SDRank: A Deep Learning Approach for Similarity Ranking of

Data Sources to Support User-Centric Data Analysis

Michael Behringer

, Dennis Treder-Tschechlov

Julius Voggesberger

, Pascal Hirmer

and Bernhard Mitschang

Institute of Parallel and Distributed Systems, University of Stuttgart, Universit

atsstr. 38, D-70569 Stuttgart, Germany

Keywords:

Data Mashup, Human-In-The-Loop, Interactive Data Analysis.

Abstract:

Today, data analytics is widely used throughout many domains to identify new trends, opportunities, or risks

and improve decision-making. By doing so, various heterogeneous data sources must be selected to form the

foundation for knowledge discovery driven by data analytics. However, discovering and selecting the suitable

and valuable data sources to improve the analytics results is a great challenge. Domain experts can easily

become overwhelmed in the data selection process due to a large amount of available data sources that might

contain similar kinds of information. Supporting domain experts in discovering and selecting the best suitable

data sources can save time, costs and signiﬁcantly increase the quality of the analytics results. In this paper,

we introduce a novel approach – SDRank – which provides a Deep Learning approach to rank data sources

based on their similarity to already selected data sources. We implemented SDRank, trained various models

on 4 860 datasets, and measured the achieved precision for evaluation purposes. By doing so, we showed that

SDRank is able to highly improve the workﬂow of domain experts to select beneﬁcial data sources.

1 MOTIVATION

Nowadays, a large number of enterprises and insti-

tutions across all industries rely on data analytics to

identify new trends, opportunities, or risks in their

decision-making. This requires the combination of

different data sources and knowledge about the se-

mantics of data. So far, this is not possible by fully

automated methods. As a consequence, it is necessary

to involve domain experts in the analysis process in

order to exploit the existing knowledge on the mean-

ing of data (Endert et al., 2014).

As this requires to enable domain experts to per-

form data selection, data preprocessing as well as

generic analyses, so-called data mashup tools are of-

ten used at start (Daniel and Matera, 2014). These al-

low the dynamic combination of data sources and data

operators through an intuitive graphical interface. In

order to not restrict domain experts in their analyses,

as many data sources as possible should be provided.

https://orcid.org/0000-0002-0410-5307

https://orcid.org/0000-0002-2502-4215

https://orcid.org/0000-0003-4808-1922

https://orcid.org/0000-0002-2656-0095

https://orcid.org/0000-0003-0809-9159

These data sources originate from very diverse

source systems and thus mostly come with different

schemas and naming conventions. In particular, for

exploratory data analyses, this leads to the situation

that it is almost impossible for a domain expert to

decide at the start of an analysis which data sources

can make a contribution to the analysis and, there-

fore, should be used. To illustrate this challenge, an

excerpt of a possible analysis is depicted in Figure 1.

Here, two data sources are present. For an explo-

rative analysis, these data sources can either be ana-

lyzed in isolation (blue and orange, respectively) or in

combination (green). This results in three possible al-

…

Data Source A

Preprocessing Analytics

Data Source B

3 Data Sources

10 Data Sources

15 Data Sources

n Data Sources

1023

32.767

-1

Combinations

Figure 1: Possible combinations of data sources.

Behringer, M., Treder-Tschechlov, D., Voggesberger, J., Hirmer, P. and Mitschang, B.

SDRank: A Deep Learning Approach for Similarity Ranking of Data Sources to Support User-Centric Data Analysis.

DOI: 10.5220/0011998300003467

In Proceedings of the 25th International Conference on Enterprise Information Systems (ICEIS 2023) - Volume 1, pages 419-428

ISBN: 978-989-758-648-4; ISSN: 2184-4992

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

419

ternatives, which have to be considered by the domain

experts. For two data sources, this still seems feasible,

but the number of possible combinations increases ex-

ponentially with each additional data source. For in-

stance, with 10 data sources, a domain expert would

have to test 1023 combinations, and with 15 data

sources, as many as 32 767 combinations. This is al-

ready highly unrealistic, but in practice, there are sig-

niﬁcantly more than 15 data sources. Thus, we need

approaches to support domain experts in the selection

of data sources, and it is reasonable to suggest only

data sources that presumably provide added value for

the analysis. This reduces the number of performed

analyses not leading to the desired results. Thus, more

beneﬁcial analyses can be performed in the same pe-

riod of time, and results can be obtained more quickly.

In addition, the frustration about repeated and unnec-

essary activities by the domain expert is reduced, and

attention can be focused on identifying new insights.

By doing so, exploratory analysis can be accelerated,

and the domain expert’s interpretive knowledge can

be leveraged. However, the decision regarding the

added value for the analysis depends on the use case

and cannot be answered in general terms.

In this paper, we focus on ﬁnding additional bene-

ﬁcial data sources. If the data source contains further

data, which are not yet represented in the currently

evaluated data sources, these can have a decisive in-

ﬂuence on the result of the analysis. Including such a

beneﬁcial data source leads to an increased effort of

the calculations, but in return, may provide more de-

tailed and robust results. A comparatively straightfor-

ward example is the resolution of foreign keys to add

related data. In most cases, however, it is not appro-

priate to merely add more data but rather to identify

semantically related data. For this reason, we intro-

duce SDRank, a novel approach that enables domain

experts to add more data to their analysis and to se-

lect beneﬁcial data sources, even in the case of a large

number of available data sources.

Our main contributions are:

• We compare different approaches regarding their

suitability to identify semantically related fea-

tures, a so-called context group.

• We present a workﬂow pipeline to suggest a data

source based on multiple input features. This data

source is expected to contain features beneﬁcial

for the analysis conducted by the domain expert.

• We evaluate our approach SDRank based on ﬁve

different domains and 4 885 datasets and show

that SDRank outperforms the expected value,

i.e., the probability for a correct suggestion, in

all of the evaluated conﬁgurations regarding the

achieved precision.

The remainder of this paper is structured as fol-

lows: In Section 2, we introduce SDRank, an ap-

proach for semantic ranking of data sources to sup-

port domain experts to select beneﬁcial data sources

during the analysis. Section 3 shows the results of our

comprehensive evaluation, before we present related

work in Section 4. Finally, we conclude in Section 5.

2 SDRank – SEMANTIC

RANKING OF DATA SOURCES

In this section, we present SDRank, our novel ap-

proach to identify beneﬁcial data sources in the con-

text of an user-centric explorative data analysis.

In contrast to common approaches, we do not fo-

cus on ﬁnding semantically identical features in other

data sources for the sake of explaining, or organiz-

ing data. Instead, we focus on ﬁnding related data in

other data sources. Therefore, we introduce the term

context group. A context group is a set of features that

frequently occur together. For instance, if we consider

address data, multiple datasets are expected to contain

features like street name, house number, zip code or

city. These features, thus, form a context group due to

their semantics. However, since these context groups

are unknown, and the speciﬁcation in advance is al-

most impossible due to the heterogeneous origin of

the data, they have to be identiﬁed in a different man-

ner. A typical approach for such challenges is Deep

Learning to identify complex patterns in data. For our

use case, we can use a neural network to identify the

context groups and their identifying feature sets.

More formally, we deﬁne the input as a set of fea-

tures F and the result as a set of result features R, and

it holds:

F := ( f

, ..., f

), n ∈ N and R := (r

, ..., r

), m ∈ N

In general, there are four different approaches to use

a neural network for this purpose:

One-to-One.

In the most straightforward case, one input fea-

ture is associated with exactly one result feature

(Equation (1)). One example is to estimate for

an input feature postal code the result feature city

since these two features occur together in many

data sources. However, this concept does not

seem promising for the use case. For each fea-

ture of the input dataset, each other feature of the

same dataset would have to be predicted. Fur-

thermore, a context of co-occurring features could

hardly be detected. Moreover, this increases the

training complexity signiﬁcantly.

F → R, f

7→ r

i, j ∈ N, i≤ n, j ≤m (1)

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

420

One-to-Many.

In the second case, one input feature is used to

compute an arbitrary number of output features

(Equation (2)). For instance, based on the in-

put feature street name, the output features house

number, postal code and city should be suggested.

Unlike the one-to-one approach, this type of train-

ing permits detecting context groups, i.e., multi-

ple features occurring together. Since the neural

network optimizes for the resulting features, the

resulting features must always occur in the same

order to prevent ambiguity. However, this order

is not guaranteed or would have to be deﬁned in

advance by a domain expert, which is impractical.

Alternatively, a schema-matching algorithm could

be applied, which determines the order across

all datasets. However, correctness is not guaran-

teed and usually requires post-processing by do-

main experts. Again, both of these counteract

our objective. Without this order, this approach

is merely a repeated application of the One-to-

One approach with the corresponding disadvan-

tages regarding the required amount of training

data and training time.

F → R

, f

7→ N

N ⊆R, q ≤|R|, i,q ∈N, i ≤n

(2)

Many-to-One.

In the third case, we use many input features to

compute exactly one result feature (Equation (3)),

i.e., based on the input features street name, house

number, and postal code, the output feature city

should be suggested. In contrast to the preceding

approaches, the many-to-one approach solves sev-

eral of their problems. First, optimization is only

performed targeting an unique feature, i.e., ambi-

guity is no longer a problem. However, the or-

der might also be important for input features, but

this can be solved in an automated way consid-

ering all possible permutations and is, therefore,

just a limitation regarding the available training

time. Furthermore, a semantic context is usually

not deﬁned by a single feature, so multiple input

features seem more suitable.

→ R, M 7→ r

M ⊆ F, p≤ |F|, j, p ∈N, j ≤m

(3)

Many-to-Many.

Finally, we could use multiple input features to

compute multiple result features (Equation (4)).

This could lead to suggesting the result features

postal code and city based on the input features

street name and house number. In theory, this

concept offers the most possibilities since all pos-

sible conﬁgurations are covered, and all of the

previous concepts are combined here. However,

this also adds up to the disadvantages. First, con-

text groups are challenging to recognize because

they must be partitioned between input and out-

put features. This also implies that the complex-

ity increases tremendously since all combinations

have to be considered. In addition, the problem of

unambiguousness arises once again regarding the

output features, as previously encountered within

the One-to-Many approach.

→ R

, M 7→ N

M ⊆ F, N ⊆R, p≤|F|, q ≤|R|, p,q ∈N

(4)

When considering these four approaches, it is ev-

ident that the Many-to-One approach is the most suit-

able since it is the only approach that can identify

context groups in an automated manner and, at the

same time, can be trained with a reasonable amount

of time. Consequently, this approach is chosen for the

data source recommendation we aim for in this paper.

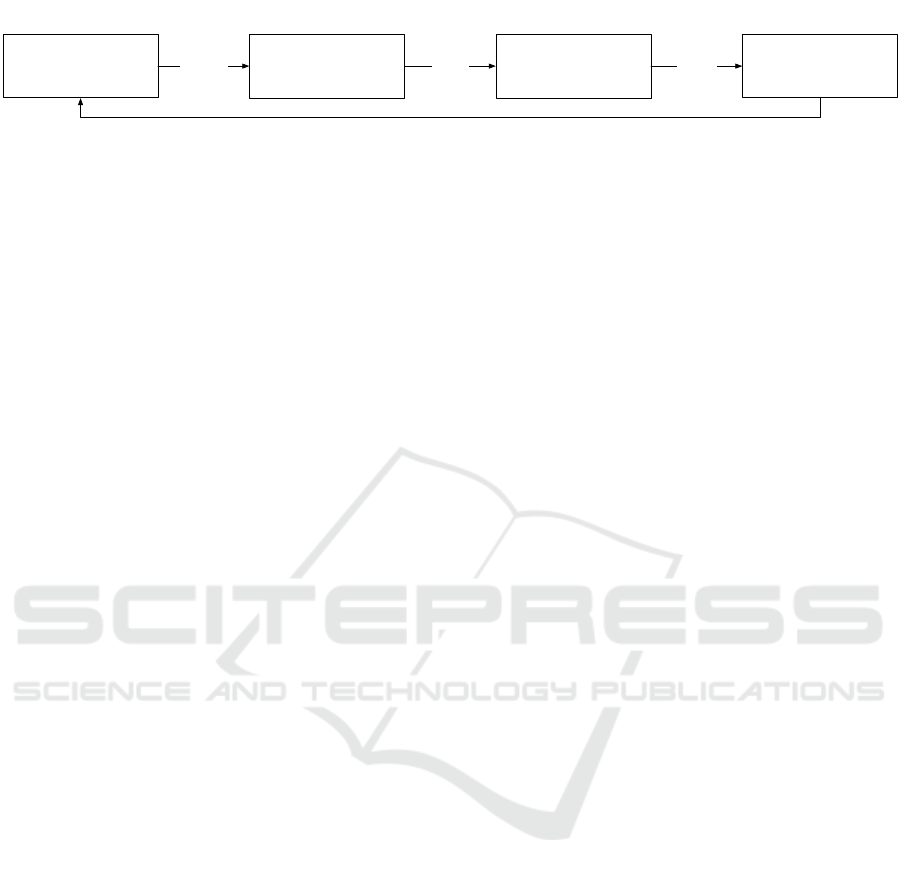
Based on this approach, the process for identify-

ing and suggesting data sources consists of four main

steps, which are shown in Figure 2 and are explained

in more detail in the following:

(1) Selection of Input Features

To be able to suggest related data sources to a domain

expert, it is ﬁrst necessary to specify an initial dataset,

i.e., one or more features of a data source, for which

related features should be found. This can be deter-

mined either in an automated manner based on the al-

ready modeled data sources or existing intermediate

results, as well as interactively by the domain expert.

While an automatic selection minimizes the cognitive

load for a domain expert, the possibility to select the

most meaningful features provides the domain expert

with a high degree of control over the suggestions.

After this step, a set of k input features is selected in

both cases.

(2) Transformation in Input Vector

In the second step, these input features must ﬁrst

be converted into a comparable form. For this rea-

son, metadata about the features is usually calculated,

which can then be used for comparison (cf. Section 4).

A promising way to generate this metadata and, thus,

to vectorize individual features is LEAPME (Ayala

et al., 2022). In contrast to LEAPME, however, we

do not aim for data integration, i.e., to recognize

and match a feature across multiple data sources, but

rather to enable suggestions of similar data sources.

SDRank: A Deep Learning Approach for Similarity Ranking of Data Sources to Support User-Centric Data Analysis

421

Automatic

- modeled data sources

Interactive

- selection of domain expert

(1) Selection

of Input Features

Vectorization

(2) Transformation

in Input Vector

Convolutional

Neural

Network

(3) Prediction

of Target Vector

Cosine Similarity

Elbow Method

Ranking

(4) Identiﬁcation

of Similar Dataset

Input

Features

Target

Vector

update modeled workﬂow / reﬁne selected features

Input

Vector

Figure 2: The four steps of our approach to suggest beneﬁcial data sources.

Thus, unlike LEAPME, our approach is intended to

recognize that a feature such as zip code frequently

co-occurs with street name but ultimately is indiffer-

ent to whether the suggested data source actually con-

tains a feature zip code as long as street name contin-

ues to be included. In our approach, we nevertheless

use parts of the dimensions deﬁned for LEAPME, i.e.,

we use 329 dimensions describing the feature using

metadata as well as the embeddings vector of the fea-

ture name (cf. Section 4). In contrast to LEAPME,

however, we get rid of all dimensions, which either

work only on text or already link features to each

other. Thus, we do not use the property pairs since

we do not need comparisons between features and di-

mensions that refer to concrete values. In addition, we

omit the average embeddings vector of all instances

of the feature, as this only works for strings and could

lead to problems in our use case since numeric fea-

tures would start with a penalty regarding similarity

to strings. The resulting dimensions are listed in Ta-

ble 1. Furthermore, these k input vectors have to be

combined and transformed into the shape expected by

the neural network as input vector.

(3) Prediction of Target Vector

In the third step, a convolutional neural network is

used to calculate a target vector from the selected and

vectorized input features. This target vector describes

a virtual feature, representing the most probable target

feature in vectorized form for the given input features.

However, this feature is not necessarily present in a

data source.

(4) Identiﬁcation of Similar Datasets

Since the feature described by the target vector most

likely does not exist, the similarity to existing features

must be evaluated in the last step. For this purpose,

the cosine similarity can be used, which describes the

similarity of two vectors. Based on this foundation,

the semantically most similar feature can already be

found quite easily, namely by selecting the existing

feature with the highest similarity to the predicted fea-

ture. However, in the context of data mashups and for

more robust suggestions, it makes sense to suggest the

most similar data sources. To this end, considering

cosine similarity alone is not sufﬁcient. While it is

possible to use the average or median of the cosine

similarity as a similarity measure of the data source,

very similar features will be blurred by a more ex-

tensive set of entirely dissimilar features by this ap-

proach. Thus, it is essential that only the most similar

features in each data source are considered. For in-

stance, the Elbow Method (Thorndike, 1953) can be

used to identify these features. Thus, the most similar

features per data source can be selected in a (semi-

)automatic way. Based on this, a ranking of the data

sources can now be created, and the best suited data

sources can be suggested to the domain expert.

In summary, these four steps allow us to recom-

mend additional data sources with a semantic rela-

tionship to the input features. These input features

can either be selected automatically based on the al-

ready modeled data sources or speciﬁed manually by

domain experts for a higher degree of adaptation to

their needs. Subsequently, the most probable (virtual)

feature is calculated, which can subsequently be used

to determine a ranking of the available data sources.

3 EVALUATION

In order to evaluate the effectiveness of our proposed

approach, we conducted a comprehensive evaluation

based on synthetic datasets from ﬁve different do-

mains. Based on these synthetic datasets, i.e., simu-

lating different data sources, we assessed the achieved

precision of our approach, both for domains known

at the time of training and for transfer learning, i.e.,

applying to previously unseen domains. More specif-

ically, we trained respective convolutional neural net-

works on different training datasets with varying data

characteristics to identify possible effects of the train-

ing data on the achieved precision. Thus, this allows

us to draw a conclusion about the robustness of our

approach and its applicability across various domains.

3.1 Datasets

We used synthetically generated datasets from differ-

ent domains as the foundation for our evaluation. In

order to generate these datasets, we initially needed

characteristic features for each domain.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

422

Table 1: Dimensions for the vectorization of input features (based on (Ayala et al., 2022)).

Description # of features

The fraction and number of occurrences of several character types, i.e., letters (uppercase, lowercase, and

both), mark characters, numbers, punctuation, symbols, separators, and others 18

The fraction and number of occurrences of several token types (words, words starting with a lowercase

letter, words starting with an uppercase letter followed by a non-separator character, uppercase words,

numeric strings)

The average of the numeric values (-1 if it is not a number) 1

The average embeddings vector of the feature name 300

Regarding our ﬁrst domain used, people, we uti-

lized Mockaroo

for this purpose. This data genera-

tor allows us to create realistic datasets, which con-

tain, for instance, name, gender, birthday or occupa-

tion. As a second domain, we used location. Again,

Mockaroo served as the data generator for this do-

main. Typical features are street, house number, city

or latitude and longitude. For the third domain cars,

we used a freely accessible database

, which con-

tains data about cars since 1945. Features include

make, model, year, trunk capacity, or the number of

doors. Our fourth domain is aircrafts. For this do-

main, we also used a freely accessible database from

the OpenSky Network

, which contains features such

as construction year, model, airline code or owner.

Finally, we used the domain movies. For this do-

main, we accessed data from DBpedia

, which con-

tains for movies among other things the release date,

title, number of awards or budget spent.

Since all these domains contain a different number

of features, for a better comparability of the domains

the feature count was homogenized, i.e., we removed

the features with more than 50 percent of null values

and afterwards randomly reduced to the feature count

of the smallest domain. Thus, 16 different features are

available for each domain to ensure that each feature

has the same probability of being selected, regardless

of the domain.

On this basis, the datasets used for the evaluation

can be generated. A training dataset initially consists

of 5, 7, or 10 features f , which were randomly se-

lected from the 16 available features of the respec-

tive domain. To simulate the inﬂuence of heteroge-

neous data sources, 0, 2, or 4 domain-foreign fea-

tures w were added to these features, i.e., features

associated with one of the remaining domains. Fur-

thermore, we varied the number of instances n for

each of these datasets between 10 000, 100 000, and

https://www.mockaroo.com/

https://database-downloads.com/

https://opensky-network.org/

https://dbpedia.org/

Table 2: Overview of the parameters for the dataset charac-

teristics. Each parameter permutation was used once.

Parameter Training-Datasets Test-Datasets

#features f 5, 7, 10 8

#domain-foreign features w 0, 2, 4 0

#instances n 10 000, 100 000, 1 000 000 100 000

#repetitions rep 10, 20, 30 5

1 000 000. Thus, for instance, a dataset assigned to

the domain cars might consist of 7 features of the do-

main cars ( f ), 2 features of the domain location (w),

and 100 000 instances (n). To further investigate the

inﬂuence of the number of data sources, we repeated

the same procedure for each combination, depending

on the parameter repetitions rep. This results in 81

possible conﬁgurations and 4 860 datasets for each

domain. For the test datasets to evaluate the achieved

precision, 8 features with 100 000 instances and 5 rep-

etitions were chosen. Thus, the trained models were

evaluated on up to 25 different datasets. All parame-

ters used are summarized in Table 2.

3.2 Training

As described in Section 2, the most suitable concept

is the many-to-one approach. Consequently, a con-

volutional neural network is used, which calculates

a (virtual) output feature based on several input fea-

tures. For the evaluation, we set the context group

size, i.e., the maximum number of input features, to

four features. This is justiﬁed by the fact that four

features are expected to be able to recognize a con-

text group already properly and due to the exponential

increase in complexity with an increasing number of

features. For instance, for a dataset with 10 available

features, 9 240 permutations have to be considered

for the training phase when the context group size is

4 input features, whereas this number grows to 76 440

permutations for a context group size of 5 features and

609 840 permutations are required for a context group

size of 6 features. We additionally decided to reduce

the required training time by using combinations in-

stead of permutations, which has a signiﬁcant impact.

SDRank: A Deep Learning Approach for Similarity Ranking of Data Sources to Support User-Centric Data Analysis

423

Input

(1@1@1316)

1,16

1,329

4,329

…

1,329

2,1

…

2,1

1,329

4,328

1,2

…

2,1

…

4,329

…

1,1

4,328

1,329

…

4,328

1,329

…

1,1

4,329

2,1

1,16

…

2,1

4,329

…

1,1

4,328

1,16

…

4,329

1,2

1,1

1,329

4,328

2,1

4,329

1,16

2,1

4,329

1,16

4,328

1,329

1,16

2,1

1,1

1,2

1,16

…

1,2

…

1,2

4,328

1,1

…

1,16

4,328

…

4,329

1,16

1,2

…

2,1

…

1,1

1,329

…

4,329

…

1,2

1,16

1,2

1,1

2,1

Conv1D

(32@1@1301)

Dense

(16@1@1301)

MaxPooling1D

(16@1@325)

Flatten

(1@1@5200)

Dense

(1@1@658)

Dense

(1@1@329)

32 layers

16 layers

Figure 3: Schematic architecture of the convolutional neural network.

The resulting convolutional neural network is

shown in Figure 3. The input layer consists of the

four vectorized input features with 329 dimensions

each (cf. Table 1). Subsequently, a Conv1D layer

with ReLu activation function follows, which detects

patterns in the input before aggregating them into a

Dense layer. A following MaxPooling1D layer iden-

tiﬁes the essential properties of the detected patterns.

These are followed by a Flatten layer and two Dense

layers to produce the desired output dimension, i.e.,

329 dimensions. Finally, the training datasets de-

scribed above were used, with a separate neural net-

work trained for each parameter conﬁguration. For

this purpose, we used Keras

with Adam as the opti-

mization function for accuracy.

3.3 Results

Our evaluation results are divided into three different

scenarios. First, we consider the results for the pre-

diction of beneﬁcial data sources for already known

domains (people, location, cars, aircrafts), i.e., do-

mains that were already available during the training

phase. This scenario will be referred to as S

in the

following. Based on this, we consider the case S

where datasets from an additional domain (movies)

are available, which in reality is very likely. This ad-

ditional domain can be suggested but is not used as

input, i.e., we do not try to query features from the

movie domain but possible false positives are taken

into account. Next, we consider the suitability of our

approach with respect to so-called transfer learning,

i.e., when additional previously unknown domains are

added and this time also queried. This scenario is re-

ferred to as S

. As a baseline for our evaluation, we

use the respective expected value, i.e., the probabil-

https://keras.io/

ity for the correct selection of a data source from the

same domain, which a domain expert would achieve

without further support. Furthermore, we use a top-k

evaluation, i.e., we consider whether at least one data

source from the same domain was identiﬁed among

the ﬁrst k suggestions.

The results for the scenarios S

and S

are almost

equivalent since all trends are similar and the achieved

precisions vary negligibly. Thus, only the expected

value differs due to a larger number of available data

sources. For the ﬁrst scenario, S

, the expected value

is approximately 0.73 for the top-4 evaluation and

0.25 for the top-1 evaluation, and for scenario S

ap-

proximately 0.61 for the top-4 evaluation and 0.2 for

the top-1 evaluation. In the following, only scenario

is considered in more detail. Figure 4 shows the

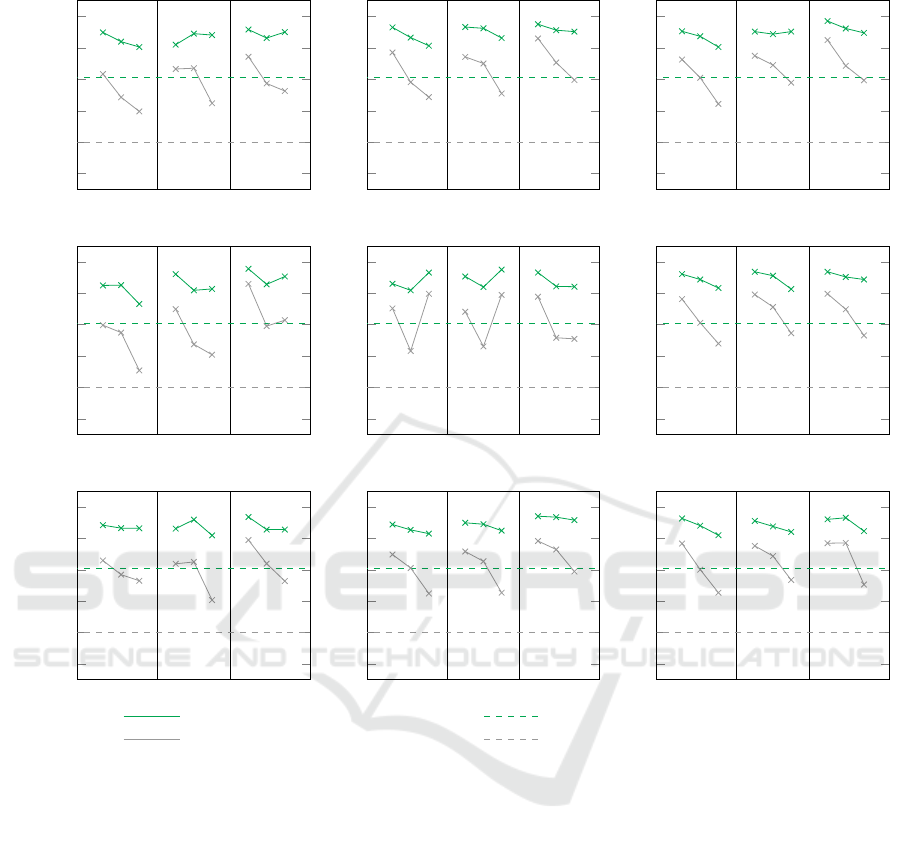
results for the second and more realistic scenario.

This ﬁgure describes the mean precision achieved

for each combination of the parameters by the respec-

tive convolutional neural network. For instance, the

sub-ﬁgure on the top left shows the mean precision

achieved for 10.000 instances and 10 repetitions on

the y-axis. In addition, the three different numbers

of features of the respective domain ( f = 5, f = 7,

f = 10) are depicted on the x-axis. Furthermore, for

each of these features, the number of domain-foreign

features (w) is plotted from left (no domain-foreign

features) to right (4 domain-foreign features). The

expected value is shown by a dashed horizontal line.

Hereby, the gray graphs refer to the top-1 evaluation,

while the green graphs refer to the top-4 evaluation.

It is evident that the expected values are exceeded

in all cases. Even for a correspondingly higher base-

line of 0.8, i.e., in 4 out of 5 cases, a beneﬁcial data

source is suggested and almost all models also ex-

ceed this baseline in the top-4 evaluation (80 out of

81 models, 98.77 percent). In the top-1 evaluation,

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

424

f=5 f=7 f=10

0.2

0.4

0.6

0.8

n = 10 000

rep = 10

f=5 f=7 f=10

0.2

0.4

0.6

0.8

rep = 20

f=5 f=7 f=10

0.2

0.4

0.6

0.8

rep = 30

f=5 f=7 f=10

0.2

0.4

0.6

0.8

n = 100 000

f=5 f=7 f=10

0.2

0.4

0.6

0.8

f=5 f=7 f=10

0.2

0.4

0.6

0.8

f=5 f=7 f=10

0.2

0.4

0.6

0.8

n = 1 000 000

f=5 f=7 f=10

0.2

0.4

0.6

0.8

f=5 f=7 f=10

0.2

0.4

0.6

0.8

Mean Precision (Top-4) of our approach Statistical Probability (Expected Value)

Mean Precision (Top-1) of our approach Statistical Probability (Expected Value)

Figure 4: Overview of the mean precision achieved for scenario S

. For each combination of instances n, repetitions rep and

features f the mean precision achieved with different number of domain-foreign features w (0, 2,4 from left to right) is shown.

such high success rates cannot be achieved, but for a

baseline of 0.6, i.e., a correct prediction in 3 out of 5

cases, still more than half of the models are suitable

(46 out of 81 models, 57 percent).

Furthermore, it can be seen that the achieved mean

precision tends to decrease with an increasing num-

ber of domain-foreign features in the training dataset.

Thus, the achieved mean precision for the top-1 eval-

uation without domain-foreign features is on average

0.74, for two domain-foreign features still 0.64 and

with 4 domain-foreign features 0.49. For the top-

4 evaluation, however, this decrease is signiﬁcantly

lower and falls from 0.91 to 0.88 to 0.84. Moreover,

this effect also weakens with an increasing number of

domain native features, which is more evident for the

top-1 evaluation. For 5 features of the same domain, a

mean precision of 0.57 is achieved, increasing to 0.62

for 7 features and to 0.67 for 10 features. For the top-4

evaluation, a mean precision of 0.86 is achieved for 5

features, 0.88 for 7 features, and 0.91 for 10 features.

With regard to the repetitions, the achieved mean

precision for the top-1 evaluation is 0.58 with 10 repe-

titions, 0.64 with 20 repetitions and 0.66 with 30 rep-

etitions. For the top-4 evaluation and 10 repetitions,

the mean precision achieved is 0.87, 0.89 with 20 rep-

etitions and 0.89 with 30 repetitions.

Finally, with respect to the number of instances,

no signiﬁcant inﬂuences are evident and the achieved

mean precision varies only slightly across the differ-

ent evaluations (top-1: 0.63; 0.62; 0.63 and top-4:

0.89; 0.88; 0.88).

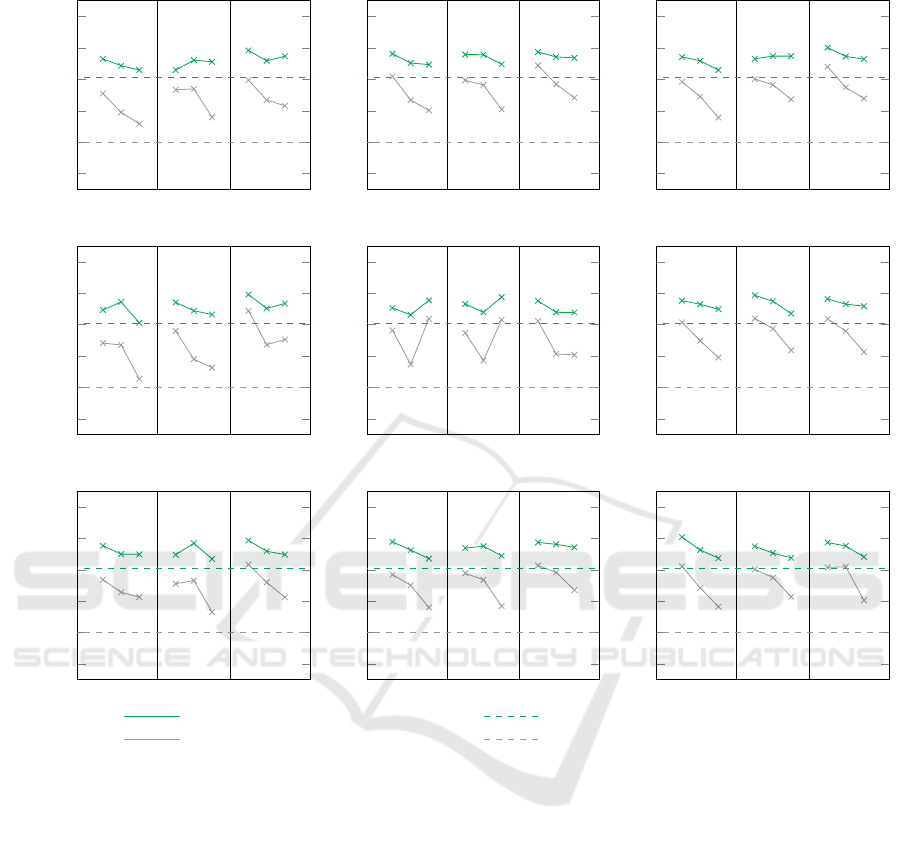
The second part of our evaluation deals with trans-

fer learning (S

). The detailed results are shown in

Figure 5. Once again, the expected value is exceeded

SDRank: A Deep Learning Approach for Similarity Ranking of Data Sources to Support User-Centric Data Analysis

425

f=5 f=7 f=10

0.2

0.4

0.6

0.8

n = 10 000

rep = 10

f=5 f=7 f=10

0.2

0.4

0.6

0.8

rep = 20

f=5 f=7 f=10

0.2

0.4

0.6

0.8

rep = 30

f=5 f=7 f=10

0.2

0.4

0.6

0.8

n = 100 000

f=5 f=7 f=10

0.2

0.4

0.6

0.8

f=5 f=7 f=10

0.2

0.4

0.6

0.8

f=5 f=7 f=10

0.2

0.4

0.6

0.8

n = 1 000 000

f=5 f=7 f=10

0.2

0.4

0.6

0.8

f=5 f=7 f=10

0.2

0.4

0.6

0.8

Mean Precision (Top-4) of our approach Statistical Probability (Expected Value)

Mean Precision (Top-1) of our approach Statistical Probability (Expected Value)

Figure 5: Overview of the mean precision achieved with regard to transfer learning (S

). For each combination of instances n,

repetitions rep and features f the mean precision achieved with different number of domain-foreign features w (0, 2, 4 from

left to right) is shown.

in all cases. For the higher baseline of 0.8 discussed

in scenario S

, this baseline can only be exceeded by 2

models in this scenario (2.5 percent). However, when

the baseline is lowered to 0.6, i.e., in 3 out of 5 cases a

beneﬁcial data source is suggested and all models are

again able to outperform the baseline. For the top-1

evaluation, the results are similar, and the mean pre-

cision decreases to 21 percent (17 out of 81 models).

If we once again lower the baseline by one step to

0.4, i.e., a beneﬁcial data source is found in 2 out of

5 trials, the baseline is exceeded in 83 percent of the

conﬁgurations examined (67 out of 81 models).

Regarding the domain-foreign features, the

achieved mean precision lowers again. For the top-1

evaluation, the achieved mean precision is 0.6 with-

out domain-foreign features, 0.52 with 2 domain-

foreign features and 0.4 with 4 domain-foreign fea-

tures. For the top-4 evaluation, the mean precision

decreases from 0.75 without domain-foreign features

to 0.73 with 2 domain-foreign features and 0.69 with

4 domain-foreign features.

In terms of repetitions, the achieved mean preci-

sion for the top-1 evaluation is 0.47 with 10 repeti-

tions, 0.52 with 20 repetitions, and 0.53 with 30 rep-

etitions. For the top-4 evaluation and with 10 repeti-

tions, the mean precision achieved is 0.71, 0.73 with

20 repetitions, and 0.73 with 30 repetitions.

Once again, no inﬂuence of a different number of

instances is apparent, and the achieved mean preci-

sion varies only slightly (top-1: 0.51; 0.5; 0.5 and

top-4: 0.73; 0.72; 0.73).

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

426

3.4 Discussion

In our evaluation, we trained different neural net-

works based on varying parameters and assessed their

precision with respect to the suggestions of beneﬁ-

cial data sources. First of all, it should be noted that

the expected value, i.e., the baseline, was always ex-

ceeded. For the setup of our evaluation, only 5 dif-

ferent domains were used, which is why the expected

value is comparatively high. In reality, it can be as-

sumed that there are many more different domains

available to a domain expert, and with each additional

domain, the expected value drops signiﬁcantly. How-

ever, the comparison of the ﬁrst two scenarios S

and

shows that our approach is not noticeably affected

by an additional unfamiliar domain available. Thus,

we can expect that similarly promising results can be

achieved if additional domains are provided and that

the selection of beneﬁcial data sources can be aided

tremendously for a domain expert.

A more detailed analysis of the various parameters

shows that the models that were trained on a larger

number of features achieved better results on the test

datasets. Therefore, we conclude that context groups

become more apparent with more features. In addi-

tion, the fact that context groups are detected less ef-

fectively with less features could also be related to the

fact that we relied on combinations instead of permu-

tations in order to reduce training complexity.

The number of domain-foreign features also has a

noticeable effect. Here, we found that the achieved

mean precision decreases, in particular for the top-1

evaluation. However, a beneﬁcial data source would

still be suggested in approximately every second at-

tempt and the expected value is signiﬁcantly ex-

ceeded. Since our approach targets domain experts,

they can manually check the suggestions. We expect

the top-4 performance to be more relevant for this rea-

son, since four data sources can be easily reviewed for

suitability and the most beneﬁcial data source can be

manually selected. In this case, there is hardly any

inﬂuence by domain-foreign features.

With regard to the number of instances, no partic-

ular inﬂuence of the different parameterization could

be found. Yet, this is not surprising and meets our

expectation, since for the vectorization of a feature

mainly a fraction of metrics is used, which does not

change much by including more data. Similarly, we

did not ﬁnd a stronger inﬂuence of the number of rep-

etitions. Indeed, the precision increases slightly, but

at the expense of a longer training time.

In terms of the evaluated transfer learning, it

should be noted that the achieved mean precision de-

creases notably and the results on unfamiliar domains

are lower than those on familiar domains. However,

even data sources from unfamiliar domains are pre-

dicted successfully and the expected value is still eas-

ily outperformed.

In summary, the detailed results show that our ap-

proach provides signiﬁcant beneﬁts for domain ex-

perts. Moreover, different models were compared

during the evaluation and no matter which parame-

terization was used, the expected value, i.e., the base-

line, was always exceeded. Likewise, the same trends

are evident for all parameterizations (with the excep-

tion of n=100 000 and rep=20). This indicates a high

robustness of our approach.

4 RELATED WORK

A common approach to identify related data is the

use of similarity metrics. In general, similarity met-

rics aim to measure the similarity between instances.

Common metrics applied for this purpose are, for

instance, euclidean distance (O’Neill, 2006), Man-

hattan distance (Craw, 2017; Krause, 1975) or co-

sine similarity (Han et al., 2012). These metrics

work on numeric values only, for text, we can ap-

ply metrics like Levensthein distance (Levenshtein,

1966) or Hamming distance (Hamming, 1950). How-

ever, these metrics are limited to pairwise compar-

isons and do not allow comparisons between text

and numeric values. To overcome this issue, often-

times a vectorization of instances or features is ap-

plied. Hereby, various characteristics of the instance

or feature are measured, e.g., occurrences of charac-

ters or number of lowercase characters. As a result,

an instance or feature is transformed into a vector of

meta-features, typically required for deep learning ap-

proaches. However, this kind of meta-features are

limited to statistical information about the data. To

integrate a semantic information, a state-of-the-art ap-

proach is the use of Word2Vec (Mikolov et al., 2013).

Word2Vec calculates a vector for each word based on

a neural network trained on large text corpora. Thus,

a text value is represented by an n-dimensional nu-

meric vector, a so-called embedding. This approach

allows to perform calculations on the representations,

e.g., king-man+woman = queen. Even if similarity

metrics can be applied to measure the similarity be-

tween two vectors, the underlying semantic relation

is not considered, i.e., in the example above it is not

speciﬁed if a vector represents a title (queen/king) or

gender (man, woman) or cards in a game. One ap-

proach to add semantic knowledge to data is the use

of so-called context clusters (Rekatsinas et al., 2015),

which structure the semantics in a knowledge base.

SDRank: A Deep Learning Approach for Similarity Ranking of Data Sources to Support User-Centric Data Analysis

427

However, to create such context clusters, a semantic

annotation is required, either manually, or oftentimes

by exploiting existing knowledge bases like DBPedia

Spotlight

or web crawling (Limaye et al., 2010), and,

thus, is time-consuming or limited to generic pub-

lic available information. In addition, this approach

requires a clear separation between different context

clusters. Furthermore, closely related to our approach

is the research discipline of schema matching (Rahm

and Bernstein, 2001; Bernstein et al., 2011), which

aims to identify semantically identical features across

different datasets. One approach in this area, which

also relies on vectorization and is able to deal with

both, text and numerical data, is LEAPME (Ayala

et al., 2022). However, we do not aim to identify

identical features, but to identify similar features with

a possible beneﬁcial impact on the analysis.

In summary, all described approaches that deal

with both, text and numeric values are either lacking

the ability to consider semantic information, aiming

on identifying identical features, or require tremen-

dous effort from domain experts for speciﬁc domains.

5 SUMMARY AND CONCLUSION

Data mashup tools are often used when domain ex-

perts are involved into interactive data analysis. In

such tools, it is common to work on a large num-

ber of data sources from various domains. Thus, it

is quite difﬁcult for a domain expert to be aware of

all data available, and it is not feasible to review all

data sources by hand. Consequently, a domain ex-

pert needs support in selecting beneﬁcial data sources.

Such a task is challenging because some features can

be assigned to different domains but in principle de-

scribe the same thing, e.g., year numbers can rep-

resent either a car’s model year or a person’s birth

year. To cope with this challenge, we introduced our

novel approach SDRank based on Convolutional Neu-

ral Networks. SDRank allows to suggest additional

beneﬁcial data sources that could contribute to the

analysis based on a set of input features, a so-called

context group. In our extensive evaluation, we trained

different models based on a large number of different

datasets. We showed that the expected value, i.e., our

baseline, was signiﬁcantly exceeded and this applies

to all trained models. Hence, SDRank is very robust

w.r.t. varying training data. Furthermore, SDRank is

also able to signiﬁcantly outperform the baseline even

for previously unknown domains. On the one hand,

training can take place in the ofﬂine phase before de-

https://www.dbpedia-spotlight.org/

ployment, and on the other hand, the training time can

be reduced without loosing much precision by fewer

repetitions and due to the robustness against different

training data. In summary, SDRank provides signiﬁ-

cant advantages for a domain expert in the context of

a user-centric interactive analysis. In the future, we

plan to conduct a user study to evaluate the beneﬁts

of SDRank in real-world use cases.

REFERENCES

Ayala, D., Hern

andez, I., Ruiz, D., and Rahm, E. (2022).

LEAPME: Learning-based Property Matching with

Embeddings. Data & Knowledge Engineering, 137.

Bernstein, P. A. et al. (2011). Generic Schema Matching,

Ten Years Later. VLDB Endowment, 4(11):695–701.

Craw, S. (2017). Manhattan distance. In Sammut, C. and

Webb, G. I., editors, Encyclopedia of Machine Learn-

ing and Data Mining, pages 790–791. Springer.

Daniel, F. and Matera, M. (2014). Mashups - Concepts,

Models and Architectures. Springer.

Endert, A. et al. (2014). The human is the loop: new direc-

tions for visual analytics. Journal of Intelligent Infor-

mation Systems, 43(3):411–435.

Hamming, R. W. (1950). Error detecting and error cor-

recting codes. The Bell System Technical Journal,

29(2):147–160.

Han, J., Kamber, M., and Pei, J. (2012). Data Mining: Con-

cepts and Techniques.

Krause, E. F. (1975). Taxicab Geometry: An Adventure in

Non-Euclidean Geometry. Dover Publications, Inc.

Levenshtein, V. I. (1966). Binary codes capable of correct-

ing deletions, insertions and reversals. Soviet Physics

Doklady, 10(8):707–710.

Limaye, G. et al. (2010). Annotating and Searching Web

Tables Using Entities, Types and Relationships. VLDB

Endowment, 3(1–2):1338–1347.

Mikolov, T. et al. (2013). Efﬁcient Estimation of Word Rep-

resentations in Vector Space. In ICLR’2013, Work-

shop Track Proceedings.

O’Neill, B. (2006). Elementary Differential Geometry.

Academic Press.

Rahm, E. and Bernstein, P. A. (2001). A survey of ap-

proaches to automatic schema matching. The VLDB

Journal, 10(4):334–350.

Rekatsinas, T. et al. (2015). Finding Quality in Quantity:

The Challenge of Discovering Valuable Sources for

Integration. In Proceedings of CIDR’15.

Thorndike, R. L. (1953). Who belongs in the family? Psy-

chometrika, 18(4):267–276.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

428