Managing Trade-off Between Cost and Time in Project Scheduling

Problems Using Discrete Event Simulation

Sena Senses

and Mustafa Kumral

Mining and Materials Engineering Department, McGill University, 3450 Rue University, Montréal, QC H3A 2A7, Canada

Keywords: Project Management, Time-Cost Trade-off, Electrical Substation Construction, Discrete-Event Simulation.

Abstract: Project Management is a key activity in engineering and business entities to achieve specific objectives (e.g.,

construction, expansion, supply chain, and replacement). Effective project management includes a detailed

investigation of the project's costs and benefits and examining the short- and long-term effects of project

design and implementation. In the mining industry, due to the operations' inherent complexity and uncertainty

associated with geological and financial inaccuracies, there is a substantial risk that the project may run over

budget and schedule. It is vital to consider the project's uncertainties to meet the project's goals. This paper

proposes a combined simulation and optimization model for time-cost trade-off project scheduling problems

under uncertainty. A numerical example is conducted to demonstrate the effectiveness of the developed model

through an electrical substation construction project conducted in a mine. By introducing numerous crashing

scenarios to quantify the impact of uncertainty on the entire project and to assess the risks, the trade-off

between time and cost is achieved under the project budget and deadline constraints. The proposed research

has a significant potential to improve the management of construction projects considering a detailed project

management methodology.

1 INTRODUCTION

Project implementation has three dimensions: (1)

completing the project in a possible earliest time, (2)

minimizing the cost through minimizing resource

usage, and (3) providing a high-quality, safe, and

environmentally friendly project outcomes. This

indicates when scheduling a project, there are

inevitable trade-offs that must be dealt with. This

paper seeks a balance between cost and completion

time. It should be noted that environmental and safety

issues cannot be balanced because they are the

uppermost priorities for a project. The first dimension

involves the decisions and questions regarding the

project completion time, project bottlenecks, and

what can be done to prevent the project from being

delayed. The second dimension addresses the

resources that need to be used such that the project is

accomplished within the budgeted cost, while at the

same time not delaying the project completion time.

The third dimension refers to scope which is difficult

to quantify. The project must provide all the

https://orcid.org/0000-0001-9145-585X

https://orcid.org/0000-0003-1370-7446

requirements included in the project scope such

as quality, safety, environmental concerns,

sustainability, or any other performance

measurements (Hickson and Owen, 2015). Large-

scale engineering projects such as mine development

call for the efficient coordination of numerous

operations carried out by several organisational units.

These projects should be handled carefully to avoid

interrupting the turnover of project length while

avoiding capital overruns because they are inherently

complicated and uncertain due to the influence of

internal and external factors. Since the value of

mining projects is sensitive to time and cost, the time

and cost management of a construction project is of

vital importance. Project planning problems

investigating the trade-off between cost and time of

the project is called time-cost trade-off (TCT)

problems in the literature.

178

Senses, S. and Kumral, M.

Managing Trade-off Between Cost and Time in Project Scheduling Problems Using Discrete Event Simulation.

DOI: 10.5220/0012004900003546

In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 178-185

ISBN: 978-989-758-668-2; ISSN: 2184-2841

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 LITERATURE REVIEW

In this regard, Xu et al. (2018) developed an

integrated dynamic approach for analyzing the

project schedule risk by combining discrete event

simulation (DES) with system dynamics. The

developed model is applied to a bridge construction

project to reveal the effect of risk factors on the

schedule. Romanskaya and Berdnikov (2020)

proposed an integrated methodology for schedule risk

management, combining the The Project Evaluation

and Review Technique (PERT) with the decision tree

method. Acebes et al. (2021) proposed a new metric

to measure the impact of each activity on the total

project risk while it is underway. The probability

factor is evaluated by Monte Carlo simulation, while

the impact factor is built on the schedule risk baseline

concept. Song, Martens, and Vanhoucke (2022)

aimed to measure and evaluate if the project progress

is acceptable for resource-constrained projects

considering project delays and resource restrictions

by applying schedule risk analysis. Chen, Lu, and

Han (2022) investigated the interdependency

between the sequence of risk occurrence for

construction schedule under uncertainty by the

Bayesian-driven Monte Carlo approach. Mostafaei et

al. (2022) examined a granite mine project to carry

out a financial analysis for the exploitation duration.

Defining the sale price and annual production is

uncertain, two net present value (NPV) models were

generated utilizing Monte Carlo simulation and

Support Vector Machine (SVM).

In addition, the time-cost trade-off problems have

been studied by various simulation techniques in the

field of project management. Simulation is a powerful

tool for modelling complex problems and its ability

to accurately reflect the structure of the real world

(Hillier and Lieberman, 2010). To optimise the time-

cost trade-off scheduling problem considering the

stochastic character of the project network, Feng, Liu,

and Burns (2000) suggested a hybrid technique

including genetic algorithms with simulation

methods. A DES methodology was developed by Li

and Lei (2010) to analyse the time-cost trade-off in

uncertain construction scheduling problems. To

calculate the critical path and the project duration

under uncertainty, Jolai et al. (2013) researched a

project network problem. A numerical example was

used to compare a DES model to the conventional

deterministic approaches. In a DES environment

coupled with a system dynamics model, Alzraiee,

Zayed, and Moselhi (2015) studied a hybrid project

planning and scheduling method on a Critical Path

Method (CPM) -based network. Regarding the

uncertainties of the project costs and durations, the

proposed hybrid modelling method sought to obtain

realistic project networks and discover the

interconnections of the project's components. Botín,

Campbell, and Guzmán (2015) explored a very

complex mine development system by integrating a

stochastic DES with a Monte Carlo simulation and

PERT to minimize the pre-production development

period. For planning a hydroelectric project, Mubin,

Jahan, and Gavrishyk (2019) investigated a time-cost

trade-off problem using Monte Carlo simulation to

analyze the project completion risk. Using discrete-

event simulation, Moreno et al. (2020) proposed the

fixed start technique for construction projects. By

regulating the start time of the activities, the approach

aimed to meet the project deadline while reducing the

variability in project delay. By combining DES with

a genetic algorithm, Nili, Taghaddos, and Zahraie

(2021) introduced a new simulation-based

optimization approach for obtaining the best

sequence of tasks in maintenance projects such that

the costs are minimized.

Even though there have been several studies on

project management, multi-scenario simulation

modelling of a project planning problem considering

project crashing has not been thoroughly investigated

in the literature. In this paper, a simulation-based

approach is proposed to optimize time-cost trade-off

project planning problem under uncertainty. By using

random activity durations, the stochastic nature of the

model representing the uncertainties in project

execution is addressed. A multi-scenario framework

is developed by creating various activity crashing

scenarios in which the durations of the activities are

shortened by allocating additional resources causing

additional cost. A case study on a mine development

project is conducted to validate the proposed model.

Hence, this paper offers a thorough analysis of the

impacts of uncertainty and multiple project crashing

scenarios on project cost and completion time.

The novel contribution of this study is the

introduction of a simulation-based optimization

algorithm to address the project scheduling problem

under uncertainty, considering project deadline and

budget constraints. The algorithm also allows for the

identification of critical project activities, statistical

analysis of activity criticalities and project

completion time, as well as the development of

multiple project crashing scenarios to minimize total

cost and completion time.

The proposed methodology and algorithm are

presented in Section 2, followed by a numerical

example and computational results in Section 3.

Managing Trade-off Between Cost and Time in Project Scheduling Problems Using Discrete Event Simulation

179

Finally, the study concludes with closing remarks and

suggestions for future research in Section 4.

3 METHODOLOGY

3.1 Network Models

The network analysis in project planning, scheduling,

and controlling has become a common application in

the past decades. The CPM and the PERT, both

proposed in the late 1950s, are the two most popular

network-based project management techniques

(Kelley and Walker 1959; Winston 2004). They are

effective methods for identifying the critical tasks and

the shortest completion time and assessing the impact

of changes on project cost and duration (Agyei 2015;

Lujić, Barković, and Jukić 2019). These methods also

introduced the concept of "project crashing", which

involves allocating more labour, equipment, and

material to one or more project tasks to reduce total

project duration. Project crashing must be applied

based on a trade-off analysis between project duration

and cost because increasing the number of resources

leads to additional project cost. The trade-off between

time and cost can be seen in Figure 1.

Figure 1: Time-Cost Trade-off.

The project network can then be constructed

based on Activity-On-Arc (AOA) graph or Activity-

On-Node (AON) graph. CPM is a deterministic

method to schedule well-defined activities assuming

that all activities can be scheduled with certainty. On

the other hand, PERT is a probabilistic method where

the uncertainties in each activity duration are

considered and the probability of completing the

project within a given deadline can be estimated. For

the estimation of duration values of each activity 𝑖,

three-point estimates, which are the optimistic

estimation 𝑎



, the most likely estimation 𝑚



, and the

pessimistic estimation 𝑏



are utilized. Considering 𝑇



is the duration of activity 𝑖 , PERT requires the

assumption that 𝑇



follows a beta distribution. Thus,

the mean and variance of 𝑇



may be approximated by

Eq. (1-2).

𝐸(𝑇



𝑎



+4𝑚



+𝑏



(1)

𝑣𝑎𝑟(𝑇



(𝑏



−𝑎



)



(2)

PERT requires the assumption that the durations

of all activities are independent. Then for any path in

the project network, the mean and variance of the

time required to complete the activities on the path

are given by Eq. (3-4).

𝐸(𝑇



)

∈





(3)

𝑣𝑎𝑟(𝑇



)

∈





(4)

One of the most difficult problems in project

planning is finding a trade-off between time and cost

that will allow the project to be completed within the

specified deadline while minimizing costs. The

project length can be shortened by crashing the

critical activity durations to meet the deadline of the

project. Crashing is achieved so that the critical

activity durations are shortened by assigning

additional resources to them. Thus, the objective is to

shorten the project duration while minimizing the

crashing cost. The relationship between normal time

and cost, and crash time and cost are represented in

Figure 2.

Figure 2: The Relationship between Normal Time and Cost,

and Crash Time and Cost.

The normal point on the graph corresponds to the

time and cost of the activity when it is executed in the

normal way. On the other hand, the crash point

represents the time and cost when the activity is fully

crashed. The crash cost per period for each activity in

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

180

the network can be calculated using Eq. (5), assuming

that the crash costs are linear over periods.

𝐶𝑟𝑎𝑠ℎ 𝑐𝑜𝑠𝑡 − 𝑁𝑜𝑟𝑚𝑎𝑙 𝑐𝑜𝑠𝑡

𝑁𝑜𝑟𝑚𝑎𝑙 𝑡𝑖𝑚𝑒 − 𝐶𝑟𝑎𝑠ℎ 𝑡𝑖𝑚𝑒

(5)

3.2 Discrete-Event Simulation Model

Discrete Event Simulation (DES) is a dynamic

simulation technique that can be used to model a

project management system that has a discrete

sequence of activities over the project duration. It is a

powerful technique in terms of the modelling of

uncertain and complex project management

problems. In this study, a dynamic, stochastic, and

discrete-event simulation model is developed based

on PERT.

In this study, a stochastic simulation-based

approach is proposed to examine the trade-off

between time and cost of a project planning problem

under the project deadline and budget constraints.

Randomized activity durations are used to address the

stochastic structure of the model, and a multi-scenario

framework is developed by creating various activity

crashing scenarios. Thus, determining the impact of

uncertainty and project crashing scenarios on project

completion time and cost is detailed in the current

study. The DES model is used to identify bottlenecks

in the project network and estimate the risks related

to the project's uncertain characteristics. The

objective of simulation-based optimization is to find

the best solution among multiple project crashing

scenarios such that the total cost of the project and its

completion time is minimized.

The project is divided into tasks in accordance

with the work breakdown structure (WBS). The

project network is established as an Activity-On-

Node (AON) graph 𝐺(𝑁,𝐴), where N denotes the

node sets identifying project activities and A denotes

the arc sets indicating the precedence relationships

between those activities. There are 𝑛 different project

activities in the established network model. The

predecessor and successor activity sets are designated

as 𝐽



and 𝐾



, respectively, for each activity 𝑖. Using

the crashed activity times 𝑋



and stochastic activity

durations 𝐷



for each activity 𝑖 , the precedence

relationships between activities are developed by

calculating the earliest start 𝐸𝑆



and earliest finish

𝐸𝐹



times in the forward pass, and the latest start 𝐿𝑆



and latest finish 𝐿𝐹



times in the backward pass,

through the network. The project completion time and

the critical path are determined based on the

parameters calculated in forward and backward

passes. The normal cost 𝑁𝐶, delay cost 𝐷𝐶, and

crashing cost 𝐶𝐶 are obtained at the end of the

simulation run. The normal cost is calculated as the

summation of each activity execution cost, 𝑁𝐶𝑃



. By

multiplying the delayed number of periods by the

delay penalty 𝑃, the delay cost, which only occurs if

the project completion time 𝑇



exceeds the target

project time 𝑇



, is determined. In addition, the

crashing cost is obtained by multiplying the duration

of the crashed activity 𝑋



by the activity's associated

crash cost per period, 𝐶𝐶𝑃



. As a result, the function

consisting of these three cost items is given as the

project's total cost function 𝑇𝐶 in the proposed

simulation model. The model also incorporates an

optimization tool where the objective function and

constraints of the network are introduced. The

equations specified in the optimization tool to

minimize the function of the total project cost are

displayed below.

𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒

𝑓



(

𝑥

)

𝑓



(

𝑥

)

𝑓



(𝑥)

)

𝑓



(𝑥) = (𝑁𝐶𝑃



)



)

𝑓



(𝑥) = 𝑇



−𝑇



∙𝑃

)

𝑓



(𝑥) = (𝑋



∙ 𝐶𝐶𝑃



)



)

𝑇𝐶 ≤ 𝐵



(10

)

𝑇



≤𝑇



(11

)

The overall project cost, including normal, delay,

and crashing cost, is minimised by Equation (6),

respectively. Equations (10) and (11) make sure that

the project budget 𝐵



and project deadline 𝑇



cannot be exceeded by the total project cost 𝑇𝐶 and

project completion time 𝑇



, respectively. In addition,

the system's control and response variables are

chosen for the simulation-based optimization

approach. The decision variables of the system are

referred to as control variables, whereas the output of

a simulation run includes the response variables.

The crashing times of the activities, which are

measured as the difference between the normal

execution time and the shortest completion time of

the activity, are defined as the decision variables of

the system. As a result, multiple scenarios are built

using numerous crashing time combinations for the

activities. Hence, a stochastic discrete-event

simulation model is developed to obtain the optimal

project schedule, yielding the cost-wise best scenario

among all.

Managing Trade-off Between Cost and Time in Project Scheduling Problems Using Discrete Event Simulation

181

4 CASE STUDY

Mining construction projects are made up of

operational activities that take place over a

predetermined time. To reveal the model's capability

and applicability, the proposed simulation model is

applied to an electrical substation construction project

conducted in a mine. Table 1 represents the

construction project consisting of 19 activities.

Precedence relationships and activity durations are

determined based on expert opinions. Activity

durations are represented as minimum, most likely,

and maximum duration required to complete the

corresponding activity. The activity list includes every

step of electrical substation building, from conducting

economic feasibility study to supplying power.

Table 1: Activity list of the electrical substation

construction project.

ID Predecessors Duration

(

)

1 - (38,56,60)

2 1 (25,28,35)

3 2 (15,19,25)

4 3

(

75,84,152

)

5 3

(

90,105,125

)

6 3 (12,14,17)

7 6 (8,11,14)

8 6 (12,15,20)

9 6

(

5,6,8

)

10 7,8,9

(

30,34,40

)

11 10

(

38,40,45

)

12 5,11 (48,52,54)

13 5,11 (14,18,22)

14 12,13 (44,48,53)

15 12,13

(

17,20,23

)

16 4,14

(

57,62,65

)

17 15,16 (10,12,15)

18 17 (15,18,22)

19 18 (0,0,0)

On this basis, Arena® Simulation Software is

used to build the activity network diagram in a

dynamic simulation environment. The simulation

model is run considering the deterministic input

dataset which is addressed as the most likely activity

duration given in Table 1. As shown in Figure 3, the

critical path includes 10 activities, including 1, 2, 3,

5, 12, 14, 16, 17, 18, and 19. The calculated time to

complete the project is 400 days.

Following the introduction of the stochastic input

dataset as probability distributions, the developed

algorithm is computed to identify the project

bottleneck activities and analyse the risk associated

with project completion time under stochastic activity

durations. Activity durations are designated by

assigning random numbers from triangular

distributions with the parameters of minimum, most

likely, and maximum activity durations, as they are

given in Table 1.

Figure 3: The Critical Path Schedule for Path-1.

The simulation model is replicated 1,000 times to

remove the initial bias when a balancing point is

found, because of the stochasticity included into the

model. This approach enables estimation of the

distribution of the project completion times and the

associated uncertainty in the level of desired relative

precision. According to the given random activity

durations, the constructed model selects one of three

paths as the critical path, as shown in Figure 3, 4 and

5. Activities 1, 2, 3, 12, 14, 16, 17, 18, and 19 are

present on both paths. Since their probability to be on

the critical path is determined as 100%, they are

designated as bottleneck activities. The probability of

occurrence of Path-1 is calculated as 54.9%, Path-2

as 44.6%, and Path-3 as 0.5%.

Figure 4: The Critical Path Schedule for Path-2.

Figure 5: The Critical Path Schedule for Path-3.

1/1/2023 2/20/2023 4/11/2023 5/31/2023 7/20/2023 9/8/2023 10/28/2023 12/17/2023 2/5/2024

Time (dd/mm/yyyy)

Activity

Critical Path - 1

1/1/2023 2/20/2023 4/11/2023 5/31/2023 7/20/2023 9/8/2023 10/28/2023 12/17/2023 2/5/2024

Time (dd/mm/yyyy)

Activity

Critical Path - 2

1/1/2023 2/20/2023 4/11/2023 5/31/2023 7/20/2023 9/8/2023 10/28/2023 12/17/2023 2/5/2024

Time (dd/mm/yyyy)

Activity

Critical Path - 3

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

182

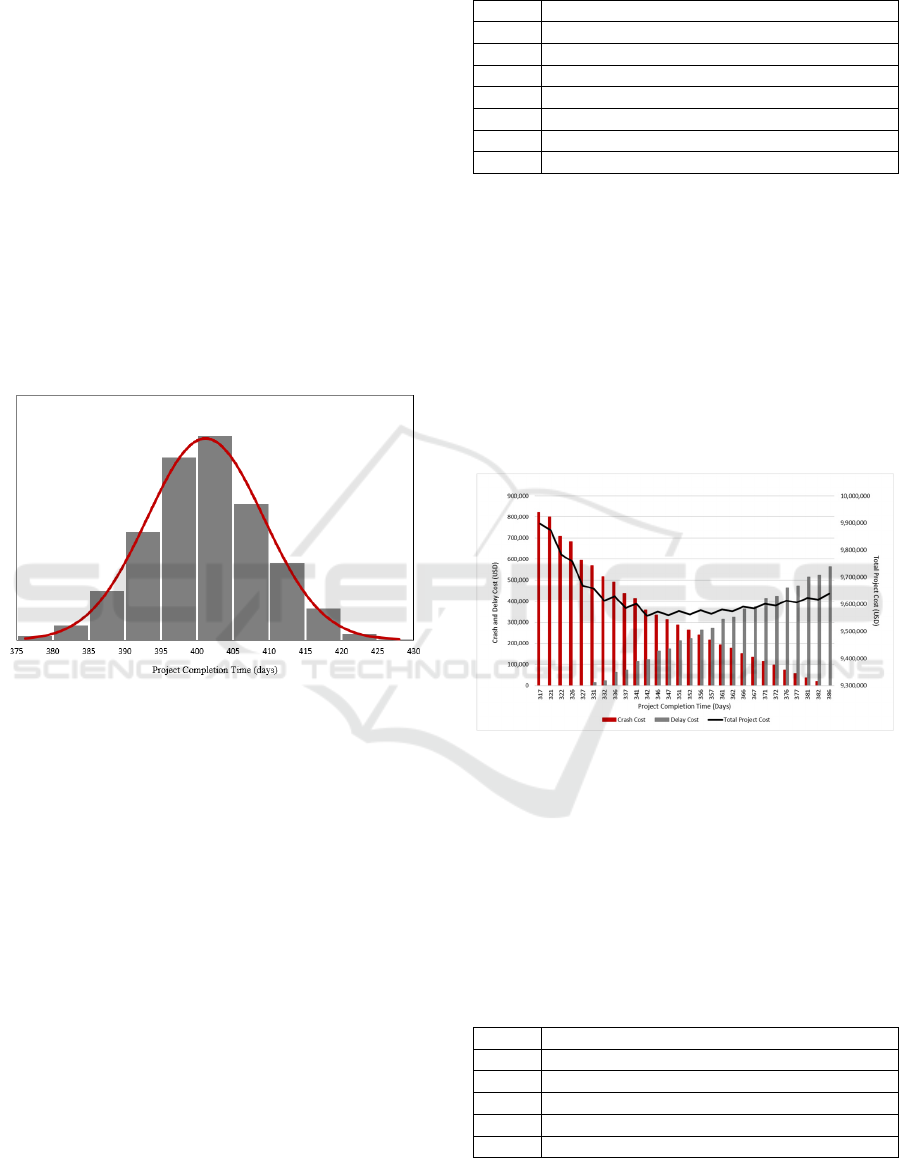
In addition, the project completion times are fitted

into the best distributions. A normal distribution with

a mean of 401.2 days and a standard deviation of 8.1

days is discovered to be able to accurately predict

project completion durations. The histogram of the

original output data and the fitted normal distribution

are shown in Figure 6. Based on the stochastic

activity durations, it is evident that the project will be

completed within 414.46 days with a 95%

probability. Additionally, it is observed that there is a

44.22% probability that the project will be completed

within 400 days. In contrast to deterministic

approach, stochastic model produces probabilistic

data that takes project uncertainties into account,

allowing the risk of delay to be evaluated. The

outcomes under these uncertainties demonstrate how

the deterministic approach deviates significantly in

terms of project completion time.

Figure 6: Fitting Normal Distribution for Project

Completion Times without Crashing.

Besides, the simulation-based optimization model

is modified to consider multiple project crashing

scenarios to reduce the overall project cost while still

adhering to the deadline and budget constraints. The

objective function and the constraints specified by

Equation (6-11) are included into the simulation

model using the OptQuest® for Arena® Simulation

Software. The crashed activity durations are defined

as the control variables of the system. Based on the

maximum crashing times listed in Table 2 and the

step of 5, 6,912 different crashing scenarios are

generated and integrated into the model. As the

response variables of the system, the activity

criticality, crashed durations, all the cost items, and

the project completion time factors are indicated.

Thus, the stochastic simulation algorithm is solved

such that the optimal project completion time is

attained through project crashing, giving the best

output among all the scenarios in terms of costs.

Table 2: Maximum crashing time of the activities.

ID Maximum Crashed Time

(

)

5 25

10 10

11 15

12 15

14 10

16 15

The simulation results of the project crashing

scenarios are shown in Figure 7. Crashing is seen to

reduce project completion time while gradually

increasing project cost. Similarly, as the delay penalty

is only paid when the project completion time reaches

a threshold value, which is set at 330 days, the delay

cost steadily rises as the project completion time

increases. Moreover, based on these two cost

elements, the project cost indicates a trade-off point,

showing the financially best schedule. The project

completion time of 342 days results in the best

solution.

Figure 7: Multi-Scenario Simulation Results on Cost Items.

According to the results, the critical path is seen

to span 10 activities, including 1, 2, 3, 5, 12, 14, 16,

17, 18, and 19, as shown in Figure 3. The optimal

crashed durations are demonstrated in Table 3 for the

cost-wise best scenario. The overall project cost is

calculated at $9,557,588.98 with 70 days of crashing,

with 94.95% of it being seen as normal cost, 3.76%

as crashing cost, and 1.29% as delay cost.

Table 3: Optimal crashed durations of DES solution.

ID Optimal Crashed Time (days)

5 25

10 10

11 15

16 15

Managing Trade-off Between Cost and Time in Project Scheduling Problems Using Discrete Event Simulation

183

Considering of the cost-wise optimal scenario

with the crashing durations listed in Table 3, the

simulation model is replicated 1,000 times and the

statistical analysis showed that the model constructs

three paths as the critical path, each of which covers

the activities 1, 2, 3, 12, 14, 16, 17, 18, and 19. Since

there is a 100% probability that these activities will

occur on the critical path, they are identified as

bottleneck activities. The schedules of Path-1, Path-

2, and Path-3 is depicted in Figures 3, 4, and 5,

respectively. The probability of occurrence of Path-1

is calculated as 77.4%, Path-2 as 22.3%, and Path-3

as 0.3%. In addition, the project completion times are

fitted into the best distributions. A normal distribution

with a mean of 359.5 and a standard deviation of 8.8

is also indicated to be able to identify the project

completion times. The histogram of the original

output data is shown in Figure 8, and the fit line

indicates the line of the normal distribution.

Figure 8: Fitting Normal Distribution for Project

Completion Times with Crashing.

The probability that the project will be completed

within 342 days is computed as 2.34%, when the

stochastic activity durations and 70 days of crashing

activity are considered. Additionally, it is observed

that the project will be completed within 374 days

with a 95% probability.

5 CONCLUSIONS

Predicting overall project cost and project completion

time is especially difficult for time-sensitive

engineering projects when operational uncertainties

are extremely noticeable. The timing of a

construction project is crucial in the mining industry

since a mining operation's worth depends on the gaps

in the commodity price of the mineral produced, price

cycles, the degree of market demand, the size of the

costumers, and sales potential. The risk of a project

should be controlled in accordance with the

company's willingness to take operational and

financial risk, which is highly variable depending on

the nature and objectives of the project.

In this study, a discrete-event simulation model

with multiple crashing scenarios is developed for the

time-cost trade-off project planning problems

considering stochastic and dynamic structure. The

model is then applied for an electrical substation

construction project conducted in a mine with the

total of 19 activities. To describe the scheduling of

activities, the basic project network is built as an

Activity-On-Node graph. The Arena® Simulation

Software is used to construct and run the model with

deterministic input dataset, and the project

completion time is observed as 400 days. On the other

hand, the criticality of the activities is assessed, and

the bottlenecks of the project are identified based on

simulation replications carried out with stochastic

input dataset. Statistical analysis is conducted on the

outputs of project completion times from 1,000

simulation replications. When stochastic activity

durations are considered, it is shown that there is a

44.22% probability that the project will be completed

within 400 days. Additionally, the multiple crashing

scenarios are integrated into the simulation-based

optimization model to minimize the overall project

cost under deadline and budget constraints. The

objective function and the constraints are established

and included in the generated simulation model using

the OptQuest® for Arena® Simulation Software. In

the cost-wise best scenario, the total project cost and

the project completion time are calculated

as $9,557,588.98 and 342 days, respectively, with a

total of 70 days of project crashing. 1,000 simulation

replications are run to find the best solution for the

DES model giving the most cost-effective scenario

considering the crashing durations, and the results are

statistically analysed. It is observed that the project

duration can be reduced by 9.89% under stochastic

activity durations, and the crashing durations

obtained from the best-case scenario of the DES

model. The project's outcomes produced a collection

of representations that reflect an equally probabilistic

understanding of reality including the uncertainties

encountered throughout project execution. Using this,

the decision-makers can make inference about the

risk of projects.

The model can be expanded in future research to

projects with more complicated structures. Further

research can focus on resource availability

constraints. On this basis, robust schedules can be

created that consider various schedule interruptions,

such as resource shortages and disruptions in the

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

184

material supply chain. Furthermore, the activity

disruptions, caused by environmental and operational

conditions such as the seasonality effect, can be

integrated to have more accurate schedules.

ACKNOWLEDGEMENTS

This research was supported by the Natural Sciences

and Engineering Research Council of Canada

(NSERC) (Fund number: NSERC RGPIN-2019-

04763). The authors are grateful for this support.

REFERENCES

Acebes, Fernando, Javier Pajares, José M. González-

Varona, and Adolfo López-Paredes. 2021. “Project

Risk Management from the Bottom-up: Activity

Risk Index.” Central European Journal of

Operations Research 29(4):1375–96. doi:

10.1007/s10100-020-00703-8.

Agyei, Wallace. 2015. “Project Planning And Scheduling

Using PERT And CPM Techniques With Linear

Programming: Case Study.” INTERNATIONAL

JOURNAL OF SCIENTIFIC & TECHNOLOGY

RESEARCH 4:8.

Alzraiee, Hani, Tarek Zayed, and Osama Moselhi. 2015.

“Dynamic Planning of Construction Activities Using

Hybrid Simulation.” Automation in Construction

49:176–92. doi: 10.1016/J.AUTCON.2014.08.011.

Botín, José Antonio, Nicholas Alexander Campbell, and

Ronald Guzmán. 2015. “A Discrete-Event

Simulation Tool for Real-Time Management of Pre-

Production Development Fleets in a Block-Caving

Project.” International Journal of Mining,

Reclamation and Environment 29(5):347–56. doi:

10.1080/17480930.2015.1086548.

Chen, Long, Qiuchen Lu, and Daguang Han. 2022. “A

Bayesian-Driven Monte Carlo Approach for

Managing Construction Schedule Risks of

Infrastructures Under Uncertainty.” SSRN Electronic

Journal 212(September 2022):118810. doi:

10.2139/ssrn.4119747.

Feng, Chung Wei, Liang Liu, and Scott A. Burns. 2000.

“Stochastic Construction Time-Cost Trade-off

Analysis.” Journal of Computing in Civil

Engineering 14(2):117–26. doi: 10.1061/(ASCE)

0887-3801(2000)14:2(117).

Hickson, R., and T. Owen. 2015. Project Management for

Mining Handbook for Delivering Project Success.

Colorado,: Society for Mining, Metallurgy &

Exploration Inc.

Hillier, Frederick S., and Gerald J. Lieberman. 2010.

Introduction to Operations Research. New York:

McGraw-Hill.

Jolai, Fariborz, Shahab Amelian, Sayyed Mohammad, Reza

Davoodi, and Abolfazl Sherafat. 2013. “Determining

Project Completion Time in Stochastic Networks

Using Discrete Event Simulation Method 1.”

Journal of Applied Sciences Research 9(4):2697–

2701.

Kelley, James E., and Morgan R. Walker. 1959. “Critical-

Path Planning and Scheduling.” Proceedings of the

Eastern Joint Computer Conference, IRE-AIEE-

ACM 1959 160–73. doi: 10.1145/1460299.1460318.

Li, Hong-xian, and Zhen Lei. 2010. “Discrete-Event

Simulation ( DES ) of Uncertainty-Based Time-Cost

Trade-off Analysis.” 2010 IEEE 17Th International

Conference on Industrial Engineering and

Engineering Management 196–99.

Lujić, Roberto, Dražen Barković, and Josip Jukić. 2019.

“Minimizing the Pessimistic Time of Activity in

Overhaul Project.” Tehnicki Vjesnik 26(2):391–97.

doi: 10.17559/TV-20180410114808.

Moreno, Francisco, Francisco Orozco, Omar Rojas, Bolivar

Senior, Mani Poshdar, and Eric Forcael. 2020. “A

Fixed Start Scheduling Approach for Repetitive

Construction Projects.” KSCE Journal of Civil

Engineering 2020 24:6 24(6):1671–82. doi:

10.1007/S12205-020-1429-8.

Mostafaei, Kamran, Shaho maleki, Mohammad Zamani

Ahmad Mahmoudi, and Dariusz Knez. 2022. “Risk

Management Prediction of Mining and Industrial

Projects by Support Vector Machine.” Resources

Policy 78(November 2021):102819. doi: 10.

1016/j.resourpol.2022.102819.

Mubin, Sajjad, Shah Jahan, and Ekaterina Gavrishyk. 2019.

“Monte Carlo Simulation and Modeling of Schedule,

Cost and Risks of Dasu Hydropower Project.”

Mehran University Research Journal of Engineering

and Technology 38(3):557–70. doi: 10.22581/

MUET1982.1903.03.

Nili, Mohammad Hosein, Hosein Taghaddos, and

Banafsheh Zahraie. 2021. “Integrating Discrete

Event Simulation and Genetic Algorithm

Optimization for Bridge Maintenance Planning.”

Automation in Construction 122(February

2020):103513. doi: 10.1016/j.autcon.2020.103513.

Romanskaya, Anastasia, and Anatoliy Berdnikov. 2020.

Project Risk Management Methodology. Vol. 1113

AISC. Springer International Publishing.

Song, Jie, Annelies Martens, and Mario Vanhoucke. 2022.

“Using Earned Value Management and Schedule

Risk Analysis with Resource Constraints for Project

Control.” European Journal of Operational

Research 297(2):451–66. doi: 10.1016/J.EJOR.

2021.05.036.

Winston, Wayne L. 2004. Operations Research:

Applications and Algorithms. 4th ed. Thomson

Learning, Inc.

Xu, Xiaoxiao, Jiayuan Wang, Clyde Zhengdao Li, Wenke

Huang, and Nini Xia. 2018. “Schedule Risk Analysis

of Infrastructure Projects: A Hybrid Dynamic

Approach.” Automation in Construction 95

(July):20–34. doi: 10.1016/j.autcon.2018.07.026.

Managing Trade-off Between Cost and Time in Project Scheduling Problems Using Discrete Event Simulation

185