Dynamic Numerical Model for a Geothermal Well

Francesco Calise

, Francesco Liberato Cappiello

, Luca Cimmino

and Maria Vicidomini

DII, University of Naples Federico II, P.le Tecchio, 80, 80125 Naples, Italy

Keywords: Geothermal Well, Downhole Heat Exchanger, Renewable Source of Energy, Dynamic Model.

Abstract: The paper proposed a detailed mathematical model that uses the TRNSYS environment to dynamically assess

the thermodynamic performance of a geothermal well. This research aims to provide a fast and reliable

dynamic mathematical model able to mimic the real-time operation of a geothermal well, given the depth of

the well and the temperature of the surrounding soil. In addition, this model can simulate the energy

performance of the downhole heat exchangers installed into the geothermal well. The results of the model

indicate that the proposed model can accurately assess and simulate the performance of the geothermal well

also including the energy performance of the downhole heat exchangers. In addition, this model may be

exploited for dimensioning proper control strategies able to manage the temperature of the downhole heat

exchanger.

1 INTRODUCTION

The growing concerns due to the impacts of climate

change on the worldwide communities (Tapia, 2017)

is increasing the interest in renewable energy sources

(Calise, 2022). Geothermal energy source is constant,

predictable, and reliable (Glassley, 2014, McClean

and Pedersen, 2023). In addition, it is unaffected by

significant seasonal variations, which dramatically

affect other renewable energy sources, such as solar

and wind (Glassley, 2014, McClean and Pedersen,

2023). The main issue with geothermal energy is

related to the excessive costs of drilling and the

complexity of the plants (Stefánsson, 2002). In this

framework the development of a proper simulation

model able to mimic the dynamic performance of a

geothermal plant is crucial, for assessing the

feasibility (Calise, 2020). Thus, the mathematical

modelling of the geothermal well performance is

useful for accurately describing the energy

performance of geothermal plants (Buonomano,

2015). Several numerical models were developed for

assessing the thermal performance of geothermal

wells including downhole heat exchangers. In this

framework, Ref. (Yuan, 2023) modelled vertical and

https://orcid.org/0000-0002-5315-7592

https://orcid.org/0000-0001-6292-686X

https://orcid.org/0000-0001-6382-3619

https://orcid.org/0000-0003-2827-5092

inclined wellbore to assess the profitability of

advanced geothermal systems. The authors developed

a 3-D model using the COMSOL software. The

results provided by such model are validated against

experimental measurements. The proposed model

resulted reliable in evaluating the thermal energy

performance of a closed-loop geothermal technology-

based plants. Ref. (Yuan, 2023) proposed a 3-D

mathematical model of a deep borehole heat

exchanger (DBHE), developed in MATLAB

environment. The main assumptions of such model

are that: i) the underground thermal reservoir is

isotropic and homogeneous; ii) the underground

thermal reservoir physical parameters are constant

over the times; iii) the heat transfer along the axis of

the heat exchanger is negligible; iv) no contact

thermal resistance between the pipe of DBHE and the

thermal reservoir; v) the soil temperature is constant

over the time. The results of such model are validated

against experimental data. In conclusion, this work

assessed that for the selected boundary conditions the

heat transfer rate per unit of buried depth is equal to

21.99 W/m with a heat exchanger water flow rate of

60 m

/h. Ref. (Dalala, 2022) proposed a novel 1-D

multi-segment model able to simulate the deep and

144

Calise, F., Cappiello, F., Cimmino, L. and Vicidomini, M.

Dynamic Numerical Model for a Geothermal Well.

DOI: 10.5220/0012007900003491

In Proceedings of the 12th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2023), pages 144-150

ISBN: 978-989-758-651-4; ISSN: 2184-4968

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

superhot geothermal wells. This model is validated by

a code-to-code approach, particularly the results

provided by the commercial software Eclipse are

assumed as benchmark. However, the study resulted

almost generic and more relevant results would be

provided applying this model to more realistic and

detailed cases study. Ref. (Lamy-Chappuis, 2022) in

detail models the heat transfer phenomena occurring

in a geothermal well. The main assumptions of this

model are: i) 1-D approach; ii) constant temperature

at an infinite distance from the geothermal well; iii)

heat transfer does not occur in the extraction zone and

injection zone; iv) constant working fluid velocity; v)

the heat exchange occurs only in radial way; vi) the

heat exchange along the axis of the pipe is neglected.

The simulation model is developed using MATLAB

software. This model simulates a desalination plant

which exploits the geothermal energy for producing

drinkable water. The proposed model resulted

extremely sensitive to: i) the geothermal gradient; ii)

geothermal well depth and iii) water to be desalinated

dissolved solids. The model proved that a geothermal

well of a depth of 4000 m, featured by geothermal

gradient of 0.05°C/m, may produce roughly 600

/day of freshwater.

1.1 Aim and Novelty

As investigated in the literature review, many works

simulate the performances of geothermal wells,

comparing with experimental data. Unfortunately, in

the framework of geothermal well mathematical

modelling, none of the available models is focused on

the dynamic response of the well and on the coupling

with a detailed geothermal plant. Therefore, the aim

and novelty of the present work are:

• Present a model which is suitably detailed but

not too computationally heavy to carry out

dynamic simulations in complex and detailed

geothermal plant layouts.

• Investigate the behavior of the transient model

when the operating parameters are varied.

• Evaluate the optimal control strategies for the

different operating conditions analyzed, during

transient operation.

2 MODEL

This work presents the evaluation of the performance

of a geothermal well, focusing on the heat exchange

phenomena, by means of a thermodynamic model

developed in a previous work by some of the authors

of this paper. Note that the focus of this work is on

the heat exchange phenomena that occur within the

well, which are important for assessing the overall

energy performance of the well and the related

geothermal plant. In addition, the thermodynamic

model will be used to simulate the heat transfer and

fluid flow within the well, and to predict the thermal

response of the well under different operating

conditions. This model simulates a stratified well,

including two downhole heat exchangers and ten

potential double ports. The double ports are employed

for describing the water withdrawn from the well, by

means of a submerged pump, which can be located at

any well depth. However, in the framework of this

research the submerged pumps are located at a

selected height (close to the well top). The internal

heat exchangers are used with the aim of modelling

the downhole heat exchangers installed inside the

well. Figure 1 displays the simplified scheme of the

geothermal well. In particular, only two heat

exchangers and one double port are considered. A

double port represents a couple of inlet/outlet to/from

the well. The mass balance must be maintained

through the double port. This means that the amount

of mass flowing into the well through the inlet port

must be equal to the amount of mass flowing out of

the well through the outlet port. When the geothermal

brine is withdrawn from the top of the geothermal

well by means of the submerged pump, the

geothermal brine simultaneously enters the bottom of

the well from the geothermal ground. Thus, the heat

continuously enters the well by inlet groundwater

openings. The two heat exchangers (Figure 1) are

linked for modelling the performance of a downhole

heat exchanger inside the geothermal well. The

geothermal well is divided in a suitable number of

nodes (N

node

). Each node represents a layer of the

stratified well as a function of the vertical gradient of

the temperature. In each layer the volume is assumed

fully mixed. The energy balance is performed for

each layer of the well to perform a detailed

calculation of each node's temperature. Obviously,

this approach leads to a discrete temperature

stratification. The nodes temperatures are evaluated

by solving a set of differential equations. The data

necessary for describing the well thermodynamic

performance are stored in a N

node

×3 array. The first

column (j=1) consists of the data about the first heat

exchanger, the second one (j=2) includes the data of

the well, and the last column (j=3) consists of the data

of the second heat exchanger. The energy balance of

each well (j=2) node (i) is displayed in the following

equation:

Dynamic Numerical Model for a Geothermal Well

145

()()

()

()()

()

, 1 1,2 , 2 2 ,2 1,2

node

1, 2,

3,1,24 ,3,2

node 1,2 ,2 1,2 ,2 ,2

wwpw

dp p w i i i i

hw h w

ii i i

con i i i i i ww

mc t t t t

UA UA

tt tt

Ntttt tt

Hndzk

ξξ

−+

+−

⋅⋅

∂





⋅= ⋅⋅⋅ −+⋅− +





∂

⋅ ⋅−+⋅ ⋅−+



⋅⋅ ⋅ −+ − − ⋅−



⋅





(1)

where: n

is the number of nodes occupied by the

heat exchangers 1; U is the overall heat transfer

coefficient; A is the exchange area; n

is the number

of nodes occupied by the heat exchangers 2; λ

con

is the

effective thermal conductivity in the well.

A mass flow from the top to the bottom counts

negative, and vice versa positive, the logical

variables, ξ

are evaluated as follows:

• ξ

= 0 if



<0, else ξ

= 1;

• ξ

= 0 if



> 0, else ξ

= 1;

• ξ

= 0 if the store node i is not in contact with the

node i of heat exchanger 1, else ξ

= 1;

• ξ

= 0 if the store node i not is in contact with the

node i of heat exchanger 2, else ξ

= 1.

The first term of equation 1 described the internal

energy variation of each node as function of the time.

Considering the right-hand side of the equation, the

fist sum describes the heat transfer due to the mass

flows throughout the nodes. The second and third

term describe the heat transfer between well node and

heat exchanger node. The fourth represents the

thermal conduction between the layers in the well.

The last term describes the heat losses to the well

surroundings, i.e. the rock of the groundwater. The

energy balance of heat exchanger nodes is described

by the following equation:

() ()

()

5 , 1, , 6 , , 1,

,2 , ,

hy hy p hy i j

hy p hy i j i j hy p hy i j i j

iij

hw hw

ij ww

hy h

Vct

mc t t mc

UA U

tt tt

ξξ

−+

⋅⋅ ∂

⋅=⋅⋅⋅ −+⋅⋅⋅− +

∂

⋅−− ⋅−



(2)

where t

i±1,j

represents the inlet (i+1) and outlet (i-1)

temperature of the heat exchanger. In particular:

• ξ

= 1 if



> 0, else

= 0;

• ξ

= 1 if



< 0, else

= 0.

Note that (UA)

hy,ww

, which describes the heat loss

capacity rate from the heat exchangers to

surroundings, is assumed equal to zero. The heat

exchangers are totally immersed into the geothermal

brine.

Obviously, this model dynamically describes the

energy performance of the geothermal well and of the

considered heat exchangers. The temperature of the

well is selected according to experimental

measurements carried out by INGV (Kiaghadi, 2017)

(Italian National Institute of geology and

volcanology). The main simulation assumptions are

displayed in Table 1.

Table 1: Geothermal well data and simulation assumptions.

Definition Value Unit

well

Temperature of the well 96 (http://terremoti.ingv.it/contact2018) °C

Mass flow rate of HE 500 kg/h

brine

Brine mass flow rate 0 kg/h

Height of the well 69 m

node

Number of nodes 150 -

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

146

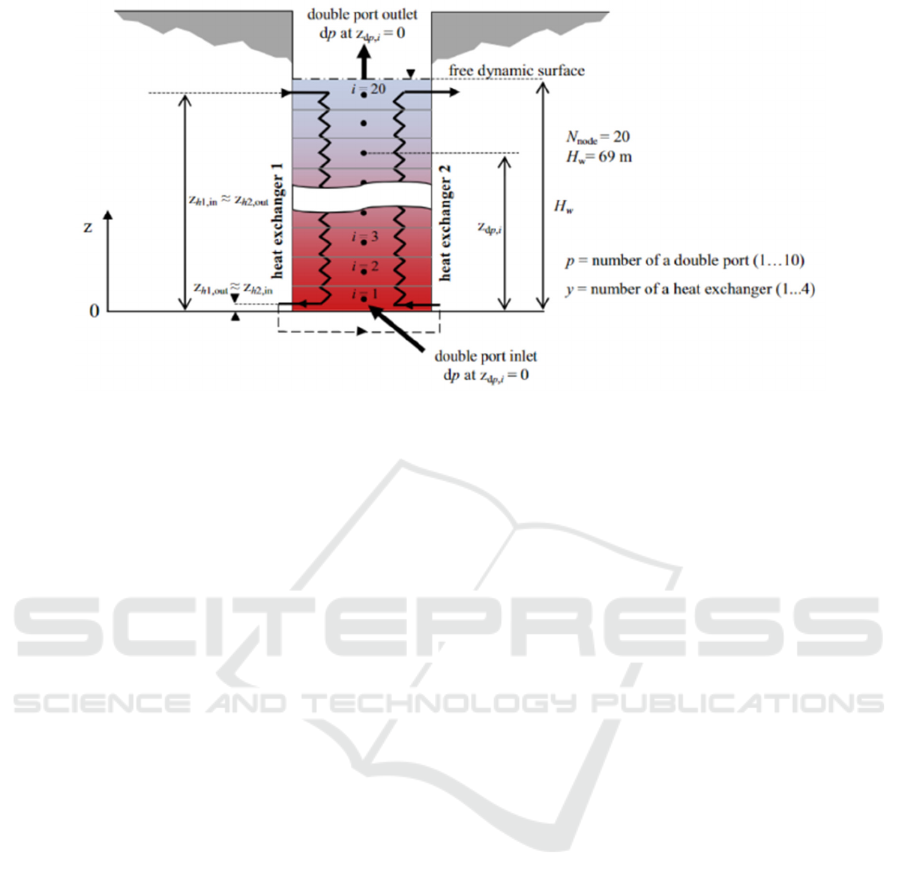
Figure 1: Scheme of the proposed model of the geothermal well.

3 RESULTS

The processor Interl(R) Core(TM) i7-7700 with a ram

of 8 GB is used for carrying out the simulations.

Adopting a time step of 0.01 h, and a time horizon of

100 hours a simulation time of 180 s is detected.

Figure 2 displays the outlet temperature of the

downhole heat exchanger (T

HEout

) as a function of the

time, for two different user thermal load, i.e., P

th,user

5 kW

and P

th,user

= 8 kW

. With a withdrawn thermal

flow rate of 5 kW

, the temperature decreases from

the initial value of 95.90 °C to 91.98 °C, reaching the

steady state. Note that the steady state is reached in

about 25 hours for both the analyzed cases (Figure 2).

These results show that the model can mimic the

dynamic evolution of a geothermal well in operation.

Note that the selected submerged pump is supposed

to be switched off (Table 1).

Figure 3 shows dynamic response of the geothermal

well under several different operative conditions, i.e.,

different user thermal loads (P

HEout

), without

activating the submerged pump. Obviously, the

greater the withdrawing of thermal flow rate, the

lower the outlet temperature of HE (T

HEout

). In

particular, with a withdrawn thermal flow rate of 15

, the HE outlet temperature falls below 85 °C in

about 8 hours. Thus, the proposed model is quite

responsive to the thermal load. This feature could be

useful for predicting whether a thermal load would

dramatically reduce the well temperature beyond an

assumed threshold temperature. It is worth nothing

that the selected geothermal well is mainly heated by

the hot groundwater. In fact, the rocks surrounding

the geothermal well have a hot temperature, i.e.,

roughly 90-96°C, but the convective and conductive

heat transfer phenomena are not able to balance high

heat transfer rate loads. Conversely, the withdrawal

of geothermal brine makes the hotter brine located

beyond the geothermal well enter the geothermal

well, heating it up. Therefore, to increase the

available heat, without reducing the heat exchanger

outgoing temperature, a suitable amount of

geothermal brine should be withdrawn. In this

framework, a parametric analysis is carried out to

analyze the combined effect of brine flow rate and

downhole heat exchanger thermal load on the

geothermal well performance (Figure 4). The growth

of the brine mass flow rate (m

brine

) increases the

thermal energy charged in the geothermal well,

increasing the thermal capacity of the geothermal

well. In fact, as discussed before, the increase in the

brine flow rate makes higher amount of hot water

brine

= 97°C) to enter the well. Thus, the well can

match extremely high thermal load without a

significant reduction of the heat exchanger outlet

temperature. For example, T

HEout

is equal to 90°C with

a withdrawn thermal flow rate of 50 kW

and a m

brine

of 4100 kg/h, (Figure 4). In addition, this figure may

be useful for dimensioning the geothermal well plant.

To match a thermal load of 21 kW

, without reducing

the heat exchanger temperature below 90°C, the

submerged pump should withdraw a brine flow rate

brine

) greater than 2100 kg/h.

Dynamic Numerical Model for a Geothermal Well

147

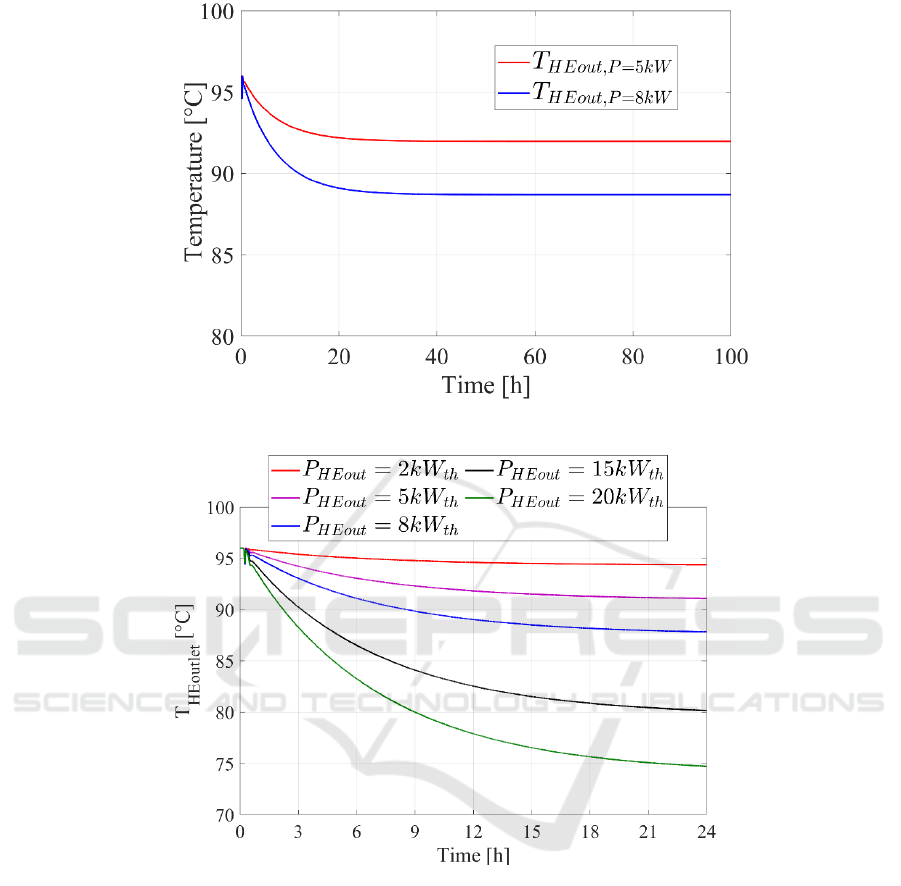
Figure 2: Geothermal well model dynamic thermal performance.

Figure 3: Well discharging as function of different operative conditions.

In addition, this model provides useful guidelines for

the development of proper control strategies to ensure

the correct operating conditions of the geothermal

well. Figure 5 displays the dynamic response of the

geothermal well under two different control

strategies: C1 proportional control strategy and C2 on

off control strategy. In particular, control strategies

C1 and C2 are designed for keeping the heat

exchanger outlet temperature within the range 85-

90°C. Then, the controlled variable is the temperature

of the water leaving the downhole heat exchanger,

while the control signal of the controller manages the

submerged pump, withdrawing geothermal brine

from the geothermal well. Note that a constant

thermal load of 10 kW

is withdrawn from the

download heat exchanger and the rated mass flow rate

of the submerged pump is equal to 2100 kg/h.

According to C1, m

brine

resulted equal to 1152 kg/h,

with a T

HEout

equal to 87.3°C. Therefore, the

controller achieves the goal of keeping the downhole

heat exchanger outlet temperature within the assumed

range. Regarding control strategy C2, when the T

HEout

decreases to 85°C the submerged pump is activated,

withdrawing the rated brine flow rate, equal to 2100

kg/h. This allows the surrounding water, which is at a

higher temperature level, to enter the well and

increase its temperature. Then, when the T

HEout

reaches the selected upper bound (95°C), the pump is

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

148

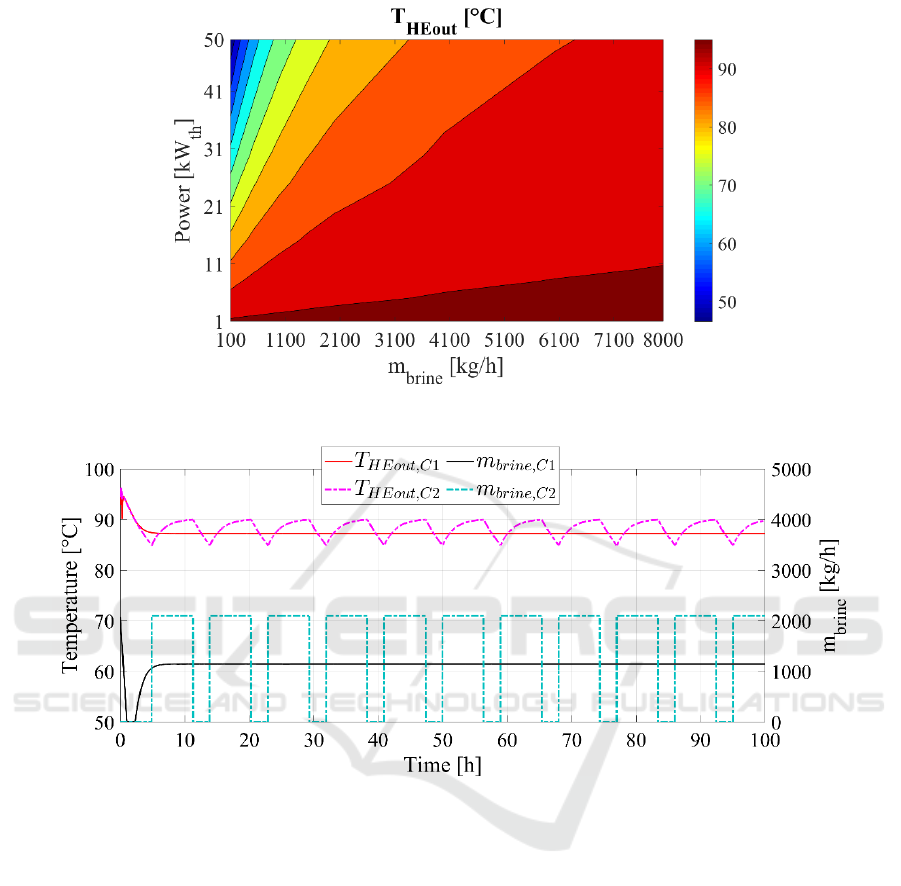
Figure 4: Parametrical analysis changing both brine mass flow rate and heat exchanger withdrawn power.

Figure 5: Downhole heat exchanger outlet water temperature, under two different geothermal well control strategy, namely

C1 dead band on-off controller and C2 proportional controller.

switched off. Figure 6 displays the response of the

proportional controller when the thermal energy

demand of the user fluctuates. In particular, two

different forcing functions are selected for testing the

geothermal well model and the controller. The first

one consists of a sinusoidal thermal energy demand

with an amplitude of 1 kW and a period of 14 hours,

the second one consists of a sinusoidal thermal energy

demand with an amplitude of 5 kW and a period of 20

hours. This figure proves the stability and reliability

of the proposed model and of the controller. In fact,

the controller can keep the temperature within the

selected range, i.e., 85-90°C. In particular, the

controller follows the fluctuating thermal energy

demand properly modulating the brine flow rate,

leading to very slight oscillation of the temperature.

In fact, T

HEout

varies between 86.9-87.4°C for the first

forcing function, while T

HEout

varies between 88-

86.4°C for the second forcing function. In conclusion,

thanks to the great accuracy and sensibility of the

proposed model, this could be also adopted for

developing proper control strategies to manage

geothermal well dynamic operations.

4 CONCLUSIONS

This work deals with a numerical model of a

geothermal well, allowing one to dynamically

simulate the energy performance of the well and the

related downhole heat exchangers. The model of the

geothermal well is developed in TRNSYS

environment. In addition, this model is designed for

being reliable and computationally fast, to integrate

Dynamic Numerical Model for a Geothermal Well

149

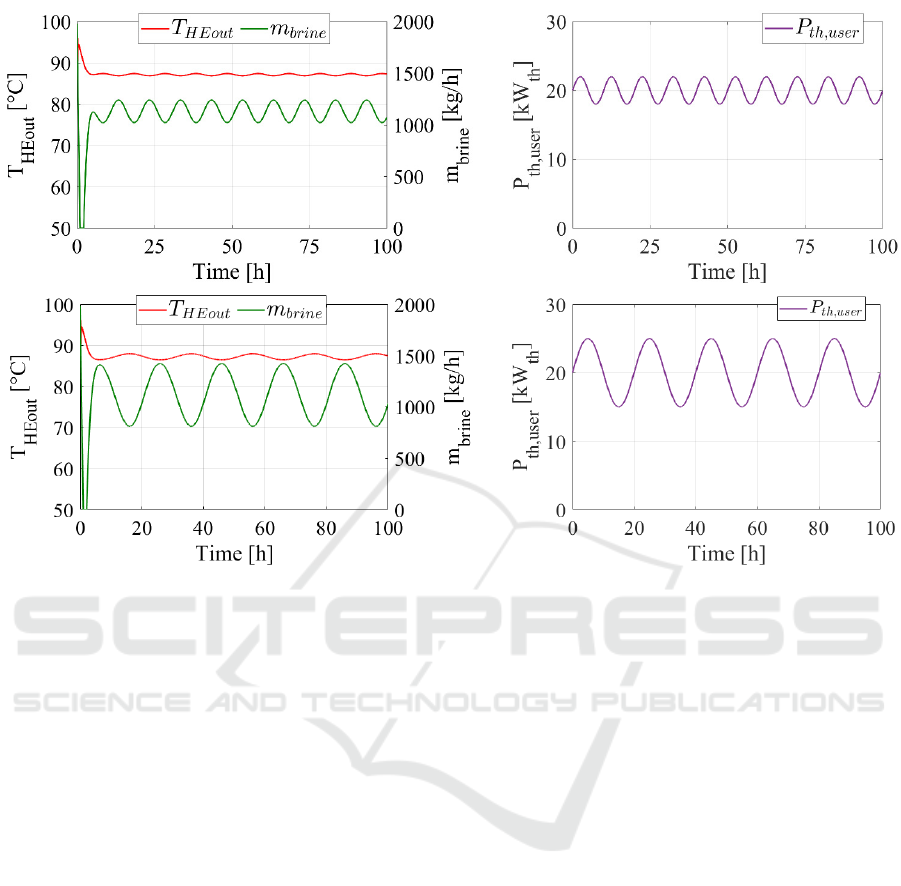
Figure 6: Heat exchanger outlet temperature controlled by means of proportional controller, under two different user thermal

energy demands.

such model in more detailed dynamic model of

geothermal power plants. The results show that the

model can mimic the dynamical performance of the

well under several operative condition and control

strategies. In particular, the model resulted extrimely

responsive to the user termal load and to the

withdrawn brine.

REFERENCES

Buonomano, A., F. Calise, A. Palombo and M. Vicidomini

(2015). "Energy and economic analysis of geothermal–

solar trigeneration systems: A case study for a hotel

building in Ischia." Applied Energy 138: 224-241.

Calise, F., F. L. Cappiello, M. Dentice d'Accadia, F.

Petrakopoulou and M. Vicidomini (2022). "A solar-

driven 5th generation district heating and cooling

network with ground-source heat pumps: a thermo-

economic analysis." Sustainable Cities and Society 76:

103438.

Calise, F., F. L. Cappiello, M. Dentice d’Accadia and M.

Vicidomini (2020). "Thermo-Economic Analysis of

Hybrid Solar-Geothermal Polygeneration Plants in

Different Configurations." 13(9): 2391.

Dalala, Z., M. Al-Omari, M. Al-Addous, M. Bdour, Y. Al-

Khasawneh and M. Alkasrawi (2022). "Increased

renewable energy penetration in national electrical

grids constraints and solutions." Energy 246: 123361.

Glassley, W. E. (2014). Geothermal energy: renewable

energy and the environment, CRC press.

http://terremoti.ingv.it/contact. (2018). "http://terremoti.

ingv.it/contact." from http://terremoti.ingv.it/contact.

Kiaghadi, A., R. S. Sobel, and H. S. Rifai (2017).

"Modeling geothermal energy efficiency from

abandoned oil and gas wells to desalinate produced

water." Desalination 414: 51-62.

Lamy-Chappuis, B., A. Yapparova and T. Driesner (2022).

"Advanced well model for superhot and saline

geothermal reservoirs." Geothermics 105: 102529.

McClean, A., and O. W. Pedersen (2023). "The role of

regulation in geothermal energy in the UK." Energy

Policy 173: 113378.

Stefánsson, V. (2002). "Investment cost for geothermal

power plants." Geothermics 31(2): 263-272.

Tapia, C., B. Abajo, E. Feliu, M. Mendizabal, J. A.

Martinez, J. G. Fernández, T. Laburu and A. Lejarazu

(2017). "Profiling urban vulnerabilities to climate

change: An indicator-based vulnerability assessment

for European cities." Ecological Indicators 78: 142-155.

Yuan, W., Z. Chen, S. E. Grasby, E. Little and G. Zhao

(2023). "Thermodynamic Modeling of the Advanced

Geothermal System Using Inclined Well Applications."

Applied Thermal Engineering 220: 119709.

Yuan, W., Z. Chen, S. E. Grasby, E. Little and G. Zhao

(2023). "Thermodynamic Modeling of the Advanced

Geothermal System Using Inclined Well Applications."

Applied Thermal Engineering 220: 119709.

SMARTGREENS 2023 - 12th International Conference on Smart Cities and Green ICT Systems

150