Feedback in Online Mathematics Tutoring

Antonín Jančařík

, Jakub Michal

and Jarmila Novotná

1,2 c

Faculty of Education, Charles University, Prague, Czech Republic

CeDS, Université Bordeaux, France

Keywords: Online Tutoring, Feedback, Mathematics, Algebra, Geometry, Chatbot.

Abstract: The goal of this paper is to present issues related to assessment and feedback in the framework of online

mathematics tutoring implemented with the help of a chatbot using Artificial intelligence (AI) (Jančařík et al.,

2022). The presented project aims to create a teaching course that is intended to help the pupil in independent

preparation for the national entrance exams in mathematics for upper secondary schools in the Czech

Republic. The course takes the form of a chatbot with which a pupil can communicate in a web browser

environment or the Telegram communication application designed for all common operating systems

(Windows, macOS, Linux, iOS, Android, ...). The chatbot also includes a communication module using

artificial intelligence that can communicate with the pupil beyond the scope of the designed course. The

following two questions are addressed in the part of the research that is presented in this paper. The first

question is what form of feedback is effective in the given environment and most reflect the nature of tutoring.

The second question is how the chosen procedures must be modified for the different areas of mathematics

the course focuses on. The paper presents an implementation within the area of algebra and geometry.

1 INTRODUCTION

The use of technology in the teaching of mathematics

is a relatively new area of interest for mathematicians

and educators, not only in the area of mathematics.

Drijvers et al. (2010) summarize the stages of

development in the years 1960 to 1990. Already from

1942, there was a significant development in

computing technologies, but only in the late 1960s,

the focus of mathematicians and mathematics

educators turned their attention to the effects of

computing on the content of school-level and

university-level mathematics (Fey, 1984). One of the

main goals of the use of technology is to promote a

more active form of student learning.

Technology has also affected the teaching of

mathematics, and in the 1980s, theoretical

frameworks were developed in which the use of

technological tools in education was investigated.

Drijvers et al. (2010) draw attention to the

Tutor/Tool/Tutees (Taylor, 1980) and White

Box/Black Box (Buchberger, 1990) frameworks,

https://orcid.org/0000-0003-3331-2396

https://orcid.org/0000-0003-3522-8411

https://orcid.org/0000-0002-5306-2315

among others. In the mode Tutor, the technology

presents the materials which the student answers and

the technology evaluates their answers. The mode

Tool has a similar focus but requires less

programming than the mode Tutor. The mode Tutee

was described by Taylor as follows: “To use the

computer as tutee is to tutor the computer; for that,

the student or teacher doing the tutoring must learn to

program, to talk to the computer in a language it

understands” (Taylor, 1980, p. 4).

The use of ICT in education continues to be at the

centre of interest of mathematics educators

(Verschaffel et al., 2019; Hardman, 2019, Phuong et

al., 2022). Lagrange et al. (2001) present a survey of

literature about the educational uses of ICT in

mathematics education up to 2001. Gissel et al.

(2019) published a critical review of various meta-

studies about the impact of ICT use on students’

learning. Much attention is paid to the use of

Artificial Intelligence in education. This is also the

focus of this article, which focuses on questions

related to evaluation and feedback in the framework

of online mathematics tutoring implemented with the

374

Jan

rík, A., Michal, J. and Novotná, J.

Feedback in Online Mathematics Tutoring.

DOI: 10.5220/0012017500003470

In Proceedings of the 15th Inter national Conference on Computer Supported Education (CSEDU 2023) - Volume 1, pages 374-381

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

help of a chatbot with the use of AI. The aim is to

develop a system of structurally homogenous courses

with a focus on the nationwide entrance examination

for Czech secondary schools where the AI would

support the learners' experience by answering pupils'

questions related or non-related to a given topic.

2 MATERIALS AND METHODS

This section is discussed in two parts. Firstly the

definition of tutoring and related research is

described; secondly, the section talks about artificial

intelligence in education.

2.1 Tutoring

The term tutoring in this paper refers to tutoring in a

school subject which is taught in addition to

mainstream schooling. Tutoring is a worldwide

phenomenon that has been paid attention to especially

in recent decades (Hille et al., 2016; Bray & Silova,

2006). Its main focus is on the “core” subjects, i.e.

language and mathematics (Mischo & Haag, 2002).

Tutoring in mathematics, albeit in various forms, can

be found in the vast majority of countries (Song,

2013). Even though there are several different forms

of tutoring, the prevailing form is the form of private

supplementary tutoring, i.e. paid tutoring focusing on

content from school lessons or preparation for

entrance exams (Novotná, 2019). As this is a paid

activity, private supplementary tutoring is not

available to all students to the same extent.

Differences in family socioeconomic status are

further exacerbated by a system in which students

who are tutored achieve better results (Safarzyńska,

2013). Tutoring used to be typically carried out face-

to-face when a pupil or a group of students came to

see the tutor, or the tutor came to see the students.

Online tutoring expanded during the covid-19

pandemic. The fact that there is no direct contact

between the tutor and the student opens up space for

the automation of activities. Some studies show the

effectiveness of providing online tutoring (e.g. Beal

et al. (2007)). Artificial intelligence can contribute to

an increase in the frequency of use of online tutoring

and can partly or even completely replace the tutor.

The tutor can be replaced in the selection of the study

trajectory, in the evaluation of results, as well as in

communication with the student (Shahbazi & Byun,

2022). These changes aim to improve the quality and

accessibility of tutoring forms and thereby reduce the

impact of socioeconomic background on a student’s

performance and achievement (Alhossaini &

Aloqeely, 2021). That's why systems like the one

described here, which will use the latest technologies,

including AI, to deliver free education content to all

learners, have a big role to play.

2.2 AI in Education

The Research into the use of AI in education focuses

on the following four areas (Zawacki-Richter et al.,

2019):

1. Profiling and prediction;

2. Assessment and evaluation;

3. Adaptive systems and personalization;

4. Intelligent tutoring systems.

The here presented research focuses only on one

of the forms of using artificial intelligence, namely on

its use in the creation of an intelligent tutoring system,

i.e. a system in which one-to-one personal tutoring

takes place, where the tutor’s role is fully or partially

taken over by a computer system – artificial

intelligence. Despite the significant progress in the

development of artificial intelligence in recent years,

the difference between AI and a live tutor is still

evident. However, research conducted with the first

such systems shows that some students may find it

much easier to communicate with AI than with a

teacher or a tutor (Kim et al., 2020). In another study

(E. Park et al., 2011), when educating participants on

a certain topic, a robot tutor that provided positive

feedback was perceived as attractive and acceptable.

As part of Attard’s (2021) research, it was found that

when using an AI chatbot in the explanation of the

mathematics, 73% of the users enjoyed making use of

the chatbot, and the same percentage of respondents

also expressed a desire to use the chatbot again in the

future. In all, these studies support the review of

research showing that social robots in educational

settings have positive effects on student learning

(Belpaeme et al., 2018). In sum, although not always

the case, most research on robots in education has

shown promising ways that can facilitate effective

learning experiences.

AI instruction may provide an effective means for

delivering instruction when current events prohibit

face-to-face human interaction. Although the first

results show the great potential of using AI in

tutoring, research in this area is at the very beginning

and many questions are still open. One of the most

important issues is the design of an appropriate

structure for the course and the form of providing

feedback.

Tutoring differs from school education in many

ways. Thus, assessment and feedback must be

Feedback in Online Mathematics Tutoring

375

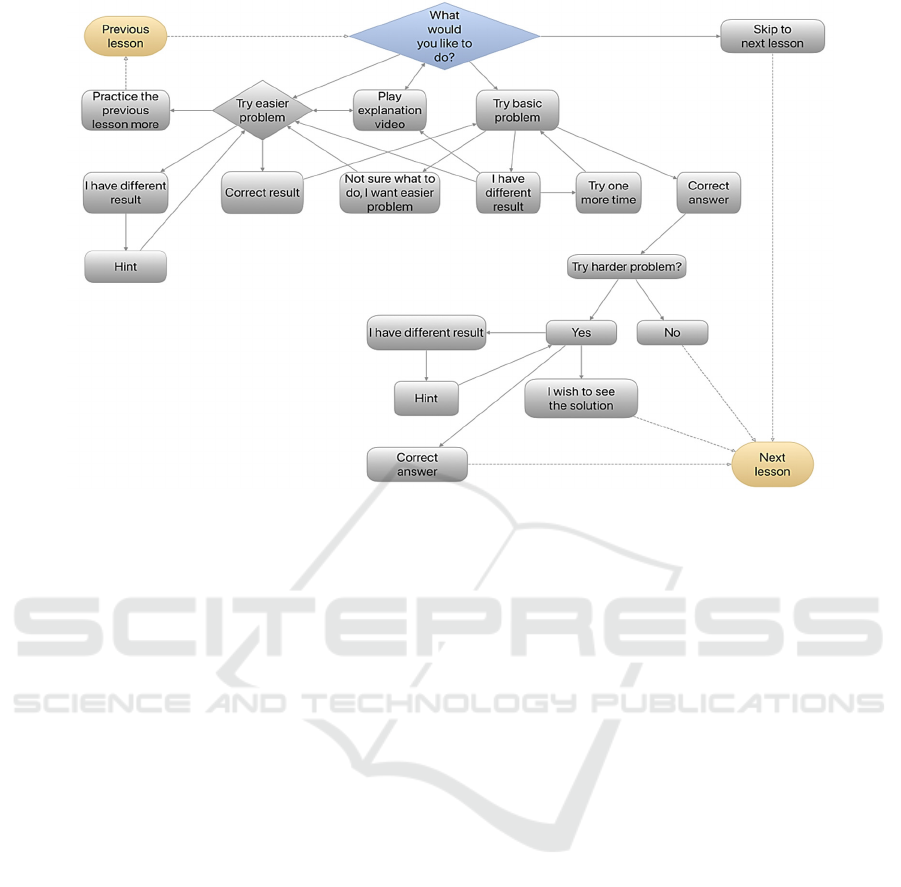
Figure 1: Options the user can choose from at each step.

adapted to these differences. Summative assessment,

which is often used in schools, does not seem

appropriate in the context of tutoring. Based on an

analysis of the effects of summative assessment

(Harlen et al., 2002), two reasons can be given why it

is advisable not to rely merely on summative

assessment in tutoring. The first reason is that

summative assessment motivates only some students

and increases the gap between higher and lower-

achieving students. By tutoring, however, we want to

reduce the differences between higher and lower-

achieving students (without reducing the

performance of high achievers). The second reason is

that summative assessment motivates students

towards performance goals rather than towards

learning goals, as required for continuing learning

(Harlen et al., 2002). The goal of tutoring should not

only be to achieve short-term results but to prepare

for continuous learning. The aim of assessment

should therefore not be an evaluation of achieved

goals, but rather the level of mastery of the needed

knowledge, procedures and skills. Fiori et al. (2004)

work with the term process-oriented assessment and

state that by assessing students’ problem-solving

processes rather than products alone, we may provide

them with more formative feedback as compared with

the other techniques. We consider the provision of

this kind of feedback to be essential for effective

tutoring. Roa (2006) states that when using ICT in

education it is important to utilize both formative and

summative evaluation. On the one hand, it is

important to determine not only the tools that allow

for the learning of a particular subject area but those

that allow for the correct feedback. Sadler (Sadler,

1998) points out that the quality of feedback is a

crucial issue.

In the paper, we focus on the use of AI for two

purposes. One of them is its independent use by

students as a tool for self-checking the correctness of

the solution or as an aid to finding a possible way to

the right results. We classify this as used in the Tutee

role (Taylor, 1980). The system can also be used by a

teacher who wants to introduce students to some

procedures that they do not know yet or do not know

how to use. This is the mode of the Tutor (Taylor,

1980).

Petty (2002) states the following motivational

reasons from a survey among students:

• The things I am learning are useful to me;

• The qualification I will get is good for me;

• I usually have good results in my studies and

this success boosts my self-confidence;

• If I study well, it will be appreciated by my

teacher or my classmates;

• If I don't study, there will be unpleasant (and

quite immediate) consequences;

• The things I am learning are interesting and

make me curious to learn more;

• The teaching is fun.

CSEDU 2023 - 15th International Conference on Computer Supported Education

376

3 RESULTS

The goal of our research is to design an online course

that will help students to prepare on their own for the

national entrance exams from mathematics for upper

secondary schools in the Czech Republic. The course

covers the following four areas: Number and

Arithmetic Operations, Dependencies, Relations and

Work with Data, Geometry in Plane and Space, and

Non-Standard Application Problems.

The course takes the form of a chatbot and can be

run in a web browser or the Telegram communication

application designed for all common operating

systems. Due to the need to implement the course into

the Telegram environment, the user interface consists

exclusively of elements suitable for touch phones and

tablets. Thus, the user communicates with the chatbot

mainly using selection fields or text fields. The

chatbot's response is typically verbal, with an image,

a gif, an URL link, or another decision-making level

with a selection from the pre-offered response fields.

Thanks to the integration of artificial intelligence, the

student can even drop the discussed topic and ask

questions to which the chatbot responds. This AI

system can also supply relevant information pupils

might need to solve the task. For example AI

responds pupil when he or she asks about

reconnecting to the course and starting over.

Questions and answers of a pupil are continuously

reflected upon and new functions are added (such as

searching for relevant information on wikipedia or

other databases of educational resources). AI is being

trained on questions and reactions of pupils’.

The aim of the course is not to test the student, but

to improve their abilities in and understanding of the

given areas. That is why we decided to implement the

course in a form where students do not get the usually

presented choice of answers of which only one is

correct and the others are wrong. Instead, we decided

to use a form where only one answer is given and this

answer is correct. The other options allow the student

to ask for advice or to give up on the solution. It is

thus up to the student to solve the task and then

answer whether they have reached the desired result.

We expect a higher level of motivation from this form

(Petty, 2002) when the student does not feel that he is

being tested and is not penalized for choosing the

wrong answer or for asking for advice. If the student

selects that they need advice, the chatbot will show

them a detailed solution to the given task, or a

procedure that can be used for the solution of the task

after some minor modification. For each topic,

questions are graded according to difficulty, allowing

the student to skip an easy task if they feel confident

in the area. Moreover, after solving a standard task, it

is up to the student to decide whether they want to try

to solve a difficult task. While working in the course,

the student is also allowed to play a video with an

explanation that will link them to YouTube or another

video server. Since our goal is to find out whether a

student has improved in the area after completing the

course and how they worked with the multiple-choice

format without distractors, their progress is recorded

anonymously. Among other things, the time between

displaying a question and selecting an answer or the

performance on a pre-test and post-test is monitored.

The student has the opportunity to generate topics for

the course based on the results of the pre-test. They

do not have to go through all the areas if they for

example only have problems in algebra.

Figure 2: Chatbot environment for Algebraic expressions

topic.

A more detailed functioning of the chatbot is

illustrated in Figure 1, which shows what options the

student chooses from at each step. Specific examples

of the use of algebraic identities and unit conversions

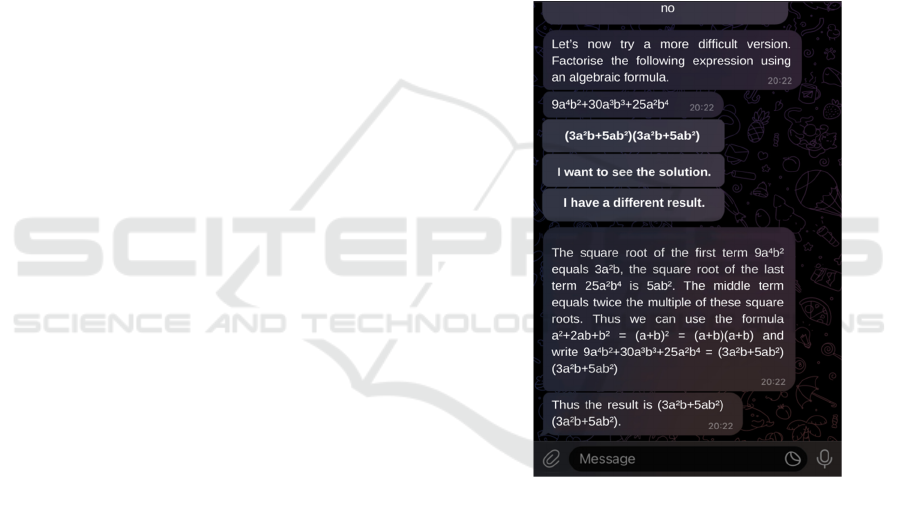
are shown in Figures 2 and 3. In Figure 2, the

student’s task is to factorise an algebraic expression

using the formula for the square of the sum. As the

student did not know what to do, they selected the

option “I want to see the solution”. Through this, the

student got access to an in-detail explained solution

to the problem. In Figure 3, the student’s task is to

convert units of length. The student chose the correct

answer, and in response, the chatbot commended the

Feedback in Online Mathematics Tutoring

377

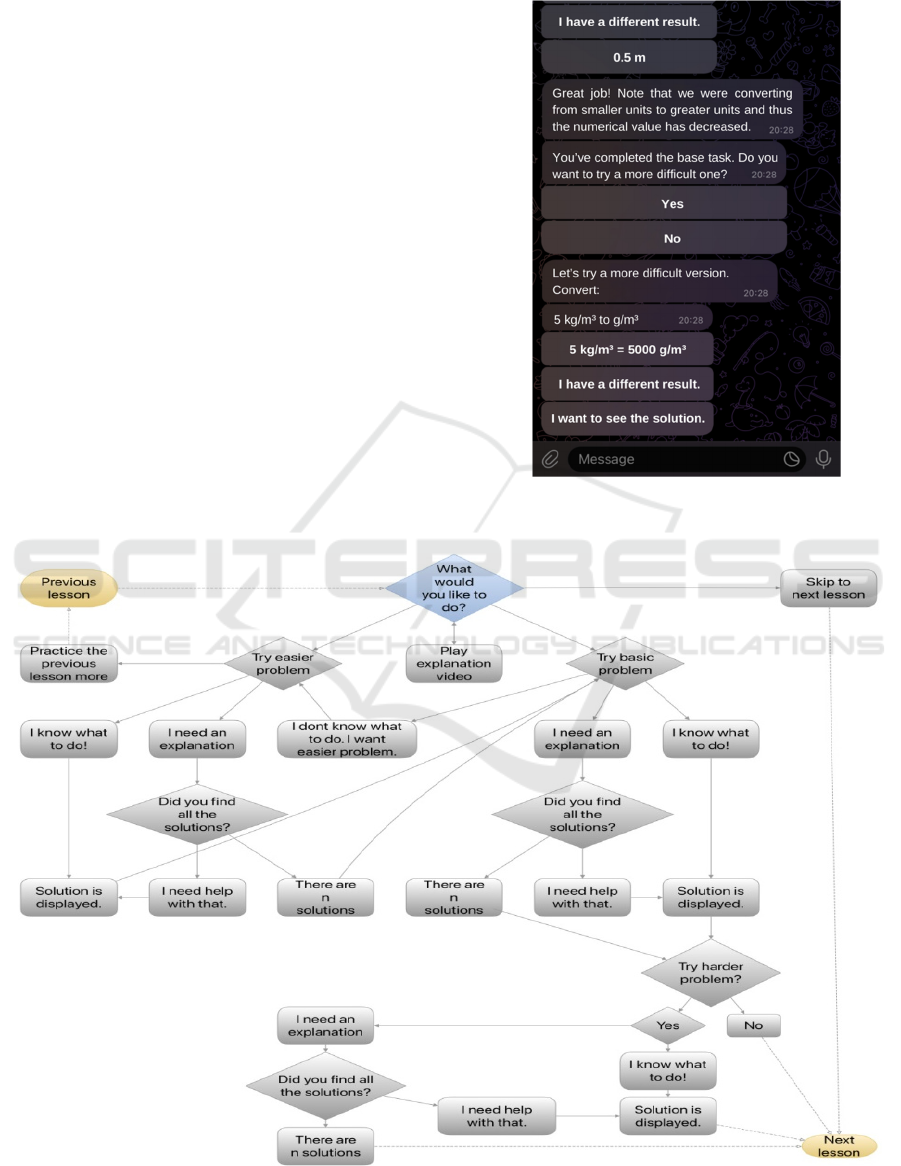
student as well as gave them useful tips on what to

look out for when converting.

The fundamental question addressed in our

research was whether this principle can be applied in

all areas of mathematics that the course focuses on.

Our original intention was to apply a uniform scheme

across all topics so that the student could get used to

the homogeneity of the environment and could work

in it effectively. However, this turned out to be

impossible, as different areas of mathematics require

different ways of presentation. While, for example, in

algebra, it is possible to offer an answer in the form

of an algebraic expression, there is no such possibility

in the field of geometry. Not only is it not possible to

express the solution with a one-line verbal answer,

but also a solution in the form of a picture may not be

sufficient for the student to understand. The

nonlinearity of the answer in the form of a picture

combined with the fact that the construction can

usually be done in many ways means that we have to

approach it differently than to offer one correct

answer. While displaying the correct solution in

arithmetic and algebra allows the student to check

their understanding of the procedure and helps to

eliminate numerical errors, in geometry showing one

solution may confuse the student, especially if the

student proceeded differently or found a different

solution.

Figure 3: Chatbot environment for Unit conversions.

Figure 4: Options the user can choose from at each step in the field of construction tasks.

CSEDU 2023 - 15th International Conference on Computer Supported Education

378

In the case of algebraic problems, the chosen

procedure was implemented in such a way that the

student was shown the correct answer together with

the assignment. The implementation of the entire

procedure can be found in Figure 1. In the case of

construction tasks, the correct answer cannot be given

immediately for the above reasons. This was solved

by giving the student the choice between the options

“I need an explanation” and “I know how to do it”.

This means that the second option is different from

how it works in the previous areas as there is no

visible solution or advice on how to proceed directly

on the button.

Figure 5: Chatbot environment for geometry.

Figure 4 shows how the chatbot works in the field

of construction tasks. Having asked for an

explanation, the student is offered a detailed verbal

answer, an animation (gif) showing the step-by-step

construction in a graphical software, a stationary

image of the solution, or a link to a video explaining

the phenomenon/construction/validity of a critical

step. The student’s task is then to determine whether

the problem has more than one solution. Having

clicked on the option “I know how to do it”, the

student is shown only a stationary image of one of the

solutions. The student is then asked if they have found

other solutions. They can choose from the options

“Yes, the task has n solutions (congruent solutions are

taken as 1)”, where n is dynamic, depending on the

task, and the option “I need advice on the number of

solutions”. Selecting the latter option means the

student is shown a detailed solution as if they selected

the option “I need an explanation” in the very

beginning. Examples of construction problems are in

Figures 5 and 6.

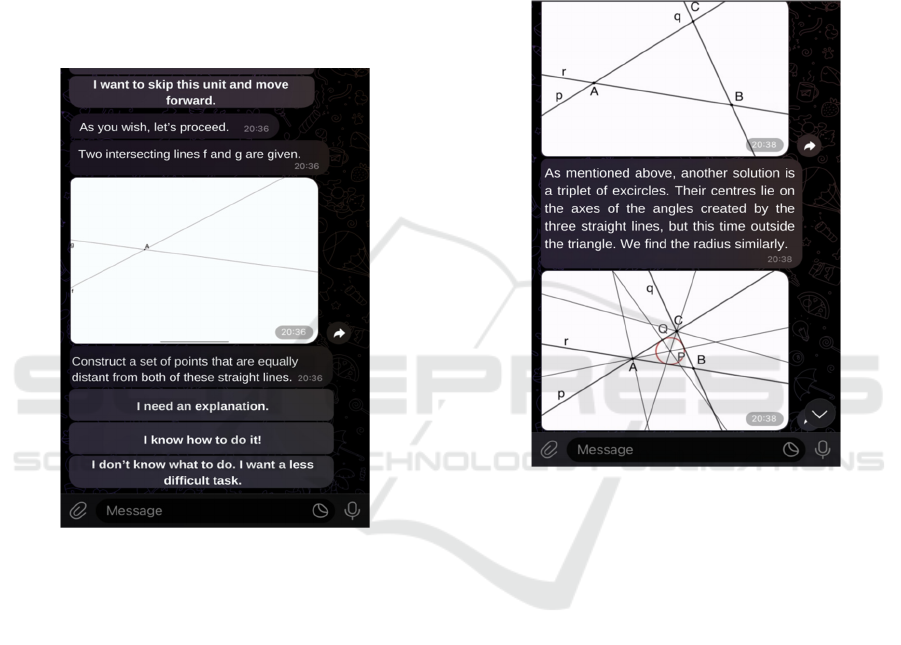
Figure 5 shows the assignment that the student

gets having chosen the difficulty of the task they want

to solve. This is described in words, sometimes it is

supplemented with an illustrative picture. Figure 6

shows an explanation of another problem is

displayed, where the student first sees the described

animation and then a picture of the solution. A set of

other solutions to the problem are also discussed here.

Figure 6: Offered solution of geometry task.

For each of the areas, at the end of the unit, the

student is offered links to other tasks or units of a

similar type created by teachers and uploaded to the

Ema.cz server. The tasks that are recommended to

students have been evaluated by the authors of the

paper in terms of quality and only the most suitable

ones have been selected. The course thus primarily

helps the student identify which areas they still need

to practice, it offers tasks and explanations but also

other resources where the student can improve or

practice their knowledge.

Before making the course available to students, we

plan to add links to interactive applets created in

GeoGebra (https://www.geogebra.org/, accesed on

March 2023) that will allow the student to

construct in a graphical software environment with a

limited palette of tools (circle, line, line segment,

compass, intersection, ...) and the software will

automatically evaluate the correctness of the solution,

similar to the Euclidea application (https://www.

euclidea.xyz/, accesed on 15

March 2023).

Feedback in Online Mathematics Tutoring

379

4 DISCUSSION & CONCLUSIONS

Our research confirms that it is necessary to proceed

differently in different areas of mathematics. In the

paper, this is documented in two different areas of

school mathematics – algebraic problems and

construction problems in geometry.

Petty (2002) states that anything that surprises,

arouses curiosity or anticipation or provokes thought

helps to motivate students. Pupils can be encouraged

to take an active approach to learning, among other

things, by presenting them with activities in which

they will correct and check their work (either on their

own or with each other), by making them study at

least some topics on their own from books and by

using inquiry-based approach and by allowing them

to experiment actively.

As we have shown in the paper, the use of a

chatbot meets these recommendations and can be

considered a suitable tool for fostering understanding

in problem-solving in mathematics. In further

research, we plan to focus on the use of the chatbot in

other areas of school mathematics, and on examining

the relationship between teachers and pupils to it.

Attention should also be paid to the introduction of

AI tools in teacher education.

The tutoring system is about to be tested with

pupils during the spring of 2023. Their feedback as

well as data from their answers (the time it took for

them to click the right answer) will be collected and

analyzed to further improve the system.

ACKNOWLEDGEMENTS

This research was funded by the Technology Agency

of the Czech Republic, grant number TAČR N.

TL05000236 – AI assistant for pupils and teachers.

REFERENCES

Alhossaini, M., & Aloqeely, M. (2021, December). Causal

Analysis of On-line Math Tutoring Impact on Low-

income High School Students Using Bayesian Logistic

and Beta Regressions. In 2021 IEEE Symposium Series

on Computational Intelligence (SSCI) (pp. 1-10). IEEE.

Attard, A. E. (2021) AI assisted pedagogical chatbot

(Bachelor's thesis, University of Malta).

Beal, C. R., Walles, R., Arroyo, I., & Woolf, B. P. (2007).

On-line tutoring for math achievement testing: A

controlled evaluation. Journal of Interactive Online

Learning, 6(1), 43-55.

Bray, M., & Silova, I. (2006). The private tutoring

phenomenon: International patterns and perspectives.

In I. Silova, V. Būdienė, & M. Bray (Eds.). Education

in a hidden marketplace: Monitoring of private tutoring.

Overview and country reports (pp. 27–40). New York:

Open Society Institute. DOI: 10.1080/030579206010

24974.

Belpaeme, T., Kennedy, J., Ramachandran, A., Scassellati,

B., & Tanaka, F. (2018). Social robots for education: A

review. Science Robotics, 3(21), eaat5954.

https://doi.org/10.1126/scirobotics.aat5954

Buchberger, B. (1990). Should students learn integration

rules? SIGSAM Bulletin, 24(1), 10–17.

Drijvers, P., Kieran, C. and Mariotti, M.A., with Ainley, J.,

Andresen, M., Cheung Chan, Y., Dana-Picard, T.,

Gueudet, G., Kidron, I., Leung, A. and Meagher, M.

(2010). Integrating Technology into Mathematics

Education: Theoretical Perspectives. In C. Hoyles and

J.-B. Langrange (Eds.), Mathematics Education and

Technology-Rethinking the Terrain (pp. 89-132).

Springer Science + Business Media. DOI 10.1007/978-

1-4419-0146-0_7

Fey, J.T. (Ed.) (1984). Computing and Mathematics: The

Impact on Secondary School Curricula. College Park:

The University of Maryland.

Fiori, N., Boaler, J., Cleare, N., DiBrienza, J., & Sengupta,

T. (2004). What discussions teach us about

mathematical understanding: exploring and assessing

students’ mathematical work in classrooms? In D. E.

McDougall & J. A. Ross (Eds.), Proceedings of the

twenty-sixth annual meeting of the North American

Chapter of the International Group for the Psychology

of Mathematics Education, 2, 491-498. Toronto:

OISE/UT.

Gissel, S. T., Ramos Artuso, A., & Køhrsen, L. (2019).

Does the use of ICT in education promote student

learning?.

https://iartemblog.wordpress.com/conferences/odense/

Hardman, J. (2019). Towards a pedagogical model of

teaching with ICTs for mathematics attainment in

primary school: A review of studies 2008–2018.

Heliyon, 5(5), e01726.

Harlen, W., Crick, R. D., Broadfoot, P., Daugherty, R.,

Gardner, J., James, M., & Stobart, G. (2002). A

systematic review of the impact of summative

assessment and tests on students’ motivation for

learning.

Hille, von A., Spieß, K., & Staneva, M. (2016). Immer mehr

Schülerinnen und Schüler nehmen Nachhilfe,

besonders in Haushalten mit mittleren Einkommen.

DIW Wochenbericht, 83(6), 111–120. DOI:

10.5684/soep.v30

Jančařík, A., Novotná, J., Michal, J. (2022) Artificial

Intelligence Assistant for Mathematics Education. In:

P. Fotaris, Panagiotis, Blake, A (Eds.),. Proceedings of

the 21st European Conference on e-Learning - ECEL

2022 (pp. 143-148). 1. Reading. ISBN 978-1-914587-

56-6. ISSN 2048-8637

Kim, J., Merrill, K., Xu, K. and Sellnow, D. D. (2020) My

teacher is a machine: Understanding students’

perceptions of AI teaching assistants in online

CSEDU 2023 - 15th International Conference on Computer Supported Education

380

education. International Journal of Human–Computer

Interaction, Vol 36, No. 20, pp 1902-1911.

Lagrange JB, Artigue M, Laborde C, Trouche L. (2001). A

meta study on IC technologies in education. Towards a

multidimensional framework to tackle their integration.

In PME CONFERENCE 2001 (Vol. 1, pp. 1-111).

Mischo, C. & Haag, L. (2002). Expansion and effectiveness

of private tutoring. European Journal of Psychology of

Education, 17(3), 263–273, DOI: 10.1007/BF03173

536.

Novotná, G. (2019). Pupils' perception of their understand-

ing in mathematics and its connection to private

supplementary tutoring. Proceedings of CERME 11.

https://www.researchgate.net/publication/348579569

Petty, G. (2002). Moderní vyučování. Praha, Portál. ISBN

80-7178-681-0. Translated from Petty, G. Teaching

Today, Cheltenham: Stanley Thornes Ltd.

Robová, J., & Moravcová, V. (2019). Vývoj

matematického vzdělávání v České republice po roce

1989. Scientia in educatione, 10(3), 143-162.

Roa, H.B., Nariño, A. (2006). A model for teaching

mathematics via problem-solving supported by

technology. In: C. Hoyles, Lagrange, J./b/, Son, Le H.

& Sinclaire, N. (Eds.), Proceedings of the Seventeenth

ICMI Study Conference (pp. 66-73).

Sadler, D. R. (1998). Formative assessment: revisiting the

territory. Assessment in Education: Principles, Policy

& Practice, 5(1), 77-84.

Safarzyńska, K. (2013). Socio-economic determinants of

demand for private tutoring. European Sociological

Review, 29(2), 139-154

Shahbazi, Z. and Byun, Y-Ch.(2022). Agent-Based

Recommendation in E-Learning Environment Using

Knowledge Discovery and Machine Learning

Approaches. Mathematics 2022, 10(7), 1192;

https://doi.org/10.3390/math10071192

Song, K. O., Park, H. J., & Sang, K. A. (2013). A cross-

national analysis of the student-and school-level factors

affecting the demand for private tutoring. Asia Pacific

Education Review, 14(2), 125-139.

Taylor, R. (Ed.) (1980). The Computer in the School: Tutor,

Tool, Tutee. New York: Teachers College Press.

Trinh Thi Phuong, T., Nguyen Danh, N., Tuyet Thi Le, T.,

Nguyen Phuong, T., Nguyen Thi Thanh, T., & Le Minh,

C. (2022). Research on the application of ICT in

Mathematics education: Bibliometric analysis of

scientific bibliography from the Scopus database.

Cogent Education, 9(1), 2084956.

Verschaffel, L., Depaepe, F., & Mevarech, Z. (2019).

Learning Mathematics in metacognitively oriented

ICT-Based learning environments: A systematic review

of the literature. Education Research International,

2019.

Zawacki-Richter, O., Marín, V.I., Bond, M., and

Gouverneur, F. (2019). Systematic review of research

on artificial intelligence applications in higher

education – where are the educators? International

Journal of Educational Technology in Higher

Education, 2-27. https://doi.org/10.1186/s41239-019-

0171-0

Feedback in Online Mathematics Tutoring

381