Vector Tile Geospatial Data Protection Using Quantization-Based
Watermarking
Danila Glazkov
1,2 a
, Nikolay Chupshev
1,2 b
and Victor Fedoseev
1,2 c
1
Samara National Research University, Samara, Russia
2
Samara-Informsputnik JSC, Samara, Russia
Keywords: Mapbox Vector Tiles, MVT, Geospatial Data, GIS, Geospatial Data Protection, Watermarking, QIM.
Abstract: The paper proposes a watermarking method for protecting geodata presented in the Mapbox Vector Tile
(MVT) format against theft. MVT is an open format that is gaining popularity in web mapping services due
to efficient storage and fast rendering. However, the vector nature of the format makes it an easy target for
attackers who want to steal data and use in their services. The method proposed in this paper protects MVT
data with a digital watermark based on re-quantization of point coordinates of object geometry. The method
can be adjusted using a number of parameters that allow finding a balance between the robustness of the
digital watermark to map distortions and the error introduced when embedding. A series of experiments
performed showed the robustness of this method to several distortions: removal of some objects and layers,
reduction in the number of points of existing objects, addition of new objects, controlled shift of points in the
tile geometry. With a proper choice of the watermark parameters, even with a moderate level of each of the
listed distortions, which does not lead to a loss of significance of the protected geodata, the method can reach
100% watermark extraction accuracy of all bits of the built-in watermark.
1 INTRODUCTION
Geospatial web services are becoming more popular
every year. Modern design standards for such systems
require compliance with several requirements
(Wallner, 2022). The most crucial of these
requirements include efficient data storage, fast and
high-quality rendering, and open format support.
Based on these requirements, the Mapbox Vector
Tile (MVT) format is increasingly being used in
modern web services. MVT is a relatively new open
standard for storing and displaying geospatial data
(Mapbox, 2023). Along with the traditional Web Map
Tile Service (WMTS), it is a hierarchical tile format
that is the most convenient for the web. However,
unlike WMTS, it stores data not in raster but in vector
form, reducing the amount of stored data and
improving the rendering quality. The benefits of
MVT have been demonstrated in several research
papers (Netek, 2020), (Yu, 2017).
a
https://orcid.org/0000-0002-4499-1489
b
https://orcid.org/0000-0002-8521-0423
c
https://orcid.org/0000-0003-1750-1920
However, using a vector format increases the risk
of theft and manipulation of geospatial data. This is
because vector tiles contain more detailed and
accurate vector geospatial data, making them more
valuable to potential attackers. Additionally, Mapbox
Vector Tiles can be easily converted to geoJSON or
KML, allowing an attacker to use stolen high-
precision data in their GIS products without the
permission of the copyright holder.
In contrast, raster tiles contain pre-rendered
images of the geospatial data. They are also more
challenging to extract and manipulate because they
are composed of pixels rather than vectors. While it
is possible to extract some information from raster
tiles using image processing techniques, the quality
of the recovered vector data is generally lower
compared to vector tiles.
Despite the security risks associated with the use
of vector tiles, the authors of this article could not find
any publications in the scientific literature dedicated
to the study of the security of MVT, nor the
Glazkov, D., Chupshev, N. and Fedoseev, V.
Vector Tile Geospatial Data Protection Using Quantization-Based Watermarking.
DOI: 10.5220/0012044500003473
In Proceedings of the 9th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2023), pages 251-258
ISBN: 978-989-758-649-1; ISSN: 2184-500X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
251

development of algorithms, protocols, or scenarios
for using MVT sources that increase the security of
MVT data. The only work that can be mentioned is
(Zhang, 2022), which is dedicated to the MVT-based
data collection and publishing technology based on
Apache Sedona. The conclusion of this article states
that the authors plan to improve the security of MVT
data in further studies, but without specifying the
methods they plan to use.
One of the most effective and widespread
solutions for protecting data from theft and
unauthorized manipulation is digital watermarking.
This technology consists in a subtle managed change
in the data representation or the way of its storage.
This change makes it possible to embed some
protective information, called a watermark, into the
data. This approach was used for more than two
decades to protect images, videos, audio, some kinds
of medical and engineering data etc. (Cox, 2008).
Watermarking methods were also used to protect
raster tile maps (Ren, 2014).
Vector geospatial data do not have the same
storage redundancy as raster geodata. Therefore, they
are less suitable for digital watermarking. Despite
this, there are many algorithms for protecting vector
cartographic data with digital watermarks based on
changing point coordinates, the order of vertex
traversal, the index of the initial vertex in the polygon,
etc. (Lee, 2013), (Cao, 2015), (Peng , 2018),
(Vybornova, 2020). However, all of them are not
designed to protect tile vector data, which have some
specific features distinguishing them from digital
maps.
This article proposes a method for protecting
MVT from unauthorized use (theft) based on a robust
watermarking method based on re-quantizing the
points of polylines or polygons. At the time of
writing, the authors could not find any paper
describing methods for MVT watermarking.
The following section provides a summary of the
MVT format that is important for understanding the
proposed method. The method itself is described in
Section 3. Section 4 presents the results of
experimental studies, and Section 5 gives the main
conclusions.
2 THE MAPBOX VECTOR TILE
FORMAT
According to the specification (Mapbox, 2023), by
default, MVT uses the Web Mercator projection and
the Google Tile scheme, which determines the
coordinates and IDs of tiles at each zoom level. Tile
data is stored using the Google Protocol Buffers
serialization mechanism.
The internal structure of a tile is a collection of
layers. Each layer must contain the extent property
that describes the width and height of the tile in
integer coordinates. In fact, the extent, together with
the tile scale level, determines the discretization step
of object point coordinates when converting them
from a GIS vector map to MVT. The discretization
step of the entire tile tree is determined by the
maximum scale level for which the data is defined, as
well as the extent value of the layers of this level.
Thus, MVT provides the copyright holder with the
opportunity to publish data at an arbitrarily high
resolution.
A layer is a collection of objects (features)
characterized by their geometry and semantics. Three
types of geometry are available: POINT,
LINESTRING (polylines), and POLYGON. In
multipoint objects, points are connected only by line
segments. Circular arcs, Bezier curves, etc. are not
supported. Thus, only three commands are used to
describe the geometry: MoveTo, LineTo, and
ClosePath. The first two commands have parameters
that are the number of repetitions and point
coordinates. Point coordinates are specified as a pair
of integers between 0 and the extent. It is allowed to
use points that are not included in this interval.
However, only those line fragments that lie in the
range

0, 𝑒𝑥𝑡𝑒𝑛𝑡

×

0, 𝑒𝑥𝑡𝑒𝑛𝑡

will be displayed.
3 PROPOSED MVT
WATERMARKING METHOD
The proposed method is based on the re-quantization
of point coordinates and is suitable for all three types
of MVT features. This makes it possible to classify
this method as one of the methods based on
Quantization Index Modulation (QIM) (Chen, 2001).
Moreover, due to the two-dimensional nature of the
protected data (plane coordinates), the proposed
method is closely related to the geometric
interpretation of the QIM method presented in the
cited paper.
Each vector tile contains a fragment of a
watermark with a length of 𝑁

≥1 bits. To embed a
watermark, a tile is represented as a set of 𝑀×𝑀
non-intersecting squares. If 𝐸 is the extent of the tile
(its width and height in integer coordinates), then the
size of each square is 𝐸/𝑀 × 𝐸/𝑀. 𝑀 is preferably a
divisor of 𝐸 . This makes it easier to translate a
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
252

specific coordinate in meters to a coordinate in the tile
space.
Each of these squares is embedded with one
watermark bit. Thus, if the embedding is done
without repeats, 𝑁

=𝑀

. However, in practice, one
of the most effective ways to increase the robustness
is to embed the same bit in several squares. Let 𝑟 be
the number of squares in which the same bit is
embedded. Then we arrive at the following equation
𝑁

=
⌊
𝑀

/𝑟
⌋
,
(1)
linking 𝑁

with two other parameters. It is desirable
to choose the parameters so that 𝑀

is evenly
divisible by 𝑟. In this case, the entire area of the tile
will be used to protect it. Embedding in a square can
be performed if at least one geometry point falls into
this square. Thus, for each bit of the input digital
watermark to be embedded, it is necessary that at least
one of the 𝑟 squares corresponding to it contains one
point. Certainly, in practice, there should be many
more such points to increase the robustness of the
watermark.
Let 𝑊_𝑖𝑛𝑥 be an 𝑀×𝑀 matrix determined for
each tile ID separately based on the secret key,
containing numbers from 0 to 𝑁

−1. Moreover,
each of them must occur exactly 𝑟 times. This matrix
specifies the correspondence between the index of the
embedded bit and the squares in which it is
embedded.
Also, based on the secret key for each tile ID, an
𝐸×𝐸 matrix 𝑀𝑎𝑝 is generated containing the values
{0,1}. The generation is carried out in such a way that
for any element of the matrix, the 4-connected
distance to the nearest element of the matrix with the
opposite value does not exceed the specified value 𝑞.
We will use small 𝑞 values, not exceeding 3.
To increase the robustness of the embedded
watermark, we also consider a version of the method
with 𝑀𝑎𝑝 initially formed as a 𝑝 times smaller
matrix, and then it is resized to 𝐸×𝐸.
We will design a couple of related algorithms for
embedding and extracting information according to
the informed embedding scheme. In this scheme, the
information extraction algorithm is designed first,
followed by the information embedding algorithm
corresponding to it. So let us start with extraction.
Consider two versions of the information extraction
algorithm that differ in the order of data aggregation
from different squares containing a watermark bit
with the same index. The first version is based on
majority voting, while the second one is based on the
formation of general statistics.
Extraction algorithm (version 1):
1. Loop through all squares 𝑖 = 0..𝑀

−1:
1.1. Find all geometry points of all tile objects
that fall into the i-th square.
1.2. If their number is less than 𝑇

, then it is
decided that this square is not taken into
account in the watermark extraction
procedure since it can introduce an error.
Go to step 1.1 for the square 𝑖+1.
1.3. Each point in the geometry corresponds to
a binary value in 𝑀𝑎𝑝. Count the number
of zeros 𝑠

and ones 𝑠

in the square.
1.4. If
|
𝑠

−𝑠

|
/(𝑠

+𝑠

)<𝑇

, then this
square is also not taken into account when
extracting the watermark. Go to step 1.1 for
square 𝑖+1.
1.5. If 𝑠

>𝑠

, then we decide that the i-th
square contains 1, otherwise it contains 0.
2. Loop over watermark bits 𝑗= 0..𝑁

−1:
2.1. Define the set of square indices {𝑖}
containing bit index 𝑊_𝑖𝑛𝑥
(
𝑗
)
.
2.2. The j-th bit is determined by the majority
voting method for those squares that are
decided to be taken into account when
extracting.
Extraction algorithm (version 2):
1. Loop through all squares 𝑖 = 0..𝑀

−1 ,
replenishing statistics 𝑠

(𝑗) and 𝑠

(𝑗) common
to the entire tile, where 𝑗 = 0..𝑁

−1 are
watermark bit indices:
1.1. All geometry points of all tile objects that
fall into the i-th square are found.
1.2. Each point of the geometry corresponds to
a binary value in the matrix 𝑀𝑎𝑝. Count the
number of zeros 𝑠
,
and ones 𝑠
,
in the i-th
square and add them to the statistics that
refers to bit 𝑊_𝑖𝑛𝑥(𝑖):
𝑠

(
𝑊_𝑖𝑛𝑥(𝑖)
)
≔𝑠

(
𝑊_𝑖𝑛𝑥(𝑖)
)
+𝑠
,
,
𝑠

(
𝑊_𝑖𝑛𝑥(𝑖)
)
:=𝑠

(
𝑊_𝑖𝑛𝑥(𝑖)
)
+𝑠
,
.
2. Loop over indices 𝑗 = 0..𝑁

−1:
2.1. If 𝑠

(𝑗) + 𝑠

(𝑗) < 𝑇

, then a decision is
made that we do not have enough data to
reliably extract the j-th bit of the digital
watermark.
2.2. If
|
𝑠

(
𝑗
)
−𝑠

(
𝑗
)|
/(𝑠

(
𝑗
)
+𝑠

(
𝑗
)
)<𝑇

,
then the j-th bit is also not extracted.
2.3. If 𝑠

(
𝑗
)
>𝑠

(
𝑗
)
, then the value of the j-th
bit is 1, otherwise 0.
Embedding algorithm:
1. Find all points of the geometry of all objects, and
calculate 𝑠

and 𝑠

for each square or bit index
depending on the extraction method chosen.
Vector Tile Geospatial Data Protection Using Quantization-Based Watermarking
253

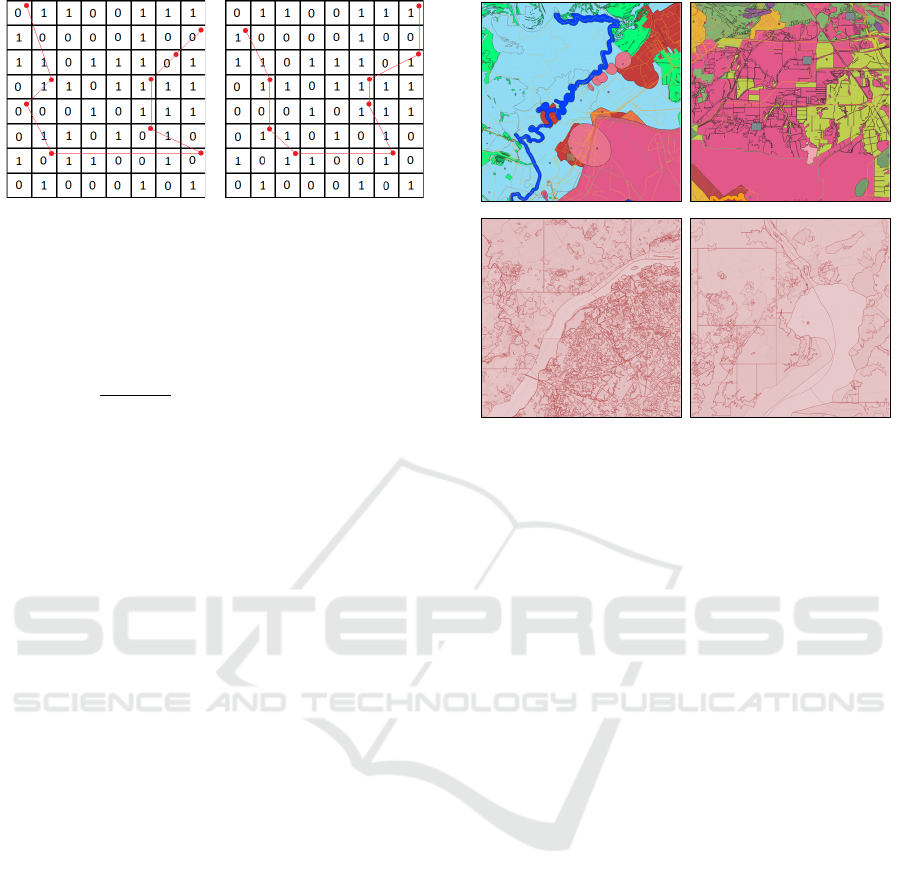
Figure 1: Illustration of the watermarking process: polyline
points move with respect to corresponding 𝑀𝑎𝑝 values.
2. If 𝑠

+𝑠

<𝑇

, move on to the next square (or
the next watermark bit).
3. Ensure that the ratio is fulfilled:
|
𝑠

−𝑠

|
𝑠

+𝑠

≥𝑇

(
1+𝑘
)
,
(2)
where 𝑘≥0 is a parameter that increases the
watermark robustness to changes in the map
contents. The sign of the difference 𝑠

−𝑠

is
determined by the value of the embedded bit. If
the initial data does not meet these conditions,
then the necessary number of points is shifted to
the nearest coordinates with the opposite binary
value in the 𝑀𝑎𝑝 . Figure 1 shows a very
simplified illustration of the embedding
approach: in this example, points located in cells
with 𝑀𝑎𝑝 = 0 are moved to neighboring cells
where 𝑀𝑎𝑝 = 1.
Thus, the proposed method is configured with the
following parameters:
 Three values
{
𝑁

,𝑀,𝑟
}
related by (1). A high
𝑁

value characterizes a large volume of the
watermark, while an increase in 𝑟 , in turn,
increases the watermark robustness.
 The extraction algorithm version.
 𝑇

,𝑇

,𝑞 – parameters that determine the
efficiency of the method and the level of
distortion when watermark embedding. They
should be selected based on the balance
between the quality of the extraction and the
quality of the protected data (closeness to the
original).
 𝑘, 𝑝 – both parameters are more convenient for
balancing the quality of extraction (robustness)
and the level of distortion caused by embedding
than the previous trio of parameters.
It should be noted that in practice it is expedient
to embed a protective digital watermark into tiles of
the most detailed levels, the theft of which is the most
sensitive for the copyright holder and commercially
justified for the attacker.
Figure 2: Test tile examples from STP (top) and Tegola
(bottom). Different colors correspond to objects of different
layers.
4 EXPERIMENTAL
INVESTIGATION
4.1 Setting Up Experiments and
Preliminary Study
To assess the performance of the proposed method,
we first evaluated the effect of the method parameters
on the quality of the digital watermark extraction and
on the level of distortions associated with embedding.
Next, a study was made of the robustness of the
digital watermark, that is the effect of subsequent
changes in protected tiles on the quality of watermark
extraction. In our experiments, we used two data
sources:
 The Samara Region Investment Map (STP);
 The Tegola demo map (https://tegola.io/).
The experiments utilized two STP tiles and two
Tegola tiles. Each test tile contained more than 3000
line and polygon objects, including objects with
complex geometry (see four examples in Figure 2).
During the research, the following quality metrics
were calculated:
 Watermark extraction accuracy (percentage of
correctly extracted bits).
 Hausdorff and Fréchet average distances as a
measure of object geometry deviation when
embedding a digital watermark (distance
between the objects of the source map and the
corresponding objects of the protected map).
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
254

 Hausdorff and Fréchet average distances as a
measure of object geometry distortion in the
study of watermark robustness (distance
between protected map objects and the
corresponding artificially distorted map
objects).
Initially, we conducted a preliminary study.
Watermark embedding was done with different
parameter values, and the average geometry deviation
was estimated. Then, the watermark was extracted,
and the extraction accuracy was computed. The
objective of this analysis was to identify the
operational ranges of the parameters of our method
that provide acceptable quality values. The results
indicated that in a relatively broad range of parameter
values, 100% accuracy of watermark extraction can
be achieved on both data sources (STP and Tegola)
with an acceptable geometry deviation (not less than
0.9 for both measures). This range includes the
following values:
 𝑇

: 0.05 to 0.95;
 𝑘: 0.08 to 1;
 𝑇

: 1 to 75;
 𝑞: 1 to 3;
 𝑟: 1 to 200;
 𝑝: 1 to 2 for STP and 1 to 8 for Tegola.
In this range of values, with p=1, the minimum
metric values were recorded as follows:
 STP: 0.946 (Hausdorff) and 0.941 (Fréchet)
 Tegola: 0.980 (Hausdorff) and 0.941 (Fréchet)
Table 1 illustrates the effect of 𝑝 on the geometry
deviation when embedding a watermark. Other
parameters were kept at average values based on the
balance between the robustness and the level of
distortion introduced. The watermark was extracted
without errors for all values of 𝑝.
Table 1: Influence of p on the geometry deviation caused
by watermark embedding
𝑝
STP Tegola
Avg
Hausdorff
Avg
Fréchet
Avg
Hausdorff
Avg
Fréchet
1 0.962 0.958 0.991 0.991
2 0.931 0.922 0.980 0.979
4 0.867 0.851 0.964 0.962
8 0.788 0.765 0.940 0.937
16 0.608 0.579 0.892 0.883
Figure 3 illustrates the influence of the developed
watermarking algorithm on the geometry of objects.
Above, the original and protected tiles are shown in
their entirety, and below are fragments of the overlay
of the two tiles, showing the difference in shapes. The
changes do not have a significant impact on the map
data and are noticeable only with explicit comparison
at a large scale. This embedding was performed with
the following set of parameters: 𝑘=0.6, 𝑇

=0.6,
𝑇

=5, 𝑝=1, 𝑞=3, 𝑁

=20, 𝑟=10. The
watermarking quality values are: 𝑎𝑐𝑐𝑢𝑟𝑎𝑐𝑦 = 1 ,
ℎ𝑎𝑢𝑠𝑑𝑜𝑟𝑓𝑓 = 0.971, 𝑓𝑟𝑒𝑐ℎ𝑒𝑡 = 0.969.
Figure 3: The effect of embedding a digital watermark:
above is the original and the corresponding protected tile,
in the middle and below are fragments of the overlay of two
tiles (the red represents the original data, while the green
represents the data with the embedded digital watermark).
4.2 Investigation of the Watermark
Robustness in Case of Map
Distortions
For reliable protection against theft, the built-in
digital watermark must remain stable when the map
changes. This should take into account changes that
may occur naturally in the course of using the stolen
data, as well as artificial changes that an attacker may
make to destroy the embedded watermark.
Vector Tile Geospatial Data Protection Using Quantization-Based Watermarking
255

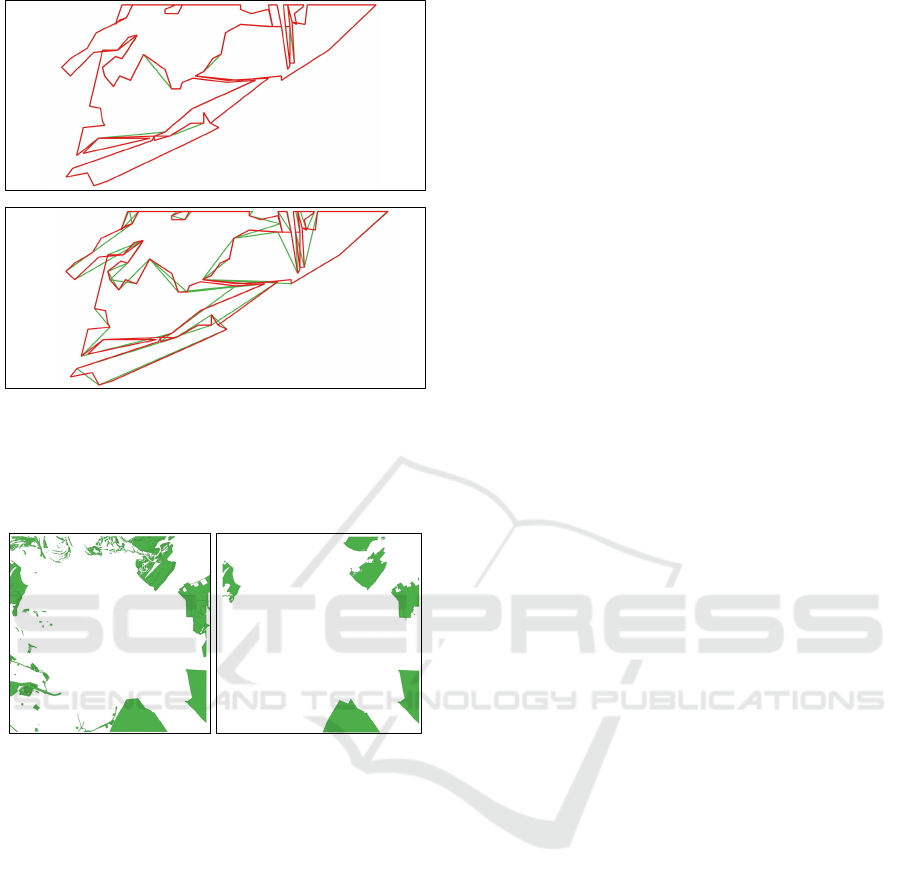
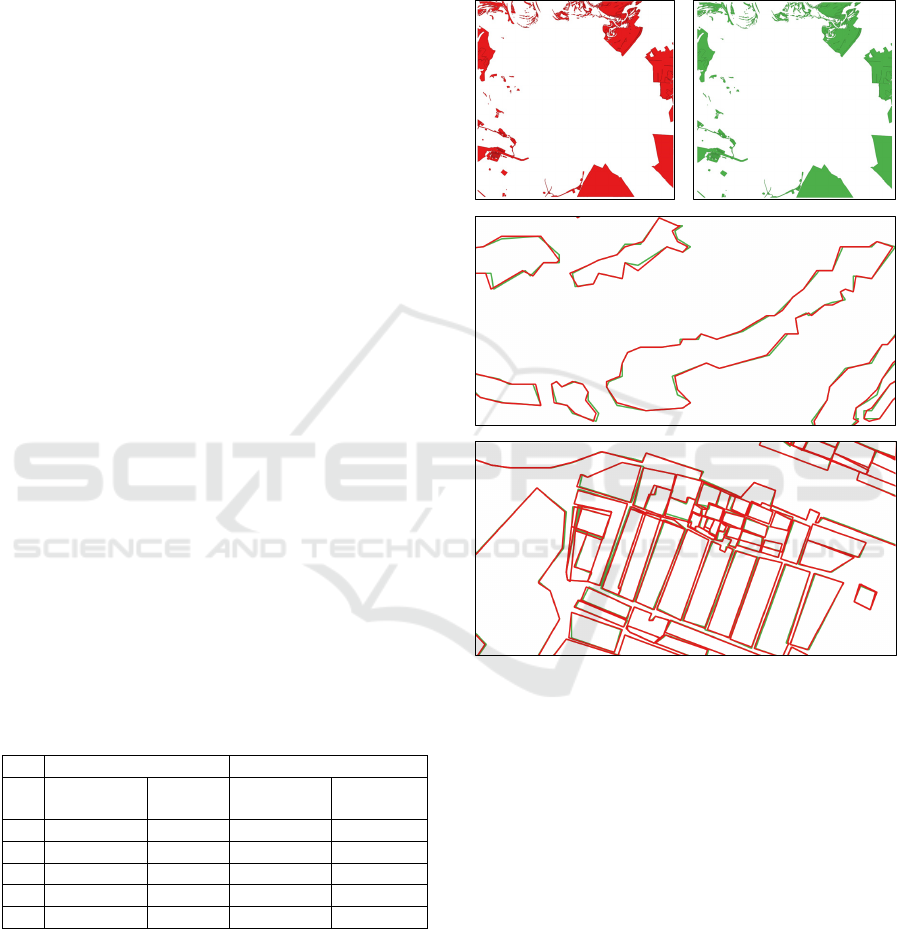
Figure 4: The effect of the ReducingNumberOfPoints
attack (zoomed tile fragments) at 𝑣𝑎𝑙𝑢𝑒 = 0.9 (upper,
hausdorff: 0.990, Fréchet: 0.961) and 𝑣𝑎𝑙𝑢𝑒 = 0.4 (lower,
hausdorff: 0.726, Fréchet: 0.616). Watermark extraction
accuracy is 1 in both cases.
Figure 5: The effect of the DeletingByArea attack (entire
tiles) at 𝑣𝑎𝑙𝑢𝑒 = 0.0001 (left) and 𝑣𝑎𝑙𝑢𝑒 = 0.3 (right).
Watermark extraction accuracy is 1 in both cases.
Of course, such distortions of the map should be
considered within a range of parameter values for
which the map retains its value as a source of reliable
data.
The second stage of the study involved
investigating the robustness of the embedded digital
watermark against map distortions. The following
distortions and their parameters were used:
1) ReducingNumberOfPoints:
This involved reducing the redundancy in the
geometry by using the Largest Triangle Three
Buckets (LTTB) algorithm (Alt, 2000), where the
parameter is the proportion of points left. This
reduction can be done naturally to decrease the size
of the database, but it can also be maliciously used to
remove the watermark.
2) DeletingByArea:
This involved removing objects with a small area,
where the parameter is the proportion of the tile area
used as a threshold for the area of objects. This
removal can be done naturally or maliciously.
3) DeletingLayers
Removal of entire MVT layers (the parameter is
the proportion of layers to be removed). It is a natural
distortion that simulates the theft of part of the data
related to some layers (if the rest of the layers are not
of interest to the attacker).
4) SeparationByGeometryType
Separation by geometry type: keep only point,
only line, or only polygonal features. It can also be
natural. Has no parameters.
5) AddingNewObjects
Adding new objects to the map (the parameter is
the number of new objects added in each layer). New
objects have random geometry; the number of points
is also random and depends on the geometry type (1
for points; from 2 to 100 for polylines; from 5 to 500
for polygons). It is a natural distortion simulating the
addition of an attacker's objects to the map after its
theft.
6) ShiftingPoints
Shift geometry points to one of the 4 adjacent cells
in the 𝑀𝑎𝑝 matrix (the parameter is the proportion of
all shifted points). Simulates an artificial action of an
attacker to remove the watermark.
Figures 4-6 show examples of map distortions for
different 𝑣𝑎𝑙𝑢𝑒𝑠 , as well as the corresponding
deviation metrics and the accuracy of watermark
extraction. All distortions were tested for various
combinations of the watermarking parameters.
Before presenting the main results of this
investigation, it should be noted that version 2 of the
information extraction algorithm proved to be less
robust to all distortions, as shown in Tables 2-3.
Table 2 provides a summary of the watermark
robustness investigation for version 1 of the
extraction algorithm. Numbers 1-6 in column headers
correspond to distortion indices, while data in rows
differ in the strength of distortions. For the
SeparationByGeometryType distortion (column 4),
the rows correspond to using only polygons, only
polylines, and only point features, respectively. Table
3 is similar to Table 2 but shows the results obtained
for version 2. It is evident from the tables that version
1 is more robust. The following embedding
parameters were used in this study: 𝑘=0.6, 𝑇

=
0.4 , 𝑇

=5, 𝑝=1, 𝑞=2, 𝑁

=5, 𝑟=20, 𝑀=
10.
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
256

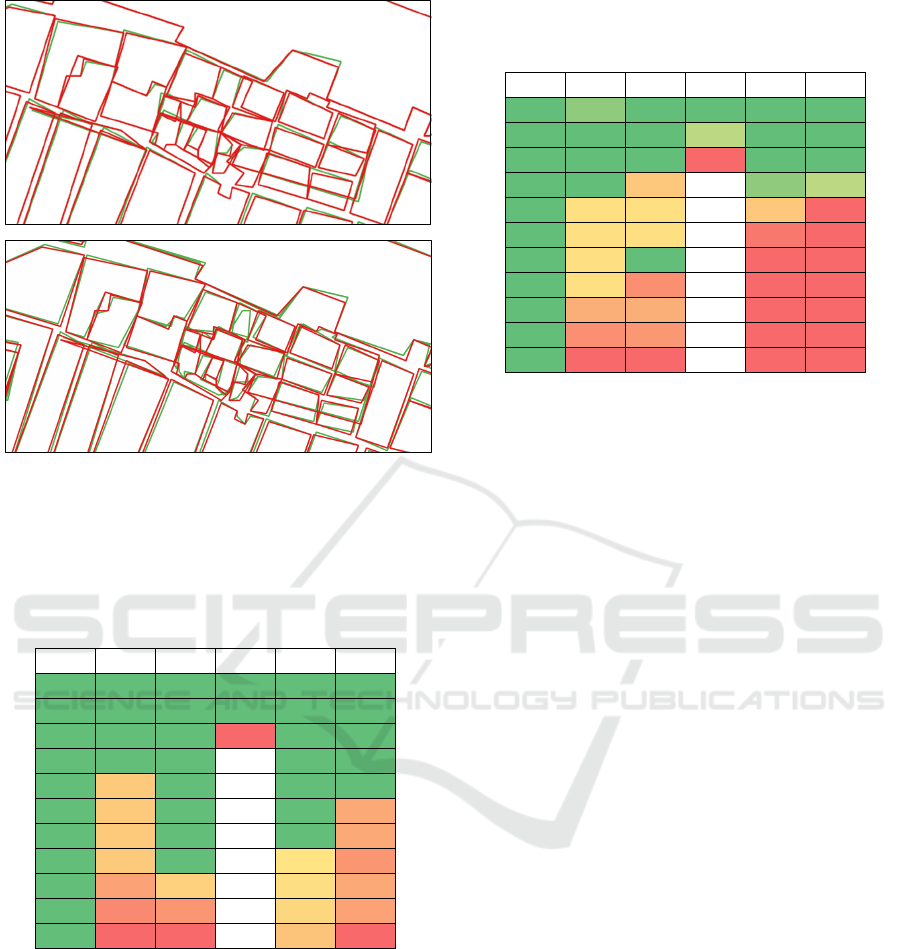
Figure 6: The effect of the ShiftingPoints attack (zoomed
tile fragments) at 𝑣𝑎𝑙𝑢𝑒 = 0.1 (upper, hausdorff: 0.957,
Fréchet: 0,944) and 𝑣𝑎𝑙𝑢𝑒 = 0.6 (lower, hausdorff: 0.949,
Fréchet: 0.948). Watermark extraction accuracy: 1 and 0.2.
Table 2: Color map representing the watermark robustness
against several distortions (columns) with several strength
values (rows) (extraction algorithm version 1).
1 2 3 4 5 6
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 0 1 1
1 1 1 - 1 1
1 0.75 1 - 1 1
1 0.75 1 - 1 0.5
1 0.75 1 - 1 0.5
1 0.75 1 - 0.95 0.35
1 0.45 0.8 - 0.9 0.5
1 0.25 0.35 - 0.85 0.45
1 0 0 - 0.7 0
In view of the large volume of studies conducted,
we will first present general conclusions based on
their results, and then we will delve in more detail into
some individual studies. To simplify, all distortion
parameters will be denoted as 𝑣𝑎𝑙𝑢𝑒, since it is clear
from the name of the distortion what value we are
talking about.
1) ReducingNumberOfPoints has almost no effect
on extraction accuracy even with severe geometric
distortions. Accuracy becomes less than 1 only when
𝑣𝑎𝑙𝑢𝑒 < 0.01.
Table 3: Color map representing the watermark robustness
against several distortions (columns) with several strength
values (rows) (extraction algorithm version 2).
1234 5 6
1 0.95 1 1 1 1
1 1 1 0.9 1 1
1 1 1 0 1 1
1 1 0.6 - 0.95 0.9
1 0.75 0.75 - 0.6 0
1 0.75 0.75 - 0.1 0
1 0.75 1- 0 0
1 0.75 0.25 - 0 0
1 0.45 0.45 - 0 0
1 0.25 0.3 - 0 0
1 0 0- 0 0
2) DeletingByArea. With 𝑣𝑎𝑙𝑢𝑒 < 0.4, extraction
accuracy equals 1 almost always, except for cases
with large 𝑁

and small 𝑟. But since 𝑣𝑎𝑙𝑢𝑒 = 0.4 is
the proportion of the area that cannot be considered
insignificant, we can conclude that the watermark is
sufficiently resistant to this distortion.
3) DeletingLayers. The quality values are not very
good in the case of this distortion, because random
layers are removed without taking into account the
number of objects and points. However, almost
always we have 𝑎𝑐𝑐𝑢𝑟𝑎𝑐𝑦 ≥ 0.9 at 𝑣𝑎𝑙𝑢𝑒  0.5 ,
which is a very good result. In practice, if necessary,
it is possible to further increase the robustness against
this distortion by embedding the watermark in
separate layers independently.
4) SeparationByGeometryType. The watermark
robustness to this distortion largely depends on the
distribution of points across the different geometry
types. Since there are relatively few point objects in
the test tiles, removing all polyline and polygon
objects leads to the destruction of the watermark.
However, for other types of geometry, the watermark
can be extracted with high accuracy. As with the
previous distortion, the robustness to
SeparationByGeometryType can be easily increased
by embedding separate watermarks for different
geometry types.
5) AddingNewObjects.
On average, when around 40 new objects are
added to each layer, the extraction accuracy begins to
decrease linearly. However, this drop can be
significantly mitigated by using high values of 𝑘
and 𝑟.
6) ShiftingPoints. This is a targeted attack
designed to exploit weaknesses in the developed
method, and therefore it has a greater effect compared
to more natural attacks. However, the impact of this
Vector Tile Geospatial Data Protection Using Quantization-Based Watermarking
257

distortion can be reduced by selecting appropriate
watermark embedding parameters. For example, it
was found that using 𝑘=1 and 𝑇

=0.5, makes it
possible to achieve the absolute watermark extraction
accuracy for 𝑣𝑎𝑙𝑢𝑒 < 0.5.
Thus, we can conclude that the proposed
watermark embedding method can be configured to
be highly robust to distortions 1-4 for any 𝑣𝑎𝑙𝑢𝑒 and
to distortions 5-6 with an average level of 𝑣𝑎𝑙𝑢𝑒𝑠.
Such results make the proposed method very
attractive for practical use.
5 CONCLUSIONS
In this paper, we proposed a watermarking method to
protect geodata in the Mapbox Vector Tile (MVT)
format against theft. Despite its popularity in web
mapping services due to its efficient storage and fast
rendering, the vector nature of the MVT format
makes it vulnerable to theft by attackers. The method
proposed in the paper protected MVT data with a
digital watermark that was based on the re-
quantization of point coordinates of object geometry.
The method could be adjusted using several
parameters to balance the robustness of the digital
watermark to map distortions and the error introduced
when embedding.
A series of experiments were performed to test the
robustness of the method against various distortions,
including the removal of objects and layers, reduction
in the number of points, adding new objects, and
shifting some points in the tile geometry. We found
that with a proper choice of watermark parameters,
the proposed method could achieve a 100%
watermark extraction accuracy for all bits of the built-
in watermark, even with a reasonable level of the
listed distortions that did not lead to a loss of
significance of the protected geodata.
Planned areas for further work include further
improvement and deeper investigation of the
proposed method.
ACKNOWLEDGEMENTS
This study was supported by Russian Science
Foundation, project 22-71-10097. https://rscf.ru/en/
project/22-71-10097/.
REFERENCES
Alt, H., & Guibas, L. J. (2000). Discrete Geometric Shapes:
Matching, Interpolation, and Approximation. In J.-R.
Sack & J. Urrutia (Eds.), Handbook of Computational
Geometry (pp. 121–153). North-Holland.
Cao, L., Men, C., & Ji, R. (2015). High-capacity reversible
watermarking scheme of 2D-vector data. Signal, Image
and Video Processing, 9(6), 1387–1394.
Chen, B., & Wornell, G. (2001). Quantization Index
Modulation: A Class of Provably Good Methods for
Digital Watermarking and Information Embedding.
IEEE Transaction on Information Theory, 47(4), 1423–
1443.
Cox, I., Miller, M., Bloom, J., Fridrich, J., & Kalker, T.
(2008). Digital Watermarking and Steganography.
Elsevier.
Lee, S.-H., & Kwon, K.-R. (2013). Vector watermarking
scheme for GIS vector map management. Multimedia
Tools and Applications, 63(3), 757–790.
Mapbox Vector Tile Specification. (2023). Mapbox.
https://github.com/mapbox/vector-tile-spec (Original
work published 2014)
Netek, R., Masopust, J., Pavlicek, F., & Pechanec, V.
(2020). Performance Testing on Vector vs. Raster Map
Tiles—Comparative Study on Load Metrics. ISPRS
International Journal of Geo-Information, 9(2), 101.
Peng, Y., Lan, H., Yue, M., & Xue, Y. (2018).
Multipurpose watermarking for vector map protection
and authentication. Multimedia Tools and Applications,
77(6), 7239–7259.
Ren, N., Zhu, C., Ren, S., & Zhu, Y. (2014). A Digital
Watermark Algorithm for Tile Map Stored by Indexing
Mechanism. In M. Buchroithner, N. Prechtel, & D.
Burghardt (Eds.), Cartography from Pole to Pole:
Selected Contributions to the XXVIth International
Conference of the ICA, Dresden 2013 (pp. 79–86).
Springer.
Vybornova, Y., & Sergeev, V. (2020). Copyright Protection
Method for Vector Map Data. In M. S. Obaidat (Ed.),
E-Business and Telecommunications (pp. 180–202).
Springer International Publishing.
Wallner, A. G., Piechl, T., Paulus, G., & Anders, K.-H.
(2022). Open source vector tile creation for spatial data
infrastructure applications. AGILE: GIScience Series,
3, 1–7.
Yu, E. G., Di, L., Rahman, Md. S., Lin, L., Zhang, C., Hu,
L., Shrestha, R., Kang, L., Tang, J., & Yang, G. (2017).
Performance improvement on a Web Geospatial service
for the remote sensing flood-induced crop loss
assessment web application using vector tiling. 2017
6th International Conference on Agro-Geoinformatics,
1–6.
Zhang, H., Du, M., Huang, W., Ding, L., Tang, D., & Jiang,
J. (2022). Research of the vector tile construction
technology based on Apache Sedona. ISPRS Archives,
XLIII-B4-2022, 639–6
GISTAM 2023 - 9th International Conference on Geographical Information Systems Theory, Applications and Management
258