Incremental Reliability Assessment of Large-Scale Software via

Theoretical Structure Reduction

Wenjing Liu

1,2

, Zhiwei Xu

, Limin Liu

and Yunzhan Gong

College of Data Science and Application, Inner Mongolia University of Technology, Hohhot 100080, China

State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications,

Beijing 100876, China

Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China

Keywords:

Large-Scale Software, Incremental Reliability Assessment, Structure Sequentialization, Theoretical

Reduction, Importance Sampling Based Reliability Assessment.

Abstract:

Problems of software quality assurance and behavior prediction of large-scale software systems have high

importance due to the fact that software systems are getting more prevalent in almost all areas of human

activities, and always include an large number of modules. To continuously offer signiﬁcant changes or major

improvements over the existing system, software upgrading is inevitable. This involves additional difﬁculty

to assess reliability and guarantee the quality assurance of the large-scale system. The existing reliability

assessment methods cannot continuously yet effectively assess the software reliability because the program

structure of the software is not taken into account to drive the assessment process. Thus, it is highly desired to

estimate the software reliability in an incremental way. This paper incorporates theoretical sequentialization

and reduction of the program structure into sampling-based software reliability evaluation. Speciﬁcally,

we leverage importance sampling to evaluate reliability rates of sequence structures, branch structures and

loop structures in the software, as well as transition probabilities among these structures. In addition, we

sequentialize program structures to support the aggregation of reliability assessment results corresponding to

different structures. Finally, a real-world case study is provided as a practical application of the proposed

incremental assessment model.

1 INTRODUCTION

Large-scale software is a term used in ﬁelds

including system engineering, computer science,

data science and artiﬁcial intelligence to refer to

software intensive systems with a large amounts of

hardware, lines of source code, numbers of users,

and volumes of data. The obstacles of large-scale

systems in defect discovery and reliability

assessment have become the crucial factors that

affect the application of modern software systems in

more ﬁelds. In October 2018 and March 2019, the

Boeing 737 Max 8 crashed twice due to the design

defects in its software system, causing 346 people

dead (TRAVIS, 2019). Similar system failures

caused by software defects always lead to serious

accidents that result in death, injury, and large

ﬁnancial losses. To evaluate the risk of system

failures, software reliability is introduced and

represents the probability of software running

without failure in a given time and under given

conditions (Committee et al., 1990). During the

process of software development, reliability

assessment helps project managers to evaluate the

reliability level of the product, so as to make

scientiﬁc management decisions on the software

development. On the other hand, users can also have

a quantitative understanding about the quality-related

factors of software products. Therefore, the research

of software reliability assessment has important

theoretical and practical value. Without software

reliability assessment, the increasingly pervasive use

of software may bring about more frequent and more

serious accidents. Measuring and predicting software

reliability has become vital in software

engineering (Bistouni and Jahanshahi, 2020).

Reliability assessment solutions can be roughly

divided into black-box methods and white-box

methods (Go

seva-Popstojanova and Trivedi, 2001).

Regard as a black-box, software is studied while only

Liu, W., Xu, Z., Liu, L. and Gong, Y.

Incremental Reliability Assessment of Large-Scale Software via Theoretical Structure Reduction.

DOI: 10.5220/0012052600003538

In Proceedings of the 18th International Conference on Software Technologies (ICSOFT 2023), pages 241-248

ISBN: 978-989-758-665-1; ISSN: 2184-2833

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

241

the interaction between the software and the external

environment is considered. These methods rely

heavily on the collection of test data and failure data.

In some safety-critical application ﬁelds, such as

aviation, aerospace, etc., failure data is scarce or

even non-existent, and thus it is impossible to

accurately estimate the reliability of such systems.

On the other hand, to assess the reliability of the

software in an accurate way, the white-box methods

combine the dynamic information of the software

structure with the failure behavior of the software.

These methods quantitatively analyze the degree of

dependence among modules and determine the

crucial parts in the software. Considering the

complex dependence among modules of a large-scale

software, the existing white-box reliability

assessment methods(Gokhale, 2007) still need to be

improved to enhance assessment efﬁciency.

To speed up reliability assessment of large-scale

software systems and discover the potential failure

risk before it gets too late, an incremental assessment

method is highly desired. The white-box evaluation

process relies on the run-time sequence of modules

or statement blocks, and this sequence is determined

by both of the program structure and the input data of

the software. In sight of this fundamental principle,

we study the essential structures of a software to

guide the reliability assessment process. In this way,

the reliability rates of software modules or statement

blocks are aggregated in terms of different run-time

sequences. Since this aggregation process is

performed according to a determined sequence, we

can update each part of the reliability assessment

result without any intervene of the others. The

primary contributions of this work are listed as

follows.

Contributions:

• Base on importance sampling, we propose a

scheme to efﬁciently estimate reliability unit

parameters (node reliability rate and transition

probability). In this way, it becomes feasible to

study software reliability in a modular way.

• We design a structural reduction and reliability

assessment model to aggregate unit parameters

with respect to three types of control structures.

Moreover, an incremental assessment updating

algorithm is developed to update the assessment

result without model reconstruction.

• The proposed method can effectively assess

software reliability in an incremental way (a

real-world software module is provided as a use

case in a technical report with the same title).

2 RELATED WORKS

Software reliability is an essential subject in the

development stage, which is a combination of

software engineering and reliability engineering, and

can be roughly divided into black-box methods and

white-box methods.

The black-box software reliability methods only

concern the functionality of software without an

attempt to understand its internal structure.

Generally, reliability analysis is conducted mainly

depending on failure data, assuming a parametric

model of failure data. In this way, the statistical

models (Pressman, 2005) and the software reliability

growth models(SRGM) (Stringfellow and Andrews,

2002) are proposed. Kumar et al. proposed an Ideal

solution for the selection of a suitable SRGM and

applied it for optimal selection and ranking of

SRGMs (Kumar et al., 2021). With considerations of

the phenomenon of imperfect debugging, varieties of

errors and change points during the testing period,

Huang et.al extend the practicability of

SRGMs (Huang et al., 2022). Black-box-based

models need to continuously collect run-time failure

data to estimate the software reliability in different

scenarios. Actually, a failure occurs when the user

perceives that the software has ceased to deliver the

expected result with respect to the speciﬁc input

values. Considering the complex structure of

large-scale systems, the presence of errors in the

large-scale systems does not always lead to system

failures. We have little or no opportunity to observe

such problems and collect failure data, and cannot

achieve an accurate estimation of software reliability

in practice.

White-box methods (Hsu and Huang, 2011;

Bistouni and Jahanshahi, 2020) are proposed and

leverage the hierarchical structure of modular

software systems to access software reliability. The

primary objective of white-box models has been

applied to obtain the software reliability among

modular interactions in large-scale systems.

Compared with the black-box-based software

reliability growth model, this type of

white-box-based method has two advantages: (1)

Considering the internal structure information of the

software, it can evaluate the system more reasonably

and accurately; (2) The system reliability can be

evaluated in the early stage of software development,

and errors can be found. Littlewood (Littlewood,

1979) constructed a software structure model

comprised of a ﬁnite number of states developed by a

semi-Markov process. Hsu (Hsu and Huang, 2011)

proposed an adaptive framework to incorporate path

ICSOFT 2023 - 18th International Conference on Software Technologies

242

testing into reliability estimation for software

systems. Though more accurate assessment has been

achieved, lacking of the structural parameter

reduction mechanism in terms of different basic

program units, the existing white-box-based

reliability methods need to reconstruct the model

from the very beginning to update the reliability

assessment result. To efﬁciently analyze and update

the reliability evaluation results of modern

large-scale software systems, an incremental

estimation method is highly desired.

3 PROBLEM FORMULATION

The software system can be deconstructed with

modules, and these modules may be further divided

into sub-modules. Exchanging of control among

modules is related to the hierarchical structure of the

logical module dependencies. Assuming the modules

and their sub-modules have their independent

functions, this type of dependencies can be modeled

as a Markov process (Cheung, 1980; Wang et al.,

2006). Thus, we assume that the software system can

be designed in a structural or modular way so that

composition or decomposition into its constituent

units is possible (Myers et al., 2011; Shooman, 1976;

Jorgensen, 2013). Due to the complex characteristics

of large-scale software systems, the reliability of

software systems depend on not only the failure

behavior of individual module but also the relations

among different modules. To formulate the impact of

these two facts, the related concepts are deﬁned

below. First of all, the control ﬂow graph is used to

model the dependencies of modules yet the overall

software system.

Deﬁnition 1 (Control ﬂow graph). The control ﬂow

graph of a unit (a function or a statement block) can

be represented as G =< N,E,N

>, where

N = {N

|i = 1,2,. . . ,n} is a set of nodes, node N

corresponds to a unit in the software system.

E = {E(i, j)|i, j = 1,2,. . . ,n} is a set of directed

edges, and edge E(i, j) corresponds to the control

ﬂow from node N

to node N

, where N

is the entry

node of software system, and N

is the exit node of

the software system.

To enable reliability assessment based on a

control ﬂow graph, parametric estimations of node

reliability and transition probability among nodes

should be performed in advance. Among them, node

reliability indicates the probability that a node

provides the correct output. Meanwhile, the

transition probability expresses the characteristics of

different branches in the software structure (Yacoub

et al., 2004).

Deﬁnition 2 (Node reliability rate). The reliability

rate of node N

is R

, which represents the probability

that node N

performs the correct output, and

transfers to the next node N

, R

∈ (0,1].

Deﬁnition 3 (Transition probability). Edge E(i, j) ∈

G corresponds to a transition probability P

i, j

between

node N

and node N

. If P

i, j

= 0, it is impossible that

node N

is performed after node N

. Otherwise, P

i, j

∈

(0,1], and N

is followed by node N

by probability

i, j

. The sum of the transition probabilities regarding

to predecessor node N

is 1, that is,

∑

i6= j

i, j

= 1.

In summary, our proposed method is based on the

following assumptions:

• All program units are physically independent of

each other. Modiﬁcation of one unit has no

impact on others. This assumption implies that

we can independently design, implement, and

test each unit and module in a complex

system (Gokhale, 2007; Go

seva-Popstojanova

and Trivedi, 2001; Gokhale and Trivedi, 2002).

Thus, the faults in each unit are also independent

from each other. Moreover, each discovered

defect can be easier to be isolated and ﬁxed in a

speciﬁed module during the processes of defect

detection and correction.

• The transfer of control between units can be

described by a Markov process. The Markov

process depends on the structure of the software

system so that it is helpful in modeling the

execution between the functional units and

branching characteristics (Gokhale, 2007). This

assumption also indicates that the next unit to be

executed depends only on the present unit and is

independent of the past history. Without loss of

generality, in this paper we only focus on the

single-input and single-output program graph (Lo

et al., 2002; Lo et al., 2003; Lo et al., 2005).

4 INCREMENTAL SOFTWARE

RELIABILITY ASSESSMENT

To facilitate the incremental software reliability

assessment, we analyze software structures and

aggregate the reliability assessment results on

different structures of the software. It has been

proved by theory and practice that no matter how

complicated a software system is, it can be

deconstructed into three types of basic control

Incremental Reliability Assessment of Large-Scale Software via Theoretical Structure Reduction

243

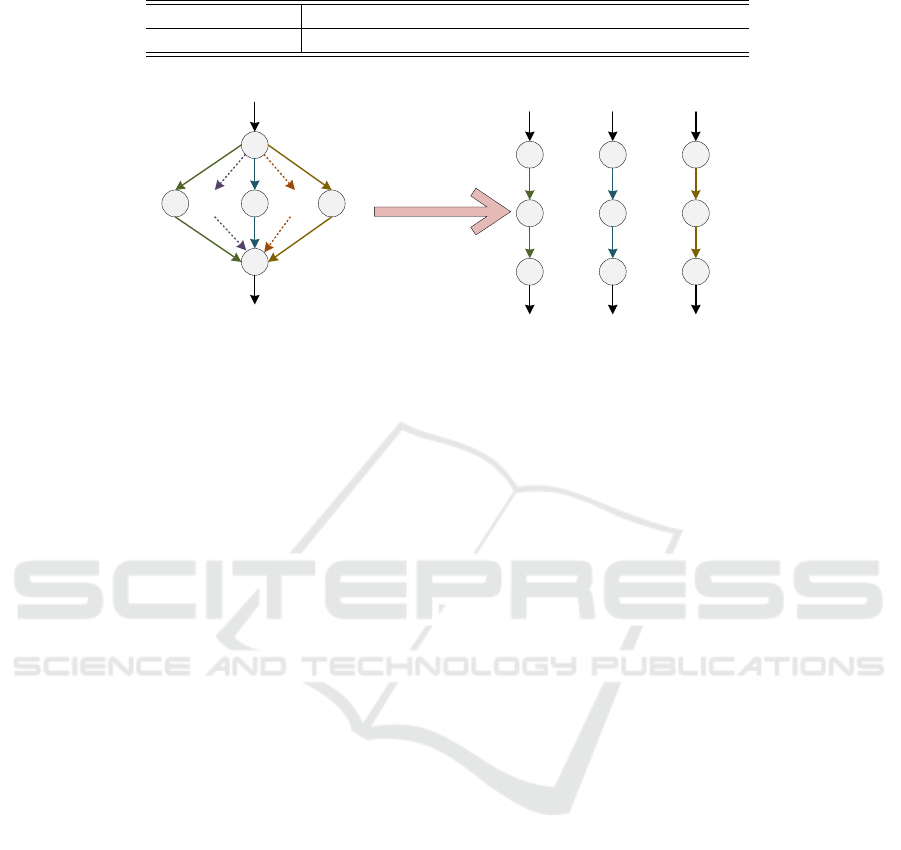
Table 1: CMMI level and the corresponding defect number per thousand lines.

CMMI level level 1&others level 2 level 3 level 4 level 5

#Defects/KLOC 11.95 5.52 2.39 0.92 0.32

Nn-1NiN2

P1,2

P1,n-1

P1,i

Pi,n

P2,n

Pn-1,n

… …

N1 N1

N2 Ni Nn-1

Nn Nn Nn

P1,2

P2,n

P1,i

Pi,n

P1,n-1

Pn-1,n

…

Sequentialization

Seq[1] Seq[i] Seq[n-1]

R1 R1

Rn Rn Rn

Rn-1

Figure 1: Sequentialization of the branch structure.

structures, i.e., sequence structure, branch structure

and loop structure. These structures regulate the

order in which node (i.e., program statements) in a

software are executed. Therefore, we analyze the

software reliability in terms of different control

structures. Speciﬁcally, we incorporate the control

ﬂow graph of the software into this structural

analysis process to represent different structures.

Through traversing the control ﬂow graph, the

parameters related to reliability assessment in terms

of different structures are marked in the the control

ﬂow graph and aggregated to achieve the reliability

assessment result of the entire software. Ultimately,

if the statement block included in a node has been

upgraded, the reliability rate corresponding to this

node in a control structure should be updated.

Therefore, an incremental assessment process is

highly desired.

4.1 Node Reliability Rate and

Transition Probability

Nodes and edges are the essential elements of a

control ﬂow graph, and correspondingly, the node

reliability and transition probability between nodes

are required for the reliability assessment process

based on the control ﬂow graph. The node reliability

rate depends on the probability that this node can be

executed correctly to obtain the intended output.

Theorem 1 (Necessary Condition for Execution

Failure). ∀s is a node (statement block), X is the

input set of s. When a failure occurs, ∃x ∈ X, the

corresponding output of s, s(x), is not the same as

the intended output ˆs(x), that is s(x) 6= ˆs(x). This is a

necessary condition for execution failure.

The proof of Theorem 1 follows by inspection.

On the other hand, the transition probability

between two adjacent program nodes indicates the

probability that a successor node will be performed

after a predecessor node. The probability is equal to

”1” unless there exists a branch condition involved in

the predecessor node. In this case, the input domain

of the predecessor node should be taken into

consideration to determine which successor node

will be performed. It is in appearance that the

estimation of node reliability rates or transition

probabilities relies on the input domain of the

predecessor node. Considering the input domain is

always quite large and various, we leverage sampling

technology on the path-based test suite to approach

efﬁcient estimation of node reliability rates and

transition probabilities.

Though the existing theories, e.g, Interval

arithmetic, etc., facilitate test data generation, all test

data for a speciﬁc node on the test path cannot be

completely determined. Therefore, their distribution

is under-determined. Since the data that can accuse a

failure is quite rare, most of sampling technology

cannot cover all possible test data and evaluate their

distribution comprehensively. If the focus is on a

problem related to system reliability, the probability

of rare events is better approximated with appropriate

proposals. Even if a large number of samples have

been drawn, it is possible that none of them will

accuse a failure or a jump to the branch determined

by a special condition. To tackle this problem, we

collect test data of every node (statement block), and

then leverage importance sampling to draw samples

from the collected test data. As a widely applied

system simulation technology, importance

sampling (Tokdar and Kass, 2010) estimates

ICSOFT 2023 - 18th International Conference on Software Technologies

244

P1,2

P2,3

P3,n

1,2

P2,3

P3,2

P2,3

P3,n

…

1,2

P2,3

P3,2

P3,n

P1,2

P2,3

P3,2

P2,3

P3,n

P1,2

P2,3

P3,2

P2,3

P3,n

P2,3

P3,2

Seq[0] Seq[1] Seq[2]

R1 R1 R1

R2 R2

Expansion

Sequentialization

b. branch structurea. loop structure c. sequence structure

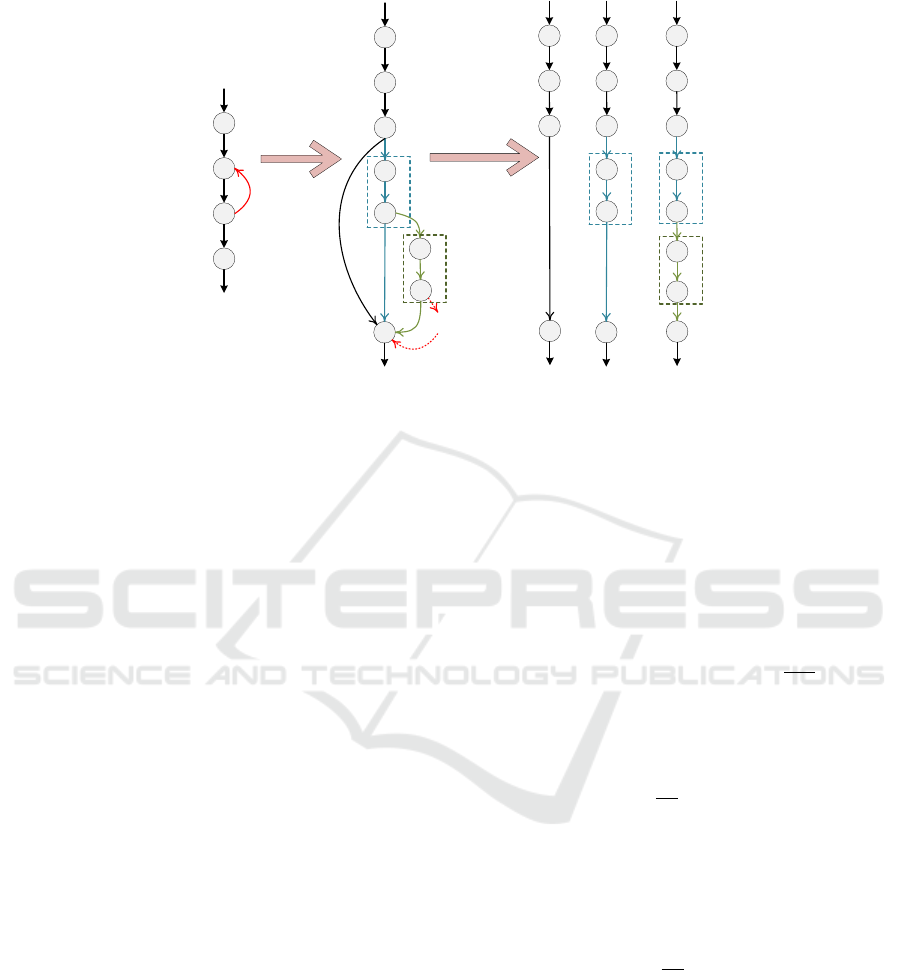
Figure 2: Sequentialization of the loop structure.

properties of a distribution, while only having less

samples generated from a proposal distribution than

the distribution of interest. Targeting to sampling

different types of test data comprehensively, a

proposal distribution is involved, with respect to

which among the test data are drawn as samples. The

density function of the proposal distribution is q(x).

According to importance sampling theory, q(x)

should dominate the density function of the

distribution of test data, p(x), and consequently, we

can cover the distribution of test data with less

samples. That means, q(x) = 0 ⇒ p(x) = 0.

To cover rare events during the sampling process,

we take a Poisson distribution, Pois(λ), as the

proposal distribution. λ is determined according to

the CMMI level of the software designer. The CMMI

model is used to assess the maturity of an designer’s

ability and to provide guidance on improving

processes, with a goal of the advanced software

systems. There is a relation between CMMI level l

and the corresponding defect number per thousand

lines of code, namely, dKLOC (see

Table 1) (CMMI-Institute, 2022). To dominate the

density of the distribution of test data, we conﬁgure λ

with a value lower than the corresponding dKLOC,

equal to

β × klDe f ects(l) × #statements (1)

where β is a constant less than 1, klDe f ects() is a

function to look up the defect number per thousand

lines of code, l is the CMMI level corresponding to

the software designer, and #statements is the number

of statements in this node.

The sampling process consists of four steps:

• Collect test data used to test a node (statement

block), and insert these data into a test suite X,

until their distribution converge to a stable

density, p(X ).

• Draw samples from X with respect to Pois(λ), n

samples and the density function values of these

samples are obtained, i.e., x

,...,x

, and

q(x

),...,q(x

• Weight the sample x

with w(x

) =

p(x

)

q(x

)

,i ∈ [1, n].

• Using the samples and weights, the reliability

rates and transition probabilities can be

approximated by a self-normalized estimator as

` =

∑

k=1

f (x

), (2)

where

Z = (1/n)

∑

k=1

is an unbiased estimator

of Z =

p(x)dx (Bugallo et al., 2017).

The detailed estimation process of node reliability

is formulated as the follows:

= 1 −

∑

k=1

I(x

), (3)

where I(x

) is an indicator function that takes the

value 1 if the output of statement block s

corresponding to test data x

is not the same as the

intended output ˆs(x

), and 0 otherwise. Statement

block s constitute node N

. That is

I(x

) =



1 s(x

) 6= ˆs(x

)

0 s(x

) = ˆs(x

)

Similarly, the transition probabilities from the i-th

node to the j-th node can be calculated as the

Incremental Reliability Assessment of Large-Scale Software via Theoretical Structure Reduction

245

following:

i, j

∑

k=1

i, j

) (4)

Another indicator function I

i, j

) is used, which

outputs 1 if the satisﬁed condition of s indicates a

jump to the j-th node, and 0 otherwise.

4.2 Sequentialization and Reliability

Evaluation of Control Structures

To efﬁciently analyze the reliability of a large-scale

software system, we need to simplify its complex

structure. To achieve that, we traverse and

sequentialize program units by using a hierarchical

approach (Hsu and Huang, 2011). The sequence

structure is the basic control structure for a program.

The program units (statement blocks) are executed

according to their sequence. In a modular way, a

program can be written using the sequence

structures, and thus, with respect of the concepts

introduced in Section 3, its reliability rate can be

computed as the following,

R = R

∏

i=2

∏

j=2

j−1, j

(5)

where R

represents the reliability rate of the i − th

node (statement block), and P

i, j

is the transition

probability between the i − th node and the j − th

node.

The other two types of control structures, branch

structures and loop structures.They also only have an

entry node N

and an exit node N

. Among them, the

branch structure determines the execution sequence

of different branches according to a condition. The

loop structure is an instruction that repeats until a

speciﬁed condition is reached. In order to simplify

these program structures, we sequentialize branch

structures and loop structures to sequence structures,

which is the preliminary work of structural reduction.

As shown in Fig. 1, each of these branch structures

can be transformed into a sequence structure through

sequentialization. Only if all branches are reliable, the

entire structure is reliable. Therefore, the reliability of

the branch structure is calculated by considering the

reliability rates of all branches.

Bran

n−2

∏

i=1

Seq[i]

(6)

where R

Bran

represents the reliability rate of the

branch structure, R

Seq[i]

represents the reliability rate

of the i −th sequence structure.

Algorithm 1: Structural reduction and

reliability assessment.

Input : control ﬂow graph G

Output: reliability rate R

1 iterate(G,P) /* P is the probability

transiting to the module

corresponding to G. */

2 state = next(G); // A statement block

3 sstate = next(G); // Next statement block

4 while sstate belongs to a sequence structure

5 R = R × nr(state)

; /* Function nr is

used to estimate node reliability

rates */

6 P = P ×t p(state,sstate);/* Function tp

is used to estimate transition

probabilities */

7 mark(state,P); /* Mark node

reliability rates & transition

probabilities */

8 state = sstate;

9 sstate = next(G);

10 R = R × nr(state)

;

11 pstate = state;

12 state = sstate;

13 sstate = next(G);

14 if state belongs to a branch structure then

15 foreach G

in seq(subGraph(G,state)) do

// Iterate sequentialization

results of the rest part of G

16 R = R × iterate(G

,P);

17 mark(state,P);

18 if state belongs to a loop structure then

19 mark(state,P);

20 P

t p(pstate,state)

1−t p(state,sstate)t p(ssstate,state)

;

21 P

t p(pstate,state)×t p(state,sstate)

1−t p(ssstate,state)t p(state,sstate)

;

22 R = R × nr(state)

iterate(subGraph(G, state), P)

;

23 return R

A loop structure executes iterative statements or

procedures, according to a condition or an iteration.

Whilst the condition is true or the iteration has not

stopped, the loop body will be carried out

repetitively. In sight of the run-time process of the

loop structure, a loop structure can be expanded into

a branch structure. For each branch of this structure,

the loop body is executed different number of times.

In this way, this loop structure is equivalent to one

branch structure. As illustrated in Fig. 2.b, when the

ICSOFT 2023 - 18th International Conference on Software Technologies

246

Loop

= (R

× R

1×P

1,2

× R

1×P

1,2

×P

2,3

× R

1×P

1,2

×P

2,3

×P

3,n

)

× (R

1×P

1,2

×P

2,3

×P

3,2

× R

1×P

1,2

×P

2,3

×P

3,2

×P

2,3

× R

1×P

1,2

×P

2,3

×P

3,2

×P

2,3

×P

3,n

)

× (R

1×P

1,2

×(P

2,3

×P

3,2

)

× R

1×P

1,2

×P

2,3

×(P

3,2

×P

2,3

)

× R

1×P

1,2

×P

2,3

×(P

3,2

×P

2,3

)

×P

3,n

)

× ...

× (R

1×P

1,2

×(P

2,3

×P

3,2

)

× R

1×P

1,2

×P

2,3

×(P

3,2

×P

2,3

)

× R

1×P

1,2

×P

2,3

×(P

3,2

×P

2,3

)

×P

3,n

)

= R

× R

∑

i=0

1,2

×(P

2,3

×P

3,2

)

× R

∑

i=0

1,2

×P

2,3

×(P

3,2

×P

2,3

)

× R

∑

i=0

1,2

×P

2,3

×(P

3,2

×P

2,3

)

×P

3,n

m→∞

= R

× R

1,2

1−P

2,3

×P

3,2

× R

1,2

×P

2,3

1−P

3,2

×P

2,3

× R

1,2

×P

2,3

×P

3,n

1−P

3,2

×P

2,3

(7)

Algorithm 2: Incremental updating of the

assessment result.

Input : G, R, state, state

Output: R

1 < NR,NT P >= search(G,state);// Search

statement blocks in G

2 NR

= nr(state

);// Get the updated

reliability rate

3 R = R × (

)

NT P

;

4 return R

condition in node N

becomes false, the exit node N

of the loop structure is executed, and the loop body

will not be executed again. Otherwise, loop body N

will be executed repeatedly. The blue box and green

box indicate the node sequences for the ﬁrst and

second time when the loop body is executed.

Ultimately, distinct sequence structures are obtained.

When the number of loop times approaches inﬁnity,

the reliability of the loop structure can be executed as

follows:

4.3 Incremental Reliability Evaluation

with Structural Reduction

Based on the above sequentialization results, we can

incorporate the control ﬂow graph of the software

into an incremental structural reduction and

reliability analysis process. Through traversing the

control ﬂow graph, three basic program control

structures are identiﬁed and sequentialized.

Meanwhile, their reliability rates are evaluated (see

Section 4.2). The propsed incremental reliability

evaluation process includes 6 steps:

• The parameters (node reliability rates and

transition probabilities) related to reliability

assessment in terms of different structures are

estimated and marked on the control ﬂow graph.

• Since the control ﬂow graph accurately

represents the ﬂow inside of nodes (statement

blocks), we traverse the control ﬂow graph of the

software to look up control structures included in

the software.

• With respect to statement blocks included every

structure, their node reliability rates and

transition probabilities to the successors are

estimated through importance sampling and

marked in the the control ﬂow graph.

• Sequentialize the statement blocks in every

structure in terms of the structure type (i.e.,

sequence, branch or loop), and aggregate the

node reliability rates of these blocks.

• Reduce different structures and obtain the

reliability assessment result of the software

(detailed in Algorithm 1).

• If the reliability rate of a node has changed, taking

advantage of the node parameters marked in the

control ﬂow graph, the corresponding assessment

result can be updated according to Algorithm 2.

5 CONCLUSION

In this paper, a structure-based reliability assessment

model is proposed. We ﬁrst take importance

sampling to evaluate reliability rates of three types of

control structures in a software, as well as transition

probabilities among these structures. Then, we

reduce these structures while aggregating their

reliability rates to the overall assessment result of the

software. With a case study on a elevator system, it is

shown that the proposed model can give a promising

estimation of software reliability. In summary, we

can conclude that in an incremental way, the

proposed incremental assessment model is viable for

estimating reliability of a large-scale software

system. There exist more open theoretical issues

Incremental Reliability Assessment of Large-Scale Software via Theoretical Structure Reduction

247

about Structure Reduction for future research. For

instance, dependent faults may occur if the data

exchanges among distributed sub-systems, this

increase complexity of structure-based reliability

assessment.

ACKNOWLEDGEMENTS

This work was supported by the Basic Scientiﬁc

Research Expenses Program of Universities directly

under Inner Mongolia Autonomous Region,

Grant/Award Number: JY20220273.

REFERENCES

Bistouni, F. and Jahanshahi, M. (2020). Evaluation

of reliability in component-based system using

architecture topology. Journal of the Institute of

Electronics and Computer, 2(1):57–71.

Bugallo, M. F., Elvira, V., Martino, L., Luengo, D., Miguez,

J., and Djuric, P. M. (2017). Adaptive importance

sampling: The past, the present, and the future. IEEE

Signal Processing Magazine, 34(4):60–79.

Cheung, R. C. (1980). A user-oriented software reliability

model. IEEE transactions on Software Engineering,

(2):118–125.

CMMI-Institute (2022). White papers. Last accessed 21

January 2022.

Committee, I. S. C. et al. (1990). Ieee standard glossary

of software engineering terminology (ieee std 610.12-

1990). los alamitos. CA: IEEE Computer Society,

169:132.

Gokhale, S. S. (2007). Architecture-based software

reliability analysis: Overview and limitations. IEEE

Transactions on dependable and secure computing,

4(1):32–40.

Gokhale, S. S. and Trivedi, K. S. (2002). Reliability

prediction and sensitivity analysis based on software

architecture. In 13th International Symposium on

Software Reliability Engineering, 2002. Proceedings.,

pages 64–75. IEEE.

seva-Popstojanova, K. and Trivedi, K. S. (2001).

Architecture-based approach to reliability assessment

of software systems. Performance Evaluation, 45(2-

3):179–204.

Hsu, C.-J. and Huang, C.-Y. (2011). An adaptive reliability

analysis using path testing for complex component-

based software systems. IEEE Transactions on

Reliability, 60(1):158–170.

Huang, Y.-S., Chiu, K.-C., and Chen, W.-M. (2022).

A software reliability growth model for imperfect

debugging. Journal of Systems and Software,

188:111267.

Jorgensen, P. C. (2013). Software testing: a craftsman’s

approach. Auerbach Publications.

Kumar, V., Saxena, P., and Garg, H. (2021). Selection

of optimal software reliability growth models using

an integrated entropy–technique for order preference

by similarity to an ideal solution (topsis) approach.

Mathematical Methods in the Applied Sciences.

Littlewood, B. (1979). Software reliability model for

modular program structure. IEEE Transactions on

Reliability, 28(3):241–246.

Lo, J.-H., Huang, C.-Y., Chen, Y., Kuo, S.-Y., and Lyu,

M. R. (2005). Reliability assessment and sensitivity

analysis of software reliability growth modeling based

on software module structure. Journal of systems and

software, 76(1):3–13.

Lo, J.-H., Huang, C.-Y., Kuo, S.-Y., and Lyu, M. R.

(2003). Sensitivity analysis of software reliability

for component-based software applications. In

Proceedings 27th Annual International Computer

Software and Applications Conference. COMPAC

2003, pages 500–505. IEEE.

Lo, J.-H., Kuo, S.-Y., Lyu, M. R., and Huang, C.-Y.

(2002). Optimal resource allocation and reliability

analysis for component-based software applications.

In Proceedings 26th Annual International Computer

Software and Applications, pages 7–12. IEEE.

Myers, G. J., Sandler, C., and Badgett, T. (2011). The art of

software testing. John Wiley & Sons.

Pressman, R. S. (2005). Software engineering: a

practitioner’s approach. Palgrave macmillan.

Shooman, M. L. (1976). Structural models for software

reliability prediction. In Proceedings of the 2nd

international conference on Software engineering,

pages 268–280.

Stringfellow, C. and Andrews, A. A. (2002). An

empirical method for selecting software reliability

growth models. Empirical Software Engineering,

7(4):319–343.

Tokdar, S. T. and Kass, R. E. (2010). Importance

sampling: a review. Wiley Interdisciplinary Reviews:

Computational Statistics, 2(1):54–60.

TRAVIS, G. (2019). How the boeing 737 max disaster looks

to a software developer. Last accessed 21 January

2022.

Wang, W.-L., Pan, D., and Chen, M.-H. (2006).

Architecture-based software reliability modeling.

Journal of Systems and Software, 79(1):132–146.

Yacoub, S., Cukic, B., and Ammar, H. H. (2004).

A scenario-based reliability analysis approach for

component-based software. IEEE transactions on

reliability, 53(4):465–480.

ICSOFT 2023 - 18th International Conference on Software Technologies

248