A Music Programming Course for Undergraduate Music Conservatory

Students: Evaluation and Lessons Learnt

Marcella Mandanici

1 a

and Simone Spagnol

2 b

Music Conservatory “L. Marenzio”, Brescia, Italy

Iuav University of Venice, Venice, Italy

Keywords:

Computational Thinking, Music Programming, Technology Integration.

Abstract:

This paper introduces the content and organisation of a music programming course offered to undergraduate

Conservatory students in the spring of 2022. A number of evaluation procedures, including pre- and post-

course questionnaires and exercises, and a ﬁnal assignment have been administered by the teacher. Results

indicate an increased conﬁdence in the use of computers and programming, although some aspects of creativity

and computational thinking need further revision. The authors examine the course content in light of the results

obtained, discuss the followed approach, and make assumptions for the improvement of both course content

and assessment methods.

1 INTRODUCTION

According to G. R. Skuse (Skuse et al., 2017), algo-

rithmic thinking can beneﬁt scholars and students of

any discipline. If it is true that computer technology

has pervaded nearly every ﬁeld of knowledge (Bai-

ley and Stefaniak, 2002), the skill of solving a prob-

lem, of reducing a process into different steps, and the

connected rational reasoning are fundamental abil-

ities to be achieved during the training process of

the XXI century learners. This means that compu-

tational thinking must also be introduced in the cur-

ricula of arts and humanities students. Music beneﬁts

from more than a century of research and artistic pro-

ductions involving ﬁrst electrical and then electronic

technologies (Collins et al., 2013). Moreover - well

before the birth of electronic music - the basic mu-

sical structures such as intervals, scales, and tuning

systems, originated from mathematical and scientiﬁc

reasoning. Just think of Pythagoras, Kepler, and Eu-

ler, to cite only a few (Fauvel et al., 2006).

However, in spite of this meaningful background,

it is still difﬁcult to explain why having a short, lim-

ited but still important experience of music program-

ming is signiﬁcant for music Conservatory undergrad-

uate students. This is due to many factors.

Firstly, electronic music has been present in Ital-

https://orcid.org/0000-0003-1863-4178

https://orcid.org/0000-0002-9309-0871

ian music Conservatoires for more than 40 years, as

one of the earliest chairs of electronic music has been

assigned to Teresa Rampazzi

at the Conservatory of

Padua in 1972 (Zattra, 2000). But the heritage of

knowledge and the evolution of the taste in sound

linked to the practices of electronic music have not

managed to leave a small circle of adepts, thus by-

passing the great potential for renewal of these tech-

nologies. The ﬂaws of technology integration have

not reached the core of professional musical training

yet, drawing a strong separation between music tech-

nologies and all the other sectors of professional mu-

sic education (Bauer and Kenton, 2005).

Secondly, music editing software such as Sounda-

tion,

PreSonus,

or Reaper

have long since come

into common use among musicians both for music

production (Burgess, 2013) and pedagogical prac-

tice (Tobias, 2013). These software usually include

tens of loops, patterns and pre-recorded music chunks

that make music creation easy and fun. However, the

strong stylistic and commercial biases connected to

their use make these environments more ﬁt for stan-

dard music production rather than for a reﬂection on

the nature of musical structures and on the way they

Teresa Rampazzi (1914-2001) composer, pianist and

researcher, is one of the pioneers in electronic music in Italy.

https://soundation.com/

https://www.presonus.com/products/studio-one/

https://www.reaper.fm/

Mandanici, M. and Spagnol, S.

A Music Programming Course for Undergraduate Music Conservatory Students: Evaluation and Lessons Learnt.

DOI: 10.5220/0012056900003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 1, pages 387-396

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

387

can be generated by an algorithm. While music edi-

tors imply a certain knowledge of music technology,

this is not aimed at content transformation (Hamilton

et al., 2016) but rather at the optimisation of the pro-

duction process. On the contrary, mastering a music

algorithm may lead to unprecedented music creation

which depends on the understanding and manipula-

tion of music elements from scratch.

Thirdly, professional musicians usually consider

themselves extraneous to the processes of technology

integration or – at best – employ technology only if

it can better realise an already well known task, such

as recording a performance or printing a score. More-

over, with more than 40% of the curriculum devoted

to individual instrumental practice,

the acoustic in-

strument learner of an Italian conservatoire has little

time left for developing abilities such as creative and

critical thinking, collaboration, and communication.

2 THE MUSIC INFORMATICS

COURSE

For these reasons the content of the Music Informat-

ics course is devoted to learning some of the funda-

mental processes of music programming. The course

is held online on the Google Classroom

platform of

the Conservatory “L. Marenzio”, Brescia (Italy). It is

subdivided into 8 lessons, each lasting 3 hours. The

course gives 3 ECTS

, which are obtained without

grading but through an internal veriﬁcation.

2.1 Objectives

The course aims at offering a very basic music pro-

gramming experience to young musicians who have

possibly never seen computer programming in their

previous educational curriculum. There are several

positive values connected to this choice.

• Learning a programming language means enter-

ing a world where everything is governed by logi-

cal reasoning. This may be a complete novelty for

a student of humanities or arts.

• Music programming requires logical reasoning

about musical structures. This implies self-

awareness, critical thinking, and analytical abili-

ties. At the end it can produce demystiﬁcation of

See this study plan from the Brescia Music Conserva-

tory as an example, https://www.consbs.it/content/uploads/

2022/02/PDS-SINT-TRI-ARPA.pdf

https://edu.google.com.au/workspace-for-education/

classroom/

European Credit Transfer System

musical concepts and a deeper knowledge about

them.

• This experience may contribute to increase digital

literacy and computer familiarisation in students

who are usually not required to use digital devices

in their learning process.

• Using a computer for music programming may

help future processes of technology integration,

i.e., the use of digital technologies for musical ac-

tivities.

• The creative activities included in the course may

complement a curriculum primarily devoted to

score reading and music performance.

In line with the concepts expressed above, the

course aims at realising the following objectives.

1. Introducing the students to computational think-

ing, i.e. the ability of “ ...formulating problems

so their solutions can be represented as computa-

tional steps and algorithms” (Aho, 2012). Com-

putational thinking also implies problem solving,

analysis, and pattern recognition (Wing, 2011).

2. Offering them the possibility of experiencing crit-

ical thinking, creativity, collaboration and com-

munication (also known as the four C’s

) as an

important complement to their academic curricu-

lum.

3. Stimulating their creativity and musicality in rela-

tion to computer programming.

2.2 Content

The course employs Pure Data

as music program-

ming software. Pure Data has been created in 1996 by

Miller Puckette, one of the fathers of computer mu-

sic. It is a multi-platform and free software and for

these reasons it is particularly suitable for use in the

course. Pure Data is also a graphical program, where

the various functions are represented by objects. The

algorithm is built by linking the objects through cords

in a tree structure that governs the ﬂow of data.

2.2.1 Inner Organisation

Table 1 shows the course content subdivided into lec-

tures, workshops, and homework. During lectures the

concepts are explained frontally through multimodal

presentations and patch examples. In workshops the

same content is presented through a set of exercises

proposed to the students. One of the students in turn

https://www.aeseducation.com/blog/

four-cs-21st-century-skills

http://puredata.info/

CSME 2023 - 4th International Special Session on Computer Supported Music Education

388

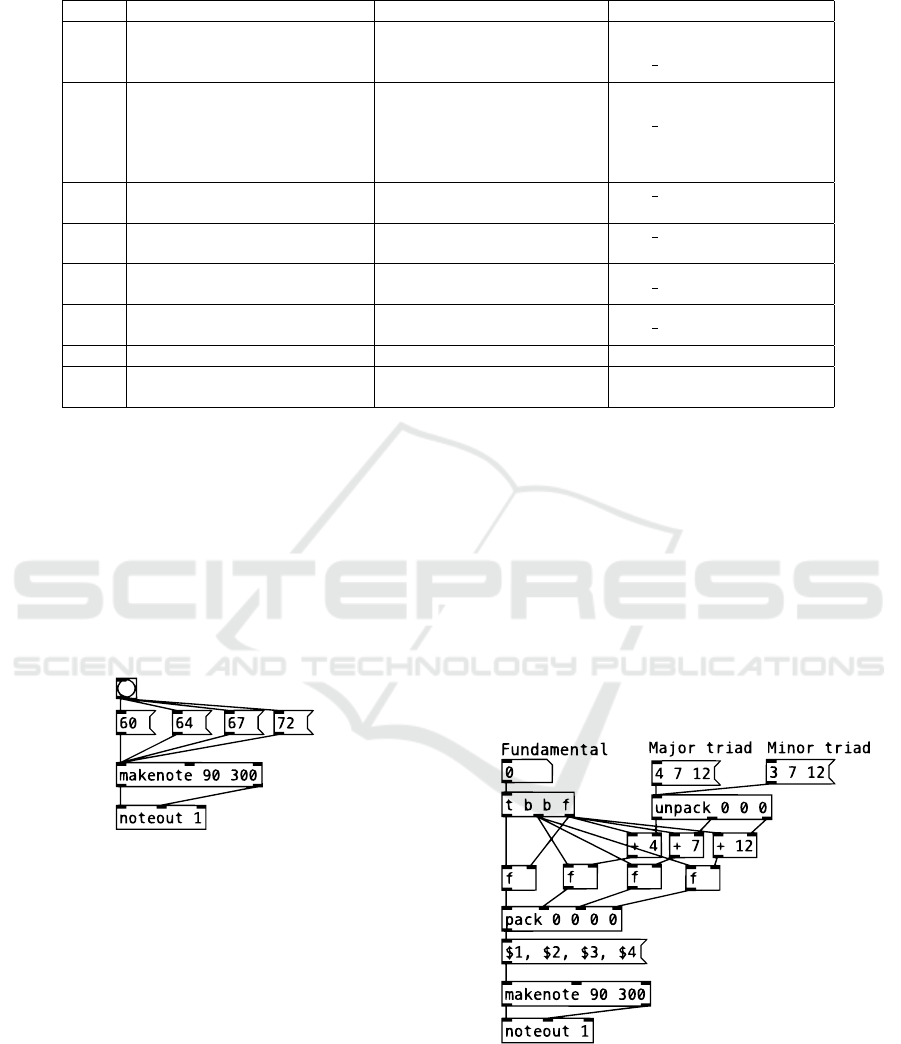
Table 1: Course organisation and content.

Week Lecture Workshop Homework

Introduction

Computational thinking

The “Four C’s”

Introduction to Pure Data

Controlling numerical ﬂow

(random, moses, clip)

Pre-course questionnaire

lab1 assignment (logic)

Audio and MIDI

MIDI events

MIDI production

(noteout, makenote)

MIDI controls

(modulation, volume,

pan and sustain)

lab2 assignment

(exploration)

Counters

(iteration, reset, loops)

The counter abstraction

A pattern of a musical form

lab3 assignment

(musical form)

4 Scales (MIDI notes and arrays)

Major and minor scales

Scale transposition

lab4 assignment

(scale fragments)

Musical structures

(patterns, polyphony, chords)

Pattern repetition (cycles),

polyphony

lab5 assignment (chords)

6 Melodies

Augmentation,

musical streams

lab6 assignment (creativity)

7 Patch modules

Bands, clusters and lines

Final group assignment

8 Group assignment discussion Group assignment discussion

Delivery of the ﬁnal project

Post-course questionnaire

tries to solve one exercise with the help of other stu-

dents. The teacher comments the solutions proposed

by the students and possibly offers alternative ways.

During the workshop, homework can be discussed

upon request. In their homework students are required

to solve problems closely related to the content of the

current lecture and workshop, but not identical to the

examples/exercises (i.e., they must demonstrate not

only to have understood the content of the lesson, but

also to be able to elaborate upon it).

Figure 1: A basic algorithm for chord production.

2.2.2 Topics

Following the approach already proposed by V. J.

Manzo (Manzo, 2016) the course starts from the al-

gorithmic implementation of basic musical structures

such as melodies, scales, and chords. The main rea-

son for this choice is that starting with concepts that

students already know may ease the process of ap-

proaching computational thinking. All these musical

structures are built following the same principle:

1. ﬁrst show the simplest implementation of the

structure, for instance a 4-part C major chord (see

Figure 1);

2. secondly, consider that this is a rigid algorithm be-

cause it requires to write down all the intervals

each time a new chord is needed;

3. ﬁnally, apply the principles of computational

thinking (decomposition, abstraction, and pattern

recognition) to produce the most ﬂexible structure

possible. As can be seen from Figure 2, the fun-

damental of the chord has been separated from the

chord pattern (decomposition), allowing an easy

transposition of the same chord (pattern recogni-

tion). The whole algorithm represents an abstrac-

tion (i.e., a general solution) with respect to the

basic version (i.e., a particular solution).

Figure 2: A more ﬂexible algorithm for chord production.

The principles of decomposition, abstraction, and

pattern recognition are introduced in the ﬁrst lesson as

theoretical assumptions. Later in week 7, the various

objects presented during the course are summarised

and grouped together according to a number of patch

modules, each performing a speciﬁc function.

A Music Programming Course for Undergraduate Music Conservatory Students: Evaluation and Lessons Learnt

389

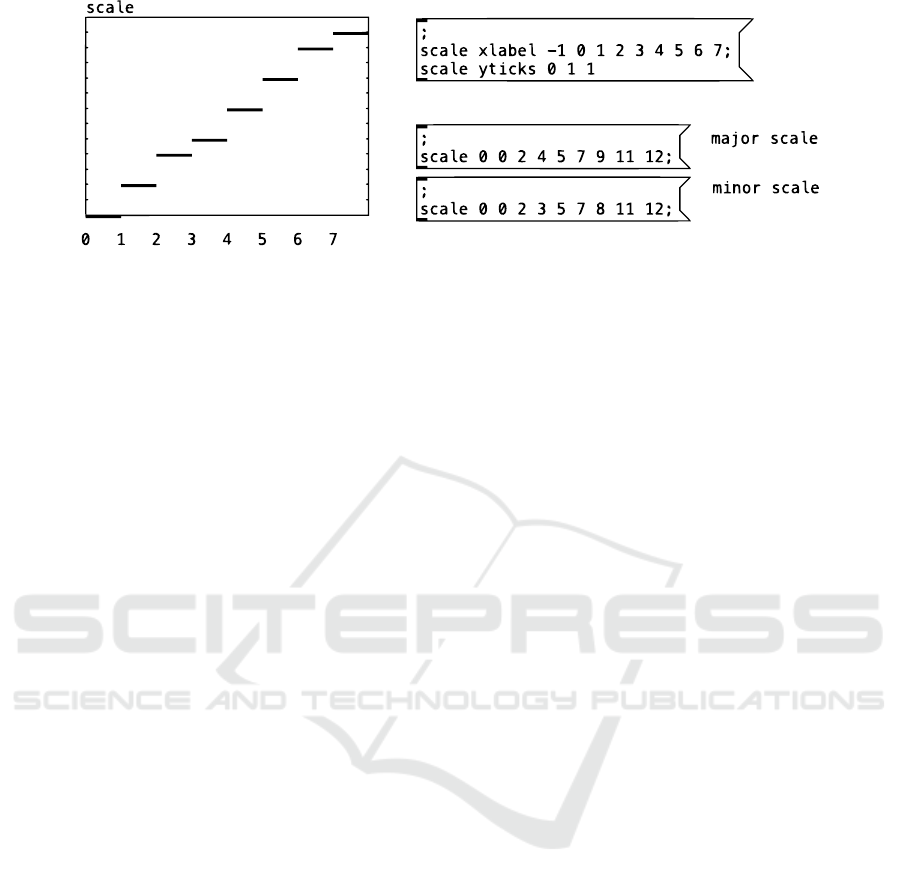
Figure 3: An array containing the sequence of intervals of a major scale. A minor scale can be obtained by clicking on the

message beneath.

These are:

1. Data storage. This function is performed by the

array object, which can store sequences of inter-

vals that can be changed dynamically with a mes-

sage (see Figure 3).

2. Timing and Initialisation. The timing function

is performed by the metro object. The trigger

object allows to simultaneously start metro and to

set the initial conditions of the patch (e.g. counters

to 0, note duration, fundamental pitch, and so on).

3. Array data scrolling and loop. The main ab-

straction here is the counter which is the true en-

gine of the patch. In conjunction with the module

object it allows to iteratively scroll the array per-

forming repetitions, loops, and transpositions.

4. Musical form. This can be controlled by a

selector object, which keeps track of the num-

bers produced by the counter and allows to stop

the performance, to change musical parameters

such as timbre, velocity and duration, or to change

the content of the array.

5. Sound production. This module groups all

the necessary MIDI objects for sound production

such as makenote and noteout .

In order to realise a melody composed of a number

of patterns, repetitions, and transpositions it is enough

to store the patterns in the array and control the range

of the scroll by adding an offset to the indices or by

changing the fundamental. But the modules and ob-

jects presented during the course can be used not only

to reproduce scales and melodies but also to create

new musical forms. This possibility is exempliﬁed in

the week 4 assignment, where starting from an array

containing the intervals of a major scale a new musi-

cal form composed of scale fragments scattered upon

various fundamental pitches is generated.

The potentialities of the various objects for com-

position of musical forms are described at the end of

the week 7 lecture. For instance, the random object is

a powerful tool for the randomisation of musical pa-

rameters (e.g. randomising the argument of the metro

object can make the musical performance irregular

and more interesting in some contexts). The spigot

object can govern streams of notes, making them ap-

pear and disappear at random intervals of time, while

pipe can provide polyphonic events at various time

delays. Moreover, in the week 7 workshop various ex-

amples of musical structures such as bands of sounds

of different direction and amplitude, clusters and lines

are presented with the aim of showing different cases

of non-traditional music elements. For their ﬁnal as-

signment, the students are required to form groups of

maximum 6 people and to produce a musical project

based on a Pure Data patch with a written description

of project analysis, aims, and limitations.

3 ASSESSMENT

The assessment of the Music Informatics course aims

at measuring the progress of the students according to

the objectives outlined in Section 2.1. For the assess-

ment we employed both quantitative and qualitative

methods. Quantitative data are collected through pre-

and post-course questionnaires and exercises, while

qualitative data are obtained from the analysis of the

ﬁnal projects of the course.

3.1 Participants

The participants who completed the course and all the

assessments are 43 in total (23 females), mean age

23.6 years, std = 8.35. The majority of the students

(69.7%) were attending the second year of their bach-

elor’s degree course, mainly in piano (18.6%), guitar

(13.9%), and singing (11.6%).

CSME 2023 - 4th International Special Session on Computer Supported Music Education

390

Table 2: The pre- and post-course questionnaire.

Group # Pre-Course Post-Course

Expectations

and outcomes

Q01

Learn something more about the integration of

computers and music

Now I understand something more about the integration of computers

and music

Q02

Learn something more about computers and

programming

I gained more knowledge about computers and programming

Q03

Learn something more about music and

composition

As a result of this course I would like to learn something more about

music and composition

Q04 Collaborate with others in my major I learned how to collaborate with others in my major

Q05 Learn to be more creative I learned to think more creatively

Q06 Learn to be more communicative I learned to be more communicative

Q07 Become more willing to take risks I am more willing to take risks

Self-perception

Q08 Technical/artistic Technical/artistic

Q09 Uncreative/creative Uncreative/creative

Q10 Do not take risks/Take risks Do not take risks/Take risks

Q11 Rules/insights Rules/insights

Q12 Big picture/Detail Big picture/Detail

Personal

opinions

Q13 I know what it means to work with computers Now I know better what it means working with computers

Q14 I enjoy working with computers As a result I am more comfortable working with computers

Q15 I know what it means to create music Now I know better what it means to create music

Q16 I enjoy creating my own music I enjoyed projects where we had to create music

Q17

I am conﬁdent using a computer language to

accomplish a complex task

Now I am more conﬁdent using a computer language to accomplish

complex tasks

Q18

I am conﬁdent in my ability to express myself

through music

Now I am more conﬁdent in my ability to express myself through music

Q19

I am good at breaking a large problem down into

its components and attacking those one at a time to

solve the bigger problem

As a result of this course I am better at breaking a large problem down

into its components and attacking those one at a time to solve the

bigger problem

Q20

I am good at diagnosing problems and

formulating solutions

As a result of this course I am better at diagnosing problems and

formulating solutions

Q21 Computers can be used to create cool music Computers can be used to create cool music

Q22 I enjoy working on group projects Now I appreciate the beneﬁts of working on group projects

Q23

There is a deep connection between music and

computer science

Now I am seeing a deep connection between music and computer

science

Q24 Computer programming is fun Computer programming is now more fun to me

Q25 Standard music notation is a form of code Now I see the connection between standard musical notation and code

Q26

Writing music down is similar to writing a

computer program

Writing music down is similar to writing a computer program

3.2 Quantitative Assessment

During the ﬁrst lecture, the teacher administered a

pre-course questionnaire aimed at evaluating the stu-

dents’ expectations on the course as well as personal

attitudes and opinions on music, computing, and their

interplay. Similarly, a post-course questionnaire (with

matching questions) was administered at the end of

the last lecture. The two questionnaires are elaborated

on the basis of the Sound thinking pre-course sur-

vey and Sound thinking post-course survey by Greher

and Heines (Greher and Heines, 2014), a pair of tools

speciﬁcally targeted at assessing how a class learns

and how attitudes change as a result of taking the class

itself. Each of the two questionnaires is composed of

twenty-six 5-point Likert scale questions, as reported

in Table 2. The original 33 questions have been re-

duced to 26 by eliminating those items that did not

pertain to the current course or did not match from

pre- to post-course.

In addition, right after the pre-course question-

naire, the teacher administered 4 exercises on music

analysis and computational thinking. In the ﬁrst exer-

cise (EX1), a melody was presented to the students

with some examples of pattern repetition and pat-

tern transposition; then, they were required to iden-

tify how many patterns they ﬁnd in a new melody.

In the second exercise (EX2), students had to iden-

tify pattern repetitions and transpositions in the same

melodic excerpt. In the third exercise (EX3), students

were presented with a ﬂowchart and asked to identify

its output when a short sequence of notes is used as

input. Similar exercises were also administered right

after the post-course questionnaire. A fourth exercise

on patch logic was considered redundant and not ad-

ministered in the post test. More details on the four

exercises can be found in (Mandanici, 2022).

A Music Programming Course for Undergraduate Music Conservatory Students: Evaluation and Lessons Learnt

391

Table 3: The 9 ﬁnal projects and their musical features.

# Name Timbres Harmony/Elements Model

1 Jazz Improvisation Drums, piano, double bass, sax Jazz harmony Accompanied melody

2 Inno alla Gioia Piano, organ, ﬂute, double bass Tonal harmony Accompanied melody

3 Grandcanon Harp, brasses, sax, guitar Tonal harmony Polyphony

4 Timbri in scala Random timbres C major scale Scale

5 Pachelbel canon Strings Tonal harmony Polyphony

6 Cum santo Vibraphone, harp

Band, crazy harp, melody

Original musical form

7 Pachelbel canon

Trumpet, french horn, ﬂute,

harpsichord, piano

Tonal harmony Accompanied melody

8 Halloween

Space voice, woodblock, ocarina,

warm pad, vibraphone, square wave

Band, melody and line Original musical form

9 Polovtsian Dances Piano, random timbre Twisted melody Polyphony

3.3 Qualitative Assessment

Qualitative assessment is based upon the analysis of

the ﬁnal assignments of the course. The 43 students

were subdivided into 9 groups with the aim of produc-

ing an original musical project composed of a com-

mented Pure Data patch and written presentation. The

aims of this ﬁnal assignment were:

1. to foster creative thinking;

2. to assess if the students are able to master the pos-

sibilities offered by the patch modules;

3. to offer the possibility of experiencing collabora-

tion and communication in a working group.

According to Sternberg and Kaufman (Sternberg and

Kaufman, 2010) creativity is a relative concept, which

depends on the interaction between the stimulus and

the receiver. Moreover, the evaluation of creativity

may be biased by cultural constraints, because a prod-

uct can be thought to be creative in one historical era

and insigniﬁcant in another. In the context of this

course we started from the implementation of sim-

ple musical structures such as scales, melodies and

polyphony, with explicit reference to the tonal lan-

guage. At the same time, however, we have pro-

posed computational structures which – in addition

to implementing the aforementioned models – also

have the power to undermine the perception of these

same structures, transforming them into something

new. This entails the application of divergent think-

ing, i.e., the ability of producing many alternative re-

sponses to the same task (Runco and Pritzker, 2020).

Thus, in order to evaluate creativity in the musical

projects presented by the students, we list the main

musical features that characterise them, i.e., the tim-

bres employed, harmony or musical structure, and the

model that inspired the project. All these elements are

summarised in Table 3.

4 RESULTS

In this section we analyse the results obtained from

the applied methods. We present quantitative pre- and

post-course data for questionnaires and exercises, and

qualitative data for the ﬁnal assignments of the course.

4.1 Quantitative Analysis

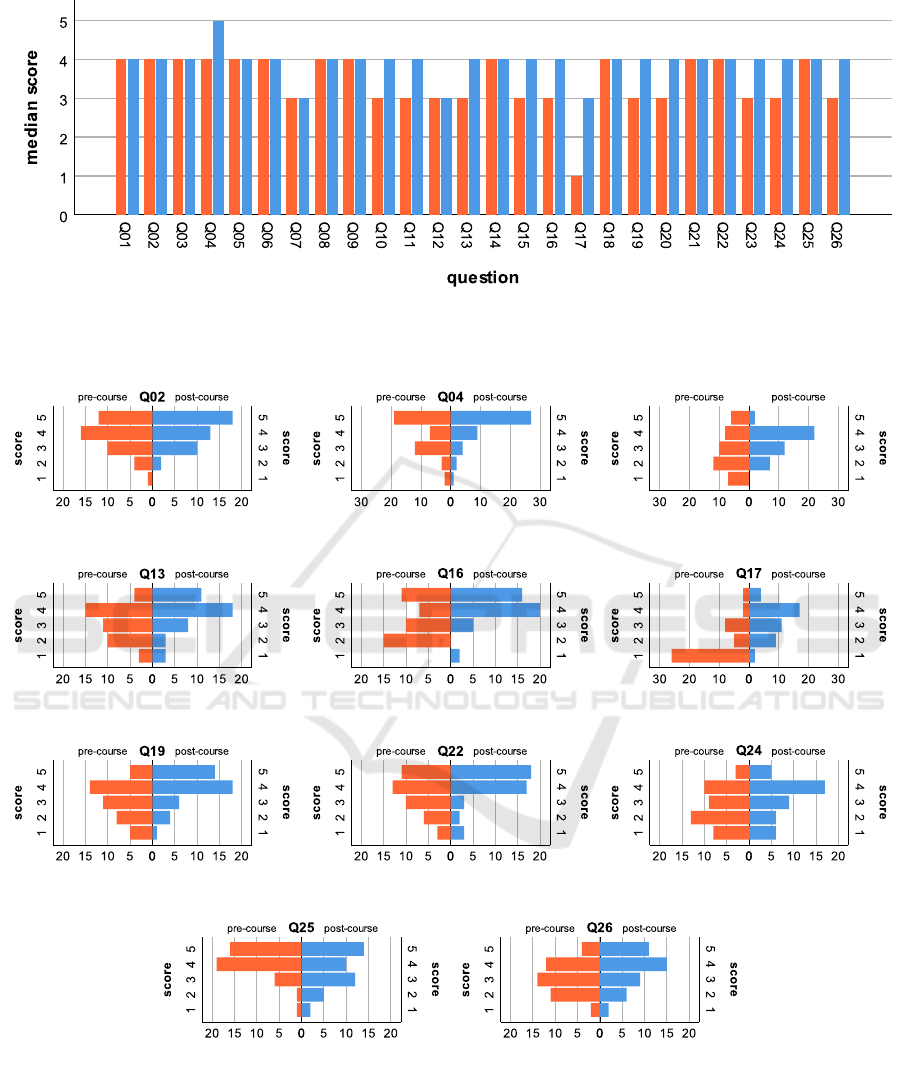
Figure 4 reports the median scores obtained for the 26

questions in each questionnaire. Notice that the large

majority of these scores is stable around 4, denoting a

clear agreement with the corresponding questions and

therefore highlighting generally positive expectations,

outcomes, and opinions on the course and on its po-

tential to improve students’ critical thinking, creativ-

ity, collaboration and communication skills. Given

the typical distribution of Likert scale data, we chose

to apply non-parametric tests to look for statistically

signiﬁcant differences between paired pre- and post-

test data. Therefore, twenty-six separate Wilcoxon

signed-rank tests, one per questionnaire item, were

run.

In the expectations and outcomes question group,

the post-course items Q02 and Q04 signiﬁcantly

ranked higher than the corresponding pre-course

items (Z = −2.068, p = .039 and Z = −2.095, p =

.036, respectively). For what concerns the self-

perception question group, the tests highlighted no

signiﬁcant difference between the outcomes of the

pre- and post-course items except for Q11, where

scores were signiﬁcantly higher in the post-course

questionnaire (Z = −3.166, p = .002). The items that

showed statistically signiﬁcant differences in the per-

sonal opinions question group are Q13 (Z = −2.118,

p = .034), Q16 (Z = −3.082, p = .002), Q17 (Z =

−4.709, p < .001), Q19 (Z = −3.089, p = .002), Q22

(Z = −2.054, p = .04), Q24 (Z = −2.586, p = .01),

Q25 (Z = −2.228, p = .026), and Q26 (Z = −2.184,

p = .029). All the related scores were signiﬁcantly

CSME 2023 - 4th International Special Session on Computer Supported Music Education

392

* *

Figure 4: Median scores for the 26 questions in the pre-course (orange bars) and post-course (blue bars) questionnaires.

Asterisks indicate statistically signiﬁcant differences between matching pairs of pre- and post-course questions: *p ≤ 0.05,

**p ≤ 0.01, ***p ≤ 0.001.

Figure 5: Histograms for the 11 items showing statistically signiﬁcant differences between pre-course (orange bars) and post-

course (blue bars) questionnaires.

higher in the post-course than in the pre-course ques-

tionnaire, except for Q25 where scores signiﬁcantly

decreased in the post-course questionnaire. Figure 5

reports all the histograms for the 11 questionnaire

items where statistical signiﬁcance was found.

Finally, we analysed the results of the three ex-

ercises. While the score in EX2 was obtained as

the fraction of correct answers on the total number

of beats, EX1 and EX3 could either have a right or

wrong answer. Therefore, we applied a Wilcoxon

A Music Programming Course for Undergraduate Music Conservatory Students: Evaluation and Lessons Learnt

393

Figure 6: The melody taken from Borodin’s Polovtsian Dances twisted by musical parameters randomisation and polyphony.

signed-rank test to EX2 scores and two McNemar’s

tests to EX1 and EX3 scores. The tests highlighted

no signiﬁcant difference between the outcomes of the

pre- and post-course exercises except for EX2, where

scores were signiﬁcantly higher in the post-course

questionnaire (Z = −4.014, p < .001).

4.2 Qualitative Analysis

The ﬁrst aim of the qualitative assessment is the eval-

uation of the amount of divergent thinking applied in

the realization of the projects (see Section 3.3). Most

of the projects in Table 3 employ tonal or jazz har-

mony as the main reference musical structures. If

we compare this with the musical models and timbres

chosen, on the whole we can afﬁrm that six projects

out of nine (i.e., projects 1, 2, 3, 4, 5, and 7) es-

sentially follow musical models belonging to the stu-

dents’ musical experience. Since group 1 was com-

posed of jazz students, they explicitly declared to

stick to jazz harmony and improvisation form. Group

2 employed the famous melody from “Ode to Joy”,

while the students of group 3 composed an original

canon to be implemented in Pure Data. This choice

explicitly assigns to the program the function of a per-

former rather than that of a creator/transformer of the

musical product. Finally, groups 5 and 7 employed

Pachelbel’s Canon,

one in a polyphonic form and

the other in a harmonised form. These projects do

not show a high degree of divergent thinking because

they basically employ Pure Data as a MIDI sequencer,

Written on the words of German poet F. Schiller

in 1785, the “Ode to Joy” is the fourth movement of

Beethoven’s Ninth Symphony, completed in 1824.

Written by the German composer Johann Pachelbel,

born in 1653.

ignoring the creative potentialities of music program-

ming.

On the other hand, projects 6, 8, and 9 contain ele-

ments such as crazy harp (taken from the assignment

of week 4), and bands and lines elaborated on the ex-

amples of week 7. Even though tonal melodies are

still present in all three cases, they are presented in

the context of an original musical form. For instance,

group 9 proposed a melody taken from Borodin’s

Polovtsian Dances

that is ﬁrst played as it is and

then completely twisted by introducing random tim-

bres, metro, and note durations (see Figure 6). Chords

and a canon are also added to the melody, obtaining

a completely different effect every time the process is

activated. In all three cases students showed to be able

to manipulate Pure Data objects in a creative way, of-

fering original solutions in the use of the objects pre-

viously presented in a tonal context.

5 DISCUSSION AND

CONCLUSIONS

From the analysis of those questions that obtained a

statistically signiﬁcant difference from pre- to post-

test, the following conclusions can be drawn:

1. Computers and programming: there is a clear

belief among the students that their abilities in

managing computers and computer programming

have increased (Q02, Q13, Q17, Q19, and Q24);

2. Collaboration: students think they have learnt

how to work in a group and better appreciate this

activity (Q04 and Q22);

These Dances belong to a scene from Act 2 of Alexan-

der Borodin’s “Prince Igor”, remained incomplete upon the

composer’s death in 1887.

CSME 2023 - 4th International Special Session on Computer Supported Music Education

394

3. Self-perception: they rely more on insights rather

than rules (Q11);

4. Music: they tend to enjoy more music creation

(Q16) and to think that writing music is similar to

computer programming (Q26). However, they are

more negative about recognising standard music

notation as a form of code (Q25).

5. Communication: there is no signiﬁcant result for

this ability.

According to points 1 and 2, undergraduate students

who are very seldom required to use electronic de-

vices in their academic career met computing pro-

gramming with a positive attitude and seem to have

become more conﬁdent with it, making progress in

computational thinking too. They enjoyed working

in groups and music creation activities, but seem to

draw a line between standard music notation and cod-

ing (point 4). They still prefer to follow insights rather

than rules (point 3), as to say “we are artists and not

computer scientists”. Moreover, the students’ percep-

tion on their communication abilities has not changed

(point 5), possibly because of their little coverage dur-

ing the course and/or presence in the questionnaire.

As far as concerns the exercises, one would ex-

pect a similar result for EX1 and EX2 since they tar-

get the same analytical ability, i.e., recognising the

repetition and transposition of the same pattern in a

melody. Alas, only EX2 showed a statistically sig-

niﬁcant improvement in the results. Actually, while

in EX1 students were asked for a synthetic answer,

EX2 is more analytical. Since it would probably have

made more sense to ﬁrst identify the patterns and then

count them, perhaps this procedure has misled many

students, causing a difference in favour of the analyt-

ical procedure. EX3 was designed for assessing if the

logic represented in a ﬂowchart could be better inter-

preted by the students after the course. Results clearly

show this is not the case. However, it has to be ac-

knowledged that ﬂowcharts have not been addressed

during the course, and this result shows that insight is

not sufﬁcient to obtain advances in this ability.

Qualitative assessment aimed at verifying the mu-

sical creativity of the students in relation to the patch

modules and musical forms presented during the

course. Three creative projects versus six based on the

persistence of already known musical models show

that the potentialities of computer programming have

not been sufﬁciently implemented by the students. It

seems instead that they need to take inspiration from

well established musical models and that they cannot

get over the limits of a musical training too tied to a

single musical style.

5.1 Lessons Learnt

The results obtained in the Music Informatics 2022

course have been employed to improve the content

and assessment methods of the 2023 course.

1. The main changes concern the questionnaire. Be-

cause of the different formulation of most ques-

tions in the post-course questionnaire 2022, many

questions may have produced unreliable results.

Therefore, in the 2023 version, the same ques-

tions are being used for the pre- and post-course

questionnaire. Moreover, to balance the question-

naire in relation to the four C’s abilities, more

questions about collaboration and communication

have been added.

2. Another change is about the use of ﬂowcharts to

represent the inner working of an algorithm, based

on the observation that ﬂowcharts are able to out-

line the logic of a music patch. For this reason,

during lectures, examples of ﬂowcharts have been

coupled to Pure Data patches to stimulate the stu-

dents’ computational reasoning.

3. A ﬁnal but very important change has been in-

troduced to aim at offering models of algorith-

mic composition to the students to improve their

creativity. Among these the Illiac Suite, by L.

Hiller and L. Isaacson (Hiller and Isaacson, 1979),

and short musical excerpts by A. Webern

and B.

Bart

5.2 Conclusions

The role and importance of a music programming

course in the curriculum integration of undergraduate

music conservatory students has been carefully eval-

uated and motivated in light of the development of

computational thinking and the four C’s. Quantitative

and qualitative methods have been tested for the as-

sessment of these abilities. The results of the assess-

ment of the 2022 course have been used to improve

the content and assessment of the 2023 course, which

is still running at the time of submission of this ar-

ticle. The authors hope that the iterative veriﬁcation

and update of its contents can improve the efﬁciency

of the course, thus contributing to a more complete

training in line with the needs of digital culture.

Anton Webern (1883–1945) is one of the members of

the “School of Wien” together with A. Sch

onberg and A.

Berg.

ela Bart

ok (1881–1945) is a Hungarian composer

who derived his musical style from his country’s popular

music.

A Music Programming Course for Undergraduate Music Conservatory Students: Evaluation and Lessons Learnt

395

REFERENCES

Aho, A. V. (2012). Computation and computational think-

ing. The Computer Journal, 55(7):832–835.

Bailey, J. L. and Stefaniak, G. (2002). Preparing the infor-

mation technology workforce for the new millennium.

ACM SIGCPR Computer Personnel, 20(4):4–15.

Bauer, J. and Kenton, J. (2005). Toward technology integra-

tion in the schools: Why it isn’t happening. Journal of

Technology and Teacher Education, 13(4):519–546.

Burgess, R. J. (2013). The art of music production: The

theory and practice. Oxford University Press.

Collins, N., Schedel, M., and Wilson, S. (2013). Electronic

Music. Cambridge University Press.

Fauvel, J., Flood, R., and Wilson, R. J. (2006). Music and

mathematics: From Pythagoras to fractals. Oxford

University Press on Demand.

Greher, G. R. and Heines, J. M. (2014). Computational

thinking in sound: Teaching the art and science of mu-

sic and technology. Oxford University Press.

Hamilton, E. R., Rosenberg, J. M., and Akcaoglu, M.

(2016). The substitution augmentation modiﬁcation

redeﬁnition (SAMR) model: A critical review and

suggestions for its use. TechTrends, 60:433–441.

Hiller, L. A. and Isaacson, L. M. (1979). Experimental Mu-

sic; Composition with an electronic computer. Green-

wood Publishing Group Inc.

Mandanici, M. (2022). Fostering computational thinking

in undergraduated music conservatory students. In

Proc. 14th Int. Conf. on Computer Supported Educa-

tion (CSEDU 2022), pages 449–457.

Manzo, V. J. (2016). Max/MSP/Jitter for music: A practi-

cal guide to developing interactive music systems for

education and more. Oxford University Press.

Runco, M. A. and Pritzker, S. R. (2020). Encyclopedia of

creativity. Academic press.

Skuse, G. R., Walzer, D. A., Tomasek, K., Baldwin, D.,

and Bailey, M. (2017). Computer science and the lib-

eral arts: Hidden synergies and boundless opportu-

nities. In New Directions for Computing Education:

Embedding Computing Across Disciplines, pages 45–

61. Springer.

Sternberg, R. J. and Kaufman, J. C. (2010). Constraints

on creativity. The Cambridge handbook of creativity,

pages 467–482.

Tobias, E. S. (2013). Composing, songwriting, and pro-

ducing: Informing popular music pedagogy. Research

Studies in Music Education, 35(2):213–237.

Wing, J. (2011). Research notebook: Computational think-

ing—what and why. The Link Magazine, 6:20–23.

Zattra, L. (2000). Da Teresa Rampazzi al Centro di Sonolo-

gia Computazionale (CSC): La stagione della musica

elettronica a Padova. Master thesis, Universit

a di

Padova.

CSME 2023 - 4th International Special Session on Computer Supported Music Education

396