Semantic Coverage: Measuring Test Suite Effectiveness
Samia Al Blwi
1
, Amani Ayad
2
, Besma Khaireddine
3
, Imen Marsit
4
and Ali Mili
1 a
1
NJIT, Newark NJ, U.S.A.
2
Kean University, Union NJ, U.S.A.
3
University of Tunis El Manar, Tunis, Tunisia
4
University of Sousse, Sousse, Tunisia
Keywords:
Software Testing, Test Suite Effectiveness, Syntactic Coverage, Mutation Coverage, Semantic Coverage.
Abstract:
Several syntactic measures have been defined in the past to assess the effectiveness of a test suite: statement
coverage, condition coverage, branch coverage, path coverage, etc. There is ample analytical and empirical
evidence to the effect that these are imperfect measures: exercising all of a program’s syntactic features is
neither necessary nor sufficient to ensure test suite adequacy; not to mention that it may be impossible to
exercise all the syntactic features of a program (re: unreachable code). Mutation scores are often used as
reliable measures of test suite effectiveness, but they have issues of their own: some mutants may survive
because they are equivalent to the base program not because the test suite is inadequate; the same mutation
score may mean vastly different things depending on whether the killed mutants are distinct from each other
or equivalent; the same test suite and the same program may yield different mutation scores depending on the
mutation operators that we use. Fundamentally, whether a test suite T is adequate for a program P depends
on the semantics of the program, the specification that the program is tested against, and the property of
correctness that the program is tested for (total correctness, partial correctness). In this paper we present a
formula for the effectiveness of a test suite T which depends exactly on the semantics of P, the correctness
property that we are testing P for, and the specification against which this correctness property is tested; it
does not depend on the syntax of P, nor on any mutation experiment we may run. We refer to this formula as
the semantic coverage of the test suite, and we investigate its properties.
1 ON THE EFFECTIVENESS OF A
TEST SUITE
1.1 Motivation
In this paper we envision to define a measure to quan-
tify the effectiveness of a test suite. The effectiveness
of an artifact can only be defined with respect to the
purpose of the artifact, and must reflect its fitness for
the declared purpose. If the purpose of a test suite is
to reveal the presence of faults in incorrect programs,
then it is sensible to quantify the effectiveness of a test
suite by its ability to reveal faults. A necessary condi-
tion to reveal a fault is to exercise the code that con-
tains the fault; hence many metrics of test suite effec-
tiveness focus on the ability of a test suite to exercise
syntactic attributes of the program (Mathur, 2014);
but while achieving syntactic coverage is necessary, it
a
https://orcid.org/0000-0002-6578-5510
is far from sufficient, and not always possible. Indeed
not all faults cause errors and not all errors lead to ob-
servable failures (Avizienis et al., 2004); also, it is not
always possible to exercise all syntactic features of a
program (re: infeasible paths, dead code), so that it
is possible to thoroughly test a program without cov-
ering all its statements (if the code that has not been
exercised contains no faults).
A better measure of test suite effectiveness is mu-
tation coverage, which is defined as the ratio of mu-
tants that it kills out of a set of generated mutants.
But while mutation coverage is often used as the gold
standard of test suite effectiveness (Inozemtseva and
Holmes, 2014; Andrews et al., 2006), it has issues of
its own:
• The same mutation score may mean vastly differ-
ent things depending on whether the killed mu-
tants are all distinct from each other, all equiva-
lent, or partitioned into some equivalence classes.
• The same test suite T may yield different mutation
Al Blwi, S., Ayad, A., Khaireddine, B., Marsit, I. and Mili, A.
Semantic Coverage: Measuring Test Suite Effectiveness.
DOI: 10.5220/0012063900003538
In Proceedings of the 18th International Conference on Software Technologies (ICSOFT 2023), pages 287-294
ISBN: 978-989-758-665-1; ISSN: 2184-2833
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
287

scores for different sets of mutants, hence the mu-
tation score cannot be considered as an intrinsic
attribute of the test suite.
• Even assuming that mutants are a faithful proxy
for actual faults (Just et al., 2014), we argue that
assessing the effectiveness of test suites by their
mutation score may be imperfect, because of the
disconnect between fault density and failure rate
(Farooq et al., 2012).
In this paper we present a measure of test suite
effectiveness which depends only on the program un-
der test, the correctness property we are testing it for,
and the specification against which correctness is de-
fined; also, this measure is intended to reflect a test
suite’s effectiveness to expose failures, rather than to
detect faults. In the next section we present and dis-
cuss some criteria that a measure of test suite effec-
tiveness ought to satisfy, and in section 1.3 we present
and justify some design principles that we resolve to
adopt to this effect.
In section 2 we introduce detector sets, and dis-
cuss their significance for the purposes of program
testing and program correctness, and in section 3 we
use detector sets to introduce our definition of test
suite effectiveness; we validate our proposed defini-
tion in section 4 by showing, analytically, that it meets
all the requirements set forth in section 1.2. In section
5 we illustrate the derivation of semantic coverage on
a sample benchmark example, and show its empirical
relationship to mutation scores. We conclude in sec-
tion 6 by summarizing our findings, critiquing them,
comparing them to related work, and sketching direc-
tions of further research.
1.2 Requirements of Semantic Coverage
We consider a program P that we want to test for cor-
rectness against a specification R and we wish to as-
sess the fitness of a test suite T for this purpose. We
argue that the effectiveness of test suite T to achieve
the purpose of the test ought to be defined as a func-
tion of three parameters:
• Program P.
• Specification R.
• The standard of correctness that we are testing
P for: partial correctness or total correctness
(Hehner, 1992).
The requirements we present below dictate how se-
mantic coverage ought to vary as a function of these
parameters.
Rq1. Monotonicity with respect to test suite size.
Notwithstanding that we favor smaller test
suites for the sake of efficiency, we argue that
from the standpoint of effectiveness, larger test
suites are better: if T
′
is a superset of T then T
′
ought to have higher semantic coverage than T.
Rq2. Monotonicity with respect to relative correct-
ness. Relative correctness is the property of
a program to be more-correct than another
with respect to a specification (Diallo et al.,
2015). A test suite T ought to have increas-
ingly greater semantic covarage as the program
grows more-correct, since more-correct pro-
grams have fewer failures to reveal.
Rq3. Monotonicity with respect to refinement. Spec-
ifications are naturally ordered by refinement,
whereby more-refined specifications represent
stronger/ harder to satisfy requirements (Mor-
gan, 1998; Hehner, 1992); a given program P
fails more often against a more-refined specifi-
cation than a less-refined specification. Hence
the same test suite ought to have greater seman-
tic coverage for less-refined specifications.
Rq4. Monotonicity with respect to the standard of
correctness. Total correctness is a stronger
property than partial correctness, hence the
same program will fail the test of total correct-
ness more often than it fails the test of partial
correctness. The same test suite T ought to have
greater semantic coverage if it is applied to par-
tial correctness than if applied to total correct-
ness.
In section 4 we prove that the formula of semantic
coverage presented in section 3 satisfies all the re-
quirements (Rq1-Rq4) discussed in this section.
1.3 Design Principles
We resolve to adopt the following design principles as
we define semantic coverage:
• Focus on Failure. We adopt the definitions of
fault, error and failure proposed by Avizienis et al
(Avizienis et al., 2004). A failure is an observable,
verifiable, certifiable effect. By contrast, a fault
(referred to in (Avizienis et al., 2004) as the ad-
judged or hypothesized cause of an error) is a hy-
pothetical cause of the observed failure; the same
failure may be caused by more than one fault or
combination of faults. Hence whereas a failure is
an objectively verifiable effect, a fault is a specu-
lative hypothesized cause; our definition is based
on failures rather than faults.
• Partial Ordering. It is easy to imagine two test
suites whose effectiveness cannot be ranked: for
ICSOFT 2023 - 18th International Conference on Software Technologies
288

example, they reveal disjoint or distinct sets of
failures. Hence test suite effectiveness is essen-
tially a partial ordering. Yet if we quantify test
suite effectiveness by numbers, we introduce an
artificial total ordering, on what is actually a par-
tially ordered set. Hence we resolve to define se-
mantic coverage, not as a number, but as an ele-
ment of a partially ordered set.
• Analytical Validation. We resolve to validate our
proposed measure of effectiveness by means of
analytical (vs empirical) methods because we do
not know of a widely accepted ground truth of test
suite effectiveness against which we can empiri-
cally validate our definition. Hence we resolve to
validate our definition by arguing that it captures
the right attributes and that it meets all the require-
ments that we mandate in section 1.2.
In section 5 we compute the semantic coverage of a
set of (20) test suites of a benchmark program for two
specifications and two standards of correctness, and
we compare the four graphs so derived against two
graphs that rank these test suites by mutation cover-
age, for two mutant generators.
1.4 Relational Mathematics
We assume the reader is familiar with elementary dis-
crete mathematics;in this section, we present some
definitions and notations that we use throughout the
paper. We define sets by means of C-like variable dec-
larations; if we declare a set S as:
xType x; yType y;
then we mean S to be the cartesian product of the
sets of values represented by types xType and yType.
Elements of S are denoted by s, and have the form
s = ⟨x, y⟩. The cartesian components of an element of
S are usually decorated the same way as the element,
so we write for example s
′
= ⟨x
′
, y
′
⟩.
A relation on set S is a subset of the Cartesian
product S×S. Special relations on S include the iden-
tity relation (I = {(s, s)|s ∈ S}), the universal relation
(L = S × S) and the empty relation (φ = {}). Opera-
tions on relations include the set theoretic operations
of union, intersection and complement; they also in-
clude the domain of a relation, denoted by dom(R)
and defined by: dom(R) = {s|∃s
′
: (s, s
′
) ∈ R}. The
product of two relations R and R
′
is denoted by R ◦ R
′
(or RR
′
for short) and defined by RR
′
= {(s, s
′
)|∃s
′′
:
(s, s
′′
) ∈ R ∧ (s
′′
, s
′
) ∈ R
′
}. Note that given a relation
R, the product of R by the universal relation L yields
the relation RL = dom(R) × S; we use RL as a repre-
sentation of the domain of R in relational form. The
inverse of relation R is the relation denoted by
b
R and
defined by
b
R = {(s, s
′
)|(s
′
, s) ∈ R}. The restriction of
relation R to subset T is the relation denoted by
T \
R
and defined by
T \
R = {(s, s
′
)|s ∈ T ∧ (s, s
′
) ∈ R}.
2 CORRECTNESS AND
DETECTOR SETS
Absolute correctness is the property of a program to
be (partially or totally) correct with respect to a speci-
fication. Relative correctness is the property of a pro-
gram to be more (partially or totally) correct than an-
other with respect to a specification. The detector set
of a program with respect to a specification is the set
of inputs (tests) that expose the (partial or total) incor-
rectness of a program with respect to a specification.
In this section, we will show how (partial, total) de-
tector sets enable us to define absolute and relative
correctness in simple, uniform terms.
2.1 Specification Refinement
In this paper, we represent specifications by relations
and programs by deterministic relations (functions).
An important concept in any programming calculus is
the property of refinement, which ranks specifications
according to the stringency of the requirements that
they represent.
Definition 1. Given two relations R and R
′
on space
S, we say that R
′
refines R (abbreviation: R
′
⊒ R, or
R ⊑ R
′
) if and only if: RL ∩ R
′
L ∩ (R ∪ R
′
) = R.
Intuitive interpretation: this definition means that
R
′
has a larger domain than R, and assigns fewer im-
ages than R to the elements of the domain of R. This
is formulated in the following Proposition.
Proposition 1. Given two relations R and R
′
on space
S. If R
′
refines R then RL ⊆ R
′
L and R
′
∩ RL ⊆ R.
2.2 Program Semantics
We consider a program P on space S and we let s be
an element of S; execution of P on initial state s may
terminate after a finite number of steps in some fi-
nal state s
′
when the exit statement of the program is
reached; we then say that execution of P on s con-
verges. Alternatively, execution of P on s may fail to
converge, for any number of reasons: it enters an in-
finite loop; it adresses an array out of its bounds; it
references a nil pointer; etc; we then say that execu-
tion of P on s diverges.
Given a program P on space S, the function of pro-
gram P (which we also denote by P) is the set of pairs
Semantic Coverage: Measuring Test Suite Effectiveness
289

of states (s, s
′
) such that execution of P on state s con-
verges and returns the final state s
′
. The domain of P
is the set of states on which execution of P converges.
2.3 Absolute Correctness
A specification on space S is a binary relation on S; it
contains all the pairs of states (s, s
′
) that the specifier
considers correct. The correctness of a program P on
space S can be determined with respect to a specifica-
tion R on S according to the following definition.
Definition 2. Given a program P on state S and a
specification R on S, we say thet P is (totally) correct
with respect to R if and only if P refines R. We say that
P is partially correct with respect to R if and only if P
refines R ∩PL.
The following proposition gives set theoretic char-
acterizations of total correctness and partial correct-
ness.
Proposition 2. Given a program P on space S and a
specification R on S, program P is totally correct with
respect to R if and only if dom(R) = dom(R ∩ P); and
program P is partially correct with respect to R if and
only if dom(R) ∩ dom(P) = dom(R ∩ P).
2.4 Detector Sets
Now that we know how to characterize correctness,
we resolve to define sets of initial states that expose
the incorrectness of a program with respect to a spec-
ification.
Definition 3. Given a program P on space S and a
specification R on S:
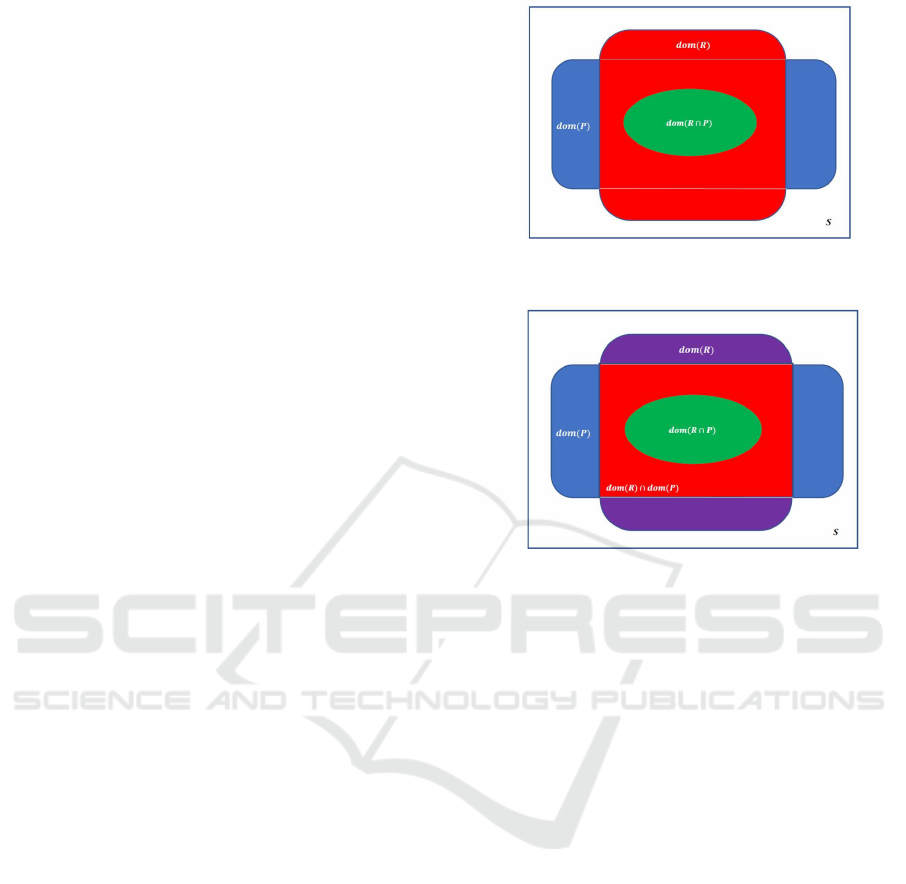
• The detector set for total correctness of program
P with respect to R is denoted by Θ
T
(R, P) and
defined by:
Θ
T
(R, P) = dom(R) \dom(R ∩ P).
• The detector set for partial correctness of program
P with respect to R is denoted by Θ
P
(R, P) and
defined by:
Θ
P
(R, P) = (dom(R) ∩dom(P)) \ dom(R ∩ P).
When we want to refer to a detector set without
specifying a particular standard of correctness (par-
tial, total), we simply say detector set, and we use the
notation Θ(R, P).
Given that detector sets are intended to expose in-
correctness, they are empty whenever there is no in-
correctness to expose; this is formualetd in the fol-
lowing proposition.
Proposition 3. Given a specification R on space S
and a program P on S.
Figure 1: Detector Set of Pprogram P with Respect to Spec-
ification R for Total Correctness.
Figure 2: Detector Set of Pprogram P with Respect to Spec-
ification R for Partial Correctness.
• Program P is totally correct with respect to spec-
ification R if and only if Θ
T
(R, P) =
/
0.
• Program P is partially correct with respect to
specification R if and only if Θ
P
(R, P) =
/
0.
2.5 Relative Correctness
Whereas absolute correctness is the property of a pro-
gram to be (totally or partially) correct with respect to
a specification, relative correctness is the property of a
program to be more-correct than another with respect
to a specification. It is natural to define relative cor-
rectness by means of detector sets: a program grows
more and more (totally or partially) correct as its (total
or partial) detector set grows smaller (in the sense of
inclusion), culminating in absolute correctness when
its detector set is empty. But relative total correctness
has already been defined, in (Diallo et al., 2015); be-
fore we redefine it using a new formula, we ensure
that the original formula is equivalent to the detector
set-based formula we envision in this paper.
Proposition 4. Given a program P and a specifica-
tion R, the following two conditions are equivalent:
f 1 : dom(R ∩ P) ⊆ dom(R ∩P
′
).
f 2 : Θ
T
(R, P
′
) ⊆ Θ
T
(R, P).
Definition 4. We consider a specification R on space
S and two programs P and P
′
on S.
ICSOFT 2023 - 18th International Conference on Software Technologies
290

Table 1: Definitions of Correctness by Means of Detec-
torSets.
Partial
Correctness
Total
Correctness
Absolute Correctness
P absolutely correct iff: Θ
P
(R, P) =
/
0 Θ
T
(R, P) =
/
0
Relative Correctness
P
′
more-correct than P iff:
Θ
P
(R, P
′
)
⊆ Θ
P
(R, P)
Θ
T
(R, P
′
)
⊆ Θ
T
(R, P)
• We say that P
′
is more-totally-correct than P with
respect to R if and only if:
Θ
T
(R, P
′
) ⊆ Θ
T
(R, P).
• We say that P
′
is more-partially-correct than P
with respect to R if and only if:
Θ
P
(R, P
′
) ⊆ Θ
P
(R, P).
Table 1 summarizes and organizes the definitions
of correctness to help contrast them. Note the follow-
ing relation between the detector sets of a program P
with respect to a specification R:
Θ
P
(R, P) = dom(P) ∩Θ
T
(R, P).
From this simple equation, we can readily infer two
properties about absolute correctness and relative cor-
rectness:
• Absolute Correctness. If a program P is totally
correct with respect to specification R, then it is
necessarily partially correct with respect to R.
• Relative Correctness. A program P
′
can be more-
partially-correct than a program P either by be-
ing more-totally-correct (hence reducing the term
Θ
T
(R, P)) or by diverging more widely (hence re-
ducing the term dom(P)), or both.
To illustrate the partial ordering properties of rela-
tive total correctness, we consider the following spec-
ification on space S of integers, defined by
R = {(s, s
′
)|1 ≤ s ≤ 3 ∧ s
′
= s
3
+ 3}.
We consider twelve candidate programs, listed in Ta-
ble 2. Figure 3 shows how these candidate programs
are ordered by relative total correctness; The green
oval shows those candidates that are absolutely cor-
rect, and the orange oval shows candidate programs
that are incorrect; the red oval shows the candidate
programs that are least correct.
3 SEMANTIC COVERAGE
We consider a program P on space S and a specifica-
tion R on S, and we let T be a subset of S. We argue
p
1
p
0
p
2
p
4
p
3
p
5
p
7
p
6
p
8
p
10
p
9
p
11
- - 
- - 
6
6
6
6
6
6
6
6















*
@
@
@
@
@I
H
H
H
H
H
H
H
H
H
H
HY
@
@
@
@
@I





@
@
@
@
@I










@
@
@
@
@I















*
@
@
@
@
@I
H
H
H
H
H
H
H
H
H
H
HY
@
@
@
@
@I








'
&
$
%





@
@
@
@
@I
Figure 3: Ordering Candidate Programs by Relative Total
(and Partial) Correctness with Respect to R.
that the purpose of test suite T is to prove or disprove
the correctness of P with respect to R: T ought to be
sufficiently thorough that, if P is incorrect with re-
spect to R, then testing it on T ought to expose the
incorrectness of P.Since the detector set of a program
includes all the initial states on which execution of P
fails, the effectiveness of a test suite T can be mea-
sured by the extent to which T encompasses all the
elements of Θ(R, P). What precludes a test suite T
from being a superset of Θ(R, P) are the elements of
Θ(R, P) that are outside T , i.e. the set
Θ(R, P) ∩ T.
The smaller this set, the higher the effectiveness of T ;
if we want a measure of effectiveness that increases
with the effectiveness of T , we take the complement
of this set.
Definition 5. We consider a program P on space S
and a specification R on S, and we let T be a subset
of S.
• The semantic coverage of test suite T for the total
correctness of program P with respect to specifi-
cation R is denoted by Γ
TOT
[R,P]
(T ) and defined by:
Γ
TOT
[R,P]
(T ) = T ∪ Θ
T
(R, P).
• The semantic coverage of test suite T for the par-
tial correctness of program P with respect to spec-
ification R is denoted by Γ
PAR
[R,P]
(T ) and defined by:
Γ
PAR
[R,P]
(T ) = T ∪ Θ
P
(R, P).
See Figure 4. If we want to talk about semantic
coverage without specifying the standard of correct-
ness, we use the notation Γ
[R,P]
(T ) defined by:
Γ
[R,P]
(T ) = T ∪ Θ(R, P).
Semantic Coverage: Measuring Test Suite Effectiveness
291

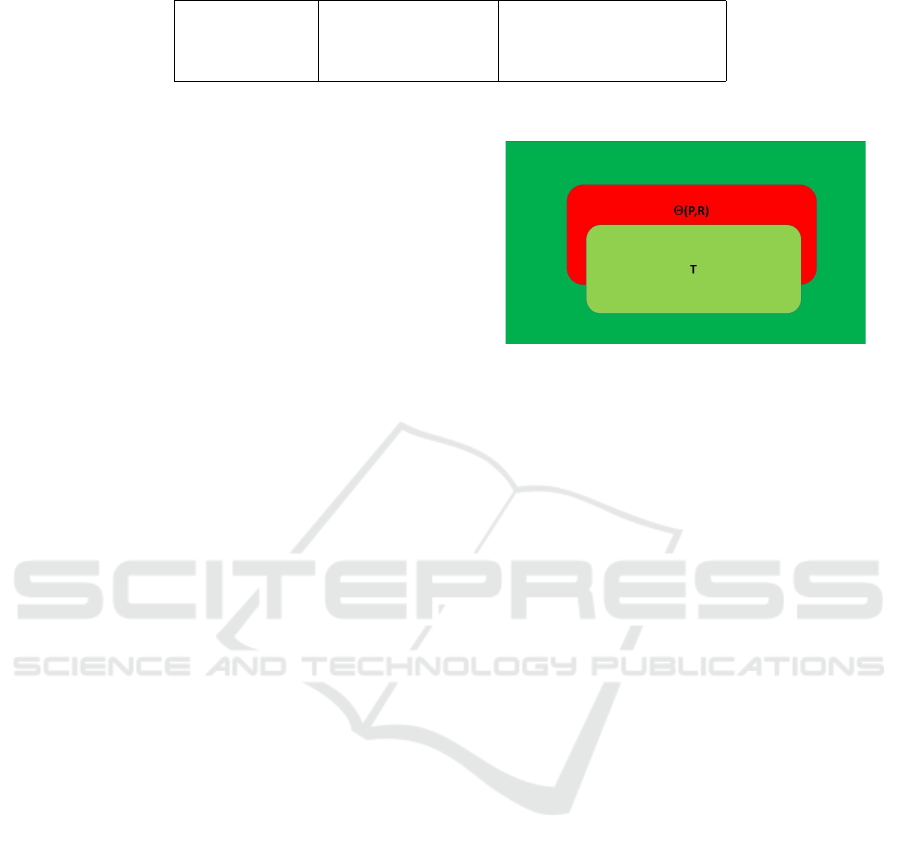
Table 2: Candidate Programs for Specification R.
p0: s=pow(s,3)+4; p4: s=pow(s,3)+s+1; p8: s=pow(s,3)+s*s-4*s+8;
p1: s=pow(s,3)+5; p5: s=pow(s,3)+s; p9: s=2*pow(s,3)-6*s*s+11*s-3;
p2: s=pow(s,3)+6; p6: s=pow(s,3)+s*s-5*s+9; p10:s=3*pow(s,3)-12*s*s+22*s-9;
p3: s=pow(s,3)+s+2; p7: s=pow(s,3)+s*s-3*s+5; p11:s=4*pow(s,3)-18*s*s+33*s-15;
4 ANALYTICAL VALIDATION
In this section we revisit the requirements put forth
in section 1.2 and prove that the formula of seman-
tic coverage proposed above does satisfy all these re-
quirements.
4.1 Rq1: Monotonicity with Respect to
the Test Suite
Definition 5 clearly provides that the semantic cover-
age of a test suite T is monotonic with respect to T .
4.2 Rq2: Monotonicity with Respect to
Relative Correctness
The effectiveness of a test suite increases as the pro-
gram under test grows more (totally or partially) cor-
rect.
Proposition 5. Given a specification R on space S
and two programs P and P
′
on S, and a subset T of S.
If P
′
is more-totally-correct than P with respect to R
then:
Γ
TOT
[R,P
′
]
(T ) ⊇ Γ
TOT
[R,P]
(T ).
Proposition 6. Given a specification R on space S
and two programs P and P
′
on S, and a subset T of S.
If P
′
is more-partially-correct than P with respect to
R then:
Γ
PAR
[R,P
′
]
(T ) ⊇ Γ
PAR
[R,P]
(T ).
4.3 Rq3: Monotonicity with Respect to
Refinement
A test suite T grows more effective as the specifica-
tion against which we are testing the program grows
less-refined.
Proposition 7. Given a program P on space S and
two specifications R and R
′
on S, and a subset T of S.
If R
′
refines R then:
Γ
TOT
[R
′
,P]
(T ) ⊆ Γ
TOT
[R,P]
(T ).
Proposition 8. Given a program P on space S and
two specifications R and R
′
on S, and a subset T of S.
If R
′
refines R then:
Γ
PAR
[R
′
,P]
(T ) ⊆ Γ
PAR
[R,P]
(T ).
Figure 4: Semantic Coverage of Test T for Program P with
respect to R (shades of green).
4.4 Rq4: Monotonicity with Respect to
the Standard of Correctness
A test suite T is more effective for testing partial cor-
rectness than for testing total correctness.
Proposition 9. Given a program P on space S, a
specification R on S, and test suite T (subset of S),
the semantic coverage of T for partial correctness of
P with respect to R is greater than or equal to the
semantic coverage for total correctness of P with re-
spect to R.
5 ILLUSTRATION
In this section we report on an experiment in which
we evaluate the semantic coverage of a set of test
suites; the sole purpose of this section is to illustrate
the derivation of semantic coverage on a concrete ex-
ample. We do compare semantic coverage against
mutation coverage, but the intent of this comparison
is not to validate semantic coverage any more than it
is to validate mutation coverage. The sole purpose of
this comparison is to satisfy our curiosity about how
these two criteria rank sample test suites.
We consider the Java benchmark program of jTer-
minal, an open-source software product routinely
used in mutation testing experiments (Parsai and De-
meyer, 2017). We apply the mutant generation tool
LittleDarwin in conjunction with a test generation
and deployment class that includes 35 test cases (Par-
sai and Demeyer, 2017); we augment the bench-
mark test suite with two additional tests, intended to
trip the base program jTerminal, by causing it to di-
ICSOFT 2023 - 18th International Conference on Software Technologies
292

verge.Application of LittleDarwin to jTerminal yields
94 mutants, numbered m1 to m94; the test of these
mutants against the original using the selected test
suite kills 48 mutants. Some of these mutants are
equivalent to each other, i.e. they produce the same
output for all 37 elements of T ; when we partition
these 48 mutants by equivalence, we find 31 equiva-
lence classes, and we select a mutant from each class;
we let µ be this set. Orthogonally, we consider set T
and we select twenty subsets thereof, derived as fol-
lows:
• T1, T2, T3, T4, T5: Five distinct test suites ob-
tained from T by removing 5 elements at random.
• T6, T7, T8, T9, T10: Five distinct test suites ob-
tained from T by removing 10 elements.
• T11, T12, T13, T14, T15: Five distinct test suites
obtained from T by removing 15 elements.
• T16, T17, T18, T19, T20: Five distinct test suites
obtained from T by removing one element.
Whereas mutation coverage is usually quantified by
the mutation score (the fraction of killed mutants), in
this paper we represent it by mutation tally, i.e. the set
of killed mutants; we compare test suites by means of
inclusion relations between their mutation tallies; like
semantic coverage, this defines a partial ordering. We
use two mutant generators, hence we get two order-
ing relations between test suites. To compute the se-
mantic coverage of these test suites, we consider two
standards of correctness (partial, total) and two spec-
ifications: We choose (the functions of) two mutants,
M25 and M50, as specifications.
Hence we get six graphs on nodes T 1...T 20, rep-
resenting six ordering relations of test suite effective-
ness. Due to space limitations, we do not show these
graphs, but we show in Table 3 the similarity ma-
trix between these six graphs; the similarity index be-
tween two graphs is the ratio of the number of com-
mon arcs over the total number of arcs.
6 CONCLUSION
6.1 Summary
In this paper, we define detector sets for partial cor-
rectness and total correctness of a program with re-
spetc to a specification, and we use them to define ab-
solute (partial and total) correctness as well as relative
(partial and total) correctness. Also, we use detector
sets to define the semantic coverage of a test suite, a
measure of effectiveness which reflects the extent to
which a test suite is able to expose the failure of an
incorrect program or, equivalently, the level of confi-
dence it gives us in the correctness of a correct pro-
gram. We illustrate the derivation of semantic cover-
age of sample test suites on a benchmark example.
6.2 Assessment
We do not validate our measure of effectiveness em-
pirically, as we do not know what ground truth to
validate it against; but we prove that it has a num-
ber of important properties, such as: monotonicity
with respect to the standard of correctness; mono-
tonicity with respect to the refinement of the specifi-
cation against which the program is tested; and mono-
tonicity with respect to the relative correctness of the
program.
Other attributes of semantic coverage include that
it is based on failures rather than faults, hence is
defined formally using objectively observable effects
rather than hypothesized causes. Also, semantic cov-
erage defines a partial ordering between test suites, to
reflect the fact that test suite effectiveness is itself a
partially ordered attribute.
6.3 Threats to Validity
The main difficulty of the proposed coverage metric is
that it assumes the availability of a specification, and
that its derivation requires a detailed semantic analy-
sis of the program. Yet as a formal measure of test
suite effectiveness, semantic coverage can be used for
reasoning analytically about test suites, or for com-
paring test suites even when their semantic coverage
cannot be computed; for example, we may be able to
compare Γ
[R,P]
(T ) and Γ
[R,P]
(T
′
) for inclusion with-
out necessarily computing them, but by analyzing T ,
T
′
, dom(P), dom(R), and dom(R ∩P).
6.4 Related Work
Coverage metrics of test suites have been the focus of
much reserch over the years, and it is impossible to do
justice to all the relevant work in this area (Hemmati,
2015; Gligoric et al., 2015; Andrews et al., 2006); as
a first approximation, it is possible to distinguish be-
tween code coverage, which focuses on measuring the
extent to which a test suite exercises various features
of the code, and specification coverage, which focuses
on measuring the extent to which a test suite exer-
cises various clauses or use cases of the requirements
specification. This can be tied to the orthogonal ap-
proaches to test data generation, using, respectively,
structural criteria and functional criteria. Mutation
coverage falls somehow outside of this dichotomy, in
Semantic Coverage: Measuring Test Suite Effectiveness
293

Table 3: Graph Similarity of Semantic Coverage and Mutation Coverage.
Graph
Similarity
Mut.
Tally 1
Mut.
Tally 2
Γ
PAR
[M25,P]
(T )
Γ
PAR
[M50,P]
(T )
Γ
TOT
[M25,P]
(T )
Γ
TOT
[M50,P]
(T )
Mut. Tally,1 1.00 0.43 0.34 0.35 0.34 0.50
Mut. Tally,2 0.43 1.00 0.67 0.70 0.67 0.53
Γ
PAR
[M25,P]
(T ) 0.34 0.67 1.00 0.66 1.0 0.46
Γ
PAR
[M50,P]
(T ) 0.35 0.70 0.66 1.00 0.66 0.62
Γ
TOT
[M25,P]
(T ) 0.34 0.67 1.00 0.66 1.00 0.46
Γ
TOT
[M50,P]
(T ) 0.50 0.53 0.46 0.62 0.46 1.00
that it depends exclusively on the program, not its
specification, and that it operates by applying muta-
tion operators; as such, it has often been used as a
baseline for assessing the effectiveness of other cov-
erage metrics (Andrews et al., 2006; Inozemtseva and
Holmes, 2014). But mutation coverage also depends
on the mutant generator, and can give different values
for different generators.
Our work differs from other research in many
ways: first, semantic coverage is not a number but a
set. Second, semantic coverage is not intrinsic to the
program, but depends also on the correctness standard
and the specification. Third, semantic coverage is fo-
cused on failures rather than faults, since unlike faults,
failures are an objectively observable attribute.
6.5 Research Prospects
We are exploring means to use the definition of se-
mantic coverage to derive a function that is indepen-
dent of the specification, and reflects the diversity of
the test suite. We are also considering to expand the
empirical study of semantic coverage.
ACKNOWLEDGEMENTS
The authors are very grateful to the anonymous re-
viewers for their valuable feedback. This work is par-
tially supported by NSF grant DGE1565478.
REFERENCES
Andrews, J. H., Briand, L. C., Labiche, Y., and Namin,
A. S. (2006). Using mutation analysis for assessing
and comparing testing coverage criteria. IEEE Trans-
actions on Software Engineering, 32(8):608–624.
Avizienis, A., Laprie, J. C., Randell, B., and Landwehr,
C. E. (2004). Basic concepts and taxonomy of de-
pendable and secure computing. IEEE Transactions
on Dependable and Secure Computing, 1(1):11–33.
Diallo, N., Ghardallou, W., and Mili, A. (2015). Correct-
ness and relative correctness. In Proceedings, 37th
International Conference on Software Engineering,
NIER track, Firenze, Italy.
Farooq, S. U., Quadri, S., and Ahmed, N. (2012). Metrics,
models and measurement in software reliability. In
Proceedings, SAMI 2012, Herlany, Slovakia.
Gligoric, M., Groce, A., Zhang, C., Sharma, R., Alipour,
M. A., and Marinov, D. (2015). Guidelines for
coverage-based comparisons of non-adequate test
suites. ACM Transactions on Software Engineering
and Methodology (TOSEM), 24(4):1–33.
Hehner, E. C. (1992). A Practical Theory of Programming.
Prentice Hall.
Hemmati, H. (2015). How effective are code coverage cri-
teria? In 2015 IEEE International Conference on
Software Quality, Reliability and Security, pages 151–
156. IEEE.
Inozemtseva, L. and Holmes, R. (2014). Coverage is not
strongly correlated with test suite effectiveness. In
Procedings, 36th International Conference on Soft-
ware Engineering. ACM Press.
Just, R., Jalali, D., Inozemtseva, L., Ernst, M., Holmes, R.,
and Fraser, G. (2014). Are mutants a valid substitute
for real faults in software testing? In Proceedings,
FSE.
Mathur, A. P. (2014). Foundations of Software Testing.
Pearson.
Morgan, C. C. (1998). Programming from Specifications,
Second Edition. International Series in Computer Sci-
ences. Prentice Hall, London, UK.
Parsai, A. and Demeyer, S. (2017). Dynamic mutant sub-
sumption analysis using littledarwin. In Proceedings,
A-TEST 2017, Paderborn, Germany.
ICSOFT 2023 - 18th International Conference on Software Technologies
294