Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption
Scheme
Muhammad Nauman Khan
1,2 a
, Asha Rao
1 b
, Seyit Camtepe
2 c
and Josef Pieprzyk
2,3 d
1
School of Science, RMIT University, Australia
2
CSIRO DATA61, Australia
3
Institute of Computer Science, Polish Academy of Sciences, Warsaw, Poland
Keywords:
Attribute-Based Encryption, Identity-Based Encryption, Proxy Re-Encryption, Post-Quantum Cryptography,
Data Confidentiality.
Abstract:
Maintaining data confidentiality at the asymmetric-resource devices across emerging technologies needs vary-
ing cryptographic algorithms. Quantum computing makes preserving data confidentiality across asymmetric
infrastructure more difficult. However, exploiting the architecture of classical cryptographic schemes to in-
tegrate the post-quantum constructs could be used to maintain post-quantum level confidentiality over the
Internet. This paper presents a post-quantum secure classical ABE-IBE proxy re-encryption scheme (L
ABE-
IBE PRE) that utilizes the classical ABE-IBE proxy re-encryption capabilities at the end nodes in a system
and raises the data confidentiality to post-quantum secure level over the Internet. The proposed L ABE-IBE
PRE transforms a ciphertext of the classical ABE scheme to a post-quantum secure ciphertext and from a post-
quantum secure ciphertext to a ciphertext of the classical IBE scheme. We compare our proposed L ABE-IBE
PRE scheme with classical ABE-IBE proxy re-encryption schemes, including Encryption Switching ABE-IBE
(ES.ABE-IBE) scheme (He et al., 2019). We discuss the security and efficiency of our proposed scheme.
1 INTRODUCTION
Integrating asymmetric devices with emerging tech-
nologies (IoT, edge, fog, cloud and quantum) opens
up new opportunities but poses new security chal-
lenges (Lohachab and Karambir, 2019). For exam-
ple, data encrypted using lightweight cryptographic
mechanisms for resource-limited devices become vul-
nerable over resourceful devices. Similarly, classical
cryptographic primitives do not address the security
needs of resource-constrained devices. Thus, exist-
ing classical cryptography does not address the se-
curity of the growing number of asymmetric devices
over the Internet. Resource-limited devices can use
resourceful parties (edge or fog platforms) for com-
putation, but these parties work in less secure envi-
ronments with a significant risk of attacks (such as
man-in-the-middle, denial-of-service) (Roman et al.,
2018). Despite this, outsourcing data to more re-
a
https://orcid.org/0000-0002-3413-1039
b
https://orcid.org/0000-0001-6222-282X
c
https://orcid.org/0000-0001-6353-8359
d
https://orcid.org/0000-0002-1917-6466
sourceful parties (cloud, edge, and fog) continues to
grow.
Identity-based encryption (IBE) and attribute-
based encryption (ABE) schemes provide fine-grain
access control over outsourced data. Proxy re-
encryption schemes, such as ABE-IBE or IBE-ABE,
have been developed for secure data outsourcing from
one domain to another without compromising the
sender’s privacy. However, these schemes ignore the
asymmetric nature of devices across the IT infras-
tructure. Furthermore, quantum computing tips the
balance against asymmetric devices using classical
cryptography. In this paper, we propose a proxy re-
encryption scheme that transforms the existing classi-
cal ciphertext to a post-quantum one for secure data
outsourcing via the insecure Internet.
This paper is organised as follows: Section 2 illus-
trates the related work. Section 3 discusses the prob-
lem statement and motivation. Section 4 gives basic
mathematical preliminaries and notations. Section 5
describes our proposed scheme. Section 6 evaluates
the security and Section 7 illustrates the efficiency of
proposed scheme. Section 8 concludes this paper.
Khan, M., Rao, A., Camtepe, S. and Pieprzyk, J.
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme.
DOI: 10.5220/0012078200003555
In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 85-98
ISBN: 978-989-758-666-8; ISSN: 2184-7711
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
85

2 RELATED WORK
The asymmetric nature of devices significantly af-
fects data outsourcing/data sharing between parties
via an insecure Internet. Several classical crypto-
graphic primitives have been developed to address the
security of individual or group devices. However,
none of these primitives addresses the security of dis-
persed and asymmetric devices and secure data out-
sourcing requirements.
Shamir (1985) proposed the first IBE scheme that
applies public identity information (such as email ad-
dresses) as public keys. IBE scheme based on bilin-
ear pairings was proposed by (Boneh and Franklin,
2001). IBE has been extensively studied, see for ex-
ample Hofheniz et al. (2018), as it simplifies pub-
lic key management without public-key infrastructure
(PKI) and certificates, and also improves efficiency
and security of asymmetric devices (Xiong et al.,
2019).
Sahai and Waters (2005) proposed the first
attribute-based encryption (ABE) scheme that re-
places the identity with attributes of an intended re-
ceiver and provides better access control over data.
Many ABE variants have been proposed, see (Li et al.,
2018, Chen et al., 2018, Li et al., 2019, Miao et al.,
2021, Li et al., 2020). Extensible and expandable
ABE methods (Susilo et al., 2017, Yang et al., 2018)
provide secure data sharing between entities. How-
ever, these methods require the valid recipients to sat-
isfy the access policies, which need to be continu-
ously updated by adding or revoking entities.
The first proxy re-encryption (PRE) scheme was
developed by Blaze et al. (1998) to transform a ci-
phertext encrypted for one receiver into a ciphertext
that a different receiver could decrypt. Several ABE-
IBE and IBE-ABE proxy re-encryption schemes have
been developed (Cao et al., 2019, He et al., 2019,
Deng et al., 2020). The security of these proxy re-
encryption schemes depends on bilinear pairing, mak-
ing them all insecure against a quantum adversary.
Post-quantum cryptography such as lattice-based
cryptography (LBC ) applies quantum intractable lat-
tice problems for designing new cryptographic algo-
rithms and protocols or re-designing existing classical
cryptography schemes to withstand quantum adver-
saries (Banerjee et al., 2019, Nejatollahi et al., 2019,
Fern
´
andez-Caram
´
es, 2020, Tao et al., 2023). LBC
also provides a rich source of cryptographic tools for
secure data sharing through resource-rich Internet or
cloud nodes.
The first LBC scheme was proposed by Ajtai
(1996) and Regev (2009) giving a rigorous security
proof of the scheme. Security of lattice-based cryp-
Figure 1: ABE-IBE Proxy Re-encryption between Alice
and Bob through Untrusted Cloud Environment.
tographic schemes depends upon intractable lattice
problems (Peikert, 2016) such as learning with er-
rors (LWE). Lattices are considered the best choice
for the design of new post-quantum cryptographic al-
gorithms and protocols in the research community.
3 PROBLEM STATEMENT
Existing classical cryptographic schemes includ-
ing ABE and IBE are vulnerable to quantum at-
tacks (Shor, 1999). It is possible to address this prob-
lem by using quantum-resistant cryptographic primi-
tives such as lattices (Asif, 2021). NIST has published
the post-quantum security recommendations for com-
mercial entities (Joseph et al., 2022). However, these
primitives have not been thoroughly tested, making it
highly likely that they will continue co-existing with
classical cryptography.
In this paper, we propose the transformation of
classical ciphertext to post-quantum secure ciphertext
using a proxy re-encryption scheme and vice versa.
Here, we solve the following problem.
How do we securely share data between two local do-
mains via the Internet under the following assumptions:
• The local domains (consisting of classical asymmet-
ric devices) predominantly use classical encryption,
and are not accessible to quantum adversaries.
• The Internet domain (consisting of cloud or quantum
devices) supports post-quantum cryptography and is
accessible to quantum adversaries.
This research aims to design a classical to
post-quantum secure ABE-IBE proxy re-encryption
(L ABE-IBE PRE) scheme for secure data sharing
between the two local domains. For this purpose, we
adapt the ABE-IBE proxy model defined by He et al.
(2019) and Deng et al. (2020) to incorporate post-
quantum secure primitives (lattice-based encryption),
transforming a classical ciphertext (ABE) to a post-
quantum secure ciphertext for secure data sharing.
SECRYPT 2023 - 20th International Conference on Security and Cryptography
86

Figure 2: Proxy Re-encryption on Edge Nodes for secure
communication between Alice and Bob via unsecure and
untrusted network with the presence of quantum adversary.
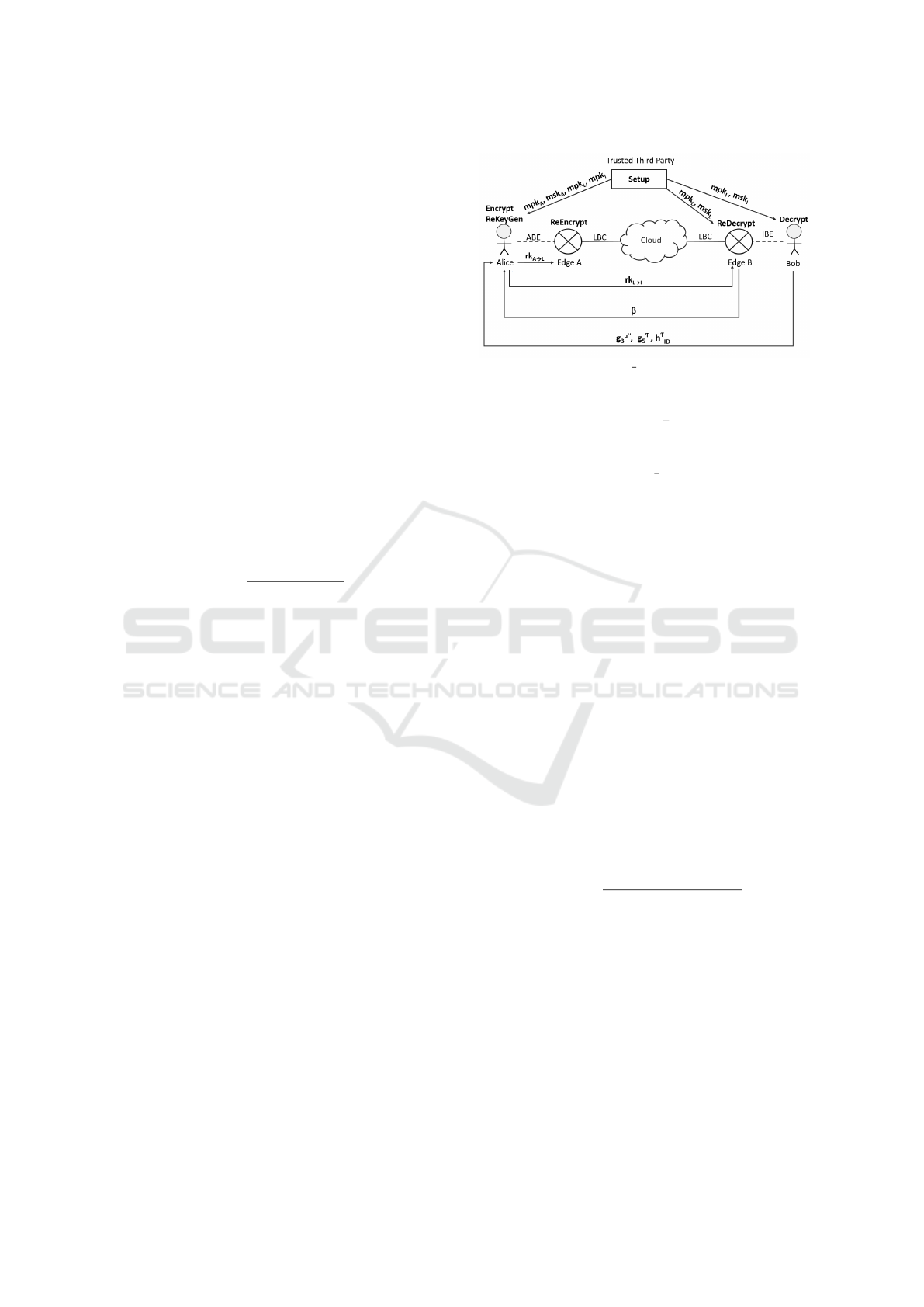
The idea is illustrated in Fig. 1. Consider a com-
pany ABC with two isolated departments, A and B
(local domains). Alice and Bob work in departments
A and B, respectively. Department A deploys several
asymmetric devices connected to a local Edge node
to monitor the environment (such as an early storm
warning system). The data inside Department A is en-
crypted using an access-control policy (ABE) based
on the attributes of the devices and people working in
Department A. Bob is interested in the encrypted data
from department A. When he asks Alice for the data,
she uses the ABE-IBE proxy (He et al., 2019) model
to allow him to access data without changing depart-
ment A’s access-control policy. That is, ABE-IBE re-
encryption facilitates one-way data sharing over the
Internet. Once quantum adversaries are allowed over
the Internet, the ABE-IBE cryptographic scheme (He
et al., 2019) becomes vulnerable due to the Shor al-
gorithm (Monz et al., 2016).
To solve this problem, we propose secure proxy
re-encryption at the local Edge nodes, which “isolate”
the local domains from the untrusted Internet – see
Fig. 2. Alice sends ABE ciphertext (secure against
a classical adversary) to the local Edge node (in her
local domain), which re-encrypts the ABE ciphertext
to post-quantum secure ciphertext (secure against the
quantum adversary) and either stores it on cloud or
sends it to Bob’s local domain via the insecure Inter-
net. When Bob requests the outsourced ciphertext, the
local Edge node on his side receives it and applies re-
decryption to transform the post-quantum secure ci-
phertext to IBE ciphertext. Finally, Bob decrypts the
generated IBE ciphertext using his private key.
This scenario motivates our work, and our solu-
tion applies novel classical to post-quantum secure
ABE-IBE proxy re-encryption (L ABE-IBE) to se-
cure data over the Internet from quantum adversaries.
The main contributions in this paper are:
• We design a proxy re-encryption scheme
(L ABE-IBE PRE) that securely transforms
the attribute-based ciphertext to post-quantum
secure ciphertext (at sender’s local Edge-A) and
post-quantum secure ciphertext to identity-based
ciphertext (at receiver’s Edge-B). Our scheme
is post-quantum-safe because its security relies
on the quantum intractability of NP-hard lattice
problems.
• Our scheme provides an effective and secure com-
munication channel between two local domains
via an insecure cloud/Internet that could be con-
trolled by a powerful quantum adversary. The
re-encryption operations are performed by local
Edge nodes – see Fig. 2.
• We evaluate the performance and security of
our scheme. We also demonstrate that our
scheme is selectively secure against indistinguish-
able chosen-ciphertext attacks (IND-sCCA).
4 PRELIMINARIES
This section illustrates the mathematical definitions,
notations, and concepts related to bilinear pairing and
lattice-based cryptography.
4.1 Bilinear Pairing
Definition 4.1 (Bilinear Pairing (Deng et al., 2014)).
Given cyclic groups G
1
, G
2
and G
T
of prime order p,
where g
1
is a generator of G
1
and g
2
is a generator
of G
2
, a bilinear pairing is a map e : G
1
× G
2
→ G
T
with the following properties:
i. Bilinearity: ∀
h
1
,h
2
∀
a,b
e(h
a
1
,h
b
2
) = e(h
1
,h
2
)
ab
,
where h
1
∈ G
1
,h
2
∈ G
2
and a,b ∈ Z
p
.
ii. Non-degeneracy: e(g
1
,g
2
) ̸= 1.
iii. For G
1
and G
2
, there exists an algorithm that can
efficiently compute the bilinear map e : G
1
× G
2
→ G
T
. □
The bilinear map e(,) is symmetric if G
1
= G
2
.
Definition 4.2 (Linear Secret Sharing Scheme
(LSSS) (Beimel, 1996, Susilo et al., 2017)). Given a
set of n parties P = {P
1
,P
2
,...,P
n
} as an access struc-
ture, a secret sharing scheme Π is a LSSS over Z
p
if
i. Each party’s shares of the secret form a vector
over Z
p
.
ii. There is an (l × n) matrix M (share generating)
matrix. The i
th
row of M, M
i
is assigned to the
party P
i
according to a function ρ(i), for all i =
1,...,n. Let vector v = (s,r
2
,...,r
n
), where s ∈
Z
p
is the secret to be shared and r
2
,...,r
n
∈ Z
p
randomly chosen, then M · v represents l shares of
s. The share of P
i
is given by λ
i
= M
i
· v. □
Recovery of a secret proceeds as follows. Given
an authorized set
b
U ∈ U and I ⊆ {1, 2, · · · ,l} defined
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme
87

as I = {i : ρ(i) ∈
b
U}, then there exist some constants
{ω
i
∈ Z
p
} such that
∑
l
i
ω
i
λ
i
= s for each valid share
{λ
i
} of secret s.
Definition 4.3 (Computational Bilinear Diffie-Hell-
man (CBDH) Problem (Joux and Nguyen, 2003)).
Let e : G
1
× G
2
→ G
T
be a non-degenerate bilinear
pairing. Then
• The bilinear Diffie-Hellman problem 1 (BDH-1)
asks to find z = e(R,S)
ab
for given R,aR,bR ∈ G
1
,
S ∈ G
2
and random a,b.
• The bilinear Diffie-Hellman problem 2 (BDH-2)
asks to find z = e(R,S)
ab
for given R ∈ G
1
, S, aS,
bS ∈ G
2
and random elements a,b.
4.2 Lattices
Definition 4.4 (Lattices (Micciancio and Regev,
2009)). Given a collection B = {b
1
,...,b
n
} consist-
ing of n linearly independent vectors b
1
,...,b
n
∈ R
m
,
an n-dimensional lattice Λ generated by B (further
called a basis) is defined as:
Λ = L(b
1
,. .. ,b
n
) = {
n
∑
i=1
c
i
· b
i
: c
i
∈ Z
n
, ∀1 ≤ i ≤ n}, (1)
where n is the rank of lattice Λ. Λ is called full rank
if and only if n = m. □
Definition 4.5 (q-ary Lattice (Micciancio and Regev,
2009)). Given a vector ⃗u ∈ Z
n
q
and a matrix A ∈ Z
n×m
q
,
whose entries are chosen uniformly at random, a q-
ary lattice for prime q is defined as:
Λ
⃗u
q
(A) := {⃗e ∈ Z
m
s.t. A⃗e =⃗u(mod q)},
Λ
⊥
q
(A) := {⃗e ∈ Z
m
s.t. A⃗e = 0(mod q)}.
(2)
The security of LBC schemes rests on the in-
tractability assumptions of lattice problems, such as
learning with error (Lindner and Peikert, 2011).
4.2.1 Learning with Error (LWE)
Let Ψ be a security parameter and X = X (Ψ) be a
Gaussian distribution over Z
q
(Gentry et al., 2008).
The LW E
n,m,q,X
assumption requires that, if A ∈
Z
m×n
q
,
⃗
s ∈ Z
n
q
, ⃗e ∈ X
m
, ⃗u ∈ Z
m
q
, then (A,A
⃗
s +⃗e) ≈
c
(A,⃗u), where ≈
c
is computational approximation.
The prime q must be sufficiently large such that
∑
i∈S
e
i
≤ q/4 holds.
Definition 4.6 (TrapGen (Micciancio and Peikert,
2012)). Let A ∈ Z
n×m
q
and G ∈ Z
n×(k−1)z
q
be matrices
with m ≥ z ≥ n and k ≥ 2. A trapdoor for A is a ma-
trix T
A
∈ Z
m×(k−1)z
, where m = m+(k −1)z, such that
A

T
A
I

= HG for some invertible matrix H ∈ Z
n×n
q
and identity matrix I ∈ Z
(k−1)z×(k−1)z
. H is the tag
matrix and can be the identity matrix I.
5 PROPOSED SCHEME
In this section, we detail the algorithms related to the
basic building blocks (ABE, IBE and Lattice-based
cryptographic) and then use these algorithms to con-
struct our proposed scheme.
5.1 Building Blocks
We start with the mathematical details of ABE, IBE
and Lattice-based schemes.
5.1.1 ABE
The Waters (2011) scheme consists four algorithms:
Setup
ABE
(U): Let U be a set of attributes, and G
1
and G
2
cyclic groups of prime order p with the bi-
linear pairing (Definition 4.1). First choose g
1
∈ G
1
,
g
2
∈ G
2
and random elements h
1
,...,h
l
∈ G
2
associ-
ated with attributes from U, where l is the number of
attributes. In addition, choose two random exponents
α
A
, a ∈ Z
p
(where the A in α
A
represents ABE). The
function Setup
ABE
outputs a master public key mpk
A
and a master private key msk
A
as follows:
mpk
A
= (g
1
,e(g
1
,g
2
)
α
A
,g
a
2
,h
1
,...,h
l
), msk
A
= g
α
A
2
.
(3)
Encrypt
ABE
(mpk
A
,M ,(M, ρ)): It takes mpk
A
, a message
M and access structure (M, ρ), where M is the share
generating matrix and ρ is a function that links at-
tributes in U to the rows of M (Definition 4.2). Choose
a random secret s and variables y
2
,...,y
n
∈ Z
P
, and
define a vector v = (s,y
2
,...,y
n
) ∈ Z
n
p
. Then calcu-
late λ
i
= M
i
· v from (Definition 4.2). The Encrypt
ABE
function chooses random r
1
,...,r
l
∈ Z
p
and calculates
ciphertext C
A
= (C,C
′
,{C
i
,D
i
}
l
i=1
) as follows:
C = M · e(g
1
,g
2
)
α
A
s
, C
′
= g
s
1
,
{C
i
= g
aλ
i
2
h
−r
i
i
, D
i
= g
r
i
1
}
i∈I
.
(4)
The Encrypt function outputs C
A
.
KeyGen
ABE
(mpk
A
,msk
A
,
b
U): Given the master public
key mpk
A
, the master secret key msk
A
, an attributes
set
b
U and a random t ∈ Z
p
, generate a private key
sk
S
= (K,L,K
ρ(i)
) as follows:
K = g
α
A
2
g
at
2
,L = g
t
1
, ∀ρ(i) ∈
b
U,i ∈ I : K
ρ(i)
= h
t
i
.
(5)
Decrypt
ABE
(C
A
,sk
S
): Given mpk
A
, sk
S
, and U, which
qualifies access structure (M,ρ) and I ⊂ {1,2,...,l}
as I = {i : ρ(i) ∈
b
U}, there exists a set of constants
{ω
i
∈ Z
p
}
i∈I
} such that
∑
i∈I
ω
i
λ
i
= s (Definition 4.2).
The Decrypt
ABE
function decrypts as follows:
M =
C ·
∏
i∈I

e(L,C
i
) · e(D
i
,K
ρ(i)
)

ω
i
e(C
′
,K)
,
=
M · e(g
1
,g
2
)
α
A
s
·
∏
i∈I
e(g
1
,g
2
)
aω
i
λ
i
t
e(g
1
,g
2
)
α
A
s
· e(g
1
,g
2
)
ast
.
(6)
SECRYPT 2023 - 20th International Conference on Security and Cryptography
88

5.1.2 IBE
The IBE scheme designed by Boneh and Boyen
(2004) is a collection of four algorithms.
Setup
IBE
: Let G
1
and G
2
be cyclic groups of prime
order p (Definition 4.1). First, choose elements
g
5
,h
ID
∈ G
1
, g
3
,g
4
∈ G
2
, and α
I
∈ Z
p
(where the I
in α
I
represents IBE) to calculate g
4
= g
3
α
I
. Then,
Setup
IBE
outputs a master public key mpk
I
and a mas-
ter secret key msk
I
as follows:
mpk
I
= (g
3
, g
4
, g
5
, h
ID
), msk
I
= α
I
.
(7)
Encrypt
IBE
(mpk
I
,M ,ID): Taking an identity ID, mpk
I
and M ∈ G
T
as input and choosing random w
′
∈ Z
p
to output a ciphertext C
I
as follows:
C
I
= (C
1
I
,C
2
I
,C
3
I
) = (g
w
′
3
,(g
ID
5
h
ID
)
w
′
,M .e(g
5
,g
4
)
w
′
). (8)
KeyGen
IBE
(mpk
I
,msk
I
,ID): Given mpk
I
, msk
I
and ID as
input, this function picks a random u ∈ Z
p
and gener-
ates a private key sk
ID
for ID as follows:
sk
ID
= (SK
1
ID
,SK
2
ID
) = (g
α
I
5
(g
ID
5
h
ID
)
u
,g
u
3
). (9)
Decrypt
IBE
(C
I
,sk
ID
): Given CT
ID
and sk
ID
as input,
this function computes M as follows:
M =
C
3
I
· e(C
2
I
,SK
2
ID
)
e(SK
1
ID
,C
1
I
)
. (10)
5.1.3 Learning with Error - Lattice-Based
Cryptography (LWE-LBC)
LWE-LBC (Lindner and Peikert, 2011) scheme is a
collection of the following four algorithms.
Setup
LBC
takes a system security parameter Ψ and de-
fines X = X (Ψ) to be a Gaussian distribution D
Z
q
. It
chooses positive integers m, n, q, where q is prime,
and generates a lattice (Definition 4.4) of n linearly
independent vectors of length m with an m × n ma-
trix A = {a
1
,...,a
n
} ∈ Z
n
q
using uniform distribution
and a trapdoor T
A
using TrapGen(n) (Definition 4.6),
where the master public key mpk
L
= A and the master
secret key msk
L
= T
A
.
KeyGen
LBC
(A,m,n,q,X ) takes positive integers m, n,
q, and X as input and chooses random error vector
{e
1
,...,e
m
} ∈ X . Then it chooses uniform short vector
γ ∈ Z
n
q
from a Gaussian distribution for basis of T
A
as
a secret key and generates the public key as follows:
pk
L
= {β
i
}
n
i=1
where β
i
=< A,γ > +e
i
mod q.
(11)
Encrypt
LBC
(mpk
L
,pk
L
,M ) takes mpk
L
, pk
L
and m ∈ M
as input. Then, it chooses random s
′
∈ Z
m
q
to generate
the ciphertext C
L
= (u,v) as follows:
u := (A
T
s
′
+ e
1
) v := β
T
s
′
+ e
2
+ ⌈q/2⌋.m. (12)
Decrypt
LBC
(C
L
,γ): This function takes a secret key γ
and C
L
and outputs a message m ∈ M as follows:
m := (v − γ
T
u). (13)
Figure 3: Construction of L ABE-IBE Proxy Re-encryption
Scheme between Alice and Bob.
5.2 Construction of L ABE-IBE PRE
We construct a classical to post-quantum secure ABE-
IBE proxy re-encryption (L ABE-IBE PRE) scheme
using the basic building blocks. Our scheme consists
of seven algorithms, and four of them are as follows:
• Setup = ⟨Setup
ABE
,Setup
IBE
,Setup
LBC
⟩.
• KeyGen = ⟨KeyGen
ABE
, KeyGen
IBE
, KeyGen
LBC
⟩.
– Alice chooses a random t ∈ Z
p
and executes
KeyGen
ABE
to generate her private key sk
S
for
a set of attributes U.
– Bob chooses a random u ∈ Z
p
and executes
KeyGen
IBE
for his ID to generate his private key
sk
ID
.
– Edge-B chooses a random uniform secret vec-
tor γ ∈ Z
n
q
and generates β for a uniform random
matrix A using KeyGen
LBC
algorithm.
• Encrypt = ⟨Encrypt
ABE
(mpk
A
,M ,(M, ρ)⟩: Alice ex-
ecutes the Encrypt
ABE
algorithm defined in Eq. (4).
• Decrypt(C
I
,sk
ID
): This function is derived from
Eq. (10). Bob receives an IBE ciphertext C
I
from
Eq. (18) and uses his private key sk
ID
to execute
the following Decrypt algorithm to get a message
M .
M =
C
I
e(sk
1
ID
· (g
ID
5
h
ID
)
u
′
,g
τ
3
)
.
(14)
The other three algorithms are: ReKeyGen, ReEncr ypt
and ReDecrypt.
More precisely, Alice executes ReKeyGen algo-
rithm, and Edge-A and Edge-B execute ReEncrypt and
ReDecrypt algorithms, respectively, and finally Bob
executes Decrypt algorithm (Eq. (14)). The working
of our proposed scheme using these algorithms is il-
lustrated in Fig. 3.
(rk
A→L
,rk
L→I
) ←ReKeyGen(mpk
A
,mpk
I
,mpk
L
,
b
U, ID, sk
S
,
sk
2
ID
′
,g
τ
5
,h
τ
ID
): Given the parameters mpk
A
(Eq. (3)),
mpk
I
(Eq. (7)), mpk
L
(Eq. (11)), Alice’s private key sk
S
,
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme
89

Bob’s identity ID, three components sk
2
ID
′
, g
τ
5
and
h
τ
ID
from Bob, and pk
L
from Edge-B. Alice and Bob
execute the following steps to generate re-encryption
and re-decryption keys:
• Bob chooses two random variables u
′
,τ ∈ Z
p
, and
computes sk
2
ID
′
= sk
2
ID
.g
u
′
3
= g
u
′′
3
and g
τ
5
, where
u + u
′
= u
′′
. Bob shares sk
2
ID
, g
τ
5
, and h
τ
ID
with
Alice.
• Edge-B chooses β and generates a secret γ from
a Gaussian distribution for a uniform random ma-
trix A. Edge-B share β with Alice.
Alice generates the re-encryption key rk
A→L
for Edge-
A and re-decryption key rk
L→I
for Edge-B as follows:
R
a
=K · g
a·ID
2
· sk
2
ID
′
= g
α
A
2
g
at
2
g
a·ID
2
g
u
′′
3
,
R
b
={
ˆ
L,
ˆ
K
ρ(i)
} = {L · g
ID
1
,K
ρ(i)
· h
ID
i
}
ρ(i)∈
b
U
,
R
c
=g
τ·ID
5
· h
τ
ID
, R
d
= ⟨A, β⟩, R
e
= e(g
τ
5
,g
4
).
(15)
Edge-A receives r k
A→L
= (R
a
, R
b
, R
c
, R
d
) to re-
encrypt ABE ciphertext to post-quantum ciphertext
and Edge-B receives rk
L→I
= (R
e
) to transform post-
quantum ciphertext to IBE ciphertext.
C
L
←ReEncrypt(rk
A→L
,C
A
): For rk
A→L
and ABE ci-
phertext C
A
= (C,C
′
,{C
i
,D
i
}
l
i=1
) (Eq. (4)), Edge-A
performs ReEncrypt to output a post-quantum cipher-
text C
L
= (C
1
L
,C
2
L
). Let {ω
i
∈ Z
p
}
i∈I
be a set of con-
stants such that if λ
i
are valid shares of any secret s,
then
∑
i∈I
ω
i
λ
i
= s (Definition 4.2). Then compute C
2
using C
i
and D
i
for all i = 1,··· , l, where
C
′
1
=
C · e(C
′
R
c
,g
u
′′
3
)
e(C
′
,R
a
)
,
C
′
2
=
l
∏
i=1
(e(
ˆ
L,C
i
) · e(D
i
,
ˆ
K
ρ(i)
))
ω
i
.
(16)
C
′
1
and C
′
2
lie on the bilinear vector space e : G
1
×
G
2
→ G
T
. Using the bilinear vector space, given bi-
linear results C
′
1
= {x
1
,y
1
} and C
′
2
= {x
2
,y
2
}, we use
the Encode function as
⃗
a1 = Encode(x
1
,y
1
) where
{a1
1
,··· ,a1
n/2
} ← x
1
and {a1
n/2+1
,··· ,a1
n
} ← y
1
.
Similarly, we use the Encode function for C
′
2
to
get
⃗
a2. Transformed vectors are symmetric, non-
degenerate and bilinear under vector space of map
e. These transformed vectors
⃗
a1 and
⃗
a2 are used as
an input to a black box lattice-based encryption func-
tion (Ioannou and Mosca, 2011) to output the post-
quantum secure ciphertext as follows:
C
1
L
= (u
1
,v
1
) = (A
T
s
′
+ e
1
,β
T
s
′
+ e
2
+ ⌈q/2⌋ ·a1),
C
2
L
= (u
2
,v
2
) = (A
T
s
′
+ e
1
,β
T
s
′
+ e
2
+ ⌈q/2⌋ ·a2),
(17)
where the output is C
L
= (C
1
L
,C
2
L
).
C
I
←ReDecrypt(rk
L→I
,C
L
,γ) takes C
L
, rk
L→I
and a se-
cret vector γ. Edge-B performs ReDecrypt algorithm
and decodes the results to bilinear vectors (Bartocci
et al., 2009) using the Decode function as follows:
r1 := (v
1
− γ
T
u
1
), r2 := (v
2
− γ
T
u
2
),
D
1
L
(x,y) =Decode(r1),
D
2
L
(x,y) =Decode(r2),
C
I
=rk
L→I
· D
1
L
· D
2
L
.
(18)
The ciphertext C
L
is post-quantum secure and
stored on the cloud, while Bob works in the classical
IBE domain. Therefore, the ReDecrypt algorithm on
the Edge-B transforms this post-quantum secure ci-
phertext into classical IBE ciphertext, making it suit-
able for Bob to decrypt using his secret key. More-
over, Edge-B also performs multiplication operations
on decoded ciphertexts to reduce the number of oper-
ations on Bob’s side without leaking any information
about the encrypted message (i.e., IBE ciphertext) to
Edge-B. Bob uses the output ciphertext C
I
to perform
decryption as defined in Eq. (14).
5.3 CBDH Assumption
Given cyclic groups G
1
, G
2
and G
T
of prime order p,
generators g
x
of G
1
and g
y
of G
2
, and bilinear map-
ping e : (G
1
×G
2
) → G
T
(Definition 4.3), let a, b ∈ Z
p
be randomly chosen. Consider a polynomial time ad-
versary A in the CBDH problem who takes the tuple
(G
1
,G
2
, p,g
x
,g
y
,g
a
x
,g
b
x
,g
a
y
,g
b
y
) as an input, and outputs
e(g
x
,g
y
)
ab
with advantage
Adv
A
= Pr
h
A(G
1
,G
2
, p, g
x
,g
y
,g
a
x
,g
b
x
,g
a
y
,g
b
y
) = e(g
x
,g
y
)
ab
i
(19)
Definition 5.1. The CBDH assumption holds if there
exists no PPT adversary with non-negligible advan-
tage (defined above) in solving the CBDH problem.
5.4 Hard Assumptions of L ABE-IBE
The key actors involved are Alice as a sender, Bob as
a receiver, and a trusted third party (TTP). In the pro-
posed scheme, the collusion of all the communicating
parties, except Alice, will not allow an adversary to
retrieve Alice’s secret key. Trusted third parties (TTP)
may be compromised, and corruption of master secret
keys can affect re-encryption and re-decryption algo-
rithms. However, TTP will not leak any information
about Alice and Bob’s encrypted message or secret
keys to adversary at edge nodes.
Moreover, the local edge nodes perform re-
encryption and re-decryption of ciphertexts. How-
ever, the generation of correct or incorrect ciphertexts
SECRYPT 2023 - 20th International Conference on Security and Cryptography
90

from these algorithms entirely depends on parame-
ters, such as master keys, private keys, random and in-
dependent variables. Based on hardness assumptions
i.e., CBDH and LWE, in our proposed L ABE-IBE
PRE scheme, if all the parties involved in communi-
cation are corrupted, the ReEncrypt and ReDecrypt al-
gorithms will still generate random indistinguishable
ciphertexts. In the following subsection, the security
of the proposed scheme is modeled as a game.
5.5 Security Game of Proposed Scheme
The indistinguishability security of our proposed
L ABE-IBE scheme is modeled by a game played be-
tween a challenger C and an adversary A. C generates
L ABE-IBE, while A tries to break it. To start, C gen-
erates the master key pairs (mpk
A
,msk
A
) and (mpk
I
,msk
I
).
A has access to master public keys mpk
I
and mpk
A
,
while master secret keys msk
A
and msk
I
are not known
to A. A then outputs two message m
0
and m
1
from
the message space, an access structure (M, ρ)
∗
for a
set of attributes
b
U
∗
and identity ID
∗
to be challenged.
The challenger C generates two classical challenge ci-
phertexts C
∗
A
and C
∗
I
for the given (M,ρ)
∗
and ID
∗
,
and one post-quantum secure challenge ciphertext C
∗
L
for the given A
∗
and β
∗
. Note a classical adversary A
tries to break C
∗
A
and C
∗
I
while a quantum adversary
A
L
tries to break C
∗
L
.
During the game, A can make private key queries
on any access structure and identity other than the
challenge access structure and challenge identity. In
particular, A can make re-encryption and decryp-
tion queries on ((M, ρ), ID,C
A
,C
I
) satisfying either
(M,ρ) ̸= (M,ρ)
∗
or ID ̸= ID
∗
or C
A
̸= C
∗
A
or C
I
̸= C
∗
I
.
Similarly A
L
make post-quantum encryption queries
on (A,γ,T
A
C
L
), where A ̸= A
∗
or γ ̸= γ
∗
or T
A
̸= T
∗
A
. A
guesses the chosen message in the challenge cipher-
texts C
∗
A
and C
∗
I
, and A
L
guesses the encrypted cipher-
text C
A
in the post-quantum challenge ciphertext C
∗
L
.
Here we only give the classical security game. The
details of post-quantum security of challenge cipher-
text C
∗
L
against A
L
are given under Theorem 3.
The selective indistinguishability game against
chosen-ciphertext attacks (IND-sCCA) is as follows:
1. Setup: Challenger C runs this algorithm to gen-
erate master key pairs (mpk
A
,msk
A
) and (mpk
I
,msk
I
)
and sends mpk
A
and mpk
I
to A, but keeps master
keys msk
A
and msk
I
secret for queries from A.
2. Phase 1: A can make the following queries.
• Key Queries: A chooses a set of attributes
U and an identity ID. Then A makes key
queries and C runs key generation algorithms
KeyGen
ABE
and KeyGen
IBE
to return the sk
S
and
sk
ID
respectively to the A .
• Decryption Queries: For chosen C
A
and C
I
,
the A makes decryption queries. C runs
Decrypt
ABE
and Decrypt
IBE
and returns result to
the A.
• ReKey Queries: A makes re-encryption
key queries on (U,(M, ρ), sk
S
,ID), C runs
ReKeyGen and returns rk
A→L
and rk
L→I
to the A.
3. Challenge: A adaptively chooses two mes-
sages m
0
and m
1
from a message space, an ac-
cess structure (M, ρ)
∗
and an identity ID
∗
to
be challenged. We restrict the access structure
(M,ρ)
∗
and the identity ID
∗
to that not previ-
ously queried in Phase 1. C randomly chooses
c ∈ {0, 1} and computes the two classical chal-
lenge ciphertexts; one before re-encryption C
∗
A
=
E[mpk, (M, ρ)
∗
,m
c
] and other after re-decryption
C
I
∗
= ReDec[rk
∗
L→I
,ReEnc[mpk, rk
∗
A→L
,C
A
∗
]], and
one post-quantum ciphertext C
∗
L
where rk
∗
A→L
̸=
rk
A→L
and rk
∗
L→I
̸= rk
L→I
.
4. Phase 2: C responds to all private-key queries,
re-key queries and decryption queries from A
in the same way as in Phase 1 with restriction
that the A can not make private key queries on
(M,ρ)
∗
and ID
∗
, and no decryption queries on ei-
ther ((M,ρ)
∗
,C
∗
A
) or (ID
∗
,C
∗
I
).
5. Guess: The adversary A outputs a guess c
′
of c
and wins the game if c
′
= c. The advantage ε of
the A in winning this game is defined as
ε = 2(Pr

c
′
= c

− 1/2). (20)
Definition 5.2. The scheme is said to be IND-sCCA
secure, if there exists no probabilistic polynomial time
(PPT) adversary having non-negligible advantage in
the above mentioned game.
5.6 Correctness of L ABE-IBE PRE
We prove the correctness of L ABE-IBE PRE using
the following Theorem.
THEOREM 1 (Correctness). Given a L ABE-IBE
PRE scheme. If the reverse substitution of parame-
ters from the Decrypt function to Encrypt function (from
Section 5) yields the message M , then the scheme is
correct.
Proof: We start with the IBE decryption algorithm
(Eq. (14)) and apply reverse substitution of security
parameters or equations up to the encryption algo-
rithm given in Eq. (4). We start with Eq. (14) and
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme
91

substitute Bob’s private secret key as follows:
M =
C
I
e(sk
1
ID
· (g
ID
5
h
ID
)
u
′
,g
τ
3
)
,
=
C
I
e(g
α
I
5
· (g
ID
5
h
ID
)
u
· (g
ID
5
h
ID
)
u
′
,g
τ
3
)
,
where u + u
′
= u
′′
. Substituting C
I
from Eq. (18):
M =
R
L→I
· D
1
L
· D
2
L
e(g
α
I
5
· (g
ID
5
h
ID
)
u
′′
,g
τ
3
)
.
We apply decode function on D1 and D2 (Eq. (18)),
and re-decryption function for a secret vector γ and
rk
L→I
(Eq. (15)) to reduce the above as:
M =
e(g
τ
5
,g
4
) · (v
1
− γ
T
u
1
) · (v
2
− γ
T
u
2
)
e((g
α
I
5
· g
ID
5
h
ID
)
u
′′
,g
τ
3
)
.
Applying g
4
= g
α
I
3
from Eq. (7), substituting func-
tions from Eq. (17) and Encode to transform resulting
{x
1
,y
1
} and {x
2
,y
2
} to C
′
1
and C
′
2
respectively, gives:
M =
e(g
τ
5
,g
α
I
3
) · {x
1
,y
1
} · {x
2
,y
2
}
e(g
α
I
5
· (g
ID
5
h
ID
)
u
′′
,g
τ
3
)
,
=
C
′
1
·C
′
2
e((g
ID
5
h
ID
)
u
′′
,g
τ
3
)
.
Substituting C
′
1
and C
′
2
from Eq. (16):
M =
C · e(C
′
R
c
,g
u
′′
3
) ·
∏
l
i=1
(e(
ˆ
L,C
i
) · e(D
i
,
ˆ
K
ρ(i)
))
ω
i
e(C
′
,R
a
).e((g
ID
5
h
ID
)
u
′′
,g
τ
3
)
.
Substituting C, C
′
, C
i
and D
i
from Eq. (4):
M =
M · e(g
1
,g
2
)
α
A
s
· e(g
s
1
R
c
,g
u
′′
3
) · e(g
t
1
g
ID
1
,g
as
2
)
e(g
s
1
,R
a
).e((g
ID
5
h
ID
)
u
′′
,g
τ
3
)
,
where
∑
l
i=1
ω
i
λ
i
= s. Applying re-encryption key
rk
A→L
(Eq. (15)) and bilinear pairing properties as fol-
lows.
M =
M · e(g
1
,g
2
)
α
A
s
· e(g
s
1
g
τ·ID
5
h
τ
ID
,g
u
′′
3
) · e(g
t
1
g
ID
1
,g
as
2
)
e(g
s
1
,g
α
A
2
g
at
2
g
a·ID
2
g
u
′′
3
).e((g
ID
5
h
ID
)
u
′′
,g
τ
3
)
,
= M . □
Based on this, we give the following corollary.
Corollary 1.1. If reverse substitution method yields
a message M , then our proposed L ABE-IBE proxy
re-encryption scheme is correct.
6 SECURITY ANALYSIS
We consider the following theorem to analyze that
our proposed L ABE-IBE PRE scheme is selectively
IND-sCCA secure (Section 5.5):
THEOREM 2. Given a L ABE-IBE PRE scheme.
Assuming the CBDH problem is intractable, then the
scheme is IND-sCCA secure.
Sketch of Proof. We illustrate the security of the
proposed scheme as a game played between adversary
A and challenger C . In Setup phase, C computes the
master public keys and shares them with A. In Phase
1, A can make an unlimited number of private key,
re-key, and decryption queries for the challenge ci-
phertexts. Once Phase 1 is over, we restrict A from
making any key or decryption queries to C . Then A
selects two messages from the message space, any at-
tribute set, and identity for a challenge with restric-
tions that A has not queried these attributes and iden-
tity in Phase 1. C randomly selects one of the mes-
sages and computes the challenge ciphertexts using
encryption and re-encryption algorithms. C presents
challenge ciphertexts to A to break. The target of A
is to correctly guess the ciphertext generated from one
of the two known messages. Here the CBDH assump-
tions come into play when C generates the challenge
ciphertexts for A. Moreover, the simulator B sim-
ulates the scheme as closely related to the proposed
scheme as possible such that A cannot distinguish be-
tween the simulated and real schemes. Below in de-
tailed proof, we use B instead of the challenger C to
respond to the adversary’s queries (Guo et al., 2018).
Detailed Proof. Let there exist a PPT adversary
A who can (t,q
k
,q
d
,ε)-break the L ABE-IBE PRE
scheme, where t is time cost, q
k
is number of key
queries, q
d
is number of decryption queries, and ε
is the advantage of A. We construct a simulator B
to solve the CBDH problem. Given the instance of
the problem (g
x
,g
a
x
,g
b
x
,g
c
x
,g
y
,g
a
y
,g
b
y
,g
c
y
) over the pair-
ing group PG = (G
1
,G
2
,G
T
, p,g
x
,g
y
,e) as an input,
B runs A and works as follow:
Init: A outputs an access structure (M,ρ)
∗
and an
identity ID
∗
.
Setup: B randomly selects x
1
,x
2
,x
3
,y
1
,y
2
∈ Z
p
and
computes master public keys:
e(g
1
,g
2
)
α
A
=e(g
x
,g
y
)
x
1
+ab
= e(g
x
,g
y
)
x
1
e(g
x
,g
y
)
ab
,
g
1
=g
x
, g
2
= g
x
2
+a
y
, g
3
= g
y
,
g
4
=g
α
I
3
= g
y
1
+ac
y
= g
y
1
y
g
ac
y
, g
5
= g
b
x
,
where α
A
= x
1
+ab, α
I
= y
1
+ac, and a,b,c are from
problem instance. The master public keys are
mpk
A
= {G
1
,G
2
,G
T
,g
x
,g
x
2
+a
y
,e(g
x
,g
y
)
x
2
e(g
x
,g
y
)
ab
,h
l
i=1
},
mpk
I
= {G
1
,G
2
,G
T
,g
y
,g
y
1
y
g
ac
y
,g
b
x
,h
ID
}.
h
i
Queries: For the set of attributes
b
U, B chooses h
i
for 1 ≤ i ≤ l uniformly from G
2
and sends to A.
h
ID
Queries: For the identity ID, B chooses a random
value h
ID
from G
1
and sends to A.
SECRYPT 2023 - 20th International Conference on Security and Cryptography
92

Phase 1: A makes private-key, re-key, and decryption
queries in this phase. For the private-keys and re-key
queries, A chooses (M, ρ) ̸= (M,ρ)
∗
and ID ̸= ID
∗
.
B chooses t
′
,t
′′
∈ Z
p
and computes
K =g
x
1
+ab
y
g
(x
2
+a)t
′
y
, L = g
t
′
x
,K
i
= h
t
′
i
,
SK
1
ID
=g
b(y
1
+ac)
x
(g
bID
x
h
ID
)
t
′′
, SK
2
ID
= g
t
′′
y
,
and constructs: sk
S
= (K,L,K
i
), sk
ID
= (SK
1
ID
,SK
2
ID
).
For re-key queries, B chooses random τ, t
1
′′
∈ Z
p
where t
′′
+t
′′
1
= t
′′
2
and computes:
R
a
=K.g
(x
2
+a)ID
y
sk
2
ID
′
= g
x
1
+ab
y
g
(x
2
+a)t
′
y
g
(x
2
+a)ID
y
g
t
′′
2
y
,
R
b
=(L · g
ID
x
,K
i
· h
ID
i
) = (g
t
′
x
g
ID
x
,h
t
′
i
h
ID
i
),
R
c
=g
bτID
x
· h
τ
ID
, and R
e
= e(g
bτ
x
,g
y
1
+ac
x
),
where rk
A→L
= (R
a
,R
b
,R
c
) and rk
L→I
= R
e
.
For a decryption queries on ((M,ρ),ID,C
A
,C
I
),
suppose C
A
= (C,C
′
,C
i
,D
i
) and C
I
derives from D
1
L
and D
2
L
. If (M,ρ) ̸= (M, ρ)
∗
and ID ̸= ID
∗
, B gener-
ates the corresponding private keys and re-keys to per-
form decryption of C
A
and C
I
. For (M,ρ) = (M,ρ)
∗
,
B continuous the simulation if it satisfies
∑
i∈I
ω
i
λ
i
=
s for a set of constants ω
i
. If
∑
i∈I
ω
i
λ
i
̸= s, it aborts
the simulation. Then B uses (M,ρ) to compute
d =
∏
i∈I
(e(L,C
i
) · e(D
i
,K
i
))
ω
i
,
=
∏
i∈I

e(g
t
′
x
,g
(x
2
+a)λ
i
y
h
−r
i
i
) · e(g
r
i
x
,h
t
′
i
)

ω
i
,
=
∏
i∈I
e(g
x
,g
y
)
(x
2
+a)ω
i
λ
i
t
′
,
=
∏
i∈I

e(g
x
,g
y
)
x
2
ω
i
λ
i
t
′
· e(g
x
,g
y
)
aω
i
λ
i
t
′

.
Therefore for valid (M,ρ) satisfying
∑
i∈I
ω
i
λ
i
= s,
the simulator B uses d to decrypt C
A
.
Similarly for ID = ID
∗
, B continues the decryp-
tion (Decrypt
IBE
) of C
I
. B searches h
ID
from the list of
h
ID
and chooses random τ, t
′′
2
∈ Z
p
where t
′′
+t
′′
1
= t
′′
2
satisfying ID. B computes d
′
as
d
′
=e

sk
1
ID
· (g
bID
x
h
ID
)
u
′
,g
τ
y

,
=e

g
b(y
1
+ac)
x
(g
bID
x
h
ID
)
t
′′
· (g
bID
x
h
ID
)
t
′′
1
,g
τ
y

,
=e(g
x
,g
y
)
by
1
τ
· e(g
x
,g
y
)
abcτ
· e(g
x
,g
y
)
bIDt
′′
2
τ
· e(h
ID
,g
y
)
t
′′
2
τ
.
Let IDt
′′
2
= −b(y
1
+ ac), then we have d
′
=
e(h
ID
,g
y
)
t
′′
2
τ
. Therefore, B uses d
′
for valid t
′′
2
and
randomly chosen τ to decrypt ciphertext C
I
. Here we
distinguish two cases as follow:
• Case I: For the queries satisfying the conditions
and hash mentioned above, B returns the correct
challenge ciphertext to A.
• Case II: For the queries not satisfying the condi-
tions mentioned in the above equations, the simu-
lator returns incorrect challenge ciphertext to A.
Challenge: A adaptively chooses two distinct mes-
sages m
0
and m
1
, a challenge access structure (M,ρ)
∗
,
and a challenge identity ID
∗
. B randomly flips the
coin c ∈ {0,1} and sets the challenge ciphertext C
∗
A
=
(C
∗
,C
′∗
,C
∗
i
,D
∗
i
) as
C
∗
A
=(m
c
· e(g
x
,g
y
)
(x
1
+ab)s
, g
s
x
,g
(x
2
+a)λ
∗
i
y
h
−r
i
i
, g
r
i
x
).
B returns challenge C
∗
A
to A. At this stage, there
exists the two more cases for computing C
∗
I
from C
∗
A
as follows.
• Case I: B utilizes the challenge C
∗
A
generated in
the above step to compute challenge C
∗
I
.
• Case II: A randomly chooses C
∗
A
and B uses that
C
∗
A
to compute the challenge C
∗
I
.
B computes the challenge C
∗
I
for the identity ID
∗
as
C
∗
I
=rk
∗
L→I
· m
c
· e

(g
bID
∗
x
h
ID
∗
)
τ
,g
t
′′
2
y

,
=e(g
bτ
x
,g
y
1
+ac
y
) · m
c
· e

(g
bID
∗
x
h
ID
∗
)
τ
,g
t
′′
2
y

,
=e(g
x
,g
y
)
bτ(y
1
+ac)
· m
c
· e(g
t
′′
2
y
,g
bτID
∗
x
).e(h
ID
∗
,g
t
′′
2
y
)
τ
,
=e(g
x
,g
y
)
bτ(y
1
+ac)
· m
c
· e(g
x
,g
y
)
bτID
∗
t
′′
2
.e(h
ID
∗
,g
y
)
t
′′
2
τ
.
Therefore, C
∗
A
and C
∗
I
for the message m
c
are cor-
rect from the point of view of A.
Phase 2: Here, A is allowed to make queries similar
as in the Phase 1 with following restrictions:
• No private key queries are allowed on any access
structure (M,ρ)
∗
or identity matching ID
∗
in the
key query phase.
• No decryption queries are allowed on
((M,ρ)
∗
,C
∗
A
), (ID
∗
,C
∗
I
), or ((M, ρ)
∗
,ID
∗
,C
∗
A
,C
∗
I
).
The challenge C
∗
I
can be computed from C
∗
A
or ran-
domly chosen ABE ciphertext using rk
∗
A→L
and rk
∗
L→I
.
Guess: A outputs a guess c
′
of c and wins the game
if c
′
= c. Otherwise, it outputs ⊥.
According to the simulation, B can compute pri-
vate keys and re-encryption keys for (M, ρ) and ID.
Then, B performs the decryption simulation correctly.
For the hash queries to h
i
and h
ID
, B randomly selects
a hash value from the hash list as the challenge hash.
B can use the hash query to solve the CBDH problem.
According to the simulation, given the decryption
query for the challenge C
A
= (C,C
′
,C
i
,D
i
), the sim-
ulator B can perform correct decryption simulation if
(M,ρ) ̸= (M,ρ)
∗
and ID ̸= ID
∗
. If (M, ρ) = (M,ρ)
∗
and ID = ID
∗
, we have following cases:
• For the access structure (M, ρ), if
∑
i∈I
ω
i
λ
i
= s, B
can compute d and perform decryption.
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme
93

• If
∑
i∈I
ω
i
λ
i
̸= s, B return the invalid d.
If A has no advantage in computing d and d
′
, B
will perform decryption simulation successfully with
negligible probability. The random and independent
numbers used in the generation of master keys, pri-
vate keys, re-encryption keys, and challenge cipher-
texts are:
master keys: x
1
+ ab,x
2
+ a,y
1
+ ac, {h
i
}
l
i=1
,h
ID
,
private keys: t
′
,t
′′
,t
′′
1
,τ,
s : ω
i
satisfying
∑
i∈I
ω
i
λ
i
= s.
This illustrates that the randomness property holds
and x
1
,x
2
,x
3
,t
′
,t
′′
,t
′′
1
,τ are randomly chosen by the
simulator. Therefore, the simulation is indistinguish-
able from the real attack.
The simulation is successful if no abort occurs in
the query or challenge phase. If the challenge access
structure (M,ρ)
∗
and the identity ID
∗
are the i-th ac-
cess structure and j-th identity queried to the h
i
and
h
ID
respectively, the adversary cannot query private
keys and re-encryption keys, so that simulation will
be successful in the query phase and the challenge
phase. The success probability is 1(q
k
1
q
k
2
), where
q
k
1
are the queries for an access structure and q
k
2
are
the queries for an identity.
Moreover, if the adversary A makes decryption
queries for randomly selected C
A
with success proba-
bility 1/p of breaking C
A
, second time it is 1/(1 − p),
and q
d
1
/(p − q
d
1
) for q
d
1
queries of C
A
. Similarly,
the success probability for the adaptive choice of C
I
is q
d
2
/(p − q
d
2
) for q
d
2
queries. Therefore, A has
success probability at most (1/2) + (q
d
1
/p − q
d
1
) of
guessing the encrypted message in C
A
and
1
4
+
q
d
2
p−q
d
2
in C
I
.
In simulation, if e(g
x
,g
y
)
(x
2
+a)ω
i
λ
∗
i
t
′
from d and
e(g
x
,g
y
)
abcτ
· e(g
x
,g
y
)
bID
∗
t
′′
2
τ
· e(h
ID
∗
,g
y
)
t
′′
2
τ
from d
′
has not been queried, the adversary has no advan-
tage in correctly guessing the c except the probabil-
ity 1/2 for the challenge ciphertext C
A
and probabil-
ity of 1/4 for the challenge ciphertext C
I
. A makes
q
d
queries to e(g
x
,g
y
)
(x
2
+a)ω
i
λ
i
t
′
and q
d
′
queries to
e(g
x
,g
y
)
abcτ
· e(g
x
,g
y
)
bIDt
′′
2
τ
· e(h
ID
,g
y
)
t
′′
2
τ
with proba-
bility ε. Therefore, the probability of correctly finding
the solution is
ε
q
d
q
d
′
.
Let T
s
denote the time cost of the simulation.
We have T
s
= O(q
k
+ q
d
), which is mainly dom-
inated by the key generation and the decryption.
Therefore, B can solve the CBDH problem with

t + T
s
,
ε
q
d
1
q
d
2
q
d
q
d
′

.
Thus, PPT A has no advantage except given above
in solving the underlying CBDH hard problem and A
cannot break the challenge ciphertexts. Therefore, our
proposed L ABE-IBE PRE scheme is provably IND-
sCCA secure as per (Guo et al., 2018). □
Note 1: Collusion resistance restricts A from ob-
taining more knowledge about C
∗
A
and C
∗
I
even when
A queries the decryption keys associated with differ-
ent attribute sets and identities. Moreover, the chal-
lenge C
∗
A
and C
∗
I
are generated by B using random
and independent numbers and A has no knowledge of
(M,ρ)
∗
and ID
∗
or any random number used in gen-
erating the challenge ciphertexts.
Using the following theorem and its brief proof,
we analyze L ABE-IBE PRE scheme is quantum se-
lectively IND-qsCCA secure:
THEOREM 3. Given a L ABE-IBE PRE scheme.
Assuming the LWE problem is intractable, then the
scheme is IND-qsCCA secure.
Brief Proof. The quantum security of the pro-
posed scheme is shown as a game played between
the quantum adversary A
L
and challenger C . Assume
there exists an quantum adversary A
L
that can break
the L ABE-IBE PRE with non-negligible probability.
We construct a quantum simulator B
q
that can solve a
LWE problem with non-negligible probability. Given
a LWE problem instance, B
q
runs A
L
as follows:
Init: A
L
outputs a noise set X
∗
, a uniform matrix A
∗
0
,
a basis T
∗
A
and a short vector γ
∗
.
Setup: B
q
randomly selects a uniform random matrix
A
0
and a basis T
A
to generate A = [A
0
| − A
0
T
A
+ G].
The master public key mpk
L
= A and master secret key
is msk
L
= T
A
.
Phase 1: In this phase, A
L
make private key and de-
cryption queries. For the private key queries, A
L
se-
lects A
0
̸= A
∗
0
and T
A
̸= T
∗
A
. For the decryption queries,
A
L
selects γ ̸= γ
∗
.
Challenge: A
L
adaptively chooses two distant ABE
ciphertexts c
1
A
and c
2
A
. B
q
randomly selects one of
the ciphertext c
c
A
, random secret s
∗
, and random errors
{e
∗
1
,e
∗
2
} ∈ X
∗
as input and generates a challenge post-
quantum ciphertext C
∗
L
as
C
∗
L
= (A
∗T
s
∗
+ e
∗
1
, β
∗T
s
∗
+ e
∗
2
+ ⌈q/2⌉ · c
c
A
).
B
q
returns C
∗
L
to A
L
.
Phase 2: In this phase, A
L
makes queries similar to
Phase 1 with restriction that A
L
can not make private
key queries for A
∗
0
and T
∗
A
. Similarly, A
L
can not make
decryption queries for γ
∗
.
Guess: A
L
guess the encrypted ABE ciphertext c
′
of
c
c
A
and wins if c
′
= c
c
A
. Otherwise, it returns ⊥.
Here we analyze the probability of a success-
ful simulation. Consider A
L
makes q
H
1
and q
H
2
queries in Phase 1 and Challenge phase respec-
tively. The success probability of the simulation is
1 − 1/(q
H
1
q
H
2
). Therefore, A
L
has advantage ε, and
SECRYPT 2023 - 20th International Conference on Security and Cryptography
94

Table 1: Comparative Analysis of our L ABE-IBE with naive ABE-Decrypt & IBE-ReEncrypt and Encryption Switching
(ES) ABE-IBE schemes.
Schemes
Theoretical Analysis
Computation Communication Storage
Naive ABE-Dec & ABE.Dec + IBE.Enc: (3 + 2l)E
p
+ (6 + 4l)E
e
ABE.CT.Size+IBE.CT.Size: ABE.CT+IBE.CT:
IBE-ReEnc IBE.Dec: 2E
p
2|G
T
| + (3 + 2l)|G
1
| 2|G
T
| + (3 + 2l)|G
1
|
ES.ABE-IBE
ES.ReKey: E
p
+ (5 + 3l)E
e
ES.ReKey.Size: ES.Enc.CT:
ABE.Enc: E
p
+ (2 + 3l)E
e
|G
T
| + (4 + l)|G
1
| |G
T
| + (1 + 2l)|G
1
|
He et al. (2019) ES.ReEnc: (2l + 1)E
p
+ (3 + l)E
e
ES.ReEnc.CT:
IBE.Dec: 2E
p
+ 3E
e
|G
T
| + 2|G
1
|
L ABE-IBE
L ReKey: E
p
+ 4E
e
+ E
v
L ReKey.Size: L Enc.CT:
L ABE.Enc: E
p
+ (2 + l)E
e
|G
T
| + 3|G
1
| +V
n
|G
T
| + (1 + l)|G
1
|
L ReEnc: 2E
p
+ lE
e
L ReEnc.CT: |G
T
| + |G
1
| + |C
l
|
L ReDec: E
p
, L IBE.Dec: E
p
+ 2E
e
L ReDec.CT: |G
T
|
Enc: Encryption, Dec: Decryption, ReKey: Re-encryption Key, ReEnc: Re-Encryption, ReDec: Re-Decryption, CT : Ciphertext, E
p
: Number of bilinear
pairing operation, E
e
: Number of exponentiation operations, E
v
: Vector multiplication operations, l: Number of attributes, V
n
: Size of n-dimensional
vector, C
l
: post-quantum ciphertext
probability |Pr[c
′
= c
c
A
]| ≥
1
2
+ ε. Thus, B
q
has ad-
vantage
1
2
(1 − 1/(q
H
1
q
H
2
)) · ε in solving hard LWE
assumption.
Conclude that the quantum adversary A
L
has no
advantage in solving underlying LWE hard problem,
and A
L
can not break challenge ciphertext. This im-
plies that the proposed scheme is quantum secure in
the IND-qsCCA model since the quantum attacker
trying to break the proposed scheme must solve the
lattice problem, which is known to be hard. □
7 DISCUSSION
In this section, we discuss a theoretical and experi-
mental analysis of our scheme in comparison with the
existing classical ABE-IBE scheme (He et al., 2019).
7.1 Theoretical Analysis
We consider communication, computation, and stor-
age complexities to perform the theoretical analysis
of our proposed scheme. For this purpose, we take
the expensive set of operations for analysis as given
at the bottom of Table 1.
The comparative analysis of our L ABE-IBE
scheme with a naive decrypt-and-reencrypt scheme
and the ES.ABE-IBE (He et al., 2019) scheme is
shown in Table 1. In the naive solution, the client
downloads the ABE ciphertext from the Cloud, de-
crypts it and then encrypts it to IBE ciphertext before
sharing. ES.ABE-IBE improves efficiency by auto-
matically transforming ABE to IBE ciphertext with-
out downloading and decrypting it. The computa-
tional complexity (Column 2, Table 1) shows that the
naive solution requires linear cost of (3 + 2l)E
p
+
(6+4l)E
e
and ES.ABE-IBE requires E
p
+(2 +3l)E
e
.
L ABE-IBE significantly reduces to E
p
+ (2 + l)E
e
reduce. Similarly, computational complexity for re-
encryption in ES.ABE-IBE is (2l + 1)E
p
+ (3 + l)E
e
,
while L ABE-IBE reduces it to 2E
p
+lE
e
. Moreover,
computational complexity for IBE.Dec in ES.ABE-
IBE is 2E
p
+3E
e
, while in L ABE-IBE it is E
p
+2E
e
.
The communication complexity (Column 3, Ta-
ble 1) illustrates the size of communication packets
between the communicating parties. The communica-
tion cost of the naive solution is 2|G
T
| + (3 + 2l)|G
1
|
and ES.ABE-IBE scheme is |G
T
|+ (4 +l)|G
1
|. How-
ever, L ABE-IBE reduces it to |G
T
| + 3|G
1
| +V
n
.
Similarly, ES.ABE-IBE reduces storage complex-
ity (Column 4, Table 1) by splitting the storage re-
quirements between sender and Cloud, while L ABE-
IBE scheme takes advantage of local edge nodes (as
shown in Fig. 3) to make it more storage efficient.
L ABE-IBE reduces the storage complexity suffi-
ciently for end nodes (sender and receiver) by moving
the complex re-encryption operations to edge nodes.
Thus, the L ABE-IBE proxy re-encryption scheme
designed in this paper can surpass existing solutions
in terms of security as well as complexity.
7.2 Experimental Analysis
Our implementation of the L
ABE-IBE scheme is
written in C-language using the PBC library (pairing-
based cryptography) (Lynn, 2007). The simulations
were tested on a Linux virtual machine with 1 GB
RAM over the host system with Intel(R) Core(TM)
i5-7200U processor with CPU of 2.50 GHz - 2.71
GHz. We implemented ES.ABE-IBE (He et al.,
2019) for comparative analysis along with our pro-
posed scheme. For this purpose, we used the bilin-
ear pairings (Definition 4.1) and LWE. We simulated
the worst-case scenario by generating access policies
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme
95

(a) (b) (c)
(d) (e)
Figure 4: Experimental Analysis of L ABE-IBE scheme with ES.ABE-IBE scheme where (a) illustrates the Re-Encryption
Key Generation Time, (b) ABE Encryption Time, (c) Re-encryption Time of ABE-quantum and ES.ABE-IBE, (d) Re-
decryption Time of quantum-IBE, and (e) IBE Decryption Time.
(U
1
,··· ,U
l
) from 10 to 100 and tested corresponding
algorithms (ES.ABE-IBE and L ABE-IBE) 20 times
for each set of attributes to take the best results.
Fig. 4 (including Figures 4a, 4b, 4c, 4d and 4e)
illustrates the experimental analysis of our proposed
L ABE-IBE proxy re-encryption scheme compared
to the classical ES.ABE-IBE (He et al., 2019) scheme.
Fig. 4a shows that L ABE-IBE takes almost con-
stant re-encryption key generation time (approxi-
mately 13 ms) with the increase in the number of at-
tributes as compared to ES.ABE-IBE. Fig. 4b shows
both ES.ABE-IBE and L ABE-IBE perform identi-
cally for a small number of attributes, but L ABE-IBE
encryption scheme performs more efficiently as the
number of attributes grows. Fig. 4c shows that both
schemes take almost equivalent re-encryption time
for a smaller set of attributes, but with the increase
in the number of attributes, L ABE-IBE outperforms
ES.ABE-IBE. Note, re-encryption in ES.ABE-IBE is
performed in the Cloud, while in L ABE-IBE, the
re-encryption is performed at the local edge nodes.
Fig. 4d shows that the re-decryption time of L ABE-
IBE is constant (approx 6 ms) when decoding post-
quantum secure ciphertext to IBE ciphertext. Finally,
Fig. 4e gives the decryption time of IBE ciphertext for
both ES.ABE-IBE and L ABE-IBE schemes. The de-
cryption function in both schemes takes almost con-
stant time but L ABE-IBE decryption consumes 2 ms
less than ES.ABE-IBE.
In general, the results of the experimental and se-
curity analysis both show that our L ABE-IBE is ef-
ficient and secure against quantum adversaries.
8 CONCLUSIONS
In this paper, we proposed a classical to post-
quantum-safe ABE-IBE proxy re-encryption scheme,
which allows the conversion of ABE to IBE via
post-quantum secure lattice-based encryption. The
proposed L ABE-IBE PRE allows secure conversion
of ABE ciphertext to post-quantum secure cipher-
text at the sender-side local Edge node and then
post-quantum secure ciphertext to IBE ciphertext at
receiver-side local Edge node to deal with the asym-
metric resources of devices. We used the game-based
framework to illustrate the selectively IND-sCCA and
selectively quantum IND-qsCCA security of the pro-
posed L ABE-IBE PRE scheme. The theoretical
analysis and experimental results highlighted that the
proposed scheme improved efficiency as well as se-
curity in comparison to both the naive solution and
classical ES.ABE-IBE proxy re-encryption scheme.
SECRYPT 2023 - 20th International Conference on Security and Cryptography
96

ACKNOWLEDGEMENTS
M. N. Khan is supported by a PhD stipend scholar-
ship from CSIRO Data61 (50050661) and an Interna-
tional Tuition Fee scholarship from the School of Sci-
ence, RMIT, Australia. Josef Pieprzyk is supported
by the Polish National Science Center (NCN) grant
2018/31/B/ST6/03003.
REFERENCES
Ajtai, M. (1996). Generating hard instances of lattice prob-
lems. In 28th ACM Symp., STOC ’96, pages 99–108.
Asif, R. (2021). Post-quantum cryptosystems for IoT: A
survey on lattice-based algorithms. IoT, 2(1):71–91.
Banerjee, U., Pathak, A., and Chandrakasan, A. P. (2019).
An energy-efficient configurable lattice cryptography
processor for the quantum-secure Internet of Things.
In 2019 IEEE ISSCC, pages 46–48.
Bartocci, C., Bruzzo, U., and Ruip
´
erez, D. H. (2009). Lat-
tices, volume 276 of PM, pages 339–345. Birkh
¨
auser.
Beimel, A. (1996). Secure Schemes for Secret Sharing and
Key Distribution. Phd thesis, Technion-Israel Inst. of
Technol., Fac. of Comput. Sci. Haifa.
Blaze, M., Bleumer, G., and Strauss, M. (1998). Divertible
protocols and atomic proxy cryptography. In EURO-
CRYPT 98, volume 1403, pages 127–144. Springer.
Boneh, D. and Boyen, X. (2004). Secure identity based
encryption without random oracles. In Advances
in Cryptology —CRYPTO 2004, pages 443–459.
Springer.
Boneh, D. and Franklin, M. (2001). Identity-based encryp-
tion from the weil pairing. In Advances in Cryptol-
ogy—CRYPTO 2001, pages 213–229. Springer.
Cao, Z., Wang, H., and Zhao, Y. (2019). AP-PRE: Au-
tonomous path proxy re-encryption and its applica-
tions. IEEE Trans. on Depend. & Sec. Comput.,
16:833–842.
Chen, J., Gong, J., Kowalczyk, L., and Wee, H. (2018). Un-
bounded ABE via bilinear entropy expansion, revis-
ited. In EUROCRYPT 2018, pages 503–534, Cham.
Springer.
Deng, H., Qin, Z., Wu, Q., Guan, Z., and Zhou, Y. (2020).
Flexible attribute-based proxy re-encryption for effi-
cient data sharing. Inf. Sciences, 511:94 – 113.
Deng, H., Wu, Q., Qin, B., Domingo-Ferrer, J., Zhang, L.,
Liu, J., and Shi, W. (2014). Ciphertext-policy hierar-
chical ABE with short ciphertexts. Inf. Sci., 275:370–
384.
Fern
´
andez-Caram
´
es, T. M. (2020). From pre-quantum to
post-quantum IoT security: A survey on quantum-
resistant cryptosystems for the Internet of Things.
IEEE Internet of Things J., 7(7):6457–6480.
Gentry, C., Peikert, C., and Vaikuntanathan, V. (2008).
Trapdoors for hard lattices and new cryptographic
constructions. In 40th Annu. ACM Symp., pages 197–
206.
Guo, F., Susilo, W., and Mu, Y. (2018). Foundations of
Security Reduction, pages 29–146. Springer, Cham.
He, K., Mao, Y., Ning, J., Liang, K., Huang, X., Panaousis,
E., and Loukas, G. (2019). A new encrypted data
switching protocol: Bridging IBE and ABE without
loss of data confidentiality. IEEE Access, 7:50658–
50668.
Hofheinz, D., Jia, D., and Pan, J. (2018). Identity-based
encryption tightly secure under chosen-ciphertext at-
tacks. In ASIACRYPT 2018, volume 11273, pages
190–220.
Ioannou, L. M. and Mosca, M. (2011). A new spin on quan-
tum cryptography: Avoiding trapdoors and embracing
public keys. In PQC 2011, pages 255–274.
Joseph, D., Misoczki, R., Manzano, M., Tricot, J., Pinu-
aga, F. D., Lacombe, O., Leichenauer, S., Hidary, J.,
Venables, P., and Hansen, R. (2022). Transitioning
organizations to post-quantum cryptography. Nature,
605(7909):237–243.
Joux, A. and Nguyen, K. (2003). Separating decision diffie–
hellman from computational diffie–hellman in crypto-
graphic groups. J. Cryptol., 16(4):239–247.
Li, J., Wang, Y., Zhang, Y., and Han, J. (2020). Full Verifi-
ability for Outsourced Decryption in Attribute-Based
Encryption. IEEE Trans. on Serv. Comput., 13:478–
487.
Li, J., Yao, W., Han, J., Zhang, Y., and Shen, J. (2018). User
collusion avoidance CP-ABE with efficient attribute
revocation for cloud storage. IEEE Syst. J., 12:1767–
1777.
Li, J., Yu, Q., and Zhang, Y. (2019). Hierarchical ABE with
continuous leakage-resilience. Inf. Sci., 484:113–134.
Lindner, R. and Peikert, C. (2011). Better key sizes (and
attacks) for LWE-based encryption. In CT-RSA 2011,
volume 6558 of LNCS, pages 319–339. Springer.
Lohachab, A. and Karambir (2019). ECC based inter-device
authentication and authorization scheme using MQTT
for IoT networks. J. of Inf. Secur. and Appl., 46:1–12.
Lynn, B. (2007). On the implementation of pairing-based
cryptosystems. PhD thesis, Stanford University Stan-
ford.
Miao, Y., Liu, X., Choo, K.-K. R., Deng, R. H., Li,
J., Li, H., and Ma, J. (2021). Privacy-preserving
attribute-based keyword search in shared multi-owner
setting. IEEE Trans. on Depend. & Secure Comput.,
18(3):1080–1094.
Micciancio, D. and Peikert, C. (2012). Trapdoors for lat-
tices: Simpler, tighter, faster, smaller. In EURO-
CRYPT 2012, volume 7237 of LNCS, pages 700–718.
Springer.
Micciancio, D. and Regev, O. (2009). Lattice-based Cryp-
tography, pages 147–191. Springer.
Monz, T., Nigg, D., Martinez, E. A., Brandl, M. F.,
Schindler, P., Rines, R., Wang, S. X., Chuang, I. L.,
and Blatt, R. (2016). Realization of a scalable Shor
algorithm. Sci., 351(6277):1068–1070.
Nejatollahi, H., Dutt, N., Ray, S., Regazzoni, F., Banerjee,
I., and Cammarota, R. (2019). Post-quantum lattice-
based cryptography implementations: A survey. ACM
Comput. Surv., 51(6):41.
Classical to Post-Quantum Secure ABE-IBE Proxy Re-Encryption Scheme
97

Peikert, C. (2016). A decade of lattice cryptography. Foun-
dations and Trends® in Theoretical Comput. Sci.,
10(4):283–424.
Regev, O. (2009). On lattices, learning with errors, random
linear codes, and cryptography. J. of the ACM, 56(6).
Roman, R., Lopez, J., and Mambo, M. (2018). Mobile edge
computing, Fog et al.: A survey and analysis of se-
curity threats and challenges. Future Gener. Comput.
Syst., 78:680 – 698.
Sahai, A. and Waters, B. (2005). Fuzzy identity-based en-
cryption. In EUROCRYPT 2005, pages 457–473.
Shamir, A. (1985). Identity-based cryptosystems and sig-
nature schemes. In CRYPTO 84, volume 196, pages
47–53.
Shor, P. W. (1999). Polynomial-time algorithms for prime
factorization and discrete logarithms on a quantum
computer. SIAM Review, 41(2):303–332.
Susilo, W., Jiang, P., Guo, F., Yang, G., Yu, Y., and Mu,
Y. (2017). Eacsip: Extendable access control system
with integrity protection for enhancing collaboration
in the cloud. IEEE Trans. Inf. Forens. Sec., 12:3110–
3122.
Tao, X., Qiang, Y., Wang, P., and Wang, Y. (2023). Lmibe:
Lattice-based matchmaking IBE for internet of things.
IEEE Access, 11:9851–9858.
Waters, B. (2011). Ciphertext-policy attribute-based en-
cryption: An expressive, efficient, and provably se-
cure realization. In PKC 2011, volume 6571, pages
53–70.
Xiong, J., Ren, J., Chen, L., Yao, Z., Lin, M., Wu, D., and
Niu, B. (2019). Enhancing privacy and availability for
data clustering in intelligent electrical service of IoT.
IEEE Internet of Things J., 6(2):1530–1540.
Yang, Y., Chen, X., Chen, H., and Du, X. (2018). Improving
privacy and security in decentralizing multi-authority
attribute-based encryption in cloud computing. IEEE
Access, 6:18009–18021.
SECRYPT 2023 - 20th International Conference on Security and Cryptography
98