Characterizing Speed Performance of Multi-Agent Reinforcement

Learning

∗

Samuel Wiggins

1 a

, Yuan Meng

1 b

, Rajgopal Kannan

2 c

and Viktor Prasanna

1 d

Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, U.S.A.

DEVCOM Army Research Lab, Los Angeles, U.S.A.

Keywords:

Multi-Agent Reinforcement Learning, AI Acceleration.

Abstract:

Multi-Agent Reinforcement Learning (MARL) has achieved signiﬁcant success in large-scale AI systems and

big-data applications such as smart grids, surveillance, etc. Existing advancements in MARL algorithms focus

on improving the rewards obtained by introducing various mechanisms for inter-agent cooperation. However,

these optimizations are usually compute- and memory-intensive, thus leading to suboptimal speed perfor-

mance in end-to-end training time. In this work, we analyze the speed performance (i.e., latency-bounded

throughput) as the key metric in MARL implementations. Speciﬁcally, we ﬁrst introduce a taxonomy of

MARL algorithms from an acceleration perspective categorized by (1) training scheme and (2) communi-

cation method. Using our taxonomy, we identify three state-of-the-art MARL algorithms - Multi-Agent

Deep Deterministic Policy Gradient (MADDPG), Target-oriented Multi-agent Communication and Cooper-

ation (ToM2C), and Networked Multi-agent RL (NeurComm) - as target benchmark algorithms, and provide a

systematic analysis of their performance bottlenecks on a homogeneous multi-core CPU platform. We justify

the need for MARL latency-bounded throughput to be a key performance metric in future literature while also

addressing opportunities for parallelization and acceleration.

1 INTRODUCTION

Reinforcement Learning (RL) is a crucial technique

for model development and algorithmic innovation in

data science. Multi-agent Reinforcement Learning

(MARL), an extension of single-agent RL, has shown

advancement in many big-data application domains

such as e-commerce (Choi et al., 2022) and surveil-

lance in large-scale systems (Ivan and Ivan, 2020).

Compared to single-agent RL, MARL introduces

agent-to-agent interactions using algorithm-speciﬁc

communication protocols. MARL also poses chal-

lenges in data processing since each agent generates a

large amount of data, which is high-dimensional and

correlated with the data from other agents. The speed

performance of processing data in MARL is critical

as MARL training is extremely time-consuming. In

https://orcid.org/0000-0002-0069-8213

https://orcid.org/0000-0001-6468-8623

https://orcid.org/0000-0001-8736-3012

https://orcid.org/0000-0002-1609-8589

∗

This work is supported by the U.S. National Science

Foundation (NSF) under grant CNS-2009057 and the Army

Research Lab (ARL) under grant W911NF2220159.

Deep MARL, using Deep Neural Network (DNN) as

a policy model, multiple autonomous agents interact

with a shared environment to achieve a joint goal. The

majority of state-of-the-art MARL algorithms utilize

DNNs, so we use MARL and Deep MARL inter-

changeably in this paper.

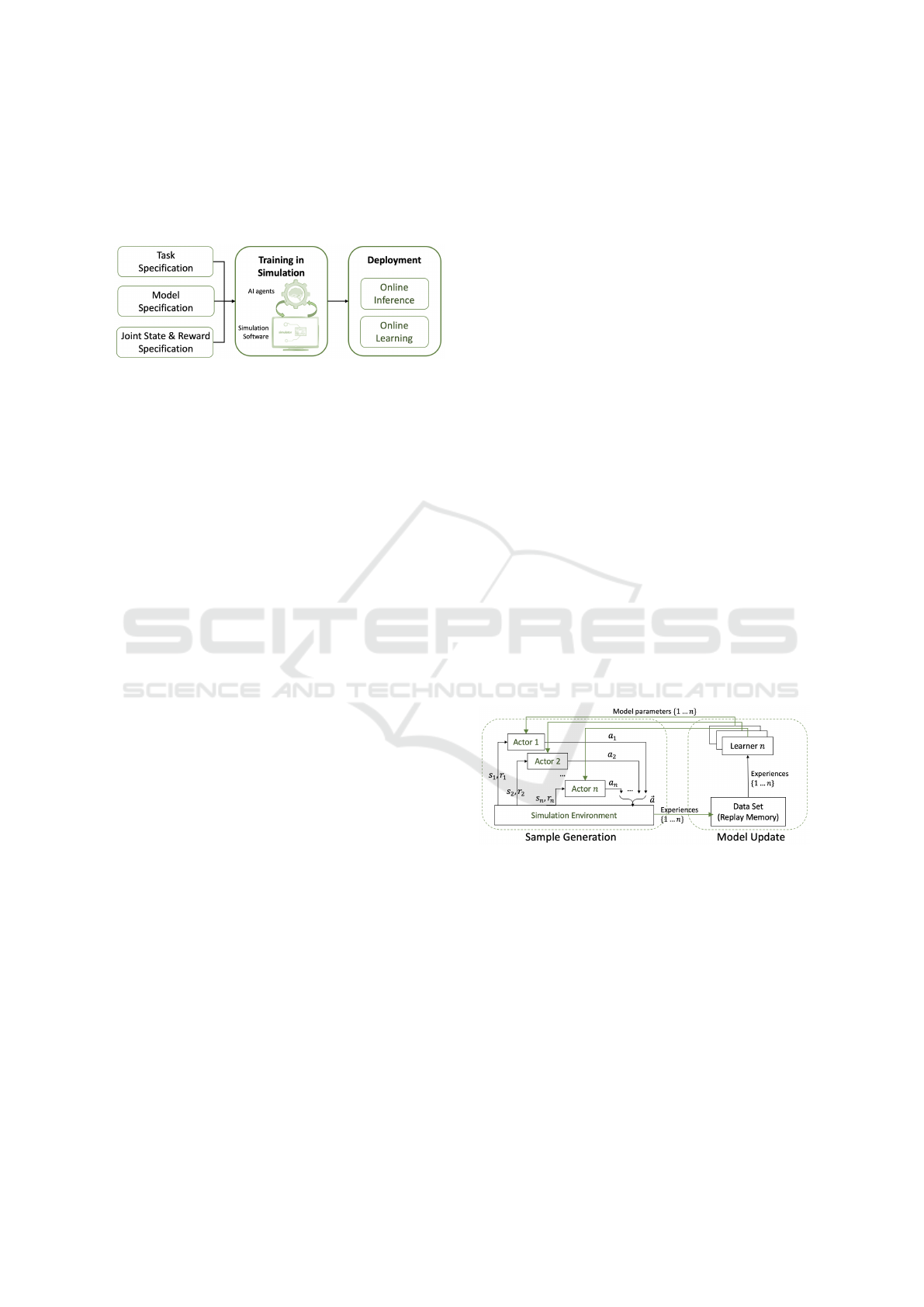
Figure 1 shows a high-level diagram of Deep

MARL in a real-world scenario. A typical work-

ﬂow consists of two major stages: Training in Sim-

ulation and Deployment. In this paper, we focus on

Training using a simulation, which is the critical pro-

cess before deploying a MARL system into its actual

physical environment. This Training in Simulation

process is the most time-consuming part of MARL

system development, often taking days to months to

train an acceptable model (Kaelbling et al., 1996).

There has been extensive work accelerating this stage

for single-agent RL. However, Training in Simulation

for MARL systems brings non-trivial computational

challenges compared to single-agent scenarios due to

the requirement of facilitating inter-agent communi-

cations. There is a lack of literature on paralleliza-

tion and acceleration in a multi-agent setting stem-

ming from the omission of MARL system execution

Wiggins, S., Meng, Y., Kannan, R. and Prasanna, V.

Characterizing Speed Performance of Multi-Agent Reinforcement Learning.

DOI: 10.5220/0012082200003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 327-334

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

327

time as a performance metric. In addition to focusing

on maximizing cumulative reward through novel al-

gorithmic optimizations, we argue that optimizing the

MARL system execution time through parallelization

and acceleration should be considered.

Figure 1: MARL application workﬂow.

In practice, the efﬁciency of developing and de-

ploying high-speed MARL systems is dependent

upon several factors such as the dependency require-

ment within RL execution loops, the various Compu-

tation intensities of MARL primitives, and the suit-

ability of the memory hierarchy. However, widely-

used homogeneous platforms (i.e., CPUs) cannot sat-

isfy all of the above factors simultaneously, leading to

various time overheads that prevent the MARL sys-

tem from achieving theoretical peak throughput. In

this paper, we provide a systematic empirical analy-

sis of the performance of three state-of-the-art MARL

algorithms - MADDPG, ToM2C, and NeurComm on

CPUs. To the best of our knowledge, this is the ﬁrst

work that analyzes MARL algorithms from a speed

performance and acceleration point of view. The main

contributions of the paper are:

• We provide a taxonomy of MARL algorithms

from an acceleration point of view, summarize

their parallelization parameters and highlight the

computation characteristics of each category.

• We compare the timing breakdown and perfor-

mance scalability with respect to the paralleliza-

tion parameters of state-of-the-art MARL imple-

mentations on a multi-core CPU platform.

• We provide reasoning into why MARL system ex-

ecution time should be considered a key perfor-

mance metric, and show new acceleration chal-

lenges and opportunities that emerge.

2 BACKGROUND

2.1 Multi-Agent Reinforcement

Learning

We formulate the decision-making problem in

MARL as an n−agent Markov game (Shap-

ley, 1953), which can be deﬁned as a tuple



S , A

, . . . , A

, R

, . . . , R

, T , γ



. In this tuple, 1...n is

the set of agents, S is the state space, A

is the ac-

tion space of agent i, R

: S × A 7→ R is the reward

function of agent i, T : S × A 7→ ∆(S ) denotes the

transition probability of each state-action pair to an-

other state, γ ∈ [0, 1) is a discount factor for future re-

wards. For agent i, we denote its policy as a probabil-

ity distribution over its action space π

: S → ∆





where π

| s

) is the probability of taking action a

upon state s

at a certain time step t. By denoting the

other agents’ actions as a

−i

j̸=i

, we formu-

late the other agents’ joint policy as π

−i



−i

| s



j∈{−i}



| s



. At each time step, actions are

taken simultaneously. Each agent i aims at ﬁnding its

optimal policy to maximize the expected return (cu-

mulative reward), deﬁned as

(

−i

)

∼T ,π

,π

−i

∞

∑

t=1



, a

−i



(1)

From Equation 1, the optimal policy of agent i de-

pends not only on its own policy but also on the be-

haviors of other agents. Depending on the assump-

tions of how agents communicate, MARL policy op-

timization can be categorized into several scenarios

which will be further discussed in Section 3.

As shown in Figure 2, each iteration of the

Training-in-Simulation process can be divided into

the Sample Generation and Model Update phases. In

Figure 2: Training in Simulation.

the Sample Generation phase, the actor of each agent

takes the environment state as input to the DNN pol-

icy and inference an action. The joint action of all the

agents is simultaneously executed to transit to a new

state. This process is repeated until a preset maxi-

mum trajectory length value is achieved or a terminal

state is reached. At the end of the Sample Genera-

tion phase, the agents produce a batch of experiences

−→

, r

, s

t+1

}. Then, in the Model Update phase,

the learner of each agent samples (mini-)batches of

experiences to train the DNN policy and propagate the

updated policy back to the actor of the same agent.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

328

2.2 Related Work

2.2.1 Reinforcement Learning Acceleration

There is a plural of work for parallelization and accel-

eration of single-agent RL. On general-purpose plat-

forms (i.e., CPU and GPU), existing work adopts

coarse-grained parallelism by deploying and dis-

tributing multiple actors and learners for the same

agent (Zhang et al., 2021; Liang et al., 2018), as

well as ﬁne-grained parallelism within each actor or

learner for simulations, batched inference, and train-

ing (Rocki and Suda, 2011). Additionally, special-

ized hardware accelerators targeting speciﬁc single-

agent RL algorithms are developed (Cho et al., 2019;

Meng et al., 2021; Meng et al., 2020). However, not

all of these acceleration techniques can be trivially

adapted to MARL. This is because MARL poses dif-

ferent challenges. For example, the latency bottleneck

of MARL may become the overhead from coordina-

tion between agents, which is nonexistent in single-

agent RL.

2.2.2 MARL Implementation: Summary and

Challenges

Compared to single-agent RL, MARL leads to ad-

ditional problems in terms of increased state-action

complexity, partial observability from each agent,

and coordination requirement in cooperative settings.

Many MARL algorithms have been proposed and im-

plemented to address these problems, where their ma-

jor contributions are targeted toward learning to com-

municate effectively between RL agents. (Lowe et al.,

2017; Jiang et al., 2018) allow agents to perform in

the environment in a decentralized way with copies

of a shared neural network and enable instantaneous

communication between all the agents for training

the policies. (Chu et al., 2020; Wang et al., 2021)

propose dedicated compute modules to learn using a

shared graph for agents to decide whether and with

whom to communicate. These works focus on in-

creasing the sample efﬁciency and communication ef-

ﬁciency to improve the convergence rate to a high

joint reward. They are implemented on multi-core

CPUs, and computationally-intensive workloads such

as neural network training are ofﬂoaded to a GPU.

However, these implementations are usually highly

time-consuming. A unique challenge that impedes the

speed performance of MARL is the overheads from

communication. The compute primitives and mem-

ory modules for learning communication, including

message generation (e.g., Recurrent neural networks

(Kim et al., 2021)) and message propagation (e.g.,

Sparse linear algebra based on Graph Neural Net-

works (Jiang et al., 2018)), are tightly coupled with

agent policy training even though they have highly

dissimilar compute patterns and memory operations

compared to policy training. This leads to various

computation overheads that lower the effective hard-

ware utilization on CPU, which in turn impedes the

policy execution and training speed. In this paper, we

aim to characterize these overheads and identify ac-

celeration opportunities in MARL training.

3 A TAXONOMY OF MARL

ALGORITHMS

We illustrate a structural way of categorizing MARL

algorithms based on their computation characteristics

and major acceleration requirements. This is shown in

two dimensions: training scheme (centralized vs. de-

centralized) and communication method (pre-deﬁned

vs. online learnt). Figure 3 shows example algorithms

in each category.

Figure 3: MARL Taxonomy.

3.1 Training Scheme

Based on the requirement of MARL applications,

each agent can learn in a decentralized way utilizing

respective local experiences, or in a centralized man-

ner where all the agents share a global pool of model

parameters and joint experiences.

Centralized Training - Decentralized Execution

(CTDE): In the Model Update phase under Central-

ized Training - Decentralized Execution (CTDE), a

centralized controller or learner is responsible for co-

ordinating the policy training of all the agents. The

centralized controller has access to global observa-

tions and rewards. Once the training is complete,

however, each agent executes its actions indepen-

dently, based on its own local observations, without

any further communication with the centralized con-

troller. Communication is required during Model Up-

date and is usually implemented using a shared mem-

ory architecture on modern CPUs and GPUs (Wang

et al., 2021; Lowe et al., 2017).

Decentralized Training: In Decentralized Training,

each agent in the system learns its own policy with-

out direct access to the experiences of other agents in

Characterizing Speed Performance of Multi-Agent Reinforcement Learning

329

the system. From the perspective of a single agent,

the environment becomes non-stationary due to the

co-adaption of the other agents, such that the pol-

icy learned can have a mismatched expectation about

the other agents’ policies. Without a centralized con-

troller, the problems of partial observability and non-

stationarity become more complex. Therefore, com-

munication that allows agents to exchange informa-

tion becomes a critical factor in the coordination of

their behaviors and overcoming the partial observabil-

ity and non-stationarity problems (Wang et al., 2022).

3.2 Communication Method

Communication Policy deﬁnes how to make the deci-

sions of ‘whom’ and ‘when’ to communicate with and

enable message transferring across agents. A commu-

nication policy can be either pre-deﬁned or learnt.

Pre-Deﬁned Communication. Pre-deﬁned commu-

nication speciﬁes a ﬁxed communication protocol and

message format before the training process begins.

Agents may perform all-to-all communication (Lowe

et al., 2017), or capture the communication paths us-

ing a pre-deﬁned graph that is associated with the

given application or environment (Chu et al., 2020;

Jiang et al., 2018).

Learnt Communication. Learnt communication of-

fers generalization abilities to more scenarios and

has become increasingly popular due to its ﬂexibility.

One popular method is to adaptively learn the evolv-

ing node and edge features of the multi-agent system

represented as a dynamic graph (Wang et al., 2021).

4 LATENCY-BOUNDED

THROUGHPUT OF MARL

ALGORITHMS: AN ANALYSIS

4.1 Metrics and Parallel Parameters

4.1.1 Latency-Bounded Throughput

Given a particular algorithm and benchmark that as-

sumes a ﬁxed sample complexity (i.e., the number

of iterations needed to reach a certain reward), the

primary metric for measuring MARL training speed

is the throughput in terms of the number of Itera-

tions executed Per Second (IPS). As the iterations in

Training-in-Simulation are sequential by nature, it is

hard to overlap consecutive iterations for faster con-

vergence (Cho et al., 2019; Meng et al., 2021), so

minimizing the latency of each iteration is critical for

high IPS throughput. Based on the Sample Genera-

tion and Model Update phases in each iteration (Fig-

ure 2), we formulate the throughput IPS as:

IPS =

iteration

⊛ (T

, T

)

, (2)

where T

and T

are the execution times of Sample

Generation and Model Update phases, respectively.

The operator ⊛(x, y) can be x + y or max(x, y) based

on whether the algorithm is on-policy (where Model

Update is strictly dependent on Sample Generation in

each iteration) or off-policy (where Sample Genera-

tion and Model Update phases can be overlapped).

In the following subsections, we provide a de-

tailed analysis of the main computation primitive la-

tency and throughput using representative algorithms

in different categories of MARL. We will show the

time breakdown and performance scalability with re-

spect to a few key parallel parameters.

4.1.2 Key Parallel Parameters

A MARL algorithm is deﬁned using a plural of hyper-

parameters, where a subset of these hyper-parameters

affects the parallelism, data processing speed, and

latency-bounded throughput of the system. We deﬁne

the following terms relevant to the key parallel param-

eters that are common in all categories of MARL:

• Agent(s). Agents execute by interacting with the

environment and improving their policies.

• Actor(s). An actor is a process used by an agent to

perform the Sample Generation phase. An actor

infers on the agent’s policy to perform an action in

a simulation environment. Each agent can spawn

multiple actors implemented on multiple rollout

thread(s) deﬁned below.

• Rollout Thread(s). A rollout thread is a CPU

thread used to execute the actor process. A rollout

thread has a local copy of the environment and

executes independently of the other actor/rollout

thread(s). Typically, each agent deploys multi-

ple actors, and each actor is mapped to a rollout

thread.

• Learner(s). A learner is the process used by

an agent to train its policy in the Model Update

phase. In CTDE, the learner is typically shared

by all the agents, so the number of learners in

the MARL system is 1. In Decentralized train-

ing, the number of learners is equal to the number

of agents.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

330

4.2 Centralized Training with

Knowledge Concatenation

Multi-Agent Deep Deterministic Policy Gradient

(MADDPG) falls under the Centralized Training De-

centralized Execution category with pre-deﬁned all-

to-all communication using knowledge concatenation

(Lowe et al., 2017). In MADDPG, each agent is

composed of four DNN models: (1) The Policy net-

work (i.e., decentralized actor) executes on the envi-

ronment using only local information independent of

other agents. (2) The Value network (i.e., centralized

critic) helps train the actor’s policy. Although it is

considered centralized, each agent still trains its own

value network. The training is centralized in the sense

that the inputs to each value network depend on the

action and observations (i.e., transition information)

of all agents. (3,4) The Target Policy and Target Value

network are used for training stability.

In the MADDPG implementation, multiple rollout

threads are deployed to sample the environment us-

ing the policies from the decentralized actors, where

the transition information is stored in a global replay

buffer. Multiple training threads can then use this

information to train the various DNN networks de-

scribed above.

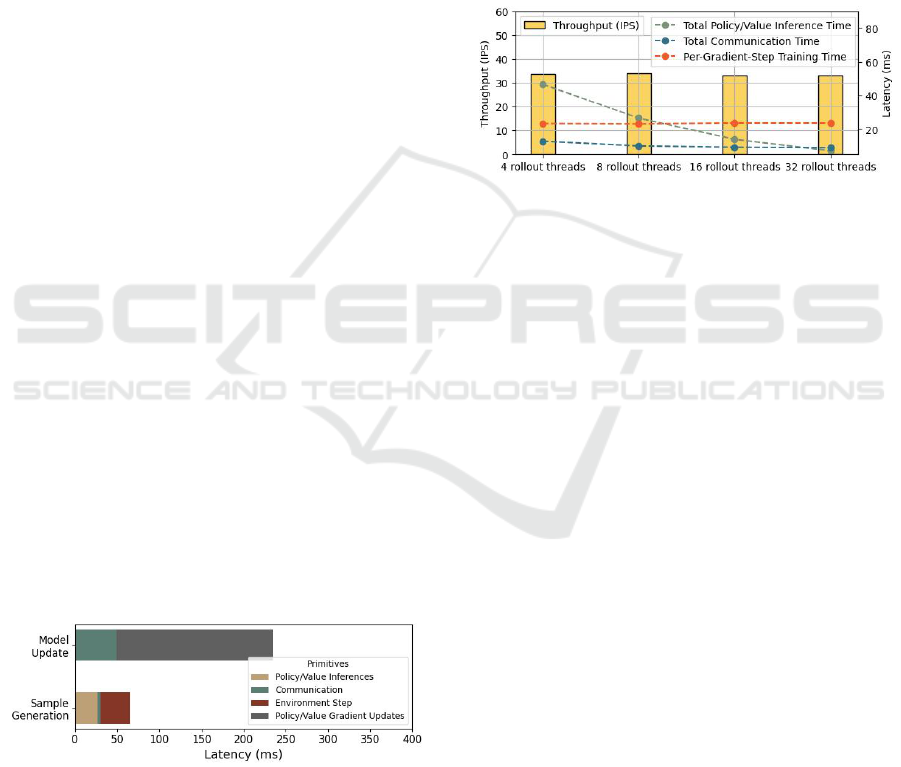
During Sample Generation, each agent samples

an action using its policy and executes it in the en-

vironment. The latency breakdown among Policy In-

ference, Communication, and Environmental Steps in

one iteration is displayed in Figure 4. During Model

Update, training occurs in an actor-critic fashion simi-

lar to the single-agent variant of MADDPG: Deep De-

terministic Policy Gradient (DDPG) (Lillicrap et al.,

2015). Overall, we observe that communication in the

sample generation and model update phase is not the

dominating factor in terms of latency during Training

in Simulation, which is attributed to the straightfor-

ward insertion and concatenation of transition infor-

mation.

Figure 4: MADDPG Training in Simulation Breakdown (8

rollout threads, 1 training thread).

We observe that the actor/critic policy and value

updates are the dominating factor in terms of latency

when varying the number of rollout threads as seen in

Figure 5. In the Sample Generation phase, the ﬁxed

amount of data generation takes a shorter amount

of time since multiple parallel actors sample copies

of the environment simultaneously while adding to

the replay buffer. During the Model Update phase,

latency for each gradient update step remains un-

changed with respect to the number of rollout threads.

This is expected given that training for each agent

happens using a single thread sequentially regardless

of the number of rollout threads. Increasing the num-

ber of rollout threads does increase the number of

gradient steps needed to complete the model update

phase in MADDPG. These additional steps cause the

overall system throughput (IPS) to remain consistent.

Figure 5: MADDPG Training Throughput Scalability vary-

ing rollout threads.

4.3 Centralized Training with Learnt

Communication

ToM2C (Target-oriented Multi-agent Communication

and Cooperation) is a recent work under the CTDE

training scheme (Wang et al., 2021). In ToM2C, each

agent learns its actions based on its local observation

space along with inference of the mental states of oth-

ers and learns the communication paths for enhancing

cooperation. Speciﬁcally, it comprises four functional

DNN models: (1) The Observation Encoder is a fully-

connected DNN layer that encodes the agent’s local

observation into a single feature using a weighted sum

mechanism. (2) The Theory of Mind network (ToM

Net) is a 2-layer Multi-Layer Perceptron on a Gate

Recurrent Unit that estimates the joint intention of all

the other agents. (3) The Message Sender is a Graph

Neural Network (GNN) that uses the ToM Net out-

put to decide the communication graph structure. (4)

The Decision Maker (i.e., policy model) learns the ac-

tions once the agent receives all the messages based

the communication graph returned by the Message

Sender of all other agents.

In the ToM2C implementation, multiple actors on

different rollout threads are used to generate datasets

and store them in a shared buffer; a single training

thread then uses the data from the shared buffer to up-

date the policy, ToM Net, and GNN described above.

During Sample Generation, each actor sequen-

tially performs inference through the four DNN mod-

Characterizing Speed Performance of Multi-Agent Reinforcement Learning

331

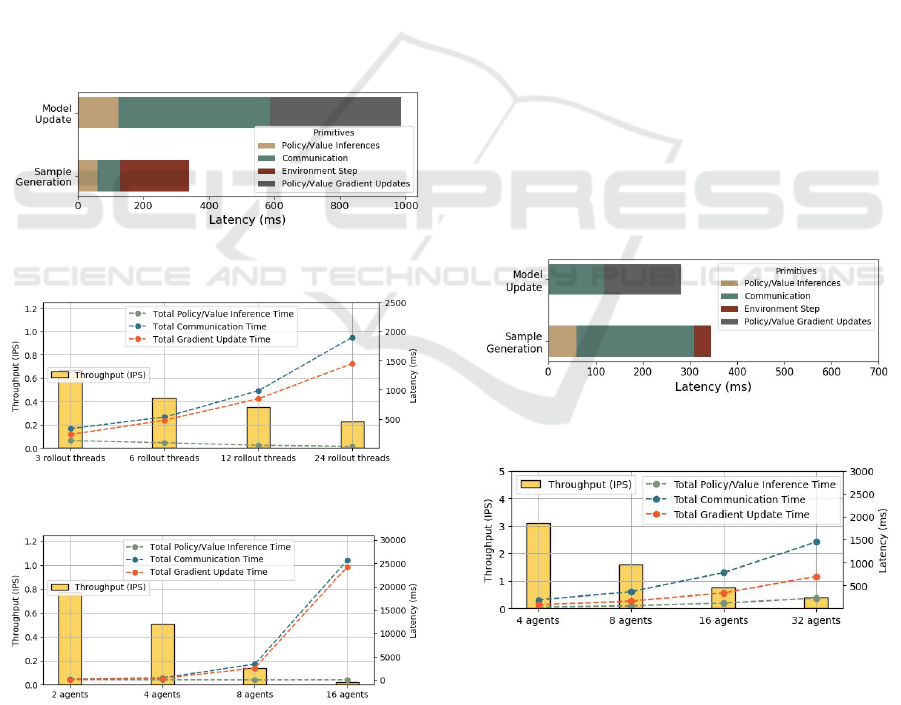
els. The time breakdown among Policy Inference,

Communication, and Environmental Interaction in

one iteration is shown in Figure 6. During Model Up-

date, the training is performed in an actor-critic man-

ner (Mnih et al., 2016), where a centralized critic (i.e.,

Value network) shared by all the agents obtain global

feature of the states to compute their values and facil-

itate the training of the policy network (i.e., the Deci-

sion Maker).

Overall, different from MADDPG which also fol-

lows the CTDE scheme, in ToM2C we observe a non-

trivial overhead from learning of communication in

the training pipeline. This is due to the added com-

putation complexity from inferring other agents’ in-

tentions and deciding the communication paths using

a graph representation of the global states of all the

agents. On the other hand, the overheads from com-

munication during agents execution (Sample Genera-

tion) are smaller compared to that in the Model Up-

date, since the decentralized execution only requires

each actor to perform one-pass inference on its own

models.

Figure 6: ToM2C Training in Simulation Breakdown (6

rollout threads, 1 training thread).

Figure 7: ToM2C Training Throughput Scalability varying

the number of rollout threads.

Figure 8: ToM2C Training Throughput Scalability varying

the number of agents.

In Sample Generation, adding rollout threads in-

creases the data generation throughput (number of

samples generated in unit time) without increasing

the total latency needed for each actor to collect data,

as shown in Figure 7. The actors and the learner

use separate threads and only synchronize through

a shared buffer; the Sample Generation and Model

Update phases can run concurrently. Therefore, the

latency of actors is completely hidden by the train-

ing process, such that increasing the number of roll-

out threads does not lead to higher system throughput

(IPS).

Figure 8 shows the execution time and IPS scal-

ability with increasing the number of agents coop-

erating in the same environment, with a ﬁxed num-

ber of rollout threads serving each agent. We ob-

serve a faster rate of latency scaling (at approximately

8× increase in gradient update time as the number of

agents doubles). This factor is contributed by both

the increased state size (processed state size dou-

bles as the number of agents doubles) and the in-

creased communication (worst-time communication

complexity is the square of the number of agents).

This means both algorithmic optimization and hard-

ware acceleration for communication reduction are

needed to increase the scalability of communication-

learning MARL systems to a large number of agents.

4.4 Decentralized Training with

Pre-Deﬁned Graph Communication

Figure 9: NeurComm Training in Simulation Breakdown (8

agents).

Figure 10: NeurComm Training Throughput Scalability

varying the number of agents.

NeurComm-enabled MARL follows the Decen-

tralized Training with Pre-Deﬁned Communication

paradigm aimed at targetting networked Multi-agent

Reinforcement Learning (NMARL) scenarios, in-

cluding trafﬁc light and wireless networks systems

(Chu et al., 2020). This is formulated using a spa-

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

332

Table 1: Comparisons of target MARL algorithms.

Algorithm MADDPG ToM2C NeurComm

Training Scheme Centralized Centralized Decentralized

Communication Method

Pre-Deﬁned,

All-to-all

Learnt

Pre-Deﬁned,

Graph-based

Comm

%: Execution 5.89% 25.8% 72.2%

Comm

%: Training 21.1% 47.0% 42.4%

Parallel Rollout Support Yes Yes No

Parallel Training Support Yes No No

SG/MU Overlapping Yes Yes No

Cumulative Rewards

: -2.75+-0.61

ATSC

: Not Supported

CN: -0.79+-0.39

ATSC: Not Supported

CN: Not Supported

ATSC: -136.1

Test Benchmarks: CN denotes Cooperative Navigation, ATSC denotes Adaptive Trafﬁc Signal Control.

Comm

% stands for Communication Time Percentage.

tiotemporal Markov Decision Process, where each

agent’s actions are learned based on the state and pol-

icy of neighboring agents. The main contributions of

this paper is a differentiable neural communication

protocol called NeurComm. NeurComm introduces

a message primitive called an agent’s “belief,” which

is propagated to the neighboring agents and optimizes

their performance iteratively. The additional commu-

nication overhead lies in the belief propagation func-

tion. Each decentralized agent uses the belief, local

states, and action probabilities of neighboring agents

in order to make a decision.

In this Decentralized NMARL using NeurComm

communication implementation, A2C agents are

used, which follow an on-policy actor-critic method

(Mnih et al., 2016). Figure 9 shows the Training in

Simulation breakdown of NeurComm during one iter-

ation of Sample Generation and Model Update. Dur-

ing Sample Generation, messages are received and

sent while control is performed. During Model Up-

date, each agent’s belief is updated along with the gra-

dients of the actor, critic, and neural communication

network. Overall, we observe that communication

takes up a large percentage of the total execution time

during an iteration of Sample Generation and Model

Update.

NeurComm lacks a parallel setup and instead uti-

lizes a single thread for both the Sample Generation

and Model Update phases. From Figure 10, we ob-

serve a 2× increase in all latency measurements when

the number of agents doubles. When increasing the

number of agents, various data structures, including

belief, agent states, number of policies, etc., also in-

crease in size proportionally. IPS decreases propor-

tionally with the number of agents, which is expected

given the single-threaded nature of this implementa-

tion and the increasing communication and state size.

While the addition of the belief primitive leads to opti-

mized control performance, each agent needs to com-

pute its own belief using the belief of other neighbor-

ing agents, leading to a large amount of communica-

tion and computation overhead.

4.5 Comparison of MARL Algorithms

Based on the analyses in Sections 4.2, 4.3 and 4.4,

we summarize some tradeoffs between these different

categories of algorithms and their parallel implemen-

tations in Table 1.

Comparison in Terms of Communication Meth-

ods. In CTDE (columns MADDPG and ToM2C of

Table 1, row “Cumulative Rewards”), it has been ver-

iﬁed that learning to communicate through predicting

other agents’ future rollouts outperforms simple all-

to-all concatenation of current experiences. However,

learnt communication also leads to higher communi-

cation cost in both decentralized execution (Sample

generation) and centralized training (Model Update),

as shown in Table 1, rows “Communication Time Per-

centage,” where the time spent on generating the mes-

sage and data transfer for communication in ToM2C

accounts for 3 times larger percentage than that in

MADDPG. This calls for ﬁne-grained acceleration of

training to alleviate the training bottleneck in MARL

frameworks supporting CTDE with learnt communi-

cation.

Comparison in Terms of Training Schemes. Note

that Centralized training vs. Decentralized training

implies different assumptions in terms of the acces-

sibility of global information on the joint policy. De-

centralized training can better support applications re-

quiring autonomous acting using local information

(e.g., trafﬁc network, stock market), but each agent

needs to cope with a non-stationary environment due

to the instability of other changing and adapting

agents. In contrast, centralized training relies on a

controlling authority of all agents’ policies and faces

a stationary environment. However, the large (expo-

nentially increasing) joint policy space could be too

difﬁcult to search. We observe that in order to learn

a stable policy, decentralized training relies more on

communication due to the lack of global information.

For instance, in NeurComm (Table 1, row “Commu-

nication Time Percentage: Agent Execution”), com-

munication accounts for as much as 70% of the to-

Characterizing Speed Performance of Multi-Agent Reinforcement Learning

333

tal training time. The additional overhead involves

DNN layer computation for the encoding and extrac-

tion of an agent’s belief. This additional communica-

tion overhead justiﬁes the need for ﬁne-grain acceler-

ation of the various added kernels.

5 DISCUSSION & CONCLUSION

In this work, we provided an extensive analysis of var-

ious MARL algorithms based on a taxonomy. This is

also the ﬁrst work in the ﬁeld of MARL that character-

izes key algorithms from a parallelization and acceler-

ation perspective. We proposed the need for latency-

bounded throughput to be considered a key optimiza-

tion metric in future literature. Based on our observa-

tion, the need for communication brings a non-trivial

overhead that needs ﬁne-grained optimization and ac-

celeration depending on the category of the algorithm

described in our taxonomy. There is a plethora of fu-

ture work that can be conducted on MARL in terms

of acceleration:

• Specialized accelerator design for reducing com-

munication overheads: Specialized acceleration

platforms such as Field Programmable Gate Ar-

rays (FPGA) offer pipeline parallelism along with

large distributed on-chip memory that features

single-cycle data access. To take full advantage

of low-latency memory, specialized data layout

and partition for the communicated message pool

need to be exploited.

• Fine-grained Task Mapping using heterogeneous

platforms: We have seen the success of bringing

single-agent RL algorithm to heterogeneous plat-

forms composed of CPU, GPU and FPGA (Meng

et al., 2021; Zhang et al., 2023) and plan to extend

this to MARL.

REFERENCES

Cho, H., Oh, P., Park, J., Jung, W., and Lee, J. (2019). Fa3c:

Fpga-accelerated deep reinforcement learning. In Pro-

ceedings of the Twenty-Fourth International Confer-

ence on Architectural Support for Programming Lan-

guages and Operating Systems, pages 499–513.

Choi, H.-B., Kim, J.-B., Han, Y.-H., Oh, S.-W., and Kim,

K. (2022). Marl-based cooperative multi-agv con-

trol in warehouse systems. IEEE Access, 10:100478–

100488.

Chu, T., Chinchali, S., and Katti, S. (2020). Multi-agent

reinforcement learning for networked system control.

arXiv preprint arXiv:2004.01339.

Ivan, M.-C. and Ivan, G. (2020). Methods of exercising

the surveillance of criminal prosecution. Rev. Stiinte

Juridice, page 160.

Jiang, J., Dun, C., Huang, T., and Lu, Z. (2018). Graph

convolutional reinforcement learning. arXiv preprint

arXiv:1810.09202.

Kaelbling, L. P., Littman, M. L., and Moore, A. W.

(1996). Reinforcement learning: A survey. CoRR,

cs.AI/9605103.

Kim, W., Park, J., and Sung, Y. (2021). Communication in

multi-agent reinforcement learning: Intention sharing.

In International Conference on Learning Representa-

tions.

Liang, E., Liaw, R., Nishihara, R., Moritz, P., Fox, R.,

Goldberg, K., Gonzalez, J., Jordan, M., and Stoica, I.

(2018). Rllib: Abstractions for distributed reinforce-

ment learning. In International Conference on Ma-

chine Learning, pages 3053–3062. PMLR.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-

uous control with deep reinforcement learning.

Lowe, R., Wu, Y. I., Tamar, A., Harb, J., Pieter Abbeel,

O., and Mordatch, I. (2017). Multi-agent actor-critic

for mixed cooperative-competitive environments. Ad-

vances in neural information processing systems, 30.

Meng, Y., Kuppannagari, S., Kannan, R., and Prasanna,

V. (2021). Ppoaccel: A high-throughput acceler-

ation framework for proximal policy optimization.

IEEE Transactions on Parallel and Distributed Sys-

tems, 33(9):2066–2078.

Meng, Y., Yang, Y., Kuppannagari, S., Kannan, R., and

Prasanna, V. (2020). How to efﬁciently train your ai

agent? characterizing and evaluating deep reinforce-

ment learning on heterogeneous platforms. In 2020

IEEE High Performance Extreme Computing Confer-

ence (HPEC), pages 1–7. IEEE.

Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T.,

Harley, T., Silver, D., and Kavukcuoglu, K. (2016).

Asynchronous methods for deep reinforcement learn-

ing. In International conference on machine learning,

pages 1928–1937. PMLR.

Rocki, K. and Suda, R. (2011). Parallel monte carlo tree

search on gpu. In Eleventh Scandinavian Conference

on Artiﬁcial Intelligence, pages 80–89. IOS Press.

Shapley, L. S. (1953). Stochastic games. Proceedings of the

national academy of sciences, 39(10):1095–1100.

Wang, X., Zhang, Z., and Zhang, W. (2022). Model-based

multi-agent reinforcement learning: Recent progress

and prospects. arXiv preprint arXiv:2203.10603.

Wang, Y., Zhong, F., Xu, J., and Wang, Y. (2021).

Tom2c: Target-oriented multi-agent communication

and cooperation with theory of mind. arXiv preprint

arXiv:2111.09189.

Zhang, C., Kuppannagari, S. R., and Prasanna, V. K. (2021).

Parallel actors and learners: A framework for gen-

erating scalable rl implementations. In 2021 IEEE

28th International Conference on High Performance

Computing, Data, and Analytics (HiPC), pages 1–10.

IEEE.

Zhang, C., Meng, Y., and Prasanna, V. (2023). A framework

for mapping drl algorithms with prioritized replay

buffer onto heterogeneous platforms. IEEE Transac-

tions on Parallel and Distributed Systems.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

334