A First Appraisal of Cryptographic Mechanisms for the Selective

Disclosure of Veriﬁable Credentials

Andrea Flamini

2 a

, Silvio Ranise

1,2 b

, Giada Sciarretta

1 c

, Mario Scuro

2 d

, Amir Sharif

1 e

and Alessandro Tomasi

1 f

Center for Cybersecurity, FBK, Trento, Italy

Department of Mathematics, University of Trento, Trento, Italy

ﬂ

Keywords:

Selective Disclosure, Veriﬁable Credentials, Zero-Knowledge Proof, eIDAS 2, GDPR.

Abstract:

Veriﬁable credentials are a digital analogue of physical credentials. Their authenticity and integrity are pro-

tected by means of cryptographic techniques, and they can be presented to veriﬁers to prove claims about the

holder of the credential itself. One way to preserve privacy during presentation consists in selectively dis-

closing the attributes in a credential. In this paper we present the most widespread cryptographic mechanisms

used to enable selective disclosure of attributes, describing their structure and comparing them in terms of

performance, size of the associated veriﬁable presentations, and the ability to produce predicate proofs and

unlinkable presentations.

1 INTRODUCTION

As more services move online, increasing importance

is given to an individual’s digital identity as the foun-

dation for secure and trusted online interactions, such

as e-government and e-commerce.

A new paradigm for identity management based

on digital identity wallets is emerging to empower

data subjects to selectively disclose credentials in a

privacy-preserving and secure way. The most promi-

nent example is the revised regulation eIDAS 2 (EU,

2021), proposing a European Digital Identity (EUDI)

Framework and Wallet to improve cross-border inter-

operability. The privacy enhancing aims of the EUDI

wallet include offering data subjects the means to con-

trol who has access to which of their personally iden-

tiﬁable information, and making it possible to selec-

tively disclose only some of the attributes in their cre-

dentials to trusted parties. These aims are technically

non-trivial to achieve; a service provider has to sat-

isfy the principles of data minimisation and privacy

by design under the GDPR (EU, 2016), while consid-

https://orcid.org/0000-0002-3872-7251

https://orcid.org/0000-0001-7269-9285

https://orcid.org/0000-0001-7567-4526

https://orcid.org/0000-0003-2410-3760

https://orcid.org/0000-0001-6290-3588

https://orcid.org/0000-0002-3518-9400

ering trade-offs between simplicity vs sophistication

of protocol, implementation, and deployment issues

including resource constraints.

Scenario. To exemplify disclosure, we consider the

following simpliﬁed scenario: a young adult wishes

to purchase alcohol and to prove that s/he is over the

legal age limit in the jurisdiction, e.g., 18, without

fully disclosing his/her entire mobile driving license

(mDL).

In this example, the agency in charge of issuing

mDL (Issuer) veriﬁes the mDL Subject’s age during

the issuance process and includes it as an attribute in

the mDL. The data Subject holding the mDL can se-

lect to disclose the single mDL attribute “age” to the

liquor store employee (Veriﬁer). The Veriﬁer can ver-

ify that the Subject is of age to buy alcohol without

learning any other personal information.

This enhances privacy for the Subject while en-

abling the Veriﬁer to verify their age in a trusted and

efﬁcient manner.

Contributions. eIDAS 2 states that EUDI wallets

“should technically enable the selective disclosure

of attributes”, and amendments to the proposal add

“where attestation of attributes does not require the

identiﬁcation of the user, zero knowledge attestation

shall be performed” (EU, 2023). The EUDI Wallet

Flamini, A., Ranise, S., Sciarretta, G., Scuro, M., Sharif, A. and Tomasi, A.

A First Appraisal of Cryptographic Mechanisms for the Selective Disclosure of Veriﬁable Credentials.

DOI: 10.5220/0012084000003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 123-134

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

123

Architecture and Reference Framework (ARF) (DG

CONNECT, 2023), intended to provide more con-

crete technical guidelines and tools, states that “attes-

tation MUST enable Selective Disclosure of attributes

by using Selective Disclosure for JSON Web Tokens

(SD-JWT) and Mobile Security Object (ISO/IEC

18013-5) scheme”.

Both schemes cited in the ARF are based on hid-

ing commitment mechanisms - generating a commit-

ment to a value while keeping it hidden, with the abil-

ity to reveal the committed value later. The ARF does

not currently cover zero knowledge proofs (ZKP) -

e.g., repeatedly proving knowledge of a value with-

out ever having to reveal it. Given the complexity and

range of available options, it is non-trivial to assess

their pros and cons. In order to facilitate an informed

choice, we start to ﬁll this gap by providing crypto-

graphic building blocks for credentials with selective

disclosure capability based on hiding commitments

and ZKP. This paper provides the following main con-

tributions:

• We summarize four cryptographic mechanisms

(cm) for selective disclosure based on hiding com-

mitment and ZKP.

• We provide the structure of Veriﬁable Credentials

and Presentations for the cm, together with the

operation of entities that must be performed for

their creation (issuing) and consumption (presen-

tation).

• We compare the cm w.r.t. several features to assist

in selecting the most appropriate for the use case

of interest.

Outline. Section 2 introduces the cryptographic

primitives used to implement the cryptographic mech-

anisms described in Sections 3 and 4. In Section 5,

we analyse and compare the mechanisms and we dis-

cuss how they support some privacy-enhancing fea-

tures. We summarize the main results and discuss fu-

ture work in Section 6.

2 SELECTIVE DISCLOSURE

Following the VC data model (Sporny et al., 2022),

a credential can be deﬁned as “a set of one or more

claims [assertions about a Subject] made by an Is-

suer”, and a Veriﬁable Credential (VC) as “a tamper-

evident credential that has authorship that can be

cryptographically veriﬁed”. We consider the follow-

ing entities and quote the descriptions from (Lodder-

stedt et al., 2023):

Issuer: “a role an entity can perform by asserting

claims about one or more subjects, creating a VC

from these claims, and transmitting the VC to a

holder”.

Holder: “a role an entity might perform by possess-

ing one or more VCs and generating presentations

from them”.

Subject: “the entity about which claims are made”.

Veriﬁer: “a role an entity performs by receiving one

or more VCs, optionally inside a veriﬁable pre-

sentation” and veriﬁes it “to make a decision re-

garding providing a service to the Subject”.

There are several methods that allow VCs to sup-

port selective disclosure. (Sporny et al., 2019), iden-

tiﬁes the following categories:

Atomic credentials contain only a single claim: the

Issuer may provide a set of atomic credentials and

the Holder presents to a Veriﬁer only those that it

wants to show.

Hashed values allow an Issuer to issue a single VC

containing multiple claims. Each claim is hidden

and committed to using hash functions, then the

commitment is signed by the Issuer. Examples

include hash lists (Section 3.1) and Merkle trees

(Section 3.2).

Selective disclosure signatures are signatures

schemes that natively support selective disclo-

sure of VC claims by using non-interactive zero

knowledge proofs. Examples are CL signature

(Section 4.1) and BBS+ signature (Section 4.2).

We provide noteworthy examples of crypto-

graphic mechanisms based on hashed values, consid-

ered as an instance of hiding commitments, which are

adopted in the standardized mobile Driving License

(ISO/IEC 18013-5, 2021) or discussed in (Steele and

Prorock, 2021) (Section 3). We also present examples

of the most relevant selective disclosure signatures

adopted in (IBM, 2010; Khovratovich et al., 2022;

Lodder et al., 2019)(Section 4). Atomic credentials

are unwieldy to manage, particularly to guarantee that

a presentation contains a collection of atomic creden-

tials that is valid as a whole, but do not introduce or re-

quire substantially different cryptographic techniques

than the other two mechanisms; therefore, we do not

discuss them further.

2.1 VC Structure and Lifecycle

We describe the general structure of VCs and Ver-

iﬁable Presentations (VPs) regardless of the crypto-

graphic mechanism used.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

124

A VC is composed of three sections: an Is-

suer protected header, containing general informa-

tion about the credential, for instance the Issuer, the

Subject and the credential type, an Issuer payload

containing information about the credential attributes,

and an Issuer proof which contains the cryptographic

material which attests the authenticity of the creden-

tial (see Table 1).

A VP is composed of three sections (see Table 2):

a presentation protected header with general infor-

mation about the credential; a presentation payload

with information related to the disclosed attributes;

and a presentation proof with the cryptographic ma-

terial that allows the Veriﬁer to check the authenticity

of the presentation.

The structure of the VC and VP we adopt is con-

sistent, albeit simpliﬁed to focus on selective disclo-

sure, with the structure of JSON Web Proof (JWP)

(Miller et al., 2023), a proposal to standardize a JSON

container which aims to describe the structure of VCs

to allow the selective disclosure of attributes.

In a preliminary set-up phase, the Issuer must

generate its private-public key pair (sk

Iss

,pk

Iss

) us-

ing the key generation function of the digital signa-

ture scheme used to sign the VCs, keyGen(). In

the issuing phase, the Issuer generates an Issuer

proof with the function genIssuerProof(−). The

Holder, upon reception of the VC created by the

Issuer, veriﬁes its validity computing the function

verIssuerProof(−).

In the presentation phase the Holder can cre-

ate a VP specifying the attributes it wants to dis-

close. In particular, the Holder creates the VP

containing the Holder-generated proof by comput-

ing the function genHolderProof(−). The Veri-

ﬁer, upon reception of the VP computes the function

verPresentProof(−) to verify it and possibly ac-

cept the Holder’s claims.

2.2 Cryptographic Building Blocks

We provide the main cryptographic notions that are

useful to understand the approaches for the creation

of VCs supporting selective disclosure of attributes:

hashing and salting for the creation of hiding com-

mitments, and ZKP to prove statements about undis-

closed attributes in selective disclosure signatures.

Digital signatures deﬁne the algorithms

keyGen() to generate the public and private

keys (pk,sk), genSig(sk,m) to sign a message m,

and verSig(pk,m,σ) to verify the signature σ.

While the algorithms to implement the above

functions mentioned in Section 3 may be any stan-

dardized digital signature algorithm, those described

in Section 4 are a special class of signatures designed

to support ZKP, and may require more structured in-

put, e.g., ordered lists of messages. We use the same

notation for brevity, but we stress that they enable dif-

ferent features.

2.2.1 Hash and Salt Technique

A commitment scheme allows a party to commit to a

value v by sending a commitment, and then to reveal

v by opening the commitment at a later point in time.

A commitment scheme is hiding if the commitment

reveals nothing about v.

In hiding commitments based on a hash function

H , the commitment creation algorithm takes as input

a value v to be committed to, and outputs H (v||s),

where s is chosen uniformly at random and is referred

to as the salt of the commitment, and v||s is the con-

catenation of the bytes strings v and s. This scheme is

said to be:

• binding: it is computationally infeasible to

ﬁnd another pair (v

′

) ̸= (v,s) such that

H (v||s) = H (v

′

||s

′

);

• hiding: no information about v can be gained by

only looking at the commitment H (v||s).

Only someone who knows both v and s can open

the commitment (by revealing v,s) and prove that the

message committed to is v.

2.2.2 Non-Interactive Zero-Knowledge Proofs

Non-interactive zero-knowledge proofs (NIZKP) al-

low an actor, called prover, to convince another actor,

called veriﬁer, of the truthfulness of some claim, with-

out revealing anything else to the veriﬁer. The proto-

col is non-interactive, meaning the prover generates a

proof π and the veriﬁer checks that π is valid without

requiring additional interactions between prover and

veriﬁer.

In Section 4 we mention two NIZKP based on the

NIZKP for linear relations: given a group G - which

in Section 4.1 will be a group of unknown order and

in Section 4.2 will be a group of prime order p - and

y,g

,.. .,g

∈ G, the prover can prove that it knows

,.. .,a

such that y =

∏

i=1

. For an introduction

to such protocols see Section 19.5.3 of (Boneh and

Shoup, 2023) and (IBM, 2010).

3 HIDING-COMMITMENT

MECHANISMS

Instances of hiding commitment mechanisms can be

obtained, for example, by using lists of hash-based

A First Appraisal of Cryptographic Mechanisms for the Selective Disclosure of Veriﬁable Credentials

125

hiding commitments (cmtList, see Section 3.1),

Merkle Trees (merTree, see Section 3.2), or vec-

tor commitments (Catalano and Fiore, 2013), as sug-

gested in (Steele and Prorock, 2021).

The Issuer commits to a set of attributes, then dig-

itally signs the commitment. The properties of hiding

commitments allow the Issuer of a credential to sign

the commitments, then a Holder, who knows the at-

tribute values of a credential, can open only some of

the committed values proving to a Veriﬁer the truth-

fulness of its claims.

Operations in the Issuing Phase. The Issuer can

create a VC with the structure of Table 1 and issues it

to the Holder. The VC is composed of the three parts

already mentioned:

• the Issuer protected header containing the cryp-

tographic mechanism identiﬁer cm, - specifying

primitives such as the chosen digital signature al-

gorithm and cryptographic hash function - and the

Issuer public key pk

Iss

;

• the Issuer payload containing a list of attributes

A = (a

,.. .,a

) certiﬁed by the Issuer who cre-

ated the credential, together with a list of random

salts, one for each attribute S = (s

,.. .,s

);

• the Issuer Proof containing the digital sig-

nature of the commitment CMT to the at-

tributes A, constructed according to the cho-

sen cryptographic mechanism and the list of

attributes and salts, signed by the Issuer, ob-

taining σ = genSig(sk

Iss

,CMT). These op-

erations are performed executing the function

genIssuerProof(sk

Iss

,A,S).

Note that the choice of the digital signature scheme

adopted by the Issuer to sign the CMT is not restricted

to a speciﬁc primitive.

The Holder can verify the VC’s validity by com-

puting the function verIssuerProof(VC), which

consists in verifying that the commitment CMT is ac-

tually a commitment to the elements in A and S, and

verifying the Issuer’s digital signature.

Operations in the Presentation Phase. The

Holder creates a VP to convince the Veriﬁer that the

attributes revealed are included in a credential issued

by a trusted Issuer.

A VP in this context has the structure described in

Table 2. It is composed by:

• a presentation protected header containing the

name of the cryptographic mechanism cm adopted

in the creation of the underlying credential and the

Issuer public key;

• the presentation payloads, containing a subset

DA ⊂ A of attributes (a

,.. .,a

) that the Holder

wants to disclose together with DS ⊂ S, the list of

associated salts (s

,.. .,s

);

• a presentation proof generated by the Holder in-

cluding the commitment CMT and its signature σ

created by the Issuer associated to pk

Iss

and the

Holder-generated proof obtained computing the

function genHolderProof(DA,DS,A, S).

Table 1: A simpliﬁed representation of VC which allows selective disclosure of attributes.

VC Hiding-commitment Selective disclosure signature

Issuer Protected Header Cryptographic mechanism: cm Cryptographic mechanism: cm

Issuer public key: pk

Iss

Issuer public key: pk

Iss

Issuer Payloads Attributes and salts: Attributes:

A = (a

,...,a

) A = (a

,...,a

)

S = (s

,...,s

)

Issuer Proof Signed commitment: Selective disclosure signature:

genIssuerProof(sk

Iss

,A,S) = genIssuerProof(sk

Iss

,A) =

= (CMT,σ = genSig(sk

Iss

,CMT)) = σ = genSig(sk

Iss

,A)

Table 2: The general structure of a VP.

VP Hiding-commitment Selective disclosure signature

Presentation

Protected Header

Cryptographic mechanism: cm Cryptographic mechanism: cm

Issuer public key: pk

Iss

Issuer public key: pk

Iss

Presentation Payloads

Disclosed attributes and salts: Disclosed attributes:

DA = (a

,...,a

) ⊂ A DA = (a

,...,a

) ⊂ A

DS = (s

,...,s

) ⊂ S

Presentation Proof

Signed commitment:

(CMT,σ)

Holder-generated Proof: Holder-generated proof:

P = genHolderProof(DA,DS,A,S) P = genHolderProof(pk

Iss

,DA,A,σ)

SECRYPT 2023 - 20th International Conference on Security and Cryptography

126

The Veriﬁer veriﬁes a VP received

from the Holder by computing the function

verPresentProof(VP), which consists in (i)

verifying the signature of the CMT created by the

Issuer, and (ii) verifying the proof that the disclosed

attributes in DA are a subset of the attributes commit-

ted to in CMT.

Once the commitment opening algorithm for

the pairs (a

) in DA × DS ⊂ A ×S is deﬁned,

the functions genHolderProof(DA,DS,A,S) and

verPresentProof(VP) are well deﬁned.

3.1 Commitment List Mechanism

In the cmtList mechanism, credentials contain or-

dered lists of attribute-salt pairs; for each pair, the is-

suer creates a hiding commitment, then signs the list

of commitments.

In genIssuerProof(sk

Iss

,A,S), the Issuer gen-

erates a random salt s

for each attribute a

and com-

putes the commitment list entries L

= H (a

||s

). Fi-

nally, CMT = [L

]

i=1

is signed by the Issuer to create

the Issuer proof.

Since the payload of a Holder-generated VP (Ta-

ble 2, column 2) contains all the information needed

to open the commitments to the disclosed attributes,

the Presentation Proof only contains the signed com-

mitment - genHolderProof is the null function.

In verPresentProof(VP) the Veriﬁer veriﬁes the

Issuer signature of CMT and compares H (a

||s

) with

, for each (a

) ∈ DA ×DS. If the signature is

veriﬁed and the digests H (a

||s

) match with L

, the

VP is accepted.

3.2 Merkle Tree Mechanism

The merTree mechanism uses Merkle trees to create

commitments CMT.

genIssuerProof(sk

Iss

,A,S): the Issuer gener-

ates one random salt s

for each attribute a

, then uses

their ordered concatenated pairs as leaves of a Merkle

tree. The Issuer sets the CMT equal to the Merkle tree

root

R = getRoot(a

||s

,.. .,a

||s

). (1)

An example of Merkle tree is given in Figure 1.

To create a VP, the Holder includes the presenta-

tion payload as in column 2 of Table 2. The presen-

tation proof, together with the signed commitment,

also requires the Holder-generated proof, which the

Holder obtains by computing the inclusion paths of

the attributes that the Holder wants to disclose.

R = H (d

||d

)

= H (d

||d

)

= H (l

)

= a

||s

= H (l

)

= a

||s

= H (d

||d

)

= H (l

)

= a

||s

= H (l

)

= a

||s

Figure 1: Merkle tree constructed over 4 leaves. Disclosing

||s

, their inclusion proof in R is [3,d

The Veriﬁer veriﬁes the presentation computing

verPresentProof(VP) verifying the signature of

CMT and verifying that the inclusion paths in P let

the Veriﬁer reconstruct the signed root R, for each

) ∈ DA × DS.

For example, the inclusion path of the leaf l

position 3 of the Merkle tree in Figure 1, given the

public root R, is [3, d

]. In order to verify the

inclusion of l

, the Veriﬁer computes d

= H (l

= H (d

||d

), and veriﬁes that H (d

||d

) = R.

4 SELECTIVE DISCLOSURE

SIGNATURE MECHANISM

Selective disclosure signatures, following the naming

in (Sporny et al., 2019), are a class of digital signa-

ture algorithms that enable (a) an Issuer to sign mul-

tiple attributes with a single signature, (b) a Holder to

prove possession of a signature and some undisclosed

attributes, generating fresh ZKP without involving the

Issuer - recall Section 2.2.2, and (c) a Veriﬁer to verify

the validity of a disclosed subset of attributes, given

only the ZKP of undisclosed attributes and signature.

Examples of selective disclosure signatures

are CL (Section 4.1) and BBS+ (Section 4.2),

which are multimessage signature algorithms

for which an ordered list is input to the signa-

ture generation genSig(sk

Iss

,(a

,.. .,a

)) =

σ and signature veriﬁcation

verSig(pk

Iss

,(a

,.. .,a

),σ) = true/false.

Operations in the Issuing Phase. The VC based on

the use of selective disclosure signature algorithms as

cryptographic mechanism is composed of three parts

(see column 3 of Table 1):

• Issuer protected header, containing the name of

the cryptographic mechanism cm i.e., the chosen

selective disclosure signature scheme, and the Is-

suer public key pk

Iss

;

• Issuer payloads, containing the list of attributes

A = (a

,.. .,a

);

A First Appraisal of Cryptographic Mechanisms for the Selective Disclosure of Veriﬁable Credentials

127

• Issuer proof, containing the selective disclosure

signature (SDSig) of the attributes in A, σ =

genSig(sk

Iss

,A).

Therefore the function that allows the

Issuer to create the Issuer proof is just

genIssuerProof(sk

Iss

,A) = genSig(sk

Iss

,A),

and the function that allows the Holder to verify it is

verIssuerProof(VC) = verSig(pk

Iss

,A,σ).

Operations in the Presentation Phase. To selec-

tively disclose some attributes of a VC to a Veriﬁer,

the Holder creates a VP (see column 3 of Table 2)

composed of:

• presentation protected header, containing the

name of the cryptographic mechanism cm and the

Issuer public key;

• presentation payload, containing the list DA =

,.. .,a

) of disclosed attributes;

• presentation proof P, generated by the Holder

executing genHolderProof(pk

Iss

,DA,A, σ), a

NIZKP of the signature σ, certifying the revealed

attributes in DA and proving in zero-knowledge the

knowledge of the hidden attributes in A \DA.

The Veriﬁer veriﬁes the NIZKP P by computing the

function verPresentProof(VP).

For both BBS+ and CL we provide a high level

description of genHolderProof(pk

Iss

,DA,A, σ) and

verPresentProof(VP), including references to

computation details omitted for brevity.

CMT vs SDSig. The purpose of CMT is to bind the

attributes into an item that is subsequently signed by

the Issuer. The Holder can perform selective disclo-

sure by revealing CMT, the attributes to be disclosed,

and a presentation proof. On the other hand, SDSig

simultaneously binds the attributes into an item that is

itself a digital signature, certifying the authorship of

the VC. To create a presentation, the Holder must not

reveal SDSig, but rather derive from SDSig a random-

ized proof that assures the Veriﬁer about the claims.

For a comparison between CMT vs SDSig w.r.t. impor-

tant features, see Section 5.

4.1 CL Signature

The CL signature scheme was presented in (Ca-

menisch and Lysyanskaya, 2002).

VC Creation and Veriﬁcation. To create SDSig

for a VC, an Issuer signs the attributes a

,.. .,a

∈ A

using the following CL digital signature algorithm as

deﬁned in (IBM, 2010).

Key generation algorithm keyGen(). Let k be the se-

curity parameter and n ← pq be an ℓ

-bit special

RSA modulus

, and choose uniformly at random

quadratic residues R

,.. .,R

,S, Z

Output the public key

Iss

= (n, R

,.. .,R

,S, Z) (2)

and the secret key sk

Iss

= (p).

Signing algorithm genSig(sk

Iss

,A). On input

A = {a

,.. .,a

},a

∈ {0, 1}

ℓ

, choose a ran-

dom prime number e ∈ {0, 1}

ℓ

, ℓ

> ℓ

+ 2,

e > 2

ℓ

−1

, and a random number v ∈ {0,1}

ℓ

where ℓ

= ℓ

+ ℓ

with ℓ

a security param-

eter (e.g. ℓ

= 80). Compute

A ←

... R

mod n. (3)

The resulting output signature is

σ = genSig(sk

Iss

,(a

,.. .,a

))

= (A, e,v). (4)

Veriﬁcation algorithm verSig(pk

Iss

,A,σ). To ver-

ify that the triple (A, e,v) is a signature on

,.. .,a

check that the following holds:

Z = A

... R

mod n (5)

∈ {0, 1}

ℓ

(6)

e ∈ [2

ℓ

−1

+ 1,2

ℓ

− 1] (7)

These functions completely deﬁne

genIssuerProof(sk

Iss

,A) which corresponds

to SDSig = genSig(sk

Iss

,A) = σ = (A, e,v) ∈

× {0,1}

ℓ

× {0,1}

ℓ

and verIssProof(VC).

VP Creation. At every presentation, the Holder

generates a new random signature from a signature

received from the Issuer; then the Holder creates a

NIZKP of knowledge of a representation for the ran-

domized signature using an argument similar to the

one about NIZKP for linear relations (Section 2.2.2)

and described in detail in (IBM, 2010).

The Holder-generated proof is a NIZKP of knowl-

edge of a signature and the attributes signed in it, gen-

erated by the function

P = genHolderProof(DA, A,σ,pk

Iss

)

= (c, A

′

,.. .,

(n−d)

) (8)

n = pq is a special RSA modulus if p = 2p

′

+ 1 and

q = 2q

′

+ 1 with p

′

prime numbers

q is a quadratic residue modulo n if there exists a ∈ Z

such that q = a

mod n

SECRYPT 2023 - 20th International Conference on Security and Cryptography

128

with pk

Iss

from Eq. (2), and σ from Eq. (4); c ∈

{0,1}

256

is the challenge of the underlying NIZKP;

′

∈ Z

∗

is a component of the randomized signa-

ture;

e ∈ {0,1}

ℓ

′

+ℓ

′

∈ {0,1}

ℓ

+ℓ

and

,.. .,

(n−d)

∈ {0,1}

ℓ

+ℓ

are the response

values of the underlying NIZKP for linear relations.

VP Veriﬁcation. The veriﬁcation function

verPresentProof(VP) consists in (i) verify-

ing the NIZKP for linear relations to prove the

Holder knows a valid undisclosed signature, and

(ii) verifying that the size of the received values

(

,.. .,

(n−d)

) lies in the expected integer interval

(IBM, 2010) to ensure that the undisclosed attributes

,.. .,a

(n−d)

and parameter e used to build the

NIZKP have the expected size.

4.2 BBS+ Signature

The BBS+ signature was presented by Au et al. (Au

et al., 2006) as a provably secure extension to BBS

group signatures (Boneh et al., 2004) and improved

by Camenisch et al. (Camenisch et al., 2016). An op-

timisation provided with a proof of security has also

recently been published (Tessaro and Zhu, 2023).

VC Creation and Veriﬁcation. To issue a VC, an

Issuer creates SDSig by producing a BBS+ signature

of the messages a

,.. .,a

with its private key sk

Iss

Let G

and G

be groups of prime order p,

and e : G

× G

→ G

be a pairing

Key generation algorithm keyGen(). Take a random

vector (h

,.. .,h

) ∈ G

m+1

, a random x ∈ Z

∗

and

sets sk

Iss

= x and pk

Iss

= (w = g

,.. .,h

)

Signing algorithm genSig(sk

Iss

= x,A). On

input the secret key x and the messages

A = (a

,.. .,a

) ∈ Z

, randomly generate e, s ∈

and compute A = (g

∏

i=1

)

e+x

. Output

the triple (A,e,s).

Veriﬁcation algorithm verSig(pk

Iss

,A,σ). On in-

put the public key

Iss

= (w,h

,.. .,h

) ∈ G

× G

m+1

, (9)

messages (a

,.. .,a

) ∈ Z

, and a

signature (A,e,s) ∈ G

× ∈ Z

, check

e(A,wg

) = e(g

∏

i=1

A pairing is a map satisfying bilinearity, i.e.

e(g

) = e(g

)

, non-degeneracy, i.e. for each gen-

erator g

∈ G

, then e(g

) generates G

, and

efﬁciency which means that the map can be efﬁciently com-

puted for any input.

These algorithms deﬁne the functions

genIssuerProof(sk

Iss

,A) which corresponds to

SDSig = genSig(sk

Iss

,A) = σ = (A,e,s) ∈ G

×Z

and verIssuerProof(VC).

VP Creation. The Holder can generate a VP with

genHolderProof(DA,A,σ, pk

Iss

) whose output is

obtained from the construction of a NIZKP of knowl-

edge of the signature and the hidden attributes based

on the NIZKP for linear relations. The function re-

turns

P = genHolderProof(DA, A,σ,pk

Iss

)

= (A

′

,A,d,c,

′

,.. .,

n−d

) (10)

where A

′

,A,d ∈ G

, and all other elements lie in Z

For a detailed description we refer to (Looker et al.,

2023; Camenisch et al., 2016).

VP Veriﬁcation. Having received a VP from

a Holder, the Veriﬁer computes the function

verPresentProof(VP), which consists in executing

the veriﬁcation steps of the underlying NIZKP for lin-

ear relations and verifying that the terms A = A

′x

using

the pairing e.

5 SOLUTION ANALYSIS

To assess the maturity of options, we consider their

standardization (Section 5.1) and their cryptographic

agility (Section 5.2). Standardization is important

for cryptographic protocols to ensure expert vetting

of correctness, security, and other properties claimed,

as well as to promote interoperability as encouraged

e.g., by the proposed Interoperable Europe Act (EU,

2022). Cryptographic agility (Sullivan, 2010) “is

achieved when a protocol can easily migrate from

one algorithm suite to another more desirable one,

over time” (Housley, 2015). The need to transition

between cryptographic algorithms and key lengths

has been steadily gaining importance, e.g., replac-

ing older versions of the Secure Hash Algorithm, and

preparing for quantum computing (Barker and Rogin-

sky, 2019).

We observe how each mechanism supports pri-

vacy and ofﬂine features with regards to presenta-

tion unlinkability (Section 5.3), and brieﬂy discuss

the advantages of predicate proofs (Section 5.4). We

compare the computation speed of each function de-

scribed in Section 2 (Section 5.5.2), and the size of

presentation elements of each mechanism (Section

5.5.3). Our assessment is summarized in Section 5.6.

A First Appraisal of Cryptographic Mechanisms for the Selective Disclosure of Veriﬁable Credentials

129

5.1 Standardization

cmtList is the only mechanism featured in ofﬁcial

standards: it is enabled by design in ISO 18013-5

(ISO/IEC 18013-5, 2021), and it is the basis for the

IETF draft SD-JWT (Fett et al., 2023). Both are con-

sidered mandatory for the European digital identity

wallet (DG CONNECT, 2023) developed in the con-

text of the revised eIDAS regulation (EU, 2021).

JSON Web Proof (JWP) (Miller et al., 2023) is a

proposed container format for VCs and VPs that aims

to be agnostic to the proof mechanism. It is currently

an IETF draft on the Standards Track. merTree has

been proposed in (Steele and Prorock, 2021) as a pos-

sible mechanism for JWP. It also appears in the exper-

imental Certiﬁcate Transparency 2.0 proposal (Laurie

et al., 2021).

The BBS+ speciﬁcation (Looker et al., 2023) is an

IRTF draft. CL signatures are not speciﬁed indepen-

dently but as part of the Identity Mixer (IBM, 2010)

and Hyperledger Ursa (Khovratovich et al., 2022)

anonymous credentials protocols.

5.2 Cryptographic Agility

cmtList and merTree offer the greatest agility: any

cryptographic hash function can be used to construct

them, and any digital signature can be chosen to sign

the hash list or tree root.

BBS+ signatures can in theory be based on any

pairing-friendly curve, of which several options have

been identiﬁed (Sakemi et al., 2022) up to 256-

bit security, and any correspondingly secure cryp-

tographic hash function. Cipher suites have been

drafted (Looker et al., 2023).

The idemix speciﬁcation (IBM, 2010) for anony-

mous credentials with CL signatures contains a default

value for 14 parameters and 7 “constraints which pa-

rameter choices must satisfy to ensure security and

soundness” (Tables 2 and 3 therein), and it is left to

the reader to adjust these as required. The default

RSA modulus is 2048 bits, which corresponds to only

112 bits of security. Other than increasing the prime

factor length, it is non-trivial to establish how param-

eters should change to increase the security level of

the scheme as a whole.

The Ursa library also defaults to 2048-bit modu-

lus; the Ursa speciﬁcation (Khovratovich et al., 2022)

lists individual parameter values scattered throughout,

including 1536-bit RSA factors, but it is left to the

reader to gather the information, to modify the source

code, and to assume that all other parameters have

been set to meet the same level of security.

5.3 Presentation Unlinkability

Unlinkability can be deﬁned as ensuring that “no

correlatable data are used in a digitally-signed pay-

load” (Sporny and Longley, 2022). Sources of corre-

lation include the signature itself and long-term iden-

tiﬁers, such as the credential subject, a credential

identiﬁer, revocation status information etc. Guaran-

teeing this property goes beyond selective disclosure

only; here we focus on signature-based correlation.

Hiding Commitment Mechanisms. Since the Pre-

sentation Proof of a VP contains the issuer-signed

commitment included in the associated VC, this iden-

tiﬁer links each VP uniquely to one VC, and there-

fore to its Holder. This means that the Holder should

use always different VCs to generate new VPs, there-

fore in the issuing phase the Issuer must provide the

Holder with several distinct versions of the same VC

where a distinct version of VC is built including the

same set of attributes hidden using different salts.

When all the distinct versions of the same VC

have been used, the Issuer must produce and send new

ones to the Holder. There must therefore be an avail-

able channel between the Issuer and the Holder device

storing the VCs that guarantees ready access to brand

new VCs that can be used to create unlinkable presen-

tations.

Selective Disclosure Signatures. As summarized

in Table 2, the presentation proof contains only the

Holder-generated proof, which is a randomized ele-

ment.

Given a VC, the Holder can create a new presen-

tation proof each time that is indistinguishable from

random, and therefore cannot be correlated to other

VPs. The Holder can use the same VC multiple times;

therefore, interaction with the Issuer is required only

when requesting a new credential or renewing an ex-

pired one.

5.4 Predicate Proofs

In some use cases, there may be an interest in ask-

ing a question (“predicate”) about an attribute, with-

out disclosing the attribute itself. For instance, a Veri-

ﬁer may need to know whether an mDL subject’s age

is over some threshold NN, or in some range, without

needing to know their full date of birth. This feature

would enhance privacy and follow the data minimiza-

tion principle.

The cmtList mechanism used in mDL allows

the Issuer to create range proofs only by treating

them as individual attributes; for instance, in the

SECRYPT 2023 - 20th International Conference on Security and Cryptography

130

AAMVA mDL implementation guidelines (AAMVA,

2023) Issuers must identify every likely threshold

value in their jurisdiction and encode a separate at-

tribute age over NN=True or False for each NN.

The disadvantages of implementing this feature

with this mechanism are: (a) an increased size of ev-

ery VC and VP, (b) requiring the Issuer to keep track

of when each threshold is crossed to issue a new VC,

the same thresholds represented every separate juris-

diction for the same VC type (e.g., age above 18, 21,

65 etc). All hiding commitment based cm including

merTree suffer the same disadvantages.

By contrast, selective disclosure signature predi-

cate proofs enable a Veriﬁer to request an evaluation

of attributes during the Presentation Phase, without

prior involvement of the Issuer: they are built by the

Holder as NIZKP of predicates about the attributes

included in the VC. For example, range proofs and

set membership proof s (Camenisch et al., 2008) al-

low the Prover to prove that an attribute a lies within

a range v < a < u, or in a given set of values a ∈ A ,

respectively. Examples of predicate proofs for the CL

mechanism can be found in Section 6 of (IBM, 2010).

5.5 Experimental Evaluation

Our use case of interest is a proximity ﬂow for EUDI

Wallets, in which the Holder and Veriﬁer are phys-

ically close and the attestation exchange and disclo-

sure occurs using proximity protocols (NFC, Blue-

tooth, QR-Code, etc.), possibly without the Holder

having internet connectivity. A concrete instance in-

volves checking a mobile driving license (mDL), as

considered in Section 1. In this scenario, the Holder

device may be resource-constrained in both compu-

tational capability and presentation exchange band-

width; we therefore measure the speed of computa-

tion, particularly genHolderProof, in Section 5.5.2

and the size of VP elements for each cm in Sec-

tion 5.5.3. Based on ISO/IEC 18013-5 (ISO/IEC

18013-5, 2021), in which an mDL consists of 11

mandatory and 22 optional attributes, we use creden-

tials with n

≤ 33 total attributes.

5.5.1 Experimental Set-up

For BBS+ and CL signature performance, we test the

Hyperledger Ursa rust implementation,

the only li-

brary with both algorithms, to the best of our knowl-

edge. For a fair comparison, we aim for an equivalent

level of security of 128 bits in all tested mechanisms -

see SP 800-57 (Barker, 2020), Table 2. Enforcing this

https://docs.rs/ursa/

common security level is non-trivial, as mentioned in

Section 5.2.

For the sake of reproducibility, the parameters and

algorithms used in our experiments are curve BLS12-

381 and BLAKE2 for BBS+, 3072-bit RSA modulus

and SHA-256 for CL, and ed25519 and SHA-256 for

hiding commitment mechanisms. For cmtList and

merTree

digital signatures we use digital signature

EdDSA over ed25519 using the same rust crate

which Ursa depends.

In order to test performance on both desktop

PCs and constrained devices with ARM CPUs more

closely resembling mobile phones - our use case for

Holder devices - experiments are run on i5-4690K

(3.50GHz, 4 cores), raspberry pi 3B+ 1GB RAM, pi

4B 4GB RAM, and Ryzen 7 5800X.

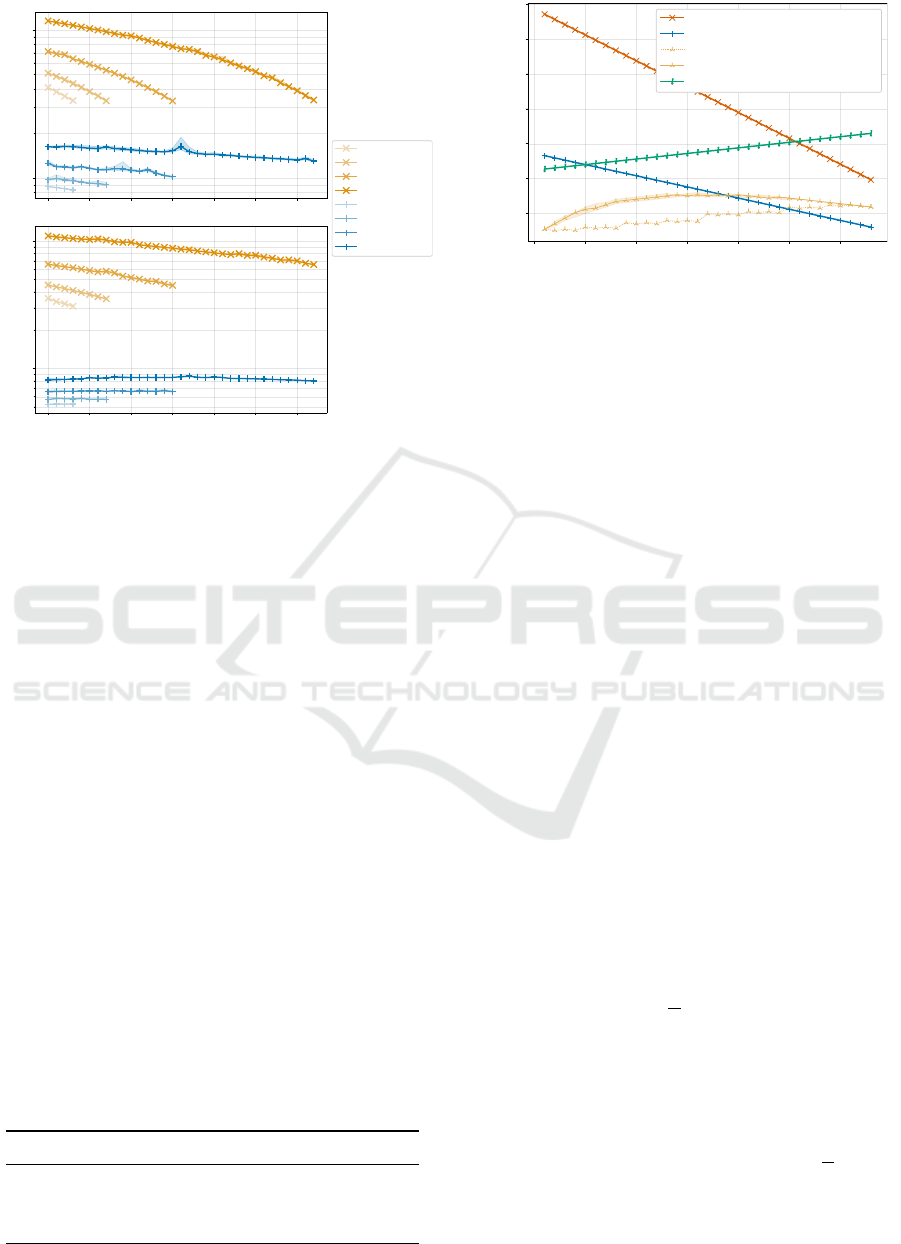
5.5.2 Speed

We measure the speed of key generation, and signa-

ture and presentation proof generation and veriﬁca-

tion - see Table 3 and Figure 2. The presentation

phase is of particular interest since it is expected to

occur frequently on constrained devices; we show re-

sults in Tables 4 and 5. There is approximately an or-

der of magnitude difference in performance between

a modern desktop CPU (Ryzen 5800X) and an ARM

raspberry pi 4B, and another between the pi 4B and pi

3B+.

The speed of hashing and of generating Merkle

inclusion paths is negligible compared with gener-

ating and verifying the digital signature in cmtList

and merTree; we therefore only report the results of

merTree speed tests.

Table 3: Speed by mechanism for each function. Approxi-

mate orders of magnitude in ms - lower is faster.

Function merTree CL BBS+

keyGen -2 4 0

genIssuerProof -1 2 0

verIssuerProof -1 2 1

genHolderProof -3 2 1

verPresentProof -1 2 1

Table 4: Presentation Proof generation test by CPU with

= 33. Times in ms are median over n

≤ n

cm 5800X 4690K pi 4B pi 3B+

merTree 0.0007 0.0015 0.0044 0.0143

CL 55.270 74.758 394.95 1475.9

BBS+ 7.127 15.109 52.03 374.7

https://docs.rs/rs merkle/

https://docs.rs/ed25519-dalek/

A First Appraisal of Cryptographic Mechanisms for the Selective Disclosure of Veriﬁable Credentials

131

time [ms]

Presentation generation

CL n

= 4

CL n

= 8

CL n

= 16

CL n

= 33

BBS+ n

= 4

BBS+ n

= 8

BBS+ n

= 16

BBS+ n

= 33

1 6 11 16 21 26 31

disclosed attributes n

time [ms]

Presentation veriﬁcation

Figure 2: Presentation Proof generation and veriﬁcation

performance test results for CL and BBS+. merTree gen-

eration and veriﬁcation speeds are 4 and 2 orders of magni-

tude faster than BBS+ and not shown. Solid lines are median

times, shaded areas are 25

and 75

percentile.

5.5.3 Presentation Size

Presentation Proof. We compare VP size contribu-

tions for each cm, with trends summarized in Figure 3.

Attribute size is arbitrary, so DA is not included. For

commitment-based mechanisms, one disclosed salt

DS per disclosed attribute must be included; there-

fore, VP size tends to grow with n

for cmtList and

merTree, while it decreases for CL and BBS+ due to

one zero-knowledge proof per undisclosed attribute.

Presentation proof size is calculated as follows:

• cmtList: one digest per attribute in the creden-

tial, a signature of the list of digests, one disclosed

salt per disclosed attribute:

CMT

= dn

+ |σ| + sn

(11)

• merTree: one tree root (of digest size), a signa-

ture of the tree root, one disclosed salt per dis-

closed attribute, an inclusion proof for disclosed

attributes. The size of an inclusion proof for a sin-

gle attribute is equal to the tree height ⌈log

)⌉

Table 5: Presentation Proof veriﬁcation test by CPU with

= 33. Times in ms are median over n

≤ n

cm 5800X 4690K pi 4B pi 3B+

merTree 0.040 0.071 0.29 1.1

CL 64.969 86.393 456.00 1687.3

BBS+ 4.875 8.383 30.56 187.9

0 5 10 15 20 25 30

Disclosed Attributes n

500

1000

1500

2000

2500

3000

3500

Holder Presentation Proof [bytes]

CL model

BBS+ model

Merkle + ed25519 sequential disclosure

Merkle + ed25519 random disclosure

cmtList + ed25519 model

Figure 3: VP proof size comparison for n

= 33. Values

used for comparison, in bytes: salt size s = 16; digest size

d = 32; cmtList and merTree signature size |σ| = 64 for

EdDSA with curve ed25519. Model equations for cmtList

(11), CL (8), BBS+ (10) shown alongside measured Merkle

implementation values for sequential attribute disclosure

(best-case) and random sampling of attribute combinations

(median with 25th and 75th percentile shaded).

times the digest size; a simple implementation

may return a separate proof per disclosed at-

tribute, an optimized implementation will be more

compact. An upper bound is therefore:

CMT

= d + |σ|+ dn

+ ⌈log

)⌉dn

(12)

• CL: SDSig: in order to make a fair comparison

between the algorithms, we consider as size of

n 3072 bits to have a security level of 128 bits.

Therefore, a NIZKP of knowledge of a signature

and of the undisclosed attributes (Eq. (8)) is given

by:

– a digest c ∈ {0,1}

256

(32 bytes);

– an element A

′

∈ Z

(384 bytes), an element

e ∈ {0,1}

457

(58 bytes), and

′

∈ {0,1}

3744

(468 bytes)

– an element

∈ {0,1}

593

(75 bytes) for each

undisclosed attribute.

• BBS+: SDSig: a NIZKP of knowledge of a sig-

nature and of the undisclosed values (Eq. (10)) is

given by:

– three elements A

′

,A,d ∈ G

;

– ﬁve elements c,

′

∈ Z

;

– one

∈ Z

for each undisclosed attribute.

BBS+ can be implemented using the pairing-

friendly elliptic curve BLS12-381, with the prime

order of the subgroup of G

being p ∈ {0, 1}

256

Therefore, the elements in G

- i.e., A

′

,A,d - can

be represented as 48-byte strings and the integer

elements as 32-byte strings.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

132

Public Keys. A VP header may contain either pk

Iss

or a reference to it. For instance, a JWS (Jones et al.,

2015) header may contain pk

Iss

as JWK or X.509 cer-

tiﬁcate, or a url as JKU, or a certiﬁcate thumbprint,

etc. pk

Iss

size may be calculated as follows.

• merTree,cmtList: the public key pk

Iss

of Ed-

DSA digital signature is a 32-byte point of the

curve ed25519.

• CL: the public key pk

Iss

of the CL signature

algorithm is (n,R

,.. .,R

,S, Z) ∈ Z

m+3

of size

384(m + 3) bytes.

• BBS+: the public key pk

Iss

of the BBS+ signature

algorithm is (w = g

,.. .,h

) ∈ G

× G

m+1

size 96 + 48(m + 1) bytes, where G

are ob-

tained using curve BLS12-381.

5.6 Assessment Summary

We ﬁnd that cmtList and merTree are more stan-

dardized, easier to implement but more cumbersome

for the Issuer to manage, very fast to compute but only

merTree is reliably small in size. Predicates must be

deﬁned by the issuer, and unlinkability requires the is-

suer to provide a supply of single-use credentials with

new attribute salts and signatures in advance. While

CL is particularly computationally expensive and large

in size, BBS+ is computationally feasible and com-

pact; in both cases, predicate proofs can be provided

by the holder, and the randomness for unlinkability is

also generated by the holder based on a single selec-

tive disclosure signature. Our assessment is summa-

rized qualitatively in Table 6.

6 CONCLUSION

There exist several approaches exist to augment VCs

with privacy-preserving selective disclosure of at-

tributes, including cryptographic mechanisms based

on hiding commitments and selective disclosure sig-

natures. We analyzed four mechanisms: salted hash

list (cmtList), salted hash tree (merTree), as well

as CL and BBS+ signatures. For each mechanism we

Table 6: cm assessment summary.

Feature cmtList merTree CL BBS+

Standard + ± − ±

Agile + + −− +

Unlinkable ± ± + +

Predicates ± ± + +

Fast + + + ++ + − ±

Compact − + − +

deﬁned the VP and VC structures, presented the oper-

ations to be performed to issue VCs and present VPs.

Finally, we examined standardization status, crypto-

graphic agility, and additional features such as pred-

icate proofs and unlinkable VPs, and experimentally

evaluated the performance of mechanisms with a view

to a practical scenario of proximity ﬂows with con-

strained devices.

We ﬁnd that merTree is the fastest mechanism of

those examined but requires constant management by

the Issuer to provide selective disclosure together with

unlinkability; BBS+ is competitive in terms of size,

does not require constant re-issuing of credentials on

the Issuer’s part, and is acceptable in speed even on

constrained devices.

Future Work. As future work, we aim to describe

additional selective disclosure mechanisms based on

e.g., vector commitments (Catalano and Fiore, 2013)

or other signatures such as PS (Pointcheval and

Sanders, 2018).

We aim to provide greater detail on the algorithms

for the creation and veriﬁcation of the Holder gener-

ated proofs for CL and BBS+, together with the neces-

sary preliminaries regarding the NIZKP.

ACKNOWLEDGEMENTS

The ﬁrst author acknowledges support from Eustema

S.p.A. through the PhD scholarship and is a member

of GNSAGA of INdAM.

This work has been partially supported by “Fu-

turo & Conoscenza Srl”, jointly created by the FBK

and the Italian Government Printing Ofﬁce and Mint,

Italy.

This work was partially supported by project

SERICS (PE00000014) under the MUR National Re-

covery and Resilience Plan funded by the European

Union - NextGenerationEU.

REFERENCES

AAMVA (2023). Mobile Driver’s License (mDL) im-

plementation guidelines, version 1.2. https://www.

aamva.org/topics/mobile-driver-license.

Au, M. H., Susilo, W., and Mu, Y. (2006). Constant-size

dynamic k-TAA. In SCN 2006, volume 4116 of LNCS,

pages 111–125.

Barker, E. (2020). NIST SP 800-57r5 Recommendation for

Key Management, Part 1: General.

Barker, E. and Roginsky, A. (2019). NIST SP 800-131A

transitioning the use of cryptographic algorithms

A First Appraisal of Cryptographic Mechanisms for the Selective Disclosure of Veriﬁable Credentials

133

and key lengths. https://nvlpubs.nist.gov/nistpubs/

SpecialPublications/NIST.SP.800-131Ar2.pdf.

Boneh, D., Boyen, X., and Shacham, H. (2004). Short

group signatures. In CRYPTO 2004, volume 3152

of LNCS, pages 41–55. https://doi.org/10.1007/

978-3-540-28628-8 3.

Boneh, D. and Shoup, V. (2023). A graduate course in ap-

plied cryptography. https://toc.cryptobook.us/.

Camenisch, J., Chaabouni, R., and Shelat, A. (2008). Efﬁ-

cient protocols for set membership and range proofs.

In ASIACRYPT, volume 5350 of LNCS, pages 234–

252.

Camenisch, J., Drijvers, M., and Lehmann, A. (2016).

Anonymous attestation using the strong Difﬁe Hell-

man assumption revisited. In Trust 2016, volume 9824

of LNCS, pages 1–20.

Camenisch, J. and Lysyanskaya, A. (2002). A signature

scheme with efﬁcient protocols. In SCN 2002, volume

2576 of LNCS, pages 268–289.

Catalano, D. and Fiore, D. (2013). Vector commitments

and their applications. In PKC 2013, volume 7778 of

LNCS, pages 55–72.

DG CONNECT (2023). The European Digital Identity Wal-

let Architecture and Reference Framework, version

1.0.0. https://github.com/eu-digital-identity-wallet/

architecture-and-reference-framework.

EU (2016). Consolidated text: Regulation (EU) 2016/679

of the European Parliament and of the Council of 27

April 2016 on the protection of natural persons with

regard to the processing of personal data and on the

free movement of such data, and repealing Direc-

tive 95/46/EC (General Data Protection Regulation)

(Text with EEA relevance). http://data.europa.eu/eli/

reg/2016/679/2016-05-04.

EU (2021). Proposal for a Regulation of the European Par-

liament and of the Council amending Regulation (EU)

no 910/2014 as regards establishing a framework for

a European Digital Identity. https://eur-lex.europa.eu/

legal-content/EN/ALL/?uri=COM:2021:281:FIN.

EU (2022). Proposal for a regulation of the euro-

pean parliament and of the council laying down

measures for a high level of public sector in-

teroperability across the Union (Interoperable Eu-

rope Act). https://eur-lex.europa.eu/legal-content/EN/

TXT/?uri=CELEX:52022PC0720.

EU (2023). Amendments by the European Parlia-

ment to the Commission proposal for a Regula-

tion of the European Parliament and of the Coun-

cil amending Regulation (EU) no 910/2014 as re-

gards establishing a framework for a European Dig-

ital Identity. https://www.europarl.europa.eu/doceo/

document/A-9-2023-0038 EN.html.

Fett, D., Yasuda, K., and Campbell, B.

(2023). Selective disclosure for JWTs

(SD-JWT). https://datatracker.ietf.org/doc/

draft-ietf-oauth-selective-disclosure-jwt/.

Housley, R. (2015). Guidelines for cryptographic algo-

rithm agility and selecting mandatory-to-implement

algorithms. https://www.rfc-editor.org/rfc/rfc7696.

IBM (2010). Speciﬁcation of the identity mixer cryp-

tographic library version 2.3.0. https://dominoweb.

draco.res.ibm.com/reports/rz3730 revised.pdf. Secu-

rity Team, Computer Science Dept., IBM Research

Zurich.

ISO/IEC 18013-5 (2021). ISO/IEC 18013-5 personal iden-

tiﬁcation - ISO-compliant driving licence - part 5:

Mobile driving licence (mDL) application.

Jones, M. B., Bradley, J., and Sakimura, N. (2015). JSON

Web Signature (JWS). https://www.rfc-editor.org/rfc/

rfc7515.html.

Khovratovich, D., Lodder, M., and Parra, C. (2022).

Anonymous credentials with type-3 revocation, ver-

sion 0.6. https://github.com/hyperledger/ursa-docs/

tree/main/specs/anoncreds1.

Laurie, B., Messeri, E., and Stradling, R. (2021). Certiﬁcate

transparency version 2.0. https://www.rfc-editor.org/

rfc/rfc9162.

Lodder, M., Zundel, B., and Khovratovich, D. (2019).

Pairings-based anonymous credentials with circuit-

based revocation and permission policies, version

0.7. https://github.com/hyperledger/ursa-docs/tree/

main/specs/anoncreds2.

Lodderstedt, T., Yasuda, K., and Looker, T. (2023). OpenID

for veriﬁable credential issuance. https://openid.net/

specs/openid-4-veriﬁable-credential-issuance-1 0.

html.

Looker, T., Kalos, V., Whitehead, A., and Lod-

der, M. (2023). The BBS signature scheme.

https://identity.foundation/bbs-signature/

draft-irtf-cfrg-bbs-signatures.html.

Miller, J., Waite, D., and Jones, M. B. (2023).

JSON Web Proof. https://datatracker.ietf.org/doc/

draft-ietf-jose-json-web-proof/.

Pointcheval, D. and Sanders, O. (2018). Reassessing se-

curity of randomizable signatures. In CT-RSA 2018,

volume 10808 of LNCS, pages 319–338.

Sakemi, Y., Kobayashi, T., Saito, T., and Wahby, R. S.

(2022). Pairing-friendly curves. https://datatracker.

ietf.org/doc/draft-irtf-cfrg-pairing-friendly-curves/.

Sporny, M. and Longley, D. (2022). Veriﬁable Cre-

dentials data integrity 1.0. https://www.w3.org/TR/

vc-data-integrity/.

Sporny, M., Longley, D., and Chadwick, D. (2022). Veriﬁ-

able credentials data model. https://www.w3.org/TR/

vc-data-model/.

Sporny, M., Longley, D., Chadwick, D., Terbu, O., Za-

gidulin, D., and Zundel, B. (2019). Veriﬁable creden-

tials implementation guidelines 1.0. https://www.w3.

org/TR/vc-imp-guide/.

Steele, O. and Prorock, M. (2021). JSON Web Proof

for binary Merkle trees. https://w3c-ccg.github.io/

Merkle-Disclosure-2021/jwp/.

Sullivan, B. (2010). Cryptographic agility. In Black

Hat USA. https://www.blackhat.com/html/bh-us-10/

bh-us-10-archives.html#Sullivan.

Tessaro, S. and Zhu, C. (2023). Revisiting BBS signatures.

In Eurocrypt 23 (forthcoming). https://ia.cr/2023/275.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

134