Does Categorical Encoding Affect the Interpretability of a Multilayer

Perceptron for Breast Cancer Classification?

Hajar Hakkoum

, Ali Idri

1,2 b

, Ibtissam Abnane

and José Luis Fernades-Aleman

ENSIAS, Mohammed V University in Rabat, Morocco

Mohammed VI Polytechnic University in Benguerir, Morocco

Department of Computer Science and Systems, University of Murcia, 30100 Murcia, Spain

Keywords: Interpretability, Machine Learning, Breast Cancer, SHAP, Global Surrogate, Categorical Encoding.

Abstract: The lack of transparency in machine learning black-box models continues to be an impediment to their

adoption in critical domains such as medicine, in which human lives are involved. Historical medical datasets

often contain categorical attributes that are used to represent the categories or progression levels of a

parameter or disease. The literature has shown that the manner in which these categorical attributes are

handled in the preprocessing phase can affect accuracy, but little attention has been paid to interpretability.

The objective of this study was to empirically evaluate a simple multilayer perceptron network when trained

to diagnose breast cancer with ordinal and one-hot categorical encoding, and interpreted using a decision tree

global surrogate and the Shapley Additive exPlanations (SHAP). The results obtained on the basis of

Spearman fidelity show the poor performance of MLP with both encodings, but a slight preference for one-

hot. Further evaluations are required with more datasets and categorical encodings to analyse their impact on

model interpretability.

1 INTRODUCTION

The use of machine learning (ML) models in

medicine has been a popular option for some time

(Kadi et al. 2017; Hosni et al. 2019; Idri and El Idrissi

2020; Zerouaoui et al. 2020). ML predictions serve as

a second opinion that can reduce human errors

(London 2019). Nonetheless, some ML models still

struggle to demonstrate their worth owing to their

obscurity (Hakkoum et al. 2022). These ML models

are also known as black-box or opaque models

(e.g. Artificial Neural Networks (ANNs)). While they

outperform transparent models (e.g., decision trees

(DTs)) in terms of performance, their lack of

interpretability is holding them back in critical fields,

such as healthcare (Hakkoum et al. 2021b).

Interpretability is the extent to which a human can

predict a model's outcome or understand the

reasoning behind its decisions (Kim et al. 2016;

Miller 2019). The term is frequently used

https://orcid.org/0000-0002-2881-2196

https://orcid.org/0000-0002-4586-4158

https://orcid.org/0000-0001-5248-5757

https://orcid.org/0000-0002-0176-450X

interchangeably with explainability, which is more

specific to a model by explaining its internals,

whereas providing mappings between the input and

output of a model without knowing its internals is

sufficient to achieve interpretability. Two criteria

distinguish interpretability techniques: 1) whether

they explain the black-box model behaviour globally

or locally (single instance), and 2) whether they are

agnostic or specific to one type of black-box model.

A systematic literature review (SLR) (Hakkoum

et al. 2021a) of 179 articles investigating

interpretability in medicine revealed that 95 (53%)

and 72 (40%) articles focused solely on global or

local interpretability, respectively, and 10 articles

(6%) proposed and/or evaluated both global and local

interpretability techniques. Additionally, most of the

data types that the selected studies worked on were

numerical (46%, 111 papers) and categorical (24%,

59 papers). The categorical features used are often

encoded using ordinal or label categorical encoding

Hakkoum, H., Idri, A., Abnane, I. and Fernades-Aleman, J.

Does Categorical Encoding Affect the Interpretability of a Multilayer Perceptron for Breast Cancer Classiﬁcation?.

DOI: 10.5220/0012084800003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 351-358

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

351

(CE) which maps the numerical values to an integer

to represent every category. Label CE can disregard

any order a feature might have like the degree of

malignancy in a cancer prognosis dataset. This can

have a negative impact on the relevance of the feature,

and therefore, on the performance of the model.

Therefore, ordinal CE is often used.

There is no doubt that data pre-processing (DP)

methods (Benhar et al. 2020), such as CE, have a

significant impact on model accuracy. According to

(Crone et al. 2006), the influence of DP is widely

overlooked, as shown in their SLR on studies

investigating data mining applications for direct

management. This SLR particularly showed that only

one publication discussed the treatment and use of

CE, despite the fact that categorical variables were

used and documented in 71% of all studies and are

commonly encountered in the application and ML

domains in general. The aforementioned authors

investigated the impact of different DP techniques

that included CE with four encoding schemes: one-

hot, ordinal, dummy, and thermometer encoding.

Tests performed on DT and a multilayer perceptron

(MLP) proved that CE can have a significant

influence on model performance.

Motivated by these findings showing the impact

of DP methods on accuracy and the lack of studies on

this effect on interpretability (Hakkoum et al. 2021a),

we investigated how interpretability techniques are

affected. Therefore, this study compares two well-

known interpretability techniques, global surrogates

using DT and Shapley Additive exPlanations (SHAP)

(Lundberg and Lee 2017), when used with an MLP

trained for breast cancer (BC) prognosis (Dua and

Graff 2017). Following the application of two

different CE, namely ordinal and hot, the MLP was

optimised using the particle swarm optimisation

algorithm (PSO) to ensure maximum accuracy. The

performance of the MLP with different CEs was first

compared using the Wilcoxon statistical test and

Borda count voting systems, after which the same

comparison was performed at the global and local

interpretability levels.

The key contributions of this study are the

identification of the impact of CEs on accuracy and

interpretability as well as the quantitative evaluation

of SHAP. In this respect, the research questions

(RQs) listed below will be addressed:

RQ1: What is the overall performance of MLP?

Which CE is the best?

RQ2: What is the overall global interpretability of

MLP? Which CE is the best?

RQ3: What is the overall local interpretability of

MLP? Which CE is the best?

The remainder of this paper is organised as

follows: Section 2 provides an overview of the chosen

black-box (MLP) as well as the interpretability

techniques (global surrogate and SHAP) used in this

study. Section 3 describes the BC dataset as well as

the performance metrics and statistical tests used to

identify the best-performing CEs. The experimental

design used in the empirical evaluation is detailed in

Section 4. Section 5 presents and discusses the

findings. Section 6 discusses the threats to the validity

of the study, and Section 7 reports the findings and

future directions.

2 METHODS

This section defines the models and methods

employed in this empirical evaluation, namely: CEs,

MLP, PSO, and the global and local interpretability

techniques.

2.1 Categorical Encodings (CEs)

Data transformation tasks are additional DP

procedures that help ML models to perform better. In

this step, the data were transformed into appropriate

forms for the mining process, resulting in more

efficient results or more understandable patterns

(Esfandiari et al. 2014). CE is a common data-

transformation method. This is the process of

converting categorical data into an integer format,

thus enabling it to be used by various ML models,

which are primarily mathematical operations that rely

entirely on numbers.

Ordinal CE is the most basic strategy for

categorical features in which observed levels from the

training set are mapped onto integers 1 to N (number

of categories) with respect to their original order. In

contrast, the indicator CE regroups one-hot and

dummy CEs. One-hot encoding refers to transforming

the categorical feature into N binary indicator

columns, in which the active category is represented

by 1. Meanwhile, dummy encoding results in only N-

1 indicator columns, and a reference feature level is

chosen, which is encoded with 0 in all indicator

columns.

2.2 Neural Networks

Black-box models are widely used in many domains

owing to their excellent performance. Their ability to

map nonlinear relationships and discover patterns in

databases that slip from white-box models has put

them in the spotlight.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

352

Neural networks are one of the most famous

black-box models. They take the topology of human

brain and can be used for classification tasks. Their

basic architecture is called MLP which is composed

of three layers of neurones. The first layer

corresponds to the input, that is, the data points. The

third and last layer is the final prediction which is

usually composed of one or two neurones for binary

classification. Each layer is connected to the others by

means of weights which are updated using a

backpropagation technique. When training an MLP,

it is important to select the hyperparameters which

determine its performance. These hyperparameters

include the number of hidden neurones and batch size

(number of data points to work through before

updating the internal model parameters), number of

epochs (number of times that the MLP will work

through the entire training dataset), and learning rate

which controls how quickly the model is adapted to

the problem.

2.3 Model Optimization

PSO is a good technique for hyperparameter

optimisation to achieve the best performance, because

it can be a hurdle to choose them manually for such

powerful black-box models. It is inspired by birds

whose discoveries can be shared with the flock that is

attempting to find the optimal solution, which is often

close to the global optimal (Brownlee 2021).

2.4 Global and Local Interpretability

There are two types of interpretability techniques:

global which examines general behaviour, and local

which focuses on a particular data point. This

evaluation study analyses the impact of CEs when

using two different interpretability techniques: global

surrogate using DT, and SHAP which can be used

globally employing features importance or locally, as

occurs in this study, by employing local surrogates.

Global surrogates are the simplest way to interpret

black-boxes. This is done by training an interpretable

model, such as DT, with black-box predictions rather

than the true labels of data points to gain insight into

the workings of the black-box workings. Nonetheless,

this global surrogate model draws conclusions based

on a black-box rather than actual data.

SHAP is based on the Shapley values game theory

technique (Shapley 1953), a method from coalitional

game theory which fairly distribute the “payout”,

which in this case is the prediction among the players

which are the features. SHAP was inspired by local

surrogates and explains predictions by assuming that

each feature value of the instance is a player in a

game, and attempts to compute the contribution of

each feature to the prediction. One innovation that

SHAP brings to the table is that the Shapley value

explanation is represented as an additive feature

attribution method, that is, a linear model. This view

connects local surrogate implementation and Shapley

values.

3 DATASET AND METRICS

This section presents the categorical BC dataset used

in this study, as well as the metrics used to evaluate

performance and interpretability, along with the

cross-validation used. Finally, the Borda count voting

system and statistical test used to define the best-

performing configuration are presented.

3.1 Dataset Description

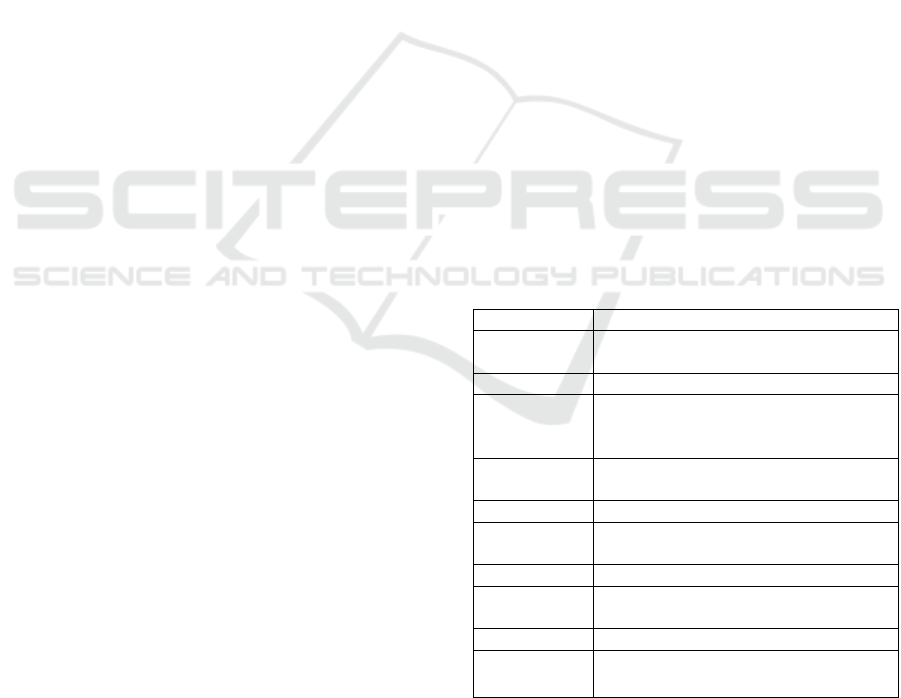
Table 1 presents the BC categorical dataset features

available online in the UCI repository (Dua and Graff

2017). It has 9 attributes and a very low number of

instances (286) with 201 instances for no recurrence

of BC and 85 for its recurrence. This class imbalance

was addressed using the synthetic minority over-

sampling technique (SMOTE), as explained in

Section 4.

Table 1: BC features description.

Attribute Possible values

Age [’20-29’, ’30-39’, ’40-49’, ’50-59’,

’60-69’, ’70-79’]

Meno

ause [’

e40’, ’lt40’, ’

remeno’]

Tumor size [’0-4’, ’10-14’, ’15-19’, ’20-24’, ’25-

29’, ’30-34’, ’35-39’, ’40-44’, ’45-49’,

’5-9’, ’50-54’]

Inv nodes [’0-2’, ’12-14’, ’15-17’, ’24-26’, ’3-5’,

’6-8’, ’9-11’]

Node Ca

s [’no’, ’

es’]

Deg of

Mali

[1, 2, 3]

Breast [’left’, ’ri

ht’]

Breast Quad [’central’, ’left low’, ’left up’, ’right

low’, ’right up’]

Irradiat [’no’, ’

es’]

Class

[‘no-recurrence-events’ (201),

‘recurrence-events’ (85)]

3.2 Evaluation Metrics

This subsection presents the metrics and tests used to

assess the performance and interpretability.

Does Categorical Encoding Affect the Interpretability of a Multilayer Perceptron for Breast Cancer Classiﬁcation?

353

3.2.1 Model Performance Metrics

The known accuracy, F1-score, Area Under Curve

(AUC), and Spearman correlation metrics were used

to evaluate and compare the constructed black-box

models. These are defined as follows:

 Accuracy: the ratio of correctly predicted

observations to total observations. Along

with the error of the model, they sum up to

 Precision: the ratio of true positive

observations to the total predicted positive

observations.

 Recall (Sensitivity/True Positive Rate): the

ratio of true positive observations to all

observations in actual class 1).

 F1-Score: the weighted average of Precision

and Recall.

 AUC: reflects how good the ROC is, a chart

that visualises the trade-off between TP rate

and FP rate; the more top-left the curve, the

higher the area and hence the higher the

AUC score (Czakon 2021).

 Spearman: the differences between ranks of

the true and predicted values are calculated

to measure the disordering of the

predictions with respect to the truth, as

shown in Equation 2.2. It takes a real value

in the range 1 ≤ ρ ≤ 1 with 1 indicates that

the function between prediction and truth is

monotonically increasing while -1 indicates

a monotonically decreasing function

(Stojiljković 2021). It is given in Equation

(1), where n is the total number of points in

each set and 𝑟







𝑋





𝑌







. Xir and Yir

are the ranks of the i

value of X and Y that

represents the sets to compare.

𝜌1



∑













²





(1)

3.2.2 Model Interpretability Metrics

To assess how well the global/local surrogate

techniques reflected the behaviour of the black-box

models, the fidelity of each surrogate technique was

computed using Spearman. Unlike the Spearman

metric calculated in the previous Subsection 3.2.1

“Model performance metrics”, fidelity using

Spearman (Equation 1) compares the predicted labels

by the surrogate against the predicted labels by the

black-box model. Consequently, fidelity does not

represent the surrogate’s performance on real data but

rather on the black-box’s predictions.

For global surrogates with DTs, the

comprehensibility of the DTs was assessed based on

the depth of the tree and number of leaves. For local

surrogates, the Mean Squared Error (MSE) was used

to measure the average of the error squares or the

average squared difference between the probability of

the predicted class by the local surrogate and that of

the MLP model.

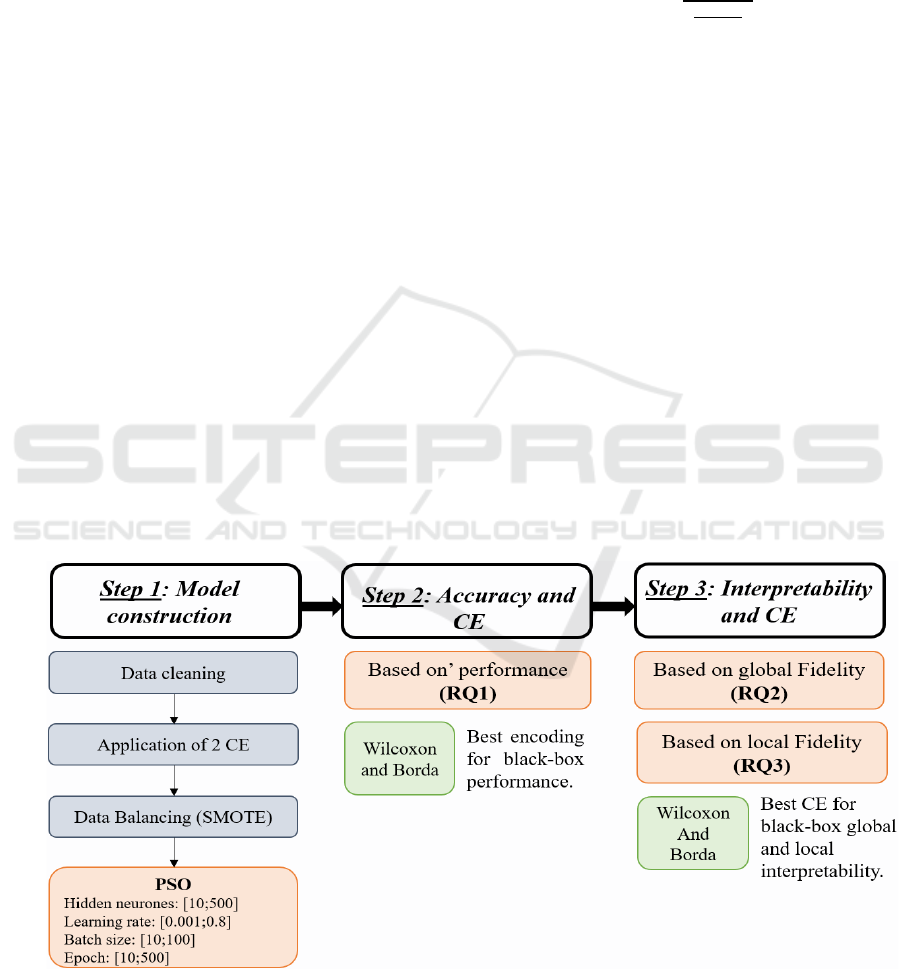
Figure 1: Experimental design.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

354

3.2.3 Validation and Statistical Testing

For validation, comparison, and testing purposes, the

present empirical evaluation uses different methods

to assess the conducted experiments.

K-folds Cross Validation was used to ensures that

the model is low on bias and to have an idea about

how it will behave/generalise over new/unseen data.

It allows better use of data and provides a robust

estimate of how well the model will perform on

unseen data. As a general rule and empirical

evidence, K = 5 or 10 is generally preferred.

Borda Count is a voting method that was used to

select the best performing CE by ranking them

according to different performance and

interpretability metrics (Borda 1784).

Wilcoxon test was used to determine whether the

two CEs were statistically different. This produces a

p-value that can be used to interpret the test results.

This can be defined as the likelihood of observing the

performance of the two CEs under the underlying

assumption that they were drawn from the same

population with the same distribution. The threshold

used in this study was set to 5%. Consequently, if the

p-value was less than 5%, the assumption of ordinal

and one-hot CEs values from the same distribution

was rejected.

4 EXPERIMENTAL DESIGN

The experimental design of this evaluation is

presented in this section, as shown in Figure 1: 1)

Model construction and evaluation, and 2) Accuracy

and CEs, in which we study the impact of the latter

on black-box performance. 3) Interpretability and

CEs, where we study the impact of the latter on global

and local interpretability techniques using the fidelity

metric.

4.1 Step 1: Model Construction and

Evaluation

The dataset was first cleaned by removing missing

values. CEs were applied to obtain two new encoded

datasets. The encoders were trained on the training-

validation set which represented 80% of the data, and

then applied to the test set (20%). The training-

validation set was balanced using the SMOTE

algorithm (Chawla et al. 2002) on which

hyperparameters were optimized using PSO

according to accuracy. The performance metrics of

the MLP models were computed using the test set.

4.2 Step 2: Accuracy and CE

After hyperparameter optimisation and model

construction, Wilcoxon and Borda count were used to

compare the two MLP models according to their

performance.

4.3 Step 3: Interpretability and CE

Similarly, this step studies the impact of the two CEs

on interpretability instead of performance. Wilcoxon

and Borda count were used to compare both models

according to their global interpretability as well as

local interpretability.

5 RESULTS AND DISCUSSION

This section presents and discusses the findings of the

empirical evaluation conducted in this study to

answer the RQs listed in Section 1. The experiments

were performed on a Lenovo Legion laptop with a

hexa-core Intel Core i7-9750H processor and 16GB

of RAM. Python libraries were used for all

experiments.

5.1 Best CE for MLP Performance

After cleaning the dataset, it was split into training,

validation, and testing, and CEs were performed. The

split resulted in 159 cases with no recurrence of BC

and 63 cases with recurrence of BC. As the

distribution of the classes for the training-validation

set is imbalanced, the SMOTE algorithm was used to

avoid biased accuracy results. The SMOTE

application resulted in 159 data points for every class

in the training-validation set.

The MLP hyperparameters were optimised using

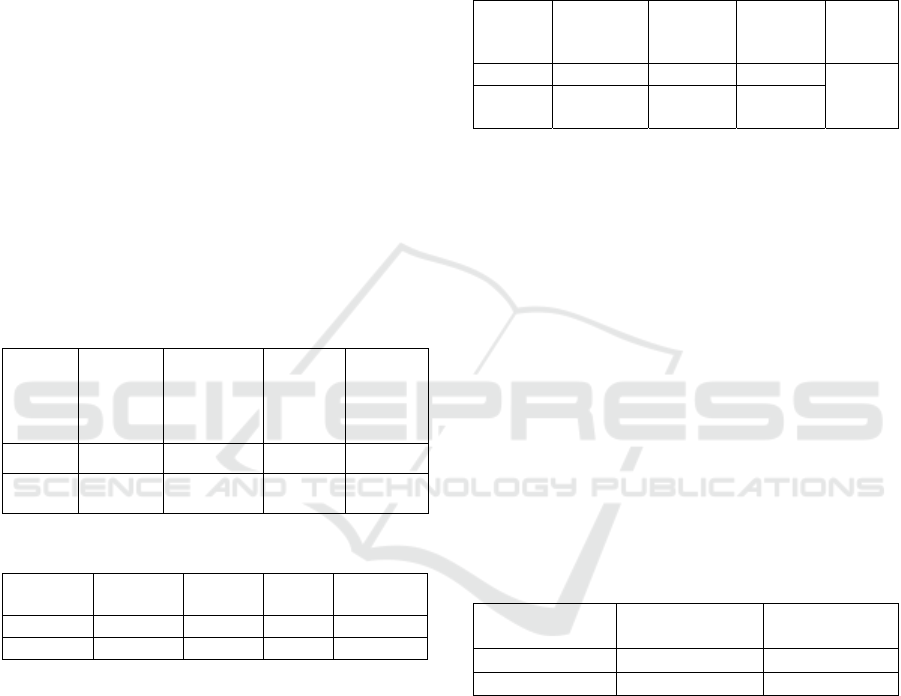
PSO. Table 2 shows the optimal hyperparameters

chosen by the PSO on the basis of accuracy with a 10-

fold cross validation using only the training-

validation set. Table 3 presents the MLP performance

results based on the optimised hyperparameters using

the test set.

As shown in Table 2, both MLP models required

the same number of hidden neurones (373) and a

slightly different batch size (79 and 91 for ordinal and

one-hot, respectively). Nevertheless, the MLP trained

with the ordinal dataset required a higher learning rate

and more than triple the number of epochs needed by

the one-hot dataset. Therefore, the use of the one-hot

dataset can reduce the computation time for the MLP.

Table 3 lists the results of model performance.

Based on accuracy and AUC, MLP trained with the

Does Categorical Encoding Affect the Interpretability of a Multilayer Perceptron for Breast Cancer Classiﬁcation?

355

one-hot dataset performed slightly better. Meanwhile,

the F1-score and Spearman correlation moderately

favoured the ordinally encoded dataset. Wilcoxon

based on the Spearman correlation reveals that the

differences between ordinal and one-hot are not

significant, while the Borda count considers the two

configurations even.

Nevertheless, it is important to mention the very

low performance of MLP on both CE. Although the

small size of the dataset might be a reason, it might

also be the fact that MLP does not perform well on

categorical datasets. To this extent, little research has

been conducted to check the performance of ANNs,

particularly MLPs, on categorical BC prognosis

datasets. Fitkov-Norris et al. (Fitkov-Norris et al.

2012) evaluated the impact of different CEs,

including ordinal and one-hot, on the performance of

ANNs. They trained an MLP with a single hidden

layer and another with two hidden layers. Results

showed that for categorical datasets, ANNs as well as

standard statistical models such as logistic regression

give similar performances, if not worse.

Table 2: PSO optimized hyperparameters.

CE Number

neurones

[10;500]

Learning

rate

[0.001;0.8]

Batch

size

[10;100]

Epochs

[10;500]

Ordinal 373 0.023 79 410

One-

373 0.012 91 182

Table 3: MLP performance results for different CEs.

Accuracy F1-

score

AUC Spearman

Ordinal 0.6 0.476 0.398 0.167

One-hot 0.618 0.399 0.404 0.120

5.2 Best CE for MLP Global

Interpretability

In this step, we compare and rank the CEs according

to the global surrogate performance using Spearman

fidelity, depth of the tree, and the number of its leaves

which are presented in Table 4 along with Borda

count decisions. The first glance shows a higher

performance of one-hot CE for the Spearman fidelity

(0.285 and 0.524 for ordinal and one-hot,

respectively), as well as the DT depth (15 and 12 for

ordinal and one-hot, respectively), while the number

of leaves was lower for the MLP trained with the

ordinal encoded dataset (67 and 77 for ordinal and

one-hot, respectively).

The Wilcoxon test yielded a p-value equal to

100% which indicates that the CEs were not

significantly different according to their fidelities.

Meanwhile, Borda count considered one-hot to be

better since it outperformed in terms of fidelity and

tree depth.

Table 4: Global surrogate performance results for different

CEs.

CE Spearman

fidelity

Depth Leaves Borda

count

winne

Ordinal 0.285 15 67 One-

hot

One-

hot

0.524 12 77

5.3 Best CE for MLP Local

Interpretability

In this phase, we determined the best CE using the

SHAP local interpretability technique to answer RQ3.

Table 5 reports the Spearman fidelity and MSE of

SHAP.

Both models did not perform well since the

Spearman are negative which assumes a slight

inclination towards negative correlation although

one-hot Spearman fidelity was very close to 0.

Meanwhile, ordinal was slightly preferred according

to MSE (0.041 and 0.090 for ordinal and one-hot

respectively). Wilcoxon reported a very high p-value

equal to 100%, implying that the SHAP fidelities to

MLP as well as the MSE for both CE were not

significantly different.

Table 5: SHAP performance results for different CEs.

Encoding

Spearman

fidelity

MSE

Ordinal -0.330 0.041

One-hot -0.146 0.090

6 LIMITATIONS

To ensure the validity of the current study, it is

necessary to highlight its possible limitations. We

think the main threats to validity are: 1) the extremely

small size of the dataset (286 instances), along with

2) the very poor performance of the MLPs as regards

categorical data. However, we believe that MLPs

generally lose their capabilities when dealing with

categorical features and are therefore a bad fit for

categorical data (Fitkov-Norris et al. 2012).

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

356

Overall, using more CEs, as well as more datasets

and models, can enrich comparisons and conclusions.

However, we believe that the small evaluation

presented in this study shows the importance of

addressing two problems of black-box models:

interpretability and categorical encoding.

7 CONCLUSION AND FUTURE

WORK

Two interpretability techniques (global surrogate and

SHAP) were empirically evaluated in this study. The

primary goal was to identify the influence of ordinal

and one-hot CE on interpretability techniques using

MLP trained for BC prognosis and compare it to the

influence on accuracy.

The main highlight of this evaluation is the

difficulty in applying ANNs to categorical data with

respect to choosing the optimal CE. Nevertheless,

performance and interpretability on both encodings

were very poor, with a slight preference for one-hot

CE which was seen in global interpretability.

Ongoing work is comparing the effect of more

CEs on the accuracy and interpretability of ML black-

box models trained on multiple datasets.

ACKNOWLEDGMENT

This work was conducted under the research project

“Machine Learning based Breast Cancer Diagnosis

and Treatment”, 2020-2023. The authors would like

to thank the Moroccan Ministry of Higher Education

and Scientific Research, Digital Development

Agency (ADD), CNRST, and UM6P for their

support.

REFERENCES

Benhar H, Idri A, L Fernández-Alemán J (2020) Data

preprocessing for heart disease classification: A

systematic literature review. Comput Methods

Programs Biomed 195:. https://doi.org/10.1016/

J.CMPB.2020.105635

Borda JC (1784) Memoire sur les elections au scrutin,

Histoire de l’Academie royale des sciences pour 1781.

Paris (English Transl by Grazia, A 1953 Isis 44)

Brownlee J (2021) A Gentle Introduction to Particle Swarm

Optimization. https://machinelearningmastery.com/a-

gentle-introduction-to-particle-swarm-optimization/.

Accessed 21 Oct 2021

Chawla N V., Bowyer KW, Hall LO, Kegelmeyer WP

(2002) SMOTE: Synthetic minority over-sampling

technique. J Artif Intell Res 16:321–357. https://doi.

org/10.1613/JAIR.953

Crone SF, Lessmann S, Stahlbock R (2006) The impact of

preprocessing on data mining: An evaluation of

classifier sensitivity in direct marketing. Eur J Oper Res

173:781–800. https://doi.org/10.1016/J.EJOR.2005.07.

023

Czakon J (2021) F1 Score vs ROC AUC vs Accuracy vs PR

AUC: Which Evaluation Metric Should You Choose? -

neptune.ai. https://neptune.ai/blog/f1-score-accuracy-

roc-auc-pr-auc. Accessed 28 Nov 2021

Dua D, Graff C (2017) UCI Machine Learning Repository

Esfandiari N, Babavalian MR, Moghadam AME, Tabar VK

(2014) Knowledge discovery in medicine: Current

issue and future trend. Expert Syst Appl 41:4434–4463.

https://doi.org/10.1016/J.ESWA.2014.01.011

Fitkov-Norris E, Vahid S, Hand C (2012) Evaluating the

Impact of Categorical Data Encoding and Scaling on

Neural Network Classification Performance: The Case

of Repeat Consumption of Identical Cultural Goods. In:

Communications in Computer and Information

Science. pp 343–352

Hakkoum H, Abnane I, Idri A (2022) Evaluating

Interpretability of Multilayer Perceptron and Support

Vector Machines for Breast Cancer Classification. 2022

IEEE/ACS 19th Int Conf Comput Syst Appl 2022-

December:1–6. https://doi.org/10.1109/AICCSA56

895.2022.10017521

Hakkoum H, Abnane I, Idri A (2021a) Interpretability in the

medical field: A systematic mapping and review study.

Appl Soft Comput 108391. https://doi.org/10.1016/

J.ASOC.2021.108391

Hakkoum H, Idri A, Abnane I (2021b) Assessing and

Comparing Interpretability Techniques for Artificial

Neural Networks Breast Cancer Classification. Comput

Methods Biomech Biomed Eng Imaging Vis 9:.

https://doi.org/10.1080/21681163.2021.1901784

Hosni M, Abnane I, Idri A, et al (2019) Reviewing

ensemble classification methods in breast cancer.

Comput. Methods Programs Biomed. 177:89–112

Idri A, El Idrissi T (2020) Deep learning for blood glucose

prediction: Cnn vs lstm. Gervasi O al Comput Sci Its

Appl ICCSA 12250:379–393

Kadi I, Idri A, Fernandez-Aleman JL (2017) Knowledge

discovery in cardiology: A systematic literature review.

Int. J. Med. Inform. 97:12–32

Kim B, Khanna R, Koyejo O (2016) Examples are not

Enough, Learn to Criticize! Criticism for

Interpretability

London AJ (2019) Artificial Intelligence and Black-Box

Medical Decisions: Accuracy versus Explainability.

Wiley Online Libr 49:15–21. https://doi.org/10.

1002/hast.973

Lundberg SM, Lee S-I (2017) A unified approach to

interpreting model predictions. In: NIPS’17:

Proceedings of the 31st International Conference on

Neural Information Processing Systems. Long Beach,

Does Categorical Encoding Affect the Interpretability of a Multilayer Perceptron for Breast Cancer Classiﬁcation?

357

California, USA. Curran Associates Inc., Red Hook,

NY, USA, pp 4768–4777

Miller T (2019) Explanation in Artificial Intelligence:

Insights from the Social Sciences. Artif Intell 267:1–38

Shapley LS (1953) A Value for n-Person Games. Contrib

to Theory Games 2:307–318. https://doi.org/10.1515/

9781400881970-018/HTML

Stojiljković M (2021) Correlation With Python.

https://realpython.com/numpy-scipy-pandas-

correlation-python/#spearman-correlation-coefficient.

Accessed 28 Nov 2021

Zerouaoui H, Idri A, Elasnaoui. K (2020) Machine learning

and image processing for breast cancer: A systematic

map. Trends Innov Inf Syst Technol 5:44–53.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

358