Predicting Academic Performance of Low-Income Students in Public

Ecuadorian Online Universities: An Educational Data Mining Approach

Jorge Rodas-Silva

1 a

and Jorge Parraga-Alava

2 b

Facultad de Ciencias e Ingenier

ıa, Universidad Estatal de Milagro, Cdla. Universitaria Km 1 1/2 v

ıa Km 26, Milagro,

Ecuador

Facultad de Ciencias Inform

aticas, Universidad T

ecnica de Manab

ı, Avenida Jos

e Mar

ıa Urbina, Portoviejo, Ecuador

Keywords:

Educational Data Mining, Predicting Academic Performance, Online Education, Low-Income Students.

Abstract:

The success of higher education institutions in the online learning environment can be measured by the per-

formance of students. Identifying backgrounds or factors that increase the academic success rate of online

students is especially helpful for educational decision-makers to adequately plan actions to promote success-

ful outcomes in this digital landscape. In this paper, we identify the factors that contribute to the academic

success of students in public Ecuadorian online universities and develop a predictive model to aid in improving

their performance. Our approach involved ﬁve stages: data collection and description, which involved gather-

ing data from universities, including social demographic, and academic features. In preprocessing, cleaning,

and transforming the data to prepare it for analysis was performed. Modeling involved applying machine

learning algorithms to identify patterns and key factors to predict student outcomes. It was validated in the

next stage where the performance of feature selection and predictive model was tackled. In the last stage, were

interpreted the results of the analysis about the factors that contribute to the academic success of low-income

students in online universities in Ecuador. The results suggest that the grade in the leveling course, the family

income, and the age of the student mainly inﬂuence their academic performance. The best performances were

achieved with Boruta + Random Forest and LVQ + SVM, reaching an accuracy of 75.24% and 68.63% for

binary (Pass/Fail) and multiclass (Average/Good/Excellent) academic performance prediction, respectively.

1 INTRODUCTION

Online education has brought about a signiﬁcant

transformation in the way people learn, making ed-

ucation more accessible and affordable to a vast num-

ber of people worldwide. With the outbreak of

the COVID-19 pandemic, the importance of online

higher education has become even more pronounced

as traditional in-person learning became challeng-

ing due to safety concerns and lockdown measures

(Stoian et al., 2022). Despite the many advantages

of online and distance learning, educational institu-

tions have become increasingly worried about the low

dropout/completion rates and academic performance

of the students. Institutional authorities often use

these outcomes as key parameters for assessing pro-

gram/course quality and assigning resources. Poor

academic performance usually translates into low cer-

tiﬁcation rates and high dropout rates can potentially

https://orcid.org/0000-0001-6526-7740

https://orcid.org/0000-0001-8558-9122

damage the reputation of the institution, funding, and

proﬁt, and they have signiﬁcant implications for the

self-esteem of the student, well-being, employment,

and likelihood of graduating (Xavier and Meneses,

2020). Hence, it is crucial to develop mechanisms

to identify students who may have low levels of aca-

demic performance as early as possible to take proac-

tive measures towards improving online learning ex-

periences and establishing intervention strategies that

cater to the needs of the students. In this sense, data

Educational Data Mining (EDM) emerges as an inter-

esting alternative for this purpose.

EDM is a ﬁeld of study that involves using data

mining and machine learning techniques to analyze

educational data in order to understand and improve

the learning process, including academic performance

and the level of learning of subjects usually with

high degrees of complexity. This becomes even more

crucial in subjects such as introductory program-

ming, which presents historically high dropout rates

(Bennedsen and Caspersen, 2019) in most careers re-

Rodas-Silva, J. and Parraga-Alava, J.

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining Approach.

DOI: 10.5220/0012086300003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 52-63

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

lated to computer science. As stated (Simeunovi

c and

Preradovi

c, 2014), these processes of analyzing edu-

cational data are important for higher education in-

stitutions given that the strategic planning of study

programs implies expanding or reducing the scope or

depth of the curriculum as well as modifying the ped-

agogical and educational process, depending on stu-

dent achievements. However, carrying out the process

of predicting student performance or level of learn-

ing is commonly difﬁcult. Machine learning tools be-

came very popular among educational researchers be-

cause of their ease of use and the ability to discover

patterns hidden in the data.

EDM has utilized Machine Learning (ML) tech-

niques to analyze academic performance data. Essen-

tially, ML algorithms perform computational tasks by

learning patterns from data samples and making au-

tomated inferences. The goal in prediction tasks is

to create a model that can distinguish between stu-

dents who will have high or low academic perfor-

mance. The prediction model is induced using certain

variables (sometimes called feature selection), some

of which are more relevant than others and can pro-

vide valuable insights into the social, demographic,

and academic history characteristics of the students.

These variables may differ between student cohorts,

revealing important factors that inﬂuence the aca-

demic success of students.

In recent years, researchers have been using ML

techniques to predict the academic performance of

university students. The work of (Ya

gcı, 2022) used

ML algorithms to predict the ﬁnal exam grades of un-

dergraduate students based on midterm exam grades

as the source data in a state University in Turkey.

Similarly, in Ecuador (Carrillo and Parraga-Alava,

2018) used data mining techniques to successfully

classify students into one of three categories: “Ac-

ceptable”, “Good”, “Excellent”, according to their

academic success in professionalizing subjects and

using personal and academic data. (Belgaum et al.,

2021) found that the use of machine learning algo-

rithms based on neural networks and logistic regres-

sion signiﬁcantly improved the accuracy of predict-

ing the academic performance of university students.

The work of (Su et al., 2022) used data from an on-

line course on data science and machine learning with

techniques such as decision trees and neural networks

to predict the academic performance of students. The

results show that student characteristics and learning

behavior can be used to predict student academic per-

formance with reasonable accuracy. A review arti-

cle with more detail on similar studies on the predic-

tion of academic performance can be consulted in the

work of (Alhothali et al., 2022).

The reviewed studies agree that the use of ma-

chine learning techniques is a promising tool for pre-

dicting student academic performance. Some studies

have used neural network algorithms and logistic re-

gression, while others have used decision trees and

other classiﬁcation techniques. These studies found

that these techniques can signiﬁcantly improve the ac-

curacy of predicting student academic performance.

However, some studies also point out that a high-

quality data set and good feature selection are nec-

essary to achieve the desired precision, and that this

quality is also inﬂuenced by the form of evaluation of

the university educational systems of each country.

Some more recent studies have used feature se-

lection techniques to ﬁnd relevant characteristics to

identify relevant characteristics that inﬂuence the aca-

demic performance of students. In the work of

(Rahimi and Shute, 2021) the authors propose a hy-

brid machine learning model that uses feature selec-

tion techniques to predict academic performance in

a blended learning environment. The results showed

that the hybrid model with feature selection outper-

forms other machine learning models and feature se-

lection techniques in terms of prediction accuracy.

(Xiao et al., 2021) used a combination of feature se-

lection and machine learning models to predict stu-

dents’ academic performance in college courses. It

was shown that feature selection improved the pre-

diction accuracy and that certain features, such as the

GPA of previous courses, had a signiﬁcant impact on

the prediction. Similarly, (Beckham et al., 2023) in

their work found that the most outstanding variables

in academic performance increased the grade point

average of previous courses, the number of previous

courses, age, and specialization of the study program.

The results suggest that the application of machine

learning techniques and feature selection can be use-

ful to predict student academic performance and to

identify the key factors that inﬂuence it. The work

of (Al-Zawqari et al., 2022) used slightly more ad-

vanced techniques. It used a genetic algorithm to se-

lect an optimal subset of characteristics from an initial

set of characteristics, including student demographic

information, online platform browsing behavior, and

social interactions with data from an Australian uni-

versity statistics and probability online course.

Studies have highlighted that individual student

characteristics are important in predicting their aca-

demic performance. These characteristics include

gender, age, parental education, socioeconomic sta-

tus, and previous educational history. Some studies

have also pointed to the importance of psychological

characteristics, such as motivation and self-efﬁcacy.

Therefore, it is important to consider a wide range

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining

Approach

of characteristics when trying to predict student aca-

demic performance. Some studies have also used data

on the use of the online learning platform and partic-

ipation in online discussions to improve the predic-

tion of academic performance. These ﬁndings suggest

that careful monitoring of student performance and

engagement over time may provide valuable informa-

tion for predicting future academic performance.

In general, the studies on predicting academic per-

formance and learning in university students using

EDM show that educational interventions are posi-

tively associated with student performance. However,

it is worth noting that the majority of these studies fo-

cus on traditional face-to-face learning and not on dis-

tance education or online learning, which is becoming

more prevalent in current times. Furthermore, more of

them have been conducted in speciﬁc countries, there-

fore, it is not clear whether the results are generaliz-

able to other countries and cultures with low incomes.

In this sense, this paper aims to perform the predicting

the academic performance of introductory program-

ming in online Ecuadorian university students using

machine learning algorithms according to their aca-

demic historic, and social demographic characteris-

tics. The main contributions are 1) To provide a pre-

dictive model for early warning for the academic per-

formance of online Ecuadorian university students in

the introductory programming subject. 2) To deter-

mine key factors associated with the academic perfor-

mance of online students of the Information Technol-

ogy career in public Ecuadorian universities.

Moreover, the study proposes the following two

research questions:

RQ1: What is the importance of socio-

demographic features in the academic performance of

online Ecuadorian university students in introductory

programming?

RQ2: Which machine learning prediction algo-

rithms are suitable for predicting the academic per-

formance of online Ecuadorian university students in

introductory programming?

The remainder of this paper is organized as fol-

lows. Section 2 presents the theoretical backgrounds

of online universities in Ecuador as well as perfor-

mance learning related to student learning. Section

3 explains the EDM-based study including the data

collection, preprocessing, feature selection, modeling

and evaluation metrics. Presentation and discussion

of the results are presented in Section 4. Finally, Sec-

tion 5 concludes the work and provides pointers for

future research.

2 BACKGROUNDS

2.1 Online Higher Education in

Ecuador

In 2018, the different institutions of the Ecuadorian

higher education system took their ﬁrst steps towards

increasing the reach of online education and helping

complete the offer of higher education in the country.

The Ecuadorian government proposed rolling out ﬁve

bachelor’s degree programs under this system in the

ﬁve public universities that have taken on this chal-

lenge: the Technical University of Manab

ı (UTM)

the State University of Milagro (UNEMI)

, the Cen-

tral University of Ecuador (UCE), the University of

the Armed Forces (UFA-ESPE) and the Technical

University of the North (UTN).

In 2023, the UTM and UNEMI are two of the

Ecuadorian public universities with the largest num-

ber of online students in Ecuador, with about 11000

and 25000 students enrolled in this modality, respec-

tively. The UTM and UNEMI have their headquar-

ters in the cities of Portoviejo and Milagro, respec-

tively. In both cases, the cities are located in least-

developed zones in Ecuador, where a large proportion

of the population lives in the countryside (C

ardenas-

Cobo et al., 2021). Students entering these universi-

ties come mostly from this social stratum. This low

socioeconomic status might have a negative inﬂuence

on academic performance (Ya

gcı, 2022), (Liu et al.,

2020) regardless of government initiatives to facilitate

access to educational centers

The information technology career is one of the

oldest online careers at both universities, according

to the database of the management systems of both

universities, careers at the beginning of 2023 had a

total of 2221 students enrolled. Over the years it was

observed that subjects such as introductory program-

ming present high failure and dropout rates coincid-

ing with experiences in other countries of the world

(Bennedsen and Caspersen, 2019). Therefore, there is

a huge challenge in developing more inclusive and ef-

fective learning environments and instructional meth-

ods to reduce these dropout and failure rates.

2.2 Student Learning Performance

Prediction

In essence, prediction involves deducing a target at-

tribute or variable that is to be predicted from a com-

bination of other aspects of the data, otherwise known

https://www.utm.edu.ec/

https://www.unemi.edu.ec/

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

as predictor variables. To accomplish this, it is neces-

sary to have output variable labels available. As men-

tioned (Huynh-Cam et al., 2022), prediction has been

a widely used technique in EDM for forecasting stu-

dent performance. Predictions can fall under either

categorical or continuous output variable categories.

The use of Student Learning Performance Predic-

tion (SLPP) can result in the development of effec-

tive strategic intervention plans well in advance of

the ﬁnal semester, as noted in reference (Huynh-Cam

et al., 2021). By identifying students who are at risk

of dropping out or struggling academically, SLPP can

facilitate the timely provision of additional support

such as tutoring or assistance, as noted in reference

(Tomasevic et al., 2020).

SLPP features are typically categorized into pop-

ular groupings, such as demographic, academic per-

formance, internal assessment, communication, be-

havioral, psychological, and family/personal back-

ground, as noted in reference (Alhothali et al., 2022).

These features are then utilized as inputs for SLPP

methods, which commonly employ supervised learn-

ing techniques. This is because the “students’ aca-

demic learning performance” serves as the class label

for these methods.

3 MATERIALS AND METHODS

The main objective of this work was to predict the

academic performance of the introductory program-

ming subject in low-income students in Ecuadorian

online universities based on social demographic and

academic history features. To accomplish this task,

we applied a pipeline inspired by (Huynh-Cam et al.,

2022) but re-adapted to our approach, as shown in

Figure 1.

Figure 1 summarizes the pipeline followed in this

study. The ﬁrst stage involves outlining the methods

used to gather data and providing an overview of the

research datasets. The second stage entails a two-

stage process of preparing the data, which includes

both data cleaning and transformation. The third

stage elaborates on a three-stage approach to imple-

menting the model, which includes data splitting, se-

lecting relevant features, and constructing the model

for making predictions. The fourth step involves as-

sessing the performance of the model, while the ﬁfth

and ﬁnal step involves summarizing the knowledge

gleaned from the research and identifying the key

factors that inﬂuence the academic performance of

the introductory programming subject in low-income

students in Ecuadorian universities online. The fol-

lowing subsections describe in detail each one of the

stages of our approach.

3.1 Stage 1. Data Collection and

Description

Data used for experiments corresponds to academic

and social demographic information of students from

the Information Technology career online modality of

the Technical University of Manab

ı (UTM) and State

University of Milagro (UNEMI). They were collected

directly from the universities database system during

the 2019–2022 academic year. The initial data set

contained a total of 3367 records of enrolled students

in the subject of introductory programming. 1610

and 1757 cases for students of the UTM and UN-

EMI, respectively. There were 24 different categories

of information for each student, including their ID,

gender, marital status, birth date, disability, school

of origin, familiar average income per month], main

source of living expenses, health condition, scholar-

ship, hours of internet use, ﬁnal grade in course of

admission, and others, all of which were used as can-

didate input variables. The introductory programming

ﬁnal grade points were used as a candidate output

variable.

3.2 Stage 2. Preprocessing

We performed a preprocessing stage to convert fea-

tures from human language into a computer-readable

format for machine learning use. During the data

cleaning step, irrelevant attributes and missing-value

samples were removed. Also, those attributes that did

not coincide in both subsets (UTM and UNEMI) were

removed. In addition, in the data transformation step,

all category features were encoded and transferred to

binary or numeric features. All features that are sensi-

tive and can reveal the identity of these students were

removed or remained anonymous for ethical reasons.

After the preprocessing stage, out of 24 initial fea-

tures, a total number of 9 features, 2 target variables,

and 1694 instances were ﬁnally selected as the dataset

to be used in experiments. we rename the dataset of

the UTM, UNEMI, and the union of both, as DS1,

DS2, and DS3, respectively. Figure 2 details the pro-

portion of instances in each of the classes of the binary

and multiclass problem.

Table 1 shows the description of selected features.

Note that ﬁnal grade was discarded because it was

used to generate two target prediction variables, i.e.,

C1=class binary and C2=class multi. The target of

predictions in this work is the academic performance

of the students which is expressed from the ﬁnal

grade feature but split-into into the two target predic-

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining

Approach

Subset A

Data collection and description

Modeling

Conclusions

9 features,

2 predictive class,

1690 instances

Preprocessing

Evaluation

Subset B

UTM

data

UNEMI

data

Dataset

DS1 DS2

DS3

2.1. Data cleaning

2.2. Data transformation

3.1. Splitting data

3.2. Feature selection

3.3. Classification model

5.1. Key factors

5.2. Predictive model

Figure 1: Pipeline of our approach for predicting academic performance of the introductory programming subject in low-

income students in Ecuadorian online universities.

Fail 39.5

Fail 44.8

Fail 41.5

UTM

UNEMI

BOTH

DS1

DS2

DS3 = DS1 + DS2

Pass 60.5

Pass 55.2

Pass 58.2

C1 %

C2 %

Excellent 17.7

Good 39.1

Average 43.2

Excellent 18.8

Good 45.4

Average 35.8

Excellent 18.0

Good 41.4

Average 40.6

Figure 2: Proportions of instances in each class and dataset.

tion variables mentioned. Thereby, they can have val-

ues as Pass/Fail and Excellent/Good/Acceptable (cat-

egories are mutually exclusive) for binary and multi-

class problems, respectively.

A student is labeled as Pass when it scores 70 or

more points, otherwise, the label is Fail. Students

who have points between 70-79, 80-89, and 90-100,

belong to the categories Average-, Good, Excellent,

respectively.

3.3 Stage 3. Modeling

3.3.1 Splitting Data

To avoid overﬁtting, we split the dataset into two sets,

i.e., assigning 75% of the instance as training and

25% as testing.

3.3.2 Feature Selection

According to (Ang et al., 2015), Feature Selection

(FS) is a crucial step in pre-processing data for build-

ing ML models. ML models generally assume that

all features are relevant to the task at hand, however,

the more features there are, the higher the computa-

tional cost of inducing the model. Additionally, ir-

relevant attributes may hinder the predictive ability of

the model. Studies by (Chen et al., 2020) and (Cilia

et al., 2019) suggest that discarding certain original

features and inducing the model on a subset of the

same data can lead to better performance of the same

learning algorithm.

In EDM, the relevant attributes often are un-

known. The FS can discover knowledge from the col-

lected data and it is performed as a selection of the

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

Table 1: Data summary of the dataset.

Code Feature name Feature values Description

F1 age

1= 17-20

The age range of the student.

2= 21-24 years

3= 25-28 years

4= 29-32 years

5= 33 or more

F2 gender

1= Male

The gender of the student.

2= Female

F3 marital status

1= Single

The marital status of the student.

2= else case

F4 housing head

1= No

Indicates if the student is the head of household.

2= Yes

F5 familiar income

1= 0-250 $

The family average income per month.

2= 251-375 $

3= 376-475 $

4 = 476-600 $

5 = 601 or more

F6 familiar help

1= No

Indicates if family-funded living expenses.

2= Yes

F7 children

1= None

The number of children of the student.

2= One or more

F8 second career

1= No

Indicates if is the second student career.

2= Yes

F9 leveling career

1 = Excellent (90–100 pts)

The performance achieved in career leveling.2 = Good (80–89 pts)

3 = Average (70–79 pts)

C1 class binary

1= Fail (0-69 pts)

Prediction class for the binary problem.

2= Pass (70-100 pts)

C2 class multi

1 = Excellent (90–100 pts)

Prediction class for the multi-class problem.2 = Good (80–89 pts)

3 = Average (70–79 pts)

most useful variables in the dataset. This can be a

dominant factor that highly affects the academic per-

formance of the students to improve pattern discov-

ery and class prediction in machine learning mod-

els. (Phauk and Okazaki, 2020). In our experiments,

we used Boruta (Kursa et al., 2010), Learning Vector

Quantization (LVQ) (Kohonen, 2001), and Recursive

Features Elimination (RFE) (Guyon et al., 2002). FS

techniques are used to ﬁlter irrelevant or redundant

features from the dataset, i.e., identifying which of the

9 socio-demographic and academic historical features

of the data set could be ignored during the predictive

process.

3.3.3 Classiﬁcation Model

The goal of a binary classiﬁcation model is to create

a model that can differentiate between successful and

unsuccessful samples from a given population. Mean-

while, in a multiclass classiﬁcation model, the goal is

to classify instances into three or more classes.

We deﬁne the problem the predicting the aca-

demic performance of low-income students in public

Ecuadorian online universities as both a binary and

multi-class classiﬁcation problem. In the binary the

performance can be successful (pass) or unsuccess-

ful (fail). In the multi-class case, each student has

an academic performance mutually exclusive (Excel-

lent, Good, Average) in the introductory program-

ming subject. Note that, both binary and multiclass

models are applied sequentially. First, we train a bi-

nary classiﬁcation model to predict whether a student

passes or fails the introductory programming course.

Then, we apply the multiclass model only to those

students who were predicted to pass the binary model.

To predict the academic performance of the on-

line students of the Information Technology career of

the UTM and UNEMI, we build prediction models

employing the well-known classiﬁcation algorithms:

random forest (RF), logistic regression (LR), Lin-

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining

Approach

ear discriminant analysis (LDA), k-nearest neighbor

(KNN), decision tree (DT) and support vector ma-

chine (SVM) in the R language which was widely

used in machine learning.

3.4 Stage 4. Evaluation

In order to evaluate the effectiveness of our classiﬁ-

cation models, we employed well-known validation

metrics. As we have the ground truth academic per-

formance (C1, C2), we use the accuracy, precision,

recall, and F-score. Here, when a student passes the

subject was called positive (P), and when it fails, neg-

ative (N). These measures are calculated as follows

(Tharwat, 2018), (Ghoneim, 2019):

Accuracy =

TP+TN

TP+FP+FN+TN

(1)

Precision =

TP+FP

(2)

Recall =

TP + FN

(3)

F-Score = 2 ×

Recall × Precision

Recall + Precision

(4)

Where:

• True positive (TP): the case is positive (P) and it

is classiﬁed as positive (P’)

• True negative (TN): the case is negative (N) and it

is classiﬁed as negative (N’)

• False positive (FP): the case is negative (N) and it

is classiﬁed as positive (P’)

• False negative (FN): the case is positive (P) and it

is classiﬁed as negative (N’)

We also considered the area under the curve

(AUC). It is a metric used to measure the classiﬁca-

tion method’s prediction performance for all classi-

ﬁcation thresholds (Niyogisubizo et al., 2022). The

AUC values range from 0.5 to 1.0, with a value of 1.0

indicating excellent performance and a value of 0.5

indicating poor performance for a particular model.

3.5 Settings and Implementation Details

The computational experiments were implemented

using R (Team, 2017) version 4.2.1, R Studio (RStu-

dio Team, 2018) version 2022.12.0. To perform

stages 4-5, we use the system of packages based

on “tidyverse” (Wickham et al., 2019) including the

“tidymodels” (Kuhn and Wickham, 2020) R libraries.

The computational tests were performed on a com-

puter with Ubuntu 22.11 OS and Intel Core i7-1065G

Processor, 2.3Ghz, 8 cores/threads, 16GB RAM,

512GB Storage.

4 RESULTS AND DISCUSSION

To perform the classiﬁcation, we consider as input

variables the nine features F1, . . . , F9 and as predic-

tion class, the features C1 and C2, which have the

values: Fail/Pass and Average/Good/Excellent for the

binary and multiclass case, respectively. It just repre-

sents the academic performance of introductory pro-

gramming of the students. As can be seen in Fig-

ure 2, the distribution of the instances in the classes

is not balanced. We apply an oversampling pro-

cess using Synthetic Minority Oversampling Tech-

nique (SMOTE) (Chawla et al., 2002) to our data. So,

we increase the number of observations in the minor-

ity class by generating synthetic samples based on the

existing ones, with the aim of balancing class distri-

bution and improving model performance. The re-

sults obtained, during 30 consecutive runs of the al-

gorithms, for the feature selection and classiﬁcation

model is shown in the following subsections.

4.1 Importance of Socio-Demographic

Features in the Academic

Performance

To answer the RQ1, we evaluated the performance of

three feature selection algorithms - Boruta, Learning

Vector Quantization (LVQ), and Recursive Feature

Elimination (RFE) - on a dataset consisting of socio-

demographic characteristics of students and their aca-

demic performance outcomes of the introductory pro-

gramming. The aim was to identify the most relevant

features for predicting academic performance. The

selected relevant features for each feature selection

(FS) method are shown in Table 2.

Furthermore, in Figure 3 we show the number of

times that each feature is selected as important by FS

algorithm. Note that when there is no frequency for

a feature, it is because none of the 3 feature selection

algorithms considered it highly important.

4.2 Performance of Machine Learning

Prediction Algorithm

To answer the RQ2, different prediction models were

evaluated considering four scenarios: the features that

contribute most to the prediction of the academic per-

formance outcomes of the introductory programming

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

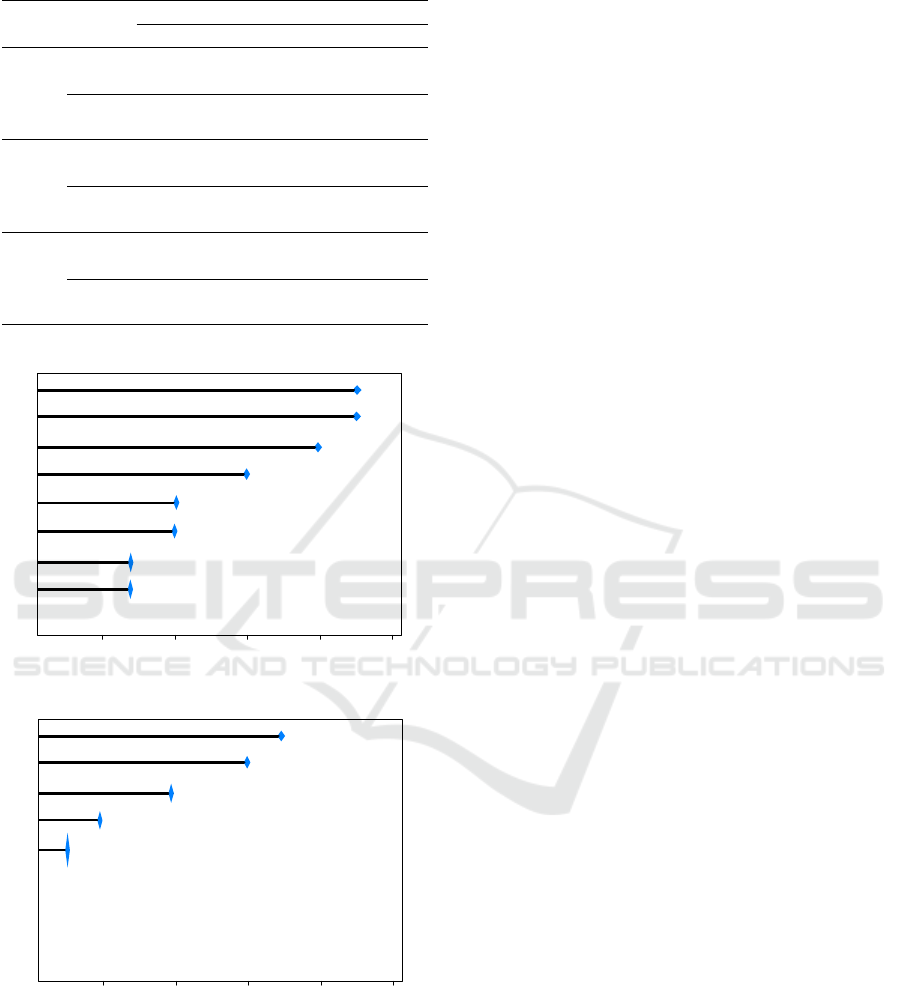
Table 2: Selected relevant features for each FS method.

Data Class

Feature selection

Boruta LVQ RFE

DS1

F1 . . . F3 F9 F9 F5

F5 F7 F9 F5 F1 F2 F7

F9 F9 F5 F9

F5 F1 F5

DS2

F1 . . . F6 F1 F2 F1 F3

F9 F5 F6 F9 F4 F5 F9

F9 F5 F6

F1 F7

DS3

F1 . . . F7 F9 F5 F9 F5

F9 F1 F1 F7 F2

F9 F5 F9 F5 F9

F7 F1 F1

a) Pass/Fail (C1)

Frequency as an important feature for prediction

2 4 6 8 10

b) Excellent/Good/Average (C2)

2 4 6 8 10

Figure 3: Number of times each feature is selected as im-

portant by FS algorithms used in experiments.

according to 1) Boruta, 2) LVQ, 3) RFE, and 4) Us-

ing all features. The average results of 30 consec-

utive runs of the prediction algorithm for the binary

and multiclass problems are shown in Tables 3-4, re-

spectively. The standard deviation is denoted as ±.

For multiclass cases, we consider the OvR (”One

vs Rest”) approach which involves one approach for

evaluating multiclass models by simultaneously com-

paring each class against all the others. To implement

this, we select one class and designate it as the “pos-

itive” class, while categorizing all remaining classes

(i.e., “the rest”) as the “negative” class (See 3.4).

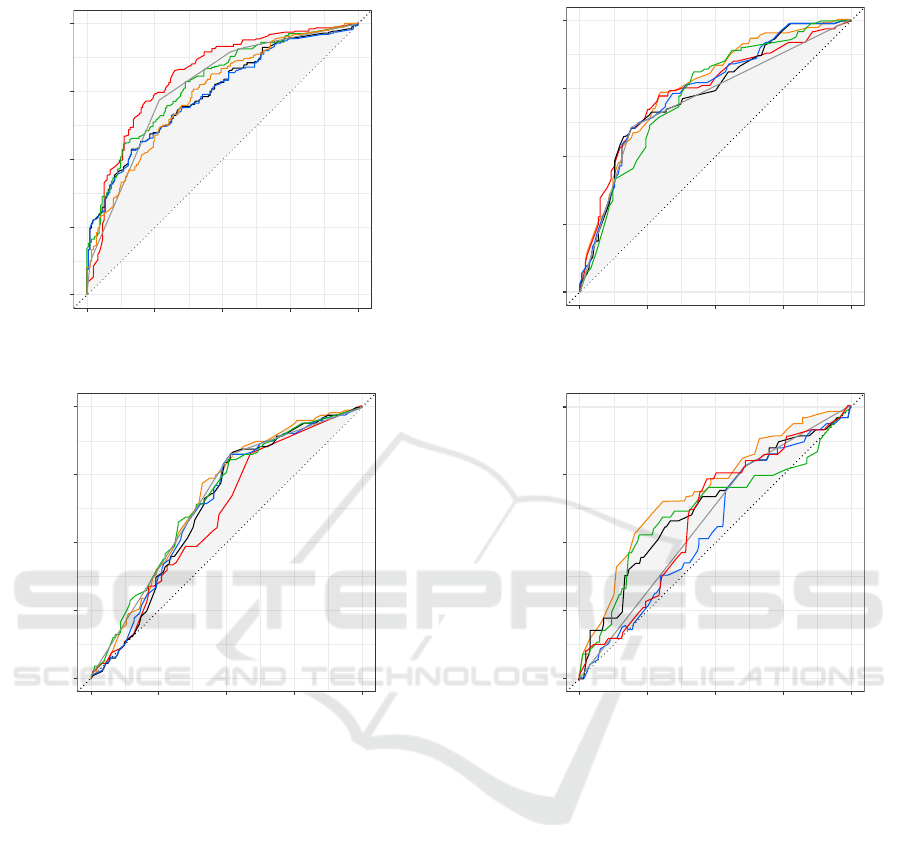
In Figure 4, we show the ROC Curve and ROC

AUC scores which are crucial resources for assessing

classiﬁcation models. Essentially, they indicate the

distinguishability of the classes across all potential

thresholds, or in simpler terms, the effectiveness of

the model to accurately classify each respective class.

We show the best performance for the models using

as input the variables selected by Boruta and LVQ,

for the binary (Figure 4a) and multiclass case (Figure

4b-d), respectively.

4.3 Discussion

We analyzed the performance of the three feature se-

lection algorithms on individual features, as shown in

Table 2. The results for DS3 indicate that to clas-

sify a student as Pass/Fail for the subject introduc-

tory programming, the Boruta algorithm considered

that F8 feature does not seem to matter, that is, if

the student is studying a second career. While LVQ

and RFE, usually consider F9, F5, and F1, as rel-

evant features to predict the academic performance

of students. This means that the grade in the level-

ing course (F9), the family income (F5), and the age

(F1) of the student mainly inﬂuence passing or not

the subject. When the performance is analyzed in

terms of Average/Good/Excellent observe that three

algorithms consider the feature F9 as the most rel-

evant, followed by F5 and F1. As seen in Figures

3a-b, these three are the features with the higher fre-

quency of selection as an important feature for pre-

diction. The importance of these socio-demographic

and academic variables has also been reported by

(Ramaswami et al., 2020), (Farissi et al., 2020) and

(Bakker et al., 2023). In fact, when analyzing in depth

the DS3 data set we notice that about 74% of the stu-

dents who achieved a minimum passing grade in the

leveling feature (coded as 1 in Table 2), failed the

subject. While those who achieved an “Excellent”

score, only 1% failed the programming fundamen-

tals course. The highest percentage (55%) of those

who passed the subject corresponds to students with

leveling grades between 80-89 points. This seems to

indicate that the student’s historical score appears to

inﬂuence future performance. Regarding the impor-

tance of familiar income, it was observed that students

whose families have incomes higher than the Ecuado-

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining

Approach

Table 3: Models evaluation using total instances of dataset (DS3) for the binary problem.

Feature selection Classiﬁcation Model Accuracy (%) Precision (%) Recall (%) F-score (%)

Boruta

RF 75.24 ±0.92 71.78 ±0.82 66.48 ±0.80 69.03 ±0.89

LR 66.04 ±0.87 58.79 ±0.87 60.8 ±0.87 59.78 ±0.86

LDA 66.04 ±0.91 58.6 ±0.90 61.93 ±0.90 60.22 ±0.95

KNN 67.69 ±0.91 58.44 ±0.91 76.70 ±0.91 66.34 ±0.91

DT 72.41 ±0.88 64.82 ±0.88 73.3 ±0.88 68.8 ±0.88

SVM 67.45 ±0.86 59.79 ±0.88 65.91 ±0.88 62.7 ±0.88

LVQ

RF 71.46 ±1.16 65.71 ±1.16 65.34 ±1.26 65.53 ±1.34

LR 65.57 ±1.01 57.81 ±1.01 63.07 ±1.00 60.33 ±1.04

LDA 65.57 ±1.01 57.81 ±1.01 63.07 ±1.09 60.33 ±1.04

KNN 64.39 ±1.01 54.24 ±1.01 60.91 ±1.01 67.94 ±1.02

DT 71.23 ±1.01 63.11 ±1.15 73.86 ±1.25 68.06 ±1.11

SVM 71.23 ±1.35 64.21 ±1.05 69.32 ±1.25 66.67 ±1.25

RFE

RF 70.28 ±1.01 63.16 ±1.01 68.18 ±1.01 65.57 ±1.01

LR 66.27 ±1.15 59.02 ±1.16 61.36 ±1.17 60.17 ±1.04

LDA 66.51 ±1.17 59.34 ±1.17 61.36 ±1.21 60.34 ±1.12

KNN 68.4 ±1.03 57.61 ±1.00 60.34 ±1.10 60.35 ±1.02

DT 71.23 ±1.14 63.11 ±1.15 73.86 ±1.15 68.06 ±1.05

SVM 68.63 ±1.19 61.26 ±1.16 66.48 ±1.11 63.76 ±1.25

None

RF 74.76 ±1.15 69.06 ±1.16 71.02 ±1.15 70.03 ±1.01

LR 66.04 ±1.14 58.79 ±1.01 60.8 ±1.25 59.78 ±1.03

LDA 66.27 ±1.17 58.92 ±1.15 61.93 ±1.10 60.39 ±1.28

KNN 68.4 ±1.19 59.29 ±1.05 76.14 ±1.25 66.67 ±1.21

DT 72.41 ±1.35 64.82 ±1.05 73.3 ±1.01 68.8 ±1.14

SVM 66.27 ±1.35 58.73 ±1.17 63.07 ±1.25 60.82 ±1.16

Table 4: Models evaluation using total instances of dataset (DS3) for the multiclass problem.

Feature selection Classiﬁcation Model Accuracy (%) Precision (%) Recall (%) F-score (%)

Boruta

RF 66.63 ±0.58 68.83 ±0.56 55.64 ±0.56 52.42 ±0.51

LR 66.63 ±0.56 68.83 ±0.56 55.64 ±0.56 52.42 ±0.52

LDA 67.44 ±0.44 66.68 ±0.55 60.04 ±0.56 50.22 ±0.53

KNN 56.59 ±0.58 68.73 ±0.41 54.89 ±0.56 56.70 ±0.53

DT 66.63 ±0.41 68.83 ±0.47 55.64 ±0.56 52.42 ±0.54

SVM 66.63 ±0.47 68.83 ±0.48 55.64 ±0.51 52.42 ±0.54

LVQ

RF 66.63 ±0.49 68.83 ±0.48 55.64 ±0.57 54.42 ±0.57

LR 66.63 ±0.51 68.83 ±0.48 55.64 ±0.48 52.42 ±0.47

LDA 67.84 ±0.54 67.88 ±0.51 61.65 ±0.48 51.56 ±0.47

KNN 55.39 ±0.55 50.18 ±0.52 50.92 ±0.60 57.22 ±0.59

DT 64.22 ±0.57 65.34 ±0.51 55.64 ±0.60 52.42 ±0.57

SVM 68.63 ±0.60 70.83 ±0.61 53.71 ±0.57 69.90 ±0.55

RFE

RF 66.63 ±0.44 68.83 ±0.40 55.64 ±0.40 52.42 ±0.42

LR 66.63 ±0.56 68.83 ±0.57 55.64 ±0.40 52.42 ±0.42

LDA 66.63 ±0.41 68.83 ±0.48 55.64 ±0.49 52.42 ±0.42

KNN 54.99 ±0.39 56.26 ±0.48 53.6 ±0.49 51.16 ±0.47

DT 66.63 ±0.48 68.83 ±0.50 55.64 ±0.58 52.42 ±0.52

SVM 66.63 ±0.62 68.83 ±0.60 55.64 ±0.58 52.42 ±0.61

None

RF 61.82 ±0.60 59.93 ±0.60 55.56 ±0.58 55.7 ±0.60

LR 65.83 ±0.57 68.38 ±0.57 54.98 ±0.54 51.51 ±0.57

LDA 67.04 ±0.57 66.43 ±0.57 59.3 ±0.54 59.23 ±0.58

KNN 57.00 ±0.57 52.97 ±0.50 52.56 ±0.54 51.41 ±0.53

DT 67.84 ±0.61 63.15 ±0.61 60.46 ±0.58 51.25 ±0.51

SVM 65.43 ±0.62 51.38 ±0.61 54.68 ±0.59 51.57 ±0.60

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

a) Pass/Fail (C1)

0.00

0.25

0.50

0.75

1.00

0.00 0.25 0.50 0.75 1.00

1 − specificity

sensitivity

AUC=73.7%

AUC=80.9%

AUC=73.7%

LDA

AUC=77.7%

KNN

AUC=76.6%

AUC=74.1%

SVM

b) Average vs Rest (C2)

0.00

0.25

0.50

0.75

1.00

0.00 0.25 0.50 0.75 1.00

1 − specificity

sensitivity

AUC=73.4%

AUC=74.3%

AUC=74.2%

LDA

AUC=73.0%

KNN

AUC=70.7%

AUC=75.6%

SVM

c) Excellent vs Rest (C2)

0.00

0.25

0.50

0.75

1.00

0.00 0.25 0.50 0.75 1.00

1 − specificity

sensitivity

AUC=68.6%

AUC=67.1%

AUC=69.1%

LDA

AUC=63.0%

KNN

AUC=58.2%

AUC=74.2%

SVM

c) Good vs Rest (C2)

0.00

0.25

0.50

0.75

1.00

0.00 0.25 0.50 0.75 1.00

1 − specificity

sensitivity

AUC=65.2%

AUC=63.4%

AUC=67.2%

LDA

AUC=57.8%

KNN

AUC=65.6%

AUC=67.7%

SVM

Figure 4: Models AUC-ROC curves plots.

rian basic salary ($475) represent about 53% of the

students who pass the subject. On the other hand,

those who earn fewer dollars than this value represent

almost 70% of the students who fail the subject. This

seems to indicate that the higher the family income,

the better the academic performance. Finally, it is ob-

served that students between 17 and 24 years old cor-

respond to 70% of the students who fail. While those

aged 25 or over are 60% of those who pass the subject.

This seems to be an indication that older students tend

to be more interested in passing the introductory pro-

gramming course. In brief, the grade in the leveling

course (F9) is likely an important predictor because

it reﬂects a student’s prior knowledge and prepara-

tion for the subject. Students who performed well in

the leveling course may have a better foundation to

build upon in the introductory programming course,

while those who struggled may face more challenges

in keeping up with the material. The family income

(F5) may be an important predictor because it can im-

pact a student’s access to resources and support that

are critical for academic success. The age (F1) may be

an important predictor because older students may ap-

proach their studies differently than younger students.

Older students may have more competing responsi-

bilities such as work or family obligations, which can

impact their ability to devote time and energy to their

studies. The ﬁndings provide insights for educators

and policymakers of the UTM and UNEMI on how to

support low-income students in online higher educa-

tion and improve their chances of success.

The experimental results with the prediction mod-

els aim to demonstrate that our approach can better

distinguish between passing and Failing the course by

the students with a high probability as well as getting

a ﬁnal grade into categories Average, Good, and Ex-

cellent. Results showed in Tables 3-4 seem to demon-

strate that the performance of the binary prediction is

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining

Approach

better when Boruta with RF model is used (except in

recall metric). Meanwhile, for the multiclass case, the

best performance is understood using LVQ + SVM

(except for the recall metric). The accuracy of 75.24%

(highlighted in gray) means that little more than 7 out

of 10 students classiﬁed as passing or failing are cor-

rectly labeled as such. While a little more than 6 out

of 10 students correctly predict their academic per-

formance in terms of average, good, or excellent ﬁnal

grades.

In Figure 4 larger area under the curve (AUC) cor-

responds to the better classiﬁcation effect. Here, we

can observe that AUC values of the RF (Figure 4a)

and SVM (Figure 4b-d) are higher than those of other

prediction models for binary and multiclass cases, re-

spectively; visually, it seems to have the best perfor-

mance for academic performance prediction. To de-

tect whether prediction models operate similarly or

not from a statistical point of view, we carried out

the ANOVA test. It veriﬁes whether the average per-

formance regarding AUC of the methods is signif-

icantly different between them. We conducted the

test and found p-values of 0.0123, 1.23e-09, 1.2e-

16, and 1.2e-16, for predictions of Pass/Fail, Average

Vs Rest, Good Vs Rest, and Excellent Vs Rest, re-

spectively. As they are lower than our threshold of

0.05, we can say that there is a statistically signif-

icant difference in the performance of classiﬁcation

models regarding AUC value. As the ANOVA test

is signiﬁcant, we can compute Tukey HSD (Tukey

Honest Signiﬁcant Differences) to perform multiple

pairwise comparisons between the means of groups.

We conducted the test and found p-values lower than

our threshold of 0.05 when comparing the AUC of RF

with LR, LDA, DT, and SVM, so we can say that there

is a statistically signiﬁcant difference between these

models for the academic performance (Pass/Fail) out-

comes of the introductory programming. However,

when it was compared with KNN, we found no dif-

ferences. For the prediction of Average vs Rest, we

found p-values lower than our threshold when com-

paring SVM with LDA and DT, with other models

we found no differences. For the prediction of Good

vs Rest, we found p-values lower than our threshold

when comparing SVM with RF, KNN, and DT, with

other models we found no differences. Finally, we

can say that there is a statistically signiﬁcant differ-

ence between SVM and other models for academic

performance (Excellent vs Rest).

5 CONCLUSIONS

This work presents a predictive model for early warn-

ing of academic performance for online Ecuadorian

university students in the introductory programming

subject.

Different feature selection and predictive models

are compared by evaluating the well-known valida-

tion metrics namely, Accuracy, Precision, Recall, F-

score as well as the ROC curve and AUC score.

In terms of the results, the computational exper-

iments shows that the grade in the leveling course,

family income, and age of the student are the main

factors inﬂuencing academic performance in terms of

passing or failing the subject and achieving an aver-

age, good, or excellent ﬁnal grade.

When our approach uses Boruta + Random Forest

and LVQ + SVM, the academic performance predic-

tion is achieved in a better way, with 7 out of 10 cases

and 6 out of 10 cases, correctly labeled for binary

(Pass/Fail) and multiclass (Average/Good/Excellent)

academic performance prediction, respectively.

REFERENCES

Al-Zawqari, A., Peumans, D., and Vandersteen, G. (2022).

A ﬂexible feature selection approach for predicting

student’s academic performance in online courses.

Computers and Education: Artiﬁcial Intelligence,

3:100103.

Alhothali, A., Albsisi, M., Assalahi, H., and Aldosemani, T.

(2022). Predicting student outcomes in online courses

using machine learning techniques: A review. Sus-

tainability, 14(10).

Ang, J. C., Mirzal, A., Haron, H., and Hamed, H.

N. A. (2015). Supervised, unsupervised, and semi-

supervised feature selection: a review on gene selec-

tion. IEEE/ACM transactions on computational biol-

ogy and bioinformatics, 13(5):971–989.

Bakker, T., Krabbendam, L., Bhulai, S., Meeter, M.,

and Begeer, S. (2023). Predicting academic suc-

cess of autistic students in higher education. Autism,

0(0):13623613221146439.

Beckham, N. R., Akeh, L. J., Mitaart, G. N. P., and Mo-

niaga, J. V. (2023). Determining factors that affect

student performance using various machine learning

methods. Procedia Computer Science, 216:597–603.

7th International Conference on Computer Science

and Computational Intelligence 2022.

Belgaum, M. R., Alansari, Z., Musa, S., Alam, M. M.,

and Mazliham, M. S. (2021). Impact of artiﬁcial

intelligence-enabled software-deﬁned networks in in-

frastructure and operations: Trends and challenges.

International Journal of Advanced Computer Science

and Applications, 12(1).

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

Bennedsen, J. and Caspersen, M. E. (2019). Failure rates

in introductory programming: 12 years later. ACM

Inroads, 10(2):30–36.

ardenas-Cobo, J., Puris, A., Novoa-Hern

andez, P., Parra-

Jim

enez,

A., Moreno-Le

on, J., and Benavides, D.

(2021). Using scratch to improve learning program-

ming in college students: A positive experience from

a non-weird country. Electronics, 10(10):1180.

Carrillo, J. M. and Parraga-Alava, J. (2018). How predicting

the academic success of students of the espam mﬂ?: A

preliminary decision trees based study. In 2018 IEEE

Third Ecuador Technical Chapters Meeting (ETCM),

pages 1–6.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: synthetic minority over-

sampling technique. Journal of artiﬁcial intelligence

research, 16:321–357.

Chen, R.-C., Dewi, C., Huang, S.-W., and Caraka, R. E.

(2020). Selecting critical features for data classiﬁca-

tion based on machine learning methods. Journal of

Big Data, 7(1):52.

Cilia, N. D., De Stefano, C., Fontanella, F., Raimondo, S.,

and Scotto di Freca, A. (2019). An experimental com-

parison of feature-selection and classiﬁcation methods

for microarray datasets. Information, 10(3):109.

Farissi, A., Dahlan, H. M., et al. (2020). Genetic algo-

rithm based feature selection with ensemble methods

for student academic performance prediction. In Jour-

nal of Physics: Conference Series, volume 1500, page

012110. IOP Publishing.

Ghoneim, S. (2019). Accuracy, Recall, Precision, F-Score

and Speciﬁcity, which to optimize on.

Guyon, I., Weston, J., Barnhill, S., and Vapnik, V. (2002).

Gene selection for cancer classiﬁcation using support

vector machines. Machine learning, 46:389–422.

Huynh-Cam, T.-T., Chen, L.-S., and Huynh, K.-V. (2022).

Learning performance of international students and

students with disabilities: Early prediction and feature

selection through educational data mining. Big Data

and Cognitive Computing, 6(3).

Huynh-Cam, T.-T., Chen, L.-S., and Le, H. (2021). Using

decision trees and random forest algorithms to predict

and determine factors contributing to ﬁrst-year uni-

versity students’ learning performance. Algorithms,

14(11).

Kohonen, T. (2001). Learning Vector Quantization, pages

245–261. Springer Berlin Heidelberg, Berlin, Heidel-

berg.

Kuhn, M. and Wickham, H. (2020). Tidymodels: a collec-

tion of packages for modeling and machine learning

using tidyverse principles.

Kursa, M. B., Jankowski, A., and Rudnicki, W. R. (2010).

Boruta–a system for feature selection. Fundamenta

Informaticae, 101(4):271–285.

Liu, J., Peng, P., and Luo, L. (2020). The relation between

family socioeconomic status and academic achieve-

ment in china: A meta-analysis. Educational Psychol-

ogy Review, 32:49–76.

Niyogisubizo, J., Liao, L., Nziyumva, E., Murwanashyaka,

E., and Nshimyumukiza, P. C. (2022). Predicting

student’s dropout in university classes using two-

layer ensemble machine learning approach: A novel

stacked generalization. Computers and Education:

Artiﬁcial Intelligence, 3:100066.

Phauk, S. and Okazaki, T. (2020). Study on dominant fac-

tor for academic performance prediction using feature

selection methods. International Journal of Advanced

Computer Science and Applications, 11:492–502.

Rahimi, S. and Shute, V. J. (2021). First inspire, then in-

struct to improve students’ creativity. Computers &

Education, 174:104312.

Ramaswami, G. S., Susnjak, T., Mathrani, A., and Umer,

R. (2020). Predicting students ﬁnal academic perfor-

mance using feature selection approaches. In 2020

IEEE Asia-Paciﬁc Conference on Computer Science

and Data Engineering (CSDE), pages 1–5.

RStudio Team (2018). RStudio: Integrated Development

Environment for R. RStudio, Inc.

Simeunovi

c, V. and Preradovi

c, L. (2014). Using data min-

ing to predict success in studying. Croatian Journal

of Education, 16(2):491–523.

Stoian, C. E., F

arcas

iu, M. A., Dragomir, G.-M., and

Gherhes

, V. (2022). Transition from online to face-to-

face education after covid-19: The beneﬁts of online

education from students’ perspective. Sustainability,

14(19).

Su, Y.-S., Lin, Y.-D., and Liu, T.-Q. (2022). Applying ma-

chine learning technologies to explore students’ learn-

ing features and performance prediction. Frontiers in

Neuroscience, 16.

Team, R. C. (2017). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing.

Tharwat, A. (2018). Classiﬁcation assessment methods. Ap-

plied Computing and Informatics.

Tomasevic, N., Gvozdenovic, N., and Vranes, S. (2020). An

overview and comparison of supervised data mining

techniques for student exam performance prediction.

Computers & Education, 143:103676.

Wickham, H., Averick, M., Bryan, J., Chang, W., Mc-

Gowan, L. D., Franc¸ois, R., Grolemund, G., Hayes,

A., Henry, L., Hester, J., Kuhn, M., Pedersen, T. L.,

Miller, E., Bache, S. M., M

uller, K., Ooms, J., Robin-

son, D., Seidel, D. P., Spinu, V., Takahashi, K.,

Vaughan, D., Wilke, C., Woo, K., and Yutani, H.

(2019). Welcome to the tidyverse. Journal of Open

Source Software, 4(43):1686.

Xavier, M. and Meneses, J. (2020). Dropout in Online

Higher Education: A scoping review from 2014 to

2018.

Xiao, W., Ji, P., and Hu, J. (2021). Rnkheu: A hybrid fea-

ture selection method for predicting students’ perfor-

mance. Scientiﬁc Programming, 2021:1–16.

gcı, M. (2022). Educational data mining: prediction

of students’ academic performance using machine

learning algorithms. Smart Learning Environments,

9(1):11.

Predicting Academic Performance of Low-Income Students in Public Ecuadorian Online Universities: An Educational Data Mining

Approach