
Robust Finite-Time Control of a Multirotor System via an Improved
Optimized Homogeneous Twisting Control: Design and Validation
Aimen Abdelhak Messaoui
1
, Omar Mechali
1
, Ali Zakaria Messaoui
2
and Iheb Eddinde Smaali
1
1
Ecole Supérieure Ali Chabati, Réghaia, Algeria
2
Laboratoire de Commande des Systèmes Complexes et Simulateurs, Ecole Militaire Polytechnique,
Bordj El-Bahri, Algeria
Keywords: The Attitude Tracking Control, Finite-Time Stability, Homogeneous Sliding Mode Control,
Pixhawk Autopilot, Quadrotor Aircraft.
Abstract: This paper presents theoretical and practical aspects of finite-time tracking control of a multirotor attitude
system. The vehicle is subjected to matched lumped disturbances. Inspired by the homogeneity theory, an
Improved Optimized Homogeneous Twisting Control (IOHTC) is proposed to deal with the fast dynamics’
response of the attitude states. Within the designed control scheme, the chattering issue of discontinuous
Sliding Mode Control (SMC) techniques can be mitigated due to the continuous control signal that is
generated by a non-switching function in the form of |𝑥|
sign(𝑥),𝑥 ∈ 𝑅,𝛼 ∈ 𝑅+. Besides, finite-time
convergence of the system’s states can be ensured to achieve accurate control. It is worth mentioning that
the disturbance rejection does not require the design of an observer since the control law integrates a
compensation term. Stability analysis of the closed-loop system is rigorously investigated by using a
homogeneous Lyapunov function. From the practical aspect, the control algorithm is embedded onboard the
quadrotor’s autopilot through a model-based design approach. A comparative study is made involving the
proposed IOHTC strategy and three other controllers. The obtained results show that the suggested controller
yields performance improvement regarding accuracy and robustness. Meanwhile, the chattering effect of
conventional SMC is remarkably alleviated.
1 INTRODUCTION
The quadrotor is among the most often used
multirotor aircraft because of its particular flight
mode, variety of sizes, and exceptional hovering
capabilities. Unfortunately, it is also considered a
well-known underactuated mechanical system.
However, since its invention in 1907, quadcopters
have found use in a wide range of application fields
(O. Mechali J. I., 2021) (O. Mechali J. I., 2021).
However, despite its alluring qualities, this kind of
system faces real challenges, especially in terms of
control. Accurate and robust aircraft attitude control
is necessary for autonomous quadrotor flying. Since
a quadrotor is a nonlinear system with highly coupled
dynamics, it is susceptible to internal modeling errors,
parametric uncertainty, and external disturbances.
Consequently, developing the system attitude
controller becomes challenging. In order to perform
the objectives of the flying mission, this aircraft’s
autonomous flight requires a sophisticated control
scheme. Additionally, the controller design appears
based on robustness, high control accuracy, and quick
convergence.
SMC, among other robust control approaches, is
an active topic in the unmanned aerial vehicle
community nowadays for controlling quadrotor
aircraft (S. Benmansour, 2023) (S. G. Khan, 2019).
The simplicity of design and the fast response are
among the benefits of such methods. In addition, it
accurately compensates for matched disturbances.
Several recent research works have focused on
synthesizing and implementing robust SMC-based
control laws for disturbance handling in the quadrotor
system. For example, through an integral SMC-based
approach, the study described in (S. Ullah, 2020)
seeks to enhance the stability of an underactuated
quadcopter. A robust backstepping-SMC control law
is suggested in a further inspired study (Almakhles,
2020) to deal with the quadrotor model with
disturbances. However, because a linear switching
manifold has been employed, it is guaranteed that the
326
Messaoui, A., Mechali, O., Messaoui, A. and Smaali, I.
Robust Finite-Time Control of a Multirotor System via an Improved Optimized Homogeneous Twisting Control: Design and Validation.
DOI: 10.5220/0012086700003546
In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 326-331
ISBN: 978-989-758-668-2; ISSN: 2184-2841
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

states will only converge asymptotically to the origin.
Additionally, Linear SMC (LSMC) is concerned with
low precision, decaying performance, and chattering
issues that might overload the actuators. Using a
nonlinear sliding manifold with continuous-based
SMC methods is one approach to get around the
chattering problem and slow convergence rate (F.
Guo, 2019). Compared with LSMC, continuous-
based SMC offers faster finite-time convergent
response and accurate tracking (Yu, 1997). For
instance, the work (O. Mechali L. X., 2022) deals
with robust trajectory tracking of a quadrotor vehicle
through a homogeneous terminal sliding mode
control. Nonetheless, the controller in (O. Mechali L.
X., 2022) is observer-based, resulting in more
computational burden. Such a method does not fit our
application, consisting of implementing the controller
in Pixhawk 1 board. Furthermore, this autopilot is
limited in terms of memory resources; thus, control
performance might be compromised. To the best of
the authors’ knowledge, only a few research studies,
such as (F. Guo, 2019) and (Falcón, Ríos, & Dzul,
2019), investigate a continuous SMC-based control
for quadrotor aircraft designs with real-time
implementation onboard a dedicated autopilot. The
current effort’s fundamental goal, inspired by (H.
Rabiee, 2019), is to report experimental findings to
bridge the gap between theoretical fronts and real-
world situations.
The main scientific contributions of the current
research can be summed up as follows:
• Inspired by the homogeneity theory, an
IOHTC is proposed to deal with the fast
dynamics’ response of the attitude states.
The proposed controller allows for
mitigating the chattering of discontinuous
SMC techniques compared to (S. Ullah,
2020) (Almakhles, 2020) (N. Wang, 2019)
(Z. Hou, 2020).
• It is worth mentioning that the disturbance
rejection does not require the design of an
observer or an adaptation mechanism since
the control law integrates a compensation
term. Thus, resulting in alleviating the
computational burden on the Pixhawk
autopilot being memory-resource limited;
• terms of application, a beneficial model-
based design methodology is used to
incorporate the control algorithm inside the
quadrotor autopilot. The suggested IOHTC
method and three other controllers are
compared in this study.
The following is the outline of this article. The
preliminaries and the problem description are
presented in Section 2. Then, in Section 3, the control
method is presented along with a thorough
mathematical analysis of the stability. The
experimental results are critically discussed in
Section 4. Finally, Section 5 concludes the paper and
considers possible research directions.
2 PRELIMINARIES AND
PROBLEM STATEMENT
2.1 Preliminaries
Lemma 1. (Xu, 2017). Consider the following
system
𝑥=
𝑓
(
𝑥
)
,𝑥
(
0
)
=𝑥
, 𝑥∈
ℝ
(1)
If there exist ∁
Lyapunov function 𝑉
(
𝑥
)
:D→ℝ
and some real constants 0<𝑐<∞ and 0<𝛼<1,
such that 𝑉
(
𝑥
)
≤−𝑐𝑉
(
𝑥
)
; then, system (1) is finite-
time stable for any given 𝑥
(
𝑡
)
∈D
⊆D.
2.2 Problem Statement
The three differential equations governing the
rotational dynamics of the quadcopter in the presence
of external disturbances are given as in (F. Guo, 2019)
𝛷
=𝐽
𝐽
−𝐽
𝜃
𝜓
−𝒸
𝛷
−𝐽
𝜔
𝜃
+𝑢
+𝑑
,
𝜃
=𝐽
(
𝐽
−𝐽
)
𝛷
𝜓
−𝒸
𝜃
+𝐽
𝜔𝛷
+𝑢
+𝑑
,
𝜓
=𝐽
𝐽
−𝐽
𝛷
𝜃
−𝒸
𝜓
+𝑢
+𝑑
,
(2)
To elaborate an adequate control model of the
quadrotor, state-space representation can be used to
reformulate the mathematical model (equation 2) as
⎩
⎪
⎪
⎨
⎪
⎪
⎧
x
=x
,
x
=𝐽
𝐽
−𝐽
x
x
+𝑢
+𝑑
,
x
= x
,
x
=𝐽
(
𝐽
−𝐽
)
x
x
+𝑢
+𝑑
,
x
= x
,
x
=𝐽
𝐽
−𝐽
x
x
+𝑢
+𝑑
,
(3)
Where x ≜
𝛷𝛷
𝜃𝜃
𝜓𝜓
∈ ℝ
the
state vector. the design of the control law follows
from the perturbated second-order nonlinear system
given below
𝜒
(
𝑡
)
=𝜒
(
𝑡
)
,
𝜒
(
𝑡
)
=𝑓
(
𝜒
,𝑡
)
+𝑔
(
𝑡
)
𝑢
(
𝑡
)
+𝑑
(
𝑑
,𝑑
,𝑡
)
,
𝒴
(
𝑡
)
=𝜒
(
𝑡
)
.
(4)
Where𝑋
≜
𝜒
𝜒
∈ ℝ
×
is the vector of
states, and 𝜒
≜𝛩=
x
x
x
=
𝛷 𝜃 𝜓
𝜒
≜𝛩
=
𝛷
𝜃
𝜓
=
x
x
x
, and
Robust Finite-Time Control of a Multirotor System via an Improved Optimized Homogeneous Twisting Control: Design and Validation
327

𝑢
≜
𝑢
𝑢
𝑢
∈ ℝ
is the vector of control
inputs, 𝒴
≜
𝛷 𝜃 𝜓
∈ ℝ
is the vector of
controlled outputs, and the uncertain function 𝑑
≜
𝑑
𝑑
𝑑
∈ ℝ
stands for the total
lumped disturbances, i.e., unmodeled dynamics and
external load perturbations. The functions
𝑓
(
𝜒
,𝑡
)
,𝑔
(
𝑡
)
are defined as follow:
𝑓
(
𝜒
,𝑡
)
≜
𝑓
𝑓
𝑓
=
𝐽
𝐽
−
𝐽
𝜃
𝜓
𝐽
(
𝐽
−𝐽
)
𝛷
𝜓
𝐽
𝐽
−
𝐽
𝛷
𝜃
(5)
𝑔
(
𝑡
)
≜
𝑔
𝑔
𝑔
=
𝐽
𝐽
𝐽
(6)
Definition 1. (Robust tracking control problem). The
considered control problem of our study consists of
designing robust finite-time SMC laws 𝒖
𝜣
=
𝒖
𝜱
𝒖
𝜽
𝒖
𝝍
𝑻
for the attitude system affected by
perturbations in (4), such that: (i) The attitude
tracking errors tend to the origin in finite-time, i.e.,
for ∀𝒆
𝟏
𝜣
(
𝒕
)
≜ 𝜣
(
𝒕
)
−𝜣
𝒅
(
𝒕
)
, There exist a constant
𝑻
𝜣
, such that: 𝐥𝐢𝐦
𝒕→𝑻
𝜣
𝒆
𝟏
𝜣
(
𝒕
)
=𝟎,∀𝒕>𝑻
𝜣
, where 𝜣
𝒅
is the desired reference signal for the attitude system.
(ii) The controller must ensure robustness against
uncertainties and disturbances. (iii) The control signal
is chattering-free.
3 CONTROL DESIGN AND
STABILITY ANALYSIS
3.1 Control Design
Let the attitude-tracking error and its dynamics be
defined as:
𝑒
(
𝑡
)
≜ 𝛩
(
𝑡
)
−𝛩
(
𝑡
)
𝑒
(
𝑡
)
≜𝛩
(
𝑡
)
−𝛩
(
𝑡
)
(7)
𝑒
(
𝑡
)
=
𝑒
𝑒
𝑒
∈
ℝ
,
𝑒
(
𝑡
)
=𝑒
,𝑒
,𝑒
∈
ℝ
,
(8)
The derivatives of the above expressions are given as:
𝑒
= 𝑒
,
𝑒
=𝛩
−𝛩
.
(9)
The Traditional Twisting Control (TTC) algorithm is
given as:
𝑢
=−𝑘
⌈
𝑒
⌋
−𝑘
⌈
𝑒
⌋
+𝜗
,
𝜗
=−𝑘
⌈
𝑒
⌋
−𝑘
⌈
𝑒
⌋
.
(10)
Remark 1. It has been shown in work (Falcón, Ríos,
& Dzul, 2019) that the TTC controller generates a
higher frequency, i.e., chattering in its control signal.
Therefore, limiting its implementation in practice.
Hence, to improve its performance, we propose to: (i)
Design a smooth hyperbolic function to mitigate the
chattering effect as ℱ
(
𝑒
)
≜
(
𝑒
)
tanh
(
𝑒
𝜐
⁄)
,
where 𝜛,𝜐 are positive constants that are related to
ℱ function. (ii) Integrate the sliding function 𝑠
=
𝑒
+𝑘
𝑒
in the TTC’s algorithm to enhance the
robustness and tracking.
Consequently, by introducing the following
control law for the attitude system
𝑢
≜−𝑘
|
𝑒
|
ℱ
(
𝑒
)
−𝑘
|
𝑠
|
ℱ
(
𝑠
)
+𝜗
,
𝜗
≜𝑘
|
𝑒
|
ℱ
(
𝑒
)
−𝑘
|
𝑠
|
ℱ
(
𝑠
)
,
𝑠
=𝑒
+𝑘
𝑒
.
(11)
The final attitude controller is formulated as:
𝑢
≜
𝑔
−𝑘
|
𝑒
|
ℱ
(
𝑒
)
−
𝑘
|
𝑠
|
ℱ
(
𝑠
)
+𝜗
−
𝑓
(12)
3.2 Stability Analysis of the Closed
Loop System
Theorem 1. Consider the nonlinear perturbated
attitude system (4) and the designed control law u_Θ
given in (11). Then, the attitude tracking errors are
globally finite-time stable at the origin.
Proof. Since the attitude dynamics are similar, we
consider the stability proof of the roll angle. The
closed-loop dynamics for the roll variable 𝛷 can be
described as:
⎩
⎪
⎨
⎪
⎧
𝑒
=𝑒
,
𝑒
=−𝑘
|
𝑒
|
ℱ
(
𝑒
)
−𝑘
|
𝑠
|
ℱ
(
𝑠
)
+𝜍
,
𝜍
=−𝑘
|
𝑒
|
ℱ
(
𝑒
)
−𝑘
|
𝑠
|
ℱ
(
𝑠
)
−𝛷
(
)
,
𝑠
=𝑒
+𝑘
𝑒
.
(13)
Where 𝜍
=𝜗
−𝛷
. The third expression in
(12) can be associated with differential inclusion (DI)
𝜍
∈−𝑘
|
𝑒
|
ℱ
(
𝑒
)
−𝑘
|
𝑠
|
ℱ
(
𝑠
)
+
−𝜆,𝜆
which is basically 𝜍
∈−𝑘
|
𝑒
|
sign
(
𝑒
)
−
𝑘
|
𝑠
|
sign
(
𝑠
)
+
−𝜆,𝜆
.Therefore, it is
associated with DI 𝑥∈F
(
𝑥
)
, where the set valued
map F is given by F
(
𝑥
)
=
𝑦∈ℝ
|𝑦=
𝑒
,𝜍
,𝜌
, for all 𝜌∈−𝑘
|
𝑒
|
ℱ
(
𝑒
)
−
𝑘
|
𝑠
|
ℱ
(
𝑠
)
+
−𝜆,𝜆
⊂ℝ . This DI is
SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
328

homogeneous of degree 𝑞
=−1 with weights 𝑟
=
3,2,1
(Falcón, Ríos, & Dzul, 2019).
Let the following candidate Lyapunov function be
proposed for system (10)
𝑉
(
𝑒
,𝑒
,𝜍
)
=𝛼
|
𝑒
|
+𝛼
𝑒
𝑠
+𝛼
|
𝑠
|
+𝛼
𝑒
|
𝜍
|
ℱ
(
𝜍
)
−𝛼
𝑠
𝜍
+𝛼
|
𝜍
|
,
(14)
Where 𝛼
=
𝛼
,…,𝛼
∈ ℝ
,𝑗=1,6
is a
coefficients vector. The time derivative of
𝑉
(
𝑒
,𝑒
,𝜍
)
is computed as:
𝑉
=ℳ=𝛽
|
𝑒
|
+𝛽
𝑒
sign
(
𝑠
)
−𝛽
sign
(
𝑒
)
𝑠
+𝛽
sign
(
𝑒
)
sign
(
𝑠
)
+𝛽
|
𝑠
|
−𝛽
𝑒
𝜍
+𝛽
|
𝑒
||
𝜍
|
−𝛽
𝑒
sign
(
𝑠
)|
𝜍
|
−𝛽
sign
(
𝑠
)
𝜍
−𝛽
𝑠
sign
(
𝜍
)
+𝛽
sign
(
𝑒
)
𝑠
|
𝜍
|
−𝛽
|
𝑒
||
𝜍
|
−𝛽
sign
(
𝑒
)
𝜍
−𝛽
sign
(
𝑠
)
𝜍
+𝛽
|
𝜍
|
+𝛽
sign
(
𝑒
)
sign
(
𝜍
)
+𝛽
sign
(
𝑒
)
sign
(
𝜍
)
.
(15)
Where 𝛽
=𝛼
𝑘
,𝛽
=𝛼
𝑘
,𝛽
=
𝛼
,𝛽
=
𝛼
𝑘
,𝛽
=
𝛼
𝑘
−𝛼
,𝛽
=𝛼
,𝛽
=
2𝛼
𝑘
,𝛽
=2𝛼
𝑘
,𝛽
=
𝛼
,𝛽
=𝛼
,𝛽
=
3𝛼
𝑘
,𝛽
=3𝛼
𝑘
,𝛽
=𝛼
𝑘
,𝛽
=
𝛼
𝑘
,𝛽
=𝛼
,𝛽
=5𝛼
𝑘
,𝛽
=5𝛼
𝑘
. The
Lyapunov function 𝑉
given in (13) is homogeneous
of degree 𝑚=5. Thus, there exist a continuous
homogeneous function ℳof degree 𝑚+𝑞
=4
such that 𝑉
≤−ℳ. Hence, there exist a real 𝛾
>0
such that ℳ≥𝛾
𝑉
. Therefore, 𝑉
≤−𝛾
𝑉
.
This implies that the tracking errors are finite-
time stable at the origin. Furthermore, since the
control system is homogeneous, the stability
property is global. The expression of the settling-
time can be obtained by solving the differential
equation 𝑉
≤−𝛾
𝑉
. This can be achieved by
appealing to the separation of variables method.
Thus, by separating the variables and then
integrating both sides of the equation, we get
𝑑𝑉
≤
−𝛾
𝑑𝑡
. Then the following
expression is obtained 5𝑉
≤−𝛾
𝑡. Finally, we
can get 𝑇
≤
5
𝑉
. It follows from Lemma 1 that the
tracking errors are finite-time stable. Thus,
completing the proof.
4 EXPERIMENT RESULTS AND
DISCUSSION
4.1 Control Gains Tuning
The gains of the controller are tuned by using the
“Optimization Toolbox”. Two blocks are used to
optimize the parameters: (i) Check Step Response
Characteristics (CSRC) block; (ii) Check Against
Reference (CAR) block. In the general case, these
two optimization blocks are inserted in the output of
the control loop, as shown in Fig. 1. The CSRC block
checks that a signal satisfies the step response bounds
during simulation (Settling-time, Rise-time, %
Overshoot, and % Undershoot). CAR block checks
that a signal remains within the tolerance bounds, at
steady-state, of a reference signal during the
simulation.
CSRC, CAR blocks ensure that a signal remains
within specified time-domain characteristic bounds.
In our case, these bounds are chosen for a unit step
response, as shown in Table.
4.2 Tracking Experiment Under Load
Disturbances
To quantify the superior performance achieved by the
presented controller, comparative studies are
conducted among the following controllers: PID
controller, Back-Stepping Controller (BSC), Integral
Back-Stepping Sliding Mode Controller (IBSSMC)
Table 1: Specified time-domain characteristic bounds for position states.
States
Optimization
Block
Characteristics Value
𝛷,𝜃,𝜓
CSRC
Settling-time (s)
≤2s
Rise-time (s)
≤4s
Overshoot (%)
≤30%
Undershoot (%)
≤5%
CAR
Amplitudes
1−exp
(
−linspace
(
0,20
)
/2
)
Absolute tolerance
eps
(/)
Relative tolerance
0.01
Robust Finite-Time Control of a Multirotor System via an Improved Optimized Homogeneous Twisting Control: Design and Validation
329
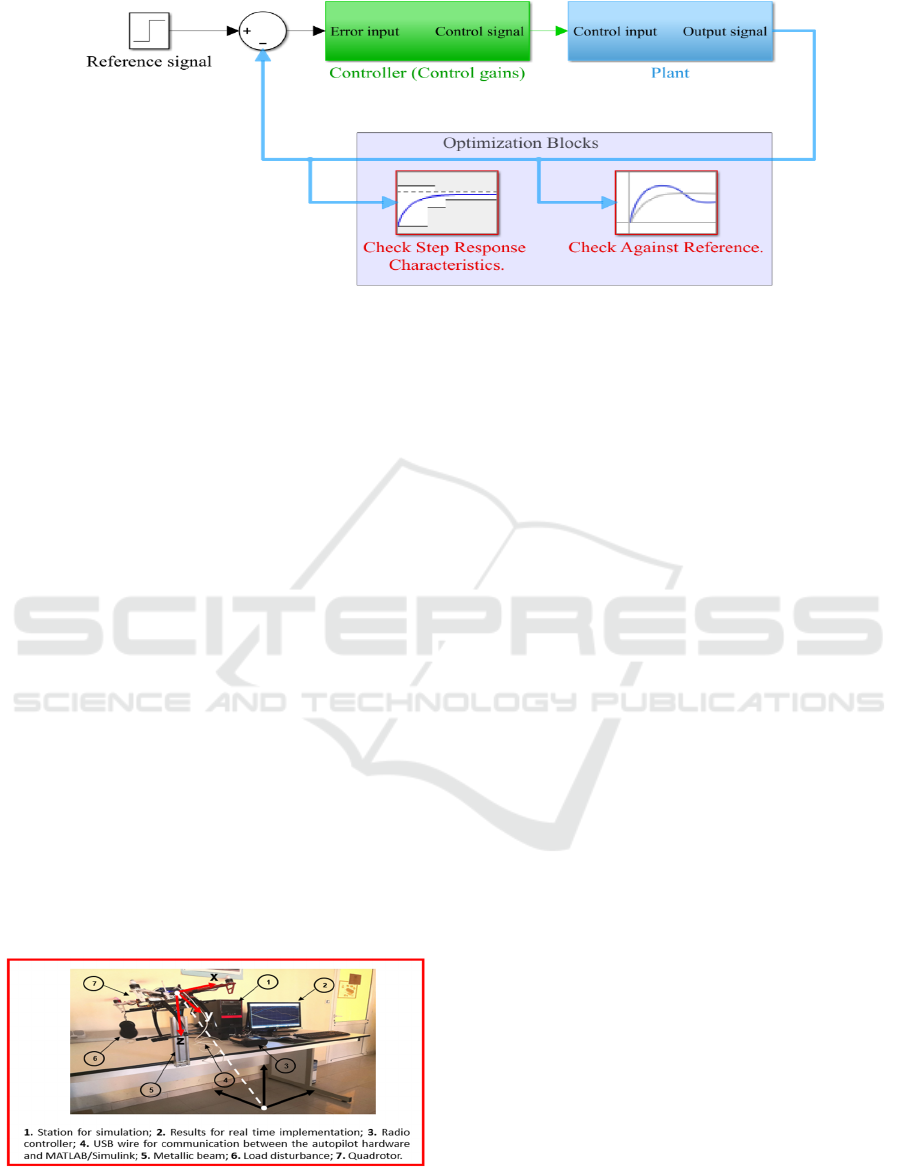
Figure 1: Integration of the optimization blocks in the closed-loop control system.
(Falcón, Ríos, & Dzul, 2019), and the proposed
controller. A load perturbation of 130 grams is
attached to the edge of the rear-left arm of the
quadrotor. The attitude variables are commanded to
track a time-varying reference trajectory given by:
𝛷
=10sin
(
0.08𝑡
)
,𝜃
=−10sin
(
0.08𝑡
)
,𝜓
=
−7.5cos
(
0.08𝑡
)
.
Fig. 2 shows the experimental setup for the real-
time controllers implementation and validation. The
tracking states are displayed in Figure 4, whereas
Figure 3 shows the tracking errors. From these two
figures, it can be observed that the proposed control
strategy ensures a robust tracking of the reference
trajectory. Figure 4 also presents the control signals
for all controllers, where we can notice that the
control inputs of the proposed controller have no
noticeable control switching (chattering). Well-
known performance indexes are used to characterize
the comparison of the achieved results. These include
the Integral of the Absolute value of the Derivative of
the input 𝑢 (IADU) and Integral of Square Error
(ISE). This improvement is quantified by the Relative
Percentage Difference (RPD) index as follows:
( 𝑢
↓60%,𝑢
↓36.08%,𝑢
↓76.60% )
compared to IBSSMC.
Figure 2: Experimental setup for real time control
implementation.
5 CONCLUSION
This work proposed an IOHTC approach to design a
robust attitude control law while considering lumped
disturbances. The stability of the control system has
been rigorously discussed based on a homogeneous-
Lyapunov function. Results based on the real-time
implementation in autopilot hardware are found to be
consistent with the theoretical foundations. To
thoroughly examine the capabilities of the
synthesized controller, a comparative analysis based
on various performance indices performed. Results
witness the effectiveness and superiority of the
proposed control law in terms of robustness,
accuracy, and elimination of the chattering effect.
Further studies will address Cartesian trajectory
tracking with a real outdoor flight experiment.
REFERENCES
Almakhles, D. J. (2020). Robust Backstepping Sliding
Mode Control for a Quadrotor Trajectory Tracking
Application. IEEE Access, 5515-5525.
F. Guo, M. W. (2019). An Unmanned Aerial Vehicles
Collaborative Searching and Tracking Scheme in
Three-Dimension Space. IEEE 9th Annual
International Conference on CYBER Technology in
Automation, Control, and Intelligent Systems
(CYBER) (pp. 1262-1266). Suzhou, China: IEEE.
Falcón, R., Ríos, H., & Dzul, A. (2019). Comparative
analysis of continuous sliding-modes control strategies
for quad-rotor robust tracking. Control Engineering
Practice, 90, 241-256.
H. Rabiee, M. A. (2019). Continuous nonsingular terminal
sliding mode control based on adaptive sliding mode
disturbance observer for uncertain nonlinear systems.
Automatica, 1-7.
SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
330
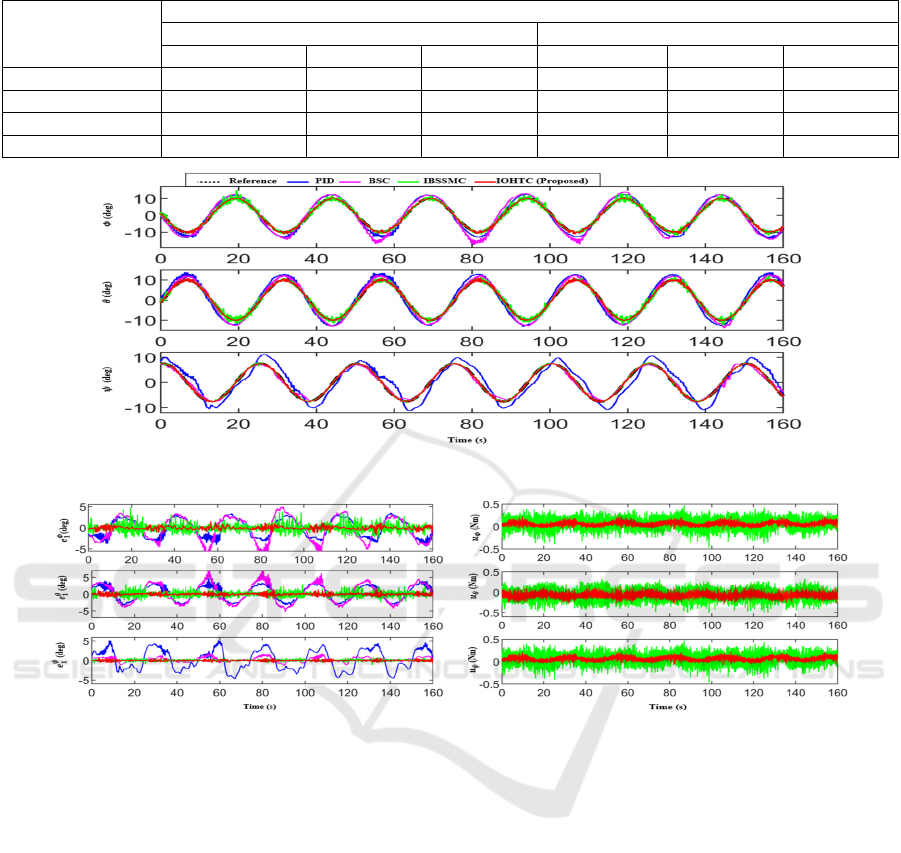
Table 2: ISE and IADU performances indices for attitude control.
Controller
Index
IADU ISE
𝛷 𝜃 𝜓 𝛷 𝜃 𝜓
PID - - - 0.818 0.835 1.252
BSC - - - 0.299 0.410 0.067
IBSSMC 1.125 1.383 1.111 0.103 0.068 0.006
PROPOSED 0.449 0.884 0.260 0.024 0.014 0.005
Figure 3: Plots of the Attitude states.
Figure 4: Plots of the tracking errors for the attitude states and the control signals.
N. Wang, Q. D. (2019). Hybrid finite-time trajectory
tracking control of a quadrotor. ISA Transactions, 278-
286.
O. Mechali, J. I. (2021). Distributed leader-follower
formation control of quadrotors swarm subjected to
disturbances. IEEE International Conference on
Mechatronics and Automation (ICMA) (pp. 1442-
1447). Japan: IEEE.
O. Mechali, J. I. (2021). Finite-Time Attitude Control of
Uncertain Quadrotor Aircraft via Continuous Terminal
Sliding-Mode-Based Active Anti-Disturbance
Approach. IEEE International Conference on
Mechatronics and Automation (ICMA) (pp. 1170-
1175). Takamatsu, Japan: IEEE.
O. Mechali, L. X. (2022). Fixed-time nonlinear
homogeneous sliding mode approach for robust
tracking control of multirotor aircraft: Experimental
validation. Journal of the Franklin Institute, 1971-
2029.
S. Benmansour, D. F. (2023). Fuzzy Integral Sliding Mode
Control of a Hyperdynamic Golf Swing Robot.
International Conference on Electrical Engineering
and Control Applications.
S. G. Khan, S. B. (2019). Experimental validation of an
integral sliding mode-based LQG for the pitch control
of a UAV-mimicking platform. Advances in Electrical
and Electronics Engineering, 275-284.
S. Ullah, A. M. (2020). Robust integral sliding mode
control design for stability enhancement of under-
actuated quadcopter. International Journal of Control,
Automation and Systems, 1671-1678.
Xu, Q. (2017). Continuous integral terminal third-order
sliding mode motion control for piezoelectric
nanopositioning system. IEEE/ASME Transactions on
Mechatronics, 1828-1838.
Yu, M. Z. (1997). Terminal sliding mode control of MIMO
linear systems. IEEE Transactions on Circuits and
Systems I: Fundamental Theory and Applications,
1065-1070.
Z. Hou, P. L. (2020). Nonsingular terminal sliding mode
control for a quadrotor UAV with a total rotor failure.
Aerospace Science and Technology, 1-18.
Robust Finite-Time Control of a Multirotor System via an Improved Optimized Homogeneous Twisting Control: Design and Validation
331
