CryptonDL: Encrypted Image Classiﬁcation Using Deep Learning

Models

Adham Helbawy, Mahmoud Bahaa and Alia El Bolock

German International University, Cairo, Egypt

Keywords:

Datasets, Convolutional Neural Networks, Image Classiﬁcation, Homomorphic Encryption.

Abstract:

Deep Neural Networks (DNNs) have surpassed traditional machine learning algorithms due to their superior

performance in big data analysis in various applications. Fully homomorphic encryption (FHE) contributes to

machine learning classiﬁcation, as it supports homomorphic operations over encrypted data without decryp-

tion. In this paper, we propose a deep learning model, CryptonDL, that utilizes TenSEAL’s CKKS scheme

to encrypt three image datasets and then classify each encrypted image. This model ﬁrst trains the image

datasets without encryption using a PyTorch convolutional neural network model. Using the weights of the

convolutional neural network model in the encrypted convolutional neural network model, each image will be

encrypted and then only decrypted in the prediction results. TenSEAL implemented the same model, but this

model was optimized to achieve higher accuracy than TenSEAL’s original model. CryptonDL achieved an

encrypted image classiﬁcation accuracy of 98.32 percent and an F1 score of 0.9832 on the MNIST dataset, an

accuracy of 88 percent and an F1 score of 0.8811 on the Fashion MNIST, and an accuracy of 92 percent and

an F1 score of 0.9207 on the Kuzushiji MNIST. CryptonDL shows that encrypted image classiﬁcation could

be achieved with high accuracy without using pre-trained models.

1 INTRODUCTION

Image classiﬁcation is a widely researched area in

computer vision, with deep learning techniques show-

ing signiﬁcant improvements in accuracy compared to

traditional methods. However, encrypted image clas-

siﬁcation is a relatively new area of research aiming

to classify images while they are encrypted. The goal

is to preserve the image’s privacy while still allowing

for its useful information to be extracted. This is a

challenging task as traditional deep learning methods

rely on the ability to process pixel values, which are

not available in an encrypted image. Some encryp-

tion techniques, when utilized with machine learning

or deep learning, do not signiﬁcantly reduce the func-

tionality and usefulness of the data. These are Homo-

morphic/Paillier Crypto-system, Secure Multi-Party

Computation, Elliptic Curve Cryptography, and Func-

tional Encryption. Additionally, the majority of cur-

rent crypto-based approaches, including (Izabach

ene

et al., 2019), (Lou and Jiang, 2021), (Wang et al.,

2021), and (Jiang et al., 2018), use homomorphic

encryption (HE) to protect the data; however, these

proposed HE-based approaches only support predic-

tion over encrypted data using existing trained mod-

els rather than training a model over encrypted data.

This is because the computed results of HE are con-

ﬁdential to the server and hence cannot be used for

evaluation with the label during the back-propagation

phase. That is, the machine learning model should

be trained on the plaintext data, and then the trained

model can be applied over encrypted data to make the

prediction. This work aims to train a convolutional

neural network to classify encrypted images using ho-

momorphic encryption. In this paper, we propose the

CryptonDL model where a convolutional neural net-

work model is trained over encrypted images without

existing trained models.

2 BACKGROUND

This paper presents work at the intersection of ma-

chine learning and cryptography. In the following, all

the needed background knowledge is brieﬂy outlined.

2.1 Datasets Selection

1. MNIST Dataset (Deng, 2012). The MNIST

dataset is an acronym that stands for the Modi-

Helbawy, A., Bahaa, M. and El Bolock, A.

CryptonDL: Encrypted Image Classiﬁcation Using Deep Learning Models.

DOI: 10.5220/0012088000003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 367-374

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

367

ﬁed National Institute of Standards and Technol-

ogy dataset. It consists of a training set of 60,000

examples and a test set of 10,000 examples. Each

example is a small square 28×28 pixel grayscale

image of handwritten single digits between 0 and

2. Fashion MNIST Dataset (Xiao et al., 2017).

Fashion-MNIST is a dataset of Zalando’s article

images—consisting of a training set of 60,000 ex-

amples and a test set of 10,000 examples. Each

example is a 28x28 grayscale image, associated

with a label from 10 classes. We intend Fashion-

MNIST to serve as a direct drop-in replacement

for the original MNIST dataset for benchmarking

machine learning algorithms. It shares the same

image size and structure of training and testing

splits.

3. Kuzushiji MNIST Dataset (Clanuwat et al.,

2018). Kuzushiji-MNIST is a drop-in replace-

ment for the MNIST dataset (28x28 grayscale,

70,000 images, a training set of 60,000 examples

and a test set of 10,000 examples.), provided in

the original MNIST format as well as a NumPy

format. Since MNIST restricts us to 10 classes,

we chose one character to represent each of the

10 rows of Hiragana when creating Kuzushiji-

MNIST.

2.2 Homomorphic Encryption

Homomorphic encryption is a form of encryption

that permits users to perform computations on its en-

crypted data without ﬁrst decrypting it. These re-

sulting computations are left in an encrypted form

which, when decrypted, results in an identical output

to that produced had the operations been performed

on the unencrypted data. Homomorphic encryption

can be used for privacy-preserving outsourced storage

and computation. This allows data to be encrypted

and outsourced to commercial cloud environments for

processing, all while encrypted. For sensitive data,

such as health care information, homomorphic en-

cryption can be used to enable new services by re-

moving privacy barriers inhibiting data sharing or in-

creasing security to existing services.

2.3 Cheon, Kim, Kim and Song Scheme

(CKKS)

The CKKS scheme (Cheon et al., 2017) is a vari-

ant of the well-known fully homomorphic encryption

(FHE) scheme that is based on the LWE (Learning

With Errors) problem. It allows for arbitrary com-

putations to be performed on encrypted data using a

technique called ”approximate homomorphism.” The

CKKS scheme is designed to work with real num-

bers, making it suitable for various applications such

as machine learning, data analysis, and cryptography.

Moreover, in the CKKS scheme, the encryption pro-

cess uses a polynomial ring over a ﬁnite ﬁeld and a

speciﬁc set of parameters. The decryption process

uses a secret key and a set of ”noise” parameters to re-

construct the original plaintext. The scheme also uses

a technique called ”relinearization” to ensure that the

correct result is obtained from the computations on

the ciphertext.

3 RELATED WORK

Lots of previous approaches investigated applying ho-

momorphic encryption techniques to preserve the pri-

vacy of data while training and applying machine

learning and deep learning models.

3.1 Homomorphic Encryption and

Machine Learning

Researchers have proposed different approaches to

secure cloud-based artiﬁcial intelligence while pre-

serving privacy. Kristin E. Lauter(Wood et al., 2020)

used homomorphic encryption (HE) and machine

learning (ML) to encrypt client data before upload-

ing it to the cloud, Edward et al.(Chou et al., 2020)

developed a privacy-preserving approach, Alexan-

der Wood et al.(Wood et al., 2020) encrypted pa-

tients’ data in bioinformatics, Xiaoqiang Sun(Sun

et al., 2020) proposed a fully homomorphic encryp-

tion scheme, K Muhammad(Muhammad et al., 2018)

showed that one machine learning model could pro-

duce an encrypted output with the same key, Sang-

wook Kim(Kim et al., 2018) proposed a privacy-

preserving Naive Bayes classiﬁer model, and Yoshiko

Yasumura proposed a secure Nave Bayes classiﬁca-

tion protocol.

3.2 Homomorphic Encryption and

Deep Learning

Ehsan Hesamifard et al.(Hesamifard et al., 2019), Ma-

lika Izabach

ene et al.(Izabach

ene et al., 2019), Qian

Lou and Lei Jiang(Lou and Jiang, 2021), Yichuan

Wang et al., and Takumi Ishiyama et al.(Ishiyama

et al., 2020) have all proposed methods to improve

the classiﬁcation accuracy of CNN inference over ho-

momorphic encryption. Ehsan Hesamifard et al. used

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

368

deep neural network algorithms on the encrypted data

by taking advantage of Homomorphic Encryption

schemes and achieved efﬁcient, accurate, and scalable

privacy-preserving predictions. Malika Izabach

ene et

al. proposed an algorithm to classify encrypted ob-

jects by means of a fully encrypted neural network

with practically relevant timings and accuracy on a

face recognition application. Qian Lou and Lei Jiang

propose a homomorphic encryption-friendly, privacy-

preserving mobile neural network architecture called

HEMET. Yichuan Wang et al.(Wang et al., 2021)

combined deep learning with a homomorphic en-

cryption algorithm to design a deep learning network

model based on secure MPC to ensure better security

of users’ private data in AIoT.

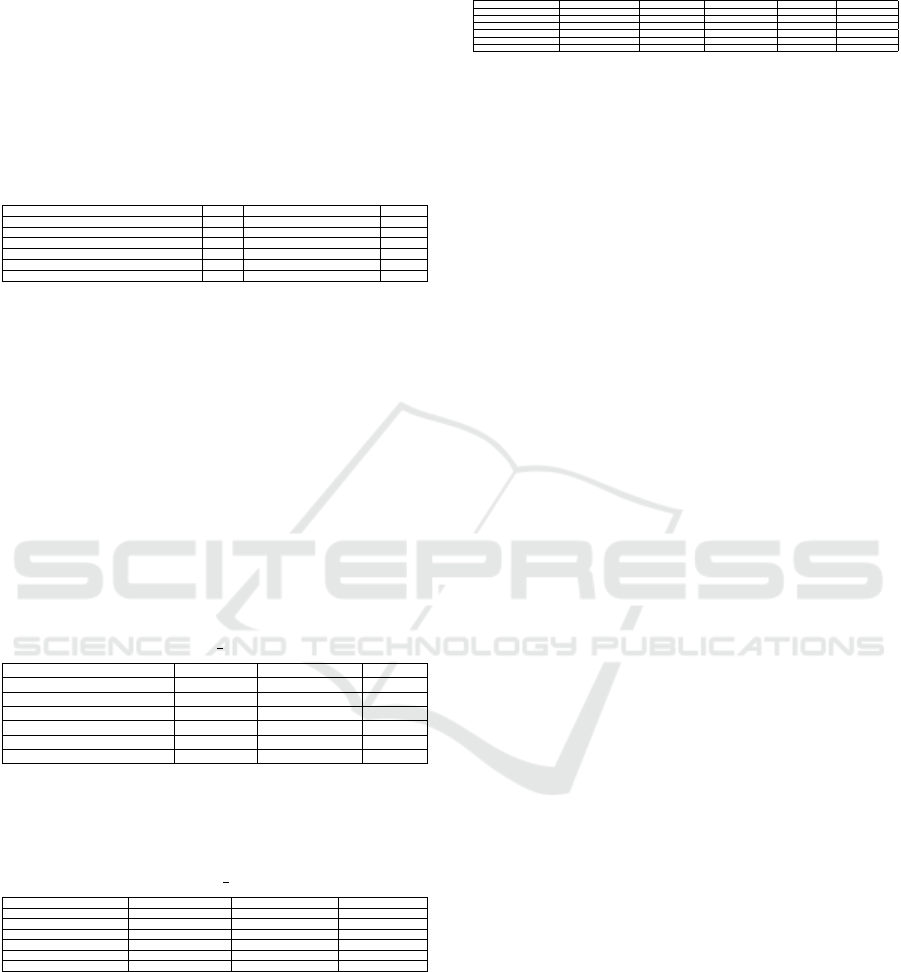
4 APPROACH OVERVIEW

As shown in ﬁgure 1, this is the whole pipeline for

the proposed model CryptonDL. The pipeline has two

parts. The ﬁrst part takes an image dataset, which is

then classiﬁed using a convolutional neural network

model either with 3 or with 4. Then the convolu-

tional neural network makes image predictions, and

the classiﬁcation accuracy is calculated with the pre-

dictions. The second part takes the weights and biases

of the ﬁrst convolutional neural network. It inputs

them to the encrypted convolutional neural network

to make the encrypted image predictions, which, with

the images still encrypted, will only decrypt the image

predictions to calculate the accuracy of the encrypted

convolutional neural network.

Figure 1: Pipeline of CryptonDL.

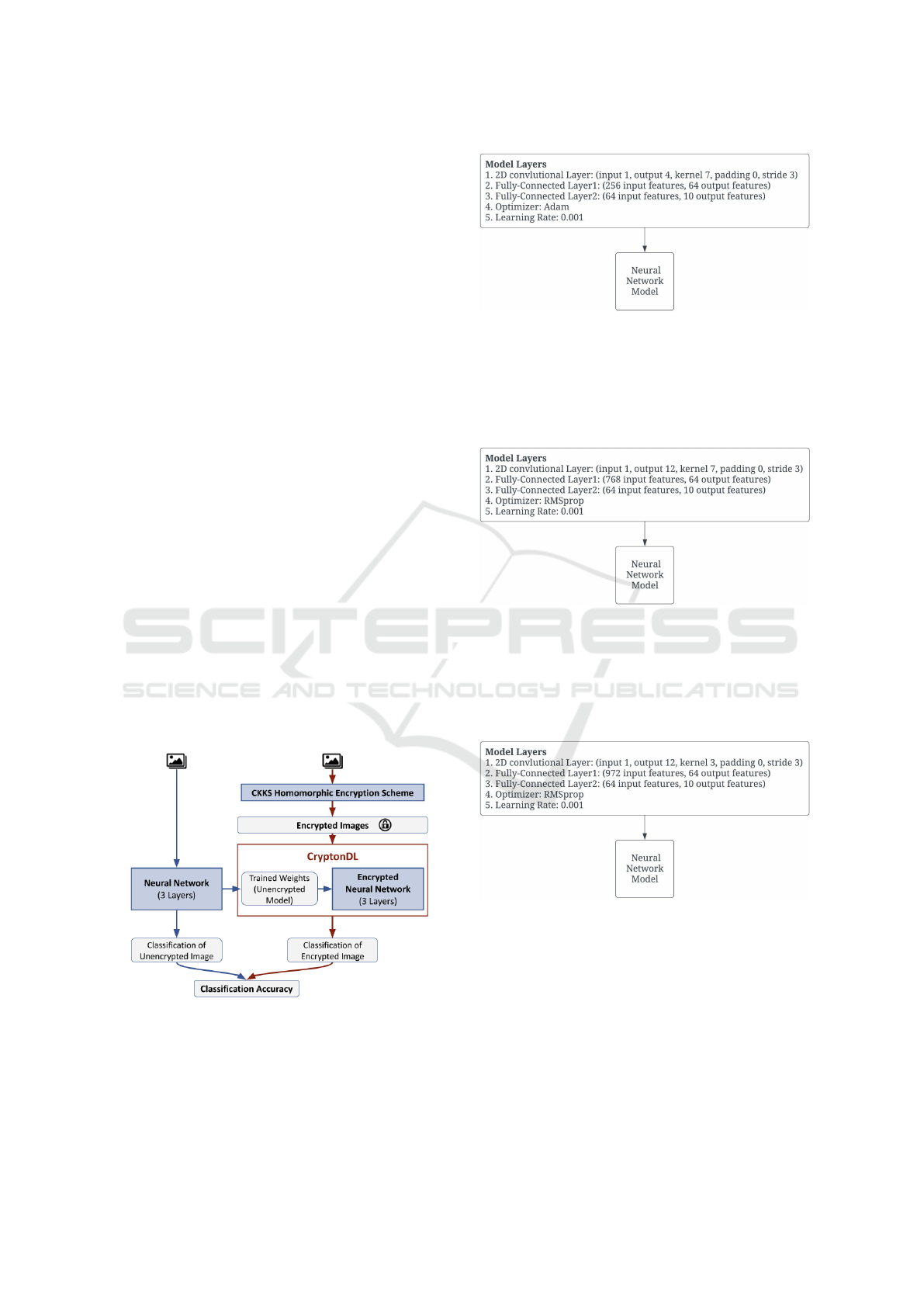
Figure 2 is the ﬁrst convolutional neural network

pipeline. This was used in TenSEAL’s original model

and was tested on three different image datasets to test

the accuracy of this model

Figure 2: TenSEAL.

Figure 3 is CryptonDL’s optimized convolutional

neural network pipeline. This second pipeline was

used in classifying the MNIST and the Kuzushiji

MNIST datasets which increased their accuracy and

f1 score compared to the ﬁrst pipeline.

Figure 3: CryptonDL1.

Figure 4 is CryptonDL’s optimized convolutional

neural network pipeline. This third pipeline was used

in classifying the Fashion MNIST dataset which in-

creased its accuracy and f1 score compared to the ﬁrst

pipeline and second pipeline.

Figure 4: CryptonDL2.

5 DEEP LEARNING MODELS

Table 1 shows the summary of all the convolu-

tional neural network inputs for the three datasets.

The TenSEAL-MNIST, TenSEAL-Fashion-MNIST

and the TenSEAL-Kuzushiji MNIST will follow

TenSEAL’s convolutional neural network pipeline.

The layer inputs are shown in ﬁgure 2 and they use 10

train epochs with optimizer Adam and learning rate of

CryptonDL: Encrypted Image Classiﬁcation Using Deep Learning Models

369

0.001. The CryptonDL-MNIST, CryptonDL-Fashion

MNIST are an optimized version of TenSEAL’s con-

volutional neural network which have different layer

inputs shown in ﬁgure 3 and they use 5 train epochs

with optimizer RMSprop and learning rate of 0.001.

Finally, the CryptonDL-Kuzushiji MNIST also use

the same training epochs, optimizer and learning rate

as the other two optimized convolutional neural net-

works but with different layer inputs as shown in ﬁg-

ure 4.

Table 1: DL Training Inputs.

2D convolution Layer Fully-connected layer1 Fully-connected layer2 Optimizer Train Epochs

TenSEAL-MNIST

Input Channels 1, Output Channels 4,

Kernel Size 7, Padding 0, Stride 3

Input Features 256, Output Features 64

Input Features 64, Output Features 10

corresponding to 10 classes of the MNIST database

Adam with Learning

Rate 0.001

CryptonDL-MNIST

Input Channels 1, Output Channels 12,

Kernel Size 7, Padding 0, Stride 3

Input Features 768, Output Features 64

Input Features 64, Output Features 10

corresponding to 10 classes of the MNIST database

RMSprop with

Learning Rate 0.001

TenSEAL-Fashion MNIST

Input Channels 1, Output Channels 4,

Kernel Size 7, Padding 0, Stride 3

Input Features 256, Output Features 64

Input Features 64, Output Features 10

corresponding to 10 classes of the

Fashion MNIST database

Adam with Learning

Rate 0.001

CryptonDL-Fashion MNIST

Input Channels 1, Output Channels 12,

Kernel Size 3, Padding 0, Stride 3

Input Features 972, Output Features 64

Input Features 64, Output Features 10

corresponding to 10 classes of the

Fashion MNIST database

RMSprop with

Learning Rate 0.001

TenSEAL-Kuzushiji MNIST

Input Channels 1, Output Channels 4,

Kernel Size 7, Padding 0, Stride 3

Input Features 256, Output Features 64

Input Features 64, Output Features 10

corresponding to 10 classes of the

Kuzushiji MNIST database

Adam with Learning

Rate 0.001

CryptonDL-Kuzushiji MNIST

Input Channels 1, Output Channels 12,

Kernel Size 7, Padding 0, Stride 3

Input Features 768, Output Features 64

Input Features 64, Output Features 10

corresponding to 10 classes of the

Kuzushiji MNIST database

RMSprop with

Learning Rate 0.001

5.1 TenSEAL-MNIST Model

5.1.1 Convolutional Neural Network

As shown in 2. First, train a convolutional neural net-

work model with the following description. 2D con-

volution layer (Input Channels 1, Output Channels

4, Kernel Size 7, Padding 0, Stride 3). Then comes

Fully-connected layer 1 (256 input features, 64 out-

put features). Fully-connected layer 2 (Input Features

64, Output Features 10 corresponding to 10 classes of

the MNIST database). There are (25664) + (6410) =

17.024 weights parameter and 64 + 10 = 74 biases pa-

rameter that can be optimized in the training process.

Afterward, using the square function as the activation

function, Train the model with the criterion CrossEn-

tropyLoss and the optimizer Adam at a learning rate

of 0.001 and 10 epochs.

5.1.2 Testing Phase

Testing the model using the Full 10000 Test images

with a batch size of 64 and giving a Test Accuracy of

97 percent and F1 Score of 0.977900.

5.2 CryptonDL1-MNIST Model

5.2.1 Convolutional Neural Network

As shown in Fig. 3. First, train a convolutional neu-

ral network model with the following description. 2D

convolution layer (Input Channels 1, Output Channels

12, Kernel Size 7, Padding 0, Stride 3). Then comes

Fully-connected layer 1 (768 input features, 64 output

features). Fully-connected layer 2 (Input Features 64,

Output Features 10 corresponding to 10 classes of the

MNIST database). There are (768 × 64) + (64 × 10) =

49.792 weights parameter and 64 + 10 = 74 biases pa-

rameter that can be optimized in the training process.

Afterward, using the square function as the activation

function, Train the model with the criterion CrossEn-

tropyLoss and the optimizer Adam at a learning rate

of 0.001 and 5 epochs.

5.2.2 Testing Phase

Testing the model using the Full 10000 Test images

with a batch size of 64 and giving a Test Accuracy of

98 percent and F1 Score of 0.983300.

5.3 TenSEAL-Fashion MNIST Model

5.3.1 Convolutional Neural Network

As shown in 2. First, train a convolutional neural net-

work model with the following description. 2D con-

volution layer (Input Channels 1, Output Channels

4, Kernel Size 7, Padding 0, Stride 3). Then comes

Fully-connected layer 1 (256 input features, 64 out-

put features). Fully-connected layer 2 (Input Features

64, Output Features 10 corresponding to 10 classes of

the MNIST database). There are (256 × 64) + (64 ×

10) = 17.024 weights parameter and 64 + 10 = 74 bi-

ases parameter that can be optimized in the training

process. Afterward, using the square function as the

activation function, Train the model with the criterion

CrossEntropyLoss and the optimizer Adam at a learn-

ing rate of 0.001 and 10 epochs.

5.3.2 Testing Phase

Testing the model using the Full 10000 Test images

with a batch size of 64 and giving a Test Accuracy of

86 percent and F1 Score of 0.869000.

5.4 CryptonDL2-Fashion MNIST

Model

5.4.1 Convolutional Neural Network

As shown in 4. First, train a convolutional neural

network model with the following description. 2D

convolution layer (Input Channels 1, Output Channels

12, Kernel Size 3, Padding 0, Stride 3). Then comes

Fully-connected layer 1 (972 input features, 64 output

features).Fully-connected layer 2 (Input Features 64,

Output Features 10 corresponding to 10 classes of the

MNIST database). There are (972 × 64) + (64 × 10) =

62.848 weights parameter and 64 + 10 = 74 biases pa-

rameter that can be optimized in the training process.

Afterward, using the square function as the activation

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

370

function, Train the model with the criterion CrossEn-

tropyLoss and the optimizer Adam at a learning rate

of 0.001 and 5 epochs.

5.4.2 Testing Phase

Testing the model using the Full 10000 Test images

with a batch size of 64 and giving a Test Accuracy of

88 percent and F1 Score of 0.880800.

5.5 TenSEAL-Kuzushiji MNIST Model

5.5.1 Convolutional Neural Network

As shown in 2. First, train a convolutional neural net-

work model with the following description. 2D con-

volution layer (Input Channels 1, Output Channels

4, Kernel Size 7, Padding 0, Stride 3). Then comes

Fully-connected layer 1 (256 input features, 64 out-

put features). Fully-connected layer 2 (Input Features

64, Output Features 10 corresponding to 10 classes of

the MNIST database). There are (256 × 64) + (64 ×

10) = 17.024 weights parameter and 64 + 10 = 74 bi-

ases parameter that can be optimized in the training

process. Afterward, using the square function as the

activation function, Train the model with the criterion

CrossEntropyLoss and the optimizer Adam at a learn-

ing rate of 0.001 and 10 epochs.

5.5.2 Testing Phase

Testing the model using the Full 10000 Test images

with a batch size of 64 and giving a Test Accuracy of

89 percent and F1 Score of 0.891100.

5.6 CryptonDL1-Kuzushiji MNIST

Model

5.6.1 Convolutional Neural Network

As shown in 3. First, train a convolutional neural

network model with the following description. 2D

convolution layer (Input Channels 1, Output Channels

12, Kernel Size 7, Padding 0, Stride 3). Then comes

Fully-connected layer 1 (768 input features, 64 output

features). Fully-connected layer 2 (Input Features 64,

Output Features 10 corresponding to 10 classes of the

MNIST database). There are (768 × 64) + (64 × 10) =

49.792 weights parameter and 64 + 10 = 74 biases pa-

rameter that can be optimized in the training process.

Afterward, using the square function as the activation

function, Train the model with the criterion CrossEn-

tropyLoss and the optimizer Adam at a learning rate

of 0.001 and 5 epochs.

5.6.2 Testing Phase

Testing the model using the Full 10000 Test images

with a batch size of 64 and giving a Test Accuracy of

91 percent and F1 Score of 0.919700.

6 ENCRYPTED DEEP LEARNING

MODELS

Figure 5 shows the pipeline of the encrypted deep-

learning model, and all of the next models use this

pipeline.

Figure 5: Encrypted convolutional neural network Pipeline.

6.1 TenSEAL Model

6.1.1 ENC-Convolutional Neural Network

As shown in 5. The process starts by initializing the

weights and biases for the three convolutional layers

in the network, using weights and biases from the pre-

vious model’s Conv1 layer and FC1 and FC2 layers.

The forward function is then called to process the in-

put data. The ﬁrst step in this function is to convert

all input data items into CKKS vectors, a format that

allows for efﬁcient computations on encrypted data.

Then, the function squares each channel in each data

item and combines them using a matrix multiplication

operation, creating a single output data item. Finally,

all three layers are combined using a simple addition

operation to produce the ﬁnal output value for this ex-

ample. The ﬁnal step in this process is the call() func-

tion, which executes the forward() function on each

input data point.

6.1.2 Encryption Parameters

Set the global scale of the context to 2, which means

that every number in the context will be doubled. It

is necessary because when encrypting or decrypting

data, you need to keep track of both the original value

and its encrypted counterpart. Then Constructing the

TenSEAL context: The ﬁrst argument speciﬁes the

scheme type as CKKS and sets the polynomial mod-

ulus degree to 8192, which determines the size of the

plaintext and ciphertext data that can be encrypted and

decrypted using the context. The ”coefﬁcient mod bit

CryptonDL: Encrypted Image Classiﬁcation Using Deep Learning Models

371

sizes” argument is a list of integers, with the ﬁrst and

last elements being 31 and all others equal to the bit

scale. The context object will store the encryption pa-

rameters for the CKKS scheme. The next step is to

set the global scale for the TenSEAL context. This

scale controls how precisely the fractional part of the

data will be encrypted or decrypted. Finally, the Ga-

lois keys function generates keys required to perform

ciphertext rotations. These keys allow the library to

perform operations on the encrypted data without de-

crypting it ﬁrst.

6.1.3 Testing Phase

Start by creating an encoding matrix using the

ts.im2col encoding. This encoding process protects

against unauthorized access to the data set. It al-

lows us to compare different models on different

datasets without worrying about differences in how

those datasets are represented in memory. This ma-

trix will be used to encode each data set column into

a different format and then create the encoding ma-

trix; it iterates through each column of data in turn and

encodes it using the ts.im2col encoding. Then the en-

crypted model inputs the encoded and encrypted val-

ues to perform the encrypted evaluation and then de-

crypts the results after the evaluation is ﬁnished. This

is performed on the 10,000 test images with a batch

size of one.

6.1.4 ENC-Convolutional Neural Network

As shown in 5. The process starts by initializing the

weights and biases for the three convolutional layers

in the network, using weights and biases from the pre-

vious model’s Conv1 layer and FC1 and FC2 layers.

The forward function is then called to process the in-

put data. The ﬁrst step in this function is to convert

all input data items into CKKS vectors, a format that

allows for efﬁcient computations on encrypted data.

Then, the function squares each channel in each data

item and combines them using a matrix multiplication

operation, creating a single output data item. Finally,

all three layers are combined using a simple addition

operation to produce the ﬁnal output value for this ex-

ample. The ﬁnal step in this process is the call() func-

tion, which executes the forward() function on each

input data point.

6.1.5 Encryption Parameters

Set the global scale of the context to 2, which means

that every number in the context will be doubled. It

is necessary because when encrypting or decrypting

data, you need to keep track of both the original value

and its encrypted counterpart. Then Constructing the

TenSEAL context: The ﬁrst argument speciﬁes the

scheme type as CKKS and sets the polynomial mod-

ulus degree to 8192, which determines the size of the

plaintext and ciphertext data that can be encrypted and

decrypted using the context. The ”coefﬁcient mod bit

sizes” argument is a list of integers, with the ﬁrst and

last elements being 31 and all others equal to the bit

scale. The context object will store the encryption pa-

rameters for the CKKS scheme. The next step is to

set the global scale for the TenSEAL context. This

scale controls how precisely the fractional part of the

data will be encrypted or decrypted. Finally, the Ga-

lois keys function generates keys required to perform

ciphertext rotations. These keys allow the library to

perform operations on the encrypted data without de-

crypting it ﬁrst.

6.1.6 Testing Phase

Start by creating an encoding matrix using the

ts.im2col encoding. This encoding process protects

against unauthorized access to the data set. It al-

lows us to compare different models on different

datasets without worrying about differences in how

those datasets are represented in memory. This ma-

trix will be used to encode each data set column into

a different format and then create the encoding ma-

trix; it iterates through each column of data in turn and

encodes it using the ts.im2col encoding. Then the en-

crypted model inputs the encoded and encrypted val-

ues to perform the encrypted evaluation and then de-

crypts the results after the evaluation is ﬁnished. This

is performed on the 10,000 test images with a batch

size of one.

7 CryptonDL EVALUATION

In this chapter, the performance of CryptonDL will be

evaluated and discussed. This will include a compar-

ison of the model’s performance with other state-of-

the-art models and with TenSEAL’s original model,

as well as a discussion of any factors that may have

affected the model’s performance

7.1 CryptonDL Against Other

State-of-the-Art Models

As shown in the table 2, most models have a high

prediction accuracy of the MNIST dataset the pro-

posed model CryptonDL has higher accuracy com-

pared to the other papers. These papers implemented

a different approach to preserving privacy. Their ap-

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

372

proach was using the same encryption type and the

tests were done on the same image dataset but the im-

ages were encrypted from the beginning of the model.

Although this approach would preserve the privacy of

the dataset which would be classiﬁed, the computa-

tional complexity is much bigger and the accuracy is

not always better than CryptonDL. This makes Cryp-

tonDL much greater than most other models at classi-

fying encrypted images.

Table 2: Results vs Other Papers.

Paper Title Dataset Encryption Type Accuracy

CryptonDL[1] MNIST Homomorphic Encryption(CKKS) 98.32%

K Muhammad et al.(Muhammad et al., 2018) MNIST Homomorphic Encryption(PHE) 92.92%

Xiaoqian Jiang et al.(Jiang et al., 2018) MNIST Homomorphic Encryption(CKKS) 98.1%

Anamaria Vizitiu et al.(Vizitiu et al., 2019) MNIST Homomorphic Encryption(FHE) 98.3%

Runhua Xu et al.(Xu et al., 2019) MNIST Homomorphic Encryption 92.5%

Ehsan Hesamifard et al.(Hesamifard et al., 2017) MNIST Homomorphic Encryption 99.25%

7.2 Results Comparison

As shown in the three tables below, the results of our

CryptonDL model are better than TenSEAL’s original

model. The testing was done using three image

datasets MNIST, Fashion MNIST and Kuzushiji

MNIST, and the results were that the accuracy and

f1 score of CryptonDL model on each of the three

datasets outperformed TenSEAL’s original model.

Table 3 shows all the deep learning models’,

the three original models of TenSEAL and the three

CryptonDL optimized models test accuracy. Table

Table 3: DL MODELS.

Test F1 Score Test Accuracy Test Time

TenSEAL-MNIST 0.977900 97% (9779/10000) 869 ms

CryptonDL-MNIST 0.983300 98% (9833/10000) 856 ms

TenSEAL-Fashion MNIST 0.869000 86% (8690/10000) 841 ms

CryptonDL-Fashion MNIST 0.880800 88% (8808/10000) 1.14 s

TenSEAL-Kuzushiji MNIST 0.891100 89% (8911/10000) 7.66 s

CryptonDL-Kuzushiji MNIST 0.919700 91% (9197/10000) 7.71 s

4 shows all the encrypted deep learning models’,

the three original models of TenSEAL and the three

CryptonDL optimized models test accuracy.

Table 4: ENC MODELS.

Encrypted Test F1 Score Encrypted Test Accuracy Encrypted Test Time

TenSEAL-MNIST 0.977400 97% (9744/10000) 2h 51min 43s

CryptonDL-MNIST 0.983200 98% (9832/10000) 5h 53min 8s

TenSEAL-Fashion MNIST 0.869900 86% (8699/10000) 3h 12min

CryptonDL-Fashion MNIST 0.881100 88% (8811/10000) 6h 52min 7s

TenSEAL-Kuzushiji MNIST 0.889900 88% (8899/10000) 2h 52min 4s

CryptonDL-Kuzushiji MNIST 0.920700 92% (9207/10000) 5h 54min 12s

Table 5 shows the accuracy of the deep learning

models and the encrypted deep learning models to-

gether. As shown below, the accuracy of CryptonDL’s

optimized models is higher than TenSEAL’s original

model.

Table 5: TenSEAL’s models against the proposed optimized

models.

Unencrypted Test Accuracy Unencrypted F1 Score Encrypted Test Accuracy Encrypted F1 Score Encrypted Test Time

TenSEAL-MNIST 97% (9779/10000) 0.977900 97% (9744/10000) 0.977400 2h 51min 43s

CryptonDL-MNIST 98% (9833/10000) 0.983300 98% (9832/10000) 0.983200 5h 53min 8s

TenSEAL-Fashion MNIST 86% (8690/10000) 0.869000 86% (8699/10000) 0.869900 3h 12min

CryptonDL-Fashion MNIST 88% (8808/10000) 0.880800 88% (8811/10000) 0.881100 6h 52min 7s

TenSEAL-Kuzushiji MNIST 89% (8911/10000) 0.891100 88% (8899/10000) 0.889900 2h 52min 4s

CryptonDL-Kuzushiji MNIST 91% (9197/10000) 0.919700 92% (9207/10000) 0.920700 5h 54min 12s

7.3 Discussion

CryptonDL ﬁnal MNIST, Fashion MNIST, and

Kuzushiji MNIST models, which used the optimized

convolutional neural network 3 or 4 and encrypted

convolutional neural network 5 had higher image

classiﬁcation accuracy and encrypted image classiﬁ-

cation as shown in table 5. Increasing the output and

kernel sizes and changing the optimizer from Adam to

RMSprop enabled the convolutional neural network

to learn more complex features in the images, which

were clearly shown in the Kuzushiji MNIST increase

in encrypted accuracy from 88 percent to 92 percent.

Furthermore, the accuracy of CryptonDL, when used

with the MNIST dataset in 2, achieved higher image

classiﬁcation accuracy than most of the other mod-

els, as all the other models use an existing pre-trained

model. Using pre-trained models is not always bene-

ﬁcial, as they are typically trained on a large dataset,

but the data may not be representative of the speciﬁc

problem or domain to which the model is being ap-

plied to. This can lead to poor performance when the

model is used on new data. Also, pre-trained mod-

els are often complex and challenging to understand,

making it hard to determine how the model is making

its predictions. This can make it difﬁcult to identify

errors or biases in the model.

8 CONCLUSION

In the domain of computer vision, the classiﬁcation of

images is a highly researched topic, with deep learn-

ing algorithms signiﬁcantly outperforming more con-

ventional approaches in terms of accuracy. The goal

of the relatively new ﬁeld of study known as ”en-

crypted image classiﬁcation” is to categorize images

even while they are encrypted. Most approaches used

homomorphic encryption to tackle this goal; how-

ever, most used existing trained models to achieve

encrypted image classiﬁcation. In this paper, the

proposed model CryptonDL achieved encrypted im-

age classiﬁcation without the use of existing trained

models. The model’s performance evaluation against

other models shows that CryptonDL achieves high ac-

curacy with less computational complexity than most

other models.

CryptonDL: Encrypted Image Classiﬁcation Using Deep Learning Models

373

9 FUTURE WORK

9.1 Datasets Scalability

Exploring the model’s capacity to handle bigger

datasets without performance problems is one direc-

tion for the future. Techniques like parallel process-

ing, distributed computing, and effective data storage

and retrieval methods can be used to accomplish this.

9.2 Convolutional Neural Network

Scalability

Prediction accuracy can be improved by altering the

convolutional neural network model’s design or pa-

rameters. The convolutional neural network model

can also be modiﬁed to handle datasets other than im-

age datasets, such as audio and text datasets, by alter-

ing the architecture or preprocessing approaches.

REFERENCES

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-

momorphic encryption for arithmetic of approximate

numbers. In Takagi, T. and Peyrin, T., editors, Ad-

vances in Cryptology – ASIACRYPT 2017, pages 409–

437, Cham. Springer International Publishing.

Chou, E. J., Gururajan, A., Laine, K., Goel, N. K., Bertiger,

A., and Stokes, J. W. (2020). Privacy-preserving

phishing web page classiﬁcation via fully homomor-

phic encryption. In ICASSP 2020 - 2020 IEEE Inter-

national Conference on Acoustics, Speech and Signal

Processing (ICASSP), pages 2792–2796.

Clanuwat, T., Bober-Irizar, M., Kitamoto, A., Lamb, A.,

Yamamoto, K., and Ha, D. (2018). Deep learning for

classical japanese literature.

Deng, L. (2012). The mnist database of handwritten digit

images for machine learning research. IEEE Signal

Processing Magazine, 29(6):141–142.

Hesamifard, E., Takabi, H., and Ghasemi, M. (2017). Cryp-

todl: Deep neural networks over encrypted data.

Hesamifard, E., Takabi, H., and Ghasemi, M. (2019). Deep

neural networks classiﬁcation over encrypted data. In

Proceedings of the Ninth ACM Conference on Data

and Application Security and Privacy, CODASPY

’19, page 97–108, New York, NY, USA. Association

for Computing Machinery.

Ishiyama, T., Suzuki, T., and Yamana, H. (2020). Highly

accurate cnn inference using approximate activation

functions over homomorphic encryption.

Izabach

ene, M., Sirdey, R., and Zuber, M. (2019). Prac-

tical fully homomorphic encryption for fully masked

neural networks. In Mu, Y., Deng, R. H., and Huang,

X., editors, Cryptology and Network Security, pages

24–36, Cham. Springer International Publishing.

Jiang, X., Kim, M., Lauter, K., and Song, Y. (2018). Se-

cure outsourced matrix computation and application

to neural networks. In Proceedings of the 2018 ACM

SIGSAC Conference on Computer and Communica-

tions Security, CCS ’18, page 1209–1222, New York,

NY, USA. Association for Computing Machinery.

Kim, S., Omori, M., Hayashi, T., Omori, T., Wang, L., and

Ozawa, S. (2018). Privacy-Preserving Naive Bayes

Classiﬁcation Using Fully Homomorphic Encryption:

25th International Conference, ICONIP 2018, Siem

Reap, Cambodia, December 13-16, 2018, Proceed-

ings, Part IV, pages 349–358.

Lou, Q. and Jiang, L. (2021). HEMET: A homomorphic-

encryption-friendly privacy-preserving mobile neural

network architecture. CoRR, abs/2106.00038.

Muhammad, K., Sugeng, K. A., and Murﬁ, H. (2018).

Machine learning with partially homomorphic en-

crypted data. Journal of Physics: Conference Series,

1108(1):012112.

Sun, X., Zhang, P., Liu, J. K., Yu, J., and Xie, W. (2020).

Private machine learning classiﬁcation based on fully

homomorphic encryption. IEEE Transactions on

Emerging Topics in Computing, 8(2):352–364.

Vizitiu, A., Nit¸

a, C. I., Puiu, A., Suciu, C., and Itu, L. M.

(2019). Towards privacy-preserving deep learning

based medical imaging applications. In 2019 IEEE

International Symposium on Medical Measurements

and Applications (MeMeA), pages 1–6.

Wang, Y., Liang, X., Hei, X., Ji, W., and Zhu, L. (2021).

Deep learning data privacy protection based on homo-

morphic encryption in aiot. Mobile Information Sys-

tems, 2021:1–11.

Wood, A., Najarian, K., and Kahrobaei, D. (2020). Homo-

morphic encryption for machine learning in medicine

and bioinformatics. 53(4).

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-

mnist: a novel image dataset for benchmarking ma-

chine learning algorithms.

Xu, R., Joshi, J. B. D., and Li, C. (2019). Cryptonn:

Training neural networks over encrypted data. CoRR,

abs/1904.07303.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

374