AIM-RL: A New Framework Supporting Reinforcement Learning

Experiments

Ionut¸-Cristian Pistol

and Andrei Arusoaie

Department of Computer Science, Alexandru Ioan Cuza University, Ias¸i, Romania

Keywords:

Reinforcement Learning, Machine Learning Framework, State-Based Models.

Abstract:

This paper describes a new framework developed to facilitate implementing new problems and associated mod-

els and use reinforcement learning (RL) to perform experiments by employing these models to ﬁnd solutions

for those problems. This framework is designed as being as transparent and ﬂexible as possible, optimising

and streamlining the RL core implementation and allowing users to describe problems, provide models and

customise the execution. In order to show how AIM-RL can help with the implementation and testing of new

models we selected three classic problems: 8-puzzle, Frozen Lake and Mountain Car. The objective results of

these experiments, as well as some subjective observations, are included in the latter part of this paper. Con-

siderations are made with regards to using these frameworks both as didactic support as well as tools adding

RL support to new systems.

1 INTRODUCTION

A very popular open-source framework built to de-

velop, test and showcase Reinforcement Learning

(RL) capabilities is Gym/Gymnasium (Brockman

et al., 2016). Studies have shown that RL within

Gym/Gymnasium can be very helpful in both solv-

ing and testing solutions for various AI problems (He

et al., 2021) and (Yu et al., 2020), as well as bench-

marking RL based solutions such as continuous con-

trol games (Duan et al., 2016) or new policy control

methods (Schulman et al., 2017).

The potential of RL is enhanced by the ability

to work both as model-free (Chen et al., 2019) and

(Yarats et al., 2021) as well as allowing users to em-

ploy and test various models to boost problem-solving

tasks (Moerland et al., 2023) and (Kaiser et al., 2019).

Due to its ﬂexibility and power, RL has been proven

useful also in education (Nelson and Hoover, 2020),

(Lai et al., 2020) and (Paduraru. et al., 2022).

As part of a larger system being built to describe,

test and employ various model based solutions for AI

problems, a need was identiﬁed for an alternative RL

framework adapted to a more ﬂexible and involved

approach as opposed to the most prominent solution

available, Gym/Gymnasium. This approach should

offer our framework advantages in streamlining ap-

https://orcid.org/0000-0002-3744-8656

https://orcid.org/0000-0002-2789-6009

plying RL to new problems and varied models as well

as being a platform to support students building and

testing RL solutions.

Contributions. The main contribution of this pa-

per is the introduction of a novel framework that

simpliﬁes the implementation of new AI problems

and associated models, using reinforcement learning

to ﬁnd solutions for those problems through experi-

ments. The framework is designed to be as transpar-

ent and ﬂexible as possible, streamlining the core im-

plementation of RL. We demonstrate the usefulness of

this framework by modeling several classic problems,

highlighting its ease of use and potential applications.

Paper Organisation. Section 2 brieﬂy describes

the challenges to adding Reinforcement Learning

support to solving AI problems. Section 3 presents

our framework and three example toy problems and

corresponding models within our framework. Sec-

tion 4 includes some experimental results, and we

conclude in Section 5.

2 RL AND GYMNASIUM

2.1 Reinforcement Learning

Reinforcement Learning (RL) is a generalisation of

Q-Learning (Watkins, 1989) introduced as a method

of combining the older “trial-and-error” learning as

412

Pistol, I. and Arusoaie, A.

AIM-RL: A New Framework Supporting Reinforcement Learning Experiments.

DOI: 10.5220/0012091100003538

In Proceedings of the 18th International Conference on Software Technologies (ICSOFT 2023), pages 412-419

ISBN: 978-989-758-665-1; ISSN: 2184-2833

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

well as delayed and probabilistic learning with the

training data independence provided by Monte Carlo

algorithms. The basic idea is that an agent explores

a state-based problem space initially at random then

guided by rewards provided according to a model

(usually a heuristic). The reward associated with each

step adjusts the score associated with the original state

and the step required to reach the current state in a ma-

trix of associations called a Q-table. This exploration,

repeated in enough epochs (from the initial state up to

a goal/fail state) should produce a Q-table which will

guide the agent so that it chooses the better rewarded

action, to a shorter path to the goal.

2.2 Gymnasium Approach

According to its authors (Brockman et al., 2016), the

Gym/Gymnasium framework was developed follow-

ing the principles:

• Environments, not agents: Separation of the prob-

lem environment, deﬁned as everything particular

to a speciﬁc problem, from the agent itself.

• Emphasise sample complexity, not just ﬁnal per-

formance: Metrics provided to measure both ﬁnal

performance as well as performance at each epoch

and even each decision.

• Encourage peer review, not competition: Allow-

ing users to easily contribute their own ”agents”

(models) to the framework and compare them

with similar contributions.

• Strict versioning for environments: Each environ-

ment is associated with a version which would al-

low only compatible agents to be used in it.

• Monitoring by default: keeping a record of all ac-

tions taken while running an agent in an environ-

ment. Since it’s initial release, Gym/Gymnasium

has emerged as the most prominent open source

environment used by RL researchers and students,

with over 5000 references in scientiﬁc papers.

3 USING AIM-RL TO

IMPLEMENT EXPERIMENTS

In this section, we describe in more detail the AIM-

RL framework, and we illustrate its ﬂexibility by

modelling several problems within this framework.

We aim to show that our approach allows users to eas-

ily customise and run their RL experiments.

3.1 The AIM-RL Design Principles

Developing AIM-RL we considered the main bene-

ﬁts of RL as being its ﬂexibility provided both by

training data independence and the ability to employ a

great variety of models to solve a wide range of prob-

lems. Our goal is to provide a framework suitable for

both students to learn and test, and for researchers to

quickly experiment with new problems and models.

Considering this, we viewed transparency as the

main objective, by allowing users full visibility and

control over all aspects of a RL environment, and ﬂex-

ibility with regards to what types of models can be

employed to solve AI problems. Both complex mod-

els and policy functions as well as model-free solu-

tions can be implemented, minimising code redun-

dancy for various experiments. We also aimed to im-

prove reproductibility and analysis of the results by

making persistent proﬁles available for input parame-

ters, trained Q-tables and experimental results.

3.2 The AIM-RL Framework

AIM-RL was implemented as a Python package

which can be compiled and installed via pip. The

main objective of our package was to provide a para-

metric implementation for RL that can be easily in-

stantiated on various problems and models.

The main component is the qlearning module

which includes the following function:

def qlearning(instance,

no_of_epochs,

epsilon,

alpha,

discount,

decay,

limit,

verbose=False,

discount_optimisation=True):

# qlearning algorithm ...

return Q, results, solutions, rate

This method takes as input the description of a prob-

lem (i.e., a concrete implementation of the abstract

Model class described below in Section 3.2) and the

usual parameters for RL. When set, the verbose ﬂag

prints the current epoch and the number of steps until

a solution is reached. The discount_optimisation

ﬂag enables a linear decrease adjustment for the

discount parameter, and it is active by default. The

function returns a tuple (Q, results, solutions,

percentage). Q is the Q table as associations be-

tween a state, an action and a value. The solutions

The source code, together with the experiments and

a README.md ﬁle which contains installation and running

instructions is available here: https://tinyurl.com/4mhx83yd

AIM-RL: A New Framework Supporting Reinforcement Learning Experiments

413

dictionary assigns to each epoch the number of steps

until a solution is found or the epoch is ended oth-

erwise, while the results dictionary stores all the

transitions made in every epoch. The rate value rep-

resents the ratio between the number of successful

epochs (when a solution has been reached) over the

total number of epochs.

The user can either call the above method directly

with the required parameters or he can deﬁne them

in a JSON ﬁle. In that conﬁguration json ﬁle the user

can provide the following parameters:

• epsilon: the ε value(s) used to determine initial

random choice chance for the epsilon-greedy ap-

proach. If not needed, ε can be set to 0.

• decay: the decay factor value(s) for ε after each

epoch. Set the value to 1 if no decay is needed.

• alpha: the learning rate α value(s) used to weight

impact of new rewards on q-table updates.

• discount: the γ value(s) used to weight impact of

older updates of q-table values.

• epochs: the number of epochs tried for each run.

• limit: the maximum number of states visited in

each epoch. If reached, the current epoch ends.

• runs: the number of repeated runs for each con-

ﬁguration of parameters.

• model: a list of references to models used in the

experiments. For each model the user has to im-

plement at least a reward function which will be

used to update the Q-table.

• generate graph: either true or false depending

whether the user wants the framework to generate

the graphical representations of each experiment.

• instances: a list of instances for the problem. For

every item in the list, every conﬁguration is exe-

cuted. The format of an instance is up to the user

to establish and parse.

In the same conﬁguration ﬁle multiple values can

be provided, as a list, for the epsilon, decay, alpha,

discount, model and instances parameters. In this case

the framework will perform a run for all possible com-

bination of these values. This can facilitate easy ex-

perimentation, the results can then be compared using

the outputted graphs and csv ﬁle (cf. Section 4).

The qlearning module also provides a function

for generating graphs using the matplotlib library.

The graphical representation includes for each epoch

the length of the solution found or the number of steps

made up to the end of the current epoch. It also in-

cludes the ratio of successful epochs.

A brief description of the steps required by the

user in order to employ this framework for a new

problem and new models is given below. In order to

run a new RL experiment two abstract classes have to

be implemented: State and Model.

The State abstract class has four abstract

methods: get_possible_actions() which returns

the next possible actions from the current state;

is_final() which returns true if the current state is

ﬁnal; get_next(action) which, given an action, re-

turns the next state; and get_id(), which returns an

unique identiﬁer for the current state.

The Model abstract class has three abstract

methods: get_no_of_actions() which returns

the total number of actions for the current problem

instance; get_initial_state() which returns

the initial state for the current problem instance;

and get_reward(state, next_state, action)

which returns the reward for the transition state to

next_state via action.

As explained above, our framework provides the

entire machinery for Reinforcement Learning at an

abstract level. Users are expected to plug in some

concrete implementations for the State and Model

abstract classes. Then, the only thing left is to write a

main.py program that uses these concrete implemen-

tation according to users’ needs. Here is a template

that we suggest for main.py:

from qlearning import aimrl as QL

from puzzleModel import PuzzleModel

from puzzleState import PuzzleState

def run(folder, fname, instance, no_of_epochs,

epsilon, alpha, discount, decay, limit):

Q, results, solutions, percentage =

QL.qlearning(instance, no_of_epochs,

epsilon, alpha, discount, decay,

limit, True, True)

QL.save_as_graph(results, solutions,

percentage, no_of_epochs, folder, fname)

return Q, results, solutions, percentage

# Steps:

# 1) create instances of PuzzleState

# and PuzzleModel

# 2) initialise parameters or read them

# from the configuration file

# 3) describe at least one problem

# instance or read them

# from the configuration file

# 4) call run on the desired inputs

The QL.qlearning(...) call inside the run

function calls our Reinforcement Learning implemen-

tation. We use the same template for all the prob-

lems that we approach in this paper. While our pri-

mary goal was to develop a user-friendly framework

for experiments, we also considered performance. To

improve the efﬁciency, we utilised various Python

tricks such as substituting for loops for while loops

and using dictionaries instead of matrices, which was

ICSOFT 2023 - 18th International Conference on Software Technologies

414

also applied to the Q table. Additionally, we metic-

ulously streamlined the number of methods required

for users to implement, further optimising the frame-

work’s overall performance.

The components of the tuple returned by

QL.qlearning(...) can be used to generate a graph

using the QL.save_as_graph(...) function. An-

other output provided for all experiments ran using

AIM-RL is a csv ﬁle including values for

• graph: the random and unique generated name for

the graph representation of this run;

• model: the model used in this run;

• instance: the input used in this run;

• epsilon, decay, alpha and discount: RL parame-

ters used in this run;

• run: the run number identiﬁer;

• time: the run duration, in milliseconds;

• percentage: the fraction of epochs ending in a goal

state versus the total number of epochs;

• Q size: the size of the ﬁnal Q table (the total num-

ber of states explored in all epochs).

3.3 Implementation of 8-Puzzle

The 8-puzzle problem (Ratner and Warmuth, 1986)

and (Piltaver et al., 2012) is one of the classical

AI puzzles used to experiment new technologies and

methods developed. It consists of a 3 × 3 grid with

eight numbered tiles and one blank space. The ob-

jective is to rearrange the tiles from their initial state

into a target state by sliding them one at a time into

the blank space. A more general formulation of this

problem consists in working with an m × n grid.

Implementing this problem using our Reinforce-

ment Learning package presented in Section 3.2 is

straightforward. First, we create a PuzzleState

class which inherits the State abstract class. In

PuzzleState we use the ﬁelds m and n as dimensions

of our grid, and a m × n-sized list A of values from 0

to m · n − 1, where 0 stands for the blank space. The

abstract methods of the State class are implemented

as explained below:

• get_possible_actions() returns the next pos-

sible actions from the current state, that is, a list of

values in the set {up, down, left, right}, where

each action is encoded as an integer. Note that the

returned list does not always include all the ac-

tions, because certain boundary conditions need

to be fulﬁlled.

Examples for both graphs and csv ﬁles generated are

provided in Section 4.1.

• is_final() returns true if the list A is ordered,

no matter what is the position of the blank space.

• get_next(action) returns an instance of

PuzzleState which is the next state obtained

when sliding a tile as speciﬁed by action.

• the get_id() function returns a number which

uniquely identiﬁes each state.

The abstract methods of the Model class are imple-

mented inside the PuzzleInstance class as follows:

• get_initial_state() returns the initial state as

an instance of PuzzleState, where m, n, and A

are provided by the user.

• get_no_of_actions() returns 4 because there is

a total of | {up, down, left, right} | actions.

• get_reward(state, next_state, action)

determines the rewards to be used to update the Q ta-

ble for the action applied to state which produces

next_state. Two different versions were tried here,

without changing any other details about the imple-

mentation. One implemented a basic model version

(no reward except for the goal state which rewards

100). The second uses the manhattan distance as re-

ward, except for the goal state which rewards 100.

Some details about the results are given in Section 4.

3.4 Implementation of Frozen Lake

The Frozen Lake problem (Brockman et al., 2016) is

a simple grid-world game where the agent has to nav-

igate a frozen lake represented as a two-dimensional

grid starting from an initial tile with the goal of reach-

ing a destination tile. Some tiles are thin ice (holes in

the overall ice cover) and when stepped one casues the

failure of the search. The player can only move one

tile at a time with no diagonal movement allowed.

The Frozen Lake state is an implementation of the

State abstract class. We use m and n as grid dimen-

sions, and we represent the grid itself as a m×n-sized

list A of labels in the set { ’S’, ’F’, ’H’, ’G’ }, where:

• ’S’ - stands for the start position;

• ’G’ - stands for the goal position;

• ’F’ - represents a frozen tile; and

• ’H’ - represents a hole (thin ice).

In addition, we also keep a poz ﬁeld which holds the

current position of the player in A. The abstract meth-

ods of the State class are implemented as below:

• get_possible_actions() returns the next pos-

sible actions of the player, that is, a list of values

in the set {up, down, left, right}, where each

action is encoded as an integer. The returned list

AIM-RL: A New Framework Supporting Reinforcement Learning Experiments

415

does not always include all the actions, because

certain boundary conditions need to be true.

• is_final() checks if the current state deter-

mines the end of the epoch and returns an integer

value. The possible values returned are 0 for fail

(the current state is not ﬁnal), 1 for success (a goal

has been reached) or greater than 1 for additional

end states. An additional end state is determined

when stepping on a hole in the ice (H tile).

• get_next(action) returns an instance of

FLState which is the next state obtained when

player moves on a tile speciﬁed by action.

• the get_id() function returns poz which

uniquely identiﬁes each state.

The abstract methods of the Model class are

implemented inside the FrozenLakeModel class.

The get_initial_state() returns the initial state

as an instance of FrozenLakeState, where m, n,

A are user provided. The get_no_of_actions()

returns 4 because there are only four actions. The

get_reward(state, next_state, action) was

tried in two versions, one model-free (maxReward for

goal, 0 otherwise), and one a model using the reward

heuristic get reward(state, next state, action):











mR, if isFinal(next state) = 1

−100, if isFinal(next state) >1

poz(state) − goal, otherwise.

(1)

The results are discussed in Section 4.

3.5 Implementation of Mountain Car

Mountain Car (Sutton, 1995) and (Heidrich-Meisner

and Igel, 2008) is yet another classic problem often

used in reinforcement learning experiments. The ob-

jective is to train an agent to move a car from the

bottom of a valley up a steep hill to a speciﬁc goal

position located at the top of another hill. The car

is subject to gravity and friction, so it cannot simply

drive up the hill. Instead, it must ﬁrst gain momentum

by moving back and forth in the valley, building up

enough speed to eventually make it up the hill to the

goal position. The agent must learn how to balance

the need to move back and forth to build up momen-

tum with the need to move up the hill towards the goal

position. This problem is challenging for RL agents

because of the sparse rewards and the long-term de-

pendencies between actions and rewards.

Unlike 8-Puzzle and Frozen Lake, this problem

has a completely different notion of state, and it is a

good example for illustrating how versatile our frame-

work is. A state in MountainState includes:

• spot- represents the position of the car on a curved

(sinusoidal) line, the initial spot value being -0.5;

• velocity - represents the velocity of the car (posi-

tive for movement to the right, negative for left),

the initial velocity being 0;

• force - the force with which the car accelerates;

• gravity - the gravitational acceleration;

• current step - the step in the current epoch.

The MountainState class implements the following:

• get_possible_actions() returns the next pos-

sible actions of the player, that is, a list of values

in the set {push_left, push_right, dont_push;

• get_next(action) returns an instance of

MountainState where the velocity is updated

according to the formula

v = v + (a − 1) ∗ f − cos(3 ∗spot) ∗ g (2)

and the spot is updated as spot = spot + v;

• the get_id() function returns a pair (spot, v)

which uniquely identiﬁes each state.

In MountainCarInstance two different rewards

were implemented: (1) a basic model version which

assigns -1 reward for each step if not reaching the goal

spot which rewards maxReward; and (2) a more com-

plicated reward heuristic get rewards(s, s’, a):











−(spot − 0.5 +v), if a = left

spot + v if a = dont push,

(spot − v − 1) otherwise.

(3)

The results are included in Section 4.

4 EXPERIMENTAL RESULTS

We performed a series of experiments for the three

implemented problems described previously. For

simplicity of explanation we used similar parameters

conﬁguration ﬁles for all three, which were:

{

"epsilon" : [1.0],

"decay": [0.9],

"alpha" : [0.1, 0.5, 0.9],

"discount" : [0.1, 0.5, 0.9],

"no_of_epochs" : 200,

"limit": 100000,

"runs" : 2,

"generate-graph" : true,

}

The model and instances parameters were speciﬁc

for each problem and are indicated below. Multiple

values were tested for both alpha and discount since

ICSOFT 2023 - 18th International Conference on Software Technologies

416

Table 1: Sample of the csv ﬁle for the 8-puzzle experiments.

graph model instance epsilon decay alpha discount run time percentage Qsize

fxttgdplljwpodu 0 [2, 5, 3, 1, 0, 6, 4, 7, 8] 1 0.9 0.5 0.9 1 60534.84 88.5 181431

vapbgsvﬁkmmcny 1 [2, 5, 3, 1, 0, 6, 4, 7, 8] 1 0.9 0.1 0.1 0 2363.86 100 63999

oglcuwowsaxikcg 0 [2, 7, 5, 0, 8, 4, 3, 1, 6] 1 0.9 0.5 0.5 1 72751.35 84 181431

wbqtvnpdmuezgur 1 [2, 7, 5, 0, 8, 4, 3, 1, 6] 1 0.9 0.1 0.1 1 180027.93 28 124819

njodxxsxttnwfae 0 [8, 6, 7, 2, 5, 4, 0, 3, 1] 1 0.9 0.5 0.9 1 73698.61 84.5 181431

eklikltolpownxu 1 [8, 6, 7, 2, 5, 4, 0, 3, 1] 1 0.9 0.1 0.5 1 166346.21 35 136110

these are the two most frequently adjusted parameters

in RL experiments. The results for each of the three

problems are brieﬂy discussed below. The examples

provided are not the extreme cases. Since the pur-

pose of this paper in not to evaluate certain models

or reward functions, they are provided just to indicate

potential beneﬁts to evaluating and adjusting the ex-

periment’s parameters and associated models.

4.1 8-Puzzle

For the classic 8-puzzle problem we ran a series of ex-

periments using the conﬁgurations described in Sec-

tion 3.3 with a limit of 100 000 steps for each epoch.

A sample of the generated csv ﬁle including the re-

sults for three instances (with short, medium and long

optimal solutions) are shown in Table 1. The com-

plete ﬁle is included in the archive provided

Even in the sample results you can easily make

some relevant observations: the ﬁrst model (model 0)

works reasonably well for all instances and is virtu-

ally unaffected by the length of the solution with re-

gards to the number of epochs required to reach a rea-

sonable performance, while also being the most con-

sistent over different runs with the same parameters.

Also, this model generates the largest Q-table, explor-

ing close to all 181 440 states which can reach a solu-

tion for the 8-puzzle problem (Johnson et al., 1879).

Figure 1: Sample representation of a run for 8-puzzle.

https://tinyurl.com/4mhx83yd

The second model, using the manhattan distance,

performs the best overall for the shortest-solution in-

stance, but would probably require more epochs to

reach the same performance for the other instances.

The number of explored states is signiﬁcantly less

than for the previous model. This indicates that the

reason for the poorer performance for the more dif-

ﬁcult instances is a tendency to reward too greatly

approaching the goal state which impedes the explo-

ration of possible paths to the goal. A sample of a

graphical representation of the second run in Table1

is shown in Figure 1.

Various data could be extracted from these results

with regards to the impact of the epsilon, decay, al-

pha and discount parameters. For example, using the

data provided by the AIM-RL output, we can observe

a correlation between the training rate, the discount

rate and the average size of the Q-tables built in vari-

ous runs. In Table 2 we can see that a higher training

rate seems to contribute to a signiﬁcant reduction in

the number of explored states. Similar statistics can

be produced for particular models or instances, which

could lead to potential adjustments of these parame-

ters or of the reward function.

4.2 Frozen Lake

The experiments used the same instance as exempli-

ﬁed in Gym/Gymnasium in the discrete (8) example

which is a 8x8 size square matrix with 7 hidden areas.

The run in Figure 2 was generated for the ﬁrst model

with the parameters epsilon = 1, decay = 0.9, alpha =

0.9 and discount = 0.5. The association between the

other details of a run, included in the csv ﬁle, and the

generated graphical representation is made by using

the name of the generated ﬁle, as indicated in Sec-

Table 2: The impact of α and γ over the average number of

explored states.

α = 0.1 α = 0.5 α = 0.9

γ = 0.1 151029.75 130502.5 125424.75

γ = 0.5 145733.1667 139352.1667 126577.4167

γ = 0.9 151429.0833 137933.75 128731.5833

https://gymnasium.farama.org/environments/toy text/

frozen lake/

AIM-RL: A New Framework Supporting Reinforcement Learning Experiments

417

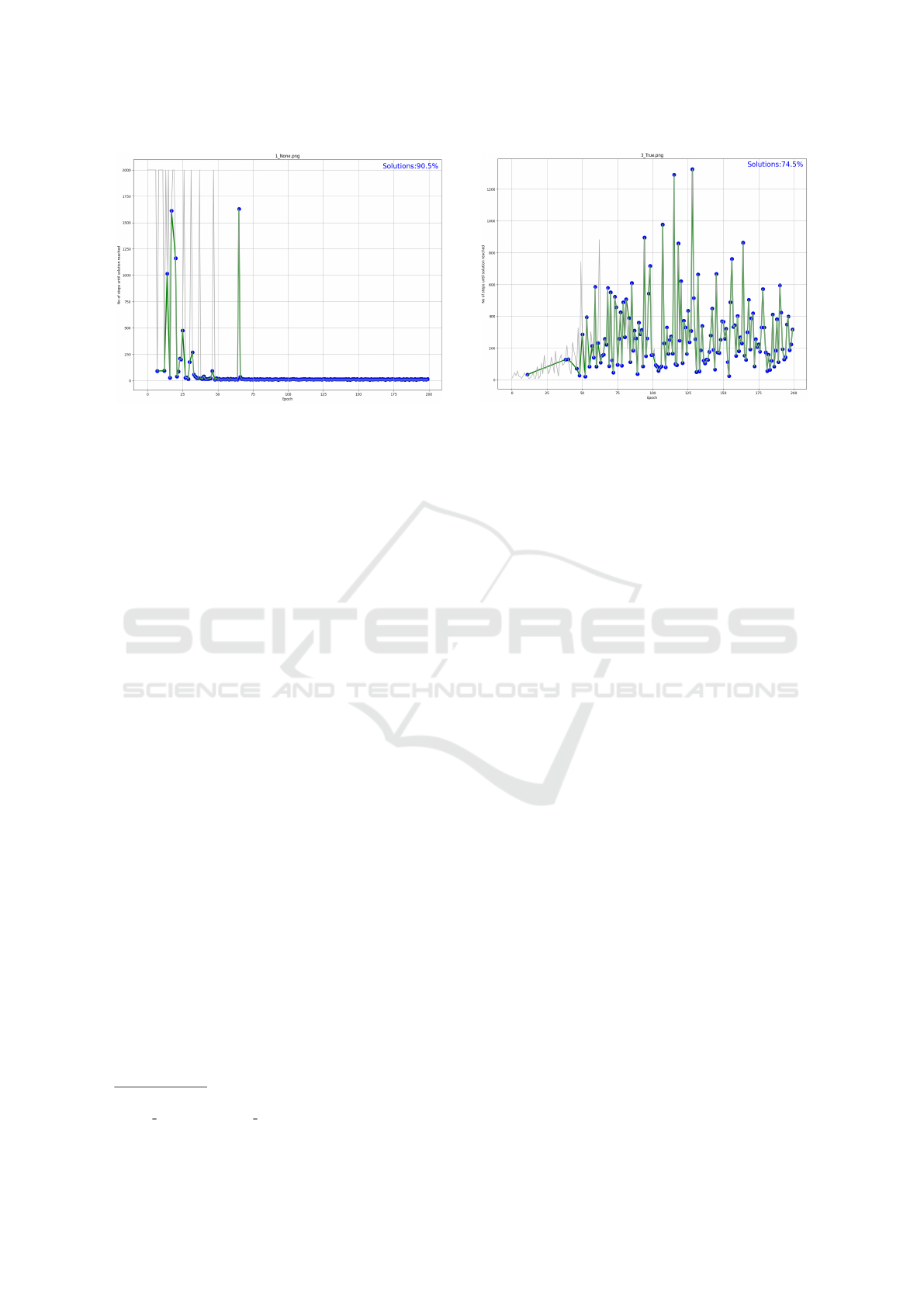
Figure 2: Sample representation of a run for FrozenLake.

tion 3.2. Using just this graph we can make various

observations about this experiment:

• Very good performance after the initial 35 epochs:

a solution (generally the shortest path) is found in

96.5% of epochs.

• This model with these parameters requires about

30 epochs from reaching a solution to stabilising

to the shortest one. An anomalous epoch is still

apparent after the stabilisation, probably due to

a catastrophic decision made early on by random

chance given by the always non-zero epsilon.

Looking at the entire set of generated graphs can also

provide signiﬁcant insights into the way various mod-

els and parameters inﬂuence the training outcome.

4.3 Mountain Car

The mountain car experiments have made apparent

the difﬁculty in handling control problems where the

association between actions and reaching the goal

state is less signiﬁcant. The instance parameters

were selected to be identical to those used in the

Gym/Gymnasium discrete(3) example

. Due to the

fact that an epoch can end if the car exists the limits

of the (−1, 1) range, and the car starts at −0.5, the

initial epoch tend to fail by the agent passing the left

side limit as seen in Figure 3. After it learns that the

goal is to the right (after about 50 epochs), it always

ﬁnds a solution even if it is of varied length.

From the csv ﬁle (included in the mentioned

archive) the user can also make a series of interest-

ing observations. One observation is that the second

more complex model explores signiﬁcantly less states

(which is of especially signiﬁcance for this problem

https://gymnasium.farama.org/environments/

classic control/mountain car/

Figure 3: Sample representation of a run for MountainCar.

with an extreme amount of states), even if it success-

fully completes just slightly more epochs than the ba-

sic model. Another interesting observation is that the

training rate has a more prominent inﬂuence over the

average Q-table size than the discount rate, for both

models, with the better value from the three tried be-

ing 0.9 with an approximate of 86% reduction of the

Q-table size as opposed to the next best value of 0.5.

5 CONCLUSIONS

Gym/Gymnasium is the most feature rich framework

for implementing and executing RL tasks, with a wide

range of implemented problems and models (envi-

ronments). As an alternative to it, AIM-RL aims to

cover particular use cases when the requirements are

focused on transparency and ﬂexibility, allowing the

user to both implement RL experiments for any prob-

lem and any model with minimum code overhead,

as well as observing the results and applying correc-

tions to the experiments parameters. In section 3.2

we have shown the steps required within AIM-RL in

order to implement a new problem and a new model

from scratch. For the three problems described the

effort is similar and proportional to the complexity of

the problem and the model employed. Efforts have

been made to optimise the speed of execution of the

actual RL, while also providing to the user metrics

to evaluate the performance of his experiments. The

results are presented in both numerical and graphical

representations, as shown in 4.1.

5.1 Future Work

Our framework is already available as a Python pack-

age, with immediate plans to be used in several di-

ICSOFT 2023 - 18th International Conference on Software Technologies

418

dactic and research RL applications. The very near

future development plans for AIM-RL include the

extension to allow as an option Deep Q-Learning

(Franc¸ois-Lavet et al., 2018) as well as alternatives

to the ε-greedy selection such as Randomised Proba-

bility Matching (Scott, 2010). As a later development

we plan to facilitate the usage of AIM-RL as a sup-

port framework for e-learning by adding a graphical

UI and a validator for implemented models.

REFERENCES

Brockman, G., Cheung, V., Pettersson, L., Schneider, J.,

Schulman, J., Tang, J., and Zaremba, W. (2016). Ope-

nai gym. arXiv preprint arXiv:1606.01540.

Chen, J., Yuan, B., and Tomizuka, M. (2019). Model-free

deep reinforcement learning for urban autonomous

driving. In IEEE intelligent transportation systems

conference (ITSC), pages 2765–2771. IEEE.

Duan, Y., Chen, X., Houthooft, R., Schulman, J., and

Abbeel, P. (2016). Benchmarking deep reinforce-

ment learning for continuous control. In International

conference on machine learning, pages 1329–1338.

PMLR.

Franc¸ois-Lavet, V., Henderson, P., Islam, R., Bellemare,

M. G., Pineau, J., et al. (2018). An introduction

to deep reinforcement learning. Foundations and

Trends® in Machine Learning, 11(3-4):219–354.

He, X., Zhao, K., and Chu, X. (2021). Automl: A sur-

vey of the state-of-the-art. Knowledge-Based Systems,

212:106622.

Heidrich-Meisner, V. and Igel, C. (2008). Variable metric

reinforcement learning methods applied to the noisy

mountain car problem. In Recent Advances in Rein-

forcement Learning: 8th European Workshop, EWRL

2008, Villeneuve d’Ascq, France, June 30-July 3,

2008, Revised and Selected Papers 8, pages 136–150.

Springer.

Johnson, W. W., Story, W. E., et al. (1879). Notes on

the “15” puzzle. American Journal of Mathematics,

2(4):397–404.

Kaiser, L., Babaeizadeh, M., Milos, P., Osinski, B., Camp-

bell, R. H., Czechowski, K., Erhan, D., Finn, C.,

Kozakowski, P., Levine, S., et al. (2019). Model-

based reinforcement learning for atari. arXiv preprint

arXiv:1903.00374.

Lai, K.-H., Zha, D., Li, Y., and Hu, X. (2020). Dual policy

distillation. arXiv preprint arXiv:2006.04061.

Moerland, T. M., Broekens, J., Plaat, A., Jonker, C. M.,

et al. (2023). Model-based reinforcement learning: A

survey. Foundations and Trends® in Machine Learn-

ing, 16(1):1–118.

Nelson, M. J. and Hoover, A. K. (2020). Notes on using

google colaboratory in ai education. In Proceedings

of the ACM conference on innovation and Technology

in Computer Science Education, pages 533–534.

Paduraru., C., Paduraru., M., and Iordache., S. (2022). Us-

ing deep reinforcement learning to build intelligent

tutoring systems. In Proceedings of the 17th Inter-

national Conference on Software Technologies, pages

288–298. INSTICC, SciTePress.

Piltaver, R., Lu

strek, M., and Gams, M. (2012). The

pathology of heuristic search in the 8-puzzle. Journal

of Experimental & Theoretical Artiﬁcial Intelligence,

24(1):65–94.

Ratner, D. and Warmuth, M. K. (1986). Finding a short-

est solution for the n× n extension of the 15-puzzle is

intractable. In AAAI, volume 86, pages 168–172.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. arXiv preprint arXiv:1707.06347.

Scott, S. L. (2010). A modern bayesian look at the multi-

armed bandit. Applied Stochastic Models in Business

and Industry, 26(6):639–658.

Sutton, R. S. (1995). Generalization in reinforcement learn-

ing: Successful examples using sparse coarse coding.

Advances in neural information processing systems, 8.

Watkins, C. J. C. H. (1989). Learning from delayed rewards.

PhD thesis, King’s College, Cambridge United King-

dom.

Yarats, D., Zhang, A., Kostrikov, I., Amos, B., Pineau, J.,

and Fergus, R. (2021). Improving sample efﬁciency

in model-free reinforcement learning from images. In

Proceedings of the AAAI Conference on Artiﬁcial In-

telligence, volume 35, no 12, pages 10674–10681.

Yu, T., Quillen, D., He, Z., Julian, R., Hausman, K., Finn,

C., and Levine, S. (2020). Meta-world: A benchmark

and evaluation for multi-task and meta reinforcement

learning. In Conference on robot learning, pages

1094–1100. PMLR.

AIM-RL: A New Framework Supporting Reinforcement Learning Experiments

419