
Heterogeneous Graph Storage and Leakage Prevention for Data
Cooperatives
Mark Dockendorf and Ram Dantu
University of North Texas, 1155 Union Cir, Denton, TX 76203, U.S.A.
Keywords:
Data Cooperatives, Privacy, Federated Graph Storage, Applications of Homomorphic Encryption (HE).
Abstract:
Current big data providers offer little-to-no control over how your data is used once it is collected. Data co-
operatives are an alternative to these companies and give control of personal data back to the data providers
(whether they be people or organizations), allowing them to determine which of their data is used and how
their data is used. Data cooperatives can serve as a more ethical alternative to other big data solutions, and have
already seen success in the real world. However, supporting software must be developed to ensure the privacy
of data providers beyond cooperative promises. In this paper, we expand upon our previous work applying
homomorphic encryption (HE) to secure the personally identifiable information (PII) of data providers in data
cooperatives that use graph storage. Data cooperatives are expected to store and query over data of varying
security levels, including PII, low-security (where anonymization alone is sufficient), and public domain in-
formation. To facilitate graph storage, we introduce a multidimensional graph storage technique designed
specifically for data cooperatives that mix cleartext, encrypted, and anonymized heterogeneous edges over a
heterogeneous set of vertices. We demonstrate a HE query watchdog, which prevents incidental data leakage
at query runtime and prior to decryption when proper rules are provided. This watchdog is complementary to
existing work preventing data leakage prior to query runtime. This watchdog’s operations are dominated by
any reasonably-complex query.
1 INTRODUCTION
1.1 The Power of Big Data
While the explosion of big data has the potential for
better decision making, there are two major problems
that have arisen in the past two decades. The first
problem has been a hotbed of research: extracting
data insights from exceptionally large data sets and
turning them into actionable business information.
The second problem has been less visible un-
til more recently: a bifurcation has developed
(D’Ignazio, 2017) where large, established companies
have all the data they need to make good decisions,
but small businesses, governments, and researchers
that would benefit immensely from access to even a
handful of queries over the data are left in the dark.
The silver lining is that general populace also has this
data. The data in question is scattered among them,
with each individual only possessing data about them-
selves.
1.2 Data as a Commodity
In 2006, Clive Humby declared “data is the new oil”.
This was meant to draw parallels between how both
data and oil are valuable only at sufficient quantity,
and both require a “refining” process to extract their
true potential. As another parallel to oil, we have a
very small number of very powerful companies mo-
nopolizing this resource (the likes of Facebook, Ap-
ple, Amazon, Google, Netflix, Microsoft, Uber, etc.).
Each of these behemoths specializes in their own type
of data. For example, Facebook knows the relation-
ships between most people and their contact informa-
tion, even if they don’t have a Facebook account (fac,
2013).
As a result, a gap has arisen between organiza-
tions that have big data and those that do not (An-
drejevic, 2014)(danah boyd and Crawford, 2012). If a
third party, such as another company, a researcher, or
a public official wants access to their data, they must
either (1) purchase a pre-made product/service from
the big data company that fulfills their need, (2) nego-
tiate access of some form to this data, or (3) purchase
192
Dockendorf, M. and Dantu, R.
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives.
DOI: 10.5220/0012091300003555
In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 192-205
ISBN: 978-989-758-666-8; ISSN: 2184-7711
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

a set of data from the big data company. While sce-
nario 1 is widely employed in the form of targeted
advertising and other pre-packaged services, general
use access is much harder to come by. Furthermore,
both scenarios 2 and 3 are likely to be very expen-
sive, putting them out of reach for most researchers
and small businesses.
1.3 Data Cooperatives
According to Pentland and Hardjono (Pentland and
Hardjono, 2020), a data cooperative is a community-
driven organization that facilitates voluntary collab-
orative data pooling to achieve some form of ben-
efit. This benefit could be as simple as improving
healthcare (Huang et al., 2017) by offering supervised
access to personal health data or splitting monetary
profits from query access to location data, web his-
tory, etc. Participants (data providers) provide data
on a voluntary basis to the data cooperative, and data
consumers use the data to gain a desired insight with-
out compromising participant privacy.
Unlike other forms of “big data” and services pro-
vided by near-monopolistic companies, all data in a
cooperative is ethically collected. Participants are
made aware of which data they are submitting, and
all data submissions are voluntary.
The primary product for data consumers is data
insight; the auxiliary product is ethical data sourcing
(Voronova and Kazantsev, 2015) (Asadi Someh et al.,
2016). In our model for a data cooperative, contrac-
tors are never given direct access to data. Rather, data
contractors may ask for insight from the data, effec-
tively granting limited query access as governed by
the data cooperative’s acceptable use policy.
1.4 Homomorphic Encryption
Homomorphic encryption (HE) is a form of encryp-
tion that allows for computation over ciphertext data.
When the result of an HE operation is decrypted, the
value is the same as it would have been if the compu-
tation were performed over cleartext data.
HE effectively allows a third party to perform
computations over data without ever knowing what
the data itself is. Current HE schemes include, but
are not limited to: BFV (Fan and Vercauteren, 2012),
which provides HE for integers; HEAAN/CKKS
(Cheon et al., 2017)(Cheon et al., 2018), which pro-
vides HE for block floating point numbers; and TFHE
(Chillotti et al., 2019)(Chillotti et al., 2016b), which
provides binary gate operations with fast bootstrap-
ping. Recently (2022), OpenFHE (Badawi et al.,
2022) has brought all of these together into a single
open-source library.
Hybrid schemes, such as CHIMERA (Boura et al.,
2020), have also arisen. CHIMERA allow for switch-
ing between TFHE, BFV, and HEAAN ciphertexts
without decryption.
HE is used in our model of a data cooperative to
preserve the privacy of participants. There has been
some study of using HE for graph schemes, as dis-
cussed below.
1.5 Related Work
Searchable symmetric encryption (Curtmola et al.,
2006) has been used to create structured encryption
with controlled disclosure (Chase and Kamara, 2010),
which can be used to encrypt graphs and run algo-
rithms over the encrypted data. This structure re-
quired several operations over encrypted data.
GRECS (Meng et al., 2015) has been used to find
efficient approximate shortest paths over encrypted
graph data. SecGDB (Wang et al., 2017) achieves
optimal storage and accurate shortest paths over en-
crypted graph data with fast O(1) updates. GraphSE
2
(Lai et al., 2019) encrypts social networks and enables
an efficient ”social search” operation.
These storage and query techniques are effective
for graphs with homogeneous vertices and homoge-
neous edges. However, a general-purpose data coop-
erative will mix heterogeneous vertices with hetero-
geneous edges, all of which will require varying de-
grees of security based on vertex and edge type. None
of these systems effectively handle varying degrees of
security, varying vertex types, and varying edge types.
2 MOTIVATION
2.1 Insufficiency of Existing Solutions
for Cooperatives
2.1.1 Corruptibility
While data cooperatives are ideally a community
driven organization with the interests of the partic-
ipants in mind, people must be selected to run a
centralized data cooperative, and insider threats have
been on the rise in recent years (ins, 2021). If the data
cooperative works on cleartext PII, snooping person-
nel will be able to skim data (Colwill, 2009). Even if
the data is encrypted, if the cooperative holds the only
key necessary to decrypt the data, then the data is ef-
fectively cleartext from the cooperative’s perspective.
Data could thus be easily exfiltrated by a corrupt indi-
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
193

vidual (or a small group of individuals) with sufficient
system access.
If the data cooperative operates on effectively-
cleartext data, then any malicious actor that compro-
mises the data cooperative’s systems now has access
to a massive collection of PII on all participants. If
data is decrypted for processing, then it can be copied
at that point by the malicious actor. Thus, a form of
encryption that allows processing of ciphertext data
(ie. homomorphic encryption such as certain RLWE-
based systems (Lyubashevsky et al., 2010)) must be
used to protect from both an insider attack and exter-
nal attackers.
2.1.2 Why a Graph Database?
With each participant able to select the types (what
they share), the verbosity (the level of detail), and
the frequency (how often they update) of the data
they provide, a suitable storage method is needed.
Irregularly-shaped data can become a problem for re-
lational databases; these omissions result in a large
number of NULL values in the tables, hindering stor-
age efficiency. Furthermore, the primary focus of a
data cooperative from the data consumer standpoint
is data insight.
Graph analytics can offer significant insight into
data (Robinson et al., 2015). Graph analysis can be
used to effectively detect money laundering (Li et al.,
2020), to optimize supply chains (Robinson et al.,
2015), predict behavior based on social media (Pitas,
2016), and more. Thus, the storage of data in graph
form facilitates production of the data cooperative’s
primary product: data insight.
Finally, graph databases are more flexible than
those with a rigid schema. This flexibility will al-
low the data cooperative to more effectively respond
to changes in demand and more readily incorporate
new data types from participants.
2.2 Encrypted Graphs
HE secures data while keeping it available for pro-
cessing and is used by SecGDB (Wang et al., 2017)
among others. However, not all data requires a high
level of secrecy. Excessive protection not only slows
down graph operations, it consumes additional stor-
age as well due to HE ciphertext expansion.
For some graph data, it may be acceptable to dis-
close the number of edges on each vertex (as would be
the case with a system based on encrypted adjacency
list). If it is necessary to hide the degree of each ver-
tex, an adjacency-list-based (AL) encryption scheme
can be padded with null edges so that all appear to
have the same degree. In extreme cases, where even
disclosing the maximum degree is a security risk, en-
crypted adjacency matrix (AM) could be used (though
this is not advised as AM size grows at Θ(|V |
2
)).
In our previous works (Dockendorf et al., 2022;
Dockendorf et al., 2021), we adapted several graph
algorithms for use over HE graph data.
2.3 Problem Definition
We address two problems in this paper. The first prob-
lem is that of over-protected data when using existing
solutions. The second problem is preventing leakage
by a well-intentioned query.
A data cooperative must be able to handle a myr-
iad of data, requiring the graph database to host PII,
public data, and anonymized data. Using a graph en-
cryption scheme that secures all data will result in
over-protection of public data. In addition to addi-
tional query time as a result of HE operations, cipher-
text expansion will result in additional storage being
consumed. As an example, a street map of a city as
well as the addresses of every property therein are
public data and can safely be left in cleartext, but the
address that each person resides at is PII and needs to
be protected.
The cooperative may receive a query that is com-
pliant with the acceptable use policy, does not intend
to violate the privacy of any individual, and is of le-
gitimate interest to the consumer (a “well-intentioned
query”); but inadvertently isolates so few participants
that disclosing the result would be a violation of their
privacy. Preventing this would be simple with cleart-
ext data: just stop the query if there are too few par-
ticipants in the query for them to remain anonymous.
However, if PII data is encrypted (as it should be),
there is no way to stop the query without decrypting
each intermediate step of the query, which would ex-
pose PII to the data cooperative in cleartext.
An example of such a situation would be a re-
searcher running queries over salary data, comparing
how different groups are paid for the same job in dif-
ferent cities. While this may be fine when run over
a large city, running this query over a small city may
result in very few or no participants in some of these
groups.
2.4 Our Contributions
2.4.1 Category Cluster Graph Storage
All of previously-explored encrypted graph solutions
either treat vertices and edges as homogeneous or as
heterogeneous but indivisible. Our solution takes ad-
vantage of the fact that the vertex type will be known
SECRYPT 2023 - 20th International Conference on Security and Cryptography
194
to the cooperative in cleartext. We use vertex type
metadata and the size of vertex sets to optimize stor-
age, updates, encryption usage, queries, and enable
the HE query watchdog to prevent leakage.
We demonstrate a heterogeneous-vertex,
heterogeneous-edge, federated graph storage scheme
supporting mixed security levels for various edge
types. Our scheme is more space-efficient than using
any one of the current encrypted graph solutions for
the entire graph, which would cause over-protection
of some data (due to ciphertext expansion). We
achieve this by separating heterogeneous data into
clusters of homogeneous data using homogeneous-set
size and type data, which must already be disclosed
by the cooperative (so that consumers know the size
of the dataset used for their queries), and allowing
the data cooperative to define per-cluster security
policies. All PII edges are encrypted, while edges
constituting public data are left in cleartext. This fed-
eral approach to graph data management ensures that
the appropriate level of protection is applied to each
edge within a heterogeneous security environment,
rather than a blanket one-size-fits-all homogeneous
security policy.
2.4.2 HE Query Watchdog
We demonstrate a simple HE query watchdog de-
signed prevent disclosure of potentially-leaky data
prior to the decryption stage. While acceptable use
validation is used to detect and prevent some queries
designed to intentionally leak data, a well-intentioned
query would still slip past these defenses and possi-
bly leak data. Our HE query watchdog enforces rules
derived from the privacy policy before the decryption
stage to prevent well-intentioned queries from leaking
data.
3 ARCHITECTURE
3.1 Data Cooperative
Our model for a data cooperative has three types of
entities: participants, consumers, and the cooperative.
The cooperative is naturally our data cooperative. It
is managed in a semi-centralized fashion, where de-
cryption of query results requires the cooperation of a
sufficient number of participants. To achieve this, we
use a multi-key fully-homomorphic encryption in our
data cooperative model.
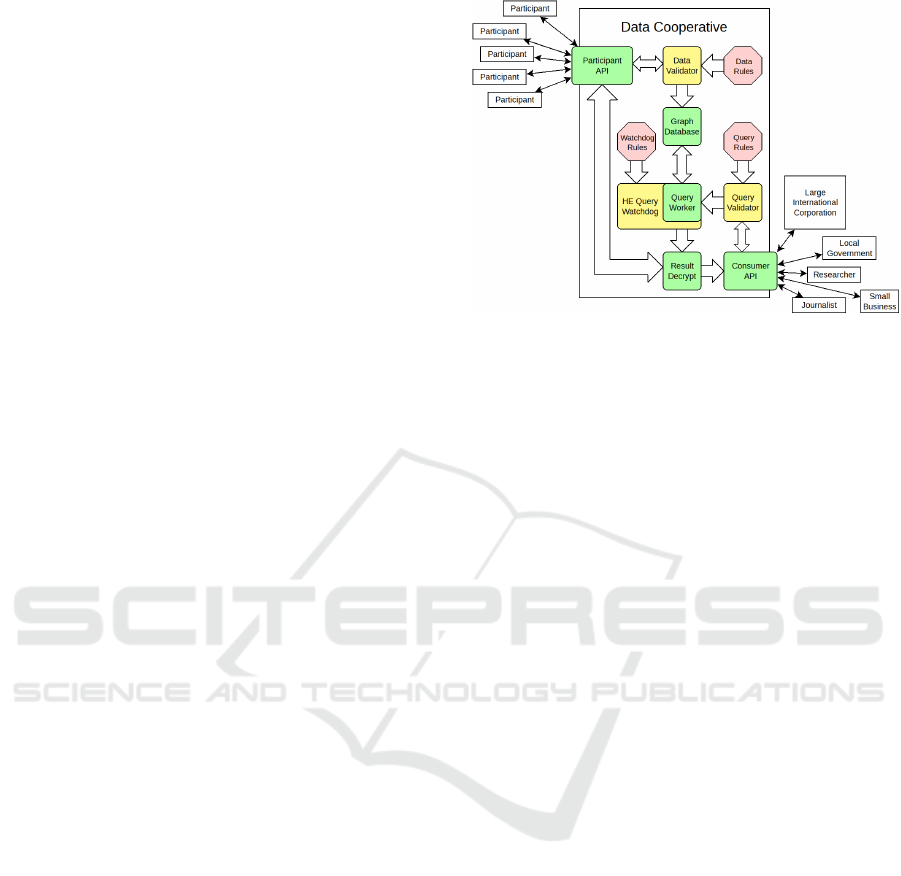
Figure 1: A block diagram of our model for a data co-
operative. The 3 pink octagons are sets of rules derived
from agreements (section 5.1). The yellow blocks are val-
idators that autonomously enforce these rules on data pass-
ing through them. The query and data validators will reject
with a response to the consumer or participant respectively,
while the watchdog is explored in section 5. Participants
(definition 2) submit data through the Participant API and
aid in the decryption process for completed queries. Data
that passes validation is forwarded on to the graph database,
which uses category cluster (section 4) to optimize stor-
age of encrypted, anonymized, and public data. Consumers
(definition 3) submit queries (or requests for data insight)
and receive results via the Consumer API. After valida-
tion, these queries are executed by the Query Worker under
the scrutinizing eye of the HE Query Watchdog, which en-
forces rules that protect the privacy of participants. When
the query finishes, the watchdog forwards the answer to Re-
sult Decryption, which works with participants to decrypt
the query result.
3.1.1 Entities
Entities are individuals or organizations, which may
include researchers, reporters, for-profit companies,
governments, charities, and more. Entities must be
able to exhibit ownership of data and accept legal re-
sponsibility for breaching an agreement. As an ex-
ample, a camera can take a video, but as an object, it
cannot express ownership of the video data. On the
other hand, the person or organization that owns the
camera would be an entity. The cooperative itself is
also considered an entity.
3.1.2 Participants
Participants are entities that submit data to the data
cooperative. Participants are never required to relin-
quish rights over their data. However, once encrypted
data enters the cooperative, it can never be retrieved.
This is due to the fact that any honest participant will
refuse to aid in the decryption of data that was not the
result of an acceptable query.
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
195

3.1.3 Consumers
Consumers are entities that submit queries (requests
for data insight) to the data cooperative. The coopera-
tive validates their queries against an acceptable use
policy, which outlines what makes a query accept-
able and how the data may be used. Importantly, a
consumer can also be a participant, so many smaller
companies could submit data to the cooperative, gain-
ing all of them better data insight.
3.1.4 Sources
Sources are individual data collectors from a device.
While a hardware example of a source would be an
IoT sensor (such as a camera), there can be software
sources. If a participant chooses to share their internet
history (likely in an anonymized or encrypted format),
each web browser on each of their devices would be a
separate source.
3.2 Participant Override
Participants capture data via their sources and sub-
mit to the cooperative through the Participant API af-
ter appropriately formatting and encrypting (if appli-
cable). Any data that is not appropriately formatted
or the Data Validator believes to be falsified or cor-
rupted will be rejected. Participants also aid in the
decryption process. If, for whatever reason, sufficient
participants lose confidence in the cooperative, they
may prevent further decryption of queries by simply
refusing to be part of the process. This gives the par-
ticipants the ability to overrule the cooperative if the
cooperative were ever to become hostile to or refuse
to work in the best interests of the participants.
4 CATEGORY CLUSTER (CC)
4.0.1 Dimensions
Dimensions are logical groupings of edges by their
type. Specifically, edges in a given dimension have
the same meaning. In a graph with multiple edge
types, there may be multiple links between the same
two vertices. However, for certain metrics and data
insights, consumers may wish to only include edges
of a specific type.
As an example, you (v
1
) may happen to both drive
and own your car (v
2
). Therefore, both v
1
→
owns
v
2
and v
1
→
operates
v
2
exist in the graph. In this case, we
have both an “ownership” dimension and an “opera-
tion” dimension. Your insurance company may only
care who operates your car when calculating your
risk, and as such, their risk calculation would include
only edges in the “operation” dimension.
4.0.2 Categories
Categories are mutually-exclusive logical groupings
of vertices by their type. No vertex may be present in
more than one category. By virtue of all vertices in
a category sharing a type, we are able to deduce that
certain edges cannot exist. We make these deductions
based on the capabilities a given type would have:
“people” can own “cars”, “people” can own “plots of
land”, but “cars” cannot own “plots of land”. In a
dimension where the presence of the edge v
1
→ v
2
means “v
1
owns v
2
”, categories such as “cars” or
“plots of land” cannot have outgoing edges as these
cannot express ownership (these are predictable as
having no edges). Importantly, the size (or its approx-
imation) of various categories must be disclosed by
the data cooperative so that consumers know the sam-
ple size used for their query.
4.0.3 Clusters
Clusters are sets of edges from a given dimension that
link vertices of a category to vertices of another cat-
egory. In the example above, the set of edges that
links the category “people” to the category “cars” in
the “ownership” dimension constitutes a single clus-
ter of the graph. The categories linked may also be
the same (ie. “people” to “people” in “friendship” di-
mension for a social network).
4.1 Federated Graph Management
Category cluster is a federated graph storage tech-
nique: after dividing the vertices by category (type)
and edges into dimensions, each “cluster” of edges
can be managed more appropriately by existing solu-
tions. We choose this federated approach for 4 rea-
sons. First, not all types of data will be optimally
stored in a single format: some clusters may be many-
to-many, others one-to-one, and still others may have
fewer edges than vertices. Second, not all data re-
quires the same level of security: personal health in-
formation needs to be protected (HIPPA, GDPR, etc.),
but a map of public roadways does not. Third, this
method effectively creates large blocks of predictable
data and cleartext data while keeping PII encrypted;
operations involving HE and cleartext data do not in-
crease the error of the encrypted sample (meaning we
avoid excessive bootstrapping, the most costly opera-
tion in HE (Jung et al., 2021)). Finally, dividing ver-
tices into categories allows us to create rules for each
category regarding the minimum number of vertices
SECRYPT 2023 - 20th International Conference on Security and Cryptography
196

involved at each stage of the query, which is impor-
tant for our HE query watchdog.
Category cluster supports using a separate graph
storage technique per-cluster: each cluster defines
how it is stored (the underlying technique, such as
AL, CSR, etc.) and which devices store it (within a
distributed system). Existing graph encryption mech-
anisms, such as GraphSE
2
(Lai et al., 2019) can be
used as the underlying storage for a cluster. This may
be optimal if the only operation(s) needed are those
supported by GraphSE
2
and the cluster is a social net-
work (ie. it maps category “people” to the category
“people”).
Each cluster is managed separately, not just in se-
curity, but commit policy and storage as well. This
improves the performance of the overall system by al-
lowing each cluster to manage its own storage scheme
and updates instead of having all clusters updated the
same way: some clusters will receive updates on the
order of seconds while others may never be updated
for the participant’s entire lifespan.
In terms of performance, category cluster allows
for isolation of any cluster (a particular edge type
mapping from one category of vertices to another)
in O(log(max(|A
d,r
|))) time, where max(|A
d,r
|) is the
maximum number of unpredictable outgoing clus-
ters from one category in one dimension. This
lookup requires zero operations over encrypted data,
which tend to take orders of magnitude longer than
cleartext operations. Our O(log(max(|A
d,r
|))) clus-
ter lookup time comes from a trivial adaptation
of compressed sparse row (where CSR would be
O(log(max(|degree|))) edge lookups) to multidimen-
sional graphs, and storing cluster identifiers (UUIDs)
and data location instead of edges.
Queries are made faster by virtue of including less
data: if only vertices that represent category A and B,
both of which are homogeneous vertex sets, need to
be used in a query, then only those vertices and their
related edges need to be loaded. This cuts down on
the amount of data that must be loaded into memory
as well as impacting the runtime based on the query’s
growth rate: if only a tenth of the vertices are in-
volved in the query, and said query has a growth rate
of O(V
2
), then the query is 100x faster than including
all vertices.
Since category cluster creates homogeneous clus-
ters, existing solutions can be plugged in to sup-
ply graph encryption, such as the aforementioned
SecGDB, GRECS, GraphSE
2
, and others (Chase and
Kamara, 2010) as well as graphs encrypted with
CHIMERA (Boura et al., 2020) or PEGASUS (jie Lu
et al., 2020) (and possibly other post-4th generation
HE in the future). For data that requires low security,
clusters can be anonymized if the intended usage per-
mits, and clusters storing public data can be stored in
cleartext.
4.1.1 Predictability
Unpredictable clusters are clusters that that cannot be
reliably reproduced by a prediction function with no
knowledge of the actual data. CC only stores unpre-
dictable clusters, using what metadata is known to en-
able the cooperative to select the optimal storage tech-
nique. If a cluster is predictable, a prediction function
is used instead. A prediction function takes the form
f
d,r,c
(i, j) → x, where i and j are row and column in-
dex of the cluster respectively and x is the computed
edge weight.
An example of a predictable cluster is the afore-
mentioned “cars” →
ownership
“plots of land”; this clus-
ter is all zeroes and is predictable with the function
f
ownership,cars,land
(i, j) → 0
which produces a zero-matrix. Another example of
a predictable cluster is “people” →
ownership
“people”,
which would be predicted by
f
ownership,people, people
(i, j) → (i = j)?1 : 0
as people cannot own other people, but are in control
of themselves in a civilized country.
4.2 Category Cluster Example
Let G be a graph on 2 dimensions. Let V , the vertex
set of G, represent devices on a computer network.
Let E be the edge set of G. Let the first dimension, D
1
,
of G represent the link speed of a direct connection
in Mbps to another device on the network. Let the
second dimension, D
2
, of G represent the total bytes
of IP-layer e-commerce data sent from another device
on the network.
V could thus be divided into several categories:
“clients”, “servers”, and “network devices” (routers,
switches, bridges, access points, etc.). After division,
we make some observations based on what we know
about each of these categories.
In D
1
, we know that “clients” (phones, laptops,
etc.) typically have 2 or fewer link-layer connections
to other devices. We can assume that client-to-client
direct connections are rare; however, this does occur
when someone uses their phone as a portable hotspot,
among other times. We also know that “servers”
will often have more than 1, but rarely more than 4
link-layer connections. Most importantly, we know
that direct physical connections between “clients” and
“servers” effectively never happen (other than in test-
ing environments).
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
197

In D
2
, we know that “network devices” are nei-
ther the origin nor the destination of e-commerce traf-
fic. We can also make the inference that “clients”
will not be browsing other “clients” when shopping.
In fact, the source and destination for layer 3 e-
commerce traffic will be client-server or server-server
(ie. database access by a web server).
Figure 2: Visualization of a 2-dimensional graph under cat-
egory cluster. The each of the 2 large squares (D
1
and
D
2
) represents what would be the adjacency matrices of the
graph in each dimension. By applying category cluster to
G, we are able to identify large, predictable sub-matrices of
zeroes that do not need to be stored, shown here as black
regions. Furthermore, we can surmise that the blue square
will have fewer edges than vertices as clients are rarely di-
rectly connected to one another. The green block is unlikely
to have more than 2 edges per row, while the grey block
is unlikely to have more than 2 edges per column (though,
these will not necessarily be a transposition of one-another).
Yellow blocks are likely to have a low number of edges per
row, and pink blocks indicate that none of the previous pat-
terns can be assumed. Using this guidance, the cooperative
can select the most optimal graph storage or graph encryp-
tion scheme for each of these clusters.
4.3 CC Storage Space
Let C = {C
1
,C
2
, ...C
n
} be the set of (mutually ex-
clusive) categories in the universal graph, with |C|
being the number of categories. Let V be the set
of all vertices (formed by the union of of the ver-
tices in each category), with subsets corresponding
to their categories on index (C
1
’s vertices are the
set V
1
, C
x
’s vertices are the set V
x
, etc.). Let D =
{D
1
, D
2
, ...D
m
} be the set of dimensions in the univer-
sal graph, with |D| being the number of dimensions.
Let E = {E
1
, E
2
, ...E
m
} be the set of edges in each
dimension, corresponding on index with dimensions.
Further, let E
d,r,c
be a subset of the edges of E
d
,
from dimension D
d
, that links the vertices, V
r
, of cate-
gory C
r
to the vertices, V
c
, of category C
c
. The cluster
that contains E
d,r,c
is designated by A
d,r,c
.
The most popular graph storage techniques are
CSR-based (compressed sparse row) or AL-based
(adjacency list) for general graphs that are sparse.
For extremely sparse graphs, where |V | > |E|, a
coordinate-based graph storage may be used. While
adjacency matrix (AM) is a possible underlying stor-
age technique for a cluster, we do not believe it to be
appropriate unless the cluster represents a dense clus-
ter.
4.3.1 Multidimensional Compressed Sparse Row
In a single dimension, compressed sparse row (CSR)
allocates 3 arrays. The first array, containing the row
start index, has |V | + 1 elements. The second and
third array contain the destination vertex (column)
and edge weight respectively; these arrays are exactly
|E| in length. Thus, storage space for CSR grows at a
rate of
Space(CSR) = e|E|+s|E|+s(|V |+1) = O(|V |+|E|)
(1)
in a single dimension, where e is the size of the edge
weight type and s is the size of the index type. Al-
ternatively, after a trivial adaptation of CSR to multi-
dimensional graphs (mCSR) would use 3 arrays: per-
dimension row start, column, and edge weight, con-
suming
Space(mCSR) = (|D||V | + |E| + 1)s +|E|e
= O(|D||V | + |E|)
(2)
space, where |E| = Σ
d=1
m
(|E
d
|) is the total number of
edges in all dimensions. To find the row start of the
i
th
row in the d
th
dimension, we use
row start(d, i) = (d − 1) ∗ |V | + (i − 1) (3)
This implementation stacks the row start array of each
dimension and combines the column and edge weight
arrays for all dimensions. This assumes edge weights
are the same type in all dimensions.
4.3.2 Category Cluster Structure
Category-clustered graph storage stores clusters
where C
r
→ C
c
is unpredictable in D
d
, the given di-
mension. Such a cluster would be referred to as A
d,r,c
and would be a |V
r
| by |V
c
| sub-matrix of the multi-
dimensional graph: a cluster can be thought of as a
mapping of V
r
to V
c
.
Important Assumptions:
1. Category types and category cardinalities (or their
approximations) can be disclosed with no signifi-
cant security implications
2. Cluster unpredictability is generally sparse
We can assume (1) is acceptable in a data coop-
erative as any consumers using the data cooperative’s
services would need to know at least the approximate
size of dataset used. We assume (2) as tighter dimen-
sions (which determine the meaning of an edge) can
SECRYPT 2023 - 20th International Conference on Security and Cryptography
198

be defined by the cooperative as necessary. If the
meaning of an edge in a dimension is too general,
then assumptions helpful to choosing optimal storage
methods cannot be made.
In category cluster, we use a mCSR to store ref-
erences to unpredictable clusters. In addition to the
underlying storage of each cluster, CC must store this
list of unpredictable clusters. Thus, mCSR structure
of CC grows at a rate of
Space(CC
struct
) = (|D||C| + |A| + 1)s + |A|u
= O(|D||C| + |A|)
(4)
where |D| is the number of dimensions, |C| is the
number of categories, |A| is the count of unpredictable
clusters in all dimensions, s is the size of the index
type, and u is the size of the cluster reference type.
We believe it is reasonable to expect |A| to dominate
just as |E| typically dominates CSR.
The storage of clustered data is heterogeneous:
different storage techniques (AM-, CSR-, AL-based,
etc.) may be combined with different privacy-
preservation measures (encryption, anonymization,
etc.) in CC. Existing work on encrypted graphs as
described in (Chase and Kamara, 2010), (Wang et al.,
2017), (Meng et al., 2015), (Lai et al., 2019), and oth-
ers as well as general-purpose HE can be applied to
clusters independently based on privacy requirements
and intended/acceptable use.
4.3.3 Worst-Case Analysis
Even if the assumptions above are not met (ie. no pre-
dictable clusters arise from using CC, the worst case
scenario), it is still possible that storage gains can be
made by selecting the optimal storage technique for
each cluster as outlined in the example above (section
4.2).
For our worst-case analysis, we will assume no
predictable clusters arise. If all clusters use a CSR-
based storage technique, then the total storage is
Space(CC
CSR
) = Space(CC
struct
)+
Σ
d=1
|D|
Σ
r=1
|C|
Σ
c=1
|C|
(|V
r
|s + |E
d,r,c
|s + |E
d,r,c
|e)
(5)
where the triple summation is the space required to
form |D| ∗ |C| ∗ |C| CSR subgraphs. Simplifying this
triple summation, we get
Σ
d=1
|D|
Σ
r=1
|C|
Σ
c=1
|C|
(|V
r
|s + |E
d,r,c
|s + |E
d,r,c
|e)
= Σ
d=1
|D|
(|V ||C|s + |E
d
|s + |E
d
|e)
(6)
where the internal expression of the single summation
on the right represents the cost of every CSR in the
d
th
dimension (remember |E
d
| is the number of edges
in the d
th
dimension). A final simplification to this
summation yeilds
Σ
d=1
|D|
(|V ||C|s + |E
d
|s + |E
d
|e)
= |D||V ||C|s + |E|s + |E|e
(7)
After back substitution of this and the value of
Space(CC
struct
), the space growth becomes
Space(CC
CSR
) =((|D||C| + |A| + 1)s + |A|u)
+ (|D||V ||C|s + |E|s + |E|e)
(8)
Converting these growth measurements to asymptotic
growth rate results in
Space(CC
CSR
) = O(|D||C|+|A|)+O(|D||V ||C|+|E|)
(9)
As we can reasonably expect there to be at least one
edge per stored cluster, we can deduce that under nor-
mal circumstances, |A| ≤ |E|. We also assume that
|C| << |V | as there should be significantly more ver-
tices than categories. Realistically, |C| is constant as
only adding support for a new type of vertex could
change this value.
Space(CC
CSR
) = O(|D||C| + |A| + |D||V ||C| + |E|)
≈ O(|D||V | + |E|)
(10)
which is the asymptotic growth rate of multidimen-
sional CSR (mCSR) from equation 2. Thus,
Space(CC
CSR
) ≈ Space(mCSR) (11)
This result shows that even in the worst case,
when CC cannot eliminate clusters from storage,
CC’s space growth rate using a CSR-based cluster
storage (or one that grows at a similar asymptotic
rate) is about the same as mCSR asymptotically.
5 HE QUERY WATCHDOG
The HE query watchdog enforces rules derived from
the privacy policy, protecting participants from infor-
mation leakage.
5.1 Cooperative Agreements
In order to fulfil their purposes, all of these documents
must be written in a manner compatible with the court
system(s) and a manner similar to a software require-
ments document. This will allow clear rules to be di-
rectly derived from them.
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
199

Table 1: An outline of binding agreements used in our data cooperative model. A bound party is responsible for upholding
the contents of the document. The protected party is the one that benefits from the document’s existence. The final column
describes which software program at the data cooperative performs automated enforcement, given a set of rules derived from
the document.
Document Binds Protects Enforced by
Participant Agreement Participants Consumers, Cooperative Data Validator
Acceptable Use Policy Consumers Participants Query Validator
Privacy Policy Cooperative Participants HE Query Watchdog
5.1.1 Participant Agreement
The participant agreement outlines what is consid-
ered acceptable behavior by a participant. This docu-
ment will typically boil down to the participant agree-
ing that they will not send incorrect, maliciously-
modified, or randomized data. Whenever new data is
submitted, it is run through the Data Validator, which
also works over encrypted data. The Data Validator
is remarkably similar to the watchdog, but the Data
Validator enforces rules derived from the participant
agreement and is designed to work over many up-
dates (specifically, working to identify inconsistent or
bad updates). Not all bad data would be a breach of
this agreement, after all, IoT sensors and other data
sources can fail.
If a participant is found to have a clearly violated
the participant agreement, the participant may have
their trustworthiness reduced or, in egregious cases,
be banned from the cooperative.
5.1.2 Acceptable Use Policy
The acceptable use policy outlines the types of queries
that are acceptable. For obvious reasons, the cooper-
ative and participants will refuse to decrypt a result
that is of certain categories (ie. a category that in-
dividually identifies people). The query validator en-
sures that no illegal query steps or query results would
come about from running the query.
Changes to the acceptable use policy that create
additional acceptable queries need to be ratified by
the participants in an update to the privacy policy.
5.1.3 Privacy Policy
The privacy policy outlines how the data cooperative
will ensure participants’ privacy while enabling query
access to data. In addition to agreeing to enforce the
acceptable use policy on the data consumers, the pri-
vacy policy states the specific metrics used to ensure
each participant remains anonymous during a query.
This will typically be a list of rules for the minimum
number of participants involved in each metric. Fi-
nally, it gives participants a way to purge their data
and close their account if they so desire.
The links between people and their PII are edges
that need to be encrypted. Within a city, each plot
of land will have some property identifier and an ad-
dress; the links between these do not need to be en-
crypted as they are a matter of public record. How-
ever, links between people and the properties that they
live at (PII) need to be encrypted.
5.2 Watchdog Operation
Figure 3: A simple query running under the watchdog. Yel-
low blocks indicate cleartext values, while green indicate
HE ciphertext values. The query in this example starts with
a cleartext vector, then performs some operation(s) with a
HE graph cluster, resulting in a ciphertext vector as an in-
termediate result. This intermediate result is then used in
another operation with a cleartext cluster, outputting the fi-
nal result ciphertext. The initial selection, along with each
intermediate result and the final result are tested against the
set of rules associated with their category. Any rule failing
will result in the “good bit”, g, becoming enc(0), which will
in turn cause the final ‘&’ operation to zero the final result
in the cleansing stage, before the result is decrypted.
5.2.1 Initialization
Each query has a validation structure associated with
it and its own instance of the watchdog. The structure
consists of the “good bit”, g, a ciphertext initialized
to enc(1) when the query starts; a list of intermedi-
SECRYPT 2023 - 20th International Conference on Security and Cryptography
200

ate results, each with a semaphore initialized to 2;
and a final result, which has a semaphore initialized
to 1. After initializing the structure, the query’s main
watchdog thread greenlights the query worker to pro-
cess the query and enters the cleansing function.
5.2.2 Query Worker
The query worker runs the query, using parallelization
where available, and writing intermediate results to
the watchdog validation structure and invoking a par-
allel watchdog result validator each time an interme-
diate result is completed. The query may continue to
run, regardless of watchdog validation status. When
the query worker no longer needs an intermediate re-
sult to compute a future result, it decrements the cor-
responding semaphore and frees the intermediate re-
sult it if the semaphore became zero. When the query
completes, the query worker decrements the final re-
sult semaphore.
5.2.3 Pseudocode
The hot loop for the watchdog is the result validator.
The result validator is invoked in parallel every time
an intermediate value is computed during a query. For
HE schemes that do not support “and”, multiplica-
tion is used. Since rule.eval on(R) returns enc(0) or
enc(1), multiplication and “and” are equivalent.
Watchdog Result Validator
Input:
R, an HE intermediate query result;
P, set of rules derived from the privacy policy;
g, atomic reference to the query’s “good bit”
Output:
signal indicating completion
validate(R,P,g):
# fetch all rules for the category
rules := P.get_rules(R.category())
# same length as rules
passed := list of ciphertext
# parallel for
for i := 0 to rules.size() - 1:
passed[i] := rule.eval_on(R)
if verbose logging enbaled:
write passed[i] to query log
# leaves result at index 0
and_all_values(passed)
atomic:
g := g and passed[0]
if logging is enabled:
write passed[0] to query log
decrement semaphore of R
free R is semaphore became 0
The rules enforced on any given intermediate re-
sult are dependent upon which category the vertices
are members of. A query may shift through several
categories, meaning different rules may be enforced
at every step. Typically, the most stringent rules will
be placed on categories that form direct or indirect
references to people (PII).
5.2.4 Logging
While logging is not required, it can be useful for in-
vestigating why certain queries are violating the pri-
vacy policy. Since we assume the most sensitive
data to be encrypted and inaccessible to the cooper-
ative, the cooperative can instead request participants
to help decrypt the watchdog log. Decrypting general
watchdog logs reveals which step the query is failing
at, while decrypting a verbose watchdog log will re-
veal the specific rules the intermediate result did not
pass.
5.2.5 Cleansing
Within the cleansing function, the main watchdog
thread for the query waits until the final result
semaphore becomes 0, then runs the result validator
on the final result. After that, this thread then waits on
all intermediate result semaphores becoming 0, sig-
naling that all of the intermediate results have been
checked. At this point, if the query’s “good bit” is
still enc(1), then every rule put forward by the privacy
policy has passed at every step; if any intermediate re-
sult (or the final result) failed to pass a rule, then the
“good bit” is now enc(0).
To avoid decrypting a potentially leaky result, the
final step the watchdog performs is R
f inal
∗ g. This
simply results in R
f inal
becoming all enc(0) if it vio-
lated the privacy policy, while maintaining its original
value if it did not. Finally, the watchdog forwards the
tuple (g, R
f inal
) to Result Decrypt.
5.2.6 Interpreting Query Results
Since the result takes the form of the tuple (g, R
f inal
),
after the decryption step, the “good bit” indicates
whether or not the result is valid. If the “good bit”
is 0, then the result is also 0 (or a vector/matrix of ze-
roes); this means the query was inconclusive. While
having a certain number of participants may be re-
quired to sufficiently anonymize each, having an in-
sufficient number of participants in a study calls into
question its validity. Therefore, in the process of pro-
tecting participants, the HE query watchdog also pro-
tects data consumers from insight based on too little
data.
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
201
6 PERFORMANCE RESULTS
All benchmarks were performed using ciphertexts en-
crypted with TFHE (Chillotti et al., 2016b) on an
AMD 3960X. The default 128-bit equivalent security
was used for all results.
6.1 Graph Assembly Results
Since CC breaks the graph into homogeneous compo-
nents, there will be occasions where these sets need
to be joined. One of the core functionalities of cat-
egory cluster is assembling clusters together to form
different subgraphs (or “data views”). This process
involves taking clusters from the selected categories
and dimension(s) and assembling them into a virtual
matrix (a matrix where blocks are references to clus-
ter) over which graph algorithms may be run.
As this function is required for nearly all graph
algorithms to be able to run over more than one clus-
ter, it may be used several times per query. Assembly
time is invariant with the number of vertices in each
category as well as the total vertices in the assembled
graph. Assembly time grows only with the number of
categories being assembled.
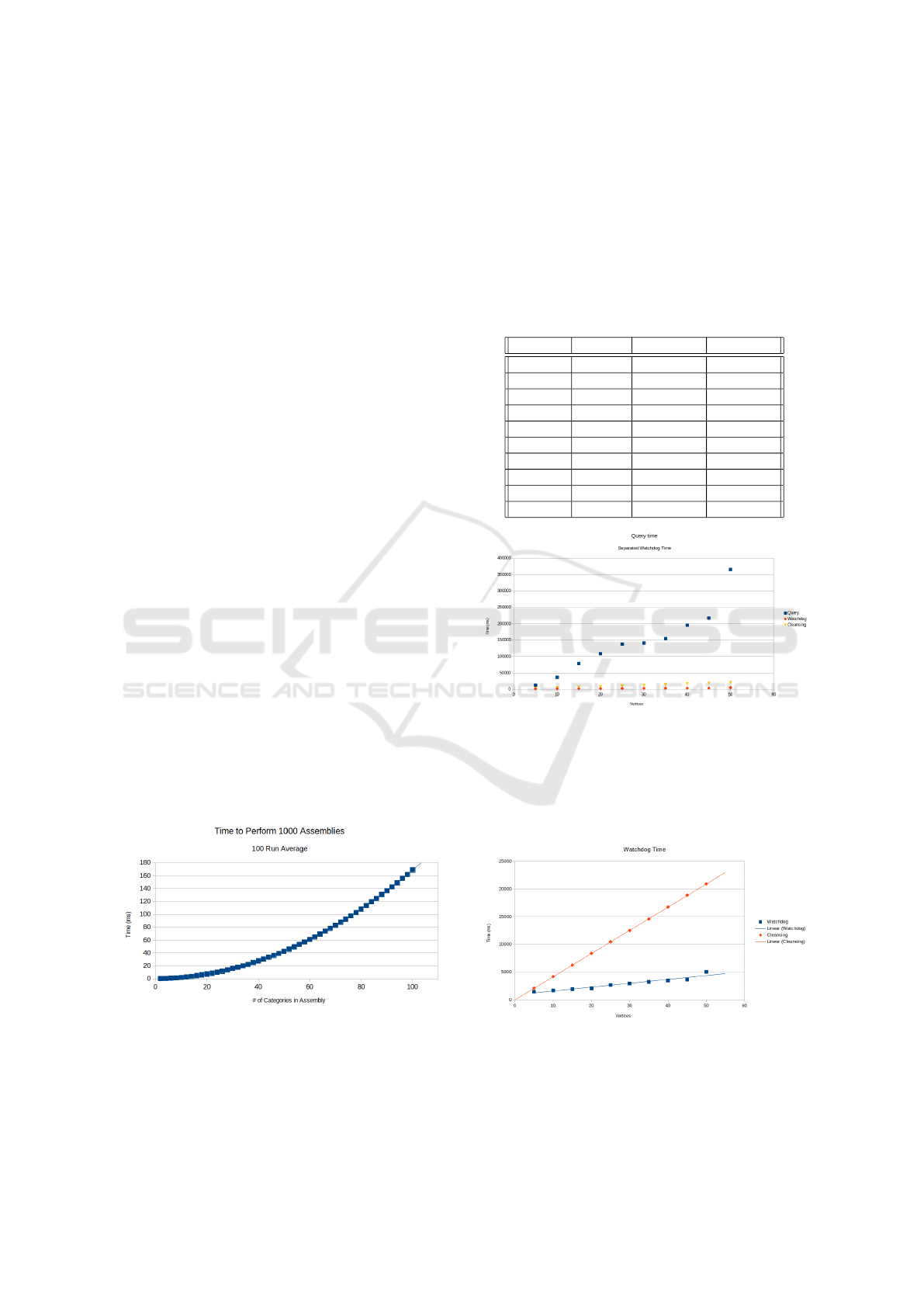
The assembly procedure is so quick that 10,000
assemblies of 2 categories (4 clusters) in a 1000-
category graph can be done in 1.4 milliseconds, which
results in an amortized rate of about 140 nanosec-
onds per assembly. Even a single HE bootstrapping
will take significantly longer than assembling the sub-
graphs together (Cheon et al., 2018) (Chillotti et al.,
2016a) (Han and Ki, 2020). The assembly operation
itself is always a cleartext operation, even when the
data is encrypted in the clusters. That is to say, even
when some or all clusters are encrypted, assembly
time does not change.
Figure 4: Assembly time grows quadratically with the num-
ber of categories in the assembly. R
2
> 0.99999.
The only case that increases assembly time is
adding more categories. Assembly time grows
quadratically with the number of categories in the
assembly. However, it should be noted that not
many implementations will have more than 1000 cat-
egories, and a separate benchmark shows that as-
sembling 1000 categories (1,000,000 clusters) is still
faster than a single HEAAN (128-bit security) boot-
strap.
6.2 Query Watchdog Results
Table 2.
Vertices Query Watchdog Cleansing
5 12564 1450 2084
10 36303 1666 4184
15 78821 1890 6248
20 108689 2064 8364
25 137678 2673 10443
30 140993 2909 12476
35 154471 3222 14561
40 195366 3475 16744
45 217135 3639 18860
50 365213 5025 20911
Figure 5: The query, shown in blue, is O(|V |
2
) with O(|V |)
parallelism, the shape is a result of running the query on a
24-core (48-thread) machine. The most important takeaway
from this chart is that the query time clearly dominates both
operations of the watchdog: the result validator (orange)
and cleansing (yellow). The watchdog times do not vary
with query result.
Figure 6: When looking at the watchdog operations without
the query, a clear linear time complexity appears for both
compliance checking (conformance to rules, shown in blue)
and the cleansing step (shown in orange).
SECRYPT 2023 - 20th International Conference on Security and Cryptography
202

In the table above the Query, Watchdog, and
Cleansing columns are times for running a simple
query of O(|V
i
|
2
) time complexity, the watchdog en-
forcing a rule on the result (more than half of ver-
tices in result), and the cleansing step; all times are in
miliseconds (ms). The simplest meaningful queries
in a data cooperative are likely to be at least O(|V
i
| ∗
|V
j
|) when dealing with encrypted AM-based clusters,
or O(|E
i j
|) when dealing with encrypted CSR-/AL-
based clusters. Thus, the O(|V
i
|) growth rate of the
watchdog rule checking and cleansing is an accept-
able outcome.
The rule checking operation (labeled “Watchdog”
in the legends of the graphs) is repeated for every in-
termediate result of the query. However, the cleansing
operation is only performed once per query (on the fi-
nal result). These results show that watchdog opera-
tions should always be dominated by the query itself.
7 LIMITATIONS
7.1 Category Cluster Graph Storage
CC relies heavily on data having logical divisions
of vertices and edges. While these logical divisions
created by various vertex/edge types are expected to
be present in nearly all data cooperatives, this is not
true for general-purpose graphs. These logical divi-
sions are used to identify clusters of edges that are
prohibited from existing in reasonable data. If the
graph’s vertices are logically indistinguishable and
edges have no patterning that can be exploited to bet-
ter store the data, then CC will simply have one cate-
gory and single cluster.
As CC was targeted at data cooperative use-cases,
we assumed that certain metadata must be disclosed
and would not constitute a disclosure on its own.
Metadata such as the number of elements in each cat-
egory (or their approximate number) were assumed to
be disclosed as this would be required for researchers
and other data consumers to understand their sample
size.
7.2 HE Query Watchdog
A clear set of rules should arise from a well-written
participant privacy policy, but said privacy policy
must be written in a manner where clear rules arise
from the document. This watchdog will not prevent
all forms of data disclosure. It is imperative that
queries be validated against an acceptable use pol-
icy prior to execution: the watchdog is not intended
to catch reconstruction attacks and the like. Rather,
this watchdog is intended to prevent legitimate (well-
intentioned) queries over encrypted data from disclos-
ing information that could weaken the privacy protec-
tions put in place by the cooperative should the result
of the query be decrypted.
8 CONCLUSION
In this paper, we present Category Cluster Graph Stor-
age as a multilevel (federated) storage solution for
data cooperatives using HE graph data. CC is de-
signed with HE graph database use-cases in mind, and
discloses to the data holder only what a data coopera-
tive would be expected to disclose anyway. Since all
clusters that could reasonably exist are stored, no fur-
ther data about the graph is disclosed other than what
the cluster storage technique discloses.
This work runs parallel to existing work on op-
timizing graph storage and encryption. Since the
cluster-find operations are cleartext, each cluster can
use an arbitrary form of cluster encryption as long
as there is either (1) a conversion from the encryp-
tion system used into other encryption system(s) used
(Boura et al., 2020) or (2) a duplicated encryption in
a general format.
CC is capable of storing graph data of varying de-
grees of sensitivity by changing the underlying stor-
age method on a per-cluster basis: HE for highest
security, structured encryption when leaking query-
relevant data is acceptable, cleartext when data is pub-
lic, and summarization when data is predictable (this
list is not exhaustive, other storage techniques can be
nested as well). In fact, this work can be combined
with SecGDB (Wang et al., 2017) to shorten query
time at the cost of a small amount of metadata dis-
closure. This metadata would need to be disclosed
anyway as a function of the data cooperative: know-
ing the sample size of some homogeneous vertex set
from among the heterogeneous vertices of a graph
database. Furthermore, any ”social media” portion of
the database could be encrypted using GraphSE
2
as
another form of nested encrypted subgraph.
Perhaps most importantly, CC creates categories
of vertices and edges, which are used by our HE
query watchdog. Our HE query watchdog prevents
accidental disclosure of insufficiently-anonymized re-
sults. The watchdog operates on data before it is de-
crypted, enforcing cooperative-defined rules (derived
from a privacy policy) on each stage of a query based
on the category of the intermediate results. Should
any rule violation occur, the results of the query
are purged prior to the decryption step: eliminating
potential leakage before it happens. We show that
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
203

watchdog operations are dominated by any reason-
ably complex query.
Ultimately, category cluster graph storage allows
for managing heterogeneous vertices, heterogeneous
edges, and heterogeneous security levels by segregat-
ing vertices and edges into homogeneous groupings
and applying existing privacy protection techniques
for single or multi-level homogeneous graphs. Dif-
ferent privacy protections may be applied to different
clusters based on the varying sensitivity of different
edge sets, allowing slower storage techniques, such as
those that use homomorphic encryption, to operate on
smaller data sets. This yields better performance by
limiting the scope of the slowest operations (HE-HE
operations) to only where they are necessary and en-
abling faster operations (HE-cleartext and cleartext-
cleartext) everywhere else.
ACKNOWLEDGEMENTS
We sincerely acknowledge and thank the National
Centers of Academic Excellence in Cybersecurity,
housed in the Division of Cybersecurity Educa-
tion, Innovation and Outreach, at the National Secu-
rity Agency (NSA) for partially supporting our re-
search through grants H98230-20-1-0329, H98230-
20-1-0414, H98230-21-1-0262, H98230-21-1-0262,
and H98230-22-1-0329.
REFERENCES
(2013). Facebook: Where your friends are your worst ene-
mies.
(2021). The fight for your data: mitigating ransomware and
insider threats. Information Age.
Andrejevic, M. (2014). Big data, big questions— the big
data divide. International Journal of Communication,
8(0).
Asadi Someh, I., Breidbach, C., Shanks, G., and Davern,
M. (2016). Ethical implications of big data analytics.
Badawi, A. A., Bates, J., Bergamaschi, F., Cousins, D. B.,
Erabelli, S., Genise, N., Halevi, S., Hunt, H., Kim, A.,
Lee, Y., Liu, Z., Micciancio, D., Quah, I., Polyakov,
Y., R.V., S., Rohloff, K., Saylor, J., Suponitsky, D.,
Triplett, M., Vaikuntanathan, V., and Zucca, V. (2022).
Openfhe: Open-source fully homomorphic encryption
library. Cryptology ePrint Archive, Paper 2022/915.
https://eprint.iacr.org/2022/915.
Boura, C., Gama, N., Georgieva, M., and Jetchev, D.
(2020). Chimera: Combining ring-lwe-based fully ho-
momorphic encryption schemes. Journal of Mathe-
matical Cryptology, 14(1):316–338.
Chase, M. and Kamara, S. (2010). Structured encryption
and controlled disclosure. IACR Cryptol. ePrint Arch.,
2011:10.
Cheon, J. H., Han, K., Kim, A., Kim, M., and Song, Y.
(2018). Bootstrapping for approximate homomorphic
encryption. In Annual International Conference on
the Theory and Applications of Cryptographic Tech-
niques, pages 360–384. Springer.
Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-
momorphic encryption for arithmetic of approximate
numbers. In Takagi, T. and Peyrin, T., editors, Ad-
vances in Cryptology – ASIACRYPT 2017, pages 409–
437, Cham. Springer International Publishing.
Chillotti, I., Gama, N., Georgieva, M., and Izabachene, M.
(2016a). Faster fully homomorphic encryption: Boot-
strapping in less than 0.1 seconds. In international
conference on the theory and application of cryptol-
ogy and information security, pages 3–33. Springer.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(August 2016b). TFHE: Fast fully homomorphic en-
cryption library. https://tfhe.github.io/tfhe/.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(2019). Tfhe: Fast fully homomorphic encryption
over the torus. Journal of Cryptology.
Colwill, C. (2009). Human factors in information security:
The insider threat–who can you trust these days? In-
formation security technical report, 14(4):186–196.
Curtmola, R., Garay, J., Kamara, S., and Ostrovsky, R.
(2006). Searchable symmetric encryption: Improved
definitions and efficient constructions. In Proceed-
ings of the 13th ACM Conference on Computer and
Communications Security, CCS ’06, page 79–88, New
York, NY, USA. Association for Computing Machin-
ery.
danah boyd and Crawford, K. (2012). Critical questions
for big data. Information, Communication & Society,
15(5):662–679.
D’Ignazio, C. (2017). Creative data literacy: Bridging the
gap between the data-haves and data-have nots. Infor-
mation Design Journal, 23:6–18.
Dockendorf, M., Dantu, R., and Long, J. (2022). Graph
algorithms over homomorphic encryption for data co-
operatives. pages 205–214.
Dockendorf, M., Dantu, R., Morozov, K., and Bhowmick,
S. (2021). Investing data with untrusted parties using
he. In International Conference on Security and Cryp-
tography Alternatively,
Fan, J. and Vercauteren, F. (2012). Somewhat practical fully
homomorphic encryption. Cryptology ePrint Archive,
Paper 2012/144. https://eprint.iacr.org/2012/144.
Han, K. and Ki, D. (2020). Better bootstrapping for ap-
proximate homomorphic encryption. In Cryptogra-
phers’ Track at the RSA Conference, pages 364–390.
Springer.
Huang, S.-K., Pan, Y.-T., and Chen, M. S. (2017). My
health bank 2.0—making a patron saint for people’s
health. Journal of the Formosan Medical Association,
116(2):69–71.
jie Lu, W., Huang, Z., Hong, C., Ma, Y., and Qu, H. (2020).
Pegasus: Bridging polynomial and non-polynomial
SECRYPT 2023 - 20th International Conference on Security and Cryptography
204

evaluations in homomorphic encryption. Cryptology
ePrint Archive, Paper 2020/1606. https://eprint.iacr.
org/2020/1606.
Jung, W., Kim, S., Ahn, J. H., Cheon, J. H., and
Lee, Y. (2021). Over 100x faster bootstrapping
in fully homomorphic encryption through memory-
centric optimization with gpus. IACR Transactions
on Cryptographic Hardware and Embedded Systems,
2021(4):114–148.
Lai, S., Yuan, X., Sun, S., Liu, J. K., Liu, Y., and
Liu, D. (2019). Graphse
2
: An encrypted graph
database for privacy-preserving social search. CoRR,
abs/1905.04501.
Li, X., Liu, S., Li, Z., Han, X., Shi, C., Hooi, B., Huang, H.,
and Cheng, X. (2020). Flowscope: Spotting money
laundering based on graphs. In AAAI.
Lyubashevsky, V., Peikert, C., and Regev, O. (2010). On
ideal lattices and learning with errors over rings. In
Annual international conference on the theory and ap-
plications of cryptographic techniques, pages 1–23.
Springer.
Meng, X., Kamara, S., Nissim, K., and Kollios, G. (2015).
Grecs: Graph encryption for approximate shortest
distance queries. In Proceedings of the 22nd ACM
SIGSAC Conference on Computer and Communica-
tions Security, CCS ’15, page 504–517, New York,
NY, USA. Association for Computing Machinery.
Pentland, A. and Hardjono, T. (2020).
2. Data Cooperatives. 0 edition.
https://wip.mitpress.mit.edu/pub/pnxgvubq.
Pitas, I. (2016). Graph-based social media analysis, vol-
ume 39. CRC Press.
Robinson, I., Webber, J., and Eifrem, E. (2015). Graph
databases: new opportunities for connected data. ”
O’Reilly Media, Inc.”.
Voronova, L. and Kazantsev, N. (2015). The ethics of big
data: Analytical survey. In 2015 IEEE 17th Confer-
ence on Business Informatics, volume 2, pages 57–63.
Wang, Q., Ren, K., Du, M., Li, Q., and Mohaisen, A.
(2017). Secgdb: Graph encryption for exact shortest
distance queries with efficient updates. In Financial
Cryptography.
Heterogeneous Graph Storage and Leakage Prevention for Data Cooperatives
205
