Optimization of a Deep Reinforcement Learning Policy for

Construction Manufacturing Control

Ian Flood and Xiaoyan Zhou

Rinker School, University of Florida, Gainesville, FL 32611, U.S.A.

Keywords: Control Policies, Construction Manufacture, Decision Agents, Deep Neural Networks, Precast Reinforced

Concrete Components, Process Simulation, Reinforcement Learning.

Abstract: The paper is concerned with the optimization of a deep learning approach for the intelligent control of a

factory process that produces precast reinforced concrete components. The system is designed and optimized

to deal with the unique challenges associated with controlling construction work, such as high customization

of components and the need to produce work to order. A deep reinforcement learning strategy is described

for training an artificial neural network to act as the factory control policy. The performance of the approach

is maximized via a sensitivity analysis that ranges key modelling parameters such as the structure of the neural

network and its inputs. This set of experiments is conducted on data acquired from a real factory. The study

shows that the performance of the policy can be significantly improved by an appropriate selection of the

modelling parameters. The paper concludes with suggestions for potential avenues for future research that

could build upon the current work and further advance the approach.

1 INTRODUCTION

Manufacturing construction components in a factory

has the potential to overcome many of the

inefficiencies of traditional on-site construction

methods. Achieving production efficiency in a

construction factory is, however, far more difficult

than for other manufacturing industries. The

techniques used in mass production are not suitable

for construction work. The workload is received in

unpredictable batches with significant variations in

demand, and the design of the work can differ widely

both within and between batches, with little or no

reproduction of the components. As a result, work

must be produced on request with limited or no

possibility for inventory accumulation, and with

significant fluctuations in the demand for productive

resources.

The uncertainties of construction operations and

demand make it challenging to formulate a

straightforward policy for efficient control. One

potential solution to this problem is to employ

artificial intelligence (AI) agents to assist with

operation control. These agents could function as

advisors in a human-in-the-loop system or as

controllers in an automated environment, providing

solutions whenever an operational decision is

required. This approach shows promise in improving

construction operations as shown by Flood and Flood

(2022).

There is limited use of AI-based decision agents

for controlling operations in the construction

industry. In a study by Shitole et al. (2019), an agent

was developed using artificial neural networks

(ANNs) and reinforcement learning (RL) to optimize

a simulated earth-moving operation. The agent

performed better than previously published heuristics

that were designed by hand. RL is a learning

technique that has demonstrated much success in

recent years by discovering and rewarding behaviour

(Sutton and Barto, 2018). The earth-moving system

in the study consisted of two excavators and a fleet of

dump trucks. The agent's role was to direct the trucks

to either of the excavators at a junction on the return

road, with the goal of maximizing the overall

production rate of the system.

A drawback of the approach adopted by Shitole et

al. (2019) is its lack of extensibility, meaning the agent

can only be applied to the earth-moving system

considered in the study. If applied to a new situation

with a different site layout or equipment combination,

the agent would require redevelopment. Although this

could be done prior to starting a new construction

Flood, I. and Zhou, X.

Optimization of a Deep Reinforcement Learning Policy for Construction Manufacturing Control.

DOI: 10.5220/0012091400003546

In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 82-91

ISBN: 978-989-758-668-2; ISSN: 2184-2841

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

operation, it would still be a significant planning

burden.

Given current technology, an alternative area

where AI can be applied more immediately without

the extensibility issue is factory-based manufactured

construction. In this context, the lifespan of an AI

agent should be relatively long and endure until any

reconfiguration of the factory system is required or a

change occurs in its operating environment. Flood

and Flood (2022) undertook a proof-of-concept study

that showed that an RL trained deep artificial neural

network (DANN) can significantly outperform a

hand-crafted rule-of-thumb approach to making

decisions in the control a construction factory. The

focus of their study was factory-based production of

precast reinforced concrete (PRC) components,

where the arrival of batches followed a Poisson

process, the number of components in a batch was

determined stochastically, and all components were

custom designed and therefore varied in their

processing times.

Researchers such as Benjaoran and Dawood

(2005), Chan and Hu (2002), and Leu and Hwang

(2001), have examined ways to optimize precast

reinforced concrete (PRC) component production

using genetic algorithms (GAs). The approach proved

to be effective although heuristic search techniques

like GAs can be computationally demanding, making

them unsuitable for scenarios where decisions need to

be made promptly.

Once trained, RL solutions based on a learned

model like the one developed by Shitole et al. (2019)

can produce prompt solutions to a decision problem.

Several researchers, such as Waschneck et al. (2018),

Zhou et al. (2020), and Xia et al. (2021), have utilized

this method for the control of factory operations and

have observed encouraging results when compared to

conventional approaches like rules-of-thumb.

However, these applications have been beyond the

scope of construction manufacturing, and therefore,

fail to address numerous challenges within this

industry.

This study represents a significant advancement

beyond the proof-of-concept work reported by Flood

and Flood (2022). It conducts a comprehensive

analysis of the impact of the DANN's structure, input

variable selection, and RL algorithm variables on the

system's performance, with the ultimate goal of

optimization. In addition, the RL policy is applied to

a genuine factory scenario, demonstrating its practical

application in a real-world context.

2 PROCESS CONTROL

2.1 Decision Agents

Both controllable and uncontrollable events shape the

trajectory of a construction manufacturing system in

the future and therefore its performance. The

controllable events can be leveraged to direct this

trajectory in a favourable direction for the

manufacturer, maximizing productivity and/or profit.

This is accomplished by making optimal decisions at

critical junctures, such as prioritizing tasks in a queue,

determining when to maintenance equipment, and

allocating machines to processes.

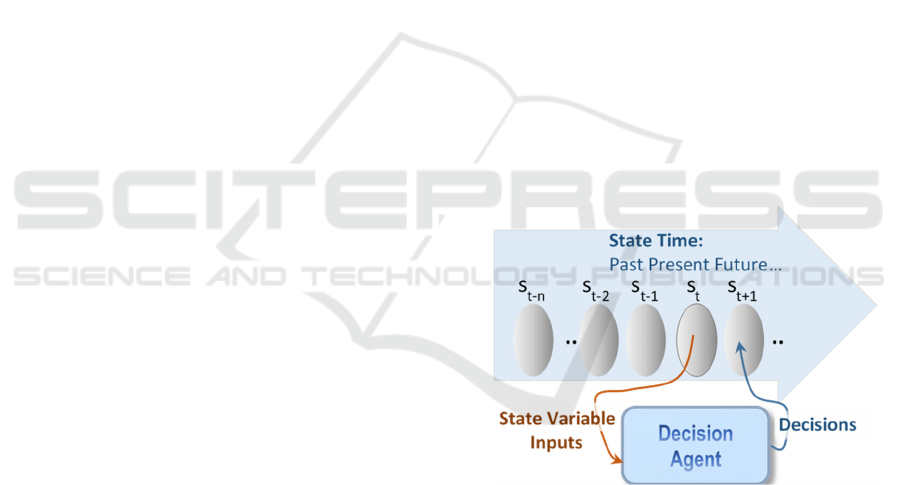
Figure 1 demonstrates how one or more agents

make decisions dynamically throughout the system's

lifetime by monitoring relevant variables that define

the system's current state (s

), and utilizes this

information to determine appropriate actions at the

next state (s

t+1

). While the agent's actions are

generally focused on the immediate future to make

use of the most relevant and accurate information,

they may also extend to events further in the future

for decisions with long lead times. The decisions

made by the agents will affect the performance of the

system over time.

Figure 1: Process control by a Decision Agent.

Decision agents can be categorized as search-

based or experience-based entities (Flood & Flood,

2022). Search-based agents, including blind and

heuristic methods, adopt a systematic approach to

explore the solution space in search of the optimal

action. They create a solution that is tailored to the

specific problem instance at hand, which can

potentially lead to better optimized solutions than

experience-based agents. Moreover, search-based

agents are highly adaptable, allowing them to be

easily modified to new versions of the problem.

However, they may not be suitable for situations that

Optimization of a Deep Reinforcement Learning Policy for Construction Manufacturing Control

require swift decision-making due to their

computational complexity.

On the other hand, experience-based agents, such

as rules-of-thumb and ANNs, rely on past exposure

to similar situations to make decisions. Once

developed, these agents can rapidly generate

decisions. However, their solutions are generic, rather

than customized to each specific situation, which can

result in suboptimal decisions compared to those of

search-based agents. Additionally, experience-based

agents typically lack extensibility, meaning that each

new version of the problem requires the agent to be

redeveloped. This redevelopment process involves

acquiring and integrating large amounts of new

information on system behaviour, making it time-

consuming and resource-intensive.

This paper compares the performances of two

experience-based agents used to decide which PRC

component to process next from a queue, baselined

against a random decision policy as detailed in

section 3.2. The two experience-based methods

considered are a rule-of-thumb and a RL trained

DANN, representing two extremes in policy

complexity. DANNs are a type of ANN that feature

multiple hidden layers or recursion between units.

This additional structure increases the functional

complexity of the model, but also presents additional

challenges in its development. Despite being an

experience-based approach, the development of the

DANN will involve the use of search techniques to

find effective training solutions, in the form of

reinforcement learning (RL) techniques.

2.2 DANN Developing Strategies

In a construction manufacturing environment,

optimal solutions to decision problems are difficult to

determine beforehand or through direct observation

of the real system. As a result, using supervised

training techniques directly for developing a DANN

is not feasible. However, there are several ways to

address this challenge, such as adopting a hindsight

strategy where the agent explores different decision

paths and chooses the most successful ones,

effectively learning through trial-and-error. The most

successful decision paths found at any one stage can

be used to train or further train the DANN. The

updated DANN can then be used search for even

better decision paths. This approach is the essence of

RL and can provide a viable alternative to direct

supervised training for developing a DANN in

construction manufacturing environments (Flood &

Flood, 2022).

Experimenting with alternative decision policies

using the real system is not feasible in construction

production, including factory-based construction

manufacturing. Construction work is typically unique

are rarely reproduced, making it almost impossible to

compare the effectiveness of alternative strategies

through direct experimentation. Artificially

reproducing work is also not a practical option, given

the cost and time required to manufacture a

construction component.

One way around this problem is to build a

simulation model of the construction production

system, and then to use this to explore and test

alternative policies. Information about the real system

and its past behaviour would be used to develop and

validate the simulation model. The information

gathered from the simulated system would be used to

develop and validate the policy, as described in

section 4.1.

3 MODELLING

3.1 Factory Production Simulator

Figure 2 shows the factory based process model used

for simulation, taken from the real system reported by

Wang et al. (2018), representing the manufacture of

precast reinforced concrete (PRC) components such

as walls, floors, beams, and column units. The system

selected was chosen as it captured the following

challenging and somewhat unique features of

construction manufacturing:



orders arrive in a sparse random manner, must be

made to order and cannot be stockpiled;



each order consists of a batch of components

variable in number;

Figure 2: Factory based process model for precast reinforced concrete (PRC) components.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

 many if not all components are unique in design

both within a batch and between batches, and

therefore have variable handling times at each

process;

 all components have uncertainty in the handling

times at each process; and

 all components must be delivered by a given date

in accordance with a site assembly schedule.

The study also incorporates several assumptions

regarding the logic of the PRC manufacturing system:

 the processes are executed sequentially by all

components, in the order shown in Figure 2;

 the order in which components are served can

change between processes; and

 each process has just enough resources to handle

one component at a time, with the exception of the

Cure process, which can process an unlimited

number of components simultaneously.

The stochastic time related data used in this study was

taken from Wang et al. (2018). This is summarized

in Table 1, along with the distribution types used. The

units of time are not given because the behaviour of

the system is given by the relative values of these data

rather than by their absolute values.

Table 1: Modelling time parameters.

stem Variable Distribution Parameters

Order arrival time

Poisson

process

Arrival rate (λ)

7,000

Batch size

Discretized

triangular

Min Mode Max

1 20 100

Forms duration

Triangular

distribution

Min Mode Max

130 150 170

Rebar duration Fixed

Min Mode Max

120 200 250

Concrete duration

Triangular

distribution

Min Mode Max

0 50 70

Cure duration Fixe

Strip duration

Triangular

distribution

Min Mode Max

80 100 120

Delivery duration

Triangular

distribution

Min Mode Max

30 50 70

Contingency relative

to site assembly time

Triangular

distribution

Min Mode Max

10 100 200

When an orders at the factory it consists of a batch

of PRC components, the number of which is sampled

from a positively skewed triangular distribution,

rounded to a positive integer. The arrival of orders is

considered to be a Poisson process, with an arrival

rate, λ, selected so that the work demand would

slightly exceed the factory production – in this way

the DANN will have something to improve upon.

Each PRC component is considered to have a

different design and therefore their process durations

(for Forms, Rebar, Concrete, Strip, and Delivery) are

sampled separately. Curing time is considered to be

the same for all PRC components. On site delivery of

a PRC component is measured as a contingency time

beyond the sum of the component’s process

durations, and sampled from a triangular distribution.

3.2 Policy Types Considered

The PRC component factory process is managed by a

decision agent, as illustrated in Figure 2. When a

process becomes vacant, the agent selects a PRC

component from the appropriate queue for

processing, using its current policy. Using the

parameters outlined in Table 1, it was found that the

only bottleneck in the system was at the Forms

process. As such, the rule-of-thumb policy (described

below) was used as the default policy type for all

processes except the Forms process. For the Forms

process, two alternative experience-based policies

were considered baselined against a random policy:

1. A DANN based policy developed using the RL

method described in section 4. The selection of a

PRC component is based on the current state of

the system and predictions about the handling

times for all the PRC components at Forms

processes.

2. A rule-of-thumb policy in which the PRC

component with the least remaining contingency

time in the queue is selected. Note, negative

contingencies (delays) are possible. This type of

policy was included as the default and, when

implemented at the Forms process, it acts as a

performance benchmark for comparison with the

DANN based policy.

3. A random policy strategy in which the PRC

component is selected from the Forms queue

using a uniformly distributed random variate.

This was included as a baseline for comparison

with the DANN policy.

3.3 DANN Structure

The DANN has a layered feedforward structure as

shown in Phase II of Figure 3.

3.3.1 Input Layer

The input layer receives spatiotemporal information

about the state of the system and the work to be

completed. The input values specify the estimated

process durations and the remaining contingencies for

Optimization of a Deep Reinforcement Learning Policy for Construction Manufacturing Control

Figure 3: Three phase reinforcement learning DANN development cycle.

the PRC components waiting to be processed. These

data are normalized at the input for each process. The

location of the values at the input indicates the

position in the queue, and the relevant process.

An issue with this approach stems from the fact

that the structure of the inputs to the DANN is fixed

(DANNs are structurally rigid) yet the number of

PRC components in the system that need to be

evaluated is variable. To get around this, the DANN

was designed to allow up to a stipulated number (N)

of PRC components to be evaluated in each queue: if

the number of PRC components in a queue is less than

N then the spare input values are set to 0.0; and if the

number of PRC components in a queue is greater than

N then only the first N PRC components will be

evaluated. Furthermore, the N PRC components

evaluated are those with the least contingency (or

greatest delay), and in this sense this the DANN is a

hybrid with the rule-of-thumb policy. For this study,

N was initially set to 20 PRC components, but then

was ranged as reported in section 5 to see how it

affects performance.

3.3.2 Hidden Layers

The number of hidden layers was initially set to 6 and

the number of hidden units per layer was initially set

to 64. These values were then ranged to seek an

optimum configuration for the DANN, as reported in

section 5. All hidden units adopted the ReLU

(rectified linear unit) activation function due its

computational efficiency and avoidance of the

vanishing gradient problem (Glorot et al., 2011).

3.3.3 Output Layer

The DANNs output layer is where the PRC

components are selected from the Forms queue for

processing. All output units use a sigmoid activation

function, thereby limiting their activation to values

between 0.0 and 1.0. Each output unit represents a

position in the Forms queue. The number of units in

a group is limited to N, the number of PRC

components to be evaluated in Forms queue (see

section 3.3.1 above). The current length of the Forms

queue or N, whichever is smallest, determines the

number of units that are active. The values generated

at the active output units are normalized to sum to 1.0.

This allows the output values to be treated as

probabilities for selecting PRC components from the

queue.

The DANN based policy has two modes of

operation:



Exploration. This mode is used to steer the

simulation through alternative partially-

randomized paths, to gathering high-reward input-

output pattern pairs for training the DANN. Monte

Carlo sampling is used to select PRC components

based on the values generated at the relevant

output units. The higher the value generated at an

output, the more likely the corresponding PRC

component will be selected. The broader strategy

adopted for learning is given in section 4 below.



Validation/Implementation. This mode operates

by selecting a PRC component from the queue

based on the output unit that generates the highest

value. The operation is entirely deterministic. It is

used to control the simulated system in non-

training mode, to validate the performance of the

current policy. In addition, this is the mode that

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

would be adopted when using the policy to control

the real system.

4 RL LEARNING STRATEGY

Figure 3 shows the overall RL strategy used to train

the DANN policy. There are three main steps: Phase

I, the collection of training patterns through the

exploration of alternative decision paths; Phase II, the

training of the DANN; and Phase III, validation of the

policy. These phases are iterated through a number of

times until learning converges, each occasion using

the most recent version of the DANN to control the

simulation. Each time the system iterates back to

Phase I, the simulation is reset to a new starting point.

These phases are described in detail in the following

two sections.

4.1 Exploration

In Phase I, the collecting training patterns is

undertaken in a series of stages ‘s’, as illustrated to

the left of Figure 3. Each stage experiments with a

predefined number of trials ‘t’ simulating the

fabrication of a set of PRC components, the reward

length. The trial with the best delivery performance

(see section 4.1.1 below) is selected for later training

of the DANN, and as the lead-in for the next stage in

the simulation. The training patterns collected are the

mappings from input to output for each state

transition in the selected trial.

This process continues until a specified number of

stages have been completed, each time collecting

training patterns from the best performing trial. After

completion of the exploration phase, the system

moves to Phase II, DANN training.

4.1.1 Delivery Performance

Delivery performance is measured in terms of delays

to the delivery of PRC components, with smaller

delays being more favourable. The cost function used

for training is the root-mean-square (RMS) of these

delays, as shown in Equation 1. Note, a PRC

component could be delivered early (indicated by a

negative delay) but the square operation would cancel

the negative sign and thereby treat it as an equivalent

delay. Therefore, the delays in this function are offset

relative to a base value to give greater emphasis to

actual delays over early deliveries.

𝑐𝑜𝑠𝑡 



∑

𝑑



𝑏









𝑛



(1)

where:

d is the delay for the i

PRC component at its

completion;

n is the number of PRC components completed

at the current trial;

b is the base value against which the delays are

offset - this value is the maximum

contingency time possible for a PRC

component.

4.1.2 Rewards

The learning strategy presented here collects training

patterns based on their success in improving delivery

performance. For this reason, a training pattern’s

output values are modified from that produced by the

DANN to increase the probability of making the same

selection in a similar circumstance. The modification

(a reward) is to move the selected output value closer

to 1.0, and to move the other relevant output values

closer to 0.0, remembering that the output values are

treated as probabilities of selecting a RC component

from the queue. The extent of the modification will

be treated as an experimental hyper-parameter,

although for this study the rewards are set to 0.0 and

1.0 without any discount.

4.2 Training

In Phase II, the training patterns collected in the

exploration phase are used to train the DANN, or to

further train it in repeat iterations, as illustrated in the

centre of Figure 3. The DANN was implemented in

Python (Van Rossum, 1995) and PyTorch (Paszke et

al., 2019), using the optimizer RMSProp (root-mean-

square propagation) and the loss function MSELoss

(mean-squared-error) with reduction set to ‘mean’.

Data loading used a mini-batch size of 64 (with a

training set size around 2,000) with shuffling

switched on. The learning rate was set to 0.001.

Training was conducted until the output from the

loss function had converged, which was found to be

within 1,000 epochs.

4.3 Validation

After training, the system moves to Phase III,

validation of the policy, as illustrated to the right of

Figure 3. This involved running the simulation in

validation/implementation mode (see section 3.3.3)

using a PRC component start point not used for

learning. After validation, the RL iteration returns to

Phase I. This cycling through the phases continues

until either the delivery performance at the validation

Optimization of a Deep Reinforcement Learning Policy for Construction Manufacturing Control

phase plateaus or tends to decline. The policy with the

with the best performance measured at the validation

phase is adopted.

5 RESULTS AND DISCUSSION

A series of experiments were undertaken to optimize

the delivery performance of the DANN (see section

4.1.1) by adjusting its structure, and to compare this

to both the rule-of-thumb and random policies

outlined in section 3.2. In the experiments reported

here, training data was collected over a 2,000 PRC

component production run, divided into 100 stages of

20 components each and with 100 trials per stage.

5.1 Performance for the DANN with

the Optimum Structure

Figure 4 shows the performance of the DANN policy

for the last 2,000 PRC components in an 8,000

validation run. Performance is measured on the

vertical axis as the mean improvement in delivery

time for each PRC component compared to the

random policy. For example, a value of 150 indicates

that the policy delivers the PRC components 150 time

units earlier on average than the random policy. The

value is the average measured from the start of the

PRC component completion sequence.

Each grey line in the figure represents the DANN

policy’s performance at different iterations in the RL

process. The dark grey line represents the iteration

that gave the best performance measured at the end of

the 8,000 PRC component validation run. The DANN

always finished learning within 10 iterations in the

experiments reported here. The green dashed curve

represents the performance of the rule-of-thumb

policy.

This figure presents the results after the DANNs

structure had been optimized, having just 1 hidden

layer, 64 hidden units, and N (the number of PRC

components that can be inspected by the policy) set

to 10. After 8,000 PRC components had been

completed in the validation run, the DANN had a

mean improvement per PRC component of about 152

time units, approximately 62 times better than the

rule-of-thumb.

5.2 Optimizing N

Figure 5 shows the relationship between performance

and N, for the first 10 RL iterations. This was for the

DANN with the optimum structure of 1 hidden layer

and 64 hidden units. The graph indicates that the

DANN with N=10 had the best overall performance,

happening at the 5

RL iteration. It is reassuring that

these curves are relatively smooth indicating that

performance dependence is well behaved.

These results are summarized in Figure 6 showing

the improvement in performance versus N. Again, the

curve is smooth giving validity to the assessment that

N=10 is around the optimum solution.

5.3 Optimizing the Internal Structure

of the DANN

Figure 7 shows the dependence of performance on the

number of hidden neurons per hidden layer, for a

Figure 4: Delivery performance for the optimum DANN structure.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Figure 5: Dependence of performance on N versus RL iteration.

Figure 6: Summary of dependence of performance on N.

DANN with 1 hidden layer. In this case, the number

of hidden units is increased logarithmically as ANNs

tend to demonstrate a linear dependence on the

number of units per hidden layer. The curve suggests

the optimum structure is around 64 hidden units.

Finally, Figure 8 shows how performance

changes with the number of hidden layers, assuming

there are 64 hidden units per hidden layer. There is a

clear vertical trend in performance as the number of

hidden layers decreases, with 1 hidden layer being the

optimum. This is somewhat surprising as deep

structures usually perform better than shallow

structures, although not all the time. This could be

due to the nature of the problem, or that the RL

algorithm is not conducive to learning composite

functional relationships. It will be intresting to see if

this basic trend holds for other case studies, or when

multiple DANN policies have to be trained and work

together, serving concurrent processes.

6 CONCLUSION AND FUTURE

WORK

The work presented in this paper was concerned with

optimizing the performance of a RL trained DANN to

provide high-performance control of factory based

construction processes. The problem is particularly

challenging given the nature of construction projects:

uneven and uncertain demand, high customization,

the need to manufacture work to order, and a lack of

opportunity to stockpile work.

Optimization of a Deep Reinforcement Learning Policy for Construction Manufacturing Control

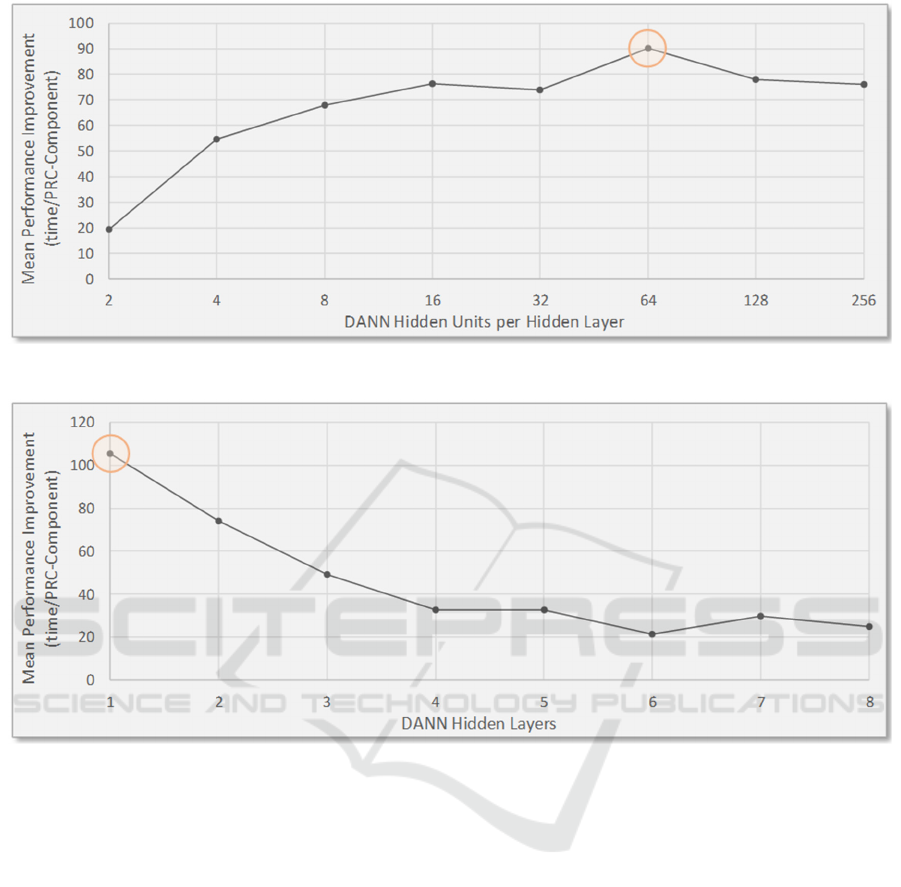
Figure 7: Dependence of performance on the number of hidden units per hidden layer.

Figure 8: Dependence of performance on the number of hidden layers.

A series of experiments, using a real factory as the

case study, showed the approach to significantly

outperform a rule-of-thumb policy and a random

policy in the control of long validation production

runs. In addition, the study demonstrated the

importance of selecting an appropriate structure for

the DANN and its inputs.

Future work will be aimed at improving the

performance of the RL approach, and increasing the

applicability of the technique to a more diverse range

of construction manufacturing problems. This will

include:



Undertaking sensitivity analyses on the RL hyper-

parameters such as the reward term lengths, the

rewards discount rate, the number of trials per

stage, and the number of stages in an iteration.



Consideration of the use of alternative RL

algorithms, and the use of heuristic search

techniques to solve the same problem.



Increasing the range of state data used for input

and the scope of the type of decisions made by the

decision agent.

REFERENCES

Benjaoran, V., Dawood, N., (2005). An application of

Artificial Intelligence Planner for bespoke precast

concrete production planning: a case study. (ISSN:

2706-6568), http://itc.scix.net/paper/w78-2005-a11-5-

benjaoran.

Chan, W.T., and Hu, H., (2002). Production scheduling for

precast plants using a flow shop sequencing model.

Journal of Computing in Civil Engineering, 16 (3), pp.

165-174.

Flood, I and Flood, PDL., (2022). Intelligent Control of

Construction Manufacturing Processes Using Deep

Reinforcement Learning. In Proceedings of the 12th

International Conference on Simulation and Modeling

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Methodologies, Technologies and Applications,

SIMULTECH 2022, Lisbon, Portugal, pp 112-122.

Glorot, X., Bordes, A., Bengio, Y., (2011). Deep Sparse

Rectifier Neural Networks. In proceedings of the

Fourteenth International Conference on Artificial

Intelligence and Statistics, Proceedings of Machine

Learning Research, 15, pp. 315-323.

Leu, S., and Hwang, S., (2001). Optimal repetitive

scheduling model with sharable resource constraint.

Journal of Construction Engineering and Management,

127 (4), pp. 270-280.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., … Chintala, S., (2019). PyTorch: An

Imperative Style, High-Performance Deep Learning

Library. In Advances in Neural Information Processing

Systems, 32, pp. 8024–8035.

Shitole, V., Louis, J., Tadepalli, P., (2019). Optimizing

Earth Moving Operations via Reinforcement Learning,

In 2019 Winter Simulation Conference (WSC), pp.

2954-2965.

Sutton, R., Barto, A. (2018). Reinforcement Learning: An

Introduction, The MIT Press. London, 2

edition.

Van Rossum, G., & Drake Jr, F. L., (1995). Python

reference manual. Centrum voor Wiskunde en

Informatica Amsterdam.

Wang, Z., Hu, H., and Gong. J., (2018). Framework for

Modeling Operational Uncertainty to Optimize Offsite

Production Scheduling of Precast Components.

Automation in Construction, 86, Elsevier, pp 69-80.

Waschneck, B., Reichstaller, A., Belzner, L., Altenmüller,

T., Bauernhansl, T., Knapp, A., & Kyek, A. (2018).

Optimization of global production scheduling with

deep reinforcement learning. In proceedings of 51

Conference on Manufacturing Systems, CIRP, 72, pp.

1264-1269.

Xia, K., Sacco, C., Kirkpatrick, M., Saidy, C., Nguyen, L.,

Kircaliali, A., Harik, R., (2021). A digital twin to train

deep reinforcement learning agent for smart

manufacturing plants: Environment, interfaces and

intelligence, Journal of Manufacturing Systems, Vol.

58, Elsevier, pp. 210-230.

Zhou, L., Zhang, L., Horn, BKP., (2020). Deep

reinforcement learning-based dynamic scheduling in

smart manufacturing. In proceedings of 53

Conference on Manufacturing Systems, CIRP, 93, pp.

383-388.

Optimization of a Deep Reinforcement Learning Policy for Construction Manufacturing Control