Simulation of Curvature Ductility of Reinforced Concrete Cantilever

Beam Under Variety of Section Ratio

Dewi Pertiwi

, Indra Komara

1,*

, Eka Susanti

1,2

, Heri Istiono

1,2

, Jaka Propika

1,2

Yanisfa Septiarsilia

1,3

, Dita Kamarul Fitria

1,3

and Firdhian Vima Rizaldy

Civil Engineering Department, Institute Technology Adhi Tama Surabaya,

Jl. Arif Rahman Hakim 100, Klampis Ngasem, Sukolilo, Surabaya, East Java, Indonesia

Civil Engineering Department, Petra Christian Unviersity,

Jl. Siwalankerto No.121-131, Siwalankerto, Surabaya, 60236, East Java, Indonesia

Civil Engineering Department, Institut Teknologi Sepuluh Nopember,

Jl. Teknik Kimia, Keputih, Sukolilo, Surabaya, East Java, Indonesia

jakapropika@itats.ac.id, yanisfa.septi@itats.ac.id, ditaka.fitriyah@itats.ac.id, firdhian@gmail.com

Keywords: Curvature Ductility, Moment Curvature, Reinforced Concrete Cantilever Beam, Numerical Analysis,

Structural Evaluation

Abstract: The purpose of this research is to look into the effects that the ductility of reinforced concrete cantilever beams

has on their curvature. A numerical program was simulated to estimate moment-curvature and available

curvature ductility of reinforced concrete cantilever beams with or without axial loads. The study evaluate

five cantilever beams with various factors were examined. Concrete strength, the quantity of longitudinal

reinforcement, and the spacing of transverse reinforcement are the factors that are measured. Beam geometry,

material characteristics, and weight make up the input. properties of the retrofitted material by using a variety

of different approaches. A confined stress-strain curve was generated for concrete using SAP2000's adopted

methods, in the same way that a steel stress-strain model was generated. From the evaluation, the curvature

ductility increases with the longitudinal reinforcement and concrete strength with it representing by the

distance length of cantilever beam. However, there is no discernible relationship between the curve ductility

and the spacing of the transverse reinforcement.

1 INTRODUCTION

When structural integrity depends on resistance to

brittle failure during flexure, reinforced structures'

ductility is a desirable characteristic. Plastic joints

placed strategically throughout the structural frame

can be used to create a ductile behavior in a structure

(Marta, 2014). These are made to be sufficiently

ductile to withstand structural failure once the

material's yield strength has been reached. Based on

the configuration of the moment-curvature relations,

https://orcid.org/0009-0008-1010-1872

https://orcid.org/0000-0001-7260-0855

https://orcid.org/0009-0009-4773-729X

https://orcid.org/0009-0002-7220-3846

https://orcid.org/0009-0008-5622-9513

https://orcid.org/0009-0008-4486-1810

https://orcid.org/0009-0008-9954-0184

the available ductility of plastic hinges in reinforced

concrete is found (Arslan and Cihanli, 2011).

Ductility is defined as the ability to endure

deformations without significantly reducing the

member's flexural capacity (Szerszen, Szwed and Li,

2007). According to the findings of previous study,

this deformability is affected by factors such as the

tensile reinforcement ratio, the quantity of

longitudinal compressive reinforcement, the degree

of lateral tie, and the strength of the concrete (Park

and Paulay, 1975). The ductility of a reinforced

310

Pertiwi, D., Komara, I., Susanti, E., Istiono, H., Propika, J., Septiarsilia, Y., ﬁtria, D. and Rizaldy, F.

Simulation of Curvature Ductility of Reinforced Concrete Cantilever Beam Under Variety of Section Ratio.

DOI: 10.5220/0012104300003680

In Proceedings of the 4th International Conference on Advanced Engineering and Technology (ICATECH 2023), pages 310-315

ISBN: 978-989-758-663-7; ISSN: 2975-948X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

concrete section could be represented as curvature

ductility, see Equation (1).

𝜇





𝜙



𝜙



(1)

𝑀





𝐴



𝑓



𝑑

(2)

𝜙





𝜀





1𝑘



𝑑



𝑓



𝐸





1𝑘



𝑑

(3)

𝑀



0.85

𝑓





𝑎𝑏

𝑑𝑎



𝐴



′

𝑓





𝑑𝑑





(4)

𝜙





𝜀



𝑐



𝜀



𝛽



𝑎

(5)

Where

𝑎

𝐴



𝑓





𝐴



′

𝑓



0.85

𝑓

′



𝑎

(6)

𝑘







𝜌𝜌







𝑛



2𝜌

𝜌



𝑑

𝑛





𝜌𝜌





𝑛

(7)

𝜌

𝐴



𝑏𝑑

(8)

Equation (1) to (8) presenting the curvature

parameter in accordance with (Park and Paulay,

1975), where 𝜇



is curvature ductility and

respectively, 𝜙



and 𝜙



, are curvature ultimate and

curvature point when the reached yield strength.

Normally, 𝜙



defined as the effect of the ultimate

strain from concrete compression and 𝜙



defined as

the influence of the yield strength of reinforcement

steel on the calculation of 𝜙



. The vast majority of

the regulations on the design curvature analysis stated

that the yield curvature of a reinforced concrete beam

should be taken when the tension steel first yields.

This condition, which may be derived from Equation

(2), and (3). Where k, 𝜌 is the tensile reinforcement

ratio and 𝜌



is the compression steel ratio. In addition,

n is the modular ratio were taken from the comparison

of modulus elasticity of steel over modulus elasticity

of concrete. 𝑑

is centroid distance over compressive

force in steel and centroid of tension over concrete.

Furthermore, to understand the ultimate

curvature, Equation (4) – (5) are used. In this stage,

evaluate the capacity of reinforced concrete where the

crushing of RC section occurred. 𝑓′



denoted as

compressive strength, 𝑓



denoted as yield strength,

where 𝛽



is the depth of equivalent rectangular stress

block. The design parameters in accordance with the

SNI 2847-2019 (Badan Standardisasi Nasional,

2019a) and ACI 318-71 (American concrete Institute,

2014) conservatively recommend stress block 0.003.

Some researchers identified the nominal value of

ultimate concrete strain (𝜀



) required to compute

Conventional Curvature Ductility Factor for

unconfined concrete is 0.0035, while it is implicitly

greater for confined concrete.

Figure 1: A moment curvature relationship under three

different stage condition (American concrete Institute,

2014).

𝐸𝐼𝑀𝑅

𝑀

𝜑

(9)

Where EI is the section flexural rigidity.

Figure 2: Curvature behaviour parameter (Olivia, Riau and

Mandal, 2005).

Theoretical moment-curvature analysis for

reinforced concrete structural components can be

performed to determine the available flexural strength

and ductility, provided the stress-strain relations for

Simulation of Curvature Ductility of Reinforced Concrete Cantilever Beam Under Variety of Section Ratio

311

both concrete and steel are known (Arslan and

Cihanli, 2011; Zhou, He and Liu, 2014). Curvature

and the bending moment of the section for a given

load raised to failure can be used to calculate the

moment-curvature relationship (Fischer and Li, 2003,

2003). The illustration of trilinear moment-curvature

in accordance with Park and Paulay can be seen in

Figure 1 (Park and Paulay, 1975). From the

illustration, the curvature classified by three different

straight stages line represent elastic conditions, after

first cracking and yielding. It is also illustrated by

classic elastic Eq. (9), relationship between moment

and curvature. Some past works also investigated

based on variety of concrete materials, which is not

included in the research. The concrete material will

also represent a different behaviour (Komara et al., no

date; Kartiko et al., 2021; Pertiwi et al., 2023)

The study evaluates five different cantilever

beams with the variable of section ratio as the demand

of section dimension which is normally used in the

midrise building. The empirical model was developed

to consent the ductility analysis. Some identifications

also included into this model to corroborate findings.

2 RESEARCH METHODS

The study was carried out by determining the range

of parameters used in the cantilever beam elements.

These parameters came in the sectional beam

property. The length of beam implied as 3 m length

and this length placed as the current case study from

office building located in East Sumatera. The

simulation appears in the same condition, elevate to

14.4 m with four lever stories with 825 m

. The

section model is in accordance with the Figure 3

where the variation presented in Table 1. The f’c used

in this simulation is factually the same for all beam

section, 30 MPa. The phase of evaluation illustrates

in Figure 4.

To identify loading mechanism, SNI 1726-2019

(Badan Standardisasi Nasional, 2019b) is used,

followed by earthquake regulation SNI 1726-2019

and concrete SNI 2847-2019 (Badan Standardisasi

Nasional, 2019a). After clarifying all preliminary

analysis, structural analysis program using SAP2000

is conducted (2000, 2008; Interface, Implemented

and Implemented, 2013). This study relates to the

implementation of load & resistance factors of

cantilever beam can be seen in Figure 4 and the 3D

model in SAP200 can be accessed on Figure 5.

Modification load factor is assigned with the value as







𝑔





9.813.27.

Figure 3: Cross section cantilever beam [unit: mm].

Table 1: Reinforcement proportion varied by length

of cantilever beam.

Section

ratio

(len

th)

Section

dimension

(mm)

Rein.

ratio

Reinforcement

section area

(mm)

L/6 500×350 0.012 1860

L/7 450×300 0.012 1412

L/8 400×300 0.012 1231

L/9 350×250 0.012 874

L/10 300×200 0.012 578

Figure 4: structure reliability concept (Frangopol, Lin and

Estes, 1997).

ICATECH 2023 - International Conference on Advanced Engineering and Technology

312

Figure 5: Three-dimensional illustration building modelling

using SAP2000.

Table 1 inform the distribution of reinforcement ratio

designed into cantilever beam. From that evaluation,

the reinforcement bar used for mid and start point,

respectively 4D15, 150-∅12 and 4D15, 180-∅12.

The total dead load (DL) according to the office

building summarized with the total 1.5 kN/m2 and

DL for roof particularly given less, with 0.65 kN/m2.

The life load (LL) is given higher than DL, count as

2.5 kN/m

and for roof, LL 1.0 kN/m

. The

fundamental period parameter considering the

location, with the detail data are S

= 0.29 with F

0.9 and S

=0.25 and F

= 0.8, is 0.7593.

The computational approach for deriving the

curvature ductility from the moment curvature

behavior of the cross section is as follows, see Eq. 10,

assess the ultimate axial load, and then derive the

curvature ductility (Badan Standardisasi Nasional,

2013).

𝑃







𝐴





𝐴





𝑚𝑎𝑥.𝑠𝑡𝑟𝑒𝑠𝑠





𝐴



𝑓



(10)

𝐴



is the gross area of confined concrete, 𝐴



is the

area of longitudinal steel, 𝑓



is the yield strength.

The strain at the extreme compressive fibre is then

analysed as if the section were applied with a single

axial load without any moment (Mihashi and Leite,

2004; Yu et al., 2017). For the value of fibre strain,

the strain profile is created. It is presumable that strain

varies linearly with beam cross section. As shown in

Figure 4, the section is cut into rectangular strips to

estimate compressive forces in concrete. The relevant

stress-strain models are used to compute the

corresponding stresses in concrete and steel.

Calculations are made for the internal forces

supporting steel (Gagg, 2014; Jensen, Kovler and

Belie, 2016).

Figure 6: Stage of evaluation moment curvature (Zhou, He

and Liu, 2014).

3 RESULTS AND DISCUSSION

In order to conduct an analysis of the 5 beams, the

numerical model was utilized. The output of the

program comprises of numerical results as well as

values for the curvature ductility. The ductility

calculation took into account the parameters that were

taken into consideration. In this section, it will discuss

the effects that the key factors have on the moment-

curvature curves. The stage of the evaluation can be

seen in Figure 6. A comparison of the moment-

curvature relationship for five beams is provided in

Figure 7. These beams have the same concrete

strength and longitudinal reinforcement but differing

confinement reinforcement spacing. When a segment

is constricted, both the ultimate compressive strain

and the ductility of the material are increased. The

Simulation of Curvature Ductility of Reinforced Concrete Cantilever Beam Under Variety of Section Ratio

313

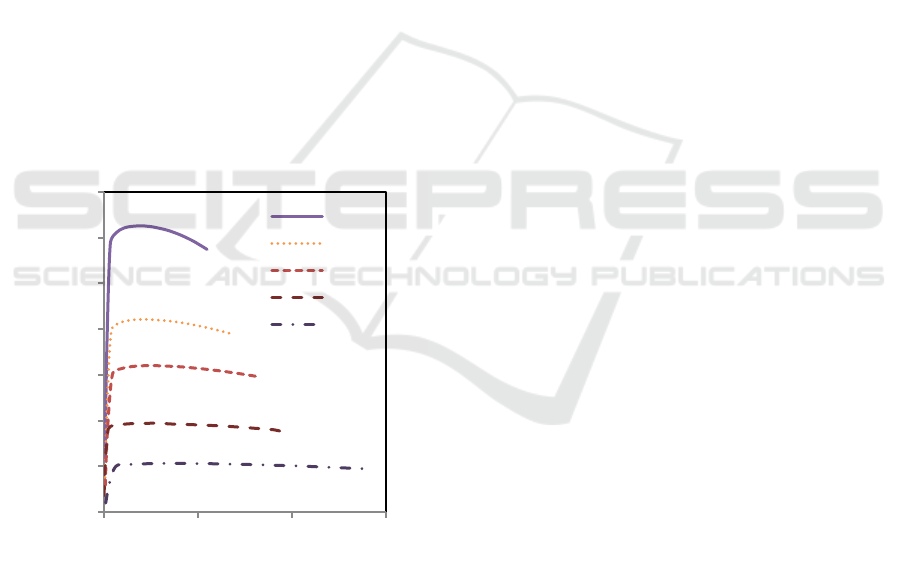
yield and maximum moment capacity of the section

are unaffected by the transverse steel because the

stress-strain model used in the numerical analysis

assumes that the shape of the initial ascending

segment is unaffected by the amount of transverse

steel. Transverse steel reinforcement does not change

yield curvature. However, compressive strain

increases curvature.

It is also determined that closer spacing delays the

buckling of the compressive reinforcement but has no

effect on the material's ductility because failure

occurs in tension steel. In light of this, the researchers

conducting the present study have concluded that a

tighter confinement spacing is ineffective. Figure 7

also shows that parameter of ρ’/ ρ classifying from ¼

to 1.0 which come to be one of the important aspects.

Cantilever beam L/10 shows the lowest moment

curvature ductility, relating to the parameter of

longitudinal reinforcement. The reason is considerate

by the increase amount of tension steel as well as the

depth of the neutral axis. When yield is reached in

longitudinal steel, the stress remains fixed, and the

depth of the neutral axis increases with curvature.

When the strain at the maximum compressive fiber of

concrete is fixed at ultimate condition, the curvature

at ultimate condition reduces.

Figure 7: Moment curvature curves for cantilever beam

with different length.

On the other hand, cantilever beam L/6 illustrates

to have the highest moment curvature ductility. It is

informed that having the very low amount of tension

steel. The breaking of tension steel is a possibility that

could lead to the ultimate situation. In this scenario,

the strain on the tension steel is held constant at the

ultimate condition; hence, the curvature at the final

condition grows. As a consequence of this, the

ductility of the curvature improves in proportion to

the reduction in the amount of tension steel. When

yield is reached in longitudinal steel, the stress

remains fixed, and the depth of the neutral axis

increases with curvature. When the strain at the

maximum compressive fiber of concrete is fixed at

ultimate condition, the curvature at ultimate condition

diminishes.

Curvature ductility decrease gradually as the

variable length is extended, L/6 – L/10. It needs to

improve the confined parameter and also the relation

of various steel reinforcement ratio to accommodate

the difference.

4 CONCLUSIONS

This research is evaluated on verifying the model of

cantilever reinforced concrete beam using SAP2000,

which indicate the value of moment curvature. This

such evaluation to anticipate the fracture condition to

the structure. The modelling process include 5

different cantilever beams classified by length

different. According to the findings, the effect of

materials properties and its geometric on the

curvature ductility of cantilever reinforced concrete

under this case study is very low. As expected, it was

found that length variable determines the value of

moment curvature. The availability of curvature

decreased by the length of span of cantilever beam

which is composed of longitudinal reinforcement.

One that should be noted, there is no significant affect

increase on the confined reinforcement while the

model and the numerical analysis having a good

agreement.

ACKNOWLEDGEMENTS

The author wishes to express their gratitude to the

Ministry of Research, Technology, and Higher

Education of the Republic of Indonesia for their

financial assistance with this research project, as well

as for the support and facilities that were made

available to them. In addition, we would like to

extend our gratitude to ITATS for providing support

within the scope of the study project.

REFERENCES

2000, S. (2008) ‘SAP2000 Basic Analysis Reference

Manual’, in Computers & Structures.

500

1000

1500

2000

2500

3000

3500

0 0,0001 0,0002 0,0003

Moment M (kNm)

Curvature φ (1/mm)

L/6

L/7

L/8

L/9

L/10

ICATECH 2023 - International Conference on Advanced Engineering and Technology

314

American concrete Institute (2014) Building Code

Requirements for Structural Concrete, American

Concrete Institute.

Arslan, G. and Cihanli, E. (2011) ‘Curvature ductility

prediction of reinforced high ‐ strength concrete beam

sections’, 3730. doi: 10.3846/jcem.2010.52.

Badan Standardisasi Nasional (2013) ‘Beban minimum

untuk perancangan bangunan gedung dan struktur lain.

SNI 1727:2013’, in Bandung: Badan Standardisasi

Indonesia, p. 196. Available at: www.bsn.go.id.

Badan Standardisasi Nasional (2019a) ‘Persyaratan Beton

Struktural Untuk Bangunan Gedung Dan Penjelasan

Sebagai Revisi Dari Standar Nasional Indonesia. SNI

03-2847:2019’, Badan Standarisasi Nasional, (8), pp.

1–695.

Badan Standardisasi Nasional (2019b) ‘Sni 1726-2019’,

Tata Cara Perencanaan Ketahanan Gempa Untuk

Struktur Bangunan Gedung dan Non Gedung, (8), p.

254.

Fischer, G. and Li, V. C. (2003) ‘Deformation behavior of

fiber-reinforced polymer reinforced engineered

cementitious composite (ECC) flexural members under

reversed cyclic loading conditions’, ACI Structural

Journal, 100(1), pp. 25–35. doi: 10.14359/12436.

Frangopol, D. M., Lin, K.-Y. and Estes, A. C. (1997)

‘Reliability of Reinforced Concrete Girders under

Corrosion Attack’, Journal of Structural Engineering,

123(3), pp. 286–297. doi: 10.1061/(asce)0733-

9445(1997)123:3(286).

Gagg, C. R. (2014) ‘Cement and concrete as an engineering

material: An historic appraisal and case study analysis’,

Engineering Failure Analysis. Elsevier Ltd, 40, pp.

114–140. doi: 10.1016/j.engfailanal.2014.02.004.

Interface, U., Implemented, E. and Implemented, E. (2013)

21.

Jensen, O. M., Kovler, K. and Belie, N. De (2016) Concrete

with Supplementary Cementitious Materials.

Kartiko, A. S. et al. (2021) ‘Analisis Geometri Bangunan

Terhadap Kinerja Seismik Menggunakan Direct

Displacement Based Design Method’, 04(September).

Komara, I. et al. (no date) ‘Experimental investigations on

the durability performance of normal concrete and

engineered cementitious composite’.

Marta, S. (2014) ‘Shear failure mechanism in concrete

beams’, Procedia Materials Science. Elsevier B.V.,

3(Vd), pp. 1977–1982. doi:

10.1016/j.mspro.2014.06.318.

Mihashi, H. and Leite, J. P. D. B. (2004) ‘State-of-the-art

report on control of cracking in early age concrete’,

Journal of Advanced Concrete Technology, 2(2), pp.

141–154. doi: 10.3151/jact.2.141.

Olivia, M., Riau, U. and Mandal, P. (2005) ‘Curvature

Ductility of Reinforced Concrete Beam’, Jurnal Teknik

Sipil, 6(June), p. 13.

Park, R. and Paulay, T. (1975) Reinforced Concrete

Structure Strength and Deformation of Members with

Shear

Pertiwi, D. et al. (2023) ‘Performance of High-Strength

Concrete Properties for Two Locally Available

Aggregates : Partial Gradation Approaches’, 20(3).

Szerszen, M. M., Szwed, A. and Li, V. C. (2007) Flexural

Response of Reinforced Beam with High Ductility

Concrete Material, Brittle Matrix Composites 8.

Woodhead Publishing Limited. doi:

10.1533/9780857093080.263.

Yu, K. et al. (2017) ‘A strain-hardening cementitious

composites with the tensile capacity up to 8%’,

Construction and Building Materials. Elsevier Ltd,

137, pp. 410–419. doi:

10.1016/j.conbuildmat.2017.01.060.

Zhou, J., He, F. and Liu, T. (2014) ‘Curvature ductility of

columns and structural displacement ductility in RC

frame structures subjected to ground motions’, Soil

Dynamics and Earthquake Engineering. Elsevier, 63,

pp. 174–183. doi: 10.1016/j.soildyn.2014.03.009.

Simulation of Curvature Ductility of Reinforced Concrete Cantilever Beam Under Variety of Section Ratio

315