Structural Modelling and Assessment of RC Beam-Column Joints

Subjected to Seismic Loads for Progressive Collapse Approach

Jaka Propika

1,2 a

, Yanisfa Septiarsilia

1,3 b

, Dita Kamarul Fitria

1,3 c

, Eka Susanti

1,3 d

Dewi Pertiwi

, Heri Istiono

1,2 f

and Indra Komara

1,* g

Civil Engineering Department, Institute Technology Adhi Tama Surabaya, Jl. Arif Rahman Hakim 100, Klampis Ngasem,

Sukolilo, Surabaya, East Java, Indonesia

Civil Engineering Department, Petra Christian Unviersity, Jl. Siwalankerto No.121-131, Siwalankerto, Surabaya, 60236,

East Java, Indonesia

Civil Engineering Department, Institut Teknologi Sepuluh Nopember, Jl. Teknik Kimia, Keputih, Sukolilo, Surabaya, East

Java, Indonesia

dewipertiwi@itats.ac.id, heriistiono@itats.ac.id, indrakomara@itats.ac.id*,

Keywords: RC Beam-Column Joints, Progressive Collapse, Reinforced Concrete Finite Element Analysis, Structural

Modelling

Abstract: The surrounding elements of a reinforced concrete frame generally undergo a significant overload that may

result in their own collapse when the frame is subjected to progressive collapse as a result of the loss of a

structural column. This may cause the frame to collapse. One of the most important factors in establishing the

structural resiliency is the rotational capacity of the beams and, as a result of this, the beam-column

connections. The response of the beam-column junction needs to be accounted for in any numerical models

that are developed to analyse the response of the structure in the event of a progressive collapse. In this

research, a systematic literature review of the different modelling approaches for beam-column joints, as well

as the different constitutive models and how easy it is to implement them numerically, are presented. Some

of these models are used to simulate the reaction of a reinforced concrete frame that has already been put

through its paces. The structural response parameters that were calculated are compared to the experimental

findings, and a discussion is had regarding the accuracy of each constitutive model.

1 INTRODUCTION

The term "progressive collapse" refers to a localized

structural failure that causes the neighbouring

members to fail, thereby setting off a domino effect.

It can also be referred to as "disproportionate

collapse." The progressive collapse of a structure can

be caused by a wide variety of events, including but

not limited to earthquake, localized fires, natural

catastrophes, vehicle impacts, terrorist attacks, and

https://orcid.org/0009-0008-5622-9513

https://orcid.org/0009-0008-4486-1810

https://orcid.org/0009-0008-9954-0184

https://orcid.org/0009-0009-4773-729X

https://orcid.org/0009-0008-1010-1872

https://orcid.org/0009-0002-7220-3846

https://orcid.org/0000-0001-7260-0855

many others (Yap and Li, 2011; Salgado and Guner,

2017).

In order to lessen the severity of the effects of a

progressive collapse, a structure needs to incorporate

a variety of different load routes (Lew et al., 2014).

In a prototypical instance of progressive collapse,

wherein a structural column is absent, three

significant load-resisting mechanisms emerge: The

three mechanisms that contribute to the flexural

resistance of structures under load are the

compressive arch action, the plastic hinge action, and

316

Propika, J., Septiarsilia, Y., Fitria, D., Susanti, E., Pertiwi, D., Istiono, H. and Komara, I.

Structural Modelling and Assessment of RC Beam-Column Joints Subjected to Seismic Loads for Progressive Collapse Approach.

DOI: 10.5220/0012105800003680

In Proceedings of the 4th International Conference on Advanced Engineering and Technology (ICATECH 2023), pages 316-323

ISBN: 978-989-758-663-7; ISSN: 2975-948X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

the catenary action. The compressive arch action is a

result of the axial restraint of the surrounding

structure, which provides additional flexural

resistance. The plastic hinge action occurs when the

formation of a plastic hinge causes large structural

displacements on the beams. Finally, the catenary

action is characterized by the development of tensile

resistance due to the presence of cracks (see Figure

1).

Previous research has indicated that the ability of

beams to rotate can effectively regulate the

emergence of catenary actions. This phenomenon is

attributed to the localized deformations that occur at

the connections between the concrete beams and

columns (Parastesh, Hajirasouliha and Ramezani,

2014). Furthermore, beam-column joints are essential

for the purposes of resisting and distributing loads

(Elsouri and Harajli, 2013), in addition to determining

the rotational capability of the beams.

Figure 1: Plastic hinge mechanism (Lew et al., 2014).

Figure 2: Illustrative common models to classify

assessment analysis of RC joints.

In this study, both existing state-of-the-art

numerical beam-column joint modelling

methodologies as well as constitutive behaviors taken

from the existing body of literature are analyzed and

compared. The creation of novel modelling

approaches that are both optimized for effectiveness

and capable of duplicating the behavior of RC joints

is a topic that is now the focus of academic

investigation. In the most recent few decades, a

considerable amount of research has been carried out

on the topic, and a wide variety of modelling

strategies have been proposed (Azoti et al., 2013;

Elsouri and Harajli, 2013; Lew et al., 2014; Parastesh,

Hajirasouliha and Ramezani, 2014; Khan, Basit and

Ahmad, 2021). In general, existing beam column

joint models can be divided into two categories:

mathematical models and experimental models, as

shown in Figure 2.

Figure 3: Scope of investigation; research impact –

experimental models and analytical models.

This scope of the investigation also includes the

research impact considering from various studies,

including experimental program models and

analytical models, as illustrated in Figure 3. This

model criteria inputted on aspects of the collapse

mechanism for RC structures (Lew et al., 2014; De

Risi et al., 2016; Salgado and Guner, 2017).

Structural Modelling and Assessment of RC Beam-Column Joints Subjected to Seismic Loads for Progressive Collapse Approach

317

Previous research developed a number of models

that describe the cyclic behavior of beam–column

connections and explain the gradual decrease in

strength and stiffness that occurs over the course of

multiple cycles (Parastesh, Hajirasouliha and

Ramezani, 2014). In terms of the experimental

program, these formulations were able to accurately

represent the cyclic behavior of the beam–column

couplings (Hosseini et al., 2012). When several

different formulations for the first quarter cycle are

combined, the controlling equation that results are as

follows:

𝑀



=0.172 + 1.03𝛾− 0.167𝛾



− 0.00846𝛾



(1)

where γ is the value that represent the stiffness when

the hinge rotation and the derivative of M/My gives

joint stiffness.

2 SIMULATION AND

NUMERICAL MODELLING OF

BEAM COLUMN JOINTS

Panel shear and bond-slip actions are the two primary

variables that influence the behaviour of the beam-

column joint. When extreme loading is applied to

members that are adjacent to a beam-column

junction, the joint panel zone experiences significant

shear deformation as a consequence of the loading. In

addition, decreasing the flexural resistance of the

beams is a frequent practice that involves terminating

the longitudinal reinforcing rebar inside the joint

(Ilyas et al., 2022).

Because of this, the frame's strength and stiffness

are reduced due to the joint damage mechanism that

is caused by high shear and bond pressures. As a

direct result of this, the frame has less strength and

less stiffness (Celik and Ellingwood, 2008). The

rigid-joint, rotational-hinge, and component models

are the three modelling strategies that have seen the

most widespread application among the many beam-

column joint modelling strategies.

Because rigid-joint models simulate an entirely

rigid connection between the beam and column

elements, joint deterioration can be omitted in these

models (Salgado and Guner, 2017). As a result,

moments can be entirely transferred from one element

to the other. The physical joint core is contained

within the rigid element region, which, as a result of

its more responsive nature, causes the joint injury to

become more concentrated at the point of contact

with the beam or column. Rigid joints yield results

that are somewhat accurate when beam-column joint

degradation is not the dominating structural behavior.

When this is not the case, these models fail to take

into account the actual deformations of the joint

panels, which leads to an inaccurate calculation of

strength and deformation (Pantazopoulou and

Bonacci, 1994).

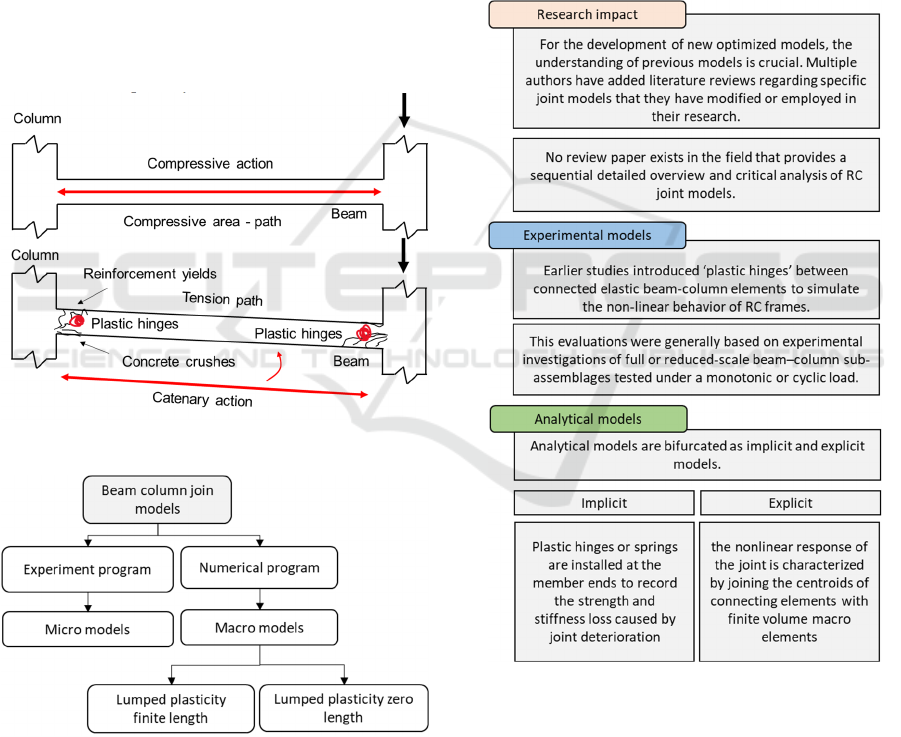
Figure 4: Simulation of Beam column joint modelling

(Khan, Basit and Ahmad, 2021).

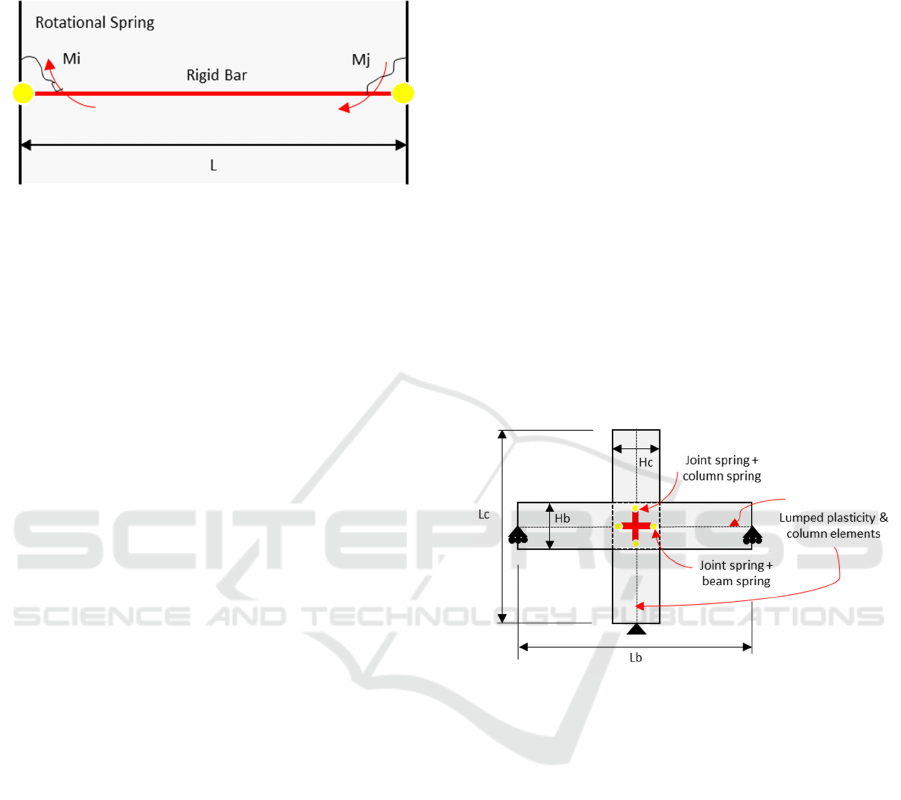
In the models of rotational hinge joints, there is a

single rotational spring that is incorporated at the

center of the beam-column connection. This

rotational spring is responsible for the shear panel

stress-strain displacement and nothing else. The

connection is modelled with rigid-end offsets (Ilyas

et al., 2022). While the moment rotation constitutive

behavior of the center spring is used to simulate joint

deformations, the rigid links are used to ignore any

damage that may have occurred in the components

that make up the joint panel. This model was utilized

quite frequently in the published works for example,

(Celik and Ellingwood, 2008; Salgado and Guner,

2017; Khan, Basit and Ahmad, 2021), and despite the

fact that its methodology was oversimplified, it

produced findings that were reasonably accurate.

However, when the bond-slip action is an essential

behavior, you shouldn't use this model at all.

Component models incorporate a more realistic

constitutive model, which specifically models joint

panel shear deformation and bond-slip. This makes

the component models more accurate representations

of the underlying material. Continuous panel

components or springs usually account for shear

deformation, but 1-D springs account for bond-slip

interactions. There have been many component

models proposed in the scientific literature for

example (Grande et al., 2021; Khan, Basit and

Ahmad, 2021; Ilyas et al., 2022)); however, these

ICATECH 2023 - International Conference on Advanced Engineering and Technology

318

models require many constitutive models for each

considered behavior (such as a spring), which, in

most cases, are not easily accessible or are difficult to

obtain, which hinders their ability to be effectively

applied in real-world situations.

2.1 Shear Panel

A calibrated joint-panel shear stress-strain response

from experimental testing of specimens with a given

shape and reinforcing configuration is used in most

models (De Risi et al., 2016). When using these

models to perform an analysis of a structure that

already exists or is in the planning stages, the

accuracy of the calculations will be significantly

impacted by the degree of similarity that exists

between the structure being modelled and the

experimental dataset that is being used in the model

calibration (Ricci et al., 2016). As a result, the

currently available joint models ought to be utilized

with extreme prudence.

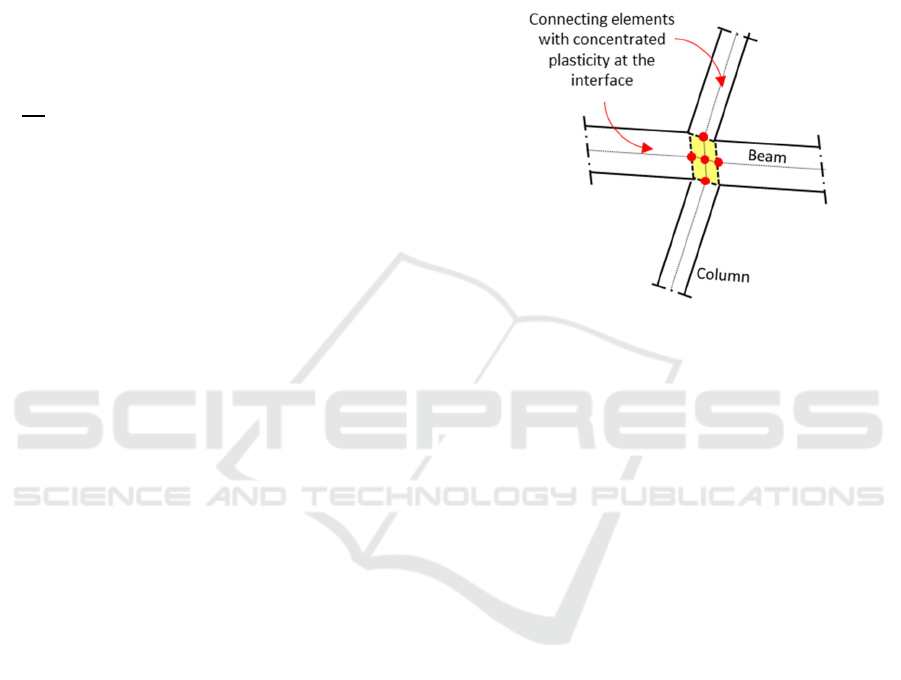
Figure 5 shows that concrete cracking, stirrup

yielding, shear strength, and residual joint shear

capacity regulate joint panel shear stress-strain

response (De Risi and Verderame, 2017). These four

damage states serve as the backbone of the response

(Celik and Ellingwood, 2008; Nawy, 2008;

Alexander, Dehn and Moyo, 2015; De and Wallace,

2015).

Figure 5: Shear panel damage conditions (Kim and Lafave,

2008).

The constitutive model developed by Teraoka and

Fujii characterizes each damage state with a

predetermined strain pattern that is derived from an

experimental collection through curve fitting. The

relationships were established purely on the basis of

the properties of the concrete and the type of joint (i.e.,

an exterior or an interior joint, and transverse beams

or not). As a direct result of this, the model allows for

the rapid definition of four joint backbone locations.

On the other hand, the reduced complexity may lead

to a reduction in dependability and accuracy (Pacific

Earthquake Engineering Research Center, 2000).

Another study proposed a constitutive joint

backbone reaction model (De Risi et al., 2016; Ricci

et al., 2016) and uses fixed strain values and

percentages of the maximum shear stress. The

theoretical shear capacity of the joint is calculated

using the modified compression field theory (Kim

and Lafave, 2008). However, the model uses an

iterative, 17-step calculation process to determine the

shear stress capacity, which limits the model's ability

to be used in real-world situations. The fixed stiffness

values for each segment used in the presented model

(Filippou, Popov and Bertero, 1982), which are based

on the joint maximum shear stress, are used to

compute the stress and strain backbone points.

Because it was calibrated for internal beam-column

joint assemblies with inadequate transverse

reinforcement, it may not be as accurate for joints

with proper design.

Additionally, the joint-shear backbone can be

defined using the variety model with only two points

(Khan, Basit and Ahmad, 2021): brittle failure after

the adjacent beam's flexural yield and maximal shear

capacity. This model is at the beam-joint contact, not

the beam-column connection. Model joint reaction

limits beam moment capacity. The method is

comparatively straightforward due to the bilinear

constitutive behavior. However, this model, which

employs fixed maximal strain and stiffness values,

was created exclusively for interior joints. According

to Kim and LaFave (Kim and Lafave, 2008, 2009),

the damage states of crack, yield, and residual

strength are inversely correlated with the highest

shear and strain values. Its "unified" constitutive

model, which does not use fixed values of stress or

strain, is its primary benefit. It considers the

concrete's compressive strength, in-plane and out-of-

plane geometry, joint eccentricity, beam

reinforcement, and joint transverse reinforcement to

calculate maximum shear and strain.

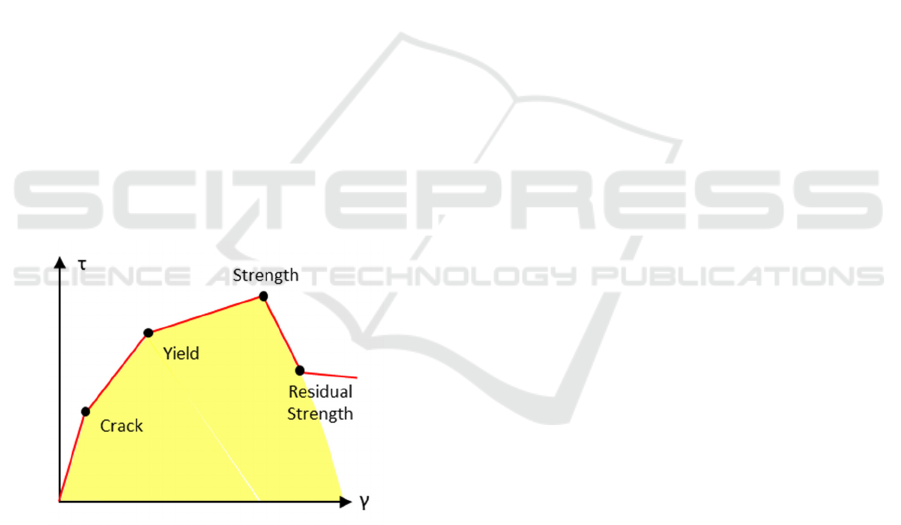
2.2 Cyclic Model

The hysteresis response at beam-column joints under

cyclic loading conditions is usually very pinched. The

beam column joint still experiences unloading as a

result of the compression-tension alternation between

each mechanism, despite the fact that this study only

conducts nonlinear static analyses. For analyses of

progressive collapse, it is crucial to take the joint's

hysteretic reaction into account. The combined cyclic

behavior suggested by Khan et al. is depicted in

Figure 6 (Khan, Basit and Ahmad, 2021).

Structural Modelling and Assessment of RC Beam-Column Joints Subjected to Seismic Loads for Progressive Collapse Approach

319

Figure 6: Hysteretic loop behaviour of beam column joint

(Dabiri, Kaviani and Kheyroddin, 2020).

The majority of current studies determine the

cyclic pinching parameters based on an experimental

approach to curve fitting, much like the backbone

response of the joint; very few studies suggest

pinching that is generally applicable. Due to the

study's understandable analysis of 124 beam-column

joint specimens.

2.2.1 Rotational Hinge Models

The stress–strain envelope and cyclic hysteretic rules

are standard input parameters in rotational hinge

models. A multilinear monotonic curve with many

constitutive models based on empirical equations and

experimental observations controls these models.

This curve controls these models. Several calibration

parameters determine the pinching effect, strength,

stiffness, and energy degradation in following cycles

based on structural reaction. Structural response

determines these characteristics. The original model

in this field was based on the idea that the joint should

flex plastically under lateral loads (Ilyas et al., 2022).

This concept served as the framework upon which the

model was built. The non-linear response that was

created by the shear demand that was made on the

beam as a result of the flexural response of the

connecting elements was able to be captured by the

two rotational hinges that were placed at the

extremities of the member. These hinges were able to

do this because they were located at the extremities of

the member.

In rotating hinge models, examples of typical

input parameters are the stress–strain envelope and

hysteretic rules that explain cyclic activity. Both of

these types of rules describe cyclic behavior. A

multilinear monotonic curve guides these models.

Using empirical equations and actual measurements,

different constitutive models define this curve's

important points. This curve controls and directs the

majority of these models. This curve is also the

primary controller for these models, acting in that

capacity here. Depending on the structural reaction,

calibration factors regulate the pinching effect,

strength, stiffness, and energy degradation in

subsequent cycles. These parameters are determined

by the actual structural response. The real structural

response serves as the foundation for all of these

factors. Ilyas et al., (Ilyas et al., 2022) developed the

first model in this field, and it was founded on the

concept that the joint should be allowed to deform

plastically when it is subjected to lateral loads. This

idea was the foundation of the model. The non-linear

response that was created by the shear demand that

was placed on the beam as a result of the flexural

response of the connecting parts was able to be

captured by the member thanks to the placement of

two rotational hinges that were positioned at the

member's extremities. This can be seen on Equation

(2-3).

𝐾



𝑀



−𝑀



𝜗





(2)

𝑧



𝑀−𝑀



𝑉

(3)

Equation (1) states that each link has a bilinear

elastic strain – hardening relationship-based M-curve.

The equation provided effectively maintains the

length of the plastic zone. The real-time value of the

shear force is represented by the variable M. This

approach is popular to be taken into design due to the

easiest approach and its accuracy related to the joint

mechanics. Notwithstanding, the design intent to fail

on the part of simulate shear panel and diagonal

cracks under cyclic loads. Further development to

include shear panel and bar slip was studied by Ilyas

et al., (Ilyas et al., 2022) represented from various

research with proposed (Celik and Ellingwood, 2008;

Ricci et al., 2016; Salgado and Guner, 2017; Grande

et al., 2021; Ilyas et al., 2022) Equation (4) – (5) as

follows:

𝐴



𝑙



𝑙



×𝐴



(4)

𝑀



𝑙



𝑙



×𝑀



(5)

𝐷=

𝛿



𝛿



𝛽

𝛿



𝑃



𝑑𝐸

(6)

Where

𝑙



is the embedment length while 𝑙



is the

development length and 𝐴



is reinforcement area. D is

illustrated as index of

damage

(0-1), 𝛿



is presented

ICATECH 2023 - International Conference on Advanced Engineering and Technology

320

maximum deformation, 𝛿



is the ultimate deformation, 𝛽 is

the strength of deterioration rate, 𝑃



is yield capacity and



𝑑𝐸 represents hysteretic energy dissipation.

Figure 7: Fixed-end rotation considering deterioration in

joint hysteretic behaviour (Ilyas et al., 2022).

When considering the damage, (De Risi and

Verderame, 2017) the model was developed to

estimate the intensity of damage in relation to

deformation and energy dissipation, as demonstrated

in Equation (6).

The following case is flexural rigidity. Normally,

the flexural rigidity is not considered into joints

mechanics. The previous research learn and take into

consideration the flexural rigidity of the joints, a

model used rigid connections as illustrated in Figure

7 (Celik and Ellingwood, 2008; Ilyas et al., 2022).

The ability of these methods to forecast responses for

a joint panel with a finite length is constrained. Joint

mechanics did not take the joint's flexural stiffness

into account. The corresponding constitutive models

and hysteresis rules depicted the individual rotations

of connecting elements. The cyclic hysteretic

response was founded on experimental findings,

whereas the shear stress-strain behavior was

empirically derived. A rotational spring that simulates

the shear behavior of the concrete core serves as the

joint's sole non-linear reaction prediction device.

Furthermore, the interface shear or bond-slip process

cannot be predicted by this model.

A simplified rotational spring model was put forth

by Khan et. al.(Khan, Basit and Ahmad, 2021) for the

nonlinear cyclic response estimate of RC beam-

column joints. As shown in Figure 8, the joint model

was configured to have rigid offset components and

focused plasticity. A shear-demand ratio was used to

calibrate the rigid offsets, giving a reasonable

approximation of the joint's initial stiffness. Each

connecting member had two springs in sequence at

the end. The non-linear reaction of the connecting

element and joint was recorded by means of the two

springs located at the end of each member. A distinct

M- relationship was employed to ascertain the

individual rotational springs. Each rotational spring

exhibited a distinct moment-rotation reaction curve.

The experimental findings of RC joints are very

closely supported by the model-simulated response.

The research did not include any corner or exterior

joints, only internal joints where the confinement

effects of the transverse beams are significant. The

joint's bond mechanism was also not taken into

consideration in the research.

Typically, the load-drift curve must exhibit a

closure of approximately 20% and 5% as per the

standard parameters established by FEMA356 and

ASCE/SEI 41-06. Based on the studies examined by

Khan et al. (Khan, Basit and Ahmad, 2021). The

preliminary rigidity was observed to be closely

approximated, exhibiting disparities of 20.3% and

5.4% for both FEMA356 and ASCE/SEI 41 – 06. The

proposed beam design beam-column joint element

with rigid offset and details of rotational springs,

based on literature. On the basis of the available

literature, the suggested beam design includes a

beam-column joint element with a rigid offset and

specifics of rotational springs (see Figure 7).

Figure 8: Experimental program – beam column joint

element with rigid offset and proposed rotational springs

(Khan, Basit and Ahmad, 2021).

The utilization of rotational hinge joint models

allows for the autonomous evaluation of the non-

elastic joint reaction while incurring only a negligible

escalation in computational expenses. This approach

offers a simpler and more dependable alternative to

the traditional method of representing joints as rigid

elastic components, while incurring only a marginal

rise in computational expenses. On the other hand,

this modeling technique makes it more difficult to

achieve design objectives and achieve precise

calibration in respect to a variety of loading scenarios

and orientations. For the purpose of constructing an

M-θ curve, it is necessary to make use of a significant

amount of experimental data. In order to develop a

model that is capable of simulating the joint response

with a variety of design features, either a complicated

calibration method that uses enormous data sets or

Structural Modelling and Assessment of RC Beam-Column Joints Subjected to Seismic Loads for Progressive Collapse Approach

321

numerous joint models that each have their own

unique design details are required. Because

experimental data of all potential orientations and

loading scenarios are not currently accessible for

calibration, the applications of these models are

severely restricted. Utilizing the constitutive models

that have been suggested by a variety of researchers

in the past (Pantazopoulou and Bonacci, 1994; Celik

and Ellingwood, 2008; Ricci et al., 2016; De Risi and

Verderame, 2017; Salgado and Guner, 2017; Khan,

Basit and Ahmad, 2021; Ilyas et al., 2022), will allow

for the development of the M-θ curves. The

constitutive models found in the scientific literature

are expressed in terms of shear stress and strain, both

of which can be transformed to M via joint

mechanics.

The proposed cracking onset studied by Uzumeri,

shear stress (τ

) under Equation (7), while its

maximum shear stress value (τ

max

) represented from

various studies as inform as follow Equation (8) –

(11).

𝜏



=0.92



𝑓

𝑐



1+0.29𝜎



(7)

𝜏



= 0.483(𝐵𝐼)

.

(

𝑓

𝑐)

.

(8)

𝐵𝐼 =

𝐴

,

𝑓

,

𝑏



×ℎ



𝑓



(9)

𝜏



=0.642𝛽 1 + 0.5551 −

ℎ



ℎ







𝑓

𝑐 (10)

𝜏



=0.409(𝐵𝐼)

.

(

𝑓

𝑐)

.

(11)

The Equation (8-9) is in accordance with Kim and

LaFave, where Equation (10) follow the calculation

of Vollumn and Newman. As the other illustrations,

Jeon proposed Equation (11). The models that have

been suggested by a variety of researchers can be used

(Yap and Li, 2011; De Risi et al., 2016; Ricci et al.,

2016; Salgado and Guner, 2017; Grande et al., 2021;

Khan, Basit and Ahmad, 2021) for the purposes of

calculating the remaining values of pre-peak and

post-peak shear stress and strains.

3 CONCLUSIONS

A level of understanding, analysis, and evaluation of

the response of RC beam–column joints that has not

been seen in previous decades has been attained

thanks to the significant advancements achieved in

these areas. The non-linear reaction of joints in RC

frames that have been subjected to lateral loads has

been modeled using a variety of different modeling

approaches and methods. The non-linear response of

RC joints is dominated by two primary mechanisms:

panel shear deformation and the bar–slip mechanism.

These mechanisms, which have been modeled using

a variety of different approaches, are responsible for

the majority of the non-linear response. In recent

times, there has been a substantial development in the

modeling techniques, which has resulted in an

improvement in accuracy and a reduction in the

amount of computational effort required. The early

models were built on the results of experimental

research; however, it was discovered that these

models were unreliable because they were contingent

on a large amount of experimental data. As our

knowledge of how connections behaved expanded,

more complex and accurate models were put forward

to explain this behavior.

For the purpose of connecting the elastic beams

and columns to the joint in rotational spring models,

a central zero-length element is utilized as the

connection point. Because the complete non-linear

behavior is combined into a single rotational spring,

it is challenging to individually evaluate the joint

panel shear, interface shear, and bar–slip mechanism.

This is because the non-linear behavior is

encapsulated in a single rotational spring.

REFERENCES

Alexander, M. G., Dehn, F. and Moyo, P. (2015) Concrete

Repair, Rehabilitation and Retrofitting IV, Concrete

Repair, Rehabilitation and Retrofitting IV. doi:

10.1201/b18972.

Azoti, W. L. et al. (2013) ‘Analytical modeling of

multilayered dynamic sandwich composites embedded

with auxetic layers’, Engineering Structures. Elsevier

Ltd, 57, pp. 248–253. doi:

10.1016/j.engstruct.2013.09.030.

Celik, O. C. and Ellingwood, B. R. (2008) ‘Modeling beam-

column joints in fragility assessment of gravity load

designed reinforced concrete frames’, Journal of

Earthquake Engineering, 12(3), pp. 357–381. doi:

10.1080/13632460701457215.

Dabiri, H., Kaviani, A. and Kheyroddin, A. (2020)

‘Influence of reinforcement on the performance of non-

seismically detailed RC beam-column joints’, Journal

of Building Engineering. Elsevier Ltd, 31(March), p.

101333. doi: 10.1016/j.jobe.2020.101333.

De, Z. T. and Wallace, J. W. (2015) ‘Seismic performance

of reinforced concrete dual-system buildings designed

using two different design methods Seismic

performance of reinforced concrete dual-system

ICATECH 2023 - International Conference on Advanced Engineering and Technology

322

buildings designed using two different design

methods’, (June 2019). doi: 10.1002/tal.1227.

Elsouri, A. M. and Harajli, M. H. (2013) ‘Seismic response

of exterior RC wide beam – narrow column joints :

Earthquake-resistant versus as-built joints’,

Engineering Structures. Elsevier Ltd, 57, pp. 394–405.

doi: 10.1016/j.engstruct.2013.09.032.

Filippou, F. C., Popov, E. P. and Bertero, V. V. (1982)

‘Mathematical Modeling of R/C Under Cyclic

Excitations.’, Proceedings of the U.S. National

Congress of Applied Mechanics, 109(11), p. 489.

Grande, E. et al. (2021) ‘A Nonlinear Macro-Model for the

Analysis of Monotonic and Cyclic Behaviour of

Exterior RC Beam-Column Joints’, Frontiers in

Materials, 8(July), pp. 1–26. doi:

10.3389/fmats.2021.719716.

Hosseini, A. et al. (2012) ‘Analytical Investigation of

Seismic Performance of Exterior RC Beam-Column

Joints Rehabilitated with New Scheme’, 15th World

Conference on Earthquake Engineering, (September

2012). doi: 10.13140/2.1.1750.0167.

Ilyas, M. et al. (2022) ‘Review of Modeling Techniques for

Analysis and Assessment of RC Beam–Column Joints

Subjected to Seismic Loads’, Materials, 15(21). doi:

10.3390/ma15217448.

Khan, M. S., Basit, A. and Ahmad, N. (2021) ‘A simplified

model for inelastic seismic analysis of RC frame have

shear hinge in beam-column joints’, Structures.

Elsevier Ltd, 29(August 2020), pp. 771–784. doi:

10.1016/j.istruc.2020.11.072.

Kim, J. and Lafave, J. M. (2008) ‘Joint Shear Behavior

Prediction in Rc Beam-Column Connections Subjected

To Seismic Lateral Loading’, October.

Kim, J. and Lafave, J. M. (2009) ‘Joint Shear Behavior of

Reinforced Concrete Beam-Column Connections

subjected to Seismic Lateral Loading’, Database,

61(November), pp. 119–132. Available at:

http://www.icevirtuallibrary.com/content/article/10.16

80/macr.2008.00068.

Lew, H. S. et al. (2014) ‘Experimental study of reinforced

concrete assemblies under column removal scenario’,

ACI Structural Journal, 111(4), pp. 881–892. doi:

10.14359/51686739.

Nawy, E. G. (2008) Concrete Construction Engineering

Handbook Second Edition. 2nd edn. New Jersey: CRC

Press.

Pacific Earthquake Engineering Research Center (2000)

‘The Second U.S.-Japan Workshop on Performance-

Based Earthquake Engineering Methodology for

Reinforced Concrete Building Structures’, in

Proceedings of the 2nd US-Japan Workshop PBEE

Methodology for RC Building Structures, p. 419.

Pantazopoulou, S. J. and Bonacci, J. F. (1994) ‘On

earthquake-resistant reinforced concrete frame

connections’, Canadian journal of civil engineering,

21(2), pp. 307–324. doi: 10.1139/l94-032.

Parastesh, H., Hajirasouliha, I. and Ramezani, R. (2014) ‘A

new ductile moment-resisting connection for precast

concrete frames in seismic regions: An experimental

investigation’, Engineering Structures. Elsevier Ltd,

70, pp. 144–157. doi: 10.1016/j.engstruct.2014.04.001.

Ricci, P. et al. (2016) ‘Experimental tests of unreinforced

exterior beam-column joints with plain bars’,

Engineering Structures. Elsevier Ltd, 118, pp. 178–

194. doi: 10.1016/j.engstruct.2016.03.033.

De Risi, M. T. et al. (2016) ‘Experimental assessment of

unreinforced exterior beam-column joints with

deformed bars’, Engineering Structures. Elsevier Ltd,

112, pp. 215–232. doi:

10.1016/j.engstruct.2016.01.016.

De Risi, M. T. and Verderame, G. M. (2017) ‘Experimental

assessment and numerical modelling of exterior non-

conforming beam-column joints with plain bars’,

Engineering Structures. Elsevier Ltd, 150, pp. 115–

134. doi: 10.1016/j.engstruct.2017.07.039.

Salgado, R. A. and Guner, S. (2017) ‘Modelling beam-

column joints for progressive collapse analysis’, IABSE

Conference, Vancouver 2017: Engineering the Future -

Report, pp. 592–599. doi:

10.2749/vancouver.2017.0592.

Yap, S. L. and Li, B. (2011) ‘Experimental investigation of

reinforced concrete exterior beam-column

subassemblages for progressive collapse’, ACI

Structural Journal, 108(5), pp. 542–552. doi:

10.14359/51683211.

Structural Modelling and Assessment of RC Beam-Column Joints Subjected to Seismic Loads for Progressive Collapse Approach

323