Design and Build Two Wheel Balancing Robot Simulation with
Fuzzy PID
Santoso, Izzah Aula Wardah, Puji Slamet, Aris Heri Andriawan and Abdul Rahman Algopiki
Electrical Engineering Study Program, Faculty of Engineering, University of 17 August 1945, Surabaya, Indonesia
Keywords: Robot, Fuzzy, PID, Human.
Abstract: This research produces a two-wheeled equilibrium robot with Fuzzy PID as its motion control. Generate
designs and simulations of robotic systems namely gyroscope, PID, Fuzzy simulation, and motor control. In
the PID simulation the stability values are obtained at Kp = 100, Ki = 200, Kd = 10, and from the gyroscope
simulation results obtained a minimum value of 0.074616, a maximum value of 0.110321, an average value
of 0.092469, a standard deviation of 0.025247, sum of data (sum) 0.184937, mean 0.092469. The results of
this study are expected to be developed using a stepper motor, improving the complement or Kalman filter
algorithm to produce a gyroscope sensor signal that is clean from noise interference, as well as adding an
input membership function to get a better motion response.
1 INTRODUCTION
The development of robotics technology has made the
quality of human life even higher. Currently the
development of robotics technology has been able to
increase the quality and quantity of production in
various industries(Tugaev & Kulibaba, 1986; Weik,
2000). Robotics technology has also reached the side
of entertainment and education for humans. One way
to increase the level of intelligence of a robot is to add
sensors, control methods and even provide artificial
intelligence to the robot. Robots that have intelligence
One of them is a self-balancing robot (Frankovský et
al., 2017; Gonzalez et al., 2017; Mai et al., 2019;
Santoso & Mursyid, 2017). balance robot (balancing
robot) is a robot that has two wheels on the right and
left which will not be balanced without a controller.
This balance robot is the development of an inverted
pendulum model that is placed on a wheeled train
(Odry & Fuller, 2018; Xin et al., 2011). Balancing a
two-wheeled robot requires a good hardware circuit
and a reliable control method to maintain the robot's
position perpendicular to the earth's surface. The
concept of a balance robot has been used as a means
of transportation called a segway(Yun et al., 2019).
To
be able to see the performance response of a system
with various combinations of input signals and control
actions is a difficult thing. to perform these steps
required high accuracy and the depiction is often less
accurate. because the transfer function in a system is
in the s region or in the laplace function, to analyze a
system response it is necessary to perform the inverse
laplace function or change from the s region to the t
region. Of course, this is very inefficient and time
consuming. Therefore, software is used, to make it
easier to understand, analyze, and get the desired
system response.
2 LITERATURE REVIEW
2.1 Inverted Pendulum
The equilibrium robot applies an inverted pendulum
model, with the ability to maintain an upright position
with respect to an object(Huang et al., 2011; Odry &
Fuller, 2018). The process of equilibrium is usually
called stability control (Yıldırım & Arslan, 2018).
Two wheels are placed on the ground surface and
allow the robot body to maintain an upright position
and move forward, backward, rotating in an effort to
maintain the center of mass above the axles (Huang
et al., 2011).
124
Santoso, ., Aula Wardah, I., Slamet, P., Heri Andriawan, A. and Rahman Algopiki, A.
Design and Build Two Wheel Balancing Robot Simulation with Fuzzy PID.
DOI: 10.5220/0012108300003680
In Proceedings of the 4th International Conference on Advanced Engineering and Technology (ICATECH 2023), pages 124-128
ISBN: 978-989-758-663-7; ISSN: 2975-948X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Figure 1: Schematic of an inverted pendulum.
As a result of the earth's gravitational force, an
inverted pendulum which is initially perpendicular
then begins to form a tilt angle of theta (θ) and over
time it will fall. Therefore, in maintaining and
maintaining the pendulum's position at a point, a force
action is needed that can restrain the pendulum's
movement. The method used to produce this force is
by making the train go forward in the direction in
which the pendulum will fall (Fahmizal et al., 2017).
2.2 Two-Wheeled Robot Kinematics
In the case of a two-wheeled robot, as presented in
Figure 2, each wheel is controlled by an independent
motor. XG and YG represent the global framework,
while XL and YL represent the local framework. The
speed of the robot is determined by the linear and
angular velocity, which is a function of the linear and
angular speed of each wheel and the distance L
between the two wheels, is the linear and angular
speed of the right wheel, is the linear and angular
speed of the left wheel, θ is robot orientation and (ω)
are the radius of the left and right wheels
V

(
t
)
ω

(
t
)
ω

(
t
)
V

(
t
)
ω

(
t
)
V

(
t
)
ω

(
t
)
r

r

(1)
The linear speed of each wheel is determined by
the relationship between the angular velocity and the
radius of the wheel(Chhotray et al., n.d.).
V

(
t
)
ω

(
t
)
r

,V

(
t
)
ω

(
t
)
r

(2)
The speed of the robot consists of the center mass
linear velocity and the angular velocity generated by
the difference between the two wheels.
V

(
t
)
V

(
t
)





ω

(
t
)
,V

(
t
)

V

(
t
)





ω

(
t
)
(3)
Figure 2: Two-wheeled robot kinematics.
2.3 PID
The PID controller is a combination of three types of
controllers, namely proportional controllers, integral
controllers, and derivative controllers. The purpose of
combining the three types of controllers is to improve
system performance where each controller will
complement and cover each other's weaknesses and
strengths. proportional, integral, and derivative terms
are added up to calculate the output of the PID
controller. By defining a controller output, the final
form of the PID algorithm is:
u
(
t
)
P
(
t
)
K

e
(
t
)
K


e


(
τ
)
dτ  K

()

(4)
𝐾

: Proportional gain, tuning parameters
𝐾

: Integral Gain, tuning parameters
𝐾

: Derivative Gain, tuning parameters
𝑒: Error = 𝑌

𝑌

𝑌

: Setpoint
𝑌

: Process variable
𝑡: Time
𝜏: Integration variable; the value is taken from
time zero to 𝑡
L
(
s
)
K

K

/s  K

s (5)
with
𝑆: The frequency of complex numbers
2.4 Fuzzy Logic
Fuzzy logic is a way of mapping the input space into
the output space, with continuous values(Zadeh,
2009, 2015). Fuzzy expressed in degrees of
membership and degrees of truth. Therefore
something can be said to be partly right and partly
wrong at the same time. In fuzzy logic are
Design and Build Two Wheel Balancing Robot Simulation with Fuzzy PID
125

fuzzification, rule evaluation (inference) based on
rule base, and defuzzification(Medynskaya, 2015;
Sadegh-Zadeh, 1999).
3 DESIGNS
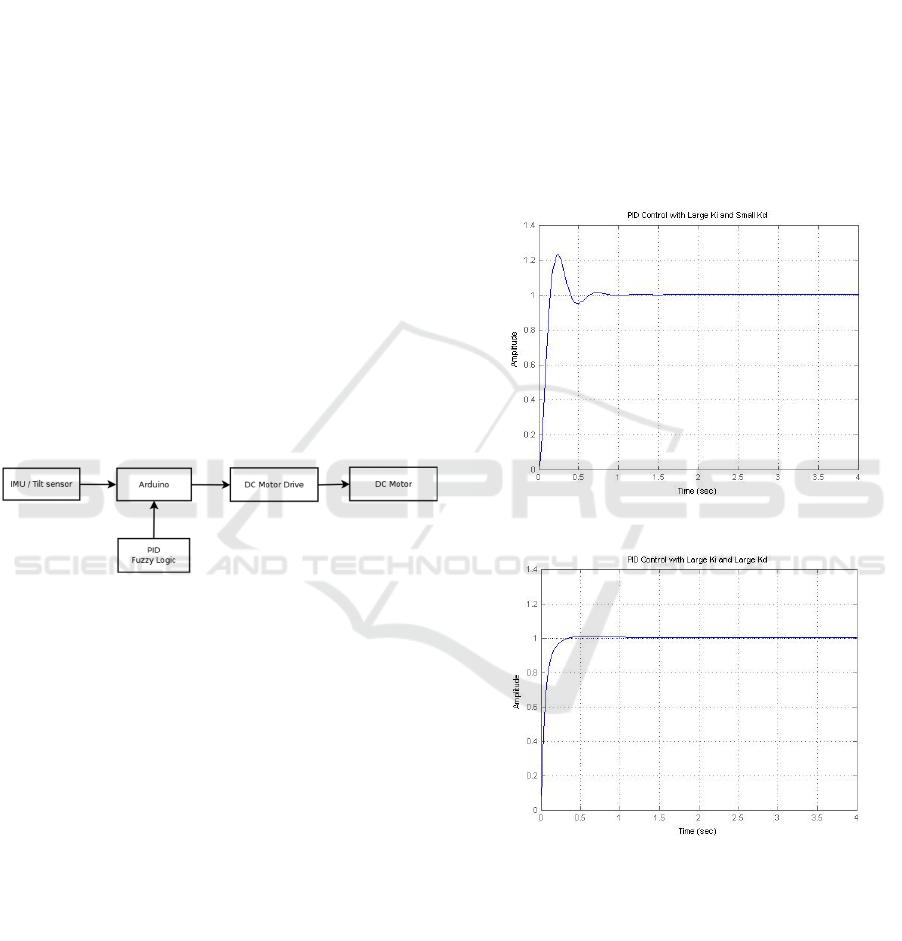
The proposed system design is shown in Figure 3.
PID Fuzzy control is the main control used in this
system. The main input parameter used in PID control
is the error value or the difference between the system
output value (process variable) and the expected
value (set point).(Bimarta et al., 2015). The addition
of Fuzzy control is expected to help improve the
performance of the equilibrium robot. With the
addition of fuzzy logic for the magnitude of the
coefficient value of the PID and combined with the
setpoint of the sensor data value, errors and error
differences will be obtained, to be used as fuzzy logic
input values, the control results will be fed to the
controller to then produce PWM, the value of the
PWM will control DC motor movement(Mai et al.,
2019; Yu et al., 2017).
Figure 3 Balancing robot block diagram
3.1 A Two-Wheeled Balanced Robot
The design of the balancing robot is built using two
wheels, the Arduino controller is placed between the
two wheels, the support circuit is arranged to produce
a balanced pressure between the two wheels, the
sensor circuit is placed on top of the robot, in order to
produce maximum power change, accepted by
Arduino as input data (position) is processed in fuzzy
logic and PID, to then be fed to the DC motor drive
circuit by controlling the PWM to be kept constant
according to the desired value setting, the coefficients
will be displayed on the LCD display, changes in
position x, y, z(Anitha et al., 2019; Cameron, 2019;
Odry & Fuller, 2018; Pan & Zhu, 2018).
4 RESULTS AND ANALYSIS
Using two motors, an L298 motor control, arduino
uno, virtual serial (compin), and virtual terminal, the
software is built on the Arduino IDE, simulation is
carried out by setting pin IN1=0, IN2=1, IN3=0,
IN4=1 , ENA=1, ENB=1, the motor speed is set by
setting the value of ENA, ENB from the lowest value
0 to the highest value 255(Frankovský et al., 2017;
Hsu & Lee, 2011).
4.1 PID Simulation
PID control will produce a response that is influenced
by the parameters Kp, Ki and Kd(Mai et al., 2019;
Odry & Fuller, 2018). The test is carried out by
changing the parameters and paying attention to the
results of the robot's movement, the value and shape
of the signal are obtained as follows:
(a)
(b)
Figure 4 (a) Kp=100, Ki=200, Kd=1, (b) Kp=100, Ki=200,
Kd=10
Figure 4 (b) shows the step response graph has a long
value to be stable, this is because the integral gain
value is small (Ki = Small), so it takes a long time for
the unification action and reduces the fixed condition
error, with the addition of the Ki value the process can
be accelerated, Figure 4(a). With the addition of the
Ki value, the steady-state error can be reduced faster
ICATECH 2023 - International Conference on Advanced Engineering and Technology
126

than before, but also increasing the spikes, with the
addition of the Kd value will reduce the spikes, shown
in Figure 4(b).
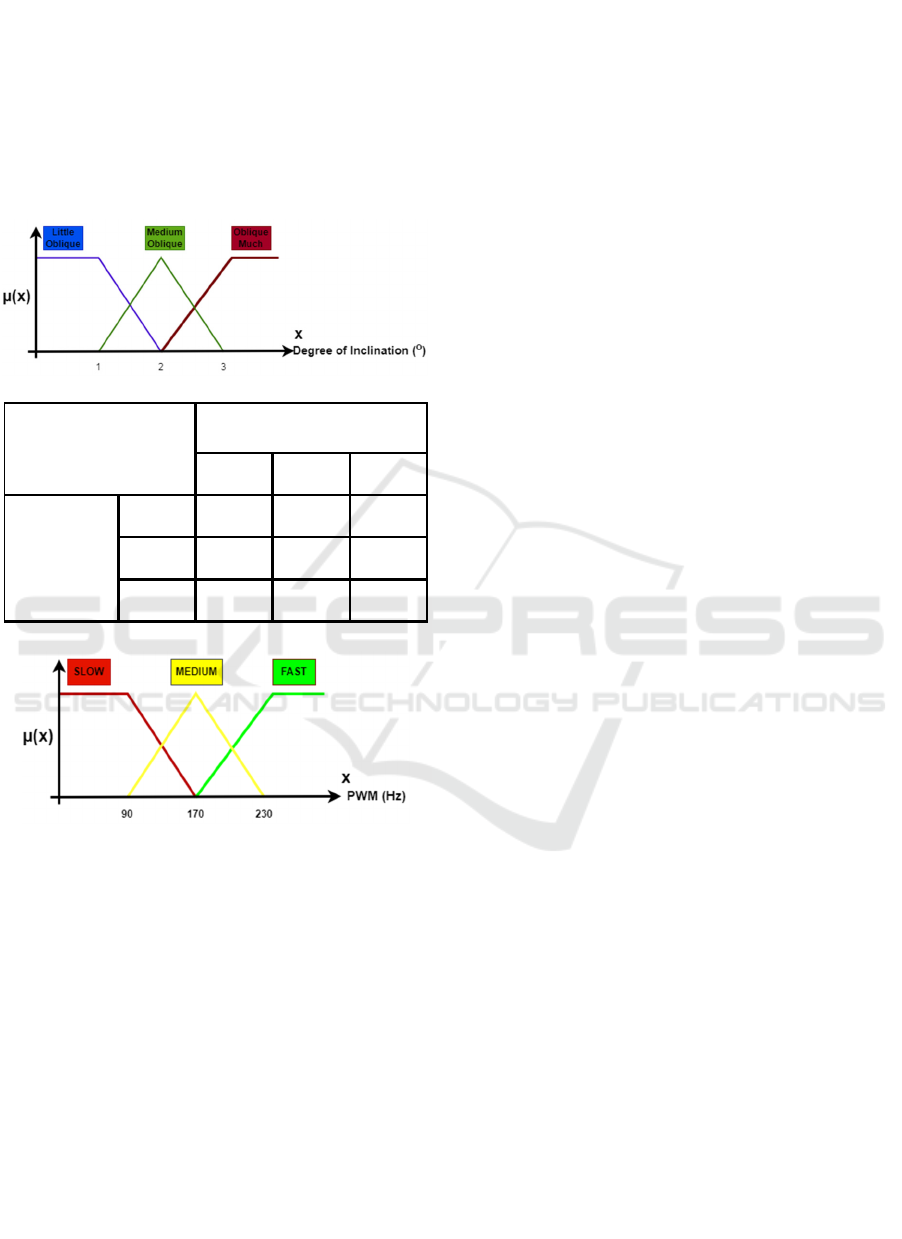
4.2 Fuzzy Logic Simulation
Fuzzy control will produce a final value according to
a predetermined value, in this study the angle value is
obtained from the IMU MPU6050 sensor.
(a)
(b)
(c)
Figure 5 (a) Angle change input membership function, (b)
PWM output membership function, (c) Correlation of angle
change to PWM value
From Figure 5 (d) it can be seen that the pwm
value increases as the angle changes, the pwm value
is 0-120, at an angle movement between 0-5
degrees, the pwm is stable at 130, at an angle
movement of 4.7-13 degrees, the pwm increases at
angle change between 14-20 degrees.
4.3 Gyroscope Simulation
The simulation was made using the proteus program,
by simulating three signals from the gyro sensor with
three variable resistors, and connected to A0, A1, and
A2 from the Arduino. The received value data is
randomized, and forwarded to Matlab for storage and
signal plots.
5 CONCLUSIONS
The results of testing the balancing robot using angle
value data according to the variable input previously
mentioned, it can be seen that the robot graph is able
to balance with a balance range between (-3 to 3
degrees) on a flat plane even with fairly constant
noise or error. From the simulation results, the
minimum value is 0.074616, the maximum value is
0.110321, the average value is 0.092469, the standard
deviation is 0.025247, the sum of data (sum) is
0.184937, the mean is 0.092469.
REFERENCES
Anitha, T., Gopu, G., Nagarajapandian, M., & Devan, PAM
(2019). Hybrid Fuzzy PID Controller for Pressure
Process Control Applications. 2019 IEEE Student
Conference on Research and Development (SCORED),
129–133.
https://doi.org/10.1109/SCORED.2019.8896276
Bimarta, R., Putra, AE, & Dharmawan, A. (2015).
Balancing Robot Using Derivative Integral
Proportional Control Method. IJEIS (Indonesian
Journal of Electronics and Instrumentation Systems),
5(1), 89. https://doi.org/10.22146/ijeis.7157
Cameron, N. (2019). Robot Car. In N. Cameron, Arduino
Applied (pp. 467–497). Apress.
https://doi.org/10.1007/978-1-4842-3960-5_24
Chhotray, A., Pradhan, MK, Pandey, KK, & Parhi, DR (nd).
Kinematic Analysis of a Two-Wheeled Self-Balancing
Mobile Robot. 8.
Fahmizal, F., Setyawan, G., Arrofiq, M., & Mayub, A.
(2017). Fuzzy Logic in Two-Wheeled Inverted
Pendulum Robot. Journal of Information Technology
and Computer Science, 4(4), 244.
https://doi.org/10.25126/jtiik.201744484
Frankovský, P., Dominik, L., Gmiterko, A., Virgala, I.,
Kurylo, P., & Perminova, O. (2017). Modeling of Two-
Wheeled Self-Balancing Robot Driven by DC
Gearmotors. International Journal of Applied
Mechanics and Engineering, 22(3), 739–747.
https://doi.org/10.1515/igame-2017-0046
Gonzalez, C., Alvarado, I., & Peña, DML (2017). Low cost
two-wheel self-balancing robot for control education.
IFAC-PapersOnLine, 50(1), 9174–9179.
https://doi.org/10.1016/j.ifacol.2017.08.1729
Hsu, C.-F., & Lee, B.-K. (2011). FPGA-based adaptive PID
control of a DC motor driver via a sliding-mode
approach. Expert Systems with Applications, 38(9),
Little
Oblique
Medium
Oblique
Oblique
Much
Lit tle
Oblique
Slow Slow Slow
Medium
Oblique
Slow Medium Fast
Oblique
Much
Fast Fast Fast
Fuzzy Logic Ru les
OBLIQUE A NGLE DA TA OF
CURRENTLY
OBLIQUE
ANGLE DATA
OF
PREVIOUSLY
Design and Build Two Wheel Balancing Robot Simulation with Fuzzy PID
127

11866–11872.
https://doi.org/10.1016/j.eswa.2011.02.185
Huang, C.-H., Wang, W.-J., & Chiu, C.-H. (2011). Design
and Implementation of Fuzzy Control on a Two-Wheel
Inverted Pendulum. IEEE Transactions on Industrial
Electronics, 58(7), 2988–3001.
https://doi.org/10.1109/TIE.2010.2069076
Kecskés, I., & Odry, P. (2014). Optimization of PI and
Fuzzy-PI Controllers on Simulation Model of
Szabad(ka)-II Walking Robot. International Journal of
Advanced Robotic Systems, 11(11), 186.
https://doi.org/10.5772/59102
Mai, TA, Dang, TS, Anisimov, DN, & Fedorova, E. (2019).
Fuzzy-PID Controller for Two Wheels Balancing
Robot Based on STM32 Microcontroller. 2019
International Conference on Engineering Technologies
and Computer Science (EnT), 20–24.
https://doi.org/10.1109/EnT.2019.00009
Matsui, N., & Shigyo, M. (1992). Brushless DC motor
control without position and speed sensors. IEEE
Transactions on Industry Applications, 28(1), 120–127.
https://doi.org/10.1109/28.120220
Medynskaya, MK (2015). Fuzzy set theory. The concept of
fuzzy sets. 2015 XVIII International Conference on
Soft Computing and Measurements (SCM), 30–31.
https://doi.org/10.1109/SCM.2015.7190402
Noga, S. (2006). Kinematics and dynamics of some
selected two-wheeled mobile robots. Archives of Civil
and Mechanical Engineering, 6(3), 55–70.
https://doi.org/10.1016/S1644-9665(12)60241-6
Odry, A., & Fuller, R. (2018). Comparison of Optimized
PID and Fuzzy Control Strategies on a Mobile
Pendulum Robot. 2018 IEEE 12th International
Symposium on Applied Computational Intelligence and
Informatics (SACI), 000207–000212.
https://doi.org/10.1109/SACI.2018.8440947
Pan, T., & Zhu, Y. (2018). Using Sensors with the Arduino.
In T. Pan & Y. Zhu, Designing Embedded Systems with
Arduino (pp. 45–100). Springer Singapore.
https://doi.org/10.1007/978-981-10-4418-2_3
Perdukova, D., Fedor, P., & Fedak, V. (2019). A Fuzzy
Approach to Optimal DC Motor Controller Design.
2019 International Conference on Electrical Drives &
Power Electronics (EDPE), 48–53.
https://doi.org/10.1109/EDPE.2019.8883896
Sadegh-Zadeh, K. (1999). Advances in fuzzy theory.
Artificial Intelligence in Medicine, 15(3), 309–323.
https://doi.org/10.1016/S0933-3657(98)00060-8
Santoso, S., & Mursyid, S. (2017). PROPORTIONAL
INTEGRAL (PI) CONTROL ON LINE FOLLOWER
ROBOT. Journal of Science and Informatics, 1(1), 10–
10.
Tugaev, VD, & Kulibaba, V. Ya. (1986). Introduction of an
industrial robot in a machine shop. Metallurgist, 30(10),
380–381. https://doi.org/10.1007/BF00741414
Weik, MH (2000). Manipulating industrial robots. In MH
Weik, Computer Science and Communications
Dictionary (pp. 972–972). Springer US.
https://doi.org/10.1007/1-4020-0613-6_11017
Xin, Y., Xu, B., Xin, H., Xu, J., & Hu, L. (2011). The
Computer Simulation and Real-Time Control for the
Inverted Pendulum System Based on PID. In M. Ma
(Ed.), Communication Systems and Information
Technology (Vol. 100, pp. 729–736). Springer Berlin
Heidelberg. https://doi.org/10.1007/978-3-642-21762-
3_95
Yıldırım, Ş., & Arslan, E. (2018). ODE (Open Dynamics
Engine) based stability control algorithm for six legged
robots. Measurements, 124, 367–377.
https://doi.org/10.1016/j.measurement.2018.03.057
Yu, G.-R., Leu, Y.-K., & Huang, H.-T. (2017). PSO-based
fuzzy control of a self-balancing two-wheeled robot.
2017 Joint 17th World Congress of International Fuzzy
Systems Association and 9th International Conference
on Soft Computing and Intelligent Systems (IFSA-
SCIS), 1–5. https://doi.org/10.1109/IFSA-
SCIS.2017.8023296
Yun, H., Bang, J., Kim, J., & Lee, J. (2019). High speed
segway control with series elastic actuator for driving
stability improvement. Journal of Mechanical Science
and Technology, 33(11), 5449–5459.
https://doi.org/10.1007/s12206-019-1039-x
Zadeh, LA (2009). Toward extended fuzzy logic—A first
step. Fuzzy Sets and Systems, 160(21), 3175–3181.
https://doi.org/10.1016/j.fss.2009.04.009
Zadeh, LA (2015). Fuzzy logic—A personal perspective.
Fuzzy Sets and Systems, 281, 4–20.
https://doi.org/10.1016/j.fss.2015.05.009
ICATECH 2023 - International Conference on Advanced Engineering and Technology
128