Modified Particle Swarm Optimization for Clustering

Muchamad Kurniawan

, Rani Rotul Muhima

, Maftahatul Hakimah

, Siti Agustini

and Rahmi Rizkiana Putri

Department of Informatics, Institut Teknologi Adhi Tama Surabaya, Indonesia

rahmi@itats.ac.id

Keywords: PSO, Clustering, Gaussian Distributional, Internal Cluster Analysis, External Cluster Analysis.

Abstract: The traditional clustering analysis algorithm grouped into several types, one of the most popular is clustering

based on partition. One of the limitations of partition clustering is that the initial centroid. initialization is

critical. Previous studies have used optimization algorithms such as Particle Swarm Optimization (PSO) to

obtain initial centroids. The first contribution in research is to use PSO with the addition of the Mean process

to produce a clustering analysis we call it PSO Mean Clustering (PMC). The second contribution is to use a

partial Gaussian distribution to generate the initial population in the PMC method, and we call it Gaussian

PSO Mean Clustering (GPMC). The datasets used in this research are six clustering datasets to get an internal

and external evaluation. The results obtained by the two proposed methods are better than the PSO clustering

method and traditional K-means based on internal and external evaluation methods compared. Average value

internal evaluation percentage of GPMC across K-means is 3.94%.

1 INTRODUCTION

The Clustering analysis is a branch of science in data

mining that is used to grouping data. Clustering

Analysis is also known as the Unsupervised method.

In other words, the data used does not have classes or

labels. Clustering methods are divided into five types:

clustering based on partition, hierarchical, density-

based, grid-based clustering, and model-based

clustering (Anuradha et al., 2014). Some partition

clustering methods are K-means, K-medoids,

minimum spanning trees, and others (Arthur and

Vassilvitskii, 2007). The clustering based on

hierarchy divided into two approaches: bottom-up

(agglomerative) and top-down (divisive). The next

approach is the density approach, with the most

popular used algorithm is DBSCAN (Auliya, 2019).

STING, OptiGrid, and MAFIA are several clustering

algorithms with a grid clustering approach. And the

last approach based on the model with the most used

algorithm is the Self Organized Map (SOM).

https://orcid.org/0000-0002-8982-4641

https://orcid.org/0000-0002-9746-4973

https://orcid.org/0000-0002-4070-3312

https://orcid.org/0000-0002-6955-9465

https://orcid.org/0000-0002-2755-6039

K-means is the most popular algorithm clustering

based on a partition that is predefined in various

fields(Auliya et al., 2019), (Capó et al., 2020). K-

means is a simple algorithm and makes this algorithm

into the top ten most popular algorithms in data

mining. This algorithm is divided into two parts, the

first part is an initialization, and the other part is

iterative (El-Khatib et al., 2016).

The limitations of the K-means algorithm are:

initialization centroid, optimal cluster, there are

outliers, no cluster members, unbalanced clusters

(Fränti and Sieranoja, 2019), (Gao et al., 2020).

Research (G.G. and K., 2017) specifically describes

local optimal K-means due to the determination

initialization of centroids. Techniques used for the

initialization of centroids are random point, furthest

point, sorting, density-based, projection-based, and

splitting. The test results with many types of datasets,

sorting techniques (max and min) get the most

optimal results.

Kurniawan, M., Muhima, R., Hakimah, M., Agustini, S. and Putri, R.

Modiﬁed Particle Swarm Optimization for Clustering.

DOI: 10.5220/0012111800003680

In Proceedings of the 4th International Conference on Advanced Engineering and Technology (ICATECH 2023), pages 89-96

ISBN: 978-989-758-663-7; ISSN: 2975-948X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

A solution of limitation K-means is to determine

the initial centroid point using the center of data each

cluster (Gupta and Chandra, 2019a), (Gupta and

Chandra, 2019b), (Irani et al., 2016), (Janani and

Vijayarani, 2019). The taking of the first and last

elements is used for determining the starting point.

The spherical technique was used to determine the

initialization centroid of K-means (Kapil et al., 2016).

Initialization partition centroid (p-k-Means) was used

in research (Kim et al., 2020) to obtain more optimal

results. The dataset used for this research includes

Pen Digits, Iris flowers, image segmentation,

Spambase, Wine, and Animal Milk. By adopting the

same motivation as a research (Kim et al., 2020),

modifications are made to improve the K-means

performance. The modification used by removing

outliers on each partition is called MP-K-Means

(Kumar et al., 2020). Hybrid K-means and bagging

for clustering Social Data tweeter media (Kurniawan

et al., 2020).

Several studies used optimization metaheuristic to

improve the performance of the K-means algorithm.

A combination of Genetic Algorithm (GA)

optimization with K-means results in more

competitive performance (Lakshmi et al., 2019),

(Lakshmi et al., 2020), (Madhukar and Verma, 2019).

The combination of Ant Colony Optimization (ACO)

and K-means has been developed by several studies

(Marom and Feldman, 2019), (Muhima et al., 2022).

Particle Swarm Optimization (PSO) algorithm is a

popular optimization algorithm used to improve K-

means performance. PSO K-means was improved by

the implementation of Gaussian Estimation

Distribution and Lévy Flight (Nerurkar et al., 2018).

Traditional PSO is used for the determination of the

initial centroid K-means value(Pacifico and

Ludermir, 2019). Research (Paul et al., 2020) used

spectral clustering as the data distribution for

individual PSO K-means. The silhouette coefficient

is used as an objective function in the combined PSO

and K-means method (KCPSO) (Sajana et al., 2016),

(Shukla and S., 2014). Multi-objective PSO

(MOPSO) combined with K-means to determine the

initial centroid point (Verma and Bharadwaj, 2017).

PSO with operator Crossover from GA is suggested

as a locally optimal solution(Xiaoqiong and Zhang,

2020). Optimization of the PSO inertia parameter is

applied to modify the K-means PSO (Yang et al.,

2020), (Yu et al., 2018). A different approach was

carried out by study (Zeebaree et al., 2017) for

clustering analysis, this approach taken is to use a

heuristic optimization algorithm for clustering.

Heuristic optimization is finding a solution with an

estimated solution with an acceptable time. This

heuristic clustering technique combines Particle

Swarm Optimization (PSO) and K-means (PSO-K-

means) Optimization. PSO is used to initialize

centroid values, and K-means are used to decided data

to certain clusters based on a certain distance.

By looking at previous studies, in this study, we

propose two contributions. The first contribution is

adding mean to update PSO individuals for clustering

we called PSO Mean Clustering (PMC). This

contribution is based on research (G.G. and K., 2017)

by taking the min-max value of sorted data that can

improve the results of K-means. By adding the mean

to PSO clustering will produce more precise centroid

points. The same motivation is used for other

algorithm, this algorithm is generate random based on

the gaussian model on PMC. This generate random is

used to generate an initial swarm, with a proper initial

swarm will obtain optimal fitness. We call the second

contribution is Gaussian PSO Mean Clustering

(GPMC).

The arrangement of this paper includes five parts.

The first part contains an introduction to the paper;

this section explains the research background,

contributions, and objectives of this research. Related

work and research methodology are included in part

two and part three. The fourth part contains the results

and discussion of this research. The conclusion is the

last part of this paper.

2 PROPOSED METHOD

2.1 Objective Function

Cost function or objective function that used is

according to Equation 3, this equation is divide result

from Equation 2 and Equation 1. Equation 1 is used

to calculate sum of distance each member (data) from

its centroid, and equation 2 is used to calculate sum

of distance each member from every centroid. In this

objective function, it is expected that the resulting

centroid is the centroid that has the farthest distance,

by getting the farthest centroid values it will make the

cluster more optimal.

𝑊𝐷𝐶 =

∑

𝑑𝑖𝑠𝑡 (𝑐



,𝐶)





(1)

𝐼𝐶𝐷 =

∑∑

𝑑𝑖𝑠𝑡 (𝑐



,𝐶



)









(2)

𝐶𝑜𝑠𝑡 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛

(

𝑥

)





(3)

where: 𝑛 : total members in centroid

𝑘 : total clusters

𝐶 : centroid in cluster

ICATECH 2023 - International Conference on Advanced Engineering and Technology

𝑐 : members in centroid

𝑥 : particle

2.2 Particle Swarm Optimization

Clustering

The first method proposed is to add the mean process

to the PSO clustering method previously studied

(Nerurkar et al., 2018). PSO Clustering Algorithm is

based on the PSO Algorithm, which uses internal and

external cluster distances as objective functions. The

PSO-clustering algorithm is different from the PSO

algorithm that used as a K-means optimization. In

PSO-clustering, PSO is used to find the initial point

of the centroid before being included in the K-means

process. The PSO-clustering algorithm is described

as follows: determine the starting point of the centroid

presented with the value of the individuals. The

representation of the change in the centroid matrix to

individual PSO can be seen in Figure 1, where Figure

1.a is the centroid matrix, and Figure 1.b is the

individual vector transformation. An individual will

be calculated the cost function.

Figure 1: Transformation of centroid to individual / particle

Algorithm 1: Algorithm for PSO Clustering

Input :

Output: Gbest, fitness value

Initial:

C // number of cluster

max_iter // maximum

iteration/generation

nPop // size of swarm

particles // new position particles with

random

loop : 1;

repeat

for i:1 to nPop

calculate fitness particle[i];

calculate velocity and new position

particle[i];

find and update Gbest and Pbest[i];

end for

loop++;

until loop = max_iter ;

Procedure of PSO clustering can be seen in

Algorithm 1, this algorithm is the same as traditional

PSO. To calculate velocity and update position using

Equation 4 and 5.

𝑉



(

𝑡

)

=𝑤𝑉



(

𝑡−1

)

+𝑐



𝑟





𝑋





𝑋



(

𝑡−1

)



𝑐



𝑟



(𝑋



−𝑋



(

𝑡−1

)

) (4)

𝑋



(

𝑡

)

=𝑉



(

𝑡

)

+𝑋



(

𝑡−1

)

(5)

where: 𝑡 : current time / current iteration

𝑖 : index particle

𝑤 : inertia param (0 – 1)

𝑋





: best position particle

𝑋





: best position in swarm

𝑋



: current position particle

𝑐



: coefficient of Pbest

𝑐



: coefficient of Gbest

𝑟



,𝑟



: random value (0 – 1)

2.3 PSO Mean Clustering

The limitation in PSO Clustering is on particle

updates (centroids). Change particle in PSO

clustering can be seen in Figure 2.a, for example the

black point are members of one cluster and the white

point is the centroid point, centroid will change by

calculate at the centroid on another particle. This can

become a limitation of PSO clustering because a

change in centroid point may not be in the middle of

a members.

Figure 2: Centroid simulation

Algorithm 2: Algorithm for PSO Mean Clustering (PMC)

Input :

Output: Gbest, fitness value

Initial:

C // number of cluster

max_iter // maximum

iteration/generation

nPop // size of swarm

Modiﬁed Particle Swarm Optimization for Clustering

particles // new position particles with

random

loop : 1

repeat

for i:1 to nPop

calculate fitness particle[i];

calculate velocity and new position

particle[i];

find and update Gbest and Pbest[i];

Update particle[i] position with mean

members of each cluster ;

end for

loop++;

until loop = max_iter

;

To handle this, this study proposes a new

procedure on changing the particle value with the

mean of the member each cluster. This algorithm

takes the concept of K-means algorithm works, so

changes in centroid values will be faster and more

precise in the middle of a cluster member as shown in

Figure 2.b and this algorithm for PSO clustering as

shown in Algorithm 2.

2.4 Gaussian Random PSO Mean

Clustering

To increase the speed and accuracy of the PSO Mean

Clustering algorithm, a technique for generating PSO

initial particle values was added to the research.

Random particle value generation technique is used

Gaussian distribution, each feature data will produce

mean and standard deviation values as in Equations 6

and 7 and called as gaussian partial distribution.

Gaussian partial distribution simulation we can see in

Figure 3, where each feature in each cluster is

calculated with 𝜇 and 𝜎.

The workings of the algorithm can be seen in

Algorithm 3. The striking difference is in the use of

the k-means method before initializing the particle

value, this is intended to create an initial cluster to

determine the members of each cluster. The rest of

algorithm is same with PSO Mean clustering.

Figure 3: Gaussian Partial Distribution

𝜇









∑

𝑋









(6)

𝜎











∑

𝑋



−𝑋











(7)

where: 𝑛 : number of members

𝑖 : index of feature

𝑐 : index of cluster

𝑋



: data

𝑋





: mean of data

3 RESULT AND DISCUSSION

To use the proposed method, there are 6 different

classification datasets. The source of the dataset used

comes from UCI Machine Learning

(https://archive.ics.uci.edu/) for all datasets

except

Banana dataset comes from

https://www.openml.org/. Complete attributes of all

datasets can be seen in Table 1, the number of data

that has the most dimensions is the Digital Pen (16 x

10992), the highest number of classes is also in the

Digital Pen dataset. The set parameter values for the

PSO clustering, PMC and GPMC methods can be

seen in Table 2. In this study there was no parameter

testing to find the best model.

Algorithm 3: Algorithm for Gaussian Random PSO Mean

Clustering (GPMC)

Input :

Output: Gbest, fitness value

Initial:

C // number of clusters

max_iter // maximum iteration/generation

nPop // size of swarm

dataset // dataset that used in k-means

dim // dimension of data (features of

data)

centroids, class = K-means (dataset, C);

// gaussian distribution

for i:1 to C

for j:1 to dim

stdv[i][j] = calculate standard

deviation from members in cluster[i][j];

mean[i][j] = calculate mean from

members in cluster[i][j];

end for

// generate particles with random gaussian

for i:1 to C

for j:1 to dim

particle[i][j] = rand * stdv[i][j] +

mean[i][j];

end for

loop : 1

repeat

for i:1 to nPop

calculate fitness particle[i];

calculate velocity and new position

particle[i];

ICATECH 2023 - International Conference on Advanced Engineering and Technology

find and update Gbest and Pbest[i];

Update particle[i] position with mean

members of each cluster ;

end for

loop++;

until loop = max_iter ;

The test scenario is that each method is tested 5

times for each dataset. This is done because there are

random values in these methods. The evaluation used

is internal and external evaluation. The internal

evaluation uses the total distance between the

centroid and its members and the total distance

between the centroids. External evaluation used in

this study is to calculate the accuracy of the data, by

matching the cluster value with the actual class. The

results of the average intra-cluster evaluation can be

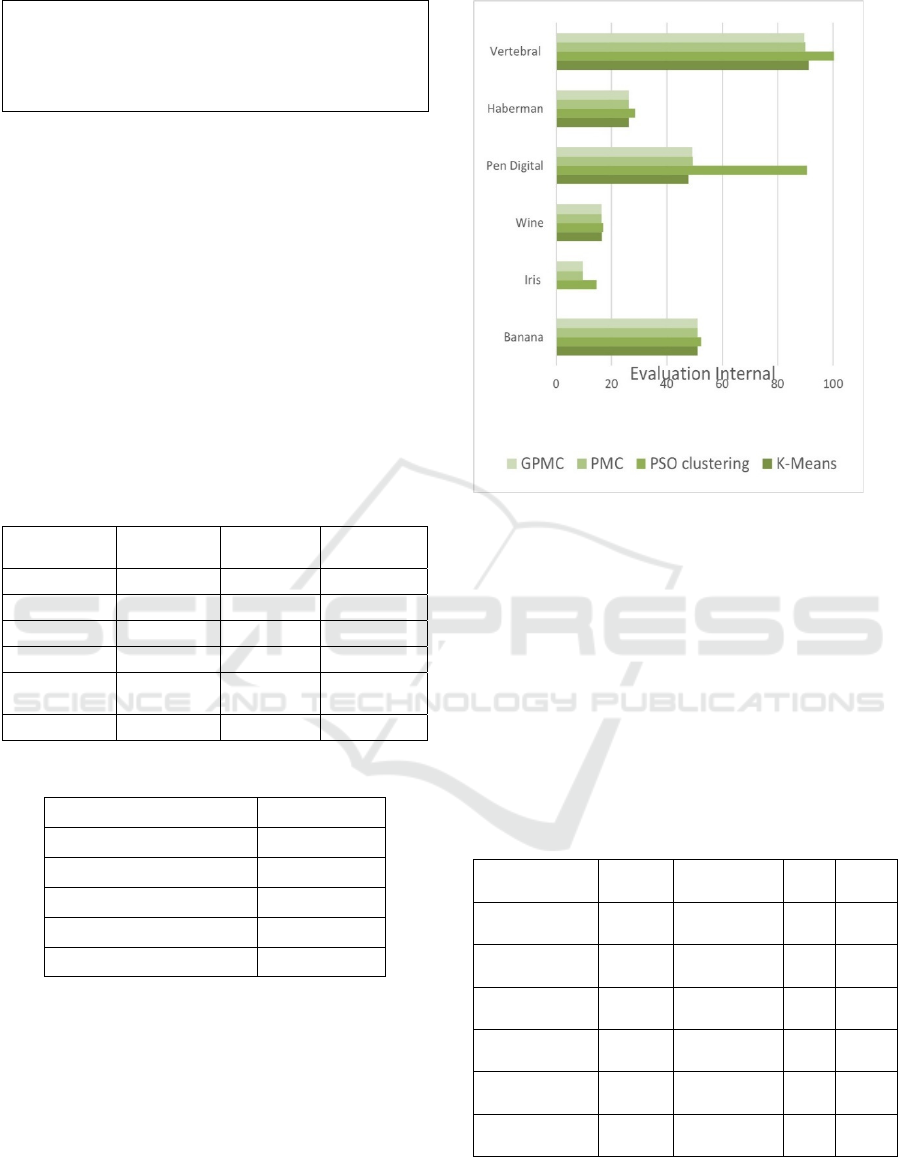
seen in Table 3. The proposed method gets the

smallest SSE value on all datasets except for the

Digital Pen as in Figure 5. If only compare the PMC

and GPMC.

Table 1: Detail attributes of dataset

Dataset

name

Number of

features

Number of

classes

Number of

Instance

Banana 2 2 5300

Iris 4 3 150

Wine 13 3 178

Pen Digital 16 10 10992

Haberman's

survival

3 2 306

Vertebral 6 2 310

Table 2: Value of parameters

Parameters Value

Number of Swarm 30

Maximum Iteration 50

C1 1.2

C2 0.12

w 1

The results of the average intra-cluster evaluation

can be seen in Table 3. The proposed method gets the

smallest SSE value on all datasets except for the

Digital Pen as in Figure 4. If only compare the PMC

and GPMC.

Figure 4: Comparation of internal evaluation

The results of the internal evaluation of the

calculation of the distance between centroids can be

seen in Table 4. The best result of this evaluation is to

optimize the maximum distance value. The results

obtained are inversely proportional to the SSE

evaluation, a good method for evaluation SSE is not

optimal at the centroid distance. The proposed

methods (PMC and GPMC) get the smallest or at least

maximum values. While the PSO clustering method

that gets uncompetitive scores is evaluated by SSE to

produce the widest distance between clusters.

Table 3: Results of intra-cluster evaluation

K-

Means

PSO

Clustering

GPM

Banana

(

E+02

)

51.2 52.29

51.

51.2

Iris

(E+01

12.40 14.61 9.7 9.7

Wine

(E+03)

16.55 16.96

16.

16.3

Pen Digital

(

E+03

)

47.74 90.55

49.

49.1

Haberman

(

E+02

)

26.26 28.45

26.

26.2

Vertebral

(E+02)

91.16 120.3

89.

89.8

Modiﬁed Particle Swarm Optimization for Clustering

Table 4: Distance Between Centroids

K-Means

PSO

Clustering

PMC GPMC

Banana 1.848 1.833 1.839 1.84

Iris 8.72 12.03 10.09 10.1

Wine (E+02) 15.74 16.96 13.98 13.5

Pen Digital

(E+02)

69.38 69.98 66.85 67.2

Haberman 17.81 22.67 17.74 17.7

Vertebral 69.03 69.31 62.86 63.4

The percentage value of the difference in SSE

between the PMC and GPMC methods with the K-

mean can be seen in Figure 8, the y-axis represents

the percentage value, and the x-axis represents the

number dataset. The average SSE difference between

the PMC method and the K-means is 3.49% and the

SSE difference between the SSE GPMC and K-means

is 3.69%. The best accuracy value for all methods is

obtained on the Iris dataset with a value of 89.33%

and the results can be seen graphically in Figure 8,

while the worst accuracy value occurs in the Digital

Pen dataset. Overall, the value generated by the

GPMC method is the most competitive compared to

the methods tested. Details of the accuracy results can

be seen in Table 5.

Table 5: Extra-cluster evaluation results (accuracy %)

K-

Means

PSO

Clustering

PMC GPMC

Banana 56.68 57.17 57.21 57.15

Iris 45.33 70.76 88.67 89.33

Wine 70.22 71.91 70.79 71.91

Pen

ital

2.98 2.16 19.78 10.76

Haberman 51.63 48.04 48.04 51.96

Vertebral 32.90 36.77 26.77 40.65

Figure 5: Comparation PMC and GPMC

4 CONCLUSIONS

From the results of trials that have been carried out,

there are differences in optimal results in the internal

(SSE) and external evaluation by evaluating the

distance between centroids. According to the results

that have been studied, the correlation between SSE

values and centroid distance is inversely related. It is

inversely proportional because the more optimal SSE

value is, the distance-centroid results are not optimal.

This can happen because the optimization methods

used the SSE value as an objective function, so the

algorithm searches to optimize SSE instead of the

centroid-distance optimization value.

According to the results of SSE values and

accuracy, the proposed method of PSO Mean

Clustering (PMC) is better than the previous method,

namely PSO Clustering and K-means. The traditional

PSO method is less able to be applied for clustering

with the objective function of SSE values. By adding

the Mean process to the PSO clustering method, this

new method (PMC) can get better SSE values than

the traditional K-means method. By adding the Mean

process to the PSO clustering method, this new

method (PMC) can get better SSE values than the

traditional K-means method.

REFERENCES

Anuradha, S., Jyothirmai, P., Tirumala, Y., Goutham, S. &

Hariprasad, V. (2014). Comparative Study of

Clustering Algorithms on Diabetes Data. 3(6), 922–

926.

Arthur, D. & Vassilvitskii, S. (2007). k-means++: The

Advantages of Careful Seeding. Proceedings of the

Eighteenth Annual ACM-SIAM Symposium on

Discrete Algorithms. Society for Industrial and Applied

Mathematics Philadelphia, PA, USA., 1027–1035.

Auliya, Y A. (2019). Improve Hybrid Particle Swarm

Optimization and K-Means by Random Injection for

Land Clustering of Potato Plants. 2019 International

Conference on Computer Science, Information

Technology, and Electrical Engineering (ICOMITEE),

192–198.

https://doi.org/10.1109/ICOMITEE.2019.8921207

Auliya, Yudha Alif, Mahmudy, W. F. & Sudarto, S. (2019).

Improve Hybrid Particle Swarm Optimization and K-

Means for Clustering. Journal of Information

Technology and Computer Science; Vol 4, No 1: June

2019DO - 10.25126/Jitecs.20194183 .

Capó, M., Pérez, A. & Lozano, J. A. (2020). An efficient

K-means clustering algorithm for tall data. In Data

Mining and Knowledge Discovery (Vol. 34, Issue 3).

Springer US. https://doi.org/10.1007/s10618-020-

00678-9

ICATECH 2023 - International Conference on Advanced Engineering and Technology

El-Khatib, S., Rodzin, S. & Skobtsov, Y. (2016).

Investigation of Optimal Heuristical Parameters for

Mixed ACO-k-means Segmentation Algorithm for

MRI Images BT - Information Technologies in

Science, Management, Social Sphere and Medicine.

355–360.

https://doi.org/https://doi.org/10.2991/itsmssm-

16.2016.72

Fränti, P. & Sieranoja, S. (2019). How much can k-means

be improved by using better initialization and repeats?

Pattern Recognition, 93, 95–112.

https://doi.org/10.1016/j.patcog.2019.04.014

Gao, H., Li, Y., Kabalyants, P., Xu, H. & Martinez-Bejar,

R. (2020). A Novel Hybrid PSO-K-Means Clustering

Algorithm Using Gaussian Estimation of Distribution

Method and Lévy Flight. IEEE Access, 8, 122848–

122863.

https://doi.org/10.1109/ACCESS.2020.3007498

G.G, G. & K, S. (2017). Improved Optimization centroid in

modified Kmeans cluster. International Journal of

Engineering and Technology, 9(2), 1511–1517.

https://doi.org/10.21817/ijet/2017/v9i2/170902224

Gupta, M. K. & Chandra, P. (2019a). MP-K-Means:

Modified Partition Based Cluster Initialization Method

for K-Means Algorithm. International Journal of

Recent Technology and Engineering, 8(4), 1140–1148.

https://doi.org/10.35940/ijrte.d6837.118419

Gupta, M. K. & Chandra, P. (2019b). P-k-means: k-means

Using Partition Based Cluster Initialization Method.

SSRN Electronic Journal, 567–573.

https://doi.org/10.2139/ssrn.3462549

Irani, J., Pise, N. & Phatak, M. (2016). Clustering

Techniques and the Similarity Measures used in

Clustering: A Survey. International Journal of

Computer Applications (0975, 134, 0975 – 8887.

https://doi.org/10.1080/00268948108072666

Janani, R. & Vijayarani, S. (2019). Text document

clustering using Spectral Clustering algorithm with

Particle Swarm Optimization. Expert Systems with

Applications, 134, 192–200.

https://doi.org/10.1016/j.eswa.2019.05.030

Kapil, S., Chawla, M. & Ansari, M. D. (2016). On K-means

data clustering algorithm with genetic algorithm. 2016

Fourth International Conference on Parallel,

Distributed and Grid Computing (PDGC), 202–206.

https://doi.org/10.1109/PDGC.2016.7913145

Kim, H., Kim, H. K. & Cho, S. (2020). Improving spherical

k-means for document clustering: Fast initialization,

sparse centroid projection, and efficient cluster

labeling. Expert Systems with Applications, 150,

113288.

https://doi.org/https://doi.org/10.1016/j.eswa.2020.113

288

Kumar, S., Kumar-Solanki, V., Choudhary, S. K., Selamat,

A. & Gonzalez-Crespo, R. (2020). Comparative Study

on Ant Colony Optimization (ACO) and K-Means

Clustering Approaches for Jobs Scheduling and Energy

Optimization Model in Internet of Things (IoT).

International Journal of Interactive Multimedia and

Artificial Intelligence, 6(1), 107.

https://doi.org/10.9781/ijimai.2020.01.003

Kurniawan, M., Muhima, R. R. & Agustini, S. (2020).

Comparison of Clustering K-Means, Fuzzy C-Means,

and Linkage for Nasa Active Fire Dataset. International

Journal of Artificial Intelligence & Robotics (IJAIR),

2(2), 34. https://doi.org/10.25139/ijair.v2i2.3030

Lakshmi, M. A., Daniel, G. V. & Contents, D. S. R. (2019).

Initial Centroids for K-Means Using Nearest Neighbors

and Feature Means. Springer, 900(February), 291–298.

https://doi.org/10.1007/978-981-13-3600-3

Lakshmi Patibandla, R. S. M., Tarakeswara Rao, B.,

Sandhya Krishna, P. & Maddumala, V. R. (2020).

Medical data clustering using particle swarm

optimization method. Journal of Critical Reviews, 7(6),

363–367. https://doi.org/10.31838/jcr.07.06.64

Madhukar, M. & Verma, S. (2019). Hybrid Kmeans with

Improved Bagging for Semantic Analysis of Tweets on

Social Causes. Proceedings of ICDMAI, 808, 283–295.

https://doi.org/10.1007/978-981-13-1402-5

Marom, Y. & Feldman, D. (2019). k-Means Clustering of

Lines for Big Data. In H. Wallach, H. Larochelle, A.

Beygelzimer, F. d\textquotesingle Alché-Buc, E. Fox &

R. Garnett (Eds.), Advances in Neural Information

Processing Systems 32 (pp. 12817–12826). Curran

Associates, Inc. http://papers.nips.cc/paper/9442-k-

means-clustering-of-lines-for-big-data.pdf

Muhima, R. R., Kurniawan, M., Wardhana, S. R., Yudhana,

A. & Sunardi. (2022). n-Mating Effect on Genetic

Algorithm-Based Clustering Performance for Hotspots

Data. 2022 IEEE International Conference on

Communication, Networks and Satellite

(COMNETSAT), 212–215.

https://doi.org/10.1109/COMNETSAT56033.2022.99

94400

Nerurkar, P., Shirke, A., Chandane, M. & Bhirud, S. (2018).

A Novel Heuristic for Evolutionary Clustering.

Procedia Computer Science, 125, 780–789.

https://doi.org/10.1016/j.procs.2017.12.100

Pacifico, L. D. S. & Ludermir, T. B. (2019). Hybrid K-

Means and Improved Self-Adaptive Particle Swarm

Optimization for Data Clustering. 2019 International

Joint Conference on Neural Networks (IJCNN), 1–7.

https://doi.org/10.1109/IJCNN.2019.8851806

Paul, S., De, S. & Dey, S. (2020). A Novel Approach of

Data Clustering Using An Improved Particle Swarm

Optimization Based K–Means Clustering Algorithm.

2020 IEEE International Conference on Electronics,

Computing and Communication Technologies

(CONECCT), 1–6.

https://doi.org/10.1109/CONECCT50063.2020.91986

Sajana, T., Sheela Rani, C. M. & Narayana, K. V. (2016).

A survey on clustering techniques for big data mining.

Indian Journal of Science and Technology, 9(3), 1–12.

https://doi.org/10.17485/ijst/2016/v9i3/75971

Shukla, S. & S, N. (2014). A Review on K-means Data

Clustering Approach. International Journal of

Information & Computation Technology, 4(17), 1847–

1860.

Modiﬁed Particle Swarm Optimization for Clustering

Verma, A. & Bharadwaj, K. K. (2017). Identifying

community structure in a multi-relational network

employing non-negative tensor factorization and GA k-

means clustering. WIREs Data Mining and Knowledge

Discovery, 7(1), e1196.

https://doi.org/10.1002/widm.1196

Xiaoqiong, W. & Zhang, Y. E. (2020). Image segmentation

algorithm based on dynamic particle swarm

optimization and K-means clustering. International

Journal of Computers and Applications, 42(7), 649–

654. https://doi.org/10.1080/1206212X.2018.1521090

Yang, K., Yu, K. & Wang, H. (2020). A hybrid method of

multi-objective particle swarm optimization and k-

means clustering and its application to modal parameter

estimation in the time–frequency domain. JVC/Journal

of Vibration and Control, 26(9–10), 769–778.

https://doi.org/10.1177/1077546319889787

Yu, S. S., Chu, S. W., Wang, C. M., Chan, Y. K. & Chang,

T. C. (2018). Two improved k-means algorithms.

Applied Soft Computing Journal, 68, 747–755.

https://doi.org/10.1016/j.asoc.2017.08.032

Zeebaree, D. Q., Haron, H., Abdulazeez, A. M. & Zeebaree,

S. R. M. (2017). Combination of k-means clustering

with genetic algorithm: A review. International Journal

of Applied Engineering Research, 12(24), 14238–

14245.

ICATECH 2023 - International Conference on Advanced Engineering and Technology