Efﬁcient Machine-Learning-Based Crypto Forecasting Analysis

Sidra Hussain, Sheikh Sharfuddin Mim and Doina Logofatu

Dept. of Computer Science, Frankfurt University of Applied Sciences, Nibelungenpl. 1, 60318 Frankfurt am Main, Germany

Keywords:

Random Forest, Hyperparameter Tuning, Cryptocurrency, Machine Learning, Loss Curves, Decision Tree,

Linear Regression, Gradient Boosting.

Abstract:

Cryptocurrency is the current evolving ﬁnancial market that gives scope for many researchers and machine

learning assets to be put into production. Cryptocurrency forecasting is a challenge as following ﬁnancial

assets is difﬁcult due to their volatility and unscalable factor dependencies. This paper puts forward the data

of fourteen different types of cryptocurrencies, which will be used to build machine learning (ML) models to

forecast the crypto scores in the next ﬁscal year. For this, four different models are used, and their performance

is evaluated and tested. The models are Linear Regression, Decision Tree, Random Forest, and Gradient

Boosting. The results obtained from the models show a perfect ﬁt and good hyperparameter tuning, giving

evidence of good feature engineering and data scraping. Overall, the models are meant to beneﬁt the ﬁnancial

market immensely by helping to forecast and help investments build in sales and purchasing.

1 INTRODUCTION

With the innovation and rise of Distributed Ledger

Technology (DLT) in the coming years, blockchain

has been reformed and has replaced stocks and shares.

Cryptocurrency is the current investing asset that uses

DLT, and its volatility has been increasing day by day

due to the ease of purchasing and selling points on the

leaderboard across the globe (Hammayel and Owda,

2021). One of the main quests of machine learning

(ML) engineers now is to predict the trend of cryp-

tocurrencies in future run cycles. As accordance to

shares and stocks that depend on intangible dependen-

cies such as utility and government inclusion, cryp-

tocurrency is quite independent of these factors and

so exposed to being forecasted using ML and data en-

gineering (Hammayel and Owda, 2021). In this paper,

ML models will be used to forecast the price values

for the future ﬁscal year.

Section 2 is about the processing of data. This

paper follows the main structure of building theoret-

ical knowledge ﬁrst (section 2.1). The dataset is in-

troduced in section 3, and data engineering is imple-

mented to maintain the model’s performance during

the process. Within the data section, exploratory anal-

ysis is used to ﬁnd associations within the ﬁnal input

data. Section 4 is dedicated to gauging the perfor-

mance of the models using different evaluations, and

lastly, results (section 5) and discussions (section 6)

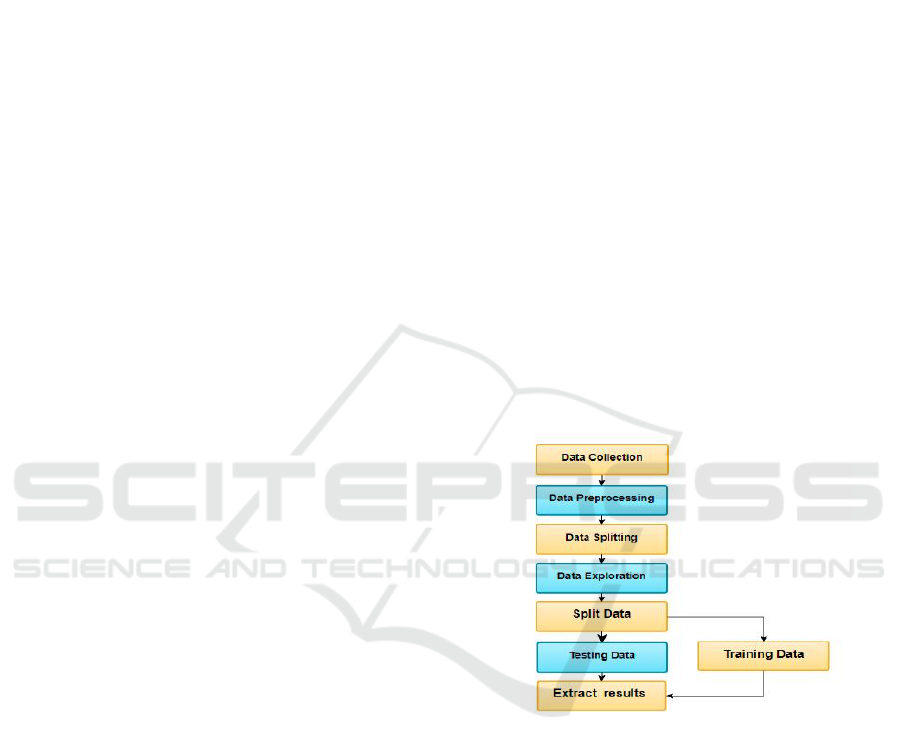
Figure 1: Methodology of processing data (Chaudhari,

2019).

are put forward. Section 7 concludes the paper.

2 METHODOLOGIES

To reach the goal of this paper, four models were

trained on the past prices of 14 cryptocurrencies

to make four price predictions for cryptocurrencies.

The data dates to 2018 and consists of an extensive

dataset. To evaluate the performance of the schemes

included in this paper, the illustrated project pipeline

is shown in Fig. 1. It shows the processing of the

dataset from inheritance to evaluation.

As mentioned in section 1, following is a discreet

352

Hussain, S., Mim, S. and Logofatu, D.

Efﬁcient Machine-Learning-Based Crypto Forecasting Analysis.

DOI: 10.5220/0012117800003546

In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 352-360

ISBN: 978-989-758-668-2; ISSN: 2184-2841

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

explanation of the ML algorithms used.

2.1 Algorithms Overview

2.1.1 Linear Regression

Linear regression was one of the ﬁrst algorithms to be

studied in detail for machine learning and forecasting.

It models the input to the output using linear predic-

tor functions, of which primarily conditional means

are used as a response or entity (Derbentsev et al.,

2021). As a linear one-to-one relationship between

the dependent and independent variables, conditional

probability distribution is the main essence of the re-

sponse calculated rather than joint probability distri-

bution, which is a multi-variable analysis (Song and

Lu, 2015).

2.1.2 Decision Tree

A supervised machine learning classiﬁcation model

with a tree topology is a decision tree. It clearly and

explicitly depicts judgments and decision-making, so

non-expert users may comprehend and successfully

draw from a dataset. The data is divided by attribute

in the decision tree. The two primary elements of a

decision tree are decision nodes, where input is di-

vided into more decision nodes, and leaves, where

we obtain the outcome. The Decision Tree method

splits data by picking the best attribute using At-

tribute Selection Measures (ASM). The data parti-

tioning heuristic ASM selects the optimum splitting

criterion. It’s called the splitting rules since it deter-

mines tuple breakpoints on a node. By explaining the

dataset, ASM ranks each function or property. The

best score characteristic will split. Information Gain,

Gain Ratio, and Gini Index are the most prevalent se-

lection criteria. (Breiman, 2001)

Entropy gives the degree of randomness or im-

purity contained within a given dataset. Information

gain calculates the difference between the entropy in

advance of the split and the average entropy after the

split the attribute values (Lui and Pareek, 2018). Vari-

able splits should have a low Gini Index (Ceriani and

Verme, 2012).

2.1.3 Random Forest (RF)

The RF classiﬁer is a supervised ML classiﬁcation

method that uses decision trees as its foundation.

A RF is a set of unbiased, unrelated, and de-

correlated decision trees. It is thus called a ‘random

forest’ (Ceriani and Verme, 2012). It’s a type of

meta-estimator that uses decision-tree classiﬁers on

random sub-spaces and dataset samples and applies

mean averaging tools to improve prediction accuracy

over time while avoiding over-ﬁtting.

RF builds a decision tree for each sample by

choosing random samples from a dataset. Each de-

cision tree’s prediction results are gathered and voted

on. The highest-voted forecast is the ﬁnal result. The

Gini impurity criteria index evaluates RF’s implicit

feature selection of variable relevance with a random

subspace approach. Based on impurity reduction the-

ory, the Gini index measures regression or classiﬁ-

cation variable predictive power. It does not require

distribution-speciﬁc data because it is non-parametric

(Sarica et al., 2017). The Gini index should be im-

proved to the greatest extent possible when splitting

a binary node. In a classiﬁcation problem, the Gini

index can be used to rank the importance of features

(Sruthi, 2021).

2.1.4 Gradient Boosting

Gradient boosting is a model used as an alternative

approach for weak prediction models as an ensemble,

which is to use multiple algorithms to learn and pre-

dict better. The main objective is to obtain a perfor-

mance that is better than the weak constituent learn-

ing algorithms (Narkhede, 2018).Gradient boosting

works by making the loss function between the in-

put and output as small as possible. It uses a greedy

approach to set the loss function into optimizing in a

maximum descent, which is represented by γ which is

a small amount for the validity of the linear approxi-

mation (Narkhede, 2018).

3 DATASET

The dataset is available in Kaggle for the competition

of G-Research Crypto Forecasting ((Kaggle, 2022)).

The dataset has a training set with 24 million records

of 14 crypto assets. That is 24236806 rows over 10

columns. This training set will be split into training

and testing sets.

The data is the information of 14 cryptocurrencies

dating back to 2018. It is public domain data from

the global stock exchange that equips over one mil-

lion high-frequency trading rows. The features for

each cryptocurrency given are: Asset ID, which is

unique to every crypto; Time stamp, which includes

the minute and date the row was caught. The dis-

criminatory features include Count, Open, High, Low,

Close, VWAP, Volume and Target. Where count is

the number of trades, open and close are the USD

prices of opening and closing the trade, volume is

Efﬁcient Machine-Learning-Based Crypto Forecasting Analysis

353

the amount of cryptocurrency traded, and VWAP is

volume-weighted average price. The target is the re-

turn on investment in a time frame of 15 minutes.

3.1 Data Preliminary Analysis

After the inheritance of data, to make the dataset ﬁt

the algorithm, it is processed beforehand. This section

investigates the preprocessing of data for the topic

sentence using two sequential methods.

3.1.1 Dataset Framing

In our case, the cryptographic data can amount to up

to 24 million records. This type of data would re-

quire extensive processing time and CPU power. To

reduce the processing time, the record of information

is reduced. It should be noted that the dataset cannot

be reduced without sacriﬁcing important trends. This

means that dataset framing can only be done when

the dataset is known and exploration is done correctly.

As discussed in Section 4, the crypto assets are non-

stationary and used for forecasting their current value.

This gives us the liberty and ﬂexibility to reduce the

data, as it is a non-stationary randomized time series.

Which means if i denotes the initial instant value of a

particular asset, the value at instant i-1, which is the

future next instant, would be a disjointed event. But

it is to be noted that this disjoint parametric does not

inﬂuence the overall forecasting, which is done on a

relatively large and sufﬁcient dataset.

For that matter, the following 24 million records

are reduced to 598k records by reducing the dataset

until November 2020. Fig. 2 is the data frame of the

reduced training dataset with the crypto assets fea-

tures for modeling.

3.1.2 Enriching Dataset

Data preliminary analysis is the pre-processing of

data that ensures the data is clean and will not stump

the model to be made. One of the most important

steps is to ensure that the data is completely popu-

lated, i.e., it does not have NAN, NA, or null values.

These values make a sparse vector and run the dan-

ger of inadequate training and a biased model. It can

also lead to less precise or inaccurate modeling. Also,

many ML algorithms do not support missing values.

The best way to avoid this is by ﬁlling in or imput-

ing these missing values or by deleting the speciﬁc

rows with missing values if the records are sufﬁcient

(Tamboli, 2021). Deletion can be done per row or per

column of the dataset. Whereas, ﬁlling can be done

in many aspects, for example, by ﬁlling the missing

locations with an arbitrary value, the mean, mode, or

median, or by doing a forward and backward ﬁll. For

categorical values, ﬁlling can be done with the most

frequent variable, or the missing values can have their

own category (Tamboli, 2021). To check for missing

values, any values that are not in a ﬁnite category are

checked.6 We found that around 1.47%, or 8814 of

the target values, are missing. To tackle this, these

rows are dropped, as 598769 records are more than

enough for training our algorithms. Fig. 3 is the resul-

tant dataset, with now 589955 records, and a general

statistical description of the feature content for each

crypto asset.

3.2 Feature Engineering

In this step of the implementation of the forecast, fea-

tures that inﬂuence the forecast are dealt with. In fea-

ture engineering, normally, features are extracted and

a transformed data frame is made from the features.

In the scope of this project, feature extraction is omit-

ted, and instead features are transformed to increase

the accuracy of the algorithm. This is important as

raw features could lead to problems with the algo-

rithms learning from themselves in the model. This

step helps the model reﬁne itself to improve perfor-

mance. These features become the important factors

that affect the business problem.

3.3 One Hot Encoding

In the dataset, there are two categorical variables that

need to be aligned with the numeric trade features.

In Fig. 3, the feature names are Asset ID, which is

unique for all fourteen crypto assets, and timestamp,

which is the minute at which the trade started. The

categorical variables are turned to numeric using one

hot encoding (Fig. 4). It is a method to better express

categorical variables. First, the feature timestamp is

divided into the weekday and hour associated with

each variable.

For all variable instances, an additional column is

added to the dataset. That is, fourteen Asset IDs with

range (Asset ID0: AssetID13), twenty-four hours

with range (hour0: hour23) and seven weekdays with

range (weekday0: weekday6). For all asset values in

a particular row, only the speciﬁc column to which

the asset belongs would be 1, and the others would be

0. This saturates the dataset with a precise value over

the whole range of categorical variables where it is on

only at the given AssetID, hour, and weekday.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

354

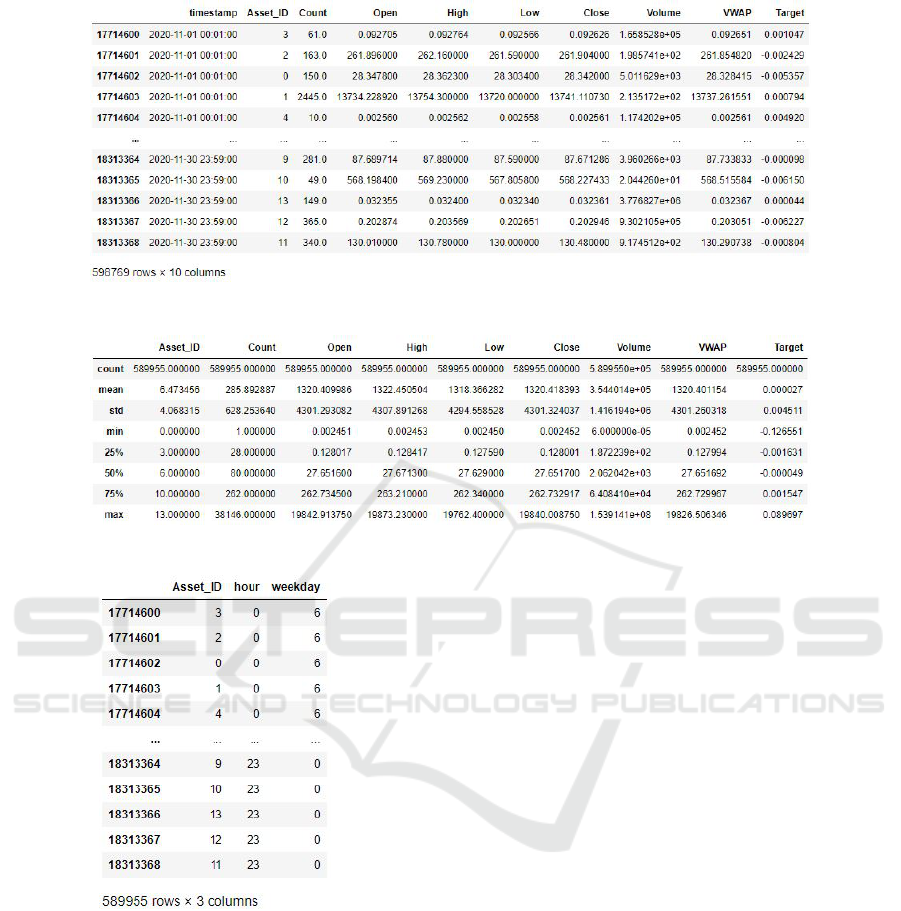
Figure 2: Framed Dataset.

Figure 3: Statistical information of the dataset.

Figure 4: One Hot Encoded Categorical Variables.

3.4 Numeric Variables

For numeric variables, there are extensive trends in

the data. In order to scale the data for each spe-

ciﬁc feature and in accordance with the speciﬁc entity,

the Min-Max scaler approach is used. The min-max

scaler takes the variables and scales the entire feature

information according to the minimum and maximum

value of the feature. This is the most efﬁcient alterna-

tive to zero mean and unit variance scaling. Without

disturbing the shape of the original distribution, the

data is transformed and scaled (Fig. 5).

3.5 Data Exploratory Analysis

Exploring datasets is important and useful for seeing

how data is spread out and how it acts. This section

explores the association of all features together. There

are two methods by which this could be achieved.

3.5.1 Time Series Plot

A time series plot would exhibit the changes in the

features of each crypto asset. This shows if the data

is co-dependent or not. Our case is a non-stationary

time-series business problem. There is no depend-

ability or inﬂuence from one crypto asset to another.

A crypto currency can only be inﬂuenced by external

factors other than the currency itself.

For the following approach, ﬁrst the time range for

each asset is captured.

Fig. 6 shows that all asset ID target variables

would be associated with the same time range. Fig. 7

is the time series plot against the target values and the

time stamp of the asset IDs. The time plot does not

provide any information on the association of vari-

ables with the target. It shows all the assets have a

unique pattern with respect to the return on invest-

ment.

Efﬁcient Machine-Learning-Based Crypto Forecasting Analysis

355

Figure 5: Scaled Dataset.

Figure 6: Time Range of Assets.

Figure 7: Time Series Plot.

3.5.2 Correlation Matrix

A correlation matrix shows associations between vari-

ables in matrix form. It demonstrates correlation be-

tween any set of variable pairs. This helps to see pat-

terns and trends in large and complex datasets easily.

Following is the correlation matrix for all the crypto

asset features.

Fig. 8 depicts that the features are highly corre-

lated with each other, which was information that was

not showcased in the time series plot. The features of

count, volume, and target are disjointed independent

variables. But the features of Open, Close, Low and

Figure 8: Correlation Matrix.

High show a trend of correlation that is also logically

understood to be linked between the crypto assets.

Overall, two conclusions are drawn from the cor-

relation matrix. First, the features are deemed ﬁt for

model training due to their high correlation. No fur-

ther features need to be engineered in. And second,

the positive correlation indicates that the crypto assets

will decrease and increase together; their behavior in

the market will be proportional.

4 EVALUATION

The evaluation of the model is the entity that shows

if the model performed well. In this case, a forecast

result is subjected to a future value. Thus, the eval-

uations are mathematical formulas implemented and

tested for errors. Following are the few ways used to

evaluate the models in use (Baeldung, 2023).

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

356

Figure 9: Hyperparameter Tuning by GridSearchCV.

4.1 Train Error

Train error is a metric to see how well the model is

trained on training data. The lower the training error,

the better the model is trained. It uses Root Mean

Squared Error (RMSE) on predicted and target values

of train dataset (Baeldung, 2023).

4.2 Validation Error

Validation error is a metric to see how well the model

performs on new or test data. The lower the valida-

tion error, the higher the accuracy of the model. It

uses RMSE on predicted and target values of the test

dataset (Baeldung, 2023).

4.3 GridSearchCV

Hyperparameter tuning is utilized for modeling all al-

gorithms. The hyperparameter tuning used in the cur-

rent case is called Grid Search. It requires a param-

eter dictionary with all the parameters to be tested in

the grid search for optimal performance, an estima-

tor that takes the algorithm model to be hyper-tuned,

a cross validation value that is the number of times

the hyperparameters will be cross validated, a scoring

method, such as the accuracy score, and the number

of jobs to be used in parallel. Processing time is grid

search’s drawback. The current work employed hy-

perparameter tuning three times, which took an hour

to process. Hyperparameter tuning helps reconstruct

regressors for optimum prediction (Team, 2022).

As illustrated in Fig. 9, the Grid search takes

the hyperparameters of max depth and min sample

splits for a decision tree estimator and cross-validates

these parameters ﬁve times for the scoring of negative

RMSE. And only one parallel job is allowed in this

case. The low output error shows the listed output

parameters are optimal.

4.4 Loss Curves

To better understand the implication of validation and

training errors, both errors are visualized together via

a graph.

• Over-Fitting Curves: A curve that demonstrates

validation error greater than training error across

a generic training duration or epoch. When vali-

dation error exceeds training error, an overﬁt oc-

curs. This shows that the model performs bet-

ter on training data and worse on new data. To

circumvent this, models might be stopped from

training for a longer duration or simpliﬁed with

fewer features to generalize to new data (Muralid-

har, 2021).

• Under-Fitting Curves: A curve that shows train-

ing error more than validation error over a gen-

eral period or epoch. Underﬁt is a situation where

training error is greater than validation error. This

indicates that the model did not accurately model

the training data. To avoid this, models need to

be trained further, i.e., features might be added,

or the dataset can be increased or cleaned better

(Muralidhar, 2021).

5 RESULTS

This section explores the results of the models. To in-

tercept the results, we gauge the overall performance

of the models as the future value of the cryptocurren-

cies and their behavior in the market will unfold in the

next stock market turn. Following are the Train and

Validation Errors of the models with (in Table. 1) and

without hyperparameter tuning (in Table. 2).

Following are the graphical representations of the

prediction scores over test data of June 13th, 2021, on

minutes 00, 01, 02, and 03 provided as test samples.

5.1 Linear Regression Evaluation

Fig. 10 shows prediction scores of all cryptocurren-

cies by the model Linear Regression. There is no par-

ticular trend, and all assets have unique behaviors.

5.2 Decision Tree Evaluation

Fig. 11 depicts Decision Tree Prediction Scores of 14

Cryptocurrencies without Hyperparamter tuning. In

the prediction scores of Decision Tree after hyperpa-

rameter tuning in Fig. 12 are ﬁnely segregated. The

max depth was given in the range of 1 to 11. It can be

seen that the predictions are all positive after hyper-

parameter tuning the model.

Efﬁcient Machine-Learning-Based Crypto Forecasting Analysis

357

Table 1: Training and Validation errors of models without hyperparameter tuning.

Train Error Validation Error

Linear Regression 0.45164954425267917 0.44541345363574125

Decision Tree 0.4514970554993003 0.44588271774088134

Random Forest 0.14292529508022003 0.524622341082601

Gradient Boosting 0.44461427028706973 0.44894542017408745

Table 2: Training and Validation errors of models with hyperparameter tuning.

Train Error Validation Error

Decision Tree 0.45186397002173306 0.4454573828646934

Random Forest 0.4471405725445213 0.44645373581115466

Gradient Boosting 0.4424690561744056 0.45001584531105976

Figure 10: Linear Regression Prediction Scores of 14 Cryp-

tocurrencies.

Figure 11: Decision Tree Prediction Scores of 14 Cryp-

tocurrencies without Hyperparamter tuning.

Figure 12: Decision Tree Prediction Scores of 14 Cryp-

tocurrencies with Hyperparamter tuning.

Figure 13: Random Forest Prediction Scores of 14 Cryp-

tocurrencies without Hyperparamter tuning.

Figure 14: Over-ﬁtting curve of hyperparameter tuning for

max depth.

5.3 Random Forest Evaluation

Fig. 13 depicts Random Forest Prediction Scores of

14 Cryptocurrencies without Hyperparamter tuning.

According to the loss curves of Random Forest for

max depth and n estimator in Fig. 14 and Fig. 15,

the values used were 5 and 10, respectively. From

that point, the losses increase in accordance with the

curves. Fig. 16 depicts Random Forest Prediction

Scores of 14 Cryptocurrencies with Hyperparamter

tuning of max depth 5 and n estimator 10. The pre-

dictions have overall increased in value after hyperpa-

rameter tuning and have become less negative.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

358

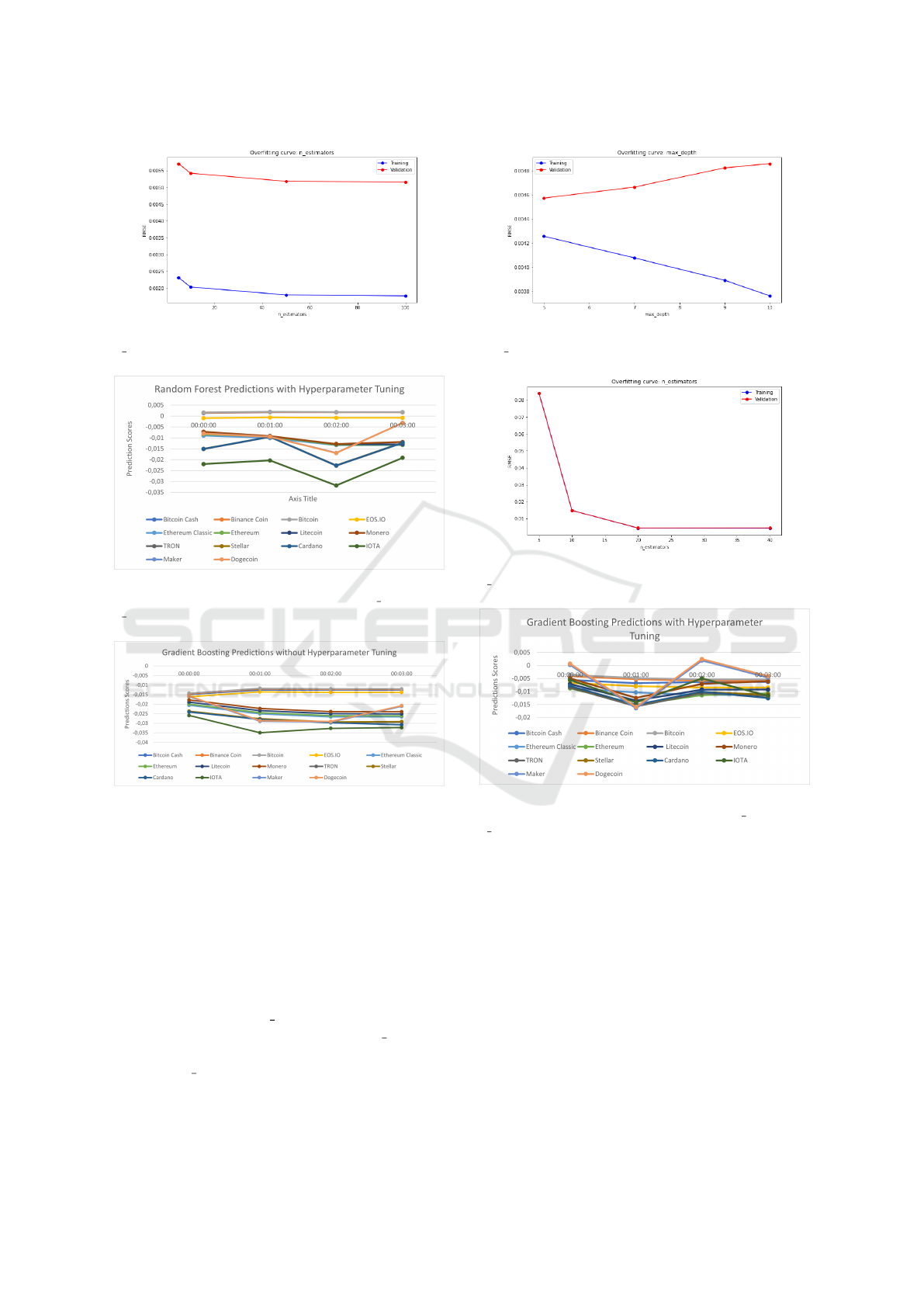
Figure 15: Over-ﬁtting curve of hyperparameter tuning for

n estimator.

Figure 16: Random Forest Prediction Scores of 14 Cryp-

tocurrencies with Hyperparamter tuning of max depth 5 and

n estimator 10.

Figure 17: Gradient Boosting Prediction Scores of 14 Cryp-

tocurrencies without Hyperparamter tuning.

5.4 Gradient Boosting Evaluation

Fig. 17 depicts Gradient Boosting Prediction Scores

of 14 Cryptocurrencies without Hyperparamter tun-

ing. The predictions of Gradiant Boosting have be-

come signiﬁcantly less negative, and a similar trend

can be seen to be followed in a few dominant cryp-

toassets such as Dogecoin, IOTA, Stellar, Litecoin,

etc. in Fig. 20. The hyperparameters used according

to the loss curves were n estimator 20 and maxdepth

5. Because at 20, the curve gets stable for n estimator

as seen in Fig. 19 and at 5, the curve is at the lowest

loss for max depth as seen in Fig. 18.

Figure 18: Over-ﬁtting curve of hyperparameter tuning for

max depth.

Figure 19: Over-ﬁtting curve of hyperparameter tuning for

n estimator.

Figure 20: Gradient Boosting Prediction Scores of 14 Cryp-

tocurrencies with Hyperparamter tuning of max depth 5 and

n estimator 20.

6 DISCUSSION

In this section, we will discuss the ﬁndings of this ex-

periment. Three things can be observed.

1. Almost all the models have the same training and

validation error which is approx. 0.44% and 0.45%.

Which is a very low value. That shows all the mod-

els are trained well and can predict with acceptable

accuracy. The model selection passes, and discreetly

no model outperformed the other. For the use case at

hand, each model has the same behavior.

2. Both the errors, training, and validation are low

and close to each other. This explains that the much-

Efﬁcient Machine-Learning-Based Crypto Forecasting Analysis

359

required middle ground is achieved. This represents a

good ﬁt model. Overall, if the errors were calculated

at different learning stages of the model (for e.g., at

increasing training set sizes or increasing features),

and the training and validation errors were drawn at

each stage, a good ﬁt model would have been when

both the values would decrease and then become con-

stant or ﬂatlined on a graph (Muralidhar, 2021).

3. Hyperparameter tuning worked signiﬁcantly better

for Random Forest than the other models. By default,

given the parameters of Random Forest, the valida-

tion error was higher than the training error. Which

means the model did not do well with predicting on

data other than the training set. After hyperparam-

eter tuning and ﬁnding the additional parameters of

maximum depth of (max depth) and number of trees

(n estimator) at which the model could be improved,

the training and validation error was brought down to

the same level as other models.

7 CONCLUSION

In this paper, four ML models were used to predict

and forecast for fourteen different types of cryptocur-

rencies. The evaluation metrics and scores show all

the models are a good ﬁt with very low losses. The

plots convey that with hyperparameter tuning, mod-

els can improve performance and learning. Also, data

engineering is seen in this paper as being a signiﬁcant

factor in the efﬁcient learning of the models.

It is to be noted that the dynamism and volatility of

the ﬁnancial crypto market make forecasting difﬁcult,

and so factors such as social media and policies also

need to be scaled for better model learning. These are

unscalable factors, which could be a future challenge

for the successor of this project.

REFERENCES

Baeldung (2023). Training and Validation Loss in Deep

Learning. https://www.baeldung.com/cs/training-

validation- loss- deep-learning [Online; accessed 25-

jan-2023].

Breiman, L. (2001). Random Forests. Machine Learn-

ing 45, 5–32, Springer. https://doi.org/10.1023/A:

1010933404324.

Ceriani, L. and Verme, P. (2012). The origins of the Gini

index: extracts from Variabilit

a e Mutabilit

a (1912)

by Corrado Gini. J Econ Inequal. Springer.

Chaudhari, A. (2019). Forecasting Cryptocurrency Prices

using Machine Learning. https: / / norma.ncirl.ie /

4272/1 / ashwinichaudhari.pdf [Online; accessed 6-

feb-2023], Ireland.

Derbentsev, V., Datsenko, N., Babenko, V., Pushko, O., and

Pursky, O. (2021). Forecasting Cryptocurrency Prices

Using Ensembles-Based Machine Learning Approach.

IEEE, Ukraine.

Hammayel, M. J. and Owda, A. Y. (2021). A Novel Cryp-

tocurrency Price Prediction Model Using GRU, LSTM

and bi-LSTM Machine Learning Algorithms. MDPI,

Switzerland.

Kaggle (2022). Dataset for the competition of G-

Research Crypto Forecasting by Kaggle. https://

www.kaggle.com / competitions / g - research - crypto -

forecasting/data.

Lui, C. and Pareek, K. (2018). Random Forest-based Voice

Activity Detector. https://github.com/karanpareek96/

Speech - Recognition - in - Urban - Setting - using -

Random- Forest- Algorithm [Online; accessed 2-jan-

2023], New York.

Muralidhar, K. (2021). Learning curve to identify Overﬁt-

ting and Underﬁtting in Machine Learning. https://

towardsdatascience.com/learning- curve- to- identify-

overﬁtting-underﬁtting-problems-133177f38df5 [On-

line; accessed 8-feb-2023].

Narkhede, S. (2018). Understanding Confusion Ma-

trix. https://towardsdatascience.com/understanding-

confusion- matrix - a9ad42dcfd62 [Online; accessed

24-jan-2023].

Sarica, A., Cerasa, A., and Quattrone, A. (2017). Random

Forest Algorithm for the Classiﬁcation of Neuroimag-

ing Data in Alzheimer’s Disease: A Systematic Re-

view. Front. Aging Neurosci.

Song, Y. and Lu, Y. (2015). Decision tree methods: ap-

plications for classiﬁcation and prediction. https:

//pubmed.ncbi.nlm.nih.gov/26120265/ [Online; ac-

cessed 12-jan-2023], China.

Sruthi, E. R. (2021). Understand Random For-

est Algorithms With Examples. https :

/ / www.analyticsvidhya.com / blog / 2021 / 06 /

understanding - random - forest/ [Online; accessed

24-jan-2023].

Tamboli, N. (2021). Effective Strategies for Han-

dling Missing Values in Data Analysis. https ://

www.analyticsvidhya.com/blog/2021/10 / handling -

missing-value/ [Online; accessed 24-jan-2023].

Team, G. L. (2022). Hyperparameter Tuning with Grid-

SearchCV. https://www.mygreatlearning.com/blog/

gridsearchcv/ [Online; accessed 10-feb-2023].

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

360