How to Plausibly Deny Steganographic Secrets

Shahzad Ahmad

1 a

and Stefan Rass

1,2 b

LIT Secure and Correct Systems Lab, Johannes Kepler University Linz, Altenbergerstrasse 69, 4040 Linz, Austria

Institute for Artiﬁcial Intelligence and Cybersecurity, Alpen-Adria-University Klagenfurt, Universit

atsstrasse 65-67, 9020

Klagenfurt, Austria

Keywords:

Steganography, Secret Sharing, Deniability, Plausible Deniability.

Abstract:

We introduce the notion of oblivious secret sharing as an enhancement of (conventional) secret sharing with

the added possibility of (plausibly) denying that some shares even exist. Secret sharing is a cryptographic

technique that allows a distributed secure storage of information across multiple parties, such that no party or

pre-deﬁned coalition of parties can reconstruct the stored secret. Conﬁdentiality, in this regard, does only apply

to the secret, but not the the shares themselves. Oblivious secret sharing extends the secrecy also to the shares,

thereby adding the additional possibility of denying the existence of shares in ﬁrst place, or to reconstruct a

different, harmless, secret upon force. We investigate a combination of steganography and secret sharing to

enhance both primitives at the same time: secret sharing adds deniability to steganography and steganography

adds extended conﬁdentiality to secret sharing. Our construction is generic in its use of steganography, but

concrete in the used secret sharing scheme. The latter is a form of multi-secret sharing, letting us secretly

hide a set of messages in a larger collection of images, such that the secrets are, in a steganographic way,

hidden, but disclosure upon force can be made with plausible deniability. This deniability even extends to the

number of secrets embedded in the picture collection. This number is as well deniable. We corroborate our

construction by providing an implementation.

1 INTRODUCTION

Information security has been subject to threats and

attacks from early espionage warfare through current

data leakage. Two often employed methods to safe-

guard communication security are steganography and

cryptography. However, coercive assaults may be

launched against either of them. Since the cipher-

text is constantly suspect to the adversary, coercive

attacks occur in cryptography. The adversary could,

in particular, force the communication parties—the

sender and receiver—to reveal the secret message and

keys. The adversary may additionally request that the

sender produce the ciphertext using the message and

secret key once more to conﬁrm the revealed message.

When a secret message is detected using steganogra-

phy, the adversary can also force the communication

parties to reveal the secret message. It is not possi-

ble to guarantee information security in such hostile

circumstances. Deniable encryption (Canetti et al.,

1997) has been suggested as a solution in cryptog-

https://orcid.org/0000-0002-9654-869X

https://orcid.org/0000-0003-2821-2489

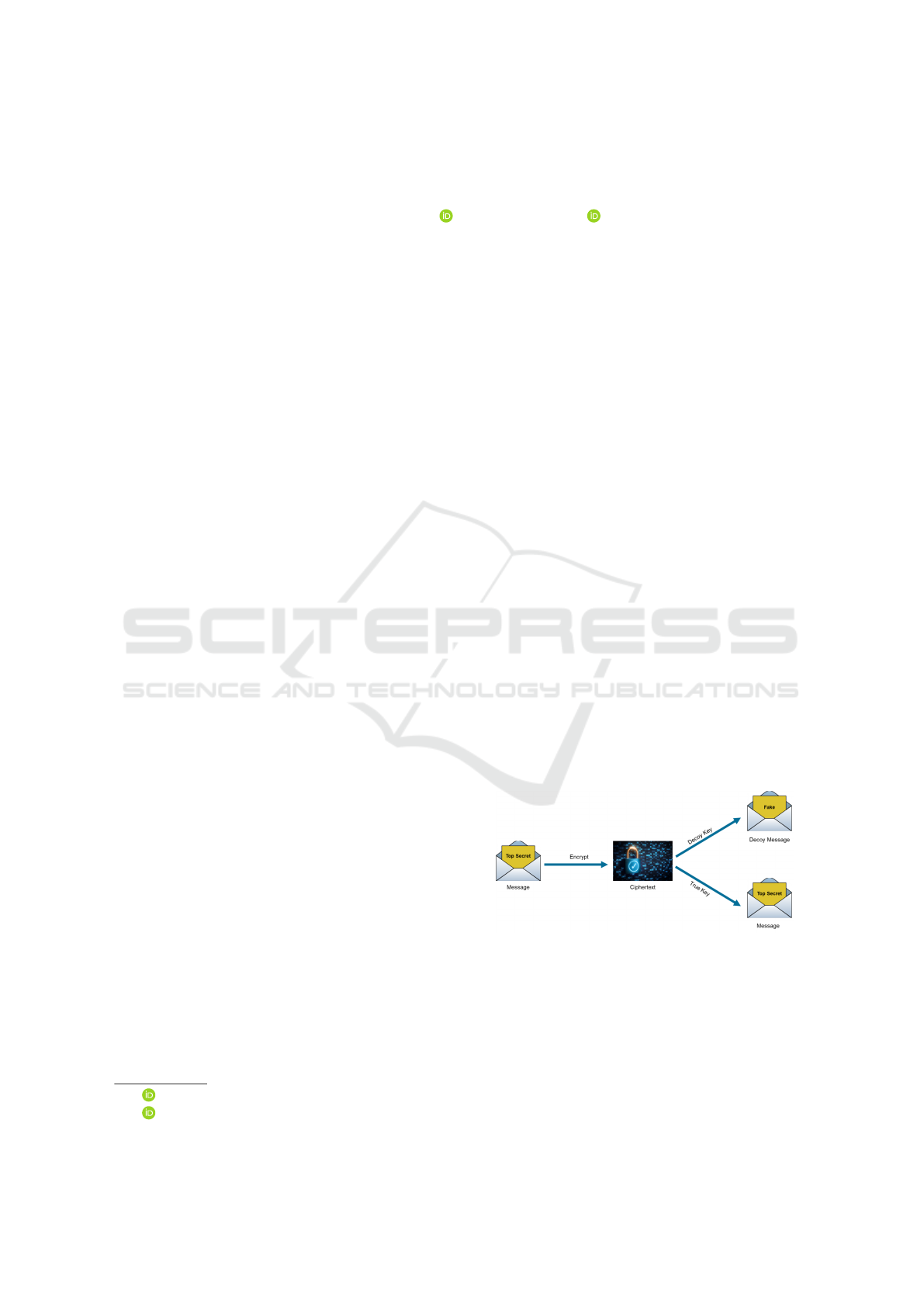
raphy to counter coercive attacks. Figure 1 displays

the idea, which employs a fake key and a real key to

decrypt either a harmless decoy message upon force,

or the real message voluntarily. However, knowing

Figure 1: Deniable Encryption.

that a mechanism like deniable encryption is in place,

what should stop the attacker from squeezing out sev-

eral secrets from the victim, perhaps based on a com-

putable maximum number of messages possibly hid-

den inside the ciphertext of n Bytes (after all, if the

decoy messages are unrelated and hence stochasti-

cally independent, the number of messages possibly

encoded in a cryptogram of size n is likely to be com-

Ahmad, S. and Rass, S.

How to Plausibly Deny Steganographic Secrets.

DOI: 10.5220/0012120100003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 731-737

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

731

putable or at least estimable for the adversary). Inter-

estingly, the concept of deniable steganography has

only been proposed recently (Xu et al., 2022), and we

extend this prior notion by making the number of se-

crets deniable, and making the construction generic in

the sense of workable with any steganographic algo-

rithm that leaves at least some portion of the picture

untouched (such as, for example, least-signiﬁcant bit

methods do, but also others). Though the focus of

present steganography research is on capacity and im-

perceptibility, deniability against coercion has yet to

be considered.

2 RELATED WORK

Some typical methods of steganography and the plau-

sible deniability are introduced here.

2.1 Steganography

Deep neural networks are commonly used for image

steganography because of their ﬂexibility. Two popu-

lar architectures for deep steganography are Encoder-

Decoder Architectures (EDA), and Generative Ad-

versarial Networks (GAN) (Goodfellow et al., 2014).

EDA uses an encoder to embed a secret message and

a decoder to extract it. Image loss and secret message

loss are common loss functions. DeepStego (Baluja,

2017) is a steganography method that encloses a cover

image within a covert image of a similar size. It

incorporates a preparation network and the encoder-

decoder network to extract more valuable features

from the secret image for efﬁcient encoding. Gener-

ative Adversarial Networks (GAN) simulate a game

between a generator and a discriminator to optimize

both. GAN thus let steganography and steganaly-

sis compete. SGAN (Volkhonskiy et al., 2020) uses

deep convolutional GAN (DCGAN) (Radford et al.,

2015) to create secure covers, and manual steganog-

raphy procedures are then used to conceal secret mes-

sages in the generated covers. Despite achieving good

undetectability, GAN-based steganography schemes

still have problems with recently proposed steganal-

ysis techniques. Tao et al. (Tao et al., 2019) created a

robust steganographic framework against JPEG com-

pression since images are often lossily compressed

over the channels. The compressed cover image and

the secret are ﬁrst used to create a stego image. They

changed the original cover image’s coefﬁcients in ac-

cordance with the stego image to produce an inter-

mediate image that, following the same channel com-

pression, is precisely like the stego image. The se-

cret can be extracted appropriately by transferring

the intermediate image across the lossy channel, even

worse, if the payload increases, it will face substantial

detection risks. Wang et al. (Wang et al., 2022) pro-

posed a repeatable data-hiding framework based on

the Least-Signiﬁcant Bit (LSB) algorithm to repeat-

edly reuse the cover image for embedding.

2.2 Secret Sharing and Steganography

Several research papers have explored the use of se-

cret sharing and steganography together, to enhance

the security and privacy of information transmission.

In 2010, Wang and Wang (Wang and Wang, 2010)

proposed a secret sharing scheme based on steganog-

raphy, where secret shares were embedded in the least

signiﬁcant bits of cover images. This is, to the best of

our knowledge, the ﬁrst work along the same lines

of this work, but with a focus on the steganographic

technique. Our work adds to this by letting the em-

bedding technique arbitrary (up to assuming that the

embedding leaves at least some part of the picture un-

altered, which is the only restriction on the stegano-

graphic algorithm that we will require), and striving

for plausible deniability in addition. In 2013, Yao

and Xiang (Yao and Xiang, 2013) developed a visual

cryptography scheme that used steganography to hide

the shares in cover images. Their work is interesting

in, among other aspects, the fact that they also address

cheating by insiders and outsides; something that we

do not address in this work, since our mode of ap-

plication is that of a sender using an image album to

transport information hiddenly and deniably to a re-

ceiver, similar to the work done by J

org et al. (Keller

and Wendzel, 2021). As such, we only have the ma-

licious outsider (attacker hereafter) that must be con-

vinced of nothing suspicious to be in our picture set.

Jaya Nirmala et al. (Jaya Nirmala, 2012) has done a

comparative study of the secret sharing algorithm for

secure data in the cloud. Most closely to our work

is the scheme of (Rajput et al., 2018), which – as we

will do – uses linear equations to represent a secret

with shares that are images themselves. The authors

note various limitations of their scheme, most impor-

tantly, the fact that “ the stego image comes out to be

random, which could alert an intruder that they are be-

ing deceived”. We propose a remedy for this problem

by enforcing the same distribution of fake and real

shares, so that the adversary cannot reliably detect the

deception.

We will make use of the above discussed tech-

niques in combination with steganography to hide

the shares, which adds new security features to both

primitives. Neither is the literature about secret shar-

ing explicitly concerned with conﬁdentiality of shares

SECRYPT 2023 - 20th International Conference on Security and Cryptography

732

(which by construction is not naturally required), nor

is steganography usually concerned with plausible de-

niability, since the secrets are hidden anyway. The

concept of plausible deniability, as we use it, ﬁrst ap-

peared in the context of encryption (Goldberg et al.,

1996), with the goal of having a cipher that lets us

decrypt either the true or a decoy ciphertext, depend-

ing on whether the decryption is done legitimately or

under pressure (Bellare and Kohno, 2003), (Asokan

et al., 1999), (Rass et al., 2022). Similarly, secret

sharing is extensible to multi-secret sharing, allowing

the reconstruction of several secrets from the same set

of shares. This is particularly interesting for matters

of deniability, since if we could reconstruct several

different secrets from the same set, some of them can

be harmless for the purpose of yielding to an attacker,

while other secrets are kept conﬁdential. This relates

our work to multi-secret sharing schemes, which have

been intensively studied in the past. For our pur-

poses, we will resort to a simple multi-secret sharing

based on intersecting hyperplanes, similar to Blake-

ley’s scheme (Blakley, 1979).

2.3 Our Contribution

We introduce the notion of Oblivious Secret Sharing

as a method to enhance steganography with plausibe

deniability, by combining the two techniques to unify

the best from both: in hiding the shares with help

of steganography, we can make the attacker uncertain

about how many shares will recover the secret. Con-

versely, in having a pool of shares from which we can

recover multiple secrets, we can steganography plau-

sibly deniable. Oblivious secret sharing is thus a form

of (regular) secret sharing that additionally hides how

many shares are there, and, is here applied to generi-

cally make a steganographic mechanism plausibly de-

niable.

3 PRELIMINARIES AND

NOTATION

In the following, m is a secret message that we as-

sume to be encoded into a matrix S that we can, in

turn, interpret as an image. Under this assumed trans-

formation, we can think of the embedding as taking an

arbitrary string, and placing it invisibly into a picture.

The intermediate representation of m as yet another

picture S (for data type compatibility in the stegano-

graphic embedding), is of no explicit interest for us

in the following. We will use m

,...,m

ℓ

each

represented as S

as the secret messages that we are

willing to hide. We let the cover images be from some

album, represented as an ordered set

{

,...,I

}

with

n ≥ ℓ. We use J ⊂

{

1,...,n

}

to denote a uniformly

random subset choice. Moreover, we will assume all

computations following hereafter to be in a suitably

deﬁned ﬁnite ﬁeld so that we do not need to worry

about overﬂows or roundoff errors. To simplify the

notation, we let the ﬁnite ﬁeld arithmetic be implicit,

without annotations to the equations.

Let us assume that the steganographic embedding

of a secret S into an image I affects only some portion

of the image, and leaves the majority part unchanged,

which we will call the “cover part” of the image I and

denote it as I

. That is, the portion I

is unchanged

whenever the secret S is steganographically put into

the image I, which – upon this embedding – has be-

come a carrier of a secret, signiﬁed by writing I

∗

. The

part of I that has changed upon this embedding is the

stego-part, denoted as I

. For example, if the embed-

ding is in the least signﬁciant bits (LSBs), I

will be

everything excluding the LSBs of each pixel.

The distinction of the cover part is important for

us in the following, since no matter what information

steganographically goes into an image I, the result-

ing stego-images I

will be different, depending on

the particular secret, but the cover part I

of I will

always be the same, as it excludes any secret (stego-

)information. We emphasize that the superscript s is

here only symbolically, and does not relate to any spe-

ciﬁc secret. Summarizing the symbols, we will thus

distinguish three versions I, I

and I

∗

of an image,

where I may or may not contain a secret (i.e., is of un-

told status), and the secret stored in I

∗

may be real or

fake. To distinguish the latter two, we reserve writing

∗

for images containing a real secret m, and write I

′

whenever I contains a fake secret, denoted as m

′

3.1 Basic Steganographic Deﬁnitions

The currently used steganographic techniques can be

divided into manual and DNN-based methods. These

two algorithms are typically used in a steganography

scheme. The deﬁnition of an embedding algorithm

(Encoder) is as follows:

∗

← E(I,m) (1)

where I is the cover image, m is the secret mes-

sage. Consequently, a deﬁnition of an extraction algo-

rithm (decoder) is: ˜m = D(I

∗

) we may obtain ˜m ≈ m

in most DNN approaches; however, additional error-

correcting encoder and decoder are required to re-

move noise to get the exact message, but we have

˜m = m in LSB or non-deep learning steganographic

methods.

How to Plausibly Deny Steganographic Secrets

733

3.2 Deniable Steganography Deﬁnitions

Steganography that is sender-deniable is resistant to

sender coercion (Xu et al., 2022). In this instance,

the adversary identiﬁes a sender and forces them to

disclose the secret information. To conﬁrm the verac-

ity of the revealed message, the adversary may force

the sender to create the same stego with the original

cover and hidden message. The sender should then

have a fake encoder E

in addition to the encoder E

used in equation (1) so that it can generate a stego

image again while using a convincing fake message

′

and cover I as follows: I

′

← E

(I, m

′

) where m

′

should be distinct from m but appear meaningful.

Let us adapt the notation from (Xu et al., 2022) for

our purposes, and think of the embedding algorithm E

and fake embedding algorithm E

as the same proce-

dure, only taking an additional auxiliary input that we

hereafter will call a secret key sk. Our new embedding

algorithm E(I, m

′

,sk) will be probabilistic and resem-

ble the algorithm E and E

from (Xu et al., 2022)

upon different auxiliary inputs sk.

Deﬁnition 1 ((Plausible) Sender-Deniability). A

steganographic embedding is called sender-deniable,

if the following scenario succeeds for the (honest)

user: having embedded a secret m into some image

(or set of images) I

∗

with a secret key sk, let the at-

tacker be in possession of the image I

∗

with m hid-

den inside. Moreover, let m and sk be unknown to the

adversary, and assume the attack goal to determine

whether or not I

∗

does contain some secret.

We call the embedding scheme sender-deniable, if

the user can, upon force, create a fake secret m

′

, and

suitable key sk

′

such that the embedding of m

′

with the

algorithm E and key sk

′

used in it, reproduces exactly

the adversary’s information I

∗

but without using the

real secret m, i.e., I

∗

= I

′

← E(I, m

′

,sk

′

), when I is the

original (clean) image.

If the real message m and the fake message m

′

have the same distribution, i.e., come from the same

source, we call the scheme plausibly sender-deniable.

Deniability thus differs from plausible deniability

in the fact that the former only demands another mes-

sage to exist, but it does not need to be meaningful.

Hence, the attacker could be suspicious when being

presented m

′

as the content of I

′

. Plausible deniability

shall resolve this issue by making m

′

indistinguish-

able from a real message, in terms of probability dis-

tribution. In both cases, the user (sender) attempts to

convince the adversary there being no sensitive infor-

mation inside the picture, by demonstrating an em-

bedding of some (random) fake message that could

have produced exactly the picture that the adversary

thinks to contain a secret.

Receiver-deniable steganography allows the re-

ceiver to open a stego image to a useless fake secret

upon force. If the adversary is sure that I

∗

contains

a secret (different to the sender-deniability situation

from above), then the receiver could be forced to dis-

close the stego content in I

∗

. In the vocabulary of (Xu

et al., 2022), the receiver would then invoke a fake

decoder D

that can extract a convincing message m

′

from the stego in addition to the ordinary decoder D.

In our notation, we will not distinguish real from fake

decoders, but rather let there be a single extraction

algorithm (Decoding) D that takes one or more im-

ages and a secret key sk to output some hidden con-

tent inside the cover images. As before, the sender

can use some suitably constructed other secret key sk

′

to extract a fake message m

′

to show to the attacker:

′

= D(I

∗

,sk

′

Deﬁnition 2 ((Plausible) Receiver-Deniability). Let

the user have embedded a secret m into an image I

∗

←

E(m,sk) and assume that the adversary knows that

∗

does contain a secret, but does not know m or sk.

Let the attacker force the user to disclose the image.

We call the extraction algorithm receiver-deniable, if

the user can (efﬁciently) construct a key sk

′

such that

the extraction returns m

′

= D(I

∗

,sk

′

) ̸= m. If m

′

and

m have the same distribution, we call the extraction

plausibly receiver-deniable.

We will, without loss of generality, allow the se-

cret to be embedded in parts over several images (up

to a full photo album) and also extracted from sev-

eral possible input images, so that both, the embed-

ding and extraction algorithms can take whole sets

of images as their (ﬁrst) inputs. To avoid overcom-

plicating our notation, we will not introduce accord-

ingly extended symbols here, and let the details be-

come clear from the constructions to follow. For en-

coding and decoding purposes in the sender-deniable

steganography and receiver-deniable steganography,

we use Open Stego (Vaidya, 2023). This has the addi-

tional purpose of showing that the constructions made

here are generic, and thus compatible with different

steganographic techniques. This ﬂexibility, however,

does not also apply for the secret sharing, for which

we require a speciﬁc method.

Plausible deniability provides an extra layer of se-

curity for the sender and can be helpful in situations

where the sender may face legal or political conse-

quences for sending the message. By having the op-

tion to deny the existence of the message, the sender

can protect themselves from potential ramiﬁcations.

It is essential to be aware that plausible deniability

does not guarantee immunity from legal action or con-

sequences. In many countries, using steganography

for illegal or unethical purposes is prohibited, and in-

SECRYPT 2023 - 20th International Conference on Security and Cryptography

734

dividuals may still be held responsible for their ac-

tions, even with the presence of plausible deniabil-

ity. This distinguishes plausible deniability from con-

vincing deniability: while plausible deniability only

means the provable possibility of a message to be real

or fake, this does not imply (nor refute) that an at-

tacker will “buy” the claim of a fake information to

be real. We cannot technologically enforce the belief

into what the user presents to the attacker, so at some

point, it will remain the subjective decision of the at-

tacker whether or not to believe that the message pre-

sented to him/her was right. A guarantee that the user

can convince the skeptic attacker would be “convinc-

ing deniability”, which is much stronger than plau-

sibly deniability, but technologically not achievable.

This paper shows how to tackle the above-mentioned

severe threat. And also, if the user possesses the

dataset and some adversary performs a steganalysis

attack on this dataset and forces him to reveal what is

hidden inside that noisy-looking picture.

Our construction will be an extension to con-

ventional multi-secret sharing with added security in

terms of deniability of content or the number, resp.

existence, of shares. We call this oblivious secret

sharing.

4 OBLIVIOUS SECRET SHARING

Our goal is hiding a secret inside a photo album in a

deniable fashion for the sender and receiver. To this

end, let the messages to be embedded, containing real

and fake messages, be m

,...,m

ℓ

, sampled at ran-

dom from the same source, and let n ≥ ℓ be the num-

ber of images in our cover photo album.

Embedding of secrets: Let the sequence of mes-

sages m

,...,m

ℓ

be coerced into respective im-

age formats S

,...,S

ℓ

, to embed the i-th secret

into our cover album. We ﬁrst choose a random set

⊂

{

1,2,...,n

}

of images, and write the secret S

representing m

, as

∑

j∈J

+ R

, (2)

with the (easily computable) residual share as

:= S

−

∑

j∈J

. Reading (2) as a form of secret

sharing, the shares are hence the cover parts I

indices j ∈ J

from the album, and the residual im-

age R

that will in most cases look like some random

noise, but not having any particularly ﬁxed distribu-

tion (it may be recognizable as a share if an attacker

extracts it). Embed the share R

inside some cover

image I

′

← E(I

′

), with I

′

∈

{

,...,I

}

taken at

random from the album at index i

′

. Note that the index

′

is not to be mixed up with the index of the i-th mes-

sage, i.e., we have i

′

̸= i in general. Create the extrac-

tion key sk

for the i-th by putting together the indices

of the shares I

in (2), and the additional index i

′

the image to contain the residual share R

, i.e., deﬁne

← (i

′

). For example: S

= (I

+ I

) + R

now the created residual share R

is put into the im-

age from the dataset. Let’s suppose we had put the

residual share of R

in the I

; then the key would be:

= (5,

{

1,14,33

}

To extract the i-th message, whether real or fake,

we proceed as: Given the secret key sk = (i

′

), ex-

tract R

from I

′

using the chosen steganographic al-

gorithm. Extract the cover parts from all images in-

dicated by the indices in J

, and recover the message

from equation (2).

To delete a secret m

from the album, we use the

corresponding secret key sk

= (i,J

) to identify the

image I

∗

′

that contains the residual share for m

. We

then simply overwrite the stego part I

′

by embedding

a newly constructed residual share R

′

for some – now

fake – message m

′

to replace m

in future.

To update a secret m

← m

i,new

, we take the se-

cret key sk

= (i

′

) and represent m

i,new

again by

equation (2), to compute a fresh residual share R

i,new

accordingly, that we embed (using the chosen proce-

dure) into I

′

5 SECURITY ANALYSIS

Since our goal is plausible deniability, we hereafter

assume that the adversary already has recovered some

secret (by steganalysis) that only needs conﬁrmation,

or is (again possibly by a prior steganalysis) already

suspicious that some secrets may exist. Sender denia-

bility works against the latter scenario, while receiver

deniability is security against the former. Steganaly-

sis itself is hence out of scope hereafter, as we assume

this to already have happened (with results used by the

attacker).

5.1 Sender Deniability

Let the attacker have image I

∗

(i.e., the image at index

t in the album) in its possession, but is uncertain about

whether this image really contains a secret (i.e., the

asterisk in our notation is not visible to the attacker

although it may exist). For the sender to plausibly

deny some real m to be inside I

∗

, assume that the cor-

responding secret S would inside I

∗

be represented by

the residual share R as

S =

∑

j∈J

+ R (3)

How to Plausibly Deny Steganographic Secrets

735

using the set J

. The secret extraction key would thus

be sk = (t, J

). The set J

is unknown to the attacker

(although it may have potential partial, but uncon-

ﬁrmed, information by knowledge of the index t), so

it is a simple matter to choose another set J

′

and a fake

secret S

′

computed as

′

= R +

∑

j∈J

′

(4)

such that (3) holds likewise with S

′

that we can reveal

to the adversary, to keep the real S secret. Thus, S

′

will

represent another message m

′

̸= m for which I

= I

′

←

E(m

′

,sk = (t, J

′

)) will be identical to the attacker’s

information and Deﬁnition 1 is satisﬁed.

To also see that the sender can plausibly deny the

embedding, consider the distributions of the terms in

(3) and (4). Let the user have created both type of

messags, real and fake, and let them be sampled from

a common probability distribution F. Moreover, let

the expression

∑

j∈J

have the distribution F

, as-

suming that J is a randomly uniform selection from

{

1,2,...,n

}

, drawn without replacement. And ﬁnally,

let the residual share have (yet another) distribution

. By (3), S will have the distribution F = F

∗ F

by convolution. However and likewise, S

′

will have

the distribution F

∗ F

= F, which is the same as the

distribution of the real message by the commutativity

of convolutions. Thus, the sender-deniability is also

plausible by Deﬁnition 1.

5.2 Receiver Deniability

Now, let the attacker be certain about there being a

secret m inside the image I

∗

in possession of the at-

tacker, and there is force on the user to disclose the

inner message m. In being forced to use some image

∗

to disclose a secret, the receiver has two options: If

there is another secret key sk

′

= (i

′

) such that t ∈ J

′

that opens a harmless (i.e., insensitive) fake message

′

, the receiver can faithfully extract the message m

′

instead of m. The process is in no aspect different to

how m would be opened, so unrecognizable for the

attacker, and delivers a message m

′

= D(I

∗

,sk

′

) ̸= m,

which accomplishes receiver deniability by Def. 2.

Otherwise, the user can proceed as with sender de-

niability, and produce a representation S

′

of a fake

message m

′

with the residual share R obtained from

∗

as in equation (4), and show the result m

′

(which is

most likely ̸= m) to the adversary, again accomplish-

ing receiver deniability by Deﬁnition 2.

In both cases, the distributions of the fake secrets

′

and the real secret m are identical by the same to-

ken as in Section 5.1, under the hypothesis that both

are sampled from the same source (owned by the cre-

Table 1: Situation of denial for the number of secrets.

attacker’s view demonstrated by the user

∗

= I

∗

. =

∗

t−1

= I

∗

t−1

(real until here) I

∗

= I

′

(fake from here)

′

t+1

= I

′

t+1

. =

′

= I

′

ator or sender of the album, resp. pictures). Hence,

the deniability is also plausible.

5.3 Deniability of the Number of Secrets

To deny the number of secrets as such, our mecha-

nism is to let the user under pressure demonstrate that

the album, exactly as the adversary has it, is repro-

ducible with less than the true number of secrets in-

side it. More formally, let the adversary’s knowledge

be the full set of images I

,...,I

, and, without loss of

generality, let us enumerate them in the order of the

ﬁrst t images containing t secrets of the user, and the

remaining n − t images being “empty” in the sense of

storing only fake residue shares. The user’s goal is to

reproduce the adversary’s information with only t − 1

of the actual secrets, thus denying the existence of the

t-th secret at all. To illustrate the situation, recall that

the asterisk marks images that contain actual secrets

of the user (speciﬁcally residue shares thereof), and

let images with a dash superscript contain fake infor-

mation. It is unknown to the adversary which pictures

contain sensitive secrets, as our goal here is denying

the number of such secrets. For the sake of illustra-

tion, however, let us arrange them in ordered rows,

where the user’s goal is to reproduce identical rows

only not using the t-th secret, hence denying that the

number of secrets was t, by demonstrating that the

number were t − 1. This in fact assumes even some

additional knowledge of the attacker, since we take it

as known that the ﬁrst t −1 images contain real secrets

(this would be unknown in reality).

To make the columns in Table 1 identical, we have

to re-create the image I

∗

as it is in the adversary’s

possession, without using the real secret with which

∗

has been made before. This works with the very

same mechanism as for sender deniability in Section

5.1, since the user can recreate the album “as is” us-

ing a fake secret in place of the real secret at image

number t. This process is repeatable for multiple im-

ages too, thus letting us also plausibly claim there to

be t − 2,t −3, . . . or fewer real secrets in the album.

For the images I

,...,I

t−1

, the user can just re-

SECRYPT 2023 - 20th International Conference on Security and Cryptography

736

veal and use the actual secrets to faithfully reproduce

,...,I

t−1

as the adversary expect. Likewise, for

t+1

,...,I

, the user can openly construct fake shares

and reproduce these pictures to the attacker’s expec-

tation. Now, the user can claim the resulting ran-

dom value S

′

to be nothing else than a legitimate fake

message that, with the choice of J

′

that the aversary

cannot recognize as being ̸= J (as it does not know

J), would reproduce exactly the residue R that the at-

tacker may have recovered from I

6 DISCUSSION

The oblivious secret sharing uses the feature of plausi-

ble deniability to provide additional security for both

mechanisms. It enhances steganography by prevent-

ing an attacker from accessing conﬁdential informa-

tion even if they can detect the presence of a hidden

message. And for secret sharing, the added value of

steganography is to prevent enforced processing of

shares, since we can plausibly deny to possess them.

A demo implementation of our method is available

for download at https://github.com/shahzadssg/How-

to-plausibly-deny-steganographic-secrets.git.

The future research in this area could be the de-

velopment of more efﬁcient and secure protocols for

oblivious secret sharing in the context of plausible

deniability. This could involve exploring new cryp-

tographic techniques, optimizing existing protocols,

and exploring the trade-offs between security, efﬁ-

ciency, and usability. Another area of research could

be the application of oblivious secret sharing to new

and emerging technologies, such as blockchain and

distributed ledger systems. These technologies often

require secure and decentralized methods for sharing

and storing sensitive information, making oblivious

secret sharing a potentially valuable tool. Addition-

ally, the research could focus on integrating obliv-

ious secret sharing with other cryptographic tech-

niques, such as homomorphic encryption and zero-

knowledge proofs, to provide even more robust levels

of security and privacy. Finally, the research could

explore the potential applications of oblivious secret

sharing outside of traditional cryptographic settings,

such as social networks, online voting systems, and

other areas where secure and private information shar-

ing is essential.

REFERENCES

Asokan, N., Niemi, V., and Nyberg, K. (1999). Man-in-the-

middle in tunnelled authentication protocols. In Proc.

8th USENIX Security Symp., pages 111–120, USA.

Baluja, S. (2017). Hiding Images in Plain Sight: Deep

Steganography. In ANIPS, volume 30.

Bellare, M. and Kohno, T. (2003). Cryptographic random

oracle utilities and proofs. In CRYPTO 2003, pages

452–469. Springer.

Blakley, G. R. (1979). Safeguarding cryptographic keys. In

Proc. of NCS, volume 48, pages 313–317.

Canetti, R., Dwork, C., Naor, M., and Ostrovsky, R. (1997).

Deniable Encryption. Lecture Notes in Computer Sci-

ence, pages 90–104, Berlin, Heidelberg. Springer.

Goldberg, I., Wagner, D., Thomas, R., and Brewer, E. A.

(1996). A secure environment for untrusted helper ap-

plications (conﬁning the wily hacker). In Proc. 6th

USENIX Security Symposium, pages 113–128, USA.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In Proc.

27th ICNIPS - Vol 2, pages 2672–2680. MIT Press.

Jaya Nirmala, S. (2012). A Comparative Study of the Se-

cret Sharing Algorithms for Secure Data in the Cloud.

International Journal on Cloud Computing: Services

and Architecture, 2(4):63–71.

Keller, J. and Wendzel, S. (2021). Reversible and Plausibly

Deniable Covert Channels in One-Time Passwords

Based on Hash Chains. Applied Sciences, 11(2):731.

Radford, A., Metz, L., and Chintala, S. (2015).

Unsupervised Representation Learning with Deep

Convolutional Generative Adversarial Networks.

arXiv:1511.06434.

Rajput, M., Deshmukh, M., Nain, N., and Ahmed, M.

(2018). Securing Data Through Steganography and

Secret Sharing Schemes: Trapping and Misleading

Potential Attackers. IEEE Consumer Electronics

Magazine, 7(5).

Rass, S., K

onig, S., Wachter, J., Egger, M., and Hobisch, M.

(2022). Supervised machine learning with plausible

deniability. Comput. Secur., 112:102506.

Tao, J., Li, S., Zhang, X., and Wang, Z. (2019). To-

wards Robust Image Steganography. IEEE TCSVT,

29(2):594–600.

Vaidya, S. (2023). OpenStego.

https://github.com/syvaidya/openstego.

Volkhonskiy, D., Nazarov, I., and Burnaev, E. (2020).

Steganographic generative adversarial networks. In

12th ICMV, volume 11433, pages 991–1005. SPIE.

Wang, X. and Wang, W. (2010). Secret sharing scheme

based on steganography. In IEEE ICNDS, pages 486–

489.

Wang, Z., Feng, G., and Zhang, X. (2022). Repeatable Data

Hiding: Towards the Reusability of Digital Images.

IEEE TCSVT, 32(1):135–146.

Xu, Y., Xia, Z., Wang, Z., Zhang, X., and Weng, J. (2022).

Deniable Steganography. arXiv:2205.12587 [cs].

Yao, J. and Xiang, Y. (2013). Secret sharing and steganogra-

phy scheme based on visual cryptography. Multimedia

Tools and Applications, 63(2):405–415.

How to Plausibly Deny Steganographic Secrets

737