An Analysis of AI Models for Making Predictions: Groundwater Case

Study

Miguel

Angel Jim

enez Garc

ıa

1 a

and Richard de Jes

us Gil Herrera

2 b

Universidad Americana de Europa, UNADE, Av. Bonampak Sm. 6-Mz. 1, Canc

un Q.R., Mexico

Universidad Internacional de la Rioja, UNIR, Logro

no, Spain

Keywords:

Artiﬁcial Intelligence, AI, Machine Learning, Linear Regression, Predictions, Groundwater.

Abstract:

The development and application of intelligent models assure continuous monitoring and improvement of

quality processes that control most of our city’s infrastructure. Regression models are a popular tool for mak-

ing predictions in multiple ﬁelds, including ﬁnance, healthcare, and weather forecasting. However, the limita-

tions of traditional regression models have prompted the development of more advanced techniques, such as

Recurrent Neural Networks (RNNs), which have revolutionized the ﬁeld of prediction modelling. This paper’s

main objective is to explore the possibilities that intelligent models offer to real-world problems, speciﬁcally

the ones that require making predictions to operate, manage, and safeguard the resources and wellbeing of

people. The study focuses on groundwater measurements and their applications in predicting reservoir levels,

as well as the possibility and criticality of ﬂoods, droughts, and other natural phenomena. By analysing avail-

able public or open data, it is possible to uncover hidden insights that lead to pattern identiﬁcation, system

behaviours, and risk modelling. The goal is to raise awareness of the power of artiﬁcial intelligence and how

to integrate them into modern business practices.

1 INTRODUCTION

Many civil and industrial projects are carried out in

the modern world using technology. The advan-

tages they bring are the optimization of resources,

safer construction, operation, and maintenance, and

increased product quality and quantity. Despite the

success above, there are always areas for improve-

ment, and with more technological advances, it is pos-

sible to automate most traditional, recurrent, and sta-

ble processes.

For example, farming and land irrigation has seen

signiﬁcantly less manual work, including ever more

efﬁcient machinery and tools, so devices are pro-

grammed to respond to environmental conditions,

crop quality, and diverse user settings.

The inner workings of these machines are due to

a better understanding and implementation of well-

known mathematical concepts. Even though their

study is not new, such concepts continue evolving to

leverage modern hardware and capabilities.

Other factors, such as the availability and price of

https://orcid.org/0009-0007-1495-1746

https://orcid.org/0000-0003-4481-7808

raw materials, contribute to the continuous develop-

ment and perfection of tools and methods. The result

is a productivity increase with a continual decrease in

expenses.

Public resource management is one industry that

has grown a fair amount thanks to technological de-

velopment. The state of California in the United

States has suffered a drought for the past couple of

decades. Hence, properly managing water, a limited

natural resource, is vital for the correct functionality

of its society.

This state has several wells and has identiﬁed

groundwater reservoir locations. Efforts to locate

more water and distribute it to needy areas are a con-

stant among public and private institutions. Formulat-

ing an algorithm or the best possible process to supply

and deal with potable water services is a constant of

the utmost importance.

Knowing the location of water and taking constant

measurements of its properties and qualities makes

it possible to generate a time series with data that,

through analysis, can uncover patterns and make pre-

dictions.

Statistical functions can highlight data correla-

tions, generating predictions based on certain con-

176

GarcÃ a, M. and Herrera, R.

An Analysis of AI Models for Making Predictions: Groundwater Case Study.

DOI: 10.5220/0012120400003552

In Proceedings of the 20th International Conference on Smart Business Technologies (ICSBT 2023), pages 176-185

ISBN: 978-989-758-667-5; ISSN: 2184-772X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ditions. Linear regressions are the most common

method to analyse these results.

A strong foundation based on concepts that guide

and adjust the project’s course is advisable to achieve

the proposed goal—knowledge in data analysis and

strategic decision-making based on mathematics, par-

ticularly statistics and computer sciences, are excel-

lent candidates for the enterprise.

The general objective of this study is to under-

stand California’s groundwater behaviours and pro-

pose an algorithmic approach to its strategic collec-

tion, distribution, and management in an efﬁciently

sustainable way.

The following are the main speciﬁc objectives of

this study:

• Provide a short description of California’s sustain-

able water management problem.

• Review Artiﬁcial Intelligence, Machine Learning,

and other computer science methods and tech-

niques to solve the problem.

• Evaluate and propose a method to select the best

AI model to address the problem.

2 CONCEPTUAL FRAMEWORK

2.1 Linear Regressions

Linear regression is a widely used statistical tech-

nique to model the relationship between a depen-

dent variable (outcome or response variable) and one

or more independent variables (predictor or explana-

tory variables). When established, the model can be

used to make predictions about the dependent vari-

able based on new values of the independent vari-

ables. The goal of linear regression is to ﬁnd the best

linear relationship between the dependent and inde-

pendent variables. (Weisberg, 2005).

There are many prevalent use cases where linear

regressions can make accurate predictions. For exam-

ple, when partial data is available that correlates with

the data in question, a linear regression can help solve

the expected results. By this method, it’s possible to

determine the most probable output based on avail-

able data.

An example could be predicting the number of

crops harvested under certain conditions. If data is

available about the soil quality, fertilizers, weather

conditions, types of seeds, and other related factors,

it’s possible to calculate with statistics which parame-

ters inﬂuence what readings. For this reason, it’s per-

fectly feasible to issue accurate predictions and plan

for an expected number of crops.

2.2 Types of Linear Regressions

There are different Linear regression classiﬁcations,

each with its strengths and weaknesses. Here are

some of the most common algorithms used in linear

regressions(Inc, 2021):

1. Ordinary Least Squares (OLS): OLS is the most

widely used algorithm in linear regression. It ﬁnds

the line of best ﬁt by minimizing the sum of the

squared differences between the predicted and ac-

tual values. OLS works well when a linear rela-

tionship exists between the dependent and inde-

pendent variables with minimal noise in the data

2. Ridge Regression: Best applied when multi-

collinearity (high correlation) between the inde-

pendent variables occurs. Ridge regression is ap-

propriate when high variance or many indepen-

dent variables exist. It adds a penalty term to the

OLS algorithm, which helps to reduce the coefﬁ-

cients of highly correlated variables.

3. Lasso Regression: Better suited when there is

multicollinearity between the independent vari-

ables, but it has a different penalty than Ridge re-

gression. Lasso regression is most effective when

there are many independent variables, and only a

few affect the outcome. Lasso regression adds an

L1 penalty to the OLS algorithm, which helps to

shrink the coefﬁcients of less important variables

to zero.

4. Elastic Net Regression: It is a combination of

Ridge and Lasso regressions, and it is most ef-

fective when the data has high multicollinearity

and many independent variables. It adds both L1

and L2 penalty terms to the OLS algorithm, which

helps to reduce the coefﬁcients of highly corre-

lated variables and shrink the coefﬁcients of less

important variables to zero.

5. Polynomial Regression: Best applied when there

is a non-linear relationship between the indepen-

dent and dependent variables. It involves adding

polynomial terms to the OLS equation, which

helps to capture the non-linear relationship. Poly-

nomial regressions are helpful when the data has

a curved relationship, such as in a parabola or a

sine wave. (Weisberg, 2005).

In summary, the choice of algorithm for linear regres-

sion depends on the speciﬁc characteristics of the data

and the research question. OLS is the most widely

used algorithm and works well when there is a lin-

ear relationship between the variables. Ridge, Lasso,

and Elastic Net regression are more convenient with

multicollinearity or when many independent variables

An Analysis of AI Models for Making Predictions: Groundwater Case Study

177

exist. Polynomial regression is a good choice for non-

linear relationships between the variables.

2.3 The ARIMA Model

The most popular statistical methods for analysing

time series are the ARIMA and Regression models.

Even though both deliver similar results, they differ in

their approach to modelling the underlying data pat-

terns.

Regression models are typically used to model the

relationship between a dependent variable and one or

more independent variables. In time series analysis,

the relationship between a dependent variable and ex-

ternal factors, such as economic indicators or weather

patterns, is frequently assigned to regression models.

The goal is to identify the most important independent

variables that explain their variation with the depen-

dent variable, then use these to predict future values

of the dependent variable.

In contrast, the ARIMA (AutoRegressive Inte-

grated Moving Average) model is a speciﬁcally de-

signed statistical model for time series data. Its goal

is to model the dependence of a time series on its past

values, capturing linear and non-linear trends in the

data. The ARIMA model is composed of three main

components: the autoregressive (AR) component, the

moving average (MA) component, and the differenc-

ing (I) component.

The AR component models the relationship be-

tween the current value of the time series and its past

values. The MA component models the relationship

between the time series current value and the past

forecast errors. Finally, the differencing component

establishes the order of differencing required to make

the time series stationary.

An example of how both tools can complement

each other is when analysing distinct scenarios based

on correlated data points yields results that may not

always match multiple predicted forecasts. Suppose a

market study for food products suggests seasonal and

regional dishes for a customer that show speciﬁc be-

haviours. Regression models could predict with high

conﬁdence what will likely be picked from the menu,

causing the restaurant to stack up and prepare for the

high season only to ﬁnd out that new customers with

different tastes visit more frequently in the forecasted

timespan. There are additional data points that could

predict what ingredients will be in high demand or

what type of menu items would be the most pleasing

for a general audience. Leveraging historical trends

using the ARIMA model would help uncover hidden

insights from the available data.

As with real-world scenarios, multiple variables

can inﬂuence a given situation. As more of them are

analysed, the more reliable the model and its predic-

tion will be. For questions of higher scope outside the

series itself, an ecosystem of models that feed into

each other will generate more stable predictions.

2.4 Recurrent Neural Networks (RNNs)

Recurrent Neural Networks (RNNs) are a type of neu-

ral network designed to work with sequential data, for

example, time series data. Unlike other neural net-

works, which process input data in a ﬁxed-size batch,

RNNs process input data one time step at a time. They

can achieve this thanks to a memory that allows them

to “remember” information from previous time steps.

The basic structure of an RNN involves a set of in-

put nodes, a set of hidden nodes, and a set of output

nodes. For each time step, the input nodes receive the

input data, allowing the RNN’s hidden nodes to use

a set of weights to process that input data and update

their internal state. The output nodes then generate

a prediction or output for that time step based on the

current hidden state.

The RNN training process for time series predic-

tion or forecasting consists of feeding a sequence of

input-output pairs to the network. RNN adjusts its

weights to minimize the difference between its pre-

dictions and the actual outputs during this process.

For example, given historical data, the RNN can pre-

dict the next value based on the previous values.

When concluded, a time series prediction or fore-

cast can be generated by feeding it a sequence of in-

put values and using the current hidden state to issue a

prediction for the next value in the chain. The process

can run until the desired number of predicted values

is delivered.

One of the advantages of RNNs for time series

prediction is that they can handle sequences of arbi-

trary length. In other words, they can forecast irregu-

lar sequences based on the inputs provided. Addition-

ally, the ability of RNNs to “remember” information

from previous time steps can help them capture pat-

terns in the data that may be difﬁcult to model with

other approaches (Salehinejad et al., 2017).

Several types of RNNs have been developed,

including vanilla RNNs, Long-Short-Term Mem-

ory (LSTM) networks, and Gated Recurrent Units

(GRUs). All these RNNs have different architectures

and update rules that make them suitable for different

types of time series prediction tasks.

Vanilla RNNs are the simplest type of RNN, and

they are best suited for modelling short-term depen-

dencies in sequential data. However, they can need

help with longer sequences, as the vanishing gradient

ICSBT 2023 - 20th International Conference on Smart Business Technologies

178

problem can make it difﬁcult to propagate informa-

tion across many time steps. For example, language

modelling may need help predicting the next word in

a sentence based on previous inputs.

Long-Short-Term Memory (LSTM) networks ad-

dress the vanishing gradient problem and improve

performance on longer sequences. They do this by

introducing a memory cell that can retain informa-

tion over many steps and a set of gates that control

information ﬂow into and out of the memory cell.

LSTMs are great for tasks like speech recognition,

where longer-term dependencies are decisive.

Gated Recurrent Units (GRUs) are a more recent

type of recurrent neural network that is simpler and

faster to train than LSTMs. GRUs are suited for tasks

like machine translation and video analysis. They are

similar in having a set of gates that control the ﬂow of

information, but they use a simpliﬁed update mecha-

nism that requires fewer parameters.

Overall, the choice of which type of recurrent neu-

ral network to use will depend on the speciﬁc require-

ments of the task at hand. For shorter sequences, a

vanilla RNN may be sufﬁcient, while for longer, an

LSTM or GRU may be more appropriate. Addition-

ally, different types of RNNs may perform differently

on different data types. Finding the optimal RNN for

a particular application is done through experimenta-

tion.

2.5 Water Management

As the proliferation of non-sustainable business prac-

tices, overpopulation, and climate change continues

to affect the west coast of the United States, it is be-

coming more urgent to optimize the natural resource

management process. California, where a decade’s

long drought has impacted public policies regarding

energy and water, needs special attention if it intends

to continue supporting its communities and economy.

(Doremus and Hanemann, 2008).

The emergence of innovative solutions in water

puriﬁcation, industrial process, and urbanization have

contributed to temporarily controlling the situation.

These practices are not permanent solutions, so the

continuous research and development of new tech-

nologies are encouraged by both local and federal

governments.

Groundwater analysis and the ability to accurately

predict its location and properties constitute a vital

supply and management issue. Among the many ef-

forts to alleviate dependency on dams and rivers is the

adequate exploitation of natural springs, fountains,

and other reservoirs (Harou et al., 2010).

Therefore, developing and implementing a pro-

cess that leverages artiﬁcial intelligence would in-

crease the effectiveness and accuracy of obtaining,

managing, and distributing water.

2.6 Groundwater Measurements and

Other Available Data

California has had 551 stations that record daily

groundwater measurements since the autumn of 1969.

Quality metrics, time, and location appear in the

records, enabling the study of time-series data in sta-

tistical analysis (Ponce, 2007).

The data format permits the initial exploration

and classiﬁcation of stations, date ranges, and quality

readings. Even though its original form allows it to be

processed directly, some preparation actions will in-

crease the effectiveness of an AI modelling technique.

2.7 AI for Problem Solving

Artiﬁcial Intelligence can solve several problems, in-

cluding logistics, business intelligence, strategic plan-

ning, and operations management. On the topic of

predictions, a project can signiﬁcantly beneﬁt from

having prior information to help decision-making.

The relevance of the information can drive the success

of an initiative by reducing time, effort, and money

when executing said initiative. Pre-processing data

and feeding it through an algorithm will not magically

grant victory to the team seeking it; there must be an

assessment and justiﬁcation for such tools to be valu-

able.

For example, it is implausible to predict winning

the lottery through information analysis. There is in-

trinsic randomness in the system’s process, so study-

ing the probabilities of guessing a winning combina-

tion will only conﬁrm that luck is the most crucial

factor in the equation.

In some cases, the study of available information

presents itself as not only plausible but mandatory be-

fore continuing into the later stages of the project. In

these cases, insights help generate hypotheses to de-

termine the direction regarding the project’s goal. For

instance, when conducting discovery work for a new

product feature, conducting experiments to assess

a market’s reception and adaption before investing

more resources can mitigate development, stafﬁng,

and budgeting risks.

In other cases, analysing data can help determine

the optimal route for solving a problem or even dis-

cover a new trial. Engineering practices recommend

designing a system that consumes only the necessary

for its operation in a determined environment. Only

considering some scenarios affecting said system will

An Analysis of AI Models for Making Predictions: Groundwater Case Study

179

cause malfunctions, and over-engineering adds un-

necessary complexity that ultimately hurts its devel-

opment and maintenance. AI tools can help uncover

insights that lead to elegant designs that optimize re-

sources for the intended and known use cases.

Even though AI has evolved impressively fast in

recent years, it has a long way to go before be-

coming strong enough to be fully autonomous. An

exciting tool that aids software engineering tasks is

GitHub Copilot, a virtual pair programmer that anal-

yses code in real-time and generates suggestions. The

user can evaluate and implement the recommendation

live into their work, reducing development time and

augmenting the quality of the code. Github Copilot

is a promising tool, but like other emerging AI-based

products, there are still areas of opportunity that pre-

vent its unsupervised implementation. Some caveats

are that the algorithm may offer quick suggestions

based on the user’s coding style or what the model has

deemed best for a particular question. The user needs

to drive the project and evaluate what suggestions are

indeed valuable. (Nguyen and Nadi, 2022).

2.8 Selecting a Convenient AI Model

ARIMA models and RNNs (Recurrent Neural Net-

works) are powerful statistical tools for time series

analysis and forecasting. As with any other method,

they have strengths and weaknesses (Ho and Xie,

1998).

ARIMA models are more practical when:

1. The time series has a deﬁned linear or seasonal

trend. Perfect case for autoregressive or moving

average terms.

2. The data is stationary, meaning it lacks signiﬁcant

trends or seasonality.

3. The goal is to model short-term (one-step) fore-

casts rather than longer-term forecasts.

4. A minor data set is available as ARIMA models

ﬁt on smaller datasets compared to RNNs.

RNNs are more suited when:

1. The time series has complex non-linear patterns

that are difﬁcult to model using traditional statis-

tical models such as ARIMA.

2. The data is non-stationary, meaning it has signiﬁ-

cant trends or seasonality.

3. The goal is to model longer-term forecasts rather

than short-term. Forecasts.

4. A large dataset is available. As RNNs are trained

on large datasets to capture complex patterns and

relationships.

5. The time series depends on multiple previous time

steps, such as lagged effects of external factors or

when the value of the series at one-time intervals

depends on values at past time intervals.

3 METHODOLOGICAL

FRAMEWORK

3.1 Implementing AI to Predict

Groundwater Levels

Groundwater is the water beneath the Earth’s sur-

face accumulated between rock and soil pore spaces

or in fractures of rock formation. About 30 percent

of all readily freshwater in the world is groundwa-

ter. A unit of rock or an unconsolidated deposit be-

comes an aquifer when it can yield a usable quantity

of water. Groundwater recharges from the surface; it

may discharge naturally at springs and seeps and can

form oases or wetlands. Private and public companies

use groundwater for agricultural, municipal, and in-

dustrial use by constructing and operating extraction

wells.

Additionally, given the growing scarcity and

strong demand for water, resource sustainability man-

agement requires urgent policies to ensure their ratio-

nal use. The heterogeneous properties of groundwater

systems are related to the dynamic temporal-spatial

patterns. In contrast, an excellent regional groundwa-

ter level forecast for managing water resources that

guarantee proper area support is necessary. Water

managers and farmers need intelligent groundwater,

irrigation planning systems, and other effective mech-

anisms to beneﬁt from the scientiﬁc and technological

revolution, particularly artiﬁcial intelligence engines,

to enhance water support in their water use planning

practices.

Additionally, California has complex water man-

agement systems across various landscapes, including

mountain snow packs, lakes, rivers, and groundwater

basins managed with engineered features like reser-

voirs, levees/ﬂood walls, weirs, culverts, bypasses,

and canals. Intelligent models represent the complex

physical interactions between these features in a con-

ceptual way. They and other analytical tools help

managers make informed decisions about managing

water for people, farms, and the environment. With

the insights and recommendations, the system offers,

it’s possible to take preventive and corrective actions

that protect lives and properties from ﬂooding.

ICSBT 2023 - 20th International Conference on Smart Business Technologies

180

3.2 Predicting the Depth Below the

Ground Surface

The study consists in answering the following ques-

tions:

• Is there any correlation between different ground-

water measurements?

• Can we predict, among other things, the ground

depth distance where water is available?

• Is it possible to predict trends and behaviours with

the resulting data?

The available data consists of a time series dataset of

measurements taken from different groundwater sta-

tions in the state of California.

1. WLM RPE: The reference point’s elevation.

2. WLM GSE: The ground surface elevation at the

well site.

3. RPE WSE: The depth to the water surface below

the reference point.

4. GSE WSE: The depth below the ground surface

or the distance from the ground surface to the wa-

ter surface.

5. WSE: The water surface elevation above sea level.

The measurement of most interest is the depth to ex-

pect water from the ground surface level. The study

consisted of selecting a random station, separating the

time series data in training and testing sets, ﬁtting and

training the model, generating predictions, and evalu-

ating them against the test data set.

The training set contained measurements from

1990 until 2019, while the testing dataset contained

2020 measurements. The objective was to determine

the accuracy and level of conﬁdence of the model’s

prediction to assess its effectiveness.

3.3 Data Mining: CRISP-DM

One of the most popular data science methodologies

for general business use cases and problem-solving is

the Cross Industry Standard for Data Mining (CRISP-

DM) which encompasses six sequential phases for its

execution and success.

1. Business understanding: What problem requires

resolution via a data science approach?

2. Data understanding: What information is avail-

able, what data points are needed, and what pro-

cesses will prepare and transform the data?

3. Data preparation: In what form and state will the

resulting data be arranged?

4. Modelling: What algorithms, experiments, and

techniques will model the data?

5. Evaluation: How will the resulting models be

measured and qualiﬁed based on their expected

results?

6. Deployment: How will the information become

available for business stakeholders and end users?

The methodology ﬁts well into various industries due

to its compatibility with agile development practices

commonly used in most product teams. It follows a

heuristic approach by experimenting through small

iterations at its most basic level. The resulting in-

crement goes into an inspecting and adapting phase

where the team adjusts based on newly available in-

formation.

Its power lies in the way product teams collabo-

rate to resolve complex problems in a natural environ-

ment. In other circumstances, it provides stability and

predictability of traditional waterfall processes by de-

termining, safeguarding, and monitoring a clear out-

come within a limited scope. The requesting party’s

regulations, culture, and needs affect how the project

is executed and delivered. In its ﬁnal phase, the re-

sulting product and its outcomes are proven valuable

and potentially deployable within the context of the

problem (Wirth and Hipp, 2000).

3.4 Cleaning the Data

The ﬁrst step is to analyse, clean, and pre-process

the data to be ready for the model to ingest. The

data source is the California Department of Water Re-

sources (Ponce, 2007). A Python function can take

an argument of its ID and the desired date ranges for

a dynamic station assignment to a given model. The

following sequence describes the logic used to pre-

pare a dataset for model ingestion:

1. Set the measurement date as the dataset’s index.

2. Drop all rows that contain null values.

3. Sort the data by index.

Create a new column with shifted data (predic-

tions).

Return the processed dataset.

By calling this function, a sample set with adequately

formatted data for a model to consume can be reached

and fed into a model or process. The last line of the

code calls the function and assigns the dataset to a

variable called ‘daily data by sample station’.

An Analysis of AI Models for Making Predictions: Groundwater Case Study

181

3.5 Initializing a Model

A Python function is ideal for encapsulating the logic

that executes a regression or any other model that gen-

erates predictions. This function can take a dataset,

model, and a list of “predictors” and pass them into

the model for training. Once the set is ready, a test-

ing dataset can run using the ﬁtted model to gener-

ate and plot prediction results to compare with actual

data. The results serve as a reference point to assess

the prediction accuracy and the model’s performance.

For the data to be ready for model ingestion, an-

other function can create two separate datasets based

on a given date. For example, the training informa-

tion could be an extensive series containing informa-

tion from the beginning until 2022 or two years before

today.

The testing set would be smaller as it only con-

tains data from yesteryear. The available data will

serve as the actual results versus the generated pre-

dictions that the model will provide.

Finally, a ‘model metrics’ function can take the

results, calculate statistical performance metrics, and

print them next to the plotted graphics.

4 RESULTS AND DISCUSSIONS

The generated predictions and overall performance

results were similar across all models due to the prob-

lem’s nature and environment. The data’s quantity

and quality also inﬂuenced the results. The experi-

mentation did not only allow the comparison with dif-

ferent mathematical approaches to solving the same

problem but also to identify the most efﬁcient and re-

liable method to implement in production.

Aspects like the processing power required for

each model or how additional data points and param-

eters affect the accuracy of the predictions were in-

sightful. For instance, the random forest algorithm

overﬁtted the model straying from the expected re-

sults, while simple regression models were less ex-

pensive and more accurate.

Below is a brief description of the ﬁndings each

model presented in the Kaggle community

4.1 Linear Regression

The simplest model implemented a linear regression

provided by SciKit Learn’s Linear Model class. As

with most of the models, the results provided a level

of conﬁdence of 99%

https://www.kaggle.com/code/mikejimenez24/notebo

ok2a2eaa55e5

Figure 1: Linear regression plot.

Independent term: 8417.138

Explained variance regression score: 0.991

Maximum residual error: 7.382

Mean squared error: 2.150

Coefficient of determination: 0.991

Root-mean-square deviation: 1.466

4.2 Ridge Regression

The Ridge regression results were almost identical to

the linear regression. The difference in mathemati-

cal approach did not show a clear distinction. On the

other hand, it begs the question of which scenarios

will it generate signiﬁcantly different results.

Independent term: -7.409

Explained variance regression score: 0.991

Maximum residual error: 7.384

Mean squared error: 2.150

Coefficient of determination: 0.991

Root-mean-square deviation: 1.466

4.3 Elastic Net Regression

The algorithm difference did not affect the results

compared to the previous models. The subtle differ-

ences in residual and mean squared error did provide

hints of how a difference in the qualities and proper-

ties of the data could produce prediction variations.

Independent term: 3.422

Explained variance regression score: 0.991

Maximum residual error: 7.026

Mean squared error: 2.062

Coefficient of determination: 0.991

Root-mean-square deviation: 1.436

4.4 Lasso Regression

The last of the classical regression models provided

the best error margins among the algorithms em-

ployed. The performance did not vary at this point

regarding the generated predictions.

Independent term: -15.956

Explained variance regression score: 0.991

Maximum residual error: 7.137

Mean squared error: 2.038

Coefficient of determination: 0.991

Root-mean-square deviation: 1.428

ICSBT 2023 - 20th International Conference on Smart Business Technologies

182

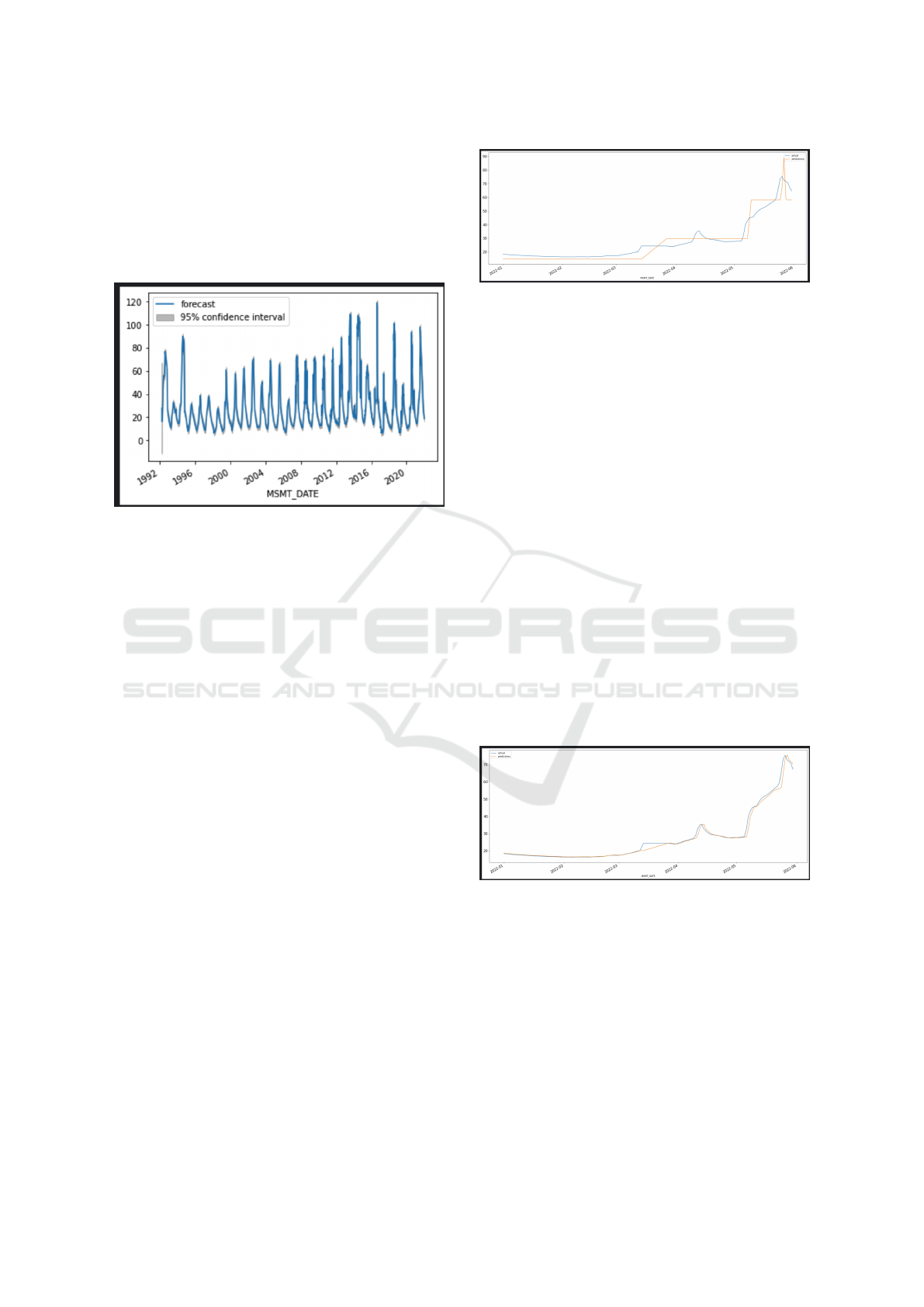
4.5 ARIMA Model

The ARIMA model is not available in SciKit Learn’s

library of classes. For its execution, it was necessary

to ﬁnd the p and q values of the entire set. Once pro-

vided to the model, the generated predictions had a

conﬁdence rate higher than 95%.

Figure 2: ARIMA model forecast plot.

Dep. Variable: GSE_WSE No. Observations: 10709

Model: ARIMA(2, 0, 3) Log Likelihood -16426.530

Date: Sat, March 04 2023 AIC 32867.060

Time: 04:15:55 BIC 32918.012

Sample: 0 HQIC 32884.248

- 10709

Covariance Type: opg

coef std err z P>|z| [0.025 0.975]

const 27.7801 4.165 6.670 0.000 19.616 35.944

ar.L1 1.9680 0.004 550.198 0.000 1.961 1.975

ar.L2 -0.9686 0.004 -272.298 0.000 -0.976 -0.962

ma.L1 -0.5857 0.004 -154.679 0.000 -0.593 -0.578

ma.L2 -0.2126 0.005 -42.423 0.000 -0.222 -0.203

ma.L3 -0.0966 0.005 -18.359 0.000 -0.107 -0.086

sigma2 1.2578 0.001 955.059 0.000 1.255 1.260

Ljung-Box (L1) (Q): 0.48 Jarque-Bera (JB): 462674860.08

Prob(Q): 0.49 Prob(JB): 0.00

Heteroskedasticity (H): 83.67 Skew: 19.02

Prob(H) (two-sided): 0.00 Kurtosis: 1020.57

4.6 Random Forest Regressor

The ﬁrst difference in prediction accuracy was from

the Random Forest Regressor. Due to its design, the

model did not behave as expected, given the time se-

ries parameters. The conﬁdence rate was not signiﬁ-

cantly low to consider it a failure, but it’s not as pre-

cise nor effective as previous models (Kadiyala and

Kumar, 2017).

Explained variance regression score: 0.909

Maximum residual error: 16.496

Mean squared error: 22.331

Coefficient of determination: 0.905

Root-mean-square deviation: 4.726

Figure 3: Random Forest regressor plot.

4.7 Multivariate LSTM Forecast Model

The process in which a recurrent neural network

model is ﬁt, and run differs from the previous exam-

ples. New Python functions are necessary to receive

extra parameters and execute more logic to prepare

the data, ﬁt the model, and generate predictions.

The model requires additional steps to encode the

data into a data series, add and conﬁgure layers, and

ﬁnally compile them to ﬁt the model for it to generate

predictions properly. The next step is to decode the

data series into a data frame, run statistics to show its

performance, and plot the results.

For the function to be dynamic, it can take addi-

tional optional parameters that conﬁgure the data se-

quencer, validations, and model layers. Ultimately,

the complexity is behind an interface that facilitates

the generation of predictions.

The results were not as accurate as the classical

linear regressions but not as low as the random forest

regressor. This other case proved that overﬁtting a

model can deviate it from its optimal state concerning

the problem (Li et al., 2019).

Figure 4: Long-short-time memory regressor plot.

Explained variance regression score: 0.989

Maximum residual error: 9.507

Mean squared error: 2.700

Coefficient of determination: 0.988

Root-mean-square deviation: 1.643

Different algorithms would be appropriate for

more speciﬁc of higher-scope questions, such as qual-

ity chemical analysis on the region over a particular

time (Czako et al., 2021). Industry best practices sup-

port delimiting a question and answer to the needs of

stakeholders (Negash et al., 2016).

An Analysis of AI Models for Making Predictions: Groundwater Case Study

183

4.8 CRISP-DM Deployment

Once the model is ready and its performance is ac-

cepted, the ﬁnal phase of the CRISP-DM methodol-

ogy is to deploy it. In most instances, software plat-

forms offer hosting services in the cloud (John et al.,

2021).

In other circumstances, a company might need to

host their in-house software, managing the entire so-

lution and its operation.

The recommendation is to follow existing guide-

lines and policies to safeguard the information and

properly operate and manage the model and its so-

lutions. Popular serverless services include Amazon,

Microsoft, and Google. (Elger and Shanaghy, 2020).

Analysing some popular approaches by the Kag-

gle community, it was evident that focusing on a sta-

tion and not on the complete universe of data yielded

better results that were easy to consume, process,

and manage. Amid the various available models, the

regression family of algorithms consumes fewer re-

sources while producing accurate predictions that suit

the problem perfectly.

An elegant solution that relies on clearly delim-

ited and manageable inputs is generally a better op-

tion than a general solution that does not consider sub-

tle nuances in the items that conform to it. Business

questions can propose scope and applicability prob-

lems, as a product’s core processes supposedly could

provide similar results across many industry and cus-

tomer use cases.

The reality is that understanding and focusing on a

particular problem and offering a solution that best ﬁts

the user’s workﬂow will undeniably be more success-

ful in the short term. Once the initial problem stops

being a concern, it is safe to switch focus to maintain,

extend, and scale the solution.

5 CONCLUSIONS

California’s groundwater ecosystem does not have

clear seasonality nor easily recognizable trends except

for diminishing water levels. The observations made

to individual stations did allow for accurate predic-

tions to locate water based on area.

With the available results, a secondary study to

map the regional water reservoirs can technically ad-

vise on a better water collection and distribution sys-

tem that uses natural deposits as reserves and as part

of the main supply stream.

The analysis showed that the data’s regularity al-

lowed multiple experiments to allocate just enough

computational power and mathematical framework to

yield an optimal answer that addresses the business

question.

Additional questions regarding the water’s quality,

the effects of continuous drainage, and the amount re-

quired to serve the population, among others, could

be the continuation of the exercise.

A more general view and a broader spectrum of

AI techniques and methods were applied to this multi-

factorial problem to properly analyse and develop the

optimal model. The problem’s characteristics, qual-

ities, and data allowed simple algorithms to gener-

ate highly accurate and effective results. Their out-

put provided high-conﬁdence predictions that satis-

ﬁed the use case from business viability and technical

feasibility perspectives. The next step is to analyse

hidden behaviours and investigate what external fac-

tors can produce additional insights.

REFERENCES

Czako, Z., Sebestyen, G., and Hangan, A. (2021).

Automaticai–a hybrid approach for automatic arti-

ﬁcial intelligence algorithm selection and hyperpa-

rameter tuning. Expert Systems with Applications,

182:115225.

Doremus, H. and Hanemann, M. (2008). The challenges

of dynamic water management in the american west.

UCLA J. Envtl. L. & Pol’y, 26:55.

Elger, P. and Shanaghy, E. (2020). AI as a Service: Server-

less machine learning with AWS. Manning Publica-

tions.

Harou, J. J., Medell

ın-Azuara, J., Zhu, T., Tanaka, S. K.,

Lund, J. R., Stine, S., Olivares, M. A., and Jenkins,

M. W. (2010). Economic consequences of optimized

water management for a prolonged, severe drought in

california. Water Resources Research, 46(5).

Ho, S. L. and Xie, M. (1998). The use of arima models

for reliability forecasting and analysis. Computers &

industrial engineering, 35(1-2):213–216.

Inc, A. (2021). 5 types of regression analysis and when to

use them.

John, M. M., Holmstr

om Olsson, H., and Bosch, J. (2021).

Architecting ai deployment: a systematic review of

state-of-the-art and state-of-practice literature. In Soft-

ware Business: 11th International Conference, IC-

SOB 2020, Karlskrona, Sweden, November 16–18,

2020, Proceedings 11, pages 14–29. Springer.

Kadiyala, A. and Kumar, A. (2017). Applications of

python to evaluate environmental data science prob-

lems. Environmental Progress & Sustainable Energy,

36(6):1580–1586.

Li, Y., Zhu, Z., Kong, D., Han, H., and Zhao, Y. (2019). Ea-

lstm: Evolutionary attention-based lstm for time series

prediction. Knowledge-Based Systems, 181:104785.

Negash, K., Khan, B., and Yohannes, E. (2016). Arti-

ﬁcial intelligence versus conventional mathematical

ICSBT 2023 - 20th International Conference on Smart Business Technologies

184

techniques: A review for optimal placement of pha-

sor measurement units. Technology and Economics of

Smart Grids and Sustainable Energy, 1:1–13.

Nguyen, N. and Nadi, S. (2022). An empirical evaluation of

github copilot’s code suggestions. In Proceedings of

the 19th International Conference on Mining Software

Repositories, pages 1–5.

Ponce, V. M. (2007). Sustainable yield of groundwater. Cal-

ifornia Department of Water Resources.

Salehinejad, H., Sankar, S., Barfett, J., Colak, E., and

Valaee, S. (2017). Recent advances in recurrent neural

networks. arXiv preprint arXiv:1801.01078.

Weisberg, S. (2005). Applied Linear Regression. Wiley

Series in Probability and Statistics. Wiley.

Wirth, R. and Hipp, J. (2000). Crisp-dm: Towards a stan-

dard process model for data mining. In Proceedings of

the 4th international conference on the practical ap-

plications of knowledge discovery and data mining,

volume 1, pages 29–39. Manchester.

An Analysis of AI Models for Making Predictions: Groundwater Case Study

185