Exploring the Effects of Subversive Agents on Consensus-Seeking

Processes Using a Multi-Agent Simulator

Johannes S. Vorster

1 a

and Louise Leenen

1,2 b

Department of Computer Science, University of Western Cape, South Africa

CAIR, South Africa

Keywords:

Consensus, Consensus Simulation, Stochastic Simulation, Synchronization, Multi-Agent Simulation,

Subversive Agents.

Abstract:

In this paper we explore the effects of subversive agents on the effectiveness of consensus-seeking processes.

A subversive agent can try and commit industrial espionage, or, could be a disgruntled employee. The ability

of an organisation to effectively execute projects, especially projects within large and complex organisation

such as those found in large corporates, governments and military institutions, depend on team members

reaching consensus on everything from the project vision through various design phases and eventually project

implementation and realisation. What could the effect be of agents trying to subvert such a process in a way

that does not raise suspicions? Such an agent cannot openly sabotage the project, but rather tries to inﬂuence

others in a way that increases the time it takes to reach consensus, thus delaying projects in subtle ways. Here

we explore the effect such agents could have on the time and effort to reach consensus though the use of a

stochastic Multi-Agent-Simulation (MAS).

1 INTRODUCTION

Project complexity, the ability of project team mem-

bers to reach consensus on the relevant topics or mov-

ing to next phases before reaching consensus have re-

peatedly been quoted as reasons for project delays and

failure (Al-Ahmad et al., 2009; Whitney and Daniels,

2013; Kian et al., 2016; Waheeb and Andersen, 2022).

In this paper we investigate the effect that sub-

versive agents (SAs) could have on project time-

lines and work effort. Our approach uses Multi-

Agent-Simulation (MAS) wherein we model agent

behaviour and in particular the behaviour of SAs. In

the text below we use the terms team members or

members to refer to the conventional members of the

team and the term agents refer to the subversive mem-

bers of the team that has as goal to delay project de-

livery by sowing discord within the team.

We regard the delivery of a project as a series of

consensus seeking processes wherein team members

have views that are debated and discussed in meet-

ings. A particular phase of a project, say the require-

ments gathering phase, can only conclude if all par-

https://orcid.org/0000-0001-6452-4186

https://orcid.org/0000-0002-9212-550X

ticipating parties agree on particular topics. Members

of the project team reach this consensus through re-

peated discussions where opinions are shared and dis-

cussed.

SAs have two goals; ﬁrstly, to promote views and

opinions that would create more debate, thus delay-

ing the project; and secondly, to not have such radical

views that they are regarded as outliers and thus ig-

nored.

We investigate, though simulation, the effect that

a small number of SAs could have on project time-

lines. First, we deﬁne and discuss our approach to

modelling this interesting problem. Then we simulate

the behaviour of team members during consensus-

seeking discussions. We investigate the ranges of

views (using statistics) that promote faster consen-

sus and which ranges delay consensus, ﬁrst theoret-

ically and then through simulation. Next, we inves-

tigate the effect of the level of subversion, from mild

to severe. Finally, we investigate the effects of a very

small number (one to four) of SAs on project delivery

if they are coordinated in their efforts.

The delivery of a project can be seen as a se-

ries of consensus-seeking processes. For example,

the project vision is discussed, reviewed, debated and

eventually agreed upon. This is a process where the

104

Vorster, J. and Leenen, L.

Exploring the Effects of Subversive Agents on Consensus-Seeking Processes Using a Multi-Agent Simulator.

DOI: 10.5220/0012123400003546

In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 104-114

ISBN: 978-989-758-668-2; ISSN: 2184-2841

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

stakeholders gravitate towards a shared single vision,

consisting of many topics, for the project.

Next, perhaps, follows an architectural design

phase. This phase will follow a similar pattern where

initial stakeholders may have widely different views

of how the design should look to fulﬁl the project vi-

sion. This phase of the project concludes when all

members agree on what the architecture should look

like.

That may be followed by systems and sub-systems

design phases, again, starting with disagreements and

various opinions that, though a process of lots of

meetings, eventually settling on a position of consen-

sus between the various stakeholders.

The use of MAS and in particular the achievement

of consensus and synchronization in these systems

have seen extensive research in the past decade, as

is evidenced by the depth of research, see Bao et al.

(2022) and Yang et al. (2022) for overviews of coop-

erative control and distributed coordination of MAS.

That line of research focus on high-speed consensus

algorithms for use in UAV and autonomous vehicles

under variations of network topology, error-rates, and

cyberattacks.

Consensus in MAS is a challenging problem

which in the literature has mostly been social sci-

ences research, economical model simulations, or

MAS consensus algorithms. Social Sciences research

focussing on crowd and voter behaviour which as a

three decade deep research history starting with Dun-

bar (1998)’s ’social brain’, Stocker et al. (2001)’s so-

cial information exchange, and the formation of con-

sensus groups discussed by Leishman et al. (2008)

also see Gilbert and Gilbert (2010). On the other

hand, MAS consensus algorithmic solutions focus al-

most exclusively on high-speed applications already

mentioned, see Amirkhani and Barshooi (2022).

This work is perhaps closest to MAS in Computa-

tional Economics discussed for example in Tesfatsion

and Judd (2006) at least in terms of project synchro-

nization as an impact factor for project economics.

Chang and Harrington (2004) described a scheme

for modelling organisations using multi-agent sys-

tems (MAS) with speciﬁc focus to answer economic

questions. Later Will et al. (2019) investigated the

role of organisational structure in innovation project

selection wherein they point out the effect of organisa-

tional structure as an enabler (or blocker) of decision-

making. In particular, they describe three organisa-

tional forms (polyarchy, hierarchical and hybrids of

the two). In a polyarchy members of the team are fully

connected and allowed to talk to each other across hi-

erarchical boundaries. We use fully connected pol-

yarchies in all the simulations discussed in this paper.

For a more detailed discussion of the three hierarchies

in terms of this simulator and simulations, see Vorster

and Leenen (2023).

The study of subversive agent behaviour and im-

pact has focused on many domains ranging from psy-

chological (McDowell, 2002), business (Manky and

Dolores, 2022), political (Barnes and Prior, 2009),

and obviously espionage (Evans and Romerstein,

2012).

The study of the impact that SAs could have on

project delivery seems, to the best of our knowledge

to not have been studied before. Furthermore, our ap-

proach to study this effect through the use of models

for consensus also seems to be novel.

In our previous paper (Vorster and Leenen, 2023)

the model and simulation implementation using MAS

for the investigation of consensus-seeking processes

such as project delivery within various organisational

architectures and project delivery methodologies has

already been reported. This paper describes the ef-

fects that a subversive agent, or a group of such agents

could have on the time and effort to reach consensus

if they try and delay the achievement of consensus

by promoting views that cause more debate and thus

longer times to reach consensus.

The approach is to simulate the consensus process

by way of team members setting up meetings with

other members on topics they do not have agreement

on and through the meeting try to resolve their differ-

ences in one of three ways. Let us say members m

and n meet. Then for every topic (k) discussed, one

of three outcomes are possible: (a) m and n reach a

consensus, a middle-ground between their two views,

(b) m convinces n or (c) m is convinced by n.

Through such a process of repeated meetings,

each issue gets resolved for all members of the team

so that at the end of the process all members agree on

all topics. Only when this state of agreement has been

reached can it be said that consensus has been reached

and can that part of the project conclude.

The SAs in these simulations have two goals (a)

to increase discord within the group thus increasing

the time it takes to reach consensus, and (b) to not

be identiﬁed as subversive, which can happen if the

SAs promote radical views or consistently promote

extreme views.

Team members initially have stochastically (sta-

tistical) chosen views and through iterative meetings

resolve differences in views while the SAs will pro-

mote the views of other team members or their own

views where those views are further away from the

mean views of the group, yet, not so far away from

the current consensus view that it creates suspicions.

The document has the following section layout:

Exploring the Effects of Subversive Agents on Consensus-Seeking Processes Using a Multi-Agent Simulator

105

• Modelling Consensus, §2, introduces the concept

of consensus as a measurable quantity as well as

how topics and each member’s view on a topic is

modelled;

• Subversive Agent Behaviour, §2.1, gives an intro-

duction to subversive agent behaviour within the

group;

• Evolution of Views, §2.2, reports on the initial re-

sults of how SAs inﬂuence the consensus process

in terms of the consensus measures and the distri-

bution of views;

• Yes-agents, §2.3, discusses the effects of agents

that constantly promote the group view and the

effect they have on the time to reach consensus;

• Subversive Agent’s Impact on Project Delivery,

§3, reports on the effectiveness of SAs to delay

projects;

• Coordinated Agents, §3.1, discusses the ways in

which SAs can cooperate to delay projects within

this narrow application;

• Level of Control, §3.2, investigates the conditions

under which SAs have such control that they can

dictate the outcome of decisions;

• Group delay & control, §3.3, discusses the over-

all effect of SAs in larger groups and the critical

number of SAs to control both outcomes and de-

lays; and

• Discussion, §4, wherein a brief overall discussion

of the results and consequences from the data pre-

sented in the various sections are discussed.

Some remarks are needed on subversive agents versus

conventional disagreement on topics between peers

trying to ﬁnd satisfactory solutions. In many projects

the issues are complex and people have justiﬁable rea-

sons for arguing positions that others may consider

unimportant. This is normal and part of ﬁnding good

solutions, the fact that there are debates imply that

topics are not simple. These debated indeed do lead

to longer times to reach consensus, but the balance

of that is that better decisions are reached, more op-

tions are considered, and more variables are investi-

gated and brought into the discussion. However, we

are using the term subversive agent to mean someone

that is pro-actively trying to ﬁnd arguments, trying to

convince others of potions that they themselves do not

believe. In short, they may be disgruntled employees

or any other range of possibilities.

(a) Normal (a) Double Normal

(b) Exponential

Figure 1: Distributions of views on a topic can take many

forms.

2 MODELLING CONSENSUS

In our model a number of members, N, try to reach

consensus through a process of repeated meetings

wherein a number of topics are discussed. Consider

a given problem under discussion, say the project vi-

sion, or the requirements speciﬁcation, or any other

aspect of the project. This problem consists of a num-

ber of topics and members of the project team will dis-

cuss these topics in a series of meetings. Each mem-

ber has a view (opinion/belief) about each topic and

as members meet, they discuss these topics and are

swayed by the presented arguments.

Let us denote two members by i and j, the spe-

ciﬁc topic they want to discuss is denoted k. Member

i has her own view of topic k, denoted by b

. Simi-

larly member j may have a different view on the same

topic, denoted b

. The mean view of all the members

on topic k are denoted

The two members may differ in opinion on topic k,

and that can abstractly be denoted by u

i j

= |b

−b

When considering these differences in views for many

members, the expected value (or mean value) for the

difference in views on topic k can be denoted ˆu

Through meetings, members will consider each

other’s views on every topic discussed. For a dis-

cussed topic there can be one of three outcomes, (a)

they reach some agreement somewhere in the mid-

dle of the two initial views; or (b) i is convinced by j,

←b

; or (c) i convinces j, b

→b

. After the meet-

ing, no matter which one of these options occurred,

i j

= 0, meaning they resolve their differences and

agree on what they believe to be the correct answer.

Throughout the process members meet each other

to discuss topics and this continues until all topics are

resolved. The total time it takes for all members to

reach consensus on all topics are denoted t

max

The distribution of real-life views could have

many forms depending on the topic and people in-

volved and has been found to have Normal, Uni-

form, Skew (Den Boon and Van Meurs, 1991), and

even Exponential (Lang et al., 2018) distributions, see

Figure 1. In our simulation members are initiated

A detailed mathematical description of this process

can be found in Vorster and Leenen (2023).

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

106

·10

Consensus (u)

Consensus for 20 simulations

Averaged Consensus

1-σ

Final consensus 1-σ

Consensus Entropy (S

)

Ln(Consensus) for 20 simulations

Ln(Consensus) averaged

1-σ

Final consensus 1-σ

0 20 40

80 100 120

Time (t

max

)

Count [%]

Histogram of t

max

LN (4.33, 0.0823)

N (76.2, 6.28)

0 10 20 30 40

50 60

70 80 90 100 110 120

Average topics discussed

per meeting

Topics per meeting (

Figure 2: (Top) Various simulations of the 10-group show-

ing the consensus measure over time. (Middle) The same

data as in top graph, but now using log

(consensus). (Bot-

tom) Histogram of the time it takes to reach consensus over

many such runs (µ = 76.2, σ = 6.28, n=10000) and Normal

and Lognormal ﬁts to the histogram data.

with random views from a Normal distribution, that

is b

∼ N (σ).

At any time during the simulation, the overall level

of consensus can be measured by summing over the

differences in view between all members on all topics.

If there are k

max

topics we can deﬁne

∑

i=1

∑

j=1

max

∑

k=1

i j

(1)

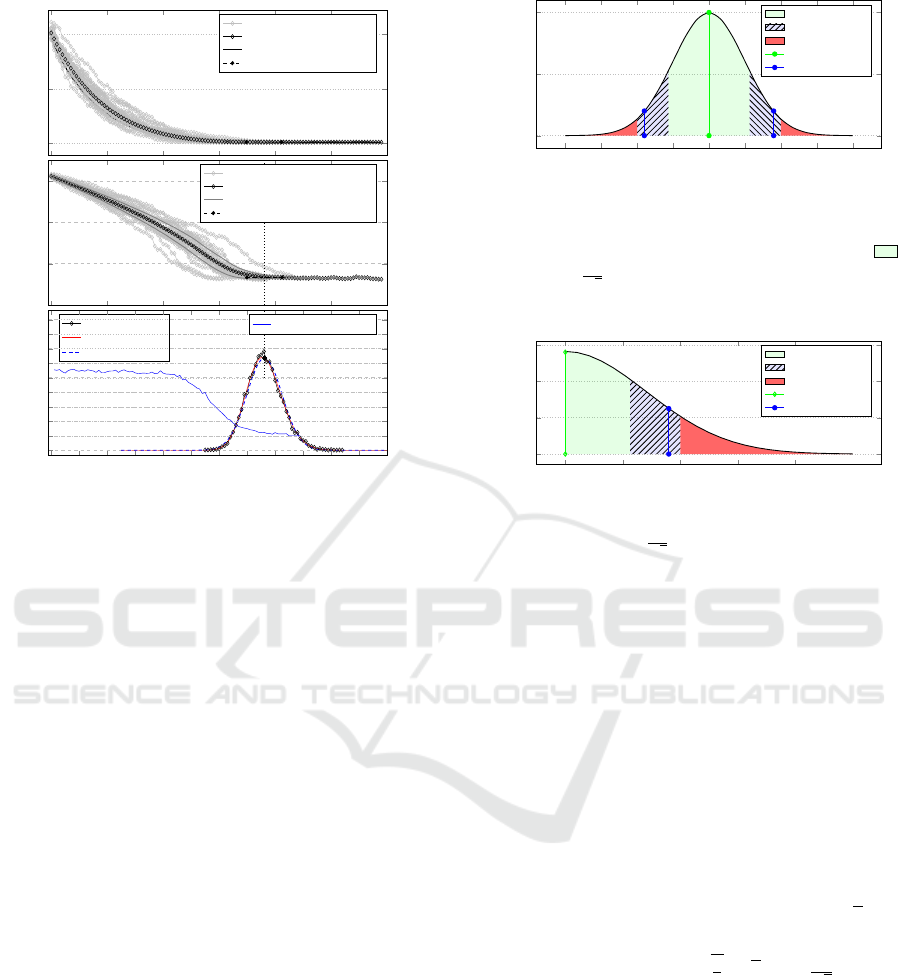
As example, consider Figure 2 that shows the

measurement of consensus over time for many simu-

lations of a group of a ten member group. Consensus

measure, as deﬁned by (1), decreases exponentially

(top diagram in Figure). The same data is presented

using a log scale (middle), and the ﬁnal time to reach

consensus is plotted in histogram form for many such

runs (bottom).

The average time to reach consensus was

max

76.2 (σ = 6.28, n = 10000). This is an abstract num-

ber representing the real time it would take to resolve

the topics and could present any time measure (hours,

days) depending on the complexity of the topics. We

are not interested in the absolute times but rather in

the relative differences in times. For example, we will

shortly compare the time it takes to reach consensus

when a subversive agent is present with the time when

−4σ −3σ −2σ −1σ 0 1σ 2σ 3σ 4σ

0.2

0.4

Members views (b

) on topic k.

Probability

Faster consensus

Slower consensus

Radical views

Yes-agent

Subversive agents

Figure 3: Distribution of views, b

∼N (σ). The opinion of

a Yes-agent (always at b

= 0) and a subversive agent in this

case with views |b

| = 1.8σ. Agents with view in the

region, |b

| <

√

σ, reduces the time to reach consensus,

otherwise it leads to longer time to reach consensus.

0 1σ 2σ 3σ 4σ

0.2

0.4

0.6

ˆu

Differences in views (u

)

Probability

Faster consensus

Slower consensus

Radical views

Yes-agent

Subversive agents

Figure 4: Distribution of differences in views, u

= |b

−

|, with average ˆu

√

σ. The opinion of a Yes-agent

(always at b

= 0 and a subversive agent in this case with

views |b

| = 1.8σ are shown in green and red respectively.

such an agent is not present.

Each member has a view (opinion, belief) on a

speciﬁc topic, which we model as a numeric value.

The views of team members have a Normal distribu-

tion, d

∼ N (σ), see Figure 3. The ﬁgure also shows

the view of an agent that always aligns its view to that

of the majority, we call such an agent a yes-agent,

always saying yes, and always agreeing with the ma-

jority. Also shown are the average positions of SAs

(at −1.8 ·σ and 1.8 ·σ).

The difference in views between members (i, j) on

a topic k is given by u

i j

= |b

−b

| and has a Folded

Normal (F N ) distribution, where N (σ

i−j

√

2 ·σ).

Then the expected value, denoted with a hat, of the

difference in views is ˆu

√

2 ·σ =

√

σ as per

the statistics of an F N distribution, see Figure 4.

An interesting aspect, key to the results discussed

later, is that if an agent, i, maintains a view b

on topic

k in the range |b

| < ˆu

then the result is shorter time

to reach consensus for the project. On the other hand,

if an agent maintains a view |b

| > ˆu

the result is

longer time to reach consensus for the project. These

theoretical results are veriﬁed by simulation later in

section §3.

Exploring the Effects of Subversive Agents on Consensus-Seeking Processes Using a Multi-Agent Simulator

107

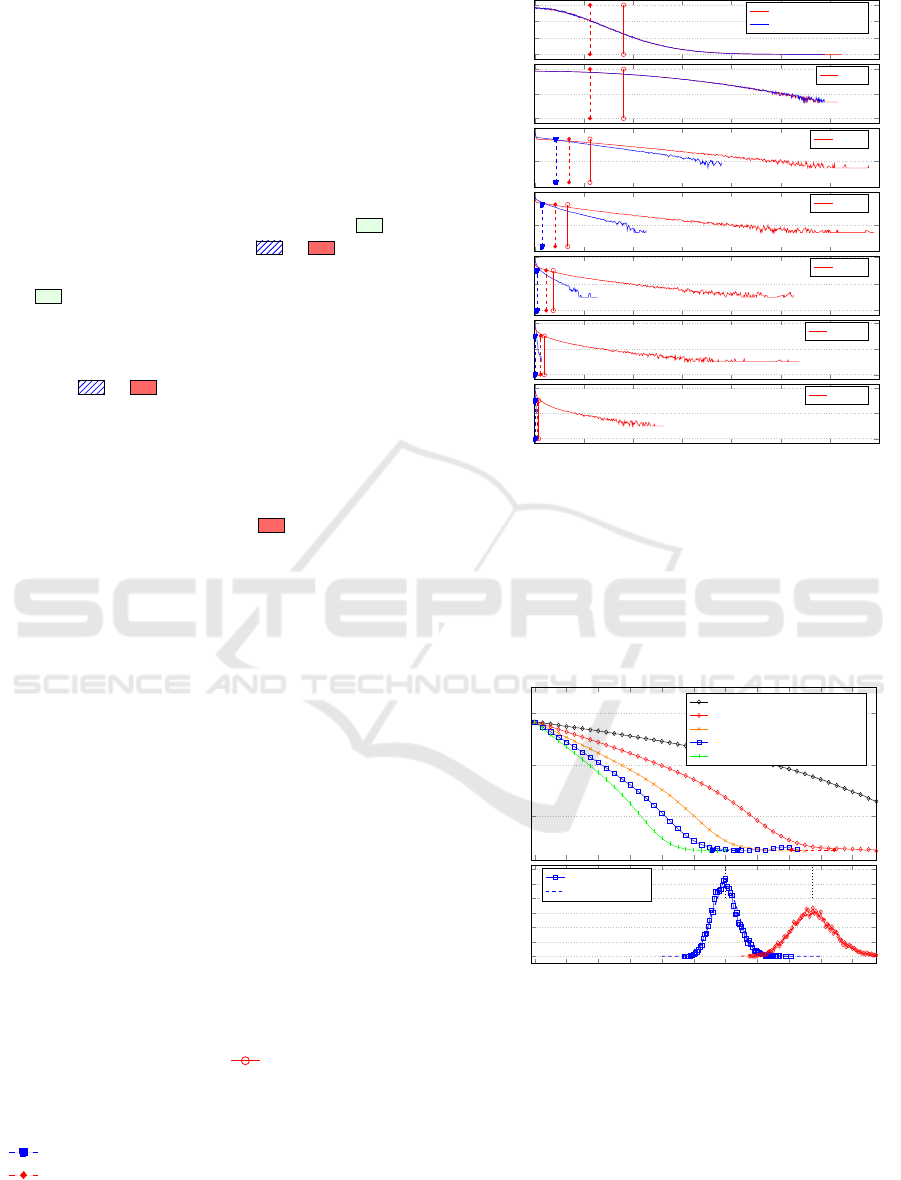
2.1 Subversive Agent Behaviour

We are interested in SAs and how they affect the pro-

cess of the group to reach consensus. SAs do not

actively sabotage projects, they are more subtle and

rather opt for creating project delays by promoting

views that will cause the group to take longer to reach

consensus. However, SAs also do not want to take

such radical positions that they are discovered.

The u

= ˆu

boundary line in Figure 4 is such that

half the view differences (u

) are to the left ( , with

< ˆu

) and half to the right ( + , with u

ˆu

). That means that an member, i, with view |b

| <

ˆu

( in Figure 3) will, through interactions with

other members, improve the overall consensus, and

thus lead to faster times to reach consensus.

Importantly, members that express views such that

> ˆu

( + ) will, through their actions, lead

to longer time to reach consensus. These are ideal

positions for SAs to promote.

However, such SAs do not want to constantly take

up controversial or fringe positions since that could

lead to their detection or labelling as subversive. We

select 2σ as the cut-off point ( in Figure 4) and

SAs will avoid expressing opinions on topics in that

range (u

> 2σ), even though other team members are

likely to have such opinions from time-to-time.

This leaves the blue hatched area in Figure 3 and

Figure 4 as the ideal ideas for SAs to promote.

The SAs change the view they project to other

members based on the overall group view. That is,

as the group as a whole moves towards consensus, so

does the SAs. They maintain their views such that

they stay in the hatched blue region, ˆu

< b

< 2, but

obviously the distribution of views contracts as the

meetings and negotiations continue.

2.2 Evolution of Views

The initial distribution of view b

∼ N (σ), as dis-

cussed in §2 and shown in Figure 4. In this subsec-

tion we discuss the evolution of this distribution as the

consensus process continue.

To illustrate the evolution of member views we

show the distribution of u

over time in Figure 5 for

a scenario with no SAs (blue) and when two SAs are

present (red, with b

= 1.8σ, ) in a group of twenty

members trying to reach consensus on twenty topics.

The top graph shows the initial distribution at

t = 0, as well as the mean values, blue solid diamond

( ) for the mean without SAs and red solid diamond

( ) when SAs are present. The graph is directly

comparable to Figure 4. The graph second from top

is the same data (at t = 0) but using a log-y scale. The

·10

−3

t = 0, 2 SAs

t = 0, no subversives

−8

−5

−2

t = 0

−5

t = 25

−5

t = 50

−8

−4

t = 75

−8

−4

t = 100

0σ 1σ 2σ 3σ 4σ

5σ 6σ

−8

−4

i j

= |b

−b

t = 125

Figure 5: As the consensus process continues, the distri-

bution of differences in opinions, u

i j

= |b

−b

|, changes.

The blue graph represent the u

values of a 20-group with

no SAs, and the red graph represent the u

values for a 20-

group with two SAs. The dashed vertical lines show the

mean values ˆu

for the two distributions, and the solid verti-

cal line shows the positions that the SAs took, at b

= 1.8σ,

where σ is the standard deviation for the group at that time.

Consensus Entropy (S

)

20-Group, three subversive agents

20-Group, two subversive agents

20-Group, one subversive agent

20-Group, no Subversive agents

20-Group, one Yes-agent

0 20 40

80 100 120 140

160

180 200

Time

Average topics discussed

per meeting

Histogram of t

max

N (175, 13.5)

Figure 6: Consensus measures over time (top) for vari-

ous numbers of subversive agents with a ﬁxed group size

(20). (Bottom) two histograms for zero subversive agents

(µ = 120, σ = 8.22) and two subversive agents (µ = 175, σ =

13.5) of time to reach consensus for n = 10000 simulations

each.

remainder of the graphs show the distribution of u

time progresses (t = 0, 25, 50, 75, 100, and 125) on a

log-y scale.

The difference in views, u

contracts until, to-

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

108

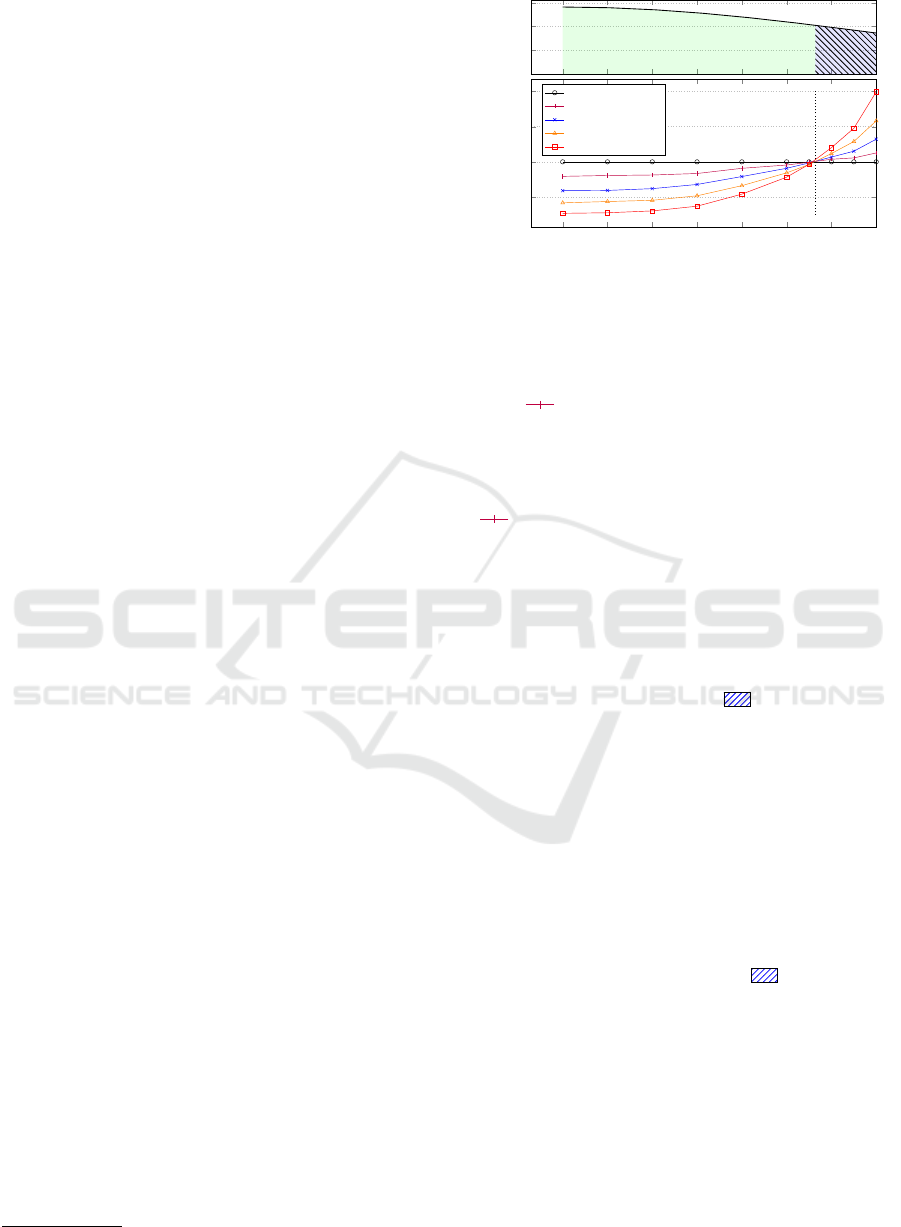
wards later time-steps, the members reach consensus

(blue graph). Here the inﬂuence of the SAs is ob-

vious, in that the distribution of views when there are

SAs present (red graphs) signiﬁcantly lag in their evo-

lution towards consensus as can be seen by visual in-

spection of the graph.

Each graph in Figure 5 is related to the data points

in Figure 6 for the same time step. Over time the

views on a topic will converge as members start to

agree on the correct position on a topic. Figure 6

shows how the sum of opinions (u) changes over time

and eventually converges. The slope of the graphs in

Figure 6 is interesting and a comparison of the graph

for a normal group with no SAs with a that of a group

with two SAs show that towards the end of the con-

sensus process the SAs have little effect (the graphs

have the same slopes). That is because the distribu-

tion of opinions is small, and thus the ability of SAs

to inﬂuence the process is also limited. In this speciﬁc

example, the dramatic difference in slope only lasts to

about t = 120 after which the slopes become similar.

The overall time to reach consensus with two SAs

has mean t = 177, so that one can postulate that SAs

do most of their damage in the ﬁrst 60% of the project,

after which group views have contracted sufﬁciently

so that the agents cannot continue being subversive

without risking being revealed.

2.3 Yes-Agents

An interesting category of non-normal agents are

those that tend towards agreeing with the majority

view on all topics, all the time. The extreme Yes-

agents

, who only take up positions that are non-

controversial, in the middle of the distribution of the

views of other members, see Figure 4, has the most

signiﬁcant impact on the time to reach consensus.

To investigate this phenomenon we simulate a

group consisting of twenty members working on a

problem with twenty topics. We vary two parameters,

ﬁrstly the number of Yes-agents in the group, and, for

every such Yes-agent conﬁguration we vary the posi-

tion, b

, that those Yes-agents take within the distribu-

tion of views (the x-axis of Figure 3). We measure the

time it takes for the group to reach consensus (t

max

The results are depicted graphically in Figure 7,

where the zero-SAs are used as reference and scaled

to 100. The Yes-agents has a positive impact on time

to reach consensus; the more Yes-agents the greater

the impact; and the more extreme their centerredness

the bigger the impact of improving t

max

A single (1 of 20) extreme Yes-agent (b

= 0, the

green line in Figure 3) improves the overall project

A sycophant in late Latin or a ’Jabroer’ in Afrikaans

0.2

0.4

0.6

ˆu

Probability

0 0.2 0.4

0.6

0.8 1 1.2 1.4

100

120

140

Subversive agent position in σ units

Time to reach Consensus

Zero SAs

One subversive agent

Two SAs

Three SAs

Four SAs

Figure 7: Simulation of various subversion factors ranging

from 0 (no subversion) up to 1.4σ. The graph shows the

effect that zero to four SAs have on the time to reach con-

sensus.

delivery from 100 time-units to 92 time-units, point

(0,92) in the Figure. That is, an 8% improvement.

However, this obviously comes at the risk of mak-

ing the wrong decision. If that agent’s views was not

needed, the agent should not have been in the group

in the ﬁrst place, some may argue. Consider the graph

( ) of a single Yes-agent as a function of the sub-

versiveness of its views b

. At b

= ˆu

this agent’s

impact is the same as if it were a conventional coop-

erative agent with its own independent views.

For b

> ˆu

the impact of the SAs causes the time

to reach consensus to increase dramatically, as can be

seen from the data, shown in the Figure. The remain-

der of this paper focuses on the impact of SAs with

views in the range ˆu

< b

< 2 ( ). In particular, the

extension of Figure 7 to that region is discussed in §3

and shown in Figure 8.

3 SUBVERSIVE AGENT’S

IMPACT ON PROJECT

DELIVERY

We now turn to the impact of SAs on the time to reach

consensus when the agents take up subversive views

on topics in the range ˆu

< b

< 2, ( in Figure 3) on

purpose. It may be that they do not even believe such

a position is correct, they may be promoting other

group-member’s views, or they try to be controver-

sial, or, even that they are pro-actively trying to ﬁnd

ways to sow disarray.

Whatever the reasoning for their actions, here we

explore the potential impact that such agents could

have on the time to reach consensus, and thus on the

time to delivery that phase of the project.

Figure 8 extends the positions taken by the SAs

from that shown in Figure 7. The results from the

Exploring the Effects of Subversive Agents on Consensus-Seeking Processes Using a Multi-Agent Simulator

109

0.2

0.4

ˆu

Probability of View

0.8 1 1.2 1.4

1.6

1.8 2

100

200

300

400

Subversive factor

Time to reach Consensus

Three SAs

Two SAs

One subversive agent

Zero SAs

Figure 8: Simulation of various subversion factors ranging

from 0.8σ up to 2σ. The graph shows the effect that zero to

three SAs have on the time to reach consensus.

simulations show that SAs can create signiﬁcant in-

creases in project times by delaying the consensus

process. The values in Figure 8 have been normal-

ized so that the consensus-time for processes with

zero SAs are scaled to 100 time-units. Recall that an

agent taking a position at ˆu

has the same effect as a

normal agent.

If SAs take up positions at ˆu

σ ≈ 1.6σ then

the simulations show that a single agent in a 20-group

can delay a project by 10.5%, two SAs can delay the

project by 27.2%, and three agents can cause 55.9%

delays, see Table 1.

If the SAs take up position at 2σ, which is only

0.9σ bigger than ˆu

, then the impact on project de-

lays are even more signiﬁcant and for one, two and

three SAs the delays are 24.3%, 83.1%, and 359.5%

respectively, see Table 1. The missing number in Ta-

ble 1 for a 4/20 ratio and b

= 2σ ( ) is because

for that conﬁguration the SAs have the ability to de-

lay the consensus process indeﬁnitely. The ability of

Table 1: The data for the delay in time to reach consensus

for different ratios of SAs to total members and different

relative positions of SAs. The ’R > b

’ row indicates for

each subversive position (b

) what percentage of the total

members have an even more radical view (statistically). All

numbers are percentages. The red bar indicate that 4 SAs at

= 2σ can indeﬁnitely delay consensus.

Ratio b

= 0 b

= 1.6σ b

= 1.8σ b

= 2σ

1/20 -8.3 10.5 15.7 24.3

2/20 -16.4 27.2 46.1 83.1

3/20 -23.3 55.9 127.3 359.5

4/20 -29.3 119.9 385.3

1/10 -10.8 18.2 26.8 41.6

2/20 -16.4 27.2 46.1 83.1

3/30 -18.8 30.3 58.2 115.4

4/40 -20.1 32.2 67.3 144.6

R > b

100 10.1 7.2 4.6

1 1.1 1.2 1.3 1.4

1.5 1.6

1.7 1.8 1.9 2 2.1

100

150

Subversive factor

% Delay

Four in forty SAs

Three in thirty SAs

Two in twenty SAs

One in ten subversive agent

Figure 9: Each simulation line keeps the ratio of SAs to

total members constant at 10%. The results show increase

in project delivery time as measured relative to groups with

zero SAs.

agents to control the outcome of decisions is brieﬂy

discussed in the next section.

The argument can be made that the reason for

these increases in delays are because a greater per-

centage of the overall number of agent are subversive.

That is, one, two, and three SAs make up 1/20, 2/20

and 3/20 of the total number of project team mem-

bers, and so, perhaps this increase percentage SAs are

creating the delays, rather than the actions that these

agents take to delay the project. To address this crit-

icism a series of simulations was conduction where

that ratio of SAs to normal members are kept static

at 10%. That is, simulations were generated with one

subversive agent in a 10-group, two in a 20-group,

three in a 30-group, and four in a 40-group.

The results are shown in Figure 9 and Table 1.

One, two, three, and four SAs at ˆu

σ ≈ 1.6σ

caused delays of 18.2%, 27.2%, 30.3%, and 32.2%

respectively and at 2σ they can create project delays

of 41.6%, 83.1%, 115.4%, and 144.6% respectively.

3.1 Coordinated Agents

A single agent is a lone wolf, however, two or more

SAs can form a pack and launch coordinated attacks,

or, in this case, coordinate in the disruption of the

project, increasing delays.

In this section we investigate the patterns of co-

operation and coordination of multiple SAs. We con-

sider the following modus operandi; they can act un-

coordinated, they can push the same side of an issue,

and they can take up opposite sides of an issue thus

trying to split the other members into two groups.

There can be other ways to coordinate, for ex-

ample targeting speciﬁc members of the team trying

to inﬂuence them rather than trying to inﬂuence all

members. These and other such strategies are not in-

vestigated and left as future research.

Consider again Figure 3 and the two marked po-

sitions of a SAs, labelled (a) and (b) in the ﬁgure.

The three patterns of cooperation we investigate are

then ﬁrstly that each agent selects a position either (a)

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

110

−2 0 2 4

8 10 12 14

18 20

100

200

Group size

Time to reach Consensus

Uncoordinated actions

Similar views

Opposing views

No subversion

Yes-agents

100

% delay

% Delay

Figure 10: The graphs show the impact on time to reach

consensus for three types of cooperation between two SAs,

uncoordinated, promotion of similar views, and promotion

of opposing views. This is plotted for various group sizes.

The bands indicate a 1 −σ spread (n=200 pp).

0 10 20 30 40

50 60

70 80 90 100

200

400

600

Group-size

Time to reach consensus

Uncoordinated

Similar views

Opposing views

Normal Agents

Yes-agent

100

200

300

400

% delay

% Delay

Figure 11: Time to reach consensus for different group sizes

and cooperation types (n=100 pp).

or (b) independent of other SAs. This pattern is the

safest in that there are no correlation between the po-

sitions that SAs take, and thus no way to link them

based on their views. The second approach, calls for

all SAs to take up the same position, either left or right

of an issue, but they are coordinated in that decision.

This is less desirable from an attempt to stay hidden.

The third method of coordination is that the SAs form

two groups, one group promoting views close to (a)

on the left of an issue and the other group promoting

position (b) on the right of an issue.

To investigate the impact of the type of coopera-

tion between SAs could have on the consensus pro-

cesses we ask the question; are some types of coop-

eration more destructive than others, if measured by

time and effort to reach consensus? To answer this

question simulations were constructed to investigate

the type of cooperation and its impact on the con-

sensus processes as a function of the group size, ﬁx-

ing the number of subversive agent and their position

(rσ, r = 1.8).

For each conﬁguration point (group-size and num-

ber of SAs), simulations were run, n = 100 per con-

ﬁguration, to achieve statistical signiﬁcance. Figure

10 shows the results for the simulations when two

SAs are present. Figure 11 shows results with four

SAs. For the graphs where two SAs are present, the

smallest group size shown is eight; this is because

for smaller groups, the SAs assert enough control that

0 1σ 2σ 3σ 4σ

0.2

0.4

0.6

ˆu

Differences in views (u

)

Probability

Figure 12: Conventional consensus processes (meetings

and discussions) acts like a force (p

) that narrows the con-

sensus distribution. SAs within that process acts like a force

) trying to widen the consensus distribution. If p

< q

then SAs control the process.

they can delay consensus indeﬁnitely. The same limit

exists for when four SAs are present but for even

larger groups.

What is surprising and interesting about the re-

sults, shown in Figure 10 and repeated in Figure 11,

is how similar, in fact indistinguishable, the three co-

operative models are from each other in terms of time

to reach consensus.

This warrants some reﬂection. The conclusion we

reached, was that in order to affect the time to reach

consensus SAs must widen the distribution of views.

It does not matter what view they put forward (left

or right of an issue); what matters is that the overall

distribution of views widen. That is, the actual po-

sition that is taken (left or right) does not matter in

terms of the time to reach consensus, since both these

views will widen the overall distribution of views. If

the agents are coordinated to the extent that they take

position on the same side of a topic (say right) then

they will widen the distribution of views and shift the

consensus view, see Figure 12.

3.2 Level of Control

In this subsection we investigate the ability of SAs to

control the outcome of a decision. We deﬁne a goal,

one that is sufﬁciently far away from the starting con-

ditions that achieving it is a clear indication of control

over the group by the SAs. We are interested in what

the boundary conditions are for allowing such control

and to what extent the SAs can achieve these goals.

We deﬁne a target for each topic, k, that is 6σ away

from the initial group mean view on that topic. SAs

still have to stay within the boundaries of ˆu

< b

< 2

to prevent detection. We vary the number of agents

and the relative subversive positions they take.

This is a theoretical exercise to test control (hence

pushing decisions in only one direction). Such a sit-

uation is not realistic in the real world, however, in

the real world SAs can use their inﬂuence to not only

delay decisions but also strive to achieve a speciﬁc

Exploring the Effects of Subversive Agents on Consensus-Seeking Processes Using a Multi-Agent Simulator

111

10-groups

0.2

0.3

0.4

0.5

0.6

ˆu

Probability

0 0.2 0.4

0.6

0.8 1 1.2 1.4

1.6

1.8 2

100

Subversive agent position in σ units

% to goal (6σ)

Six SAs

Five SAs

Four SAs

Three SAs

Two SAs

One subversive agent

0σ

1σ

2σ

3σ

4σ

5σ

6σ

Figure 13: Graphs of the % that SAs can move the outcome

of a consensus process relative to a goal of 6σ. The group

size is ten members.

20-groups

0.2

0.3

0.4

0.5

0.6

ˆu

Probability

0 0.2 0.4

0.6

0.8 1 1.2 1.4

1.6

1.8 2

100

Subversive agent position in σ units

% to goal (6σ)

Six SAs

Five SAs

Four SAs

Three SAs

Two SAs

One subversive agent

0σ

1σ

2σ

3σ

4σ

5σ

6σ

Figure 14: Graphs of the % that SAs can move the outcome

of a consensus process relative to a goal of 6σ. The group

size is twenty members.

outcome.

The main point is that SAs will often strive for a

speciﬁc outcome, and if that outcome is reasonably

within the scope of the original set of views, then it

will be easy for them to achieve while still delaying

the project.

The ﬁrst set of simulations that was constructed

focused on the effects that SAs can have when work-

ing together in controlling the outcome of the con-

sensus process when they operate within the b

range ( in Figure 3, 4, 12, and of interest here 13

and 14).

For these simulations, the delays in reaching con-

sensus are not of interest.

We believe there is a deﬁnite theoretical boundary

where the SAs can fully control the consensus pro-

cess, which means they can both control the time to

reach consensus, stretching it out as long as they want

and control the ﬁnal outcome of the process.

In a conventional consensus process through

meetings and discussion, the distribution of views

contract over time and this contraction can be seen

% Time Increase

r = 1.8 agents

r = 1.6 agents

r = 1.4 agents

100

% SAs (100-group)

% to goal (6σ)

r = 1.8

r = 1.6

r = 1.4

0σ

1σ

2σ

3σ

4σ

5σ

6σ

Figure 15: Subversive agents as percentage of total team

members. The top graphs show how much they can delay

the consensus process and bottom graphs show how much

they can inﬂuence the outcome.

as a force closing the distribution of views, p

in Fig-

ure 12. Similarly the SAs, during the same process,

acts like a force pushing the distribution wider, q

the Figure. Therefore, as long as the p

, the clos-

ing force from all the conventional team members is

greater than q

, the force from the SAs, the process

will reach consensus, though taking longer than with-

out SAs. In a scenario where p

< q

the SAs have

great control over the outcome, both in terms of time

to reach consensus and also the overall outcome.

3.3 Group Control and Delays

In this sub-section the ability of SAs to delay the pro-

cess but also control the outcome is investigated. Here

we will are interested in the effects as a function of the

% of SAs in the group.

Since it should be clear by now that if there are

sufﬁcient SAs present then they can delay the consen-

sus process indeﬁnitely. To constrain the simulation

we curtail the SAs to stop their antics once a project

had been delayed by 2500%, that is, by a factor of

more than 20.

The group-size is kept at 100, and the number of

SAs are increased from 0. Also, the positions that the

SAs occupy are varied (r = 1.4, 1.6, 1.8).

The questions we then want to answer here are

how much control does the SAs have, as a function

of the group make-up, over the (a) outcomes and (b)

total project times.

The results from these experiments are shown in

Figure 15. The top graphs show that for r = 1.8 the

SAs gain full time-control when there are more than

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

112

16% SAs. For r = 1.6 and 1.4 full control is gained at

23% and 34% respectively.

This should however be seen in context since these

measures are for a more than 20 times delay. If the

benchmark is a more reasonable 100% delay in time

to reach consensus, then for r = 1.8, 1.6, and1.4 the

resulting number of SAs needed are 10%, 15%, and

23% respectively.

The bottom graphs in Figure 15 shows the level of

control that the SAs can exert on the ﬁnal outcome,

similar to the measurements from the previous sec-

tion. Again, shifts in position are capped at 6σ. SAs

can reach this benchmark when 14% SAs are present

for r = 1.8. This changes to 17% and 25% for r = 1.6

and 1.4, respectively.

4 DISCUSSION

We started off with the simple assumption that the

delivery of a project is fundamentally a series of

consensus-seeking processes. We assumed all team

members are cooperative and work under assump-

tions of good-faith on the part of other members.

However, the introduction of a subversive agent

that pro-actively tries to inﬂuence other members to-

wards views that are plausible yet create more debate

has a signiﬁcant impact on the time and effort to reach

consensus. This was surprising.

The initial distribution of views has the effect that

SAs have a much wider range of views to promote

and thus we see that the inﬂuence of SAs are strong

initially but as the consensus distributions contracts

the SAs also loose their ability to inﬂuence. The in-

ﬂuence of SAs are stronger in the earlier parts of the

consensus process, Figure 6.

Yes-agents can signiﬁcantly improve consensus

times, however, since they are actively lobbying for

the group mean view (or any other speciﬁc view), they

can also cause the group to abandon valid views thus

increasing the probability that the wrong decisions are

reached. This is obviously not a new discovery; yes-

agents have been used to sway decisions for all of

recorded history (Browning, 2010).

However, when SAs operate to increase the range

of options or act to polarize the group then the impact

on the time to reach consensus can be signiﬁcant, Fig-

ures 8 and 9.

An interesting result from this study was that

the level of cooperation and synchronization between

SAs do not have a signiﬁcant impact on the time to

reach consensus. That is, SAs acting as a group, or

acting in isolation have the same effect as measured

by consensus time. However, SAs acting in a coordi-

nated way can signiﬁcantly inﬂuence the outcome of

a decisions, even if the SAs form a small minority in

the group, Figures 14 and 15.

Under the right conditions a small minority of SAs

(say 10%) can have a signiﬁcant impact on the time

to reach consensus, extending it by as much as 100%

(doubling the time it would have taken), Figure 15

(top). Surprisingly, a small number of SAs (20%) can

indeﬁnitely stall the consensus process. A slightly

bigger SAs group of 20% of the group membership

can have effects ranging from a doubling of the time

to reach consensus (r = 1.4) to indeﬁnitely delaying

consensus (r = 1.8).

5 LIMITATIONS

We would like to point out some limitations to this ap-

proach and results. Firstly, this is a theoretical model

showing what is possible with consistently operating

subversive agents. Reality may be vastly different and

more complex. Secondly, we see a speciﬁc topic, say

k, as a single atomic topic with a single outcome. In

reality this topic may consist of many sub-topics, and

the actual complexity of a project is much greater than

what we model. The sub-topics issue is less of a prob-

lem since that strengthen the Gaussian distribution

assumptions we made. We do not think the results

will differ if the problem size is increased, as we have

demonstrated in an earlier paper (Vorster and Leenen,

2023), however, other researchers should verify this.

Lastly and perhaps the most important limitation

is that it will be difﬁcult to verify these results in real-

world projects, since subversive agents are by deﬁni-

tion hidden. Any team member may act as a subver-

sive agent due to being disgruntled or a host of other

reasons. One way to verify these results would be to

insert such an agent into ’play’ projects, an interesting

topic for Social Psychology research.

6 CONCLUSION AND FUTURE

WORK

In this paper we investigated the effects that subver-

sive agents may have on consensus processes and in

particular the speed of project delivery if a project is

seen as a series of consensus-seeking processes.

The important results are that even small numbers

of SAs can have a signiﬁcant effect on the time it take

a group to reach consensus. The delay effects of SAs

are most signiﬁcant during the earlier parts of the con-

sensus process. SAs need not coordinate to achieve

Exploring the Effects of Subversive Agents on Consensus-Seeking Processes Using a Multi-Agent Simulator

113

signiﬁcant delays but, if they do coordinate, they can

both delay the process signiﬁcantly and also have a

signiﬁcant inﬂuence on the decision outcomes (con-

trolling which decisions are ﬁnally made).

A small number of SAs, as little as 10% can, under

the right conditions, double the time to reach consen-

sus (and thus also doubling the cost, as a measure of

effort).

A group of well coordinated SAs that make up

more than 20% of the group can cause delays ranging

from about doubling the time for project completion

to completely stall projects.

As future work we propose Social Psychology re-

search experiments to covertly observe the behaviour

of a planted agent within a mock project and the ef-

fect this could have. For one, can such an agent stay

hidden, what would be good strategies for subverting

team members, and, when to give up being subver-

sive, since our research suggest most of the damage

had been done about halfway through the project, and

thus that seems to be a good point in time to stop be-

ing subversive, or at least reduce risk of detection by

being more cooperative.

From a computational intelligence perspective,

extending a multi-agent system with AI-based sub-

versive behaviour could yield more complex strate-

gies; and, ways to address such behaviour, both form

a detection as well as a mitigation perspective.

REFERENCES

Al-Ahmad, W., Al-Fagih, K., Khanfar, K., Alsamara, K.,

Abuleil, S., and Abu-Salem, H. (2009). A taxonomy

of an it project failure: root causes. International

Management Review, 5(1):93.

Amirkhani, A. and Barshooi, A. H. (2022). Consensus in

multi-agent systems: a review. Artiﬁcial Intelligence

Review, 55(5):3897–3935.

Bao, G., Ma, L., and Yi, X. (2022). Recent advances on

cooperative control of heterogeneous multi-agent sys-

tems subject to constraints: A survey. Systems Science

& Control Engineering, 10(1):539–551.

Barnes, M. and Prior, D. (2009). Subversive citizens: Power,

agency and resistance in public services. Policy Press.

Browning, G. (2010). Agency and inﬂuence in the his-

tory of political thought: The agency of inﬂuence and

the inﬂuence of agency. History of Political Thought,

31(2):345–366.

Chang, M.-h. and Harrington, J. E. (2004). Agent-based

models of organizations working paper, no. 515.

Den Boon, A. K. and Van Meurs, A. (1991). Measuring

opinion distributions: An instrument for the measure-

ment of perceived opinion distributions. Quality and

Quantity, 25(4):359–379.

Dunbar, R. I. (1998). The social brain hypothesis. Evo-

lutionary Anthropology: Issues, News, and Reviews:

Issues, News, and Reviews, 6(5):178–190.

Evans, M. S. and Romerstein, H. (2012). Stalin’s secret

agents: the subversion of Roosevelt’s government. Si-

mon and Schuster.

Gilbert, N. and Gilbert, G. N. (2010). Computational social

science. null.

Kian, M. E., Sun, M., and Bosch

e, F. (2016). A consistency-

checking consensus-building method to assess com-

plexity of energy megaprojects. Procedia-social and

behavioral sciences, 226:43–50.

Lang, J. W., Bliese, P. D., and de Voogt, A. (2018). Mod-

eling consensus emergence in groups using longi-

tudinal multilevel methods. Personnel Psychology,

71(2):255–281.

Leishman, T. G., Green, D. G., and Driver, S. (2008). Self-

organization in simulated social networks. null.

Manky, O. and Dolores, J. (2022). Subversive en-

trepreneurs: Business agency and commodiﬁcation of

peruvian higher education (1992–2012). Latin Amer-

ican Perspectives, 49(3):162–180.

McDowell, K. (2002). Roll of thunder, hear my cry: A

culturally speciﬁc, subversive concept of child agency.

Children’s Literature in Education, 33:213–225.

Stocker, R., Green, D. G., and Newth, D. (2001). Consensus

and cohesion in simulated social networks. Journal of

Artiﬁcial Societies and Social Simulation, 4(4).

Tesfatsion, L. and Judd, K. L. (2006). Handbook of compu-

tational economics: agent-based computational eco-

nomics. Elsevier.

Vorster, J. S. and Leenen, L. (2023). Consensus simulator

for organisational structures. Proceedings of the 13th

International Conference on Simulation and Modeling

Methodologies, Technologies and Applications.

Waheeb, R. A. and Andersen, B. S. (2022). Causes of

problems in post-disaster emergency re-construction

projects—iraq as a case study. Public Works Manage-

ment & Policy, 27(1):61–97.

Whitney, K. M. and Daniels, C. B. (2013). The root cause

of failure in complex it projects: Complexity itself.

Procedia Computer Science, 20:325–330.

Will, M. G., Al-Kfairy, M., and Mellor, R. B. (2019). How

organizational structure transforms risky innovations

into performance–a computer simulation. Simulation

Modelling Practice and Theory, 94:264–285.

Yang, R., Liu, L., and Feng, G. (2022). An overview of

recent advances in distributed coordination of multi-

agent systems. Unmanned Systems, 10(03):307–325.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

114