The Imbalance Data Handling of XGBoost in Insurance Fraud

Detection

Nathanael Theovanny Averro, Hendri Murfi and Gianinna Ardaneswari

Department of Mathematics, Universitas Indonesia, Depok 16424, Indonesia

Keywords: Insurance Fraud, Machine Learning, Binary Classification, XGBoost, Imbalance Class.

Abstract: Insurance fraud is an emerging problem threatening the insurance industry because of its potential severe loss.

Many conventional efforts have been implemented to detect fraud, such as releasing blacklists and deeper

investigation on every claim, but these efforts tend to cost financial resources a lot. Because of that, machine

learning is proposed as a decision support system to detect potential insurance fraud. Insurance fraud detection

problems often have data with an imbalanced class. This paper examines the imbalanced class handling of

XGBoost in predicting insurance fraud. Our simulation shows that the weighted-XGBoost outperforms other

approaches in handling the imbalanced class problem. The imbalance-XGBoost models are quite reliable in

improving base models. They can reach up to 28% improvement of the recall score on minority class

compared to the basic XGBoost model. The precision score of both imbalance-XGBoost models decreases,

while the weighted-XGBoost model simultaneously improves the precision and recall score.

1 INTRODUCTION

Insurance fraud has become a threatening problem in

the insurance industry for its potential financial

damage. In the United States, 10% of proposed claims

were detected as fraud, contributing to around US$34

Billion loss yearly

. Association of General Insurance

in Indonesia (Asosiasi Asuransi Umum Indonesia,

AAUI) also claimed that losses incurred by fraud

could reach billions of Indonesian Rupiah for every

company. Fraud cases are also reportedly increasing

since the COVID-19 pandemic hits Indonesia

Many conventional efforts have been

implemented to fight insurance fraud. AAUI has

developed a system called AAUI Checking, which

contains blocklists of policyholders and any other

third parties accused of insurance fraud

. Deeper

investigations on proposed claims are also imposed

by many companies, though resulting in no

significant impact. Even worse, many issues were

hard to predict immediately; hence the devastating

effects were known to present up to twenty months

later

https://knowledge.friss.com/survey-insurance-fraud-2019

https://finansial.bisnis.com/read/20201127/215/1323401/dampak-

corona-industri-asuransi-mesti-antisipasi-maraknya-penipuan

Machine learning is proposed as a solution to

predict potential fraud on each claim. Historical data

that contains essential information about

policyholders, loss amount, and a description of

whether the claim was a fraud can be used to train the

model. This problem is a classification scenario in

machine learning (Duda et al., 2001). The machine

learning model is expected to shorten the time needed

to investigate every claim manually without

sacrificing accuracy. The model's decision can be

considered a decision support system or a second

opinion (Merkert et al., 2015).

Several methods have been proposed to achieve

the high accuracy of insurance fraud detection

systems. Wang and Xu (2018) proposed a text

mining-based algorithm to analyze car accident

description text to detect potential automobile

insurance fraud. The text data was then used to train

several models using support vector machine (SVM),

random forest, and deep neural networks. All models

achieve an f1-score of more than 75%. Roy and

George (2017) used random forest and naïve Bayes to

detect fraud in automobile insurance claims. Verma

et al. (2017) implemented an outlier detection model

https://www.medcom.id/ekonomi/mikro/DkqVYaZK-aaui-biki

n-daftar-hitam-nasabah-cegah-kecurangan-klaim

https://www.medcom.id/ekonomi/mikro/DkqVYaZK-aaui-biki

n-daftar-hitam-nasabah-cegah-kecurangan-klaim

460

Averro, N., Murﬁ, H. and Ardaneswari, G.

The Imbalance Data Handling of XGBoost in Insurance Fraud Detection.

DOI: 10.5220/0012126900003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 460-467

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

to find anomalies, and potential health insurance

claims fraud. Waghade and Karandikar (2018) also

discussed the need for better machine learning and

data mining methods to improve the effectiveness of

fraud detection systems in health insurance.

In 2014, Tianqi Chen invented XGBoost as a

library containing optimized tree gradient boosting. It

is designed as a highly efficient, flexible, and portable

model. The fundamental idea of XGBoost is to

optimize the tree gradient boosting model to handle

sparse data, manage large amounts of data efficiently,

implement efficient computation, and be highly

scalable. This project is often claimed to be the most

successful machine learning since XGBoost-based

models often outperform other models and dominate

data science competitions (Chen, 2016). It has also

been implemented to many problems across different

fields, including insurance. Fauzan & Murfi (2018)

implemented XGBoost for insurance claim prediction

and got better accuracy than other ensemble learning

models such as AdaBoost, Stochastic Gradient

Boosting, Random Forest, and Neural Networks.

Rusdah & Murfi (2020) also proved that XGBoost

could learn from the dataset with missing values

directly and give comparable accuracy to the

XGBoost model trained using the imputed dataset.

Yet, XGBoost is not optimized over the

imbalanced dataset in the classification problem. In

many cases, the XGBoost base model did not give

desirable results, such as in the simulation by Ruisen

et al. (2018). Several common strategies have been

invented and implemented to handle imbalanced

classes. Dhankhad et al. (2018) and Rio et al. (2015)

used undersampling and oversampling with increased

ratios to alter the dataset's composition before

implementing the machine learning model. Another

widely used approach to imbalance class problems is

Synthetic Minority Oversampling Technique

(SMOTE), which Varmedja et al. (2019)

implemented to predict credit card fraud. Some

researchers have also developed and implemented a

strategy to handle imbalance class without altering

the dataset, such as Wei et al. (2012), who integrated

contrast pattern mining, neural network, and decision

forest to predict online banking fraud activities. Wang

et al. (2020) proposed modifying the XGBoost base

model and called it Imbalance-XGBoost. The

improvement was made by adding either a weighted

function or a focal loss function on the boosting

machine. The fundamental idea of the weighted

function is to increase the penalty if the model

wrongly predicts the minority class. Meanwhile, the

focal loss function adds a multiplier factor to the

cross-entropy function for the same purpose as the

weighted function. These modifications are expected

to improve the XGBoost base model's performance.

This paper examines the imbalanced class

handling of XGBoost in predicting insurance fraud.

The comparative analysis of the existing methods is

measured based on some metrics, i.e., accuracy,

precision, recall, f1-score, and AUC. Our

implementation shows that the weighted-XGBoost

outperforms other approaches in handling the

imbalanced class problem. The imbalance-XGBoost

models are quite reliable for improving base models.

They can reach up to 28% improvement of the recall

score on minority class compared to the basic

XGBoost model. The precision score of both

imbalance-XGBoost models decreases, while the

weighted-XGBoost model simultaneously improves

the precision and recall score.

The rest of the paper is organized as follows:

Section 2 presents materials and methods that explain

the theoretical foundations of machine learning

models implemented in this research. In Section 3, we

discuss the process and the results of the simulations.

Finally, we give a conclusion of this research in

Section 4.

2 MATERIALS AND METHODS

2.1 XGBoost

XGBoost is a popular model that optimizes gradient

tree boosting and learns from tabular data. High

scalability makes XGBoost run ten times faster than

other conventional models and robust to a high-

dimensional dataset. This high scalability is

empowered by implementing a tree-learning

algorithm optimized for sparse data, a weighted

quantile algorithm for more efficient computation,

and a cache-aware block structure for parallelizing

the tree-learning process using all processor cores

(Chen & Guastrin, 2016).

The important improvement to XGBoost is how it

handles overfitting. Overfitting is a condition where

machine learning does capture not only the trend but

also the noise. Consequently, model performance on

training data will be very high, while model

performance on observations outside training data

will be far worse (Ying, 2019). The first method

implemented in XGBoost is a regularized learning

objective where weight terms are added to prevent the

model from overlearning data. Equation 1 shows

regularized learning function used in XGBoost.

The Imbalance Data Handling of XGBoost in Insurance Fraud Detection

461

𝐿

(

𝜙

)

=𝑙(𝑦



,𝑦



)



+Ω(

𝑓



)



(1)

where Ω

(

𝑓

)

=𝛾𝑇+

𝜆

‖

𝑤

‖



The second overfitting handling combines

shrinkage and column subsampling. Shrinkage was

first introduced by Friedman (2002). This technique

multiplies newly added weights by a particular 𝜂

value on every iteration in the tree-boosting machine.

Shrinkage aims to reduce the influence of every tree

built before to get an optimized tree model on the

subsequent iterations. As the name suggests, column

subsampling only uses several random columns or

features to be used in the tree-fitting process. It is also

used by Briedman (2001) and Friedman (2003) on the

Random Forest model. This technique has been

proven to prevent overfitting better than traditional

row subsampling, which only uses several randomly

sampled observations instead of features. It also

efficiently shortens the time needed in the

computational process.

The last important thing in XGBoost is how it

splits data into every branch to get a model producing

the best result possible. This problem is the best-split

problem in the decision tree. The algorithm

implemented in XGBoost as a solution is called an

approximate algorithm. This algorithm first proposes

splitting points candidates based on percentiles of

feature distribution. The algorithm then maps the

feature into buckets split based on these splitting

points candidates, aggregates the statistics, and finds

the best solution among these candidates.

Despite all these advantages, the base model of

XGBoost often struggles with imbalanced datasets.

Several methods have been proposed to handle the

imbalance class problem when implementing the

XGBoost model.

2.2 Imbalance Class Handling

2.2.1 Data-Level Approach: Oversampling

The data level approach is an imbalanced class

handling strategy that manipulates the composition of

the minority and majority classes. This approach is

usually used as a baseline model (Batista et al., 2004).

One widely used strategy in this approach is

oversampling.

In the oversampling strategy, data from the

minority class are resampled randomly until the

composition of both classes is balanced.

Oversampling has a tremendous advantage over any

https://xgboost.readthedocs.io/en/latest/parameter.html

other data-level approach method where no

information is omitted. However, after adding more

observations, the model tends to take a lot of time to

fit oversampled data due to its huge dimensionality.

In addition, models built on oversampled data are

prone to overfit because of several identical

observations in the dataset (Kaur & Gosain, 2018).

2.2.2 Weighted-XGBoost

Besides the oversampling method, there is another

standard handling of the imbalance class provided by

XGBoost. This method is usually referred to as

Weighted-XGBoost. This method is integrated into

the XGBoost package and can be activated by setting

the scale_pos_weight parameter in model fitting.

The optimal value for the scale_pos_weight

parameter does not need to be tuned through a

sophisticated optimization method. XGBoost

developers have stated that



(

 

)



(

 

)

can

be used as its value

. Negative instances here mean

majority class and positive instances represent

minority class. Adjusting the scale_pos_weight value

will penalize the algorithm more if the model

mispredicts a positive class. This approach should

also not increase the time needed to fit the model

significantly compared to oversampling strategy.

2.2.3 Imbalance-XGBoost

Imbalance-XGBoost proposes modified loss

functions to solve the heavily penalized model if it

wrongly predicts a minority class. This idea is

suggested by Wang et al. (2020) as a solution to

handle the imbalance class in XGBoost. The model

proposes two modified functions: weighted cross-

entropy function (weighted function) and focal loss

function. One should only choose a function to be

implemented before building the model.

The weighted function modifies the standard

cross-entropy loss function in XGBoost by adding the

imbalance_alpha (α). When α > 1, the extra loss will

be counted on "classifying 1 as 0". Otherwise, when

α < 1, the extra loss will be calculated on "wrongly

identified 0". Plugging α = 1 returns the modified loss

function to the base XGBoost's cross-entropy loss

function. Equation 2 shows a weighted function.

𝐿



=−

(

𝛼𝑦



log(𝑦



)





(

1−𝑦



)

log(1

−𝑦



))

(2)

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

462

The focal loss function adds focal_gamma in

exponential form to the cross-entropy loss function.

This factor serves the same purpose as

imbalance_alpha in the weighted function. Plugging

γ = 0 returns the loss function to the base XGBoost's

loss function. Equation 3 shows the focal loss

function.

𝐿



=−𝑦



(

1−𝑦





)



log

(

𝑦





)





(

1−𝑦



)

𝑦







log(1 − 𝑦





)

(3)

These imbalance parameters should be tuned to

achieve the best possible result while building the

model. As with the weighted-XGBoost method, these

two function modifications should not significantly

increase the time to fit the model.

2.3 Accuracy Measurement

Accuracy measurement is an essential step in

evaluating model performance. It serves as an

objective way to compare the model's performance.

These are the accuracy metrics that we use in this

research. Overall accuracy is the ratio between

correctly predicted and total observations. Precision

measures the classifier's ability to not label negative

observations as positive. Recall measures the

classifier's ability to find positive observations. F1-

score is the harmonic mean of precision and recall. It

compares several models instead of illustrating their

accuracy (Pedregosa et al., 2011). Area Under Curve

(AUC) is the total area under the ROC (Receiver

Operator Characteristic) curve. ROC consists of a

false positive (FP) on the x-axis and a true positive

(TP) on the y-axis. It is constructed by mapping (FP,

TP) from the model by varying its decision threshold

(Bradley, 1996).

3 IMPLEMENTATIONS

3.1 Dataset

This research uses the fraud insurance dataset

published by Roshan Sharma on Kaggle. This dataset

was published in 2019 and contained labeled data on

automobile insurance fraud. The dataset has 40

features with 18 numerical variables and 22

categorical variables. Of 1,000 observations, 24.7%

are classified as fraud observations. While this

imbalance class may not cause the model to predict

all data as majority class like in more extreme cases,

it is still prone to bias toward the majority class. The

model's performance in predicting data from minority

classes may be unreliable.

The dataset also has several features with missing

values. These features are collision_type,

property_damage, and police_report_available. Since

XGBoost can handle missing values, no imputation is

performed to fill these missing values. Table 1 lists

all features contained in the dataset.

Table 1: Features in the dataset.

Nu-

me-

rical

months_as_customer, age, policy_number,

policy_deductable, policy_annual_premium,

umbrella_limit, insured_zip, capital-gains,

capital-loss, incident_hour_of_the_day,

number_of_vehicles_involved,bodily_injuries,

witnesses, total_claim_amount, injury_claim,

roperty_claim, vehicle_claim, auto_yea

Cate-

gori-

cal

policy_bind_date, policy_state, policy_csl,

insured_sex, insured_education_level,

insured_occupation, insured_hobbies,

insured_relationship, incident_date,

incident_type, collision_type,

incident_severity, authorities_contacted,

incident_state, incident_city,

incident_location, property_damage,

police_report_available, auto_make,

auto_model, fraud_reporte

3.2 Preprocessing Data

Before fitting the model, the dataset needs to be

preprocessed first to optimize the result. Here, the

process involves dropping and joining some features,

extracting new features, one hot encoding categorical

features, and rescaling numerical features.

The first feature to be dropped is

incident_location. It has 1,000 unique string values,

which tend to act as noise since it has very detailed

data on where the incident happened. Policy_number

is also removed from the list as it only serves as a

unique identifier for each company-issued policy.

Total_claim_amount is also dropped from the feature

list since it has perfect multicollinearity with

injury_claim, vehicle_claim, and property_claim.

Even though some features are dropped from the

dataset, several new features are also generated from

existing features. They are policy_duration and auto

features. Policy_duration is obtained by calculating

how many days the policy had been in charge since

issued until the incident happened. In other words, it

is extracted by subtracting policy_bind_date from

incident_date. The idea of generating this feature

arises from the expectation that those willing to

commit insurance fraud will not wait for a very long

time (e.g., several years or more) to execute their

The Imbalance Data Handling of XGBoost in Insurance Fraud Detection

463

plan. Another feature is also generated by joining

auto_make and auto_brand. This feature is expected

to efficiently shorten the time to fit the model since it

has only 39 unique values instead of 53 unique values

from auto_make and auto_brand one-hot encoded

separately.

All numerical and categorical features need to be

further preprocessed. Categorical features are

processed using one-hot encoding. This process

creates dummy variables for every unique value in

one feature to store information related to the feature

for every observation. However, missing values (NaN

values) in some observations are retained in the

dummy variables.

Numerical features are scaled using several

rescaling methods. They are standard scaler, min-max

scaler, and robust scaler. Standard scaler is used on

normally distributed features; only the

policy_annual_premium feature satisfies this

condition. A robust scaler is used on features with

many outliers. Umbrella_limit and property_claim

are two features scaled using a robust scaler. The

other numerical features are scaled using a min-max

scaler suitable for uniformly distributed data.

3.3 Performance Evaluation

The preprocessed dataset is then used to fit all five

models mentioned earlier. The fitting process used

70% train and 30% test data to minimize bias while

inferring the result (Xu & Goodacre, 2018). Figure 1

briefly illustrates the model fitting scheme that

involved five replications in minimizing bias.

Before fitting the models, each model's

parameters must be optimized first. The optimization

processes use Bayesian Search Cross-Validation with

five-fold and 100 samples. The following scheme in

Figure 2 is used in parameter optimization processes.

Utilizing the accuracy measurements mentioned in

the previous section, the overall model performance

result can be summarized in Figure 3. Further analysis

of how each model predicts majority and minority

class is shown in Figure 4.

Based on overall results from Figure 3, imbalance

class handling using Weighted-XGBoost and both

Imbalance-XGBoost models produce slight

improvement based on overall accuracy, precision,

recall, and f1-score. Nevertheless, there is no

significant difference between these five models

measured by AUC. The lowest score is obtained by

Imbalance-XGBoost using focal loss, and XGBoost

obtains the highest with oversampling.

More exciting results are observed when detailed

performance in each class is analyzed (Figure 4). In

Figure 1: Implementation Scheme.

the majority class (non-fraud observations), the

imbalance class handling provided by both

Imbalance-XGBoost models improves the precision

score by more than 7% compared to other models—

however, the recall score on these two models and

weighted-XGBoost decrease by the same percentage.

As a result, the f1-score for all these models does not

differ much except for weighted-XGBoost, which

results 3% lower than the rest.

Significant improvements are shown in the

model's performance in predicting minority class

(fraud observations). The precision score on

weighted-XGBoost is the highest among other

models, with over 80%. Imbalance-XGBoost with

both models surprisingly suffers here, resulting in a

lower score than the base XGBoost model and

XGBoost with oversampling. However, the recall

score on these three models improved significantly,

with 91.04% compared to 63.28% on base XGBoost

and 57.91% on XGBoost with oversampling. Hence,

weighted-XGBoost produces the highest score on the

f1-score, with 88.09%. Those two Imbalance-

XGBoost models have 76% in f1-score, lower than

weighted-XGBoost but still significantly higher than

the base XGBoost model on 66.13% and XGBoost

with oversampling on 62.73%. Given this result, we

could observe that both modified objective functions

given by Imbalance-XGBoost deliver reliable

improvements compared to the base and

oversampling model. However, weighted-XGBoost

still outperforms the rest of the models.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

464

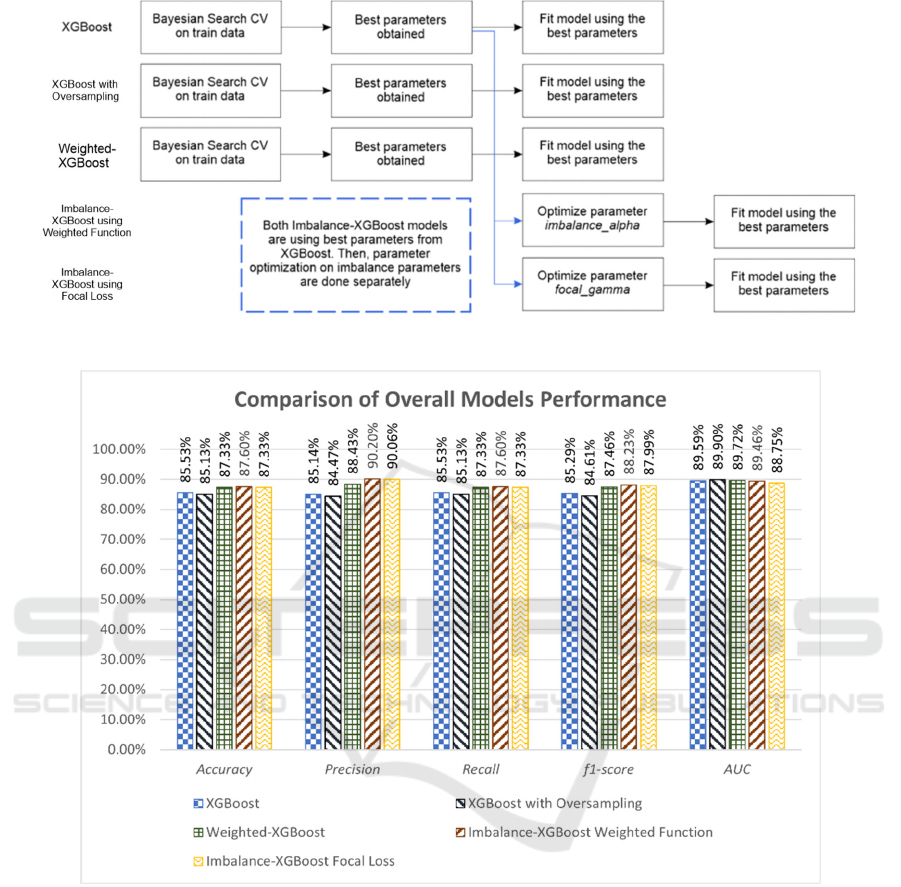
Figure 2: Parameters Optimization Scheme.

Figure 3: Comparison of Overall Models Performance.

4 CONCLUSIONS

Insurance fraud prediction is an important solution to

avoid fraud-related loss for the insurance company.

Since claims proposed to the insurance company

usually consist of many non-fraud cases and a small

percentage of fraud cases, imbalance class problems

arise when fitting machine learning models.

Predictions may be biased toward majority class or

non-fraud cases in this research. Hence, Imbalance-

XGBoost is proposed as a solution to the imbalance

dataset.

Imbalance-XGBoost with both loss functions

achieves desirable improvement, especially in

predicting minority class in the case of predicting

insurance fraud. These two models can improve up to

28% compared to the basic XGBoost model based on

minority recall scores. Yet, the standard method using

the scale_pos_weight parameter in the weighted-

XGBoost model also significantly improves.

Minority precision scores on both Imbalance-

XGBoost models decrease compared to the basic

XGBoost model, while the weighted-XGBoost model

improves minority precision and recall score

The Imbalance Data Handling of XGBoost in Insurance Fraud Detection

465

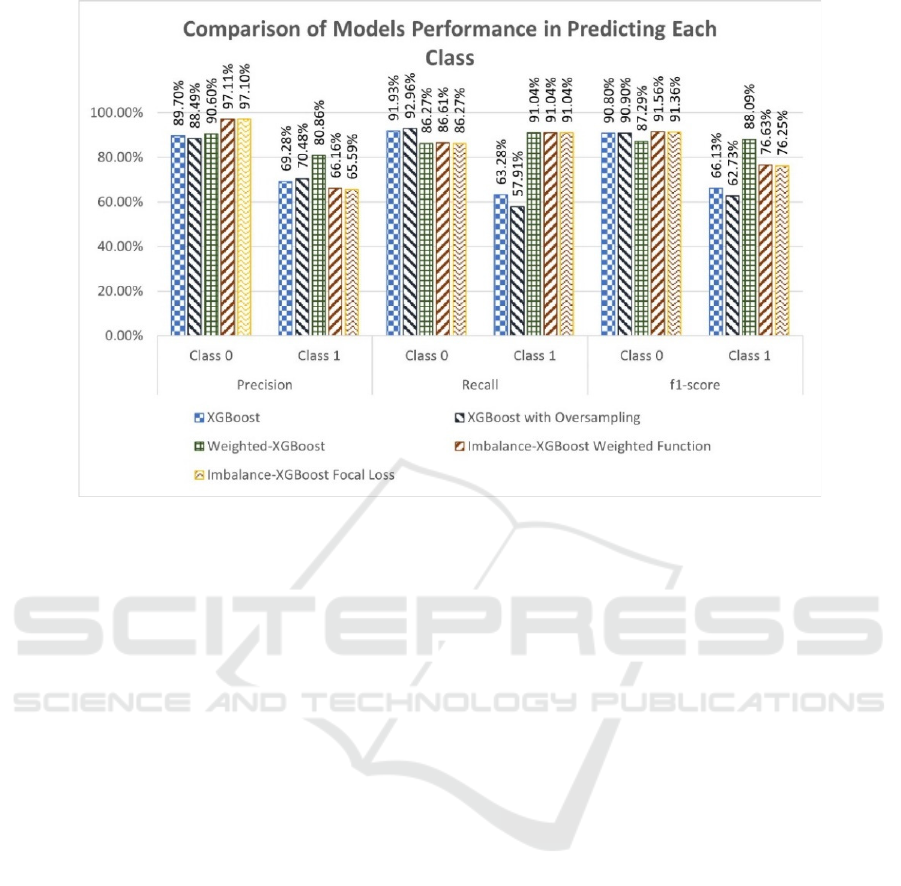
Figure 4: Comparison of Models Performance in Predicting Each Class.

simultaneously. Thus, Imbalance-XGBoost models

are quite reliable for improving base models, but

weighted-XGBoost still outperforms any other

imbalance class handling, in this case, the imbalance

class problem.

ACKNOWLEDGEMENT

The Ministry of Education, Culture, Research, and

Technology, Republic of Indonesia, funded this

research under Penelitian Fundamental 2023.

REFERENCES

Batista, G. E. A. P. A., Prati, R. C., & Monard, M. C.

(2004). A study of the behavior of several methods for

balancing machine learning training data. ACM

SIGKDD Explorations Newsletter, 6(1), 20–29.

https://doi.org/10.1145/1007730.1007735

Bradley, A. P. (1997). The use of the area under the ROC

curve in the evaluation of machine learning algorithms.

Pattern Recognition, 30(7), 1145–1159. https://doi.

org/10.1016/s0031-3203(96)00142-2

Chen, T., & Guestrin, C. (2016). XGBoost: A Scalable Tree

Boosting System. Proceedings of the 22nd ACM

SIGKDD International Conference on Knowledge

Discovery and Data Mining. KDD '16: The 22nd ACM

SIGKDD International Conference on Knowledge

Discovery and Data Mining.

https://doi.org/10.1145/2939672.2939785

Dhankhad, S., Mohammed, E., & Far, B. (2018).

Supervised machine learning algorithms for credit card

fraudulent transaction detection: A comparative study.

2018 IEEE International Conference on Information

Reuse and Integration (IRI). https://doi.org/

10.1109/iri.2018.00025

Duda, R.O., Hart, P.E., & Stork, D.G. (2001). Pattern

Classification. Wiley, New York.

Fauzan, M. A., Murfi, H. (2018). The Accuracy of

XGBoost for Insurance Claim Prediction. International

Journal of Advances in Soft Computing and its

Applications, 10(2), 159-171

J. H. Friedman and B. E. Popescu. Importance sampled

learning ensembles, 2003.

Kaur, P., & Gosain, A. (2017). Comparing the Behavior of

Oversampling and Undersampling Approach of Class

Imbalance Learning by Combining Class Imbalance

Problem with Noise. Advances in Intelligent Systems

and Computing, 23–30. https://doi.org/10.1007/978-

981-10-6602-3_3

Merkert, J., Mueller, M., & Hubl, M. (2015). A Survey of

the Application of Machine Learning in Decision

Support Systems. ECIS 2015 Completed Research

Papers. Paper 133.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,

Cournapeau, Brucher, M., Perrot, M., & Duchesnay, E.

(2011). Scikit-learn: Machine Learning in Python.

Journal of Machine Learning Research, 12, pp. 2825 –

2830.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

466

Rio, S. del, Benitez, J. M., & Herrera, F. (2015). Analysis

of data preprocessing increasing the oversampling ratio

for extremely imbalanced Big Data Classification. 2015

IEEE Trustcom/BigDataSE/ISPA. https://doi.org/10.

1109/trustcom.2015.579

Roy, R., & George, K. T. (2017). Detecting insurance

claims fraud using machine learning techniques. In the

2017 international conference on circuit, power, and

computing technologies (ICCPT) (pp. 1 – 6). IEEE.

Ruisen, L., Songyi, D., Chen, W., Peng, C., Zuodong, T.,

YanMei, Y., & Shixiong, W. (2018). Bagging of

XGBoost Classifiers with Random Under-sampling and

Tomek Link for Noisy Label-imbalanced Data. IOP

Conference Series: Materials Science and Engineering,

428, 012004. https://doi.org/10.1088/1757-899x/

428/1/012004

Rusdah, D. A., & Murfi, H. (2020). XGBoost in handling

missing values for life insurance risk prediction. SN

Applied Sciences, 2(8). https://doi.org/10.1007/s42452-

020-3128-y

Sharma, Roshan. (2019). Insurance Claim. August 31,

2021. https://www.kaggle.com/roshansharma/insuranc

e-claim

Varmedja, D., Karanovic, M., Sladojevic, S., Arsenovic,

M., & Anderla, A. (2019). Credit Card Fraud Detection

- Machine Learning Methods. 2019 18th International

Symposium INFOTEH-JAHORINA (INFOTEH).

https://doi.org/10.1109/infoteh.2019.8717766

Verma, A., Taneja, A., & Arora, A. (2017). Fraud detection

and frequent pattern matching in insurance claims using

data mining techniques. In 2017 tenth international

conference on contemporary computing (IC3) (pp. 1 –

7). IEEE.

Waghade, S.S., & Karandikar, A.M. (2018). A

comprehensive study of healthcare fraud detection

based on Machine learning. International Journal of

Applied Engineering Research, 13 (6), pp. 4175-4178.

Wang, C., Deng, C., & Wang, S. (2020). Imbalance-

XGBoost: leveraging weighted and focal losses for

binary label-imbalanced classification with XGBoost.

Pattern Recognition Letters, 136, 190–197.

https://doi.org/10.1016/j.patrec.2020.05.035

Wang, Y., & Xu, W. (2018). Leveraging deep learning with

LDA-based text analytics to detect automobile

insurance fraud. Decision Support Systems, 105, 87 –

95.

Wei, W., Li, J., Cao, L., Ou, Y., & Chen, J. (2012).

Effective detection of sophisticated online banking

fraud on extremely imbalanced data. World Wide Web,

16(4), 449–475. https://doi.org/10.1007/s11280-012-

0178-0

Xu, Y., & Goodacre, R. (2018). On Splitting Training and

Validation Set: A Comparative Study of Cross-

Validation, Bootstrap and Systematic Sampling for

Estimating the Generalization Performance of

Supervised Learning. Journal of Analysis and Testing,

2(3), 249–262. https://doi.org/10.1007/s41664-018-

0068-2

Ying, X. (2019). An Overview of Overfitting and its

Solutions. Journal of Physics: Conference Series

1168(2), 022022. https://doi.org/10.1088/1742-6596/

1168/2/022022.

The Imbalance Data Handling of XGBoost in Insurance Fraud Detection

467