Learning Heuristics for Topographic Path Planning in Agent-Based

Simulations

Henrique L. Krever

1 a

, Thiago R. S. Le

1 b

, Juliano M. Pasa

1 c

, Edison P. de Freitas

2 d

Raul C. Nunes

1 e

and Luis A. L. Silva

1 f

Graduate Program in Computer Science, Federal University of Santa Maria, Av. Roraima nº 1000,

97105-900, Santa Maria, Brazil

Graduate Program in Computer Science, Federal University of Rio Grande do Sul,

CP 15064, 91501-970, Porto Alegre, Brazil

Keywords:

Topographic Path Planning, Heuristic Learning, Deep Neural Networks, Agent-Based Simulations.

Abstract:

Path planning algorithms with Deep Neural Networks (DNN) are fundamental to Agent-Based Modeling and

Simulation (ABMS). Pathﬁnding algorithms use various heuristic functions while searching for a route with

a low cost according to different criteria. When such algorithms are applied to compute agent routes in

simulated terrain maps represented by large numbers of nodes and where topographic movement constraints

are present, the problem is that traditional heuristic functions lose quality since they do not capture important

characteristics for target simulation problems. To approach this issue, this work investigates the training of

DNNs with large numbers of (i) topographic path costs and (ii) correction factors for standard Euclidean

distance heuristic estimations. The aim is to use these DNNs as heuristic functions to guide the execution of

different A

∗

-based topographic path planning algorithms in agent-based simulations. The work approaches

the heuristic learning and computation of agent routes in topographic terrain maps of different natures. To

assess the performance of the proposed techniques, experimental results with path planning algorithms and

alternative topographic maps are analyzed according to statistical models.

1 INTRODUCTION

Deep Neural Networks (DNN) (Goodfellow et al.,

2016) are crucial to the resolution of several path

search problems of Agent-Based Modeling and Simu-

lation (ABMS) (Macal, 2016). Various challenges re-

lated to the computation of path planning algorithms

with different natures, the use of terrain map repre-

sentation and indexing structures, the exploration of

pre-processed terrain map and path information, the

search for better heuristic functions, and the consid-

eration of different types and numbers of agents are

investigated in the path planning literature (Abd Al-

gfoor et al., 2015). With the exploration of DNNs,

these issues also have an important role in planning

relief-aware movement behaviors for agents in simu-

https://orcid.org/0000-0002-5791-5557

https://orcid.org/0000-0002-6137-2751

https://orcid.org/0000-0003-0319-7817

https://orcid.org/0000-0003-4655-8889

https://orcid.org/0000-0003-3228-4071

https://orcid.org/0000-0002-6025-5270

lated virtual environments.

Heuristic path planning algorithms search for

the path with the lowest cost according to different

characteristics of the simulated application problem,

where different types of heuristic functions are used

to guide the search process. The key role of these

functions is to estimate the distance from a current po-

sition n to a goal position g. In the A

∗

-based pathﬁnd-

ing algorithms, the cost of each node n is determined

by the function f (n) = g(n)+ h(n), where g(n) is the

current path cost, h(n) is the heuristic function to esti-

mate the distance between the current and goal nodes.

The quality of a heuristic estimation is related to

the form in that the function approaches the actual dis-

tance to the goal, directly inﬂuencing the choice of

terrain map nodes analyzed during the path search.

Traditional heuristic functions (e.g., Euclidean dis-

tance) adequately guide the search for agent routes

in many simulated maps that do not have many obsta-

cles or other terrain movement constraints. The prob-

lem is that standard heuristic functions become inef-

fective when the pathﬁnding algorithms have to com-

Krever, H., LeÃ

co, T., Pasa, J., P. de Freitas, E., Nunes, R. and Silva, L.

Learning Heuristics for Topographic Path Planning in Agent-Based Simulations.

DOI: 10.5220/0012129900003546

In Proceedings of the 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2023), pages 115-125

ISBN: 978-989-758-668-2; ISSN: 2184-2841

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

115

pute realist routes for agents in terrains with varied to-

pographic characteristics. Moreover, many complex

search problems can rely on heuristics that compute

suboptimal solutions for many reasons (e.g., (Spies

et al., 2019), where computing better quality agent

routes has a fundamental role in maintaining the real-

ism and ﬂuency of the many virtual simulations.

Recent works (Takahashi et al., 2019) (Jindal

et al., 2017) (Wang et al., 2019) (Ariki and Narihira,

2019) (Li et al., 2016) (Kirilenko et al., 2022) (Neisse

et al., 2022) (Weber et al., 2022) investigate the ex-

ploration of DNNs as heuristic functions for the res-

olution of path planning problems in different appli-

cations. Although relevant proposals have been pre-

sented, exploring DNN in pathﬁnding for ABMS ap-

plications is not a mature research ﬁeld. To approach

this issue, this work investigates the computation of

paths in terrain maps with different relief character-

istics (Ganganath et al., 2014) (Chen et al., 2009)

(Chagas et al., 2022), permitting the evaluation of the

effectiveness of alternative path planning approaches

based on the DNN-based learning of heuristic func-

tions.

The pathﬁnding algorithm’s heuristic functions

guide the map node analysis during the path search

in simulated topographic terrain maps. Therefore, the

more the DNN-based heuristic function approximates

the shortest distance between two terrain map nodes,

the fewer nodes need to be analyzed by the pathﬁnd-

ing algorithm. Most importantly, these functions can

learn the topographic characteristics of a set of simu-

lated terrain maps to better estimate relief-aware dis-

tances between start and destination positions. This

work details a DNN architecture and how to prepare

the path information to train it so that the DNN learns

the heuristic function to be used by topographic path

planning algorithms. Experimental results presented

in this work are computed using two distinct A

∗

-based

pathﬁnding algorithms, where alternative forms of

training and using the DNNs in the heuristic compu-

tations are investigated. This work assesses the pro-

posed approach in terms of the number of expanded

nodes, execution time, and path cost (distance). The

various pathﬁnding results computed in different ter-

rain maps are also statistically analyzed.

The work is organized as follows: Section II starts

reviewing pathﬁnding techniques. Then it discusses

approaches for topographic path planning and the ex-

ploration of DNNs as heuristic functions for pathﬁnd-

ing; Section III details the DNN-based topographic

pathﬁnding approaches investigated in this work; Sec-

tion IV details how the proposed techniques were ex-

perimentally analyzed. Then it discusses the obtained

testing results; Section V presents ﬁnal remarks and

directions for future work.

2 BACKGROUND AND RELATED

WORK

Path planning algorithms (Abd Algfoor et al., 2015)

are based on alternative criteria to ﬁnd a route for

agents to move in a virtual terrain map. For this,

a movement cost value should be considered from

the different topographic characteristics of a terrain

map. These cost computations can involve charac-

teristics such as path distance, travel time, agent en-

ergy required for the movement, travel limitations re-

lated to the agent’s physical capacities, logistic agent

issues, and many other application-oriented factors.

Although this work focuses on the computation of

paths for agents to better move through the terrain re-

lief, it actually aims to investigate how to learn char-

acteristics like these in DNNs so that they are not

lost/underused in heuristic path search computations.

Path search algorithms can work with or without

heuristic functions composing the travel cost com-

putations. A heuristic estimates the cost between

any node and a destination on the map representa-

tion structure, being zero when applied to the destina-

tion. This estimate assists the pathﬁnding algorithm

in choosing the next node to be analyzed during the

search, indicating the most promising map node in re-

lation to ﬁnding a path that leads to the destination.

Dijkstra’s algorithm (Frana and Misa, 2010) does

not use such a heuristic function. However, it is usu-

ally a ﬁrst choice in developing many simulation sys-

tems because it has a straightforward implementation,

good performance level, and calculation of the mini-

mum path cost between nodes representing the virtual

terrain map. The A

∗

algorithm (Hart et al., 1968) and

others derived from it differ from Dijkstra in using a

heuristic function for prioritizing the choice of nodes

that should be better than others during the search.

With this, the A

∗

-family of algorithms signiﬁcantly

reduces the processing time of the path search.

The Bi-Directional A

∗

algorithm (BiA

∗

) (Pohl,

1971) is a version of graph search algorithms that, us-

ing a heuristic, does the search from the start node

towards the destination node, while simultaneously

searching from the destination node towards the start

node. The path is returned when one of these searches

ﬁnds a node opened by the other search. Because of

that, the algorithm sometimes ends up ﬁnding subop-

timal paths, as it can ﬁnish the execution without hav-

ing examined less costly nodes. That is not a problem

for many simulation applications since these subopti-

mal paths are much more efﬁciently computed, where

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

116

memory and processing time constraints have to be

considered in many agent-based simulations.

2.1 Related Works

First, this work approaches the computing of agent

routes in terrain maps with topographic characteris-

tics.

The authors of (Ganganath et al., 2014) formu-

lated a heuristic for movements with lower energy

costs for mobile robots on terrain with elevation, us-

ing an A

∗

-based algorithm. A graph was used to ab-

stract a Digital Elevation Model (DEM) of a small

area of 1 km

of a region of canyons. Each graph

vertex represents a terrain point and has 8 edges for

its neighbors. The terrain points have three coordi-

nates, two for the position and one for the elevation.

The tangent arc of the inclination between coordi-

nates gives the inclination angle between two terrain

points. This angle is used in formulating the energy

cost model for traversing graph vertices and the algo-

rithm’s heuristic.

The work in (Chen et al., 2009) presents a path-

planning algorithm for 3D game scenes. The scene is

represented by a graph, where the vertices represent

the polygons and the edges represent the polygons’

adjacencies used in the scene rendering. The heuris-

tic used by the search algorithm uses the Euclidean

distance between nodes of the terrain representation

structure. The terrain inclination information, rep-

resented by normal vectors, is used in the function

(o,n), where a linear combination of these vectors

represents the difﬁculty of moving between the nodes

o and n. A graph is used to abstract a DEM, where

the graph vertices store the height information of the

pixel it represents. The difﬁculty of local movement

between neighboring vertices, expressed in the func-

tion g of the f (n) = g(n) + h(n) cost computations,

uses the terrain height difference, where the inclina-

tion between neighboring vertices is employed when

calculating the distance between two adjacent nodes.

This distance is computed using the Euclidean dis-

tance in the R

The work in (Chagas et al., 2022) describes a

pathﬁnding algorithm that produces smoothed paths

where agents have terrain inclination constraints that

they can cross during their simulated movement tasks.

A hierarchical structure models the maps to represent

large terrains, where the leaf nodes have normal vec-

tors that represent terrain inclinations in the 4 adja-

cent directions. The angle of normal vectors is used

to compute the local cost function g(n) (i.e., the cost

to traverse adjacent positions according to the terrain

relief) of the proposed pathﬁnding algorithm. In this

way, the higher terrain inclinations are more costly to

be traversed by the simulated agents.

Second, this work also investigates the exploration

of DNNs in path search computations.

The authors of (Takahashi et al., 2019) address

the computation of path search heuristic values with

neural networks. A Convolutional Neural Network

(CNN) extracts information from map images col-

lected for heuristics learning. Having the state-space

map and a three-dimensional matrix containing infor-

mation from the goal node and the path orientation

angle, the CNN produces a heuristic value using the

map dimensions and the number of goal node orien-

tations. The work also used the Dijkstra algorithm

output to produce the training dataset. Then the A

∗

algorithm was used to evaluate the CNN results.

The neural network model detailed in (Jindal

et al., 2017) predicts the travel distance between

source and destination GPS coordinates. This algo-

rithm combines this prediction with the time of the

day to better estimate a taxi travel time. The proposed

approach uses only raw GPS origin, destination coor-

dinates, and time of day information to perform dis-

tance and time predictions.

The NASR (Neuralized A-Star) model described

in (Wang et al., 2019) proposes using DNNs to learn

the cost functions of a heuristic algorithm used by

a custom route recommendation problem. Route

suggestions are issued from path planning-oriented

queries between source and destination positions. The

model consists of a Recurrent Neural Network (RNN)

to model the cost from the source position to the cur-

rent position and a value network (functions that as-

sign weights to nodes) to estimate the cost of the can-

didate position to the target position.

A CNN-based technique for learning heuristic

functions for path planners is presented in (Ariki and

Narihira, 2019). The network input is a map of obsta-

cles and a destination position. The network output

is a heuristic map, an image containing all heuristic

values from the destination point. The heuristic map

predicted by the CNN is used as a query table to pro-

vide a heuristic value during path planning.

The ANN

∗

presented in (Li et al., 2016) relies on

a heuristic algorithm similar to the A

∗

, although it

employs a modiﬁed heuristic function. This heuris-

tic function is generated from a regression neural net-

work, which is used to learn the map characteristics

and to predict the difﬁculty of pathﬁnding. The al-

gorithm uses the same cost function as the A

∗

algo-

rithm, using a traditional heuristic function and a mul-

tiplier, aiming to predict the route complexity. This

multiplier function is the result of the neural network,

f (n) = g(n)+ hT (n) ∗ hNN(n).

Learning Heuristics for Topographic Path Planning in Agent-Based Simulations

117

In (Kirilenko et al., 2022), different ways of train-

ing DNN to aid the pathﬁnding heuristic estimation

are compared with the use of uniform cost terrain

maps. Using pre-computed path information, one per-

forms DNN training to predict the absolute path cost

(cost-to-go) and the other to predict a correction fac-

tor for a Euclidean distance heuristic estimation. Ex-

perimental results show that the second approach is

superior because it ﬁnds more optimal cost paths. The

results also demonstrate that, in some cases, A

∗

with

DNN to predict the cost-to-go opened more nodes

than the standard A

∗

algorithm. This did not occur

with the DNN trained to return a correction factor to

be used by the weighted A

∗

algorithm.

In (Neisse et al., 2022), two DNN approaches to

assist in the A

∗

-based path planning over a set of to-

pographic terrain maps are explored: (1) h

sub

(n) =

DNN(n,m), where a DNN is trained for each used

100x100 pixel map representing terrain relief charac-

teristics, making the heuristic predictions h

sub

(n) for

that map only, and (2) h

subAll

(n) = DNN(n,m), where

a single DNN is trained to make heuristic predic-

tion h

subAll

(n) for three different topographic maps,

where a map identiﬁer is used as input in the DNN

executions. Experiments showed that the second ap-

proach is more promising because it presents a good

pathﬁnding performance, guaranteeing a smaller ex-

pansion of nodes and, consequently, execution time.

DNNs are explored in (Weber et al., 2022) to sup-

port computing A

∗

-based safe paths in topographic

terrain maps: paths that deviate as much as possible

from the ﬁeld of view of observers at different map

positions. Two different DNN strategies are com-

pared: (1) h(n) = DNN

(n), where the DNN is trained

to predict an absolute path cost in the R

, while other

path cost components are considered during the path

search runtime only, and (2) h(n) = DNN

(n), where

the DNN is trained to predict topographic path costs

that include a path safety cost component. Experi-

mental results show that DNN approaches can open

fewer nodes and have lower computing time than the

topographic-aware A

∗

algorithm. Using the safety

factor in the DNN2 training showed that other path

cost components can be successfully inserted in the

learning and, consequently, in the heuristic predic-

tions used to support the path search.

3 DNNS AS HEURISTIC

FUNCTIONS FOR COMPUTING

PATHS IN TOPOGRAPHIC

TERRAIN MAPS

Agent navigation behaviors for virtual simulation sys-

tems are most often modeled and implemented to

reﬂect the actual physical behaviors of real-world

agents. When simulations are performed in moun-

tainous terrains, the agents’ movement behaviors can

be compromised because the relief roughness may

cause all sorts of simulation problems. In many sit-

uations, the wheels of the simulated vehicles slip in

the steep terrain slopes, these slops make the vehicles

capsize in the simulations, and the agents can simply

try to use routes that make the movement progress al-

most impossible. The computation of paths consider-

ing these risks is paramount for the proper function-

ing and integrity of the agent-based simulations. As

investigated in this work, path computations should

prioritize determining routes that consider the various

characteristics of the simulated terrain topographies.

To implement virtual simulation systems in which

the terrain maps represent characteristics of real-

world mountainous regions, this work models the vir-

tual terrain as a regular grid with non-uniform costs.

This representation is based on a DEM of the to-

pographic terrain, where map nodes represent each

pixel of the terrain elevation model. Elevation in-

formation is calculated similarly to in (Chagas et al.,

2022). In it, the Euclidean distance function in the

is used to compute the g(n) and h(n) values of

the f (n) = g(n) + h(n) cost function used in the path

search. Then, the topographic terrain information is

converted to cost values stored in the map mode rep-

resentation structure. This cost is used to make up

the cost of crossing two adjacent nodes of the terrain

representation map and the training of DNNs for es-

timating the topographic route costs between two ter-

rain positions.

Figure 1 describes the calculation of the topo-

graphic path cost between two adjacent terrain nodes

A and B. Each map node has a resolution of 30 me-

ters in the real world. The height of each node (i.e.,

Height(A) and Height(B)) varies according to the re-

lief elevation in that terrain position. The height dif-

ference between two adjacent map nodes |Height(B−

A)| and the map node resolution Di f f (x, y) is used

to calculate the topographic distance Cost(A,B) given

by the triangle’s hypotenuse. Then the resulting value

is used as a local cost value between adjacent map

nodes.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

118

Figure 1: Cost calculation based on the height difference

between adjacent nodes in the terrain map representation.

3.1 Heuristic Topographic Path Cost

Computations with DNNs

This work investigates DNNs as heuristic functions

for the A

∗

and BiA

∗

pathﬁnding algorithms (Abd Al-

gfoor et al., 2015) when computing paths in terrains

with topography. To assess the impact of alternative

forms of DNN training with pre-computed path costs

between start S and goal G terrain map nodes, the

f (n) = g(n) + h(n) cost function used by these algo-

rithms uses the following heuristic formulations:

• h(n) = DNN

absCost

(n), where the DNN

absCost

(n)

returns absolute path cost heuristic values;

• h(n) = DNN

errorCoe f f

(n) ∗ h

′

(n), where the

DNN

errorCoe f f

(n) returns an error coefﬁcient

value to be used with the h

′

(n), which computes

Euclidean distance heuristic values in the R

;

DNN

absCost

- the computation of paths on terrains

with topography is motivated by the works presented

in (Neisse et al., 2022) and (Weber et al., 2022). In

them, the heuristic function h(n) of the used pathﬁnd-

ing algorithm is fully replaced by the DNN(n), such

that h(n) = DNN(n). The DNN

absCost

is trained with

absolute path cost values. These path costs are pre-

computed between start S and goal G terrain map

nodes.

DNN

errorCoe f f

- the DNN is trained to compute

an error coefﬁcient value. This error is related to

the heuristic distance values computed using the Eu-

clidean distance function in the R

. Motivated by

the work presented in (Kirilenko et al., 2022), the

DNN

errorCoe f f

is trained with pre-computed error co-

efﬁcients, where the resulting DNN returns a correc-

tion rate to be applied to the path costs returned when

standard (map-independent) heuristic distance func-

tions are used. The DNN is actually trained with

the topographic path costs dist

Topog

(n) divided by

cost estimates for the same paths returned by the Eu-

clidean distance function dist

Eucl

(n). Therefore, the

values returned by the trained DNN are DNN(n) =

(dist

Topog

(n) / dist

Eucl

(n)). In the runtime pathﬁnd-

ing computations, the values returned by the DNN

are multiplied by those returned by the Euclidean dis-

tance function in the R

between the considered start

S and goal G map nodes. It means that the heuris-

tic component h(n) of the path cost calculations of

f (n) becomes dist

Eucl

(n) ∗ DNN

errorCoe f f

(n). There-

fore, the path search cost function takes the form of

a weighted cost function f (n) = g(n) + w ∗ h(n)

(Ebendt and Drechsler, 2009).

The DNN architecture (the number of neurons and

layers) used in this work was determined experimen-

tally. A fully connected Feed-Forward DNN model

is used, with the hidden layers having certain sym-

metry in relation to the number of neurons per layer.

From the performed tests, the model that obtained

the most promising results was similar to the DNN

models described in (Neisse et al., 2022) and (Weber

et al., 2022). In this model, the number of neurons is

expanded, then contracted in the hidden layers. The

DNN architecture is the following: a) the linear func-

tion for the input layer, with 7 neurons (i.e., a terrain

map ID and the (x, y, z) coordinates of start and goal

map positions), b) the ReLU function for the three

hidden layers, with [400, 500, 400] neurons, and c)

the Sigmoid function for the output layer with 1 neu-

ron to return either the absolute path cost value or the

correction factor value.

3.2 The Computation of Heuristic Maps

from DNN Estimates

The trained DNN calculates the heuristic function for

the targeted pathﬁnding algorithms. It computes the

heuristic value for the cost function in each node

analysis during the search. In doing so, the exe-

cution of the pathﬁnding algorithms may not be as

fast as required as the number of neuron calculations

in the overall DNN architecture grows. That is be-

cause heuristic calculations using standard distance

functions are much faster than those developed using

the DNN elements. The problem is that traditional

heuristic functions fail (e.g., due to the terrain topog-

raphy, the heuristic results are too different from the

actual path costs between the considered terrain po-

sitions) when other application-oriented components

must be considered in the path calculations. To ap-

proach this problem, this work explores GPU paral-

lelism functionalities to compute DNN-based heuris-

tic function values during the pathﬁnding execution.

Learning Heuristics for Topographic Path Planning in Agent-Based Simulations

119

This approach involves the computation and use of a

“heuristic map”.

A two-dimensional matrix can represent a heuris-

tic map in many terrain maps. The matrix values

record the topographic distances from all map posi-

tions S to a goal position G. This matrix is fed with the

DNN distance predictions generated via the GPU par-

allel computations. This heuristic map is computed

through the DNN execution and ﬁlled out once at the

ﬁrst step of each pathﬁnding execution. It means that

the pathﬁnding algorithm retrieves the estimated path

cost value in the previously computed heuristic map

when it requires a heuristic value for a current node

during the path search.

According to tests in this work, the delay time re-

quired to generate the heuristic map for all 300x300

topographic map instances is at most 600 ms. More-

over, this additional computing time required to gen-

erate the heuristic map starts to pay off when the

routes’ complexity in the used terrain map increases.

For large-scale and uneven terrain maps, where a

large number of heuristic computations may have to

be developed for the opening of a large number of

nodes by the pathﬁnding algorithm, the GPU paral-

lel computation of all heuristic map values in a single

run is faster than the individual DNN computations of

heuristic values when required.

4 EXPERIMENTS AND RESULTS

The experiments developed in this work aimed to

evaluate the pathﬁnding techniques resulting from the

two different DNN models as heuristic components

for path search computations. Eight maps with differ-

ent topographies were used in the tests. For each map,

pairs of S/G map positions were generated, where

the goal was to ﬁnd the shortest topographic path be-

tween these positions. The A

∗

and BiA

∗

pathﬁnd-

ing algorithms were individually executed using the

tested DNN-based heuristic functions - DNN

absCost

and DNN

errorCoe f f

- for each pair of map positions.

The heuristic function values returned by the DNNs

were recorded in the generated heuristic maps. When-

ever this map was required, it was computed and used

during the execution of the tested pathﬁnding algo-

rithms. For each algorithm execution, the resulting

path’s topographic length (distance), the number of

expanded nodes, and the execution time were mea-

sured and stored for statistical analysis.

In the terrain maps’ pre-processing activities, the

following attributes were used to generate the dataset

for the DNN training:

• mapID: representing the map used in the path

computations;

• S(x,y, z): representing the start map position S;

• G(x,y, z): representing the goal map position G;

• Either (i) the shortest distance d

Topog

(S,G) be-

tween the S and G positions, representing the ab-

solute path cost, or (ii) the heuristic correction

factor computed by d

Topog

(S,G) / d

Eucl

(S,G),

where d

Topog

(S,G) is the shortest topographic

path cost and d

Eucl

(S,G) is the Euclidean distance

in the R

A sample of map positions equivalent to 10% of

each terrain map was selected to generate the train-

ing dataset. The shortest topographic distance be-

tween these positions was calculated using a parallel

version of the topographic-aware Dijkstra algorithm

(Harish and Narayanan, 2007). Moreover, the Dijk-

stra execution was adapted not to have a target node,

expanding to all map nodes. This way, the Mini-

mum Spanning Tree (MST) was generated for the se-

lected map nodes. Thus, it was possible to obtain the

shortest topographic distance of any node n in rela-

tion to all other nodes accessible from it on the ter-

rain map. Subsequently, the generated dataset was

randomly shufﬂed, grouped, and separated into three

different datasets. Then we used the cross-validation

method during the training, where the 70/15/15 distri-

bution was selected (70% for training, 15% for test-

ing, and 15% for validation).

The computed distances between the map’s differ-

ent S and G positions were stored in the CSV format.

All computed distances are positive real values.

Table 1: Real-world topographic terrain maps and DNN

training information.

Feature Value

Different maps 8 maps (Figure 2)

Size of each map 300 x 300 pixels

Pixel resolution 30 m

Dimension of each map 81 km

Sample of each map 9,000 (10%)

Dataset size (computed paths)

8 *



9,000



= 323,964, 000

Dataset memory size 16.5 GB

Dataset generation time ∼48 hours

Train/test/validation sets 70/15/15

The DNN

absCost

and DNN

errorCoe f f

used by the

topographic A

∗

computations were trained in two

DNNs. The DNNs were trained to less than 8.5%

of error, where the Mean Absolute Percentage Error

expressed the training error (Myttenaere et al., 2016)

given by the MAPE function (1).

MAPE =

100

∑

t=1



− ˆy



(1)

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

120

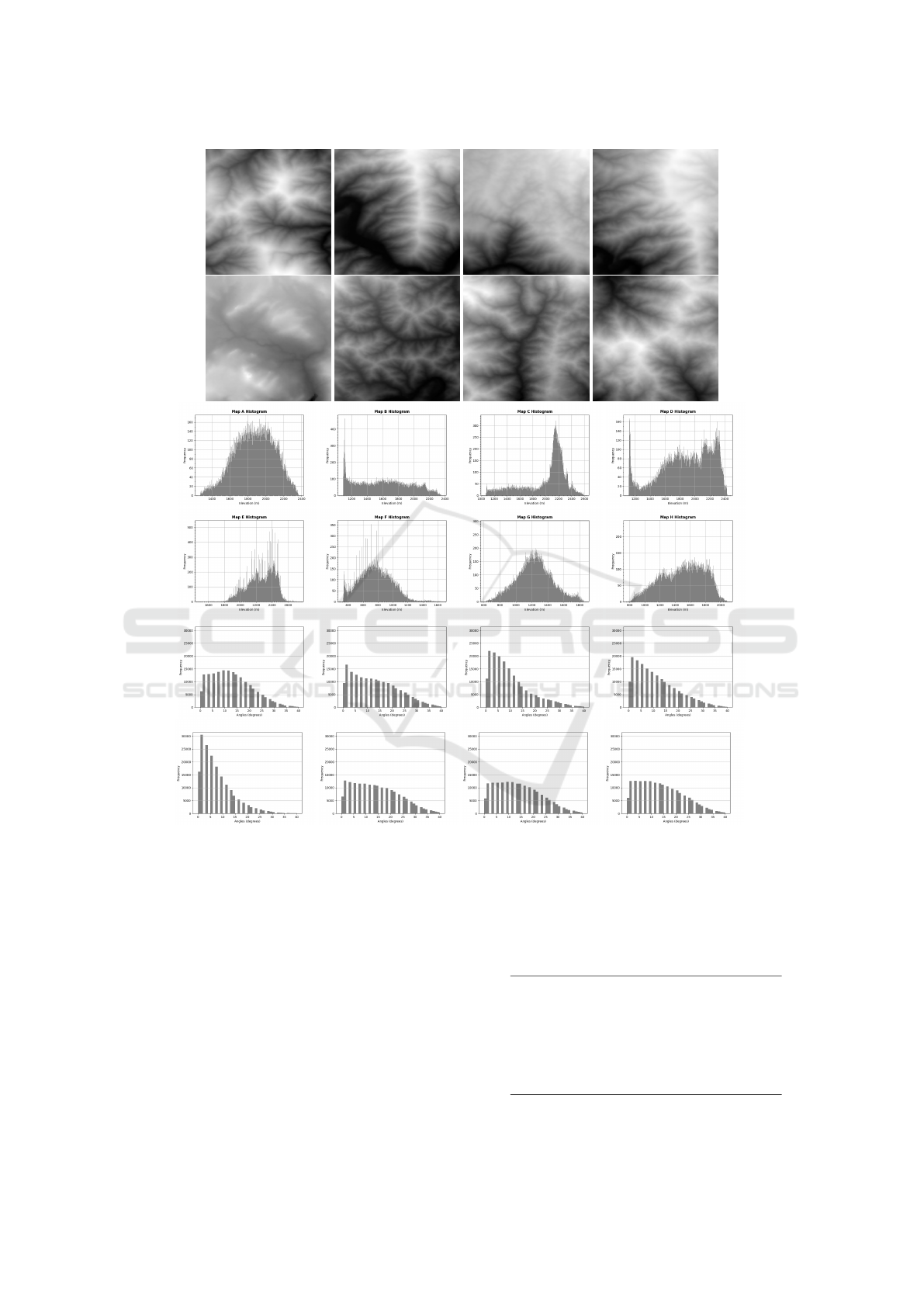
Figure 2: DEMs obtained from ((SRTM), 2013), elevation and inclination (between adjacent nodes) histograms for the real-

world topographic terrain maps used in this work.

where y

− ˆy

is the error between the predicted DNN

value and the expected value, n is the cardinality of

the dataset used to assess the trained DNN error.

In the DNN training, the two main parameters

were the loss function and optimization. While the

chosen loss function was the Mean Absolute Error,

the optimization function was ADAM (Kingma and

Ba, 2014). We explored the minibatch approach

(Goodfellow et al., 2016) with a batch size of 32. A

maximum number of 100 seasons was deﬁned for the

training duration. A premature stop criterion of 30

seasons passed without prediction improvements was

also used. The DNNs were implemented and trained

in Python using the TensorFlow library (Abadi et al.,

2016). Table 2 details the computing environment

used throughout this work’s development.

Table 2: Computing environment used in this work.

CPU Intel® Core™ i5-12400F

CPU cores 6 cores

CPU frequency 2.5 GHz / 4.4 GHz

RAM memory (2x) 16 GB DDR5 2400MHz

GPU GeForce GTX 3060

GPU cores 3,584

GPU memory 12 GB GDDR6

Operating system Windows 11 Pro

Learning Heuristics for Topographic Path Planning in Agent-Based Simulations

121

(a) (b)

Figure 3: Paths computed with (a) A

∗

DNN

absCost

, path cost = 7,788.06m; (b) A

∗

DNN

errorCoe f f

, path cost = 7,823.91m; (c)

BiA

∗

DNN

absCost

, path cost = 7,878.06m and (d) BiA

∗

DNN

errorCoe f f

, path cost = 7,817.65m.

A Generalized Linear Regression Model (GLRM)

(McCullagh and Nelder, 1989) was used to statis-

tically analyze the experimental pathﬁnding results.

This model was computed using the R statistical soft-

ware package (R Core Team, 2013). Details and

examples of such kind of statistical analysis can be

found in (Chagas et al., 2022) (Neisse et al., 2022)

and (Weber et al., 2022).

To compare the tested methods, the computed

dataset consists of 6,350 paths in each map (50,800

in total) for each tested heuristic approach. For ev-

ery path, the resulting topographic path cost (distance

in meters), the execution time, and the number of

opened nodes were recorded. To assess the effects of

the tested DNN-based heuristic setups, the pathﬁnd-

ing results were detailed in terms of a) the expanded

node values in relation to the topographic distance of

the resulting path and b) the execution time values in

relation to the distance of the resulting topographic

path.

Instances of topographic paths between the same

S and G positions computed by the tested methods in

the same terrain map are presented in Figure 3. De-

spite the differences in the plotted topographic routes,

they have quite similar costs. The statistical results

obtained with the pathﬁnding tests are presented in

Tables 3 and 4. All pathﬁnding results are statistically

signiﬁcant (Signif. level: 0.001, Std. Error: 0.01).

These (i) execution times and (ii) number of opened

nodes results are also shown in Figure 4.

The test results show that the DNN

errorCoe f f

opens a smaller number of nodes in relation to

the DNN

absCost

with the A

∗

and BiA

∗

algorithms.

With the trained DNNs, this result shows that the

DNN

errorCoe f f

better approximates the heuristic esti-

mates of the actual topographic path costs. The A

∗

with DNN

errorCoe f f

opens the lowest number of nodes

among the tested techniques. It opens 16.07% fewer

nodes than the A

∗

with the DNN

absCost

, the base tech-

nique in this statistical analysis. Regarding the num-

ber of opened nodes, the A

∗

with the DNN

absCost

second among the tested techniques. The BiA

∗

with

the DNN

errorCoe f f

opens 14.30% more nodes than the

base method, and the BiA

∗

with the DNN

absCost

opens

37.33% more nodes than the base method. The fastest

method is the BiA

∗

with the DNN

absCost

. It runs 5.21%

faster than the base method. Regarding computing

time, the A

∗

with the DNN

absCost

is second among the

tested techniques. The slowest method is the BiA

∗

with the DNN

errorCoe f f

, expending 13.20% more time

than the base method. The A

∗

with DNN

errorCoe f f

11.23% slower than the base method. The results in-

dicate that the tested pathﬁnding algorithms with the

DNN

errorCoe f f

method is slower because they require

the additional calculation of the Euclidean distances.

To assess the topographic path costs resulting

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

122

(a)

(b)

Figure 4: (a) Expanded nodes x topographic path cost, and (b) Execution time x topographic path cost.

from the tested pathﬁnding algorithms with the

heuristics proposed in this work, the Mean Absolute

Percentage Error (MAPE) function was used. Table 5

shows that the paths generated by DDN-based heuris-

tics had a maximum cost difference of 1.34% in rela-

tion to the optimal path costs returned by the A

∗

with

the Euclidean distance heuristic function.

The experiments indicate that the pathﬁnding

method choice is based on a tradeoff between ex-

panded nodes and execution time. While the

DNN

errorCoe f f

method presents fewer memory costs,

it is slower than the DNN

absCost

method. In addi-

tion, the DNN

absCost

and DNN

errorCoe f f

methods re-

sulted in shorter topographic paths when used with

the A

∗

algorithm in comparison to the topographic

path costs of the BiA

∗

algorithm. Overall, the tested

approaches generalized the eight different terrain to-

pographies well, meaning that they can approach the

training of new terrains.

In summary, the proposals and experimental re-

sults presented in this paper analyze the combina-

tion of the DNNs and pathﬁnding techniques for the

heuristic map generation and use, the exploration of

the parallel version of the topographic-aware Dijkstra

algorithm (Harish and Narayanan, 2007) to construct

the training dataset, and the DNN model to reproduce

the heuristic computations in different topographic

terrain maps. This work analyzes DNN heuristic

methods for learning a large number of path cost in-

stances (i.e., shortest topographic path distances) be-

tween two S/G terrain map positions and the conse-

quent learning of targeted map topographic character-

istics. This work also presents the statistical analysis

of experimental pathﬁnding results, where the tested

DNN-based algorithms’ performance is analyzed.

Learning Heuristics for Topographic Path Planning in Agent-Based Simulations

123

Table 3: Statistical results for execution time x topographic path cost.

Estimate Std. Error t Value Pr(>|t|)

Intercept -4.654 0.0059 -784.69 <2e-16

∗

DNN

absCost

0.0000 0.0000 70,586.76 <2e-16

∗

DNN

errorCoe f f

0.1064 0.0075 14.18 <2e-16

BiA

∗

DNN

absCost

-0.0535 0.0074 -7.27 <3.57e-13

BiA

∗

DNN

errorCoe f f

0.1240 0.0069 17.93 <2e-16

Table 4: Statistical results for expanded nodes x topographic path cost.

Estimate Std. Error t Value Pr(>|t|)

Intercept 5.4290 0.0038 1,424.73 <2e-16

∗

DNN

absCost

0.0002 0.0000 418.82 <2e-16

∗

DNN

errorCoe f f

-0.1752 0.0033 -52.39 <2e-16

BiA

∗

DNN

absCost

0.3172 0.0033 96.68 <2e-16

BiA

∗

DNN

errorCoe f f

0.1337 0.0031 43.37 <2e-16

Table 5: Percentage of DDN-based path costs compared to

the optimal path costs (computed with the A

∗

algorithm with

Euclidean distance heuristic function).

DNN

absCost

DNN

errorCoe f f

∗

1.31% 0.87%

BiA

∗

1.34% 0.92%

5 FINAL REMARKS

The computation of path routes for agents in topo-

graphic terrain maps is a relevant problem for many

agent-based simulation applications. In this context,

this work shows that the heuristic functions learned by

DNNs can support the path search in topographic map

representations. The use of the DNN allows the im-

plementation of the search for paths which combines

path pre-processed information – the pre-computed

topographic distances in the terrain map that are later

learned into DNN memory structure – with the actual

path cost computations developed during the execu-

tion time of different path planning algorithms.

Future work in our project will aim at the hier-

archical and irregular capture of the extremely large

real-world topographic terrain maps, including a large

number of maps with more distinct topographic char-

acteristics (e.g., varying from ﬂat areas to mountain

regions), in addition to other required adjustments for

DNN-based pathﬁnding algorithms. Moreover, we

aim to investigate the learning of characteristics that

could be more independent of the used terrain maps,

and the investigation of other DNN architectures, with

special attention to the computation of topographic-

aware agent routes for agent-based simulations.

ACKNOWLEDGMENT

We thank the Brazilian Army Strategic Program AS-

TROS for ﬁnancial support through the SIS-ASTROS

GMF project (898347/2020) - TED 20-EME-003-00.

REFERENCES

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,

J., Devin, M., Ghemawat, S., Irving, G., and Isard, M.

(2016). Tensorﬂow: A system for large-scale machine

learning.

Abd Algfoor, Z., Sunar, M. S., and Kolivand, H. (2015).

A comprehensive study on pathﬁnding techniques for

robotics and video games. International Journal of

Computer Games Technology, 2015.

Ariki, Y. and Narihira, T. (2019). Fully convolutional

search heuristic learning for rapid path planners. arXiv

preprint arXiv:1908.03343.

Chagas, C., Zacarias, E., de Lima Silva, L. A., and Pignaton

de Freitas, E. (2022). Hierarchical and smoothed to-

pographic path planning for large-scale virtual simula-

tion environments. Expert Systems with Applications,

189:116061.

Chen, S., Shi, G., and Liu, Y. (2009). Fast path searching

in real time 3d game. In WRI Global Congress on

Intelligent Systems, volume 3, pages 189–194.

Ebendt, R. and Drechsler, R. (2009). Weighted A

∗

search –

unifying view and application. Artiﬁcial Intelligence,

173(14):1310–1342.

Frana, P. L. and Misa, T. J. (2010). An interview with

edsger w. dijkstra. Communications of the ACM,

53(8):41–47.

Ganganath, N., Cheng, C.-T., and Tse, C. K. (2014). Find-

ing energy-efﬁcient paths on uneven terrains. In

2014 10th France-Japan/ 8th Europe-Asia Congress

on Mecatronics (MECATRONICS2014- Tokyo), pages

383–388.

SIMULTECH 2023 - 13th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

124

Goodfellow, I., Bengio, Y., Courville, A., and Bengio, Y.

(2016). Deep learning, volume 1. MIT press Cam-

bridge.

Harish, P. and Narayanan, P. J. (2007). Accelerating large

graph algorithms on the gpu using cuda. In A., S.,

P., M., B., R., and P., V., editors, High Performance

Computing – HiPC 2007, pages 197–208. Springer.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE Transactions on Systems Science and

Cybernetics, 4(2):100–107.

Jindal, I., Qin, T., Chen, X., Nokleby, M., and Ye, J.

(2017). A uniﬁed neural network approach for esti-

mating travel time and distance for a taxi trip. arXiv

preprint arXiv:1710.04350.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Kirilenko, D., Andreychuk, A., Panov, A., and Yakovlev,

K. (2022). Transpath: Learning heuristics for grid-

based pathﬁnding via transformers. arXiv preprint

arXiv:2212.11730.

Li, G., Wang, G., Wang, Q., Fei, F., L

u, S., and Guo, D.

(2016). Ann: A heuristic search algorithm based on

artiﬁcial neural networks. In Proceedings of the 2016

International Conference on Intelligent Information

Processing, pages 1–9.

Macal, C. (2016). Everything you need to know about

agent-based modelling and simulation. Journal of

Simulation, 10:144–156.

McCullagh, P. and Nelder, J. A. (1989). Generalized Linear

Models, volume 37. CRC Press.

Myttenaere, A. d., Golden, B., Grand, B. L., and Rossic, F.

(2016). Mean absolute percentage error for regression

models. Neurocomputing, 192:38–48.

Neisse, C., Soares, J. L., Silva, L. A., and Freitas, E. P.

(2022). Investigating deep neural networks as heuris-

tic functions for path planning with topographic ter-

rain characteristics in agent-based simulation. In

2022 IEEE 31st International Symposium on Indus-

trial Electronics (ISIE), pages 174–181. IEEE.

Pohl, I. (1971). Bi-directional search. in machine. Intelli-

gence, 6:124–140.

R Core Team (2013). R: A Language and Environment for

Statistical Computing. Vienna, Austria.

Spies, M., Todescato, M., Becker, H., Kesper, P., Waniek,

N., and Guo, M. (2019). Bounded suboptimal search

with learned heuristics for multi-agent systems. Pro-

ceedings of the AAAI Conference on Artiﬁcial Intelli-

gence, 33(01):2387–2394.

(SRTM), N. S. R. T. M. (2013). Shuttle radar topog-

raphy mission (srtm) global. Distributed by Open-

Topography. Accessed: 2023-04-12. Available:

https://doi.org/10.5069/G9445JDF.

Takahashi, T., Sun, H., Tian, D., and Wang, Y. (2019).

Learning heuristic functions for mobile robot path

planning using deep neural networks. In Proceedings

of the International Conference on Automated Plan-

ning and Scheduling, volume 29, pages 764–772.

Wang, J., Wu, N., Zhao, W. X., Peng, F., and Lin, X.

(2019). Empowering a* search algorithms with neural

networks for personalized route recommendation.

Weber, C. M., Freitas, E. P., and Silva, L. A. (2022). Safe

and topographic path planning with deep neural net-

works. In 2022 21st Brazilian Symposium on Com-

puter Games and Digital Entertainment (SBGames),

pages 1–6. IEEE.

Learning Heuristics for Topographic Path Planning in Agent-Based Simulations

125