A Web Scraping Algorithm to Improve the Computation of the

Maximum Common Subgraph

Andrea Calabrese

, Lorenzo Cardone

, Salvatore Licata, Marco Porro and Stefano Quer

DAUIN Department of Control and Computer Engineering, Politecnico di Torino, Turin, Italy

Keywords:

Graphs, Maximum Common Subgraph, McSplit, Heuristics, Software, Algorithms.

Abstract:

The Maximum Common Subgraph, a generalization of subgraph isomorphism, is a well-known problem in

the computer science area. Albeit being NP-complete, ﬁnding Maximum Common Subgraphs has countless

practical applications, and researchers are continuously exploring scalable heuristic approaches. One of the

state-of-the-art algorithms to solve this problem is a recursive branch-and-bound procedure called McSplit.

The algorithm exploits an intelligent invariant to pair vertices with the same label and adopts an effective

bound prediction to prune the search space. However, McSplit original version uses a simple heuristic to pair

vertices and to build larger subgraphs. As a consequence, a few researchers have already focused on improving

the sorting heuristics to converge faster. This paper concentrate on these aspects and presents a collection of

heuristics to improve McSplit and its state-of-the-art variants. We present a sorting strategy based on the

famous PageRank algorithm, and then we mix it with other approaches. We compare all the heuristics with

the original McSplit procedure, and against each other. In particular, we distinguish the heuristics based on the

node degree and novel ones based on the PageRank algorithm. Our experimental section shows that PageRank

can improve both McSplit and its variants signiﬁcantly regarding convergence speed and solution size.

1 INTRODUCTION

Graphs are ﬂexible structures that allow us to model

many elements of human knowledge through a math-

ematical abstraction. In particular, graphs can be

very good representations of relationships between

objects. Graphs ﬁnd many applications in ﬁelds

such as chemistry (Dalke and Hastings, 2013), so-

cial networks (Milgram, 1967), web searches (Brin

and Page, 1998), security threat detection (Park and

Reeves, 2011), modeling dependencies between dif-

ferent software components (Zimmermann and Na-

gappan, 2007), hardware testing and functional test

programs (Angione et al., 2022).

In this paper, we are interested in improving the

computation of the Maximum Common Subgraph

(MCS) between two graphs. Even if the problem has

been appearing in the scientiﬁc literature since the

70s (Bron and Kerbosch, 1973; Barrow and Burstall,

1976), one of the most efﬁcient state-of-the-art algo-

rithm for ﬁnding MCS is McSplit, introduced in 2017

https://orcid.org/0000-0002-8854-8171

https://orcid.org/0009-0008-7553-4839

https://orcid.org/0000-0001-6835-8277

by McCreesh et al. (McCreesh et al., 2017). Mc-

Split is a branch-and-bound algorithm that recursively

computes new solutions by pairing vertices selected

from the two graphs. The core idea is to label all ver-

tices based on the connection they have with already

selected nodes. After that, the algorithm efﬁciently

prunes the search tree taking into account those labels

and a formula computing the upper bound for the size

of the current solution. The approach is quite efﬁcient

in maintaining low memory proﬁles and pruning the

search space. Unfortunately, it considers all possible

vertex pairs, one vertex from the ﬁrst and one from the

second graph, and its performances strongly depend

on the vertex sorting heuristic. The original version

of McSplit statically sorts the vertices of both graphs

based on their degree. This order is then maintained

unaltered for the entire process, and it is the most im-

pairing element of the procedure. Many vertices may

have identical degrees, making it impossible to dis-

criminate between them. Moreover, there is no way to

prioritize a promising pair discovered during the exe-

cution of the algorithm. In our approach, we exploit

the core of the original McSplit procedure, but we re-

place the static sorting heuristic with sharper ordering

techniques.

Calabrese, A., Cardone, L., Licata, S., Porro, M. and Quer, S.

A Web Scraping Algorithm to Improve the Computation of the Maximum Common Subgraph.

DOI: 10.5220/0012130800003538

In Proceedings of the 18th International Conference on Software Technologies (ICSOFT 2023), pages 197-206

ISBN: 978-989-758-665-1; ISSN: 2184-2833

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

197

McSplitRL (Liu et al., 2020), McSplitLL (Zhou

et al., 2022), and McSplitDAL (Liu et al., 2022) al-

ready brought an improvement over the original sort-

ing heuristic of McSplit. McSplitRL uses a Rein-

forcement Learning approach to reﬁne the order of the

vertex selection. McSplitLL, based on McSplitRL,

outperforms its predecessor by using a technique

called Long Short Memory which deals with nodes

with speciﬁc characteristics. McSplitDAL builds

upon McSplitLL, introducing a technique called Dy-

namic Action Learning, which improves the reward

function of McSplitRL. However, these techniques

use the original McSplit sorting heuristic as a tie-

breaker when selecting vertices.

In this work, we present a new vertex selection

heuristic that is able to improve the performances of

McSplit, McSplitLL, and McSplitDAL. In particular,

we propose to use PageRank (Brin and Page, 1998),

the former algorithm behind the Google search en-

gine, as a vertex selection heuristic, exploiting its

capabilities to work on both directed and undirected

graphs. We use PageRank both as a standalone or as

a tie-breaking heuristic, using it to classify vertices

and then combining it with other techniques such as

McSplitLL or McSplitDAL.

In our experimental analysis, we compare our al-

gorithm with McSplit and its variants. We tested 400

graph pairs, selecting the graphs from the largest pub-

licly available graphs at (Foggia et al., 2001) and

choosing at least one graph pair for each graph cat-

egory. We set the timeout for each experiment to

60 seconds to quickly grab the convergence speed of

each algorithm. Overall, we can improve McSplit,

McSplitRL, McSplitLL, and McSplitDAL in up to

77% of the graph pairs considered. Moreover, we ob-

tain an improvement in terms of the ﬁnal size of the

solution subgraph up to 7%.

The paper is organized as follows. In Section 2,

we describe our notation and we deﬁne the problem.

We also present a set of well-known approaches for

solving it. In Section 3, we illustrate new heuristics to

enhance the original McSplit algorithm and its latest

variants. Section 4 describes our experimental results.

Finally, Section 5 draws some conclusions and give

some hints on possible future work.

2 BACKGROUND

This section introduces our graph notation and some

basic concepts on subgraph isomorphism and the

Maximum Common Subgraph problem. After that,

we present McSplit and its more recent variants,

which we consider state-of-the-art algorithms for

solving the Maximum Common Subgraph problem.

2.1 Graphs

A graph is a pair of vertices (nodes) and edges (links).

Links represent connections with nodes, making this

structure well-suited for representing relationships

between objects. In our notation, we use G and H

to represent two graphs and V (G) (V (H)) to repre-

sent the vertices belonging to G (H). Furthermore,

we use E(G) (and E(H)) to represent the set of all the

pairs of vertices connected by an edge. We use |G| or

|V (G)| to indicate the number of vertices belonging

to G, referring to it as its size. In contrast, we refer

to the number of edges of a graph as |E(G)|. Given

∈ V (G), we denote E(v

) the edge that links

to v

Graphs can come in various ﬂavors: Labeled or

unlabeled, weighted or unweighted, directed or undi-

rected. In labeled graphs, vertices have additional in-

formation described by the label; in many applica-

tions, the labels classify the vertices as sharing spe-

ciﬁc characteristics. In our notation, L(v) is the label

of the vertex v.

We say that the graph is weighted if edges present

different weights associated with them. For example,

a weight might represent the distance between two

nodes. Unweighted graphs can be seen as weighted

graphs with every weight equal to one.

We say that G is undirected if

∀v

∈ V (G) ∈ E(G) ⇐⇒

} ∈ E(G) & E(v

) = E(v

)

In other words, if a link exists between v

and v

, the

opposite link must exist and have the same weight.

We say that H is a subgraph of G if

V (H) ⊂ V (G) ∧ E(H) ⊂ E(G)

that is, the vertices and edges of H are a subset of the

vertices and edges of G. A graph H is an induced

subgraph of G if H is a subgraph of G and contains

all the edges between its vertices of the original graph

Graph isomorphism is the problem of detecting if

there is a bijection between two graphs G and H such

that

∀v

∈ H ∈ E(H) ⇐⇒ {v

} ∈ E(G)

that is, if two graphs have the same structure. Veri-

fying whether two graphs are isomorphic is known to

be NP (Sch

oning, 1988), even if the exact complexity

inside that class is unknown.

A subgraph is a subset of a graph’s vertices (or

nodes) and edges (or links). The terms vertex and

node will be used interchangeably in this paper.

ICSOFT 2023 - 18th International Conference on Software Technologies

198

The Maximum Common Subgraph (MCS) prob-

lem between graphs G and H, requires ﬁnding the

most extensive graph simultaneously isomorphic to a

subgraph of G and H. In particular, the Maximum

Common Induced Subgraph (MCIS) focuses on ﬁnd-

ing the induced subgraph with all the vertices in com-

mon between two graphs. The problem is known to

be NP-complete (Michael Garey, 1979).

In our case, we focus on undirected, unlabeled,

and unweighted graphs, as they represent the worst

case scenario for the Maximum Common Subgraph

computation.

2.2 McSplit

McSplit (McCreesh et al., 2017) is a branch-and-

bound recursive algorithm for ﬁnding the MCS be-

tween two graphs.

The authors deﬁne a label class as a set of ver-

tex pairs (belonging to the ﬁrst and the second graph)

having the same connections toward the vertices be-

longing to the current solution. As McSplit uses la-

bels to ﬁnd possible couplings between vertices, the

original algorithm also provides a way to create those

labels based on the adjacency lists of the vertices.

1 BEST ←

3 Function MCS(G, H, M)

4 if |M| > |BEST | then

5 BEST ← M

6 end

7 if CalculateBound() < |BEST | then

8 return

9 end

10 label class ← SelectLabelClass(G,H)

11 G

← G

12 while G

0 do

13 v ← SelectVertex(G,label class)

14 G

← G

\ {v}

15 forall

w ∈ getVertices(H,label class) do

16 M

← M ∪ (v, w)

17 H

← H \{w}

18 G

← U pdateLabels(G

,v)

19 H

← U pdateLabels(H

,w)

20 mcs(G

)

21 end

22 end

23 mcs(G

,H,M)

24 return

Algorithm 1: The simpliﬁed version of the original Mc-

Split algorithm.

Algorithm 1 provides a simpliﬁed version of the

McSplit algorithm. It takes as inputs the two graphs,

G and H, as well as the current solution M. La-

bel classes are used to guide the algorithm in ﬁnd-

ing the solution to the problem. The label class is a

classiﬁcation of each couple of vertices belonging to

(G,H). First, the algorithm assigns the current solu-

tion to the best one (line 5), in case the current so-

lution has a larger size (line 4). Notice that the best

solution BEST is initially empty (line 1). Then, the

algorithm calculates the upper bound B for the cur-

rent path (line 7). If this upper bound is less than the

size of the best solution, the current solution cannot

be improved along the current path; thus, the algo-

rithm backtracks (line 8). Otherwise, the algorithm

keeps improving the current solution. The bound is

computed as shown in Equation 1.

B = |M| +

∑

l∈L

min(|{v ∈ G\M : L(v) = l}|,

|{w ∈ H\M : L(w) = l}|)

(1)

When improving the current solution, McSplit tries to

build a larger solution by virtually removing a cou-

ple of vertices with the same label from the respective

graphs, updating the labels (lines 18-19) and trying

to explore recursively all possibilities starting from

the current solution (line 20). In each iteration of

the algorithm, the selection of a vertex pair occurs in

three distinct stages. Firstly, the most promising label

class is identiﬁed, followed by selecting a vertex from

the set of vertices belonging to that label class in the

graph G (line 14). Subsequently, all vertices w ∈ H of

the chosen label class are gathered (line 15), and then

individually selected one by one (line 17). Once v ∈ G

is selected, the current mcs instance uses recursion to

explore all solutions that include v and all the nodes

of the received partial solution M, therefore at line 23

an additional recursive call is introduced to explore

all the other solutions that include M but exclude v.

Ultimately, as every vertex couple has been explored

(line 12), the procedure returns the best solution.

To explore all possible vertex pairs, McSplit uses

two different heuristics. The ﬁrst one is used to se-

lect the next label class. The second one is adopted

to choose the next vertex to add to the ﬁnal graph.

The former (line 10) chooses the label class with

the smallest maximum size between G and H, i.e.,

max(|G|,|H|). The latter, instead, prioritizes vertices

in G with the most signiﬁcant degree, where the de-

gree is the number of links (inward and outward) of

the vertex. In particular, for selecting the next vertex

(line 13), McSplit heuristically considers the degree

of the vertex, choosing each time the vertex with the

most considerable degree and removing it from the

graph. We will refer to this approach as the Node De-

A Web Scraping Algorithm to Improve the Computation of the Maximum Common Subgraph

199

gree, or simply the Degree heuristic.

2.3 McSplit Variants

Many notable variants of McSplit have been devel-

oped to improve over the original algorithm. This sec-

tion brieﬂy describes some of the most noticeable and

recent ones.

2.3.1 McSplitSD

McSplit works asymmetrically on the two graphs

since it selects a vertex from G and then searches for

a matching vertex in H. This approach may unbal-

ance the algorithm, making it perform better or worse,

depending on the characteristics of the ﬁrst graph.

Among other strategies, Trimble (Trimble, 2023) pro-

poses McSplitSD, which sets as the ﬁrst graph the

denser one of the pair. The density K of a graph is

evaluated through Equation 2, using the number of

edges and vertices of the two graphs to express the

density extremeness:

K(G) =

|E(G)|

|V(G)|·(|V (G)|−1)

(2)

The two graphs G and H are swapped when the in-

equality

− K(G)| > |

− K(H)|

is true.

2.3.2 McSplitRL

Liu et al. (Liu et al., 2020) proposes McSplitRL, a

novel approach that extends the standard McSplit us-

ing Reinforcement Learning. This approach keeps

two vectors, one for the vertices of G and the other for

the vertices of H, which contain the rewards of each

node. Therefore, the node selection heuristic is based

on ﬁnding the node with the highest reward. The au-

thors devised a scoring system for a given action using

Equation 3:

R(v, w) =

∑

)∈E

min(|V

|,|V

|)−

∑

)∈E

min(|V

|,|V

(3)

Given a set of label classes of the initial graphs at a

given point of the search, E

, and the subsequent set

of label classes, E

, generated by including a new cou-

ple of vertices to the current solution, Equation 3 cal-

culates the reduction of the size of the label classes.

The size of a label class is considered as the minimum

of |V

| and |V

|, which are the number of vertices be-

longing to the label class respectively from the ﬁrst

or the second graph. Thus, this method can be seen

as a bound reduction and tends to prefer nodes whose

resulting branching cause a higher reduction of the

bound, thus cutting as many branches as possible in

subsequent steps of the algorithm.

2.3.3 McSplitLL

Zhou et al. (Zhou et al., 2022), starting from Mc-

SplitRL, build a more sophisticated version of the

tool called McSplitLL. Their solution introduces a

new heuristic called Long Short Memory (LSM) and

a method to be used in a speciﬁc situation called

Leaf Vertex Union Match (LUM). The new heuris-

tic uses Equation 3 but stores the rewards in a vector

for nodes of G and a matrix for the nodes of H, al-

lowing to reward each possible node pair separately

(v, w) ∈ (G,H).

However, since rewards may become huge, an

asymmetric decay is used, following a long-short-

term approach, which halves both G and H rewards

when their respective thresholds are exceeded. Re-

wards for single nodes v decay faster than the re-

wards for pair of nodes (v,w); thus, node pairs have a

smaller threshold.

Moreover, the LUM heuristic introduces a more

optimized strategy to handle leaf nodes. A node is

considered a leaf if it is adjacent to only one vertex

of a given graph, and it has been proved it can always

be added to the current subgraph if its only neighbor

is part of it as well. Thus, whenever a leaf from the

left graph and a leaf from the right graph is found, the

pair formed by these two nodes is added to the current

solution.

2.3.4 McSplitDAL

Liu et al. introduced McSplitDAL (Liu et al., 2022).

This algorithm is the most recent version of McSplit,

and it is built upon McSplitRL and McSplitLL. This

algorithm mainly introduces two new ideas. A new

value function called Domain Action Learning (DAL)

and a hybrid learning policy for choosing the next ver-

tex to match. The DAL value function aims to take

into account, when branching, not only the reduction

of the upper bound but also the simpliﬁcation of the

problem occurring after the branch. This feature can

be implemented by adding an additional term to the

reward deﬁned in Equation 3, granting a higher re-

ward to the vertices whose generated partitions have

a higher cardinality, when these vertices are added to

the solution:

R(v, w) =

∑

)∈E

min(|V

|,|V

|)−

∑

)∈E

min(|V

|,|V

|)+

(4)

Moreover, the hybrid branching policy of this ap-

proach has the primary goal of overcoming a possible

“Matthew effect”, which causes the algorithm to con-

tinue branching on a subset of nodes with very high

rewards getting trapped in a local optimum. The au-

thors believe this can be overcome by switching from

ICSOFT 2023 - 18th International Conference on Software Technologies

200

the RL to the DAL policy (and vice versa) after a

ﬁxed number of iterations without improvement, al-

lowing to dynamically change the strategy for select-

ing nodes.

For brevity, in this paper, we use the term Mc-

SplitX to generically identify the original McSplit or

one of its variants, i.e., McSplitLL, or McSplitDAL.

2.4 Other Approaches

Many algorithms have been presented to solve the

MCS problem, using strategies that differ from the

original McSplit. Among those, we would like to

mention the following. Levi (Levi, 1973) casts the

MCS problem onto the Maximum Common Clique

problem. McCreesh et al. (McCreesh et al., 2016)

and Vismara et al. (Vismara and Valery, 2008) fol-

low the previous approach while exploiting constraint

programming to solve the problem. Other approaches

take a step back, adopting parallel computation ca-

pabilities of General-Purpose computing on Graphics

Processing Unit (GPGPU) (Quer et al., 2020), to en-

hance McSplit on modern devices. A set of heuristics

to tackle the MCS problem with more than two graphs

has been developed by Cardone et al. (Cardone and

Quer, 2023). However, the most promising heuristics

work by analyzing graphs in couples and later merg-

ing the results, thus still motivating the research on

MCS techniques working on pairs of graphs.

3 OUR APPROACH

The main target of this work is to improve the ver-

tex selection heuristic. In particular, we are interested

in heuristics that can classify the vertices of the two

graphs. From our perspective, a good heuristic should

follow the guidelines presented by Marti et al. (Mart

and Reinelt, 2022):

• The solution should be nearly optimal.

• The heuristic should require low computational

effort.

In our heuristics, we also aim to generate classiﬁca-

tions as diverse as possible for ranking the vertices.

Moreover, we would like heuristics to classify a ver-

tex with a single number instead of representing it as

a vector. Although vectors have already been used in

MCS solutions, due to the nature of the problem, us-

ing a mathematical vector incurs possible downfalls.

More speciﬁcally, vectors may require more compu-

tational power to retrieve a classiﬁcation than using

single integers and the results may depend on the lex-

icographical order of the vertices. With these con-

siderations in mind, we focus on a classiﬁcation of

vertices based on single numbers. In particular, we

developed different heuristics for classifying vertices:

• A heuristic considering the PageRank of each ver-

tex.

• A heuristic using both PageRank and McSplit-

DAL.

• A heuristic using both PageRank and McSplitLL.

Please notice that both DAL and LL heuristics are

computed dynamically, whereas the PageRank ap-

proach is applied only once at the beginning of the

procedure.

3.1 The PageRank Algorithm

PageRank (Brin and Page, 1998) is an algorithm de-

veloped by Google that, given a network of web

pages, generates the probability of reaching a page

through a ﬁnite sequence of random clicks. PageRank

was the algorithm used by Google to sort the results

of its web engine searches. However, it is not used

anymore, as its patent expired in 2019.

PageRank is usually implemented on a generic

graph, so to account for different web pages, it con-

siders directed and unweighted graphs. A link from

one web page takes the user to another web page, but

the way back is not guaranteed. However, we can also

use it on undirected graphs, as we can think of them

as directed graphs with both forward and backward

edges between each node pair.

Algorithm 2 implements our PageRank algorithm,

and it is strongly inspired by a public version

. In

Algorithm 2, we use the notation ad j(G) to refer to

the indices of the adjacency matrix of graph G.

The Damping Factor (DF), initialized in line 1,

represented a person’s probability of stopping click-

ing random links. We decided to follow Brin et

al. (Brin and Page, 1998) recommendation for the

value of the DF, and we set its value at 0.85. In line 2,

we set the acceptable error ε at an arbitrary value. Ex-

perimentally, we discover that the smaller the epsilon

(i.e., the more we increase the precision of the pro-

cedure), the better the results, as the rankings tend to

be more diverse. However, as the original algorithm

accepts integers numbers, we also want to be able to

map integers to ranks; thus, we chose for ε a precise

enough number that would surely not overﬂow any

32-bit integer.

PageRank can be described as a Markov chain.

Thus, we build a stochastic matrix representing the

graph in line 17, based on the previously computed

https://github.com/purtroppo/PageRank

A Web Scraping Algorithm to Improve the Computation of the Maximum Common Subgraph

201

links going out from each node in line 16. Com-

puting the outgoing links is trivial and is not shown

in the algorithm. On the contrary, the computation

of the stochastic matrix is represented in function

StochasticGraph, from line 4 to line 13. Assuming

that each node has a unitary amount of information

ﬂowing outwards to the neighbors, the matrix identi-

ﬁes how much of that information is ﬂowing through

each of the adjacent edges. In line 18 we transpose

the stochastic matrix, and outgoing links are replaced

with incoming links and vice versa. PageRank ranks

nodes based on their incoming links; thus, the inver-

sion is necessary for the generality of the algorithm.

For undirected graphs, this might represent an unnec-

essary step; however, as McSplit works on directed

and undirected graphs, this must be true also for its

intermediate stages. On line 20, we pre-allocate the

results of the previous iteration and set them to zero.

In line 22 we calculate the ratio between the in-

coming or outgoing links and the size of the graph.

The core section of the evaluation is included from

line 25 to line 38. First, we zero the results for the

current iteration. Then, we compute the current rank

by adjusting the previous results, approximating at

each iteration the clicking probability, and discount-

ing them by the DF. On line 35, we update the er-

ror on the measurement, and on line 37 we update

the result vector p. The algorithm terminates when

(error < ε) in line 25; this condition is triggered when

the rankings converge, reaching a stable conﬁgura-

tion.

As we consider it trivial, we do not show the ﬂoat

to integer conversion in Algorithm 2.

3.2 McSplitX+PR

Within the framework introduced in Section 3.1, we

exploit the ideas introduced by McSplitLL and Mc-

SplitDAL, enhanced by the integration of the PageR-

ank heuristic. The union of these techniques pro-

duced two new versions of the McSplit algorithm,

speciﬁcally referred to as McSplitLL+PR and Mc-

SplitDAL+PR.

Whilst the original McSplit idea was centered

around the node degree heuristic, the subsequent vari-

ants were mainly based on McSplitRL, which used

reinforcement learning as a vertex selection heuristic.

However, whenever a tie is encountered, the heuristic

falls back to the node degree for choosing a vertex.

We propose using PageRank as a standalone or

tie-breaking heuristic, substituting it for the node de-

gree. This approach is summarized by Algorithm 3.

First, we apply the PageRank to classify the vertices

of graphs G and H (in lines 2 and 3, respectively).

1 DF ← 0.85

2 ε ← 0.00001

4 Function StochasticGraph(G,out links)

5 G

← [0.0] ∗ |G|

6 forall x,y ∈ ad j(G) do

7 if out link[x] = 0 then

8 G

[x,y] ← 1.0/|G|

9 else

10 G

[x,y] ← G[x,y]/out link[x]

11 end

12 end

13 return G

15 Function PageRank(G)

16 out links ← OutLinksForEachNode(G)

17 G

← StochasticGraph(G,out links)

18 G

← TransposeMatrix(G

)

19 result ←

0 ∗ |G|

20 p ←

21 forall x,y ∈ ad j(G

) do

22 push(G

[x,y]/|G|)

23 end

24 error ← 1.0

25 while error > ε do

26 result ←

0 ∗ |G|

27 forall x,y ∈ ad j(G

) do

28 result[x] ←

result[x] + G

[x,y] ∗ p[y]

29 end

30 forall rank ∈ result do

31 rank ← rank ∗ DF +

1.0−DF

|G|

32 end

33 error ← 0.0

34 forall rank, prev ∈ zip(results, p) do

35 error ← error + abs(rank − prev)

36 end

37 p = result

38 end

39 return result

Algorithm 2: Our version of the popular PageRank al-

gorithm, implemented on an adjacency matrix repre-

senting the graph G.

Then, we sort the vertices following their ranks ob-

tained by the previous classiﬁcation (lines 4 and 5).

Finally, we apply our McSplitLL or McSplitDAL

(i.e., McSpliX, generically speaking) on the sorted

vertices (line 6). This method leverages the Rein-

forcement Learning, to choose vertices dynamically

along the search, and guarantees the use of the PageR-

ank scores as a tie-breaker, particularly at the begin-

ning of the algorithm, when the rewards are initialized

ICSOFT 2023 - 18th International Conference on Software Technologies

202

1 Function McSplitX+PR(G, H)

2 G

ranks

← PageRank(G)

3 H

ranks

← PageRank(H)

4 G

sorted

← SortGraph(G,G

ranks

)

5 H

sorted

← SortGraph(H,H

ranks

)

6 McSplitX(G

sorted

)

7 return

Algorithm 3: The proposed McSplitX+PR algorithm

optimizing a McSplitX implementation recalled in

line 6.

to zero.

4 EXPERIMENTAL RESULTS

4.1 Experimental Setup

We ran our tests on a workstation with an Intel Core

i9-10900KF CPU and 64 GBytes of DDR4 RAM.

All our algorithms are written in C++, and we

compiled it with GCC version 9.4. For McSplit and

McSplitLL, we use the original versions obtained

from the WEB and adapted for being used with our

new heuristic. For McSplitDAL, we wrote an imple-

mentation that follows the ideas indicated by the au-

thors (Liu et al., 2022) as we were unable to ﬁnd an

ofﬁcial version publicly available. In addition, since

it has been proven to be beneﬁcial, we borrow the

graph swap idea from McSplitSD (Trimble, 2023),

and include it in all the variants of McSplit. Our

core implementation adopts the C++ parallel version

of McSplit. Unfortunately, not all versions may run

in multi-threading mode. Thus, as we are interested

in comparing our results with the ones gathered with

the previous variants of McSplit, we present all results

running all parallel versions with a single thread.

All algorithms were tested on a publicly available

dataset (Foggia et al., 2001). We focused on the most

extensive graphs, the ones with 100 nodes. Given the

size of the set, we chose at least one experiments for

each graph category, ﬁnally selecting 400 graph pairs.

Our tests are designed to evaluate the most prac-

tical aspect of all algorithms; thus, we evaluate their

ability to ﬁnd suitable solutions in a limited amount

of time, instead of ﬁnding the optimal solution with

an unlimited timeout. For each graph pair, we then

record the size of the most signiﬁcant solution found.

We compare the different methodologies in terms of

their capacity to ﬁnd the largest solution in the slotted

time.

We ﬁxed the timeout to 60 seconds for each ex-

periment. This timeout has been selected because ex-

perimentally McSplit often ﬁnds an effective solution

along the ﬁrst recursion path and it improves it only

sporadically. Figure 1 plots the typical growth of the

solution size with respect to the number of recursions.

We can see that at the beginning (within a few thou-

sand of recursions, usually performed in less than one

second in our setup) the solution size increases very

rapidly. Unfortunately, after the ﬁrst few seconds, the

solution grows slowly as most of the time is spent

searching the enormous solution space. In orange, we

highlighted the solution size at the end of the recur-

sion process. Please, notice that the number of recur-

sions is reported on the x-axis on a logarithmic scale.

Figure 1: Typical behavior of the effectiveness of the origi-

nal implementation of McSplit. The size of the solution of-

ten increases rapidly in the ﬁrst part of the process; then, the

procedure is captured by local minima which slow down the

convergence process and force the algorithm to visit enor-

mous state spaces that do not improve the solution size. In

orange, we can see the solution size at the end of the execu-

tion.

4.2 Experimental Evaluation

Figure 2 reports the number of graph pairs on which

each method ﬁnds the largest MCS out of the 400

graph experiments run. When an MCS with the same

size is returned by more than one heuristic (i.e., we

have a ex aequo) that pair is assigned to all the meth-

ods returning that result.

It is straightforward to see that our PR heuris-

tic, only applied to McSplit, McSplitLL, and Mc-

SplitDAL, easily outperforms the original strategies.

Moreover, the fastest strategy, i.e., McSplitDAL+PR,

ﬁnds the most signiﬁcant solution in almost 300 cases

out of 400.

Table 1, using no tie-breaker, shows the percent-

A Web Scraping Algorithm to Improve the Computation of the Maximum Common Subgraph

203

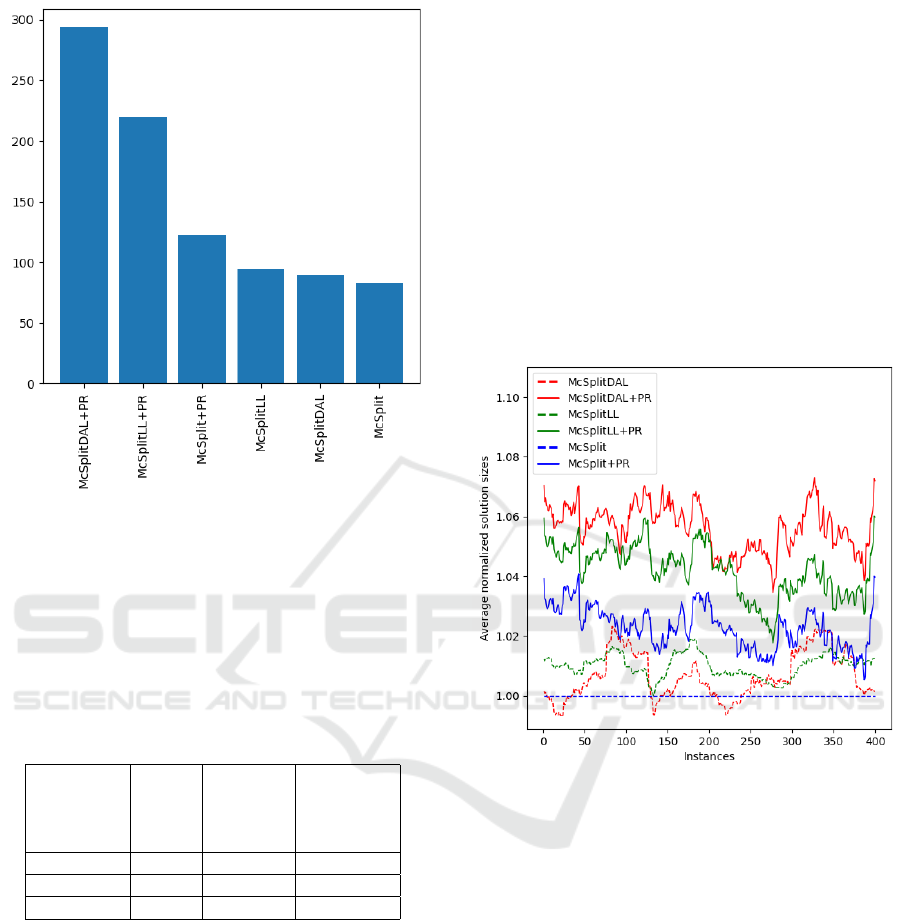
Figure 2: The histogram plots the number of times each

heuristic ﬁnds the MCS (i.e., the largest maximum com-

mon subgraph) on the 400 experiments. When a graph with

the same size is returned by more than one method, each

strategy is reported as a winner.

age of victories of all PR-improved strategies with re-

spect to each original method.

Table 1: Percentage of instances improved by the PR meth-

ods (columns) over the original methods (rows), without

breaking ties.

Heuristics

McSplit McSplitLL McSplitDAL

+ + +

PR PR PR

[%] [%] [%]

McSplit 64 72 77

McSplitLL 60 69 76

McSplitDAL 63 72 77

Figure 2 and Table 1 focus on the number of ex-

periments on which PageRank could return larger so-

lutions than the original algorithms. Overall, they

show that PR methods provide larger solutions for

most of cases. However, we can also compare the

size of the different solutions to understand the av-

erage improvements. To highlight the size of the re-

sults, we collected the size of the best solution found

by each algorithm for every graph pair. To account

for the natural variation in solution sizes between a

wide range of instances of different complexity, we

normalized all results with respect to the size of the

subgraph found by the original McSplit algorithm.

In Figure 3, we show the average performance of

our normalized heuristics. Due to the signiﬁcant dif-

ferences in solution sizes across instances, we plot a

circular rolling average with a window size of 50 to

better present the outcomes of our experiments. This

strategy implies that each point on the plot represents

the average normalized performance over a window

of 50 consecutive tests. Due to the normalization, the

original McSplit always returns solutions of size one,

whereas all other methods almost always return more

extensive solutions. Notably, PageRank demonstrates

a distinct advantage over the degree heuristic. More-

over, McSplitDAL+PR and McSplitLL+PR methods

consistently outperform their McSplitX counterparts

in any batch of 50 instances and when they fall be-

hind, they do not fall behind by a large amount.

Figure 3: A circular rolling average (with a window width

of 50 consecutive tests) of the sizes of the solutions obtained

by the McSplitX and McSpliX+PR algorithms on each in-

stance. All values are normalized with respect to the results

obtained by the original McSplit.

The heat-map in Figure 4 shows the relative per-

formance across all combinations of the algorithms.

For each method on the vertical axis, the results are

individually normalized with respect to the results of

the algorithm on the horizontal axis; then, all the nor-

malized values are averaged together.

From the map, we learn that McSplitDAL+PR ex-

hibits an average improvement of 6% over McSplit-

DAL, McSplitLL+PR yields solutions that are 4%

larger compared to McSplitLL, and McSplit+PR pro-

duces solutions 3% larger than McSplit. These re-

sults suggest that PageRank is an effective standalone

heuristic, providing even more signiﬁcant beneﬁts

when used as a tie-breaker on top of more complex

Reinforcement Learning rewards.

ICSOFT 2023 - 18th International Conference on Software Technologies

204

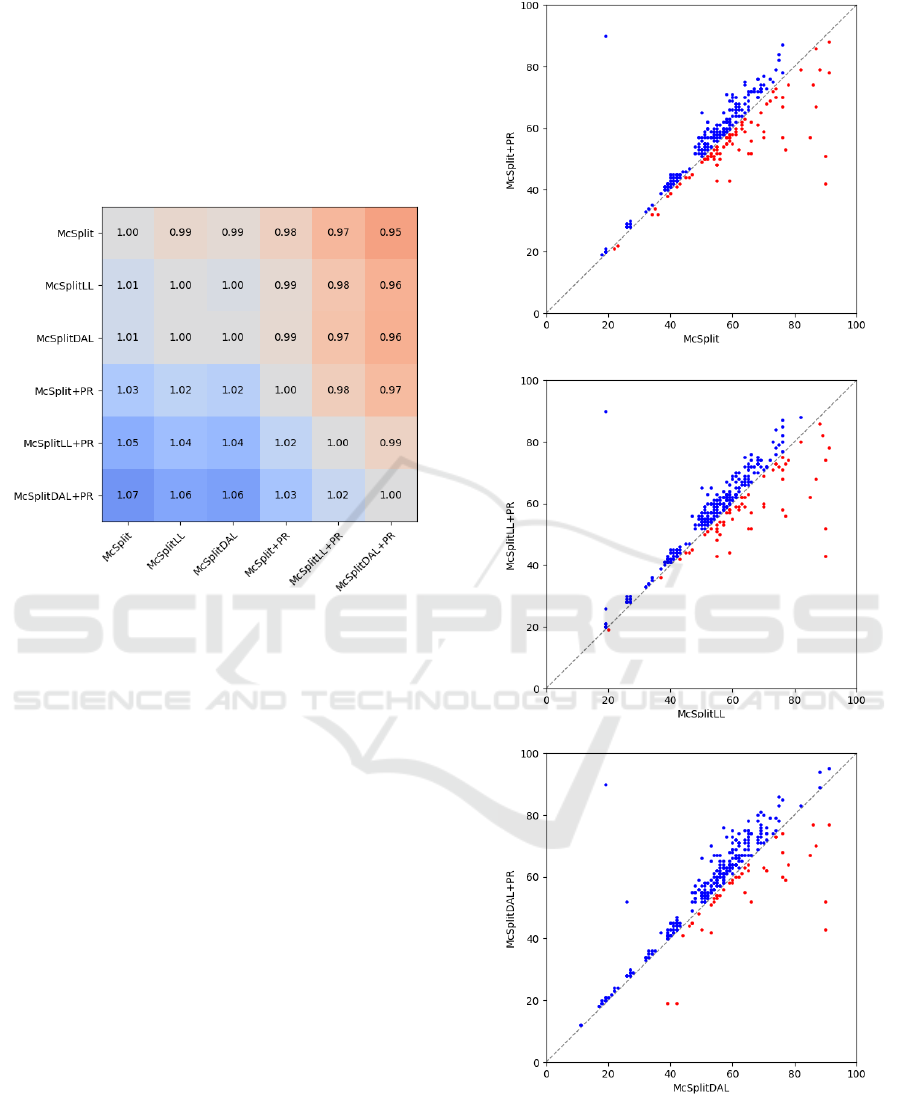
It has to be noticed that in our testing, the McSplit-

DAL policy is not always better than the McSplitLL,

unlike what was observed by Liu et al. (Liu et al.,

2022). This result is likely due to our different evalua-

tion methodologies. However, McSplitDAL+PR ben-

eﬁts from the PageRank heuristic, convincingly out-

performing both McSplitLL and McSplitLL+PR by

6% and 2%, respectively.

Figure 4: The relative performance of the McSplitX and

McSplitX+PR methods. For each row, we report the aver-

age improvement relative to the respective column. Darker

blue colors highlight the size improvements.

In Figure 5 we present a comprehensive com-

parison of the solution sizes achieved by each Mc-

SplitX+PR method and its corresponding McSplitX

counterpart. For each instance, a dot is reported to

show the size of the solutions found by the two al-

gorithms. By removing the need for the rolling aver-

age, this scatter plot offers a better view of the results

of the individual instances. Notably, the PageRank

heuristic is the winner in most cases, particularly in

the McSplitDAL+PR variant. Upon careful examina-

tion, it becomes evident that the average performance

of the McSplitX methods is inﬂuenced by a few out-

lier instances that exhibit exceptional results. How-

ever, in contrast, McSplitX+PR consistently demon-

strates improved performance across the entire range

of instances.

5 CONCLUSIONS AND FUTURE

WORKS

In this paper, we focus on solving the Maximum

Common Induced Subgraph problem. Starting from

(a)

(b)

(c)

Figure 5: The dispersion of the points above the main di-

agonal shows that McSplitX+PR ﬁnds more extensive solu-

tions in the vast majority of the cases.

a state-of-the-art algorithm called McSplit, and its

recent variants (namely McSplitLL, McSplitRL, and

A Web Scraping Algorithm to Improve the Computation of the Maximum Common Subgraph

205

McSplitDAL). we propose a family of Branch-and-

Bound algorithms called McSplitX+PR.

The original McSplit algorithm uses a node de-

gree heuristic to select the vertices of the graphs dur-

ing the recursive search. McSplitRL and its deriva-

tives use rewards obtained through Reinforcement

Learning, but still enforce the node degree to break

ties. We propose the McSplitX+PR algorithm family,

namely McSplit+PR, McSplitLL+PR, and McSplit-

DAL+PR, to replace the original node degree heuris-

tic with the ranking produced by the PageRank algo-

rithm. PageRank, famously known as the former al-

gorithm behind the Google search engine, generates

more effective node orderings compared to the de-

gree of vertices, as it prioritizes nodes that are easier

to reach across multiple hops rather than just in the

local neighborhood, effectively differentiating them

over more categories than the original heuristic.

Using publicly available graph pairs, we con-

ducted experiments on both the McSplitX+PR and

McSplitX families. We mainly focus on ﬁnding the

best solution within a limited time to simulate real-

world scenarios. Our results indicate that all Mc-

SplitX+PR algorithms consistently outperform their

McSplitX counterparts, with McSplitDAL+PR yield-

ing the most effective solutions than the other strate-

gies.

Among the possible future works, we would

like to mention the necessity of studying the multi-

threaded versions of the above tools. In this work,

this analysis has been limited by the fact that not all

the considered tools were initially implemented with

multi-threading capabilities. Consequently, one of

our targets is to improve the above heuristics obtain-

ing uniform scalability on multi-core architectures.

REFERENCES

Angione, F., Bernardi, P., Calabrese, A., Cardone, L., Nic-

coletti, A., Piumatti, D., Quer, S., Appello, D., Tan-

corre, V., and Ugioli, R. (2022). An innovative strat-

egy to quickly grade functional test programs. In 2022

IEEE International Test Conference (ITC), pages 355–

364.

Barrow, H. G. and Burstall, R. M. (1976). Subgraph Iso-

morphism, Matching Relational Structures and Maxi-

mal Cliques. Inf. Process. Lett., 4(4):83–84.

Brin, S. and Page, L. (1998). The anatomy of a large-scale

hypertextual web search engine. Computer Networks

and ISDN Systems, 30(1):107–117. Proceedings of the

Seventh International World Wide Web Conference.

Bron, C. and Kerbosch, J. (1973). Finding All Cliques of an

Undirected Graph (algorithm 457). Commun. ACM,

16(9):575–576.

Cardone, L. and Quer, S. (2023). The multi-maximum and

quasi-maximum common subgraph problem. Compu-

tation, 11(4).

Dalke, A. and Hastings, J. (2013). Fmcs: a novel algorithm

for the multiple mcs problem. Journal of cheminfor-

matics, 5(Suppl 1):O6.

Foggia, P., Sansone, C., and Vento, M. (2001). A database

of graphs for isomorphism and sub-graph isomor-

phism benchmarking. In -, page 176–187.

Levi, G. (1973). A note on the derivation of maximal com-

mon subgraphs of two directed or undirected graphs.

CALCOLO, 9(4):341–352.

Liu, Y., Li, C.-M., Jiang, H., and He, K. (2020). A learning

based branch and bound for maximum common sub-

graph related problems. Proceedings of the AAAI Con-

ference on Artiﬁcial Intelligence, 34(03):2392–2399.

Liu, Y., Zhao, J., Li, C.-M., Jiang, H., and He, K. (2022).

Hybrid learning with new value function for the max-

imum common subgraph problem.

Mart

ı, R. and Reinelt, G. (2022). Heuristic Methods, pages

27–57. Springer Berlin Heidelberg, Berlin, Heidel-

berg.

McCreesh, C., Ndiaye, S. N., Prosser, P., and Solnon, C.

(2016). Clique and constraint models for maximum

common (connected) subgraph problems. In Rueher,

M., editor, Principles and Practice of Constraint Pro-

gramming, pages 350–368, Cham. Springer Interna-

tional Publishing.

McCreesh, C., Prosser, P., and Trimble, J. (2017). A par-

titioning algorithm for maximum common subgraph

problems. In Proceedings of the Twenty-Sixth Inter-

national Joint Conference on Artiﬁcial Intelligence,

IJCAI-17, pages 712–719.

Michael Garey, D. S. J. (1979). Computers and Intractabil-

ity: A Guide to the Theory of NP-Completeness. W.

H. Freeman and Company, United States.

Milgram, S. (1967). The small world problem. Psychology

today, 2(1):60–67.

Park, Y. and Reeves, D. (2011). Deriving common malware

behavior through graph clustering. In Proceedings of

the 6th ACM Symposium on Information, Computer

and Communications Security, pages 497–502.

Quer, S., Marcelli, A., and Squillero, G. (2020). The

maximum common subgraph problem: A parallel and

multi-engine approach. Computation, 8(2).

Sch

oning, U. (1988). Graph isomorphism is in the low hi-

erarchy. Journal of Computer and System Sciences,

37(3):312–323.

Trimble, J. (2023). Partitioning algorithms for induced sub-

graph problems. PhD thesis, University of Glasgow.

Vismara, P. and Valery, B. (2008). Finding maximum com-

mon connected subgraphs using clique detection or

constraint satisfaction algorithms. In Modelling, Com-

putation and Optimization in Information Systems

and Management Sciences: Second International

Conference MCO 2008, Metz, France-Luxembourg,

September 8-10, 2008. Proceedings, pages 358–368.

Springer.

Zhou, J., He, K., Zheng, J., Li, C.-M., and Liu, Y. (2022).

A strengthened branch and bound algorithm for the

maximum common (connected) subgraph problem.

Zimmermann, T. and Nagappan, N. (2007). Predicting sub-

system failures using dependency graph complexities.

In The 18th IEEE International Symposium on Soft-

ware Reliability (ISSRE ’07), pages 227–236.

ICSOFT 2023 - 18th International Conference on Software Technologies

206