Union k-Fold Feature Selection on Microarray Data

Artur J. Ferreira

1,3 a

and M

ario A. T. Figueiredo

2,3 b

ISEL, Instituto Superior de Engenharia de Lisboa, Instituto Polit

ecnico de Lisboa, Portugal

IST, Instituto Superior T

ecnico, Universidade de Lisboa, Portugal

Instituto de Telecomunicac¸

oes, Lisboa, Portugal

ﬁ

Keywords:

Cancer Detection, Classiﬁcation, Feature Selection, Filter, Gene Expression, Microarray Data, Union.

Abstract:

Cancer detection from microarray data is an important problem to be handled by machine learning techniques.

This type of data poses many challenges to machine learning techniques, namely because it usually has large

number of features (genes) and small number of instances (patients). Moreover, it is important to characterize

which genes are the most important for a given classiﬁcation task, providing explainability on the classiﬁca-

tion. In this paper, we propose a feature selection approach for microarray data, which is an extension of the

recently proposed k-fold feature selection algorithm. We propose performing the union of the feature sub-

spaces found independently by two feature selection ﬁlters, which have been proven to be adequate for this

type of data, individually. The experimental results show that the union of the subsets of features found by

each ﬁlter, in some cases, produces better results than the use of each individual ﬁlter, yielding human man-

ageable subsets of features.

1 INTRODUCTION

Datasets with large numbers of features and relatively

smaller numbers of instances pose challenges for ma-

chine learning methods. It is often the case that many

features are irrelevant or redundant for the classiﬁca-

tion task at hand (Yu et al., 2004; Peng et al., 2005).

This may be specially harmful in the presence of rel-

atively small training sets, since the irrelevance and

redundancy are harder to assess. To deal with such

datasets, feature selection (FS) (Hastie et al., 2009;

Guyon et al., 2006; Escolano et al., 2009) methods

have been proposed with the goal of obtaining re-

duced representations of the datasets that are more ad-

equate for learning, targeting the curse of dimension-

ality problem, often allowing the learning algorithms

to obtain better performing classiﬁers.

In the last decades, there has been a great in-

terest on automated cancer detection from microar-

ray data, also known as gene expression data (Guyon

et al., 2002; Statnikov et al., 2005; D

ıaz-Uriarte and

de Andr

es, 2006; Lee, 2008; Meyer et al., 2008;

Bolon-Canedo et al., 2011; Fang et al., 2011; Lazar

et al., 2012; Manikandan and Abirami, 2018; Almu-

https://orcid.org/0000-0002-6508-0932

https://orcid.org/0000-0002-0970-7745

gren and Alshamlan, 2019; Consiglio et al., 2021).

The nature of gene expression data (many features,

small samples) is suited to the use of FS techniques.

Statnikov et al. (2005) compared multi-category

support vector machines (MC-SVM) against k-

nearest neighbors (KNN), multilayer perceptrons

(MLP), and probabilistic neural networks (PNN).

The MC-SVM classiﬁer outperformed the other tech-

niques, while FS signiﬁcantly improves the classiﬁca-

tion accuracy of all algorithms. An FS ﬁlter for mi-

croarray data proposed by Meyer et al. (2008) uses

double input symmetrical relevance (DISR) to assess

variable complementarity. Their experimental results

show that the DISR criterion is competitive with ex-

isting FS ﬁlters. An approach based on monotone de-

pendence (MD) was proposed by Bolon-Canedo et al.

(2011) to perform supervised FS using the MD cri-

terion to estimate the mutual information (MI) be-

tween features and class labels. In some microarray

datasets, the MD criterion is able to select informative

features. Fang et al. (2011) proposed an approach that

combines gene expression with other biological data,

yielding a good performance in identifying the most

informative genes (features).

The main drawback common to existing ap-

proaches is the difﬁculty to accurately handle multi-

class microarray datasets, due to the scarcity of data.

540

Ferreira, A. and Figueiredo, M.

Union k-Fold Feature Selection on Microarray Data.

DOI: 10.5220/0012135800003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 540-547

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

For a recent review on microarray data classiﬁcation,

see the work by Li et al. (2018); S

anchez-Maro

et al. (2019) and the many references therein.

In this paper, we propose a supervised FS ap-

proach suited for microarray datasets, for binary and

multi-class problems. The remainder of this paper

has the following structure. In Section 2, we analyze

some aspects regarding microarray data and feature

selection techniques. Our approach is described in

Section 3. The experimental evaluation is reported in

Section 4. Section 5 concludes the paper with some

remarks and directions of future work.

2 RELATED WORK

In this section, we review some details on microar-

ray data (Subsection 2.1). A brief review of FS tech-

niques is provided in Subsection 2.2. The FS ﬁlters

used in this work are described in Subsection 2.3.

2.1 Microarray Data

DNA microarray data (Simon et al., 2003) is com-

posed by an array of gene expression proﬁles, with

measurements of relative abundance of mRNA cor-

responding to each gene (Baldi and Hatﬁeld, 2002).

Gene expression represents the activation level of

each gene at a given point in time, identifying the

genes expressed by a cell. A DNA microarray has

the following characteristics:

• It is composed by a solid surface with thousands

of spots arranged in columns and rows.

• Each spot on the microarray evaluates only one

gene with multiple strands of the same DNA.

• Each spot location and its respective DNA se-

quence is recorded in a database.

DNA microarrays can identify dissimilarities between

cancer and healthy cells, by identifying which genes

in a cancer cell are being expressed, but not in a

healthy cell. There are different methods to extract

this type of data, such as reading from a ﬂuorescent

signal or a radioactive signal. In either case, the ac-

quisition process leads to the presence of noise in

the data. Figure 1 depicts the process of generating

a dataset from the DNA microarray technique. The

datasets considered in this work are obtained with this

process. The red color on a spot indicates the higher

production of mRNA in the cancer cell, as compared

to the healthy cell. On the other hand, the green

color speciﬁes the higher production of mRNA in the

healthy cell as compared to the cancer cell. How-

ever, a yellow spot suggests that the gene is expressed

Figure 1: Dataset generation from DNA microarray.

equally in both cells and therefore, they are not rel-

evant as the cause of the disease, because when the

healthy cell becomes cancerous its activity does not

undergo a change.

Some studies on the classiﬁcation of tissues have

shown that gene expression data is very relevant for

cancer diagnosis and prediction, thus leading to the

quest for solving a major public health problem.

Moreover, since we are dealing with large arrays of

gene expression values, it is difﬁcult to control the

correctness of the values read for each gene; this leads

to the presence of many redundant and irrelevant fea-

tures (Baldi and Hatﬁeld, 2002). From a machine

learning (ML) perspective, we typically have a super-

vised problem, in which the patterns are composed

by the gene expression proﬁles whereas the class la-

bels indicate a particular type of tumor or its ab-

sence. Typically, we have multi-class problems, due

to the existing different tumor types. The analysis of

these expression patterns is of particular importance

to classify tumor types, and it has been well stud-

ied in the literature of ML and bionformatics (Baldi

and Brunak, 2001). However, we typically have fairly

small sample sizes whereas the number of genes in-

volved is on the order of thousands. This is a high-

dimensional data problem, with curse of dimension-

ality issues posing challenges to ML techniques.

2.2 Concepts About Feature Selection

In this paper, we denote a dataset by X = {x

,... ,x

represented as a n × d matrix, in which the rows

hold the n patterns and the columns are the d fea-

tures. Each pattern x

is a d−dimensional vector, with

i ∈ {1, .. ., n}. We denote each feature vector (col-

umn of X) as X

, with j ∈ {1, .. ., d}. The number of

distinct class labels is C, with c

∈ {1,. .. ,C} denot-

ing the class of pattern x

and y = {c

,. .. ,c

} is the

set of class labels corresponding to the n patterns.

The use of FS techniques typically improves the

performance of a classiﬁer learnt from data, allow-

ing faster training than with the original data. Thus,

FS mitigates the effects of the curse of dimensional-

Union k-Fold Feature Selection on Microarray Data

541

ity, which is often the case with microarray data. In

this paper, we consider FS ﬁlter algorithms (Guyon

et al., 2006), which evaluate the goodness of sub-

sets of features using characteristics of that subset,

without the use of any subsequent learning algorithm

(they are agnostic in this sense). Filters are the sim-

plest and fastest FS approach, being the only possible

type of technique for high-dimensional data, in which

the embedded, wrapper, and hybrid approaches are

time-consuming and prohibitive (Hastie et al., 2009;

Guyon et al., 2006; Escolano et al., 2009).

Some FS ﬁlters are based on the relevance-

redundancy (RR) framework (Yu and Liu, 2003),

which assumes that a dataset is composed by four

subsets: (I) irrelevant features; (II) weakly relevant

and redundant features; (III) weakly relevant and non-

redundant features; (IV) strongly relevant features, as

depicted in Figure 2. The FS methods aim to identify

the features that compose parts (III) and (IV).

Figure 2: The relevance-redundancy framework for feature

selection regarding the existing subsets of features as pro-

posed by Yu and Liu (2003).

Recent surveys on FS techniques are provided

by Remeseiro and Bolon-Canedo (2019), Pudji-

hartono et al. (2022), and Dhal and Azad (2022). The

use of FS techniques for microarray data and related

data is surveyed in (Lazar et al., 2012; Manikandan

and Abirami, 2018; Almugren and Alshamlan, 2019;

Arowolo et al., 2021).

2.3 Feature Selection Filters

Some FS methods are based purely on the relevance

of the features. One of such methods is the Fisher

ratio (Fisher, 1936), also known as Fisher score. For

the i-th feature, the Fisher score is deﬁned as

FiR



(−1)

− X

(1)



var(X

)

(−1)

+ var(X

)

(1)

, (1)

where X

(−1)

, X

(1)

, var(X

)

(−1)

, and var(X

)

(1)

, are the

sample means and variances of feature X

, for the pat-

terns of each class. This ratio measures how well each

feature alone separates the two classes (Fisher, 1936).

It has been found that it serves well as a relevance cri-

terion for FS problems. In the multi-class case, C > 2,

the ratio for feature X

can be generalized (Duda et al.,

2001; Zhao et al., 2010) as

FiR

∑

j=1

(y)



( j)

− X



∑

j=1

(y)

var



( j)



, (2)

where n

(y)

is the number of occurrences of class j

in the n-length class label vector y, and X

( j)

denotes

the sample mean of the values of X

whose class la-

bel is j; ﬁnally, X

is the sample mean of feature X

Among many other applications, the Fisher ratio has

been used successfully with microarray data, as re-

ported by Furey et al. (2000). When using Fisher ratio

for FS, we simply keep the top-rank features.

The fast correlation-based ﬁlter (FCBF), pro-

posed by Yu and Liu (2003, 2004), follows the

RR framework by computing the feature-class and

feature-feature correlations. It starts by selecting a

set of features that is highly correlated with the class,

with a correlation value above a threshold. This cor-

relation is assessed by the symmetrical uncertainty

(SU) (Yu and Liu, 2003) measure, deﬁned as

SU(X

) =

2I(X

)

H(X

) + H(X

)

, (3)

where H(.) denotes the Shannon entropy and I(.)

denotes the mutual information (MI) (Cover and

Thomas, 2006). The SU is zero for independent

random variables and equal to one for deterministi-

cally dependent random variables. The ﬁrst step of

FCBF identiﬁes the predominant features, which are

the ones with higher correlation with the class. In the

second step, a redundancy detection analysis ﬁnds re-

dundant features among the predominant ones. The

set of redundant features is further processed to re-

move the redundant features and to keep the ones

most relevant to the class.

Recently, the k-fold feature selection (KFFS) ﬁlter

was proposed by Ferreira and Figueiredo (2023), as

described in Algorithm 1.

The key idea of KFFS is that the discriminative

power of a feature is proportional to the number of

times it is chosen, on the k-folds over the training data,

by the generic unsupervised or supervised FS ﬁlter.

KFFS has two key parameters: the number of folds k

to sample the training data and the threshold T

to as-

sess the percentage of choice of a feature by the ﬁlter

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

542

Algorithm 1: k-Fold Feature Selection (KFFS) for unsupervised or supervised FS.

Require: X : n × d matrix, n patterns of a d-dimensional dataset.

@ f ilter : a FS ﬁlter (unsupervised or supervised).

k : an integer stating the number of folds (k ∈ {2,. ..,n}).

: a threshold (percentage) to chose the number of features.

y : n× 1 class label vector (necessary only in case of a FS supervised ﬁlter).

Ensure: idx: m−dimensional vector with the indexes of the selected features.

1: Allocate the feature counter vector (FCV), with dimensions 1 × d, such that each position refers to a speciﬁc feature.

2: Initialize FCV

= 0, with i ∈ {0, .. .,d − 1}.

3: Compute the k data folds in the dataset (different splits into training and test data).

4: For each fold, apply @ f ilter on the training data and update FCV

with the number of times @ f ilter selects feature i.

5: After the k data folds are processed, convert FCV to percentage: FCV P ← FCV /k.

6: Keep the indexes of the features that have been selected at least T

times (expressed in percentage), idx ← FCV P ≥ T

7: Return idx (the vector with the indexes of the selected features that have been selected at least T

times).

on the k-folds. Figure 3 depicts the input and output

parameters of the KFFS algorithm, using a generic FS

ﬁlter denoted as @ filter, which is applied on k-folds

of the input data.

Figure 3: The k-fold feature selection (KFFS) algo-

rithm (Ferreira and Figueiredo, 2023).

3 PROPOSED APPROACH

In this paper, we propose to extend the KFFS algo-

rithm in the following way:

• To use more than one ﬁlter. We provide KFFS

with two FS ﬁlters. These algorithms should fol-

low different approaches in order to select dif-

ferent subsets of relevant and non-redundant fea-

tures, that is, they are expected to focus on differ-

ent parts of the input feature space.

• We apply each FS algorithm to the same data par-

titions and then combine the output indexes of the

different ﬁlters, by performing a union of the in-

dexes of the features selected by each ﬁlter. For

instance, say that one FS ﬁlter selects features

{10,13, 27,34} and the other FS ﬁlter selects fea-

tures {12,27, 30,34}, the resulting subset of fea-

tures will be {10,12, 13,27, 30,34}.

The key idea of this approach which we name union

k-fold feature selection (UKFFS), is that by using di-

verse ﬁlters, we focus on different parts of the input

feature space. Their union should provide an aggre-

gated selection of the input feature space (correspond-

ing to parts III and IV in Figure 2). In this work, we

consider the Fisher and FCBF FS ﬁlters, mentioned in

Subsection 2.3. The Fisher ﬁlter is a relevance-only

based method whereas the FCBF algorithm performs

a relevance-redundancy analysis. For the Fisher algo-

rithm, we select the top m most relevant features as

follows:

• Compute the Fisher ratio, FiR

, for each feature

, i ∈ {1,.. ., d}, given by equation (1) for C = 2

or by equation (2), for C > 2.

• Sort the values of the Fisher ratio by decreasing

order.

• Compute the cumulative and normalized rele-

vance values, leading to an increasing function

whose values range to a maximum of 1.

• Keep the ﬁrst top relevant m features, holding, say

90% of the accumulated relevance given by FiR

On the FCBF algorithm, we consider the implemen-

tation with its default parameter values. We evalu-

ate our proposal with microarray data. On the same

data, the use of the Fisher ratio usually yields subsets

with more features than those attained with the use of

FCBF, due to the redundancy elimination procedure

performed by the later.

4 EXPERIMENTAL EVALUATION

The proposed method is now evaluated with pub-

lic domain datasets. Subsection 4.1 describes the

datasets and the evaluation metric. In Subsection 4.2,

we check for the sensitivity of a changing thresh-

old on KFFS, for some datasets. In Subsection 4.3,

we report experimental results with all the available

datasets. Finally, Subsection 4.4 provides a discus-

sion of the experimental evaluation.

Union k-Fold Feature Selection on Microarray Data

543

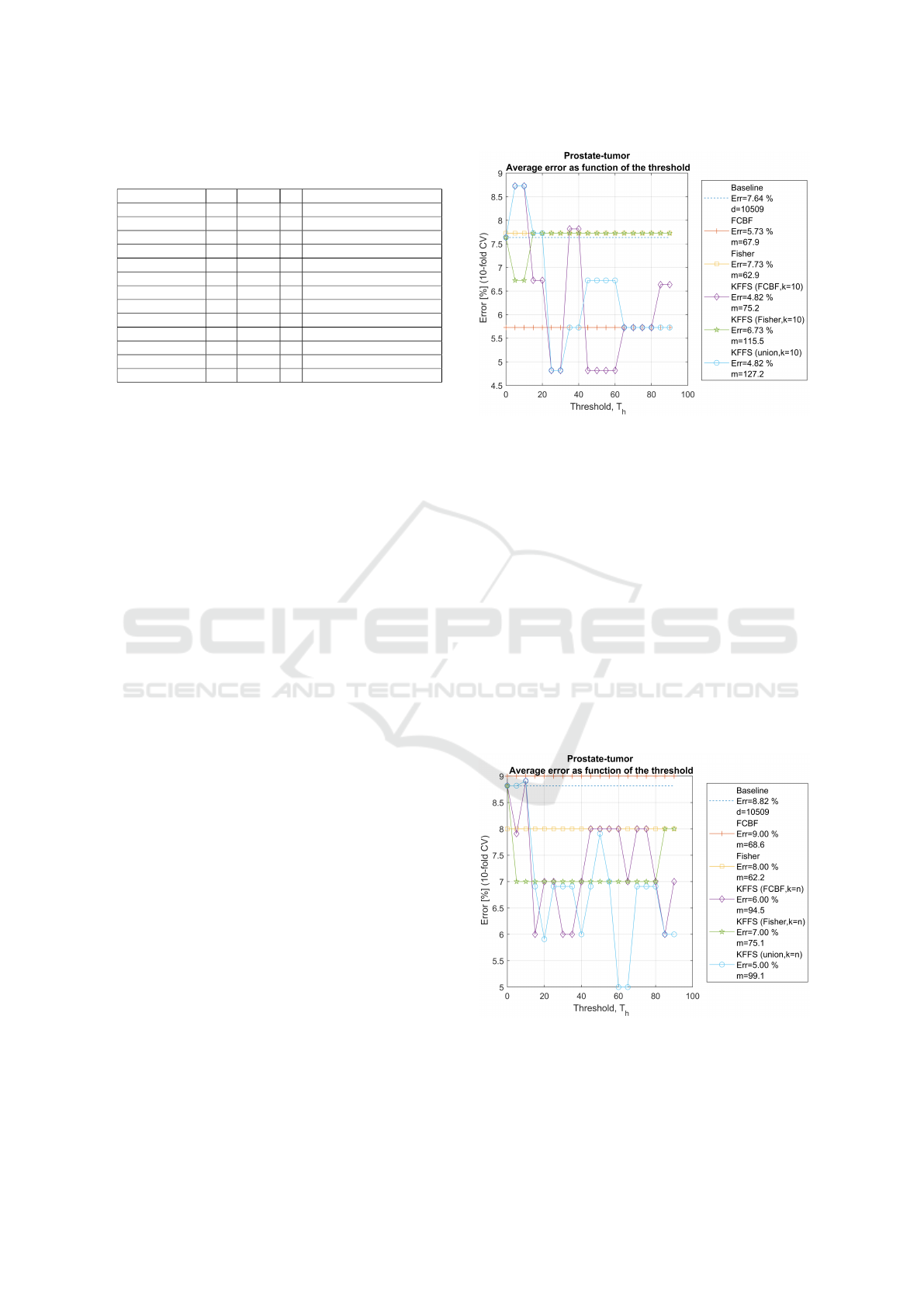
Table 1: Microarray datasets used in the experiments, with

n instances, d features, and C classes.

Name n d C Problem

Brain-Tumor-1 90 5920 5 Cancer detection

Brain-Tumor-2 50 10367 4 Cancer detection

CLL-SUB-11 111 11340 3 Leukemia detection

Colon 62 2000 2 Cancer detection

DLBCL 77 5469 2 Detect B-cell malignancies

GLI-85 85 22283 2 Glioma detection

Leukemia 72 7129 2 Leukemia detection

Leukemia-1 72 5328 3 Leukemia detection

Leukemia-2 72 11226 3 Leukemia detection

Lymphoma 96 4026 9 Lymphoma detection

Prostate-Tumor 102 10509 2 Prostate tumor detection

SMK-CAN-187 187 19993 2 Lung cancer detection

SRBCT 83 2308 4 Cancer detection

4.1 Datasets, Tools, and Metrics

Table 1 summarizes the microarray datasets (Zhu

et al., 2007) used in this work, available online at

https://csse.szu.edu.cn/staff/zhuzx/Datasets.html and

at the Arizona State University (ASU) reposi-

tory (Zhao et al., 2010). These datasets have n ≪

d, leading to challenging situations for ML tech-

niques (Bishop, 1995), which are the ones that we

intend to address in this paper. We use the FCBF im-

plementation of the Arizona State University (ASU)

repository, with its default parameters. The linear

support vector machines (SVM) and random forest

(RF) classiﬁers from Waikato environment for knowl-

edge analysis (WEKA) are considered in the experi-

ments. SVM is considered to be one of the best per-

forming classiﬁers for this type of data. The RF clas-

siﬁer is known to achieve adequate results for many

problems. The evaluation metric is the test-set error

rate, with a 10-fold cross-validation procedure. We

also analyze the size of the subset of features for each

FS ﬁlter, denoted as m.

4.2 Individual Filters and Their Union

First, we analyze the effect of changing the thresh-

old T

and k parameters for KFFS, on some datasets.

In Figure 4, we assess the test set error rate of the

SVM classiﬁer with 10-fold cross-validation (CV).

As FS ﬁlters, we consider: the standard use of the

FCBF and Fisher algorithms (mentioned in Subsec-

tion 2.3); the use of FCBF, Fisher and their union

on the KFFS algorithm denoted as KFFS(union). We

set the threshold T

∈ {0, .. ., 90} and set k = 10, for

the Prostate-Tumor dataset. Notice that the baseline,

FCBF, and Fisher methods results are represented as

horizontal lines, since their results do not depend on

the threshold. The KFFS(FCBF), KFFS(Fisher), and

KFFS(union) algorithms result is a function of the

threshold; for these algorithms, we display the low-

Figure 4: Test set error rate of the SVM classiﬁer with 10-

fold cross-validation (CV), with varying threshold, T

. We

use FS by FCBF, Fisher, KFFS(FCBF), KFFS(Fisher), and

KFFS(FCBF,Fisher), with k = 10 for KFFS on the Prostate-

Tumor dataset. The average number of selected features by

these methods is denoted as m.

est error rate in the legend of the ﬁgure.

We observe that the lowest error rate of 4.82% is

attained by KFFS(FCBF) and KFFS(union). All FS

methods achieve a considerable reduction on the size

of the subsets of features.

In Figure 5, we have the experimental results for

the same dataset, now with k = n for KFFS. In this

case, the union of FCBF and Fisher with KFFS attains

the best results, using T

∈ {60,65}.

Figures 6 and 7 show the experimental results for

the Colon and the Brain-Tumor-2 datasets. For both

datasets, the use of KFFS yields a decrease on the er-

Figure 5: Test set error rate of the SVM classiﬁer

with 10-fold CV, with varying threshold, T

. We use

FS by FCBF, Fisher, KFFS(FCBF), KFFS(Fisher), and

KFFS(FCBF,Fisher), with k = n for KFFS on the Prostate-

Tumor dataset. The average number of selected features by

these methods is denoted as m.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

544

Figure 6: Test set error rate of the SVM classiﬁer

with 10-fold CV, with varying threshold, T

. We use

FS by FCBF, Fisher, KFFS(FCBF), KFFS(Fisher), and

KFFS(FCBF,Fisher), with k = n for KFFS on the Colon

dataset. The average number of selected features by these

methods is denoted as m.

Figure 7: Test set error rate of the SVM classiﬁer

with 10-fold CV, with varying threshold, T

. We use

FS by FCBF, Fisher, KFFS(FCBF), KFFS(Fisher), and

KFFS(FCBF,Fisher), with k = n for KFFS on the Brain-

Tumor-2 dataset. The average number of selected features

by these methods is denoted as m.

ror rate, as compared to the baseline and the standard

use of the FS ﬁlters.

4.3 Evaluation with the Best Threshold

We now report the experimental results with all the

datasets, setting k = n. Table 2 presents, for each

dataset, the error rate of the linear SVM classiﬁer for

the baseline case (no FS) and for FCBF and Fisher

standard simple use. We also apply KFFS using

FCBF, KFFS using Fisher, and KFFS performing the

union of FCBF and Fisher, with a different threshold

for each dataset. For each KFFS ﬁlter, we display

the results with the threshold that yields the best re-

sults. Notice that the value of this optimal threshold

does not inﬂuence the results of the FCBF and Fisher

standard simple use. Table 3 reports the experimental

results of a similar test, with the RF classiﬁer. The

results in Table 2 and Table 3, show that in many sit-

uations the use of KFFS provides improvement, as

compared to the results of the individual FCBF and

Fisher ﬁlters. In many cases, the union of FCBF and

Fisher, under the KFFS framework attains the best re-

sults. All FS algorithms attain a signiﬁcant decrease

on the dimensionality of the data, usually improving

the classiﬁcation accuracy.

We have carried out the Friedman statistical sig-

niﬁcance test for the error rates reported in Table 2

and Table 3. The corresponding p-values are p

4.1865 × 10

−8

and p

= 2.7103 × 10

−5

, respectively,

yielding statistical signiﬁcance since these values are

below 0.05.

4.4 Discussion of the Results

The experimental evaluation on microarray data has

shown that KFFS using one FS ﬁlter or two ﬁlters,

usually yields better results than the standard use of

the individual ﬁlters. By appropriately setting the

threshold parameter, we attain lower error rate with

fewer features than using standard FS ﬁlters, at the

expense of computation time. For each dataset, there

is the need to establish an adequate threshold value to

achieve the best results. Regarding the k parameter of

KFFS, we have found that larger values of k usually

provide better results, especially on the multi-class

datasets with a few samples per class. The proposed

approach ﬁnds subsets of features with low general-

ization error, small enough to be interpreted and ana-

lyzed by humans (e.g. a medical doctor). From these

experimental evaluation results, we recommend to set

∈ {40,. .. ,60} and k = n, as a starting (default)

conﬁguration for the KFFS algorithm using one or

more ﬁlters with microarray data.

5 CONCLUSIONS

Cancer detection from microarray data is an important

and demanding task for machine learning tools. The

large number of genes poses many problems to ma-

chine learning methods, which are faced with a high-

dimensional space of features and a small number of

instances. Moreover, in some cases we have multi-

class problems with a few samples per class.

Union k-Fold Feature Selection on Microarray Data

545

Table 2: The average number of features (m) and the average test set error rate (Err, %) with the linear SVM classiﬁer with

10-fold CV, for different FS methods with the best threshold T

value for KFFS, on each dataset. For KFFS, we set k = n.

The best result (lower Err with fewer features, m) is in bold face.

Baseline SVM FCBF Fisher KFFS (FCBF) KFFS (Fisher) KFFS (Union)

Dataset d Err m Err m Err m Err T

m Err T

Brain-Tumor-1 5920 11.11 110.6 14.44 90.3 14.44 191.7 11.11 8 5920 11.11 0 143.9 11.11 75

Brain-Tumor-2 10367 22.00 70.3 22.00 83.7 24.00 184.1 16.00 6 90.7 18.00 20 176.8 16.00 20

CLL-SUB-11 11340 21.74 74.7 24.47 97.6 47.05 37.7 17.20 84 11340 21.74 0 120.3 19.02 90

Colon 2000 19.05 14.6 17.62 40.5 12.86 17.4 12.86 27 38.7 11.19 47 45.9 12.86 47

DLBCL 5469 2.68 61.3 3.93 49.6 4.11 44.1 1.25 75 46.5 2.68 60 81.0 0.00 75

GLI-85 22283 9.17 125.3 11.67 77.2 12.92 334.6 9.17 3 22283 9.17 0 399.0 9.17 3

Leukemia 7129 1.43 45.8 2.68 76.7 4.11 7129 1.43 0 7129 1.43 0 7129 1.43 0

Leukemia-1 5327 2.68 49.9 8.04 89.2 3.93 5327 2.68 0 5327 2.68 0 5327 2.68 0

Leukemia-2 11225 3.93 76.9 2.68 96.0 5.36 184.0 1.43 4 120.9 2.68 6 152.2 1.25 45

Lymphoma 4026 4.33 252 4.33 66.8 9.44 157.1 4.33 80 4026 4.33 0 204.6 4.33 80

Prostate-Tumor 10509 6.82 67.5 7.73 61.3 5.91 34.8 5.73 85 66.5 4.82 17 75.8 3.82 88

SMK-CAN-187 19993 26.73 54.6 31.05 22.6 33.65 19993 26.73 0 19993 26.73 0 19993 26.73 0

SRBCT 2308 0.00 72.7 1.25 87.3 0.00 46.7 0.00 85 78.1 0.00 90 99.3 0.00 90

Average 9068.9 10.13 82.7 11.68 72.2 13.68 2590.8 8.46 – 5881.5 8.97 – 2611.4 8.34 –

Table 3: The average number of features (m) and the average test set error rate (Err, %) with the RF classiﬁer with 10-fold

CV, for different FS methods with the best threshold T

value for KFFS, on each dataset. For KFFS, we set k = n. The best

result (lower Err with fewer features, m) is in bold face.

Baseline RF FCBF Fisher KFFS (FCBF) KFFS (Fisher) KFFS (Union)

Dataset d Err m Err m Err m Err T

m Err T

Brain-Tumor-1 5920 13.33 105.4 16.67 90.4 16.67 5920 13.33 0 5920 13.33 0 123.8 13.33 83

Brain-Tumor-2 10367 32.00 68.8 34.00 83.7 32.00 43.2 26.00 53 95.5 28.00 15 623.7 26.00 2

CLL-SUB-11 11340 18.94 74.1 24.47 97.6 41.29 11340 18.94 0 11340 18.94 0 500.7 18.94 1

Colon 2000 17.86 14.0 21.43 39.9 14.52 58.5 16.19 1 31.5 16.19 90 34.1 12.86 90

DLBCL 5469 9.29 62.2 9.11 49 7.86 99.5 5.18 10 44.6 6.61 71 60.0 7.86 90

GLI-85 22283 9.17 125.3 10.28 77.5 14.03 22283 9.17 0 150.0 6.81 1 172.6 7.92 44

Leukemia 7129 8.39 48.9 6.96 76.2 6.96 16.3 6.96 90 123.8 5.71 1 277 7.14 1

Leukemia-1 5327 6.96 49.2 12.50 88.8 8.39 5327 6.96 0 5327 6.96 0 5327 6.96 0

Leukemia-2 11225 8.39 78.8 12.50 96.0 6.79 11225 8.39 0 84.9 8.21 89 231.5 8.39 9

Lymphoma 4026 18.00 251.2 17.00 66.7 13.67 319.7 15.00 18 59.5 12.44 87 236.1 13.89 71

Prostate-Tumor 10509 8.91 65.8 6.91 61.0 7.91 33.0 5.91 89 55.5 6.91 90 77.8 5.91 89

SMK-CAN-187 19993 27.22 51 35.18 22.7 32.05 19993 27.22 0 19993 27.22 0 19993 27.22 0

SRBCT 2308 3.47 71.9 7.08 87.0 3.47 2308 3.47 0 2308 3.47 0 198.1 3.47 4

Average 9068.9 13.99 82.1 16.47 72.0 15.82 6074.3 12.52 – 3502.6 12.37 – 2142.7 12.30 –

To achieve adequate results on this type of data,

one must resort to dimensionality reduction tech-

niques. This reduction should be performed in such

a way that the number of resulting features is small

enough to be interpreted by humans, to analyze the

expressed genes. In this work, we have addressed

this problem, by proposing a strategy to combine and

perform an union of ﬁlters, under the recently pro-

posed KFFS framework. We have found that, in most

cases, the union of the feature subspaces found by

each method yields a resulting feature subspace with

better classiﬁcation performance, as compared to the

use of the individual ﬁlter, regardless if it is applied

under the KFFS framework. The KFFS union strategy

yields feature subsets with human manageable size,

that is, they can be analyzed by clinical experts.

As future work, we will ﬁne tune the parameters of

the method for each dataset, individually. We aim to

ﬁnd the best pair of parameters for each dataset and to

explore different combinations of two or more well-

known feature selection ﬁlters. We may also consider

other types of data rather than microarray data.

REFERENCES

Almugren, N. and Alshamlan, H. (2019). A survey on hy-

brid feature selection methods in microarray gene ex-

pression data for cancer classiﬁcation. IEEE Access,

7:78533–78548.

Arowolo, M., Adebiyi, M., Aremu, C., and Adebiyi, A.

(2021). A survey of dimension reduction and classi-

ﬁcation methods for RNA-Seq data on malaria vector.

Journal of Big Data, 8(50).

Baldi, P. and Brunak, S. (2001). Bioinformatics: the ma-

chine learning approach. MIT Press.

Baldi, P. and Hatﬁeld, G. (2002). DNA microarrays and

gene expression. Cambridge University Press.

Bishop, C. (1995). Neural Networks for Pattern Recogni-

tion. Oxford University Press.

Bolon-Canedo, V., Seth, S., Sanchez-Marono, N., Alonso-

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

546

Betanzos, A., and Principe, J. (2011). Statistical de-

pendence measure for feature selection in microar-

ray datasets. In 19th Europ. Symp. on Art. Neural

Networks-ESANN 011, pages 23–28, Belgium.

Consiglio, A., Casalino, G., Castellano, G., Grillo, G., Per-

lino, E., Vessio, G., and Licciulli, F. (2021). Explain-

ing ovarian cancer gene expression proﬁles with fuzzy

rules and genetic algorithms. Electronics, 10(375).

Cover, T. and Thomas, J. (2006). Elements of information

theory. John Wiley & Sons, second edition.

ıaz-Uriarte, R. and de Andr

es, S. A. (2006). Gene selec-

tion and classiﬁcation of microarray data using ran-

dom forest. BMC Bioinformatics, 7:3.

Dhal, P. and Azad, C. (2022). A comprehensive survey on

feature selection in the various ﬁelds of machine learn-

ing. Applied Intelligence, 52(4):4543–45810.

Duda, R., Hart, P., and Stork, D. (2001). Pattern classiﬁca-

tion. John Wiley & Sons, second edition.

Escolano, F., Suau, P., and Bonev, B. (2009). Information

Theory in Computer Vision and Pattern Recognition.

Springer.

Fang, O., Mustapha, N., and Sulaiman, N. (2011). Inte-

grative gene selection for classiﬁcation of microarray

data. Computer and Information Science, 4(2):55–63.

Ferreira, A. and Figueiredo, M. (2023). Leveraging explain-

ability with k-fold feature selection. In 12th Inter-

national Conference on Pattern Recognition Applica-

tions and Methods (ICPRAM), pages 458–465.

Fisher, R. (1936). The use of multiple measurements in

taxonomic problems. Annals of Eugenics, 7:179–188.

Furey, T., Cristianini, N., Duffy, N., Bednarski, D., Schum-

mer, M., and Haussler, D. (2000). Support vector

machine classiﬁcation and validation of cancer tissue

samples using microarray expression data. Bioinfor-

matics, 16(10).

Guyon, I., Gunn, S., Nikravesh, M., and Zadeh, L.

(2006). Feature extraction, foundations and applica-

tions. Springer.

Guyon, I., Weston, J., and Barnhill, S. (2002). Gene se-

lection for cancer classiﬁcation using support vector

machines. Machine Learning, 46:389–422.

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The El-

ements of Statistical Learning. Springer, 2nd edition.

Lazar, C., Taminau, J., Meganck, S., Steenhoff, D., Coletta,

A., Molter, C., de Schaetzen, V., Duque, R., Bersini,

H., and Now

e, A. (2012). A survey on ﬁlter techniques

for feature selection in gene expression microarray

analysis. IEEE/ACM Transactions on Computational

Biology and Bioinformatics, 9:1106–1119.

Lee, Z. (2008). An integrated algorithm for gene selec-

tion and classiﬁcation applied to microarray data of

ovarian cancer. Artiﬁcial Intelligence in Medicine,

42(1):81 – 93.

Li, Z., Xie, W., and Liu, T. (2018). Efﬁcient feature selec-

tion and classiﬁcation for microarray data. PLoS One,

13(8).

Manikandan, G. and Abirami, S. (2018). A Survey on Fea-

ture Selection and Extraction Techniques for High-

Dimensional Microarray Datasets, pages 311–333.

Springer Singapore, Singapore.

Meyer, P., Schretter, C., and Bontempi, G. (2008).

Information-theoretic feature selection in microarray

data using variable complementarity. IEEE Journal of

Selected Topics in Signal Processing, 2(3):261–274.

Peng, H., Long, F., and Ding, C. (2005). Feature selec-

tion based on mutual information: criteria of max-

dependency, max-relevance, and min-redundancy.

IEEE Transactions on Pattern Analysis and Machine

Intelligence (PAMI), 27(8):1226–1238.

Pudjihartono, N., Fadason, T., Kempa-Liehr, A., and

O’Sullivan, J. (2022). A review of feature selection

methods for machine learning-based disease risk pre-

diction. Frontiers in Bioinformatics, 2:927312.

Remeseiro, B. and Bolon-Canedo, V. (2019). A review

of feature selection methods in medical applications.

Computers in Biology and Medicine, 112:103375.

anchez-Maro

no, N., Fontenla-Romero, O., and P

erez-

anchez, B. (2019). Classiﬁcation of Microarray

Data, pages 185–205. Springer New York, New York,

NY.

Simon, R., Korn, E., McShane, L., Radmacher, M., Wright,

G., and Zhao, Y. (2003). Design and analysis of DNA

microarray investigations. Springer.

Statnikov, A., Aliferis, C., Tsamardinos, I., Hardin, D.,

and Levy, S. (2005). A comprehensive evaluation

of multicategory classiﬁcation methods for microar-

ray gene expression cancer diagnosis. Bioinformatics,

21(5):631–643.

Yu, L. and Liu, H. (2003). Feature selection for high-

dimensional data: a fast correlation-based ﬁlter solu-

tion. In Proceedings of the International Conference

on Machine Learning (ICML), pages 856–863.

Yu, L. and Liu, H. (2004). Efﬁcient feature selection via

analysis of relevance and redundancy. Journal of Ma-

chine Learning Research (JMLR), 5:1205–1224.

Yu, L., Liu, H., and Guyon, I. (2004). Efﬁcient feature

selection via analysis of relevance and redundancy.

Journal of Machine Learning Research, 5:1205–1224.

Zhao, Z., Morstatter, F., Sharma, S., Alelyani, S., Anand,

A., and Liu, H. (2010). Advancing feature selection

research - ASU feature selection repository. Techni-

cal report, Computer Science & Engineering, Arizona

State University.

Zhu, Z., Ong, Y., and Dash, M. (2007). Markov blanket-

embedded genetic algorithm for gene selection. Pat-

tern Recognition, 49(11):3236–3248.

Union k-Fold Feature Selection on Microarray Data

547