Anomaly Detection in Smart Grid Networks Using Power Consumption

Data

Hasina Rahman

1 a

, Priyadarsi Nanda

1 b

, Manoranjan Mohanty

1 c

and Nazim Uddin Sheikh

2 d

University of Technology Sydney, Sydney, NSW, Australia

Torrens University, Sydney, NSW, Australia

Keywords:

Smart Meter Security, Anomalies, Intrusion Detection System, False Data Injection, Deep Learning Model,

Energy Data, LSTM-DAE Model.

Abstract:

Smart meters, intelligent devices used for managing energy consumption of consumers, are one of the inte-

gral components of the smart grid infrastructure. The smart metering infrastructure can facilitate a two-way

communications through the Internet to leverage home energy management and remote meter reading by the

service providers. As a consequence, the smart meters are extremely susceptible to various potential security

threats, such as data tampering, distributed denial of services (DDoS) attack and spooﬁng attacks. In this paper,

we put forward a scheme to detect anomalies in energy consumption data using real-world datasets. Thereby,

addressing data tampering attacks. We have adapted an unsupervised machine learning method to distinguish

the anomalous behaviour from the normal behaviour in energy consumption patterns of consumers. In addi-

tion, we have proposed a robust threshold mechanism for detecting abnormalities against noise, which has not

been used in smart grids before. Our proposed model shows an accuracy of 94.53% in detecting anomalous

patterns in energy consumption data. This accuracy surpasses the existing benchmark in anomaly detection in

energy consumption data using machine learning models (Huang and Xu, 2021).

1 INTRODUCTION

Smart meters, an integral part of the smart grid infras-

tructure, play a signiﬁcant role in regulating the ad-

vanced metering infrastructure(AMI) systems (Hart,

2008). The AMI enables various services, such as

electronic billing, grid monitoring, grid operation and

demand response for both consumers and providers.

On the other hand, smart meters are deployed by

electricity providers and retailers to monitor ﬁne-

grained energy consumption of households in real-

time(Sheikh et al., 2021). Consequently, they are

physically accessible and more prone to data tamper-

ing attacks. The demand for these smart meters is

increasing with every passing day and they are be-

ing widely deployed. However, Tellbach et al. (Tell-

bach and Li, 2018) showed that cyber-attacks on these

smart meters can incur huge ﬁnancial losses. These

data are often communicated to the service providers

https://orcid.org/0000-0002-7447-3738

https://orcid.org/0000-0002-5748-155X

https://orcid.org/0000-0002-0258-4586

https://orcid.org/0000-0002-6565-9880

over a secure channel (Erkin et al., 2013), and are re-

quired to monitor and manage the grid (Knirsch et al.,

2016).

The cyber attacks in the smart grid can be detri-

mental and can cause the electronic devices like smart

devices and/or generators malfunction. The well-

known attacks are false data injection, spooﬁng, de-

nial of services (DoS), man-in-the-middle, replay and

meter bypass attacks. We discuss the severity of these

attacks below.

False Data Injection Attack: The false data injection

attack is launched to inject fake data or payloads into

the smart meters or the advanced metering infrastruc-

ture (AMI), that modiﬁes the power system data or

state of the smart meters. A number of incidents

of false data injection attacks have been launched

by customers in USA, Ireland, Virginia and Hong

Kong (Lo and Ansari, 2013).

Spooﬁng Attack: In this type of attack, a new system

element is added at one end that acts as a legitimate

body (Fan et al., 2015).

DoS Attack: The DoS attack is launched to ﬂood

any computer or network system with overwhelming

830

Rahman, H., Nanda, P., Mohanty, M. and Sheikh, N.

Anomaly Detection in Smart Grid Networks Using Power Consumption Data.

DOI: 10.5220/0012137600003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 830-837

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

packets through different sources or geographical lo-

cations to overﬂow the system buffer, thereby shatter-

ing the system and leaving it inoperable (Wang et al.,

2017). In addition, a new attack called the puppet at-

tack on smart meters can cause DoS attacks in the me-

tering networks (Yi et al., 2016). Security weaknesses

of smart meters were discussed in the 2014 Black Hat

Europe conference, where Alberto and Javier stated

how an attacker can get access to the encryption keys

(for e.g. a master key) by exploiting the hardware of

the device (Illera and Vidal, 2014).

Attacks on smart grid seriously affect the entire

ecosystems, such as smart home activities, indus-

trial operations, hospital facilities, ﬁnancial and gov-

ernment institutions. In 2014, an Australian util-

ity company was seriously affected by the DDoS at-

tack caused due to a misdirected command (Wueest,

2014). Also, the cyber-attacks on Ukrainian energy

companies in 2015

and 2016

caused power black-

outs in the region for several hours.

Contributions: The main contributors of this paper

are summarised as follows.

• In this paper, we have proposed a novel unsu-

pervised deep learning based Long Short Term

Memory-Denoising Autoencoder (LSTM-DAE)

model to detect anomalies in energy consumption

data of smart meters. As a result, we have ad-

dressed the issue of real-world anomaly detection.

This would help in detecting the energy theft by

customers, meter malfunctioning or third-party at-

tacks.

• Also, time-series energy data can be appropriately

handled using sequential model like LSTM (Long

Short Term Memory). Since, our model is built

using LSTM and Auto-encoder, unlike other ex-

isting machine learning models used for anomaly

detection in energy data, it is most beﬁtting.

• Our model achieves an accuracy of 94.53% and

false positive rate of 5.47%, thereby outperform-

ing the existing models in detecting anomalous

behaviour.

2 RELATED WORKS

In this section, we review some existing works (Nagi

et al., 2009; Nizar et al., 2008; Yip et al., 2017; Li

et al., 2020; Huang and Xu, 2021; Yip et al., 2018;

https://ics-certus-cert.gov/alerts/IR-ALERT-H-16-0

56-01

https://www.technologyreview.com/2016/12/22/5969

/ukraines-power-grid-gets-hacked-again-a-worrying-sig

n-for-infrastructure-attacks/

Cui et al., 2021) related to the detection of anoma-

lies in power consumption data of smart meters. They

speciﬁcally focused on grid’s electricity consumption

data.

Yi et.al (Yip et al., 2017) designed a linear regres-

sion based detection model for energy theft and de-

fective smart meter was used for detection of anoma-

lies. The anomalies are considered coefﬁcients to the

power consumption values of users, sampled at dif-

ferent points of the day in the form of a matrix. How-

ever, the model shows numerical discrepancies when-

ever the rate of anomaly i.e. anomaly coefﬁcient of

a particular user vary throughout the day. They had

used Irish Smart Energy trial dataset that was based

on half-hourly samples. They acquired anomaly co-

efﬁcients through t-statistics and p-values using Mat-

lab’s ﬁtlm function. Though they introduced categor-

ical values like off-peak and on-peak hours for coefﬁ-

cients of anomalies, it was not good enough to justify

situations since anomalies can vary throughout differ-

ent times. Also, the threshold set for anomaly coefﬁ-

cient to be anomaly rather than an outlier is not based

on a robust mechanism since technical errors (Yip

et al., 2018) or measurements errors from device can

likely create the noise. Additionally, they did not pro-

vided any numerical measurements on the model’s

performance. In (Yip et al., 2018), the discrepancy

in numerical value of their previously mentioned LP

model (Yip et al., 2017) was solved, by introducing

Linear Programming where varying anomaly coefﬁ-

cients were considered that made the model more re-

alistic. It further improved the threshold for anoma-

lies from 0 to 0.05 on the same dataset. However,

they still did not consider losses due to technical faults

such as cables, transmission lines and distribution sta-

tions. Therefore, we still cannot rely on the improved

threshold, which might not be reliable enough.

While, Li et.al (Li et al., 2020) proposed a

blockchain based detection method in conjunction

with unsupervised K-Nearest Neighbor(KNN) for

clustering into three categories like working class,

holiday class and outlier class. However, there is

a great uncertainty in the method of data collection

from sensors and smart meters deployed by them in

factories and homes. In addition, there was no justi-

ﬁcation for the selection of k−value in the KNN al-

gorithm. The concepts for relation between data us-

ing correlation coefﬁcient and number of occurrences

of data points using Poisson’s distribution to address

anomalies was appropriately evaluated. They neither

provide a proper justiﬁcation to distinguish anomalies

from data-points that are simply outliers, nor deploy

a robust mechanism against outliers and anomalies.

The picture of their stated analysis is rather vague and

Anomaly Detection in Smart Grid Networks Using Power Consumption Data

831

thereby makes the detection rates unreliable. More-

over, Huang et.al (Huang and Xu, 2021) used Stacked

Sparse Denoising Auto-encoder for detection of data

theft. The model is stated to be unsupervised with sin-

gle labels of honest customers obtained from the Elec-

tricity Consumption Fujian, China data-set. How-

ever, we deem it appropriate to state that it is semi-

supervised. The anomalies are obtained from the re-

construction error with a claimed optimal threshold.

The threshold is set through the ROC Curve. The

ROC curve in turn is dependent on the False positive

rate and this is acquired from the test set which is in-

appropriate (Merrill and Eskandarian, 2020) because

the threshold should have been determined from the

training set. Consequently, we need a robust mecha-

nism to determine thresholds and a better model for

real time classiﬁcation.

It is clear that almost all of the existing works have

used either supervised or semi-supervised frame-

works for the detection of data theft . However, the

supervised and the semi-supervised machine learning

algorithms cannot provide a good solution for real-

world scenarios.

3 PROPOSED HOST-BASED

INTRUSION DETECTION

SYSTEM

The Host-Based Intrusion Detection System (HIDS)

is used for detecting abnormalities in smart meter en-

ergy consumption data. These abnormalities could be

caused due to several reasons, such as energy theft,

measurement errors, technical errors and/or faulty

meters (Yip et al., 2017). The literature shows that

the majority of research works on anomaly detection

have been carried out using supervised models. The

practicality of such models is questionable as it is ex-

tremely difﬁcult to get a substantial amount of labeled

anomalous samples in a real-world scenario. On the

other hand, the semi-supervised methods work a way

around the requirement of labeled anomalous sam-

ples by completely relying on readily available nor-

mal samples. Thus, they utilise data labeled as normal

to detect anomalies and examples that do not comply

with normal samples are simply ﬂagged as anoma-

lies. However, semi-supervised approaches are sig-

niﬁcantly susceptible to model over-ﬁtting or under-

ﬁtting which leads to poor model performance in

terms of recall and precision scores (Goldstein and

Uchida, 2016). This issue is daunting for all appli-

cations and speciﬁcally for grid data where we need

very low false positives and false negatives (Mitchell

and Chen, 2013). Since, the data may or may not

contain anomalous samples, a more pragmatic ap-

proach is to use unlabeled data samples. As a re-

sult, unsupervised learning approach can essentially

be adapted to achieve such goals (Merrill and Eskan-

darian, 2020). Thus, we envisage an unsupervised

model for anomaly detection, which is relevant to any

practical scenario. Our model is based on deep neural

networks using LSTM-AE.

3.1 Anomaly Detection Model

We present a LSTM-DAE model for anomaly detec-

tion in smart meter energy data. The model is inspired

by the capability of LSTMs to predict time-series data

and auto-encoders in extracting features and recon-

structing data as mentioned in (Huang and Xu, 2021).

To the best of our knowledge, this is the ﬁrst work on

anomaly detection of smart meter power consumption

data using on LSTM-AE model, and signiﬁcantly our

approach is novel as it introduces a denoising LSTM-

AE. The denoising element is introduced to remove

the noise from the data in order to develop a robust

auto-encoder.

Structure of LSTM-DAE: Here, we discuss the follow-

ing models: LSTM, auto-encoder and denoising auto-

encoders. We do this for the ease of understanding the

overall structure of the model used.

1. LSTM is a type of recurrent neural networks

model that was introduced to solve the vanishing

gradient problem in RNNs. The vanishing gradi-

ent problem occurred when some of the weights

ceased to change during the learning process. As

a result, preference given to the current informa-

tion would lead to forget of past events. There-

fore, the model cannot learn substantially in case

of relations recurring over a long period of time.

While, LSTMs were designed to control the en-

tire information ﬂow within neurons, through a

gate that adds and deletes the information. Con-

sequently, the model can learn long-term as well

as short-term dependencies by controlling the pro-

cess of forgetting unlike RNN. However, it limits

the memory capacity in such a way that the out-

put gate infers the updated cell state. It is partic-

ularly suitable for multivariate or univariate time-

series data where it can be supervised or unsuper-

vised (i.e. the dataset can be with or without la-

bels) (Lindemann et al., 2021). Figure 1 shows a

typical structure of a cell in LSTM model.

2. Auto-encoders have been effective as unsuper-

vised model for removal of outliers since they

SECRYPT 2023 - 20th International Conference on Security and Cryptography

832

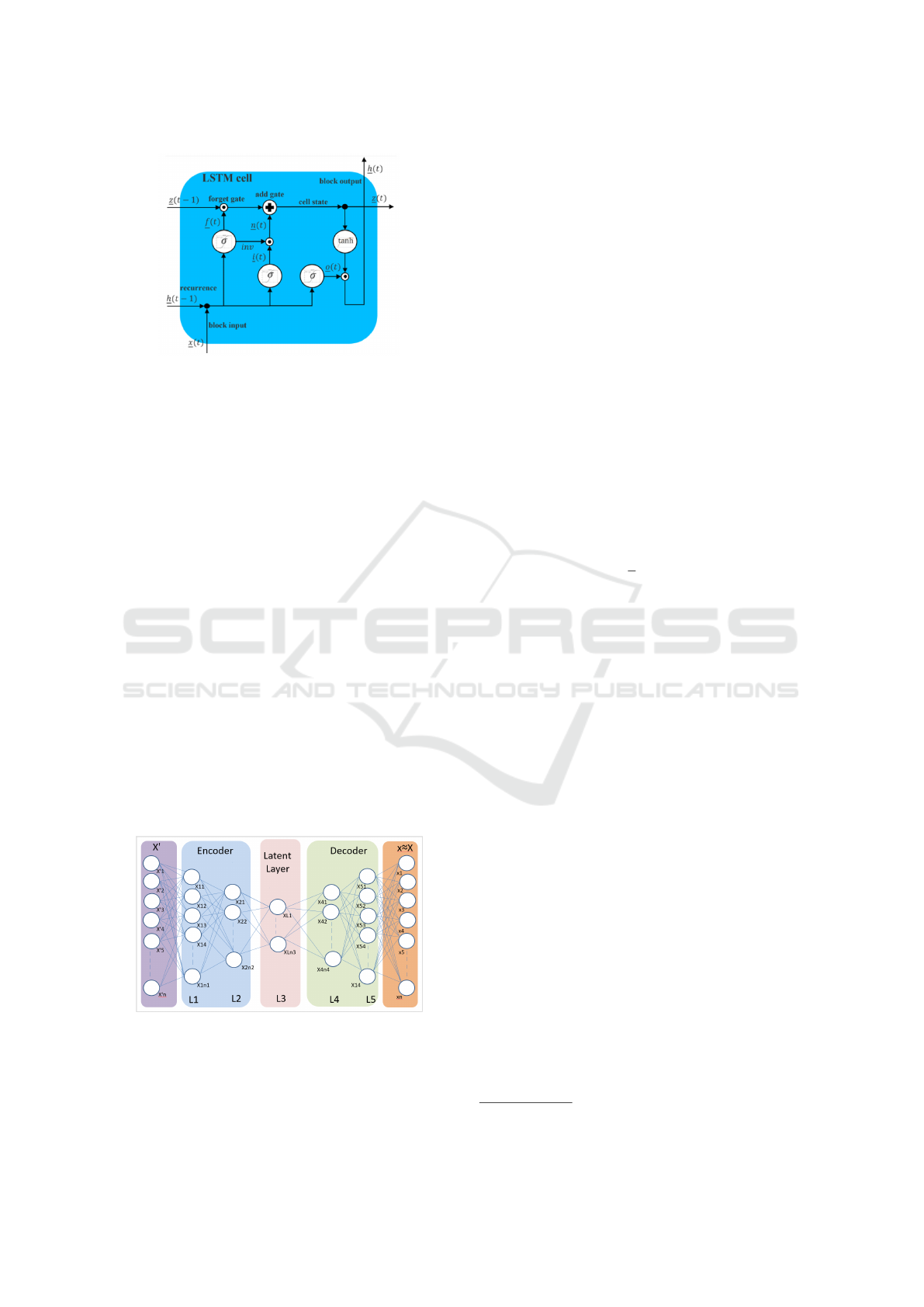
Figure 1: LSTM cell as designed by Hochreiter and

Schmidhuber in 1997.

can reconstruct data efﬁciently with higher den-

sity. The neural network has two models called

an encoder and a decoder that are trained to-

gether. The encoder compresses the initial input,

thereby learning important features, while the de-

coder reconstructs the data from its compressed

state. Therefore, the whole model can learn highly

complicated data patterns (Merrill and Eskandar-

ian, 2020).

3. When these auto-encoders are fed with noisy

inputs to reconstruct actual outputs, they are

known as denoising auto-encoders (see Figure 2

). These are more robust against noise and help

prevent learning identity function as in general

auto-encoders i.e., reconstructing X from

X (in-

put) (Vincent et al., 2008). In this model, noise

is added to the input X such that it constructs a

clean output from the noisy samples i.e.,

X (Vin-

cent et al., 2008). This corruption of inputs can be

done in several ways such as by replacing 30% of

the input values with zero, 50% of the inputs with

zero, (Huang and Xu, 2021) using random noise

or white Gaussian noise.

Figure 2: The proposed Denoising Auto-encoder where

noise is added to the real inputs before feeding it to the

model.

4 EXPERIMENTAL EVALUATION

In this section, we report the experimental ﬁndings

in detecting anomalies using smart meter energy con-

sumption data. We have envisaged an unsupervised

deep learning-enabled IDS to distinguish between

normal and anomalous behaviours in energy con-

sumption patterns of households.

4.1 Metrics

We deﬁne few metrics to evaluate the performance of

our proposed model in detecting anomalies. It is im-

portant to understand these metrics before we delve

further into the experiment section, since it describes

the way in which we have used them.

Mean Squared Error: The Mean Squared Error

(MSE) is the square of the difference between the ac-

tual and predicted values for all n samples. This can

be represented as follows where, the actual or ground

truth is denoted as X and the predicted value is de-

noted as

MSE =

∑

i=1

(X −

(1)

Model Loss: It is a scalar value that indicates how

closethe predictions of the model are as compared to

the actual labels. If the loss is low (ideally 0), the

predictions are considered to be perfect, and close to

0 are good predictions; on the contrary, if it is closer

to 1, the predictions are bad.

Threshold: It is the numerical range beyond or below

which the anomalies are ﬂagged.

False Positive (FP): The number of samples that are

non-anomalies while they are ﬂagged as anomalies.

False Negative (FP): The number of samples that are

anomalies, but are ﬂagged as non-anomalies.

True Positive (TP): The numbers that state how many

are samples are correctly predicted as non-anomalies.

True Negative (TN): It states how many samples are

correctly predicted as anomalies.

Accuracy: Accuracy is the percentage of correct pre-

diction of non-anomalies from the samples. It can be

represented as follows.

Accuracy = (T P+ T N)/(TP+T N +FP+FN) (2)

4.2 Conﬁguring Threshold

There are several methods for calculating the thresh-

old, such as the use of ROC curve (Huang and

Xu, 2021), 90 − 95% on the training data (Givnan

et al., 2022), mean and standard deviation method

https://github.com/tensorflow/docs/

Anomaly Detection in Smart Grid Networks Using Power Consumption Data

833

and kentucky’s method (Zhou et al., 2021). Though

the threshold is very much dependent on a dataset,

and each method might provide different results, we

should choose a very robust threshold that would

overcome the noise due to some outliers, such as mea-

surement errors and technical errors. Therefore, we

preferred Kentucky’s method over the rest as it is a

robust mechanism as stated in (Zhou et al., 2021).

The threshold is calculated based on the training data,

where we assume that the training data is not anoma-

lous. The threshold is evaluated using Q1, Q2 and

IQR metrics. Q1 is the ﬁrst quartile which means

that it is the value under which 25% of data points

are found when they are arranged in increasing order.

Q3 is the third quartile which thereby, the value under

which 75% of data points are found when arranged in

increasing order. IQR is the inter-quartile range where

IQR = Q3 − Q1 (3)

The formula for calculating the upper and lower

thresholds respectively are as follows.

lowerrange = Q1 − 1.5 ∗ IQR (4)

upperrange = Q3 + 1.5 ∗ IQR (5)

4.3 Datasets and Experiments

We use two different datasets for the experimenta-

tions and analyses as mentioned below: Our emperi-

cal evaluations are based on two different energy con-

sumption datasets summarised in Table 1.

The UCI Power Consumption dataset extracted

from traditional meters was chosen to consider a di-

verse range of parameters, such as current, voltage

and sub-meter data in addition to power consump-

tion. Signiﬁcantly, the dataset was unlabelled resem-

bling any real-world dataset. However, we were un-

able to validate the performance of the model due

to lack of a ground-truth. Therefore, we later used

Irish power consumption dataset that consists of half-

hourly smart meter data from honest customers only

i.e. non-anomaly labels. We did not feed labels to our

model but utilised the labels to calculate the various

performance metrics including accuracy, false posi-

tives and false negatives.

4.3.1 Experiments on UCI Dataset

We train LSTM-AE and LSTM-DAE to compare the

loss and reconstruction error for the same dataset. At

ﬁrst, we train the LSTM-AE for ﬁve epochs and it

produces satisfactory loss value (loss value is 0.05).

This is done for both training and validation set. The

model is found to be a good ﬁt since the plot of train-

ing set loss against validation seem to be converging

towards the last few epochs. The loss values are sub-

stantially low indicating that the model is performing

well in terms of learning.

Then, we train our model on the same dataset

using noisy data. After training for 12 epochs, we

observe satisfactory low loss value in the last few

epochs. Thereby, indicating that the original data is

recovered well from the noised input. Further, we use

our LSTM-DAE model. The number of samples con-

sidered is 10,000 and that constitutes nearly 1 month

of data. The model loss shows that it is considerably

low i.e.,0.06, at only 12 epochs even with noisy in-

put. Therefore, this illustrates a good learning capac-

ity and efﬁcient model performance.

The MSEs after noised inputs added to the training

set acquired from Paris Power Consumption data, are

in Figure 3.

Figure 3 shows the train MSEs on noisy inputs

to the model using Paris power consumption dataset.

The MSEs are low thereby, indicating that the model

is predicting very well. After the reconstruction er-

ror is calculated from test set, we check if that error

is beyond a selected threshold for the anomaly score.

Further, the sample would be ﬂagged as an anomaly if

the error is beyond the threshold, otherwise the con-

sumption pattern will be considered as normal.

Figure 3: MSEs from the noisy input of Train set on Power

Consumption Data-set.

Finding Anomalies. The test set for UCI dataset is

predicted and the MSEs i.e., MSE per sample is cal-

culated from the deviations of the actual test set.

Though, these MSEs in the test set are relatively

higher than those in train set, they are still visibly low

as shown in the y-axis of Figure 4. We tried to re-

construct the error through Keras’ predict function in

python. These errors are checked against the thresh-

old. Thereby, the errors found below the lower and

above the upper threshold limit are marked as anoma-

lies. We ﬁnd that out of 399 samples in the test set, 23

are ﬂagged as anomalies. However, we are unaware,

if the anomalies are correctly classiﬁed since the data-

SECRYPT 2023 - 20th International Conference on Security and Cryptography

834

Table 1: Dataset description.

Dataset Period of Consumption Number of samples Data Location

UCI Energy Consumption Dataset

December 2006 - November 2010 2075259 Paris, France

Irish Contracted Power Dataset

January 2009-June 2010 157992996 Ireland

Figure 4: MSEs from the Test set on UCI Energy Dataset.

set is unlabeled.

4.3.2 Experiments on Irish Power Data-Set

Similar to the previous dataset, we calculate the loss

for this dataset too using LSTM-DAE. The loss is

found to be as low as 0.025 in this case, within just

14 epochs, thereby, yielding model consistency on

low loss value and establishing the model as a good

learner. Here, we have chosen 180 meters out of 6444.

The data points involved with these 180 meters are

3,863,725. Therefore, we have performed our experi-

ments on substantial amount of data rather than small

to medium scale data and obtained satisfactory results

on the learning capacity.

We trained with considerably less data than the

test set. The training set was based on 16.67% of the

total data used from the dataset for training and test-

ing. This is so because, we just wanted to validate

the model performance in terms of reconstructing the

loss and minimal error with relatively lesser data. Our

model is trained using the ﬁrst 30 meters ranging be-

tween 1000 and 1030 i.e. 7,00,000 samples, while our

test data comprises of 150 meters i.e. 3,163,725 data

points.

We plot the MSEs from training data for Irish

Power Data-set(see ﬁgure 5). We ﬁnd that the MSEs

are relatively low as well.

Identifying Anomalies. We acquire the test MSEs

and anomaly scores for Irish Power Data-set samples

having only healthy data. Our model is still essen-

tially unsupervised since we train without these la-

bels. However, we are able to use the labels for com-

parison after ﬁnding the anomalies. But, before ac-

Figure 5: MSEs from the noisy input of Train set on Irish

Power Consumption Data-set.

quiring the MSEs, we divide the entire test set hav-

ing huge number of samples into chunks since we can

achieve better visualisation with lesser data points.

The MSEs for samples from meters ranging between

1031 and 1060 are low i.e. mostly within the range of

In ﬁgure 6, it is seen that the samples for meters

between 1061 and 1090 are mostly within the range of

3.5 and very few are beyond 8.The meters ranging be-

tween 1091 and 1120 too shows errors mostly within

3.5 and 4, while few are beyond 10. Similarly, meters

between 1121 and 1150 have most of the errors in low

range i.e. within 4. The last chunk for errors between

1151 and 1180 are around the range of 2 and very few

are beyond 10.

Figure 6: MSEs from the Test set obtained from Irish Power

Consumption Data-set for meter samples 1061 to 1090.

Anomaly Detection in Smart Grid Networks Using Power Consumption Data

835

Therefore, with the MSEs ranging between 2 and

10, we conclude that the model performance stands

out with relatively very less data for training in com-

parison to the testing set.

We obtained the anomaly score from training er-

rors based on the ﬁxed threshold for Irish Data-set.

The lower and upper ranges of the threshold are -

0.24896152299660124 and 1.3530767084315753 re-

spectively. We ﬁnd that 2,951,974 half-hourly data

points from among 150 meters are marked to be non-

anomalous.

Figure 7: Anomalies from meter samples ranging between

1061 and 1090.

We ﬁnd that out of 3,871,203 data points, 211,751

points were marked as anomalies. Thereby, indicating

the false-positives to be at 5.47%. The True Negatives

i.e. non-anomalies, stand at 94.53%. As a result, the

accuracy of the model or detection rate is 94.53% with

low data considered for training.

Figure 8: Confusion matrix for performance metrics based

on Irish Power Consumption Data-set.

4.4 Comparison and Discussion

A range of machine learning(ml) models like Stacked

Sparse Denoising Autoencoder (SSDAE), RDBN

which is a combination of Restricted Boltzmann ma-

chines (RBMs) and deep belief networks (DBNs),

Principal Component Analysis (PCA) and Support

Vector Machines (SVM), that have been used for

identifying data theft attacks in smart meters(Huang

and Xu, 2021). SSDAE is a set of stacked autoen-

coders with some suppressed hidden layers, noisy in-

put and clean output. RDBN allows pre-training of

a deep belief network using ideas from ’contrastive

divergence’ and adjusting the network for classiﬁca-

tion through backpropagation algorithm. PCA uses

unsupervised ml model based on correlation to carry

out applications such as exploratory data analysis, di-

mensionality reduction and data denoising. SVMs are

supervised ml model for tasks like regression, outlier

detection and classiﬁcation where a line or hyperplane

is created to separate data into classes. Our model

LSTM-DAE is compared to other models based on

two performance metrics i.e. accuracy and false pos-

itive rate. Here, we have made comparison with the

above mentioned models. We ﬁnd out that our model

has a higher accuracy level and lower FPR than the

other models as shown in Table 2, thereby outper-

forming others.

Table 2: Performance of various models on detection of

anomalies in Energy consumption.

Model Accuracy FPR

LSTMDAE (Our Work) 0.9453 0.0547

SSDAE 0.9174 0.0719

RDBN 0.8701 0.1362

PCA 0.8582 0.1793

SVM 0.8176 0.1607

Our model LSTMDAE performs better than the

ones listed in the table. This gives an indication that

the model can be utilised for detecting anomalies and

prove to be a good detector for smart meters.

5 CONCLUSION AND FUTURE

DIRECTIONS

To conclude, we develop a robust unsupervised deep

learning model to ﬁnd out cohort anomalies in the

power consumption data. We have considered every

possible parameter to make sure that we secure our

model against noise and ﬂag the actual abnormalities.

The model is reliably suitable for a real world sce-

nario because of its unsupervised nature and it’s short

inference time. Also, it performs well with compar-

atively very less training (16.67%) and more testing

https://archive.ics.uci.edu/ml/datasets/

https://www.ucd.ie/issda/data/

SECRYPT 2023 - 20th International Conference on Security and Cryptography

836

data. It surpasses the available model in accuracy

and false positive rate. Additionally, we consider the

time series data factor through LSTM, unlike other

proposed models. Therefore, it is a ﬁrst of its kind

for anomaly detection of smart meter data, keeping in

mind their resource constrained nature. In the near

future, we would focus more on the causes of anoma-

lies like anomalies due to faulty meter and anomalies

caused by theft using LSTM-DAE. Thereby, speciﬁ-

cally focusing on anomaly due to attacks and not due

to meter faults.

REFERENCES

Cui, L., Guo, L., Gao, L., Cai, B., Qu, Y., Zhou, Y.,

and Yu, S. (2021). A covert electricity-theft cyber-

attack against machine learning-based detection mod-

els. IEEE Transactions on Industrial Informatics.

Erkin, Z., Troncoso-Pastoriza, J. R., Lagendijk, R. L., and

erez-Gonz

alez, F. (2013). Privacy-preserving data

aggregation in smart metering systems: An overview.

IEEE Signal Processing Magazine, 30(2):75–86.

Fan, Y., Zhang, Z., Trinkle, M., Dimitrovski, A. D., Song,

J. B., and Li, H. (2015). A cross-layer defense mech-

anism against gps spooﬁng attacks on pmus in smart

grids. IEEE Transactions on Smart Grid, 6(6):2659–

2668.

Givnan, S., Chalmers, C., Fergus, P., Ortega-Martorell, S.,

and Whalley, T. (2022). Anomaly detection using au-

toencoder reconstruction upon industrial motors. Sen-

sors, 22(9):3166.

Goldstein, M. and Uchida, S. (2016). A comparative eval-

uation of unsupervised anomaly detection algorithms

for multivariate data. PloS one, 11(4):e0152173.

Hart, D. G. (2008). Using ami to realize the smart

grid. In Power and energy society general meeting-

Conversion and delivery of electrical energy in the

21st Century, pages 1–2.

Huang, Y. and Xu, Q. (2021). Electricity theft detection

based on stacked sparse denoising autoencoder. Inter-

national Journal of Electrical Power & Energy Sys-

tems, 125:106448.

Illera, A. G. and Vidal, J. V. (2014). Lights off! the darkness

of the smart meters. BlackHat Europe.

Knirsch, F., Eibl, G., and Engel, D. (2016). Error-

resilient masking approaches for privacy preserving

data aggregation. IEEE Transactions on Smart Grid,

9(4):3351–3361.

Li, M., Zhang, K., Liu, J., Gong, H., and Zhang, Z.

(2020). Blockchain-based anomaly detection of elec-

tricity consumption in smart grids. Pattern Recogni-

tion Letters, 138:476–482.

Lindemann, B., Maschler, B., Sahlab, N., and Weyrich, M.

(2021). A survey on anomaly detection for technical

systems using lstm networks. Computers in Industry,

131:103498.

Lo, C.-H. and Ansari, N. (2013). Consumer: A novel hybrid

intrusion detection system for distribution networks in

smart grid. IEEE Transactions on Emerging Topics in

Computing, 1(1):33–44.

Merrill, N. and Eskandarian, A. (2020). Modiﬁed autoen-

coder training and scoring for robust unsupervised

anomaly detection in deep learning. IEEE Access,

8:101824–101833.

Mitchell, R. and Chen, R. (2013). Behavior-rule based

intrusion detection systems for safety critical smart

grid applications. IEEE Transactions on Smart Grid,

4(3):1254–1263.

Nagi, J., Yap, K. S., Tiong, S. K., Ahmed, S. K., and Mo-

hamad, M. (2009). Nontechnical loss detection for

metered customers in power utility using support vec-

tor machines. IEEE transactions on Power Delivery,

25(2):1162–1171.

Nizar, A., Dong, Z., and Wang, Y. (2008). Power utility

nontechnical loss analysis with extreme learning ma-

chine method. IEEE Transactions on Power Systems,

23(3):946–955.

Sheikh, N. U., Asghar, H. J., Farokhi, F., and Kaafar, M. A.

(2021). Do auto-regressive models protect privacy in-

ferring ﬁne-grained energy consumption from aggre-

gated model parameters. IEEE Transactions on Ser-

vices Computing.

Tellbach, D. and Li, Y.-F. (2018). Cyber-attacks on smart

meters in household nanogrid: modeling, simulation

and analysis. Energies, 11(2):316.

Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-

A. (2008). Extracting and composing robust features

with denoising autoencoders. In Proceedings of the

25th international conference on Machine learning,

pages 1096–1103.

Wang, K., Du, M., Maharjan, S., and Sun, Y. (2017). Strate-

gic honeypot game model for distributed denial of ser-

vice attacks in the smart grid. IEEE Transactions on

Smart Grid, 8(5):2474–2482.

Wueest, C. (2014). Targeted attacks against the energy sec-

tor. Symantec Security Response, Mountain View, CA.

Yi, P., Zhu, T., Zhang, Q., Wu, Y., and Pan, L. (2016). Pup-

pet attack: A denial of service attack in advanced me-

tering infrastructure network. Journal of Network and

Computer Applications, 59:325–332.

Yip, S.-C., Tan, W.-N., Tan, C., Gan, M.-T., and Wong, K.

(2018). An anomaly detection framework for identi-

fying energy theft and defective meters in smart grids.

International Journal of Electrical Power & Energy

Systems, 101:189–203.

Yip, S.-C., Wong, K., Hew, W.-P., Gan, M.-T., Phan, R. C.-

W., and Tan, S.-W. (2017). Detection of energy theft

and defective smart meters in smart grids using linear

regression. International Journal of Electrical Power

& Energy Systems, 91:230–240.

Zhou, G., Liu, M., and Liu, X. (2021). An autoencoder-

based model for forest disturbance detection using

landsat time series data. International Journal of Dig-

ital Earth, 14(9):1087–1102.

Anomaly Detection in Smart Grid Networks Using Power Consumption Data

837