Optimizing Attribute-Based Encryption for Circuits Using

Compartmented Access Structures

Alexandru Ionit¸

1,2 a

Simion Stoilow Institute of Mathematics of the Romanian Academy, Bucharest, Romania

Department of Computer Science, Alexandru Ioan Cuza University of Ias¸i, Ias¸ i, Romania

Keywords:

Attribute-Based Encryption, Boolean Circuits, Access Control, Bilinear Maps, Decisional Bilinear Difﬁe-

Hellman.

Abstract:

Attribute-based encryption (ABE) is an asymmetric encryption method that allows expressive access granting

mechanisms, with high applicability in modern IT infrastructure, such as Cloud or IoT systems. (Ezhilarasi

et al., 2021; Touati and Challal, 2016) One open problem regarding ABE is using Boolean circuits as access

structures. While Boolean Formulae were supported since the ﬁrst ABE scheme proposed, there is still no

efﬁcient construction that supports Boolean circuits. We propose a new ABE scheme for a new access structure

type, situated between Boolean formulae and Boolean circuits in terms of expressiveness. This key point in

our construction is the usage of CAS-nodes, a structure modeling compartmented groups access structures.

We also show that our CAS -nodes can be used to improve the efﬁciency of existing ABE schemes for Boolean

circuits. Our construction is secure in the Selective Set Model under the bilinear Decisional Difﬁe-Hellman

Assumption.

1 INTRODUCTION

In our days, Cloud and IoT services are experiencing

continuous growth, and a large amount of data ends

up being stored in such systems. Hence, the Cloud

service provider has access to sensitive data, such as

personal documents or conﬁdential information. For

example, suppose we need an online platform for stor-

ing personal documents, medical records, and other

sensitive data, such that you should be able to down-

load your data on-demand, at any time. We do not

wish the Cloud Service provider to have access to

such information.

The natural approach to solving this problem is to

encrypt all documents containing sensitive informa-

tion. However, we then face the problem of granting

access to these encrypted documents. Using conven-

tional techniques, each user should keep a decryption

key for each encrypted document for which he has the

right to decrypt. This approach is impractical, due to

the large number of decryption keys a user may have.

A modern solution for this problem could be

Attribute-based encryption (ABE). This allows us to

grant content-based or role-based access over the en-

crypted data, depending on which ﬂavor of ABE we

https://orcid.org/0000-0002-9876-6121

are using - key-policy (KP-ABE) or ciphertext-policy

(CP-ABE).

Using a KP-ABE system, each user could have set

up an instance of the scheme, having a public key and

a secret key. With the public key, any doctor could

encrypt the respective user’s medical data, such as

test results or medical examinations. Using the pri-

vate key, the user is in full control of granting access

to its data. Not even the third party which provides

the system infrastructure will be able to decrypt these

pieces of information, as it will not have access to a

user’s decryption keys.

Each user can control who has decryption privi-

leges over his data using an access policy deﬁned over

some attributes. Thus, we can identify 2 vital features

such a system should have:

• expressiveness: to have ﬁne-grained access over

the encrypted data, using an expressive access

policy

• efﬁciency: the running time and decryption key

size of our scheme should be as low as possible

since our data should be accessible even from de-

vices with limited computational power.

Due to the expressiveness it provides, ABE is a

subject of high interest in network security. Many

researchers are developing secure ABE systems with

230

IoniÅ

cÄ

C, A.

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures.

DOI: 10.5220/0012139000003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 230-241

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

many functionalities, such as outsourced decryption

(Green et al., 2011), access revocation (Attrapadung

and Imai, 2009), or multi-authority ABE (Chase,

2007; Zhong et al., 2018). Recently, European

Telecommunications Standards Institute (ETSI) has

published technical speciﬁcations for implementing

ABE in the cloud, IoT, and other Internet services

(ETSI TS 103 458 (ETSI, 2018))

One challenge is to construct ABE systems with

more expressive access structures while maintaining

the computational cost of the scheme in reasonable

parameters. Finding the best trade-off between these

two properties has been widely studied. There are ef-

ﬁcient solutions for Boolean formulae access struc-

tures in ABE system (Goyal et al., 2006), but for more

complex ones, such as Boolean Circuits (T¸ iplea and

agan, 2014; Hu and Gao, 2017a) we only have in-

efﬁcient solutions.

1.1 Our Contribution

Starting from the secret sharing for compartmented

access structure (CAS) proposed in (Ghodosi et al.,

1998), we propose a new access structure - CAS-

circuit. We build an efﬁcient KP-ABE system for

this structure, with decryption key linear in the access

structure size. Since (Tiplea et al., 2020) showed that

compartmented access structures cannot be expressed

via access trees, our new access structure offers more

expressiveness than Boolean formulae. Our scheme

is secure in the Selective Set Model for ABE, under

the decisional bilinear Difﬁe-Hellman Assumption.

Moreover, using the CAS-nodes, we can improve

the state-of-the-art solutions in terms of ABE for

Boolean circuits, namely, (T¸ iplea and Dr

agan, 2014)

for KP-ABE and (Hu and Gao, 2017a) for CP-ABE.

The CAS-node can be used to re-write a Boolean cir-

cuit such that the decryption key will be smaller and

the decryption algorithm will run faster. This brings

us one step closer to solving the open problem of con-

structing efﬁcient ABE schemes for Boolean circuits

from bilinear maps.

1.2 Related Work

The general idea of Attribute-based encryption was

introduced in (Sahai and Waters, 2005), and the ﬁrst

ABE system was proposed one year later in (Goyal

et al., 2006). In their system, the access policy is

represented as an access tree and it is associated with

the key (hence the name Key-Policy ABE). Their con-

struction is efﬁcient, the key size being linear in the

access policy size, and it is proven to be secure in

the Selective Set Model under the decisional bilinear

Difﬁe-Hellman (DBDH) Assumption.

Later on, Bethencourt et al. in (Bethencourt et al.,

2007) proposed the ﬁrst Ciphertext-Policy ABE sys-

tem. They used the same access structure as in (Goyal

et al., 2006), an access tree, but their security was only

proven in the generic group model. The ﬁrst CP-ABE

systems proven to be secure under cryptographic as-

sumptions in the standard model were introduced a

few years later in (Goyal et al., 2008; Waters, 2011).

ABE and Boolean Circuits. Garg et al. (Garg

et al., 2013) proposed the ﬁrst ABE system with

access structures represented by Boolean circuits.

They have shown that the sharing technique used for

Boolean formulae does not work for Boolean circuits,

and proposed a new ABE scheme, based on multi-

linear maps. Later, (Dr

agan and T¸ iplea, 2015) pro-

posed a more efﬁcient system, which relies on a sim-

ple form of multi-linear maps, called chained multi-

linear maps. Since at the moment there is no se-

cure cryptographic construction for any type of multi-

linear maps (Albrecht and Davidson, 2017; T

iplea,

2018), these two systems presented above have no

practical applicability.

T¸ iplea-Dragan (T¸ iplea and Dr

agan, 2014) pro-

posed the ﬁrst ABE system for Boolean circuits that

relies solely on bilinear maps, which proves to be

secure under the bilinear Decisional Difﬁe-Hellman

(BDDH) Assumption. They make use of special fan-

out gates (FO-gates) in their Boolean circuit represen-

tation, and for each such gate they attach a group el-

ement to the decryption key. Hu-Gao (Hu and Gao,

2017a) reﬁned their result and proposed a similar sys-

tem, which removes this element associated to the

FO-gates. (Hu and Gao, 2017b) creates a similar sys-

tem for KP-ABE, by expanding the circuit, resulting

in a Boolean access tree, equivalent to the initial cir-

cuit. However, all three systems presented above have

exponential key size and decryption time in the worst-

case scenario.

More progress regarding Boolean circuits ABE

schemes was made in the system recently proposed

in (Kowalczyk and Wee, 2019), which offers efﬁcient

solutions for NC

circuits for both CP and KP ABE

systems from bilinear maps. Their system is proven

to be secure under the k-Lin Assumption.

In (Bolocan, 2020) is proposed a solution for ABE

for general circuits using bilinear maps. However, this

solution’s correctness is questionable, due to the se-

cret sharing technique they provide for NAND gates.

More precisely, an output wire of such a gate will be

divided into a

and a

such that a = −a

− a

. a

and

are forwarded to the children nodes of the gate.

However, we note that in this case, the reconstruction

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures

231

is possible only if both values from the children are

available. This leads to an incorrect construction of

the scheme.

Secure ABE schemes for Boolean circuits (Gor-

bunov et al., 2015; Agrawal and Yamada, 2020) were

proposed from Learning With Errors (LWE) assump-

tion. Although LWE offers a strong security guaran-

tee, encryption schemes based on this assumption are

often impractical due to the great computing power

that they require (Steinfeld et al., 2019).

2 PRELIMINARIES

Bilinear Maps (Goyal et al., 2006). Given G

and

two multiplicative cyclic groups of prime order p,

a map e : G

× G

→ G

is called bilinear if it satis-

ﬁes:

• e(x

) = e(x,y)

, for any x,y ∈ G

and a,b ∈

;

• g

= e(g,g) is a generator of G

, for any genera-

tor g of G

is called a bilinear group if the operation in G

and e are both efﬁciently computable.

Decisional Bilinear Difﬁe-Hellman Assumption.

Let a, b,c,z ∈ Z

chosen randomly, and g a genera-

tor of G

The decisional BDH Assumption (Sahai and Wa-

ters, 2005) is that no polynomial-time algorithm

B can distinguish between (A = g

,B = g

,C =

,e(g,g)

abc

) and (A = g

,B = g

,C = g

,e(g,g)

)

with a non-negligible advantage.

The advantage of B is:

|Pr[B (A,B,C,e(g,g)

abc

)] − Pr[B(A,B,C,e(g,g)

)]|

where the probability is taken over the random choice

of the generator g, the random choice of a,b,c,z ∈ Z

and the random bits consumed by B.

Access Structures (Beimel, 2011). Let p

,..., p

be a set of parties. A collection A ⊆ 2

,...,p

}

monotone if B ∈ A and B ⊆ C imply that C ∈ A. An ac-

cess structure is a monotone collection A ⊆ 2

,...,p

}

of non-empty subsets of {p

,..., p

}. Sets in A are

called authorized, and sets not in A are called unau-

thorized.

Boolean Formulae and Boolean Circuits. A

Boolean circuit is a directed acyclic graph over a set

of input wires, concluding to a single output wire,

with internal nodes representing logical gates of type

AND, OR, or NOT. These gates may have fan-out

greater than 1. A monotone Boolean circuit is a cir-

cuit without negation gates. A Boolean formula is a

Boolean circuit where each node is limited to a fan-

out of 1.

KP-ABE Model. A Key-Policy Attribute-based en-

cryption scheme, as ﬁrst described in (Goyal et al.,

2006), consists of four algorithms:

setup(λ) A randomized algorithm that takes as input

the implicit security parameter λ and returns the

public and secret keys (MPK and MSK).

encrypt(m,A,MPK) A probabilistic algorithm that

encrypts a message m under a set of attributes A

with the public key MPK, and outputs the cipher-

text E.

keygen(C , MPK,MSK) This algorithm receives an

access structure C , public and master keys MPK

and MSK, and outputs corresponding decryption

keys DK.

decrypt(E,DK,MPK) Given the ciphertext E and

the decryption keys DK, the algorithm decrypts

the ciphertext and outputs the original message.

Selective-Set Model for KP-ABE (Goyal et al.,

2006).

Init The adversary declares the set of attributes A,

that he wishes to be challenged upon.

Setup The challenger runs the Setup algorithm of

ABE and gives the public parameters to the ad-

versary.

Phase 1 The adversary is allowed to issue queries for

private keys for many access structures A

, where

A /∈ A

for all j.

Challenge The adversary submits two equal length

messages M

and M

. The challenger ﬂips a ran-

dom coin b, and encrypts M

with A. The cipher-

text is passed to the adversary.

Phase 2 Phase 1 is repeated.

Guess The adversary outputs a guess b

′

of b. The ad-

vantage of an adversary A in this game is deﬁned

as Pr[b

′

= b] −

Notations and Abbreviations.

Notation Meaning

Γ A node in an access structure

attr(Γ) attribute corresponding to node Γ

(Γ) value of i-th input wire of gate Γ

Out(Γ) value of the output wire of gate Γ

SECRYPT 2023 - 20th International Conference on Security and Cryptography

232

3 OUR CONSTRUCTION

While access trees offer a decent level of expressive-

ness, it has been proven in (Tiplea et al., 2020) that

they cannot represent compartmented or multi-level

access structures. One way of achieving a more re-

ﬁned access control would be by using Boolean cir-

cuits instead of access trees. Unfortunately, at the

moment there is no efﬁcient and secure construction

of ABE systems for them. We can divide the existing

schemes into three categories, based on the crypto-

graphic primitives which they are using, and show for

each case why it cannot be used in practice:

• ABE for Boolean circuits from LWE (Gorbunov

et al., 2015): although secure, current LWE-

based ABE systems have large public keys, which

makes them unpractical.

• ABE for Boolean circuits from multi-linear maps

(Garg et al., 2013; Dr

agan and T¸ iplea, 2015):

multi-linear maps are very powerful primitives,

however, there is still no secure cryptographic

solution for implementing them. (Albrecht and

Davidson, 2017; T

iplea, 2018)

• ABE for Boolean circuits from bilinear maps:

For some Boolean circuits, the current approaches

could lead to an exponential expansion of keys or

ciphertexts.

The constructions from bilinear maps are the most

promising ones at the moment. In order to develop

more expressive ABE schemes which can be used in

practice, we focus on optimizing existing schemes for

Boolean circuits from bilinear maps.

One of the reasons for the great success of Goyal’s

et al. ABE scheme (Goyal et al., 2006) is that their ac-

cess tree policy could support more than just Boolean

formulae with AND and OR nodes: their construction

uses the more expressive threshold nodes (t out of n).

Similarly, we propose extending these access struc-

tures by

adding a new node type: a compartmented access

structure - node (further referred to as C AS−node).

However, to be able to create even more expres-

sive schemes, we provide construction for secret shar-

ing through a general circuit, by adding sharing tech-

niques for FO-gates. These are special gates intro-

duced in (T¸ iplea and Dr

agan, 2014), which multiply

the output of a node in order to represent Boolean cir-

cuits more easily. More details on the efﬁciency and

the improvements added by this new construction can

be found in Section 4.

3.1 Compartmented Nodes

A CAS-node Γ will be a special node having 1 out-

put wire (values associated to this wire are stored

in Out(Γ)) and n

input wires. These wires are di-

vided into k disjoint compartments, compartment i

having n

nodes, respecting n

= n

+ n

+ .. .n

The i-th compartment input wires are denoted with:

i.1

(Γ),In

i.2

(Γ),...In

i.n

(Γ). Each compartment i

will have a threshold t

associated to it: t

≤ n

, and

the CAS-gate will also have a general threshold t, such

that t

...t

≤ t ≤ n

A C AS-node Γ is satisﬁed if and only if:

• each compartment is satisﬁed (the number of the

satisﬁed input wires in the compartment i exceeds

or equals the threshold value t

)

• the general threshold value is satisﬁed: The sum

of all satisﬁed input wires of the gate is greater or

equal to the general threshold t

Since Ghodosi et al. (Ghodosi et al., 1998) pro-

posed an ideal secret sharing scheme for Compart-

mented Groups, we can apply a slightly modiﬁed

technique to our CAS-node. Thus, the share CAS(y)

procedure receives a value from Z

at the output wire

- Out(Γ), and assigns a single value to each input wire

i. j

(Γ), while ensuring that the reconstruction of the

initial value is possible if and only if the CAS policy

is satisﬁed.

share CAS(Γ,y):.

1. Let T = t −

∑

i=1

2. For each compartment, choose randomly the par-

tial secret y

and a public parameter p

from Z

such that y

+ y

+ .. .y

+ p

= y.

3. Then, for each compartment i = 1,... ,k: se-

lect randomly and uniformly t

− 1 values

i.1

,...,a

i.t

−1

from Z

corresponding to each

compartment i, i = 1, ...,k.

4. Choose randomly and uniformly T values

,...β

in Z

5. Determine a sequence of k polynomials,

(x) = y

+ a

i.1

x + ... + a

i.t

−1

+ β

... + β

+T −1

for every level i.

6. Assign the shares for each input node: In

i. j

( j), and publish P(Γ) = g

as the gate’s pub-

lic parameter.

Similar to most ABE schemes, in the reconstruc-

tion phase, the secret must be reconstructed using el-

ements from G

. For each value α associated to some

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures

233

AND

OR OR

3/5

1.1

⟨y

⟩

1.2

⟨y

⟩

2.1

⟨y

⟩

2.2

⟨y

⟩

2.3

⟨y

⟩

CAS - node

t = 4,n = 5

= 1,n

= 2

= 2,n

= 3

P=g

1.1

⟨y

⟩

1.2

⟨y

⟩

2.1

⟨y

⟩

2.2

⟨y

⟩

2.3

⟨y

⟩

(1)

(2)

(1)

(2)

(3)

Figure 1: Replacing a sub-circuit with an equivalent CAS-node. Shares obtained in (T¸ iplea and Dr

agan, 2014) sharing

compared to our scheme.

wire at the sharing phase, we will have a correspond-

ing value g

αs

attached to the same wire during the re-

construction phase. We further present how the re-

construction should be done:

recon CAS(Γ,P(Γ) = g

,S = g

,⟨e(g,g)

( j)s

,...,⟩):.

During the reconstruction phase in out ABE sys-

tem, for each satisﬁed input wire i. j of the CAS-

node Γ, we will have some value e(g,g)

( j)s

which represents the result of an equation of form:

e(g,g)

· e(g,g)

i.1

· .. . · e(g,g)

i.t

−1

e(g,g)

· .. . · e(g,g)

T +t

−1

=e(g,g)

s(y

i.1

j+...+a

i.t

−1

+β

+...+β

T +t

−1

)

=e(g,g)

( j)s

We need to select from each compartment ℓ

wires, namely j

i.1

, j

i.2

,... j

i.ℓ

, such that ℓ

≥

,ℓ

≥ t

,...ℓ

≥ t

and

∑

i=1

ℓ

= t.

Putting all such equations together from all input

wires, we obtain the equation system from Figure

Note that in this system the values y

, a

i. j

and β

are unknown, but we do know all j indices. We

have a system of t equations with t unknowns.

Therefore, we can compute the partial secrets

,...g

. Using these partial secrets, and the

gate’s public parameter P(Γ) we can compute

= e(g

,P(Γ))·g

·...·g

= g

s(p

+...y

)

We can simply observe that the system can be

solved if and only if the CAS-node is satisﬁed.

Sharing and Reconstruction Example. For a bet-

ter understanding, we provide an example of how

these procedures work in Figure 1. First, construct

the partial secrets y

and y

and p such that y =

+ y

+ p, and then the polynomials:

(x) = y

+ β

(x) = y

+ a

2.1

x + β

Since T = t −t

−t

= 1, we require a single value

common across all compartments. Then, each ter-

minal node will receive an evaluation of the poly-

nomial of his compartment. (Node 1.1 will receive

(1), 2.3 will receive q

(3), etc..)

If at the reconstruction phase we will receive at

least one element from each compartment, with a to-

tal of at least three elements, we will be able to recon-

struct the corresponding values from G

of the partial

secrets y

and y

, namely g

and g

, and then com-

pute the corresponding value in G

for the secret y:

= g

Note that using the CAS-node, we will obtain one

share for each input node. For comparison, using

the ﬁrst approach from (Tiplea et al., 2020) (a regu-

lar Boolean circuit) will result in two shares for each

input node.

3.2 Access Structure Based on

CAS-nodes

We can use our newly deﬁned CAS-node to con-

struct expressive access structures with efﬁcient secret

sharing. We extend the access structure proposed in

(Goyal et al., 2006), namely the access tree, to CAS-

nodes, resulting in an access structure that we call a

CAS-circuit.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

234











s(y

1.1

1.2

1.1

+...+a

1.t

−1

1.1

+β

1.1

+...+β

T +t

−1

1.1

)

= e(g,g)

( j

1.1

...

s(y

1.1

1.ℓ

1.2

1.ℓ

+...+a

1.t

−1

1.ℓ

+β

1.ℓ

+...+β

T +t

−1

1.ℓ

)

= e(g,g)

( j

1.ℓ











s(y

k.1

k.2

k.1

+...+a

k.t

−1

+β

k.1

+...+β

T +t

−1

k.1

)

= e(g,g)

( j

k.1

...

s(y

k.1

k.ℓ

k.2

k.ℓ

+...+a

k.t

−1

+β

k.ℓ

+...+β

T +t

−1

k.ℓ

)

= e(g,g)

( j

k.ℓ

Figure 2: Equation system.

Deﬁnition 1. A CAS-circuit is a tree with CAS -nodes.

Since threshold gate t/n can be modeled by a

CAS-node (by setting the threshold for each compart-

ment to 0, and the general threshold to t), then we can

model a Boolean formulae access structure through

a CAS-circuit. Although it has visually the form of a

tree, we have named our access structure a circuit, be-

cause T¸ iplea et al. proved in (Tiplea et al., 2020) that

CAS cannot be represented as Boolean formulae, but

as Boolean circuits. Therefore, we have that:

Proposition 1. The class of access structures repre-

sented by CAS-circuits is a proper extension of the

ones represented by Boolean formulae

Our construction is very efﬁcient for CAS-circuits,

producing only one decryption key element in G

for

each attribute and one element in G

for each access

structure internal node. Therefore, we can say that our

decryption key has linear size in the access structure

size.

3.3 Full Construction

We provide a full construction of our scheme for

CAS-circuits. For a better understanding, we have

separated the secret sharing part from our ABE

construction, by deﬁning two special procedures:

CAS circuit and recon CAS circuit. They

share and reconstruct a secret through a CAS-circuit

access structure. The sharing procedure starts with

a single value y assigned to the CAS-circuit’s output

wire and assigns values to all leaf nodes (correspond-

ing to attributes). The reconstruction procedure starts

with values in G

at the bottom of the CAS-circuit in

order to reconstruct the value e(g,g)

required for de-

cryption. We will denote with In

(Γ)/Out(Γ) the val-

ues associated with the i-th input/output wire of gate

Γ. Note that if a gate Γ

is the i-th children of another

gate Γ

, then In

(Γ

) = Out(Γ

We start by describing the sharing and reconstruc-

tion procedure, and then our full construction of the

KP-ABE scheme.

share CAS circuit(y,C ):.

1. Initially, all gates of C are unmarked;

2. Assign y to the output wire of the circuit:

Out(C ) = y

3. Choose an unmarked CAS-gate Γ with all

input wires deﬁned, and run ⟨α, P(Γ)⟩ =

share CAS(Out(Γ)). This returns a collection of

values α, where α(x.y) represents the value of the

x-th input node from the y-th compartment. Thus,

we set In

x.y

(Γ) = α(x.y). P(Γ) is the public pa-

rameter which is associated with this gate.

4. Repeat step 3 until all gates are marked.

5. Return S(Ψ) = Out(Ψ) for all terminal nodes Ψ

and the public parameters P of CAS-gates.

recon CAS circuit(C ,V,P).

1. Initially, all gates of C are unmarked;

2. Out(Ψ) = V

, for all leaf (starting) nodes Ψ.

Mark these nodes.

3. Choose an unmarked gate Γ with all input wires

deﬁned. We consider that Γ has k input wires, and

we do the following: Mark Γ and set Out(Γ) =

recon CAS(Γ,P,g

,In(Γ)).

4. Repeat step 3 until all gates are marked.

5. return the value from the output wire of the cir-

cuit: Out(C ).

3.3.1 KP-ABE for CAS-circuits Scheme

setup(λ). This algorithm receives a security parame-

ter λ, which is used to choose two multiplicative

groups G

and G

of prime order p, g a generator

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures

235

of G

, and a bilinear map e : G

× G

→ G

. The

set of attributes is deﬁned by U = {1,2 .. .n}.

Then choose random y ∈ Z

, and generate random

∈ Z

, and sets the public key as:

MPK = ⟨p,G

,e,g,n,Y = e(g,g)

= g

⟩

and the master key:

MSK = ⟨y,(t

,1 ≤ i ≤ n)⟩

encrypt(m,A,PK). The encryption algorithm re-

ceives a message m, and encrypts it under the

set of attributes A ⊆ U, with the public key mpk.

Generate a random element s ∈ Z

, and se the ci-

phertext as:

E = ⟨A,E

′

= mY

= g

⟩

keygen(MPK,C ). The key generation algorithm

shares the y component of the MSK through the

circuit using the sharing procedure:

S,P = share CAS circuit(y,C ).

Then, for every i ∈ U, output the decryption key

as:

DK = ⟨D

= g

,P⟩, where Ψ is a leaf node

decrypt(E,DK). This algorithm receives a valid ci-

phertext and a decryption key, and returns the

original message. For all leaf nodes Ψ, and con-

sidering i = attr(ψ), compute:











e(T

) = e(g

) = e(g,g)

if i ∈ A

⊥, otherwise

R = recon CAS circuit(C ,V,P)

Then compute the message as:

m = E

′

/R = m · e(g,g)

/e(g,g)

4 EFFICIENCY AND

IMPROVEMENTS

4.1 CAS-nodes in Other ABE Systems

Our CAS-node could be easily combined with other

access structures from other KP-ABE schemes. For

example, alongside AND and OR nodes, (T¸ iplea and

agan, 2014) or (Hu and Gao, 2017b) can be mod-

iﬁed to support also CAS-nodes, by simply adding to

the scheme the secret sharing and reconstruction pro-

cedures provided in our construction.

Similarly, our construction could be applied also

to CP-ABE schemes such as (Bethencourt et al.,

2007) or (Hu and Gao, 2017a) to increase expressive-

ness or efﬁciency. We show in the following sections

how this node can improve the efﬁciency of such sys-

tems.

4.2 Comparison with Other ABE

Systems

We provide comparisons of our system with exist-

ing KP-ABE systems. The relevant schemes are

Goyal et al.’s (Goyal et al., 2006), Tiplea-Dragan

(T¸ iplea and Dr

agan, 2014) and Hu-Gao (Hu and Gao,

2017b). Regarding the scheme proposed by Goyal et

al. (Goyal et al., 2006), we have only compared our

system with the access trees version. Their construc-

tion for Monotone Span Programs could offer a solu-

tion of similar efﬁciency. However, we do not know

how to efﬁciently convert a CAS-circuit to a Mono-

tone Span Program. Using the construction provided

in (Beimel et al., 1996), which transforms any Lin-

ear secret sharing scheme to a Monotone Span Pro-

gram, we obtain an impractically large matrix, with p

columns, where p represents the order of our group

Besides our basic construction for CAS-circuits,

we also added to the comparison an altered version

of our scheme, referred to as “Ours-2”, as we said

that we are able to do in Section 4.1. This scheme

supports, besides CAS-nodes, also threshold (from

(Goyal et al., 2006)) and FO gates (as in (Hu and Gao,

2017a) or (T¸ iplea and Dr

agan, 2014)).

The Ciphertext size and the setup/encryption algo-

rithms are the same in all these schemes. The decryp-

tion time in all these schemes is proportional to the

decryption key size. Therefore, we will only analyze

the key size in these systems.

In our comparison, we have considered that the ac-

cess structure contains n input nodes, r fan-out gates,

j input wires at each fan-out gate, and a total number

of q internal gates.

Note that the running time of the algorithms in-

volved in these schemes is directly proportional with

the number of pairings compute. Therefore, we

will analyze only the decryption algorithms in these

schemes, since it is the only one where the number

of pairings computed depends on the access struc-

ture size. For the encryption and key generation al-

gorithms there are no pairings involved, and the setup

phase makes use only of a constant number of pair-

ings. In the decryption algorithm, for each share re-

SECRYPT 2023 - 20th International Conference on Security and Cryptography

236

sulted after the secret sharing upon the access struc-

ture, we must compute a pairing. Therefore, it sufﬁces

to count the number of shares. The concrete analysis

can be seen in Table 1.

The basic version of our system (Referred to as

“Ours-1”) can only support CAS-circuits. However, it

is the most efﬁcient scheme available at the moment

for such access structures. With “Ours-2” we prove

that our node is useful in providing efﬁcient secret

sharing for CAS-circuit without losing expressiveness

or efﬁciency compared to existing KP-ABE schemes.

Although “Ours-2” does not have better results in the

worst-case scenario than the other schemes, we show

in Section 4.3 that CAS-gates actually can improve the

existing ABE schemes for Boolean circuits in some

cases.

4.3 CAS-Nodes in Boolean Circuits

While generating decryption keys, one would prob-

ably construct a Boolean circuit according to its re-

quirements. Given such an already deﬁned circuit, we

explain how it could be optimized using CAS-nodes.

Many sub-circuits can be expressed as CAS-nodes,

although at ﬁrst sight they do not comply to the typical

CAS structure. The only requirements that we have

for a sub-circuit to be represented as a CAS-node are:

• An AND node Γ

at the top of the sub-circuit

• Γ

and Γ

two children of Γ

(Γ

may also have

other children besides them)

• The set of children of Γ

is a proper subset of chil-

dren of Γ

Such circuits can be expressed as CAS-nodes by

creating a virtual compartment of threshold 0 which

will contain all children of Γ

which are not children

of Γ

. This can be seen as a CAS-node with two com-

partments: the virtual one and the one consisting of

children of Γ

For such a sub-circuit, the total number of shares

are reduced by: |Out(Γ

)| − |Out(Γ

) + 1|. Note that

if this sub-circuit occurs somewhere at the top of a

large circuit, this reduction in the number of shares

propagates all over the circuit.

We provide such an example of a sub-circuit that

can be modeled as a CAS-node in Figure 3. We can

consider the children of the OR-node (Γ

) as the ﬁrst

compartment. Node Z does not have a compartment

associated, therefore we will consider it to be in a vir-

tual compartment with threshold 0.

For the sub-circuit in Figure 3 (a) the best ap-

proach used until now in ABE system for secret shar-

ing over Boolean circuit access policy would result in

a total of 5 shares at the bottom (using the scheme

proposed by (T¸ iplea and Dr

agan, 2014)), while our

approach reduces the number of shares to 3.

We observe that sub-circuits which can be ex-

pressed as CAS-nodes (as the one Figure 3(a) ) are

quite common and may occur often in some larger

circuits.

4.3.1 Experimental Results

Because we could not estimate the beneﬁt of us-

ing CAS-nodes in general Boolean circuits, we have

tested how much these nodes could reduce the de-

cryption key size in practice. Thus, we have gener-

ated various random Boolean circuits with different

parameters and then replaced as many sub-circuits as

we were able to, with C AS-nodes.

While analyzing a Boolean circuit in order to

replace sub-circuits with CAS-nodes, we can ob-

serve that some sub-circuits may overlap. There-

fore, we must choose only some (non-overlapping)

circuits to be replaced. However, the problem of op-

timally choosing which sub-circuits to use in such

cases seems difﬁcult. In our implementation, we

have chosen randomly the sub-circuits that will be

replaced with CAS-nodes. The heuristic approaches

from (Ionita et al., 2023) could be adapted to the re-

placement process in order to obtain better results.

Our results can be seen in Table 2. The ﬁrst

four columns represent parameters of generated ac-

cess structure: Number of nodes, number of edges,

number of leaf nodes and the height of the Boolean

circuit. The last column (denoted with “% Opti-

mized”) represents how much the total number of the

shares has been reduced. More exactly, it represents

p from the formula S

· (1 −

100

) = S

, where S

de-

notes the number of share obtained with regular secret

sharing, and S

represents the number of shares ob-

tained after various sub-circuits being replaced with

CAS-nodes. Note that the percent of the optimization

will also be approximately equal to the percentage of

optimization of the running time, because the running

time of the decryption algorithm is directly propor-

tional with the number of pairings, which are by far

the most expensive operations. Recall that for each

share we should compute one pairing in the decryp-

tion algorithm. The encryption and the key genera-

tion algorithms are fast, since they require no pairing

operations.

5 SECURITY

We provide the full construction of a KP-ABE system

using our share and recon procedures. We stress that

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures

237

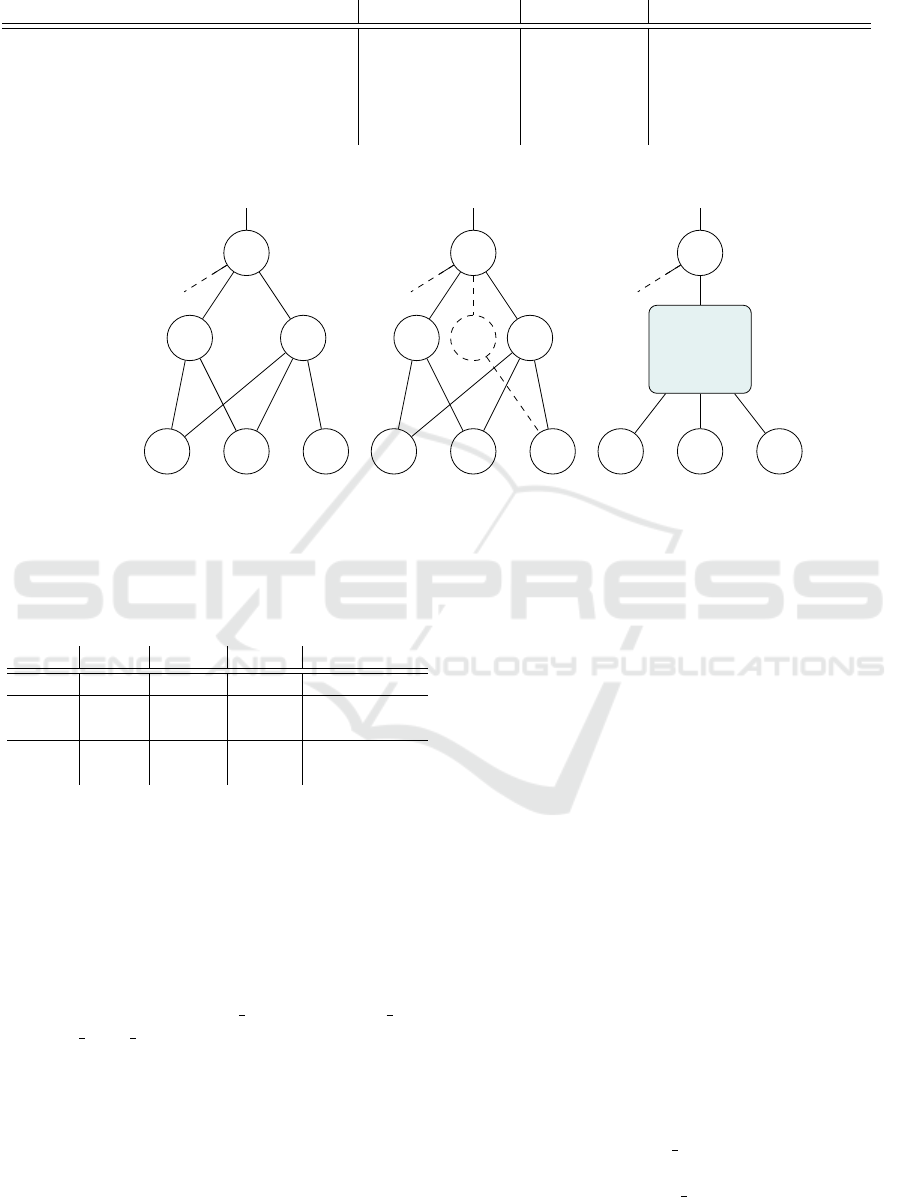
Table 1: Worst case decryption key size.

ABE system Bolean Formulae CAS-circuit General Boolean circuits

Goyal et al. (Goyal et al., 2006)

n Unsupported Unsupported

Tiplea-Dragan (T¸ iplea and Dr

agan, 2014) n n j + n + j

n j + n + j

Hu-Gao (Hu and Gao, 2017b) n n + j

n + j

Ours-1 (CAS-circuit) n + q n + q Unsupported

Ours-2 (general circuit) n n + q n + j

with access trees

AND

2/3

⟨α

,α

⟩

⟨α

,α

⟩

⟨α

⟩

(a) Secret sharing using (T¸ iplea and Dr

agan, 2014)

AND

1/2

0/1 2/3

⟨α

,α

⟩

⟨α

,α

⟩

⟨α

⟩

(b) Transformation to CAS

AND

′

CAS - node

t = 2,n = 3

= 1,n

= 2

= 0,n

= 1

P=g

⟨α

⟩

⟨α

⟩

⟨α

⟩

Figure 3: Replacing a sub-circuit with an equivalent CAS-node. Shares obtained in (T¸ iplea and Dr

agan, 2014) sharing

compared to our scheme.

Table 2: Key size.

Nodes Edges Leaves Height % Optimized

60 160 12 8 12.3%

50 100 12 7 10.24%

50 150 12 10 5.57%

70 200 12 10 21.20%

70 150 12 10 17.26%

these procedures could also be used in CP-ABE sys-

tems, such as (Bethencourt et al., 2007) or (Hu and

Gao, 2017a), to create more efﬁcient CP-ABE sys-

tems for Boolean circuits.

Our scheme is secure in the selective model under

the decisional bilinear Difﬁe-Hellman assumption.

Proof. In our security demonstration we will make

use of some special procedures, which we will de-

scribe beforehand: PolySat CAS, PolyUnSat CAS

and f ake share C AS. Due to space limitations, we

describe these procedures in detail in the Appendix.

Suppose that there exists a polynomial-time ad-

versary A that has an advantage ε for our scheme in

the Selective-Set model. We build a simulator B that

can play the decisional BDH with advantage ε/2, as

follows:

Let G

and G

be two groups, g a generator of G

and e an efﬁcient bilinear map, and the tuples (A =

,B = g

,C = g

= g

abc

) and (A = g

,B = g

,C =

= g

). The challanger ﬂips a coin p ∈ 0,1 and

chosses Z

. The adversary has to guess Z

between

and Z

Init. The simulator B runs the algorithm A, which

chooses the set of attributes A for encryption.

Setup. B simulates Setup algorithm of ABE and

sets Y = e(A, B) = e(g,g)

. Then, it generates ran-

dom r

and sets

(

, if i ∈ A

)

, otherwise

Then, it outputs the public parameters as:

⟨p,G

,e,g,n,Y,T

⟩

Phase 1. The adversary A is allowed to issue

queries for private keys for many access structures C

,such that C

(A) = 0 for all j. B will use in this scope

a procedure called f ake share, which will simulate

theese queries for A.

The deﬁnition of f ake share(g

,C ) is the follow-

ing:

SECRYPT 2023 - 20th International Conference on Security and Cryptography

238

1. Initially, all gates of C are unmarked;

2. Assign g

to the output wire of the circuit:

Out(C ) = g

3. Choose an unmarked gate Γ with all output wires

deﬁned, and then run the f ake share CAS al-

gorithm to obtain the values for child nodes

and the public values associated to the gate:

In(Γ),P(Γ) = f ake share CAS(Γ)

4. Repeat step 3 until all gates are marked.

5. Return ⟨S, PP⟩, where S(attr(Ψ)) = Out(Ψ) for

all terminal nodes Ψ.

B will run S,PP → f ake share(g

,C ) and com-

pute:

D(i) =

(

)

S(i)/r

if i ∈ A, i = attr(Ψ)

S(i)

1/r

, otherwise

Then forward to A:

DK = ⟨D, PP⟩

From A ’s point of view, the shares look as if they

were shared using the normal sharing procedure. By

using the reconstruct procedure with an approved set

of attributes, the recon procedure will return e(g,g)

abc

if applied to V (i, j) = e(g,g)

S(i, j)bc

for i ∈ A.

Challenge. A selects two equal length messages m

and m

. The challenger B ﬂips a random coin b, and

encrypts m

under the set of attributes A and by using

, p ∈ {0, 1}.

E = ⟨A,Y = m

· Z

= g

= T

⟩

If p = 0, then Z

= e(g,g)

abc

and E is a valid en-

cryption for m

. Otherwise, Y is a random element

from G

Phase 2. Phase 1 is repeated.

Guess. The adversary A outputs a guess b

′

of b. If

′

= b, then B outputs p = 0. Otherwise, it outputs

′

= 1

The advantage of B is:Phase 1 is repeated.

Adv(B) =Pr[p

′

= p] −

= Pr[p

′

= p|p = 0] · Pr[p = 0]+

+ Pr[p

′

= p|p = 1] · Pr[p = 1] −

Both Pr[p = 0] =

and Pr[p = 1] =

Next, we analyze the two cases:

• If p = 0, then A sees a valid encryption of the ci-

phertext, thus its advantage is Pr[p

′

= p|p = 0] =

+ ε.

• If p = 1, then the ciphertext offers no information

to A about the original message, thus in this case

Pr[p

′

= p|p = 1] =

Putting all toghether we obtain:

Adv(B) = Pr[p

′

= p|p = 0] · Pr[p = 0]+

+Pr[p

′

= p|p = 1] · Pr[p = 1] −



+ ε



−

5.1 CAS-node Public Parameter

Note that the public parameter of the CAS-nodes does

not provide additional security in any way. However,

it is needed in our security proof. We believe that this

parameter is not necessary, but we do not know how

to prove the security of our scheme without it.

6 CONCLUSIONS

The CAS-node adds a signiﬁcant improvement to

ABE systems for Boolean circuits from bilinear maps,

extending the class of practically efﬁcient access

structures to a new sub-class of Boolean circuits, the

CAS-circuit. Previous constructions of ABE schemes

((Goyal et al., 2006; T¸ iplea and Dr

agan, 2014)), when

adapted to CAS-circuits, are considerably less efﬁ-

cient than our version. This new access structure

proves to be a proper extension of the Boolean formu-

lae, lowering the gap between efﬁcient ABE schemes

with limited expressiveness (such as (Goyal et al.,

2006)) and the expressive ones with high computa-

tional demands (such as (Hu and Gao, 2017a; T¸ iplea

and Dr

agan, 2014)). Our construction is secure in

the Selective Set Model under the bilinear decisional

Difﬁe-Hellman Assumption.

Also, as we can see in our practical analysis,

the CAS-node can be used to optimize pre-deﬁned

circuits, by offering a more efﬁcient secret sharing

method. This could be only a ﬁrst step towards con-

structing more expressive and efﬁcient ABE systems.

Finding other structures with efﬁcient secret sharing

techniques may further enlarge the class of practically

efﬁcient access structures. A new possible direction

could be in ﬁnding such access structures and con-

structing ABE systems for them. This could, in the

end, could lead us to an efﬁcient ABE construction

for Boolean circuits.

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures

239

REFERENCES

Agrawal, S. and Yamada, S. (2020). Cp-abe for circuits

(and more) in the symmetric key setting. In Theory of

Cryptography Conference, pages 117–148. Springer.

Albrecht, M. and Davidson, A. (2017). Are graded encod-

ing scheme broken yet.

Attrapadung, N. and Imai, H. (2009). Attribute-based en-

cryption supporting direct/indirect revocation modes.

In IMA international conference on cryptography and

coding, pages 278–300. Springer.

Beimel, A. (2011). Secret-sharing schemes: a survey. In

International conference on coding and cryptology,

pages 11–46. Springer.

Beimel, A. et al. (1996). Secure schemes for secret sharing

and key distribution.

Bethencourt, J., Sahai, A., and Waters, B. (2007).

Ciphertext-policy attribute-based encryption. In 2007

IEEE symposium on security and privacy (SP’07),

pages 321–334. IEEE.

Bolocan, D. (2020). Key-policy attribute-based encryption

scheme for general circuits. Proceedings of the Roma-

nian Academy Series A-Mathematics Physics Techni-

cal Sciences Information Science, 21(1):11–19.

Chase, M. (2007). Multi-authority attribute based encryp-

tion. In Theory of Cryptography Conference, pages

515–534. Springer.

agan, C. C. and T¸ iplea, F. L. (2015). Key-policy attribute-

based encryption for general boolean circuits from se-

cret sharing and multi-linear maps. In International

Conference on Cryptography and Information Secu-

rity in the Balkans, pages 112–133. Springer.

ETSI (2018). Cyber; application of attribute based

encryption (abe) for pii and personal data

protection on iot devices, wlan, cloud and

mobile services - high level requirements.

https://www.etsi.org/deliver/etsi ts/103400 103499/

103458/01.01.01 60/ts 103458v010101p.pdf.

Ezhilarasi, T., Sudheer Kumar, N., Latchoumi, T., and Bal-

ayesu, N. (2021). A secure data sharing using idss

cp-abe in cloud storage. In Advances in Industrial

Automation and Smart Manufacturing, pages 1073–

1085. Springer.

Garg, S., Gentry, C., Halevi, S., Sahai, A., and Waters, B.

(2013). Attribute-based encryption for circuits from

multilinear maps. In Annual Cryptology Conference,

pages 479–499. Springer.

Ghodosi, H., Pieprzyk, J., and Safavi-Naini, R. (1998). Se-

cret sharing in multilevel and compartmented groups.

In Australasian Conference on Information Security

and Privacy, pages 367–378. Springer.

Gorbunov, S., Vaikuntanathan, V., and Wee, H. (2015).

Attribute-based encryption for circuits. Journal of the

ACM (JACM), 62(6):1–33.

Goyal, V., Jain, A., Pandey, O., and Sahai, A. (2008).

Bounded ciphertext policy attribute based encryp-

tion. In International Colloquium on Automata, Lan-

guages, and Programming, pages 579–591. Springer.

Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).

Attribute-based encryption for ﬁne-grained access

control of encrypted data. In Proceedings of the 13th

ACM conference on Computer and communications

security, pages 89–98.

Green, M., Hohenberger, S., Waters, B., et al. (2011). Out-

sourcing the decryption of abe ciphertexts. In USENIX

security symposium, volume 2011.

Hu, P. and Gao, H. (2017a). Ciphertext-policy attribute-

based encryption for general circuits from bilinear

maps. Wuhan University Journal of Natural Sciences,

22(2):171–177.

Hu, P. and Gao, H. (2017b). A key-policy attribute-based

encryption scheme for general circuit from bilinear

maps. IJ Network Security, 19(5):704–710.

Ionita, A., Banu, D.-A., and Oleniuc, I. (2023). Heuris-

tics optimization of boolean circuits with application

in attribute based encryption.

Kowalczyk, L. and Wee, H. (2019). Compact adaptively se-

cure abe for nc

from k-lin. In Annual International

Conference on the Theory and Applications of Cryp-

tographic Techniques, pages 3–33. Springer.

Sahai, A. and Waters, B. (2005). Fuzzy identity-based

encryption. In Annual International Conference on

the Theory and Applications of Cryptographic Tech-

niques, pages 457–473. Springer.

Steinfeld, R., Sakzad, A., and Zhao, R. K. (2019). Practi-

cal mp-lwe-based encryption balancing security-risk

vs. efﬁciency. Cryptology ePrint Archive, Report

2019/1179. https://eprint.iacr.org/2019/1179.

T¸ iplea, F. L. and Dr

agan, C. C. (2014). Key-policy attribute-

based encryption for boolean circuits from bilinear

maps. In International Conference on Cryptography

and Information Security in the Balkans, pages 175–

193. Springer.

Tiplea, F. L., Ionita, A., and Nica, A. (2020). Practically ef-

ﬁcient attribute-based encryption for compartmented

access structures. In Samarati, P., di Vimercati, S.

D. C., Obaidat, M. S., and Ben-Othman, J., editors,

Proceedings of the 17th International Joint Confer-

ence on e-Business and Telecommunications, ICETE

2020 - Volume 2: SECRYPT, Lieusaint, Paris, France,

July 8-10, 2020, pages 201–212. ScitePress.

Touati, L. and Challal, Y. (2016). Collaborative kp-abe for

cloud-based internet of things applications. In 2016

IEEE International Conference on Communications

(ICC), pages 1–7. IEEE.

Waters, B. (2011). Ciphertext-policy attribute-based en-

cryption: An expressive, efﬁcient, and provably se-

cure realization. In International Workshop on Public

Key Cryptography, pages 53–70. Springer.

Zhong, H., Zhu, W., Xu, Y., and Cui, J. (2018). Multi-

authority attribute-based encryption access control

scheme with policy hidden for cloud storage. Soft

Computing, 22(1):243–251.

iplea, F. L. (2018). Multi-linear maps in cryptography.

In Conference on Mathematical Foundations of Infor-

matics, pages 241–258.

SECRYPT 2023 - 20th International Conference on Security and Cryptography

240

APPENDIX

Procedures Used in Security

Demonstration:

PolySat CAS(y

,β) receives as input a value y

∈

and integers t

and k

representing threshold and

number of component of some compartment in a

CAS-node. β = β

,...β

represent the additional val-

ues, common in all compartments to be used as poly-

nomial coefﬁcients. Knowing y, we simply construct

a polynomial q

′

of grade t

− 1 by randomly choosing

its coefﬁcients with y

as free term. Then construct

the polynomial q(x) = q

′

(x) + β

+ .. . + β

+T −1

For every satisﬁed child j set q( j) as the value

associated to that wire, and for every unsatisﬁed wire

j set the value g

q( j)

PolyU nSat CAS(y

,β

′

): We stress that this func-

tion will receive the β coefﬁcients in G

: β

′

⟨g

,...g

⟩

• Let ℓ be the number of satisﬁed input wires, and

the wires: j

, j

,..., j

ℓ

, ℓ < t

• Choose randomly x

,...x

ℓ

and assign them to

the satisﬁed input wires

• Choose randomly ℓ

′

= t

− ℓ − 1 more values

ℓ+1

...x

−1

to completely deﬁne the polynomial

q, such that q(i) = x

• Then, the coefﬁcients a

of this polynomial can be

computed in G

·g

i.1

·.. .·g

i.t

−1

·g

·.. .·g

T +t

−1

= g

q( j)

• Evaluate this polynomial in some points to obtain

the rest of the values. Since β

′

contains values

from G

we can only compute the G

value of the

evaluation of q in some point, but this is enough,

since these values will be passed anyway to unsat-

isﬁed wires.

f ake share CAS(Γ): We consider that Γ is a CAS -

gate with k compartments with general threshold t,

and each one of the compartments has k

elements and

threshold t

, where i ∈ 1, k:

• Set T = t −t

−t

−.. .−t

the difference between

the general and the sum of partial thresholds.

• if the gate Γ is satisﬁed, then simply return

share CAS(Out(Γ)). (the secret sharing tech-

nique used in our scheme).

• if the gate Γ is not satisﬁed, then Out(Γ) = g

is a

value from G

Generate y

,...y

and compute P(Γ) from G

such that:

P(Γ) · g

∑

j=1

= Out(Γ).

Then randomly generate parameters β

,...β

from Z

, and for each compartment i choose val-

ues for its input wires In

i. j

(Γ), j ∈ 1,n

, by us-

ing PolySat CAS, or PolyUnsat CAS, depending

if the respective compartement is satisﬁed or not.

We say that a compartment i is satisﬁed if its num-

ber of satisﬁed input wires is strictly greater than

the threshold of the compartment.

• Return In(Γ) and public gate parameter P(Γ).

Optimizing Attribute-Based Encryption for Circuits Using Compartmented Access Structures

241