A Rand Index-Based Analysis of Consensus Protocols

Sangita Roy

1,∗ a

and Rudrapatna K. Shyamasundar

Thapar Institute of Engineering and Technology, Patiala, Punjab, India

Department of Computer Science and Engineering,

Indian Institute of Technology Bombay, Mumbai, Maharashtra, India

Keywords:

Blockchain, Consensus, Ripple Protocol, Fairness, Trust, Cluster.

Abstract:

Consensus is the heart of Blockchain Technology. Consensus algorithms suffer from issues of either energy

inefﬁciency in the context of Proof of Work (PoW) or monopoly in the context of Proof of Stake (PoS).

In other words, while PoW suffers from scalability and performance and PoS suffers from monopoly, both

fairness issues are from various interpretations of the blockchain platform. To overcome these issues, there

have been several hybrids of PoW and PoS consensus protocols. In this paper, we show how Rand Index can

be used for cluster analysis hence analyzing various aspects of consensus protocols. The analysis focuses on

issues like correctness, fork formation, and fairness aspects like overcoming monopoly, equal participation of

nodes in block creation, decreased latency in commit transaction, a fair selection of validators, minimizing

the size/requirement of permissioned networks, etc. We ﬁrst demonstrate our approach to the Ripple protocol

and correlate it with its’ analogies of correctness. We further show, how conditions like fork formations can

be overcome through our analysis. Toward the end of the paper, we propose a cluster environment model for

realizing a fair selection of validators.

1 INTRODUCTION

PoW is the most widely used trusted consensus in the

context of untrusted peer groups. In PoW, miners rig-

orously work on block generation requiring high en-

ergy to solve the computationally intensive puzzle. To

deal with this energy-inefﬁcient mechanism, PoS was

introduced that suffers from the “rich-gets-richer” is-

sue which is nothing but the power law distribution of

stake reward.

For considering the advantages of PoW and PoS

and their hybrid variations, we need to look at the un-

derlying fairness and trust of the system. In terms

of fairness analysis, we need to consider the advan-

tages of both mechanisms as otherwise the system

will either be energy inefﬁcient which is harmful to

the environment or it would be controlled by a few

rich miners which is totally unfair. To achieve ad-

vantages from both, the block must be generated by

PoW miners and it must be veriﬁed by PoS miners.

This mechanism will eliminate the monopoly of hash

power and it would also provide better security. So in

https://orcid.org/0000-0002-7366-0232

∗

Supported by Center for Blockchain Research funded

by Ripple Inc. USA.

fairness and trust analysis, two main concerns are in-

centive distribution and load distribution for which we

can design the network in such a way that one subset

will work as permission-less nodes where the other

subset can work as permissioned nodes.

In this paper, we consider cluster structures and

show how the hybrid concept of PoW and PoS can

be mapped into it and thus, effectively use a spectrum

of analysis measures used in cluster structure analy-

sis for analyzing the correctness or fairness issues of

consensus schemes. For instance, the entire Unique

Node List (UNL) concept used in the Ripple proto-

col to realize determinism under certain conditions of

the UNL list can be captured through such an anal-

ysis. Similarly, it is possible to derive conditions on

the underlying PoW and PoS in a hybrid consensus

protocol using cluster analysis that would diminish

the monopoly of miners of the entire network. These

mappings are formally described in section 3.

The rest of the paper is organized as follows.

Section 2 provides fairness aspects of different

blockchain consensus protocols. Section 3 discusses

the characteristics of the Ripple protocol and its anal-

ysis. Section 4 deﬁnes the cluster-based analysis of

the Ripple protocol. Section 5 provides fairness anal-

Roy, S. and Shyamasundar, R.

A Rand Index-Based Analysis of Consensus Protocols.

DOI: 10.5220/0012148200003555

In Proceedings of the 20th International Conference on Security and Cryptography (SECRYPT 2023), pages 567-576

ISBN: 978-989-758-666-8; ISSN: 2184-7711

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

567

ysis through cluster modeling environment and con-

cludes with section 6.

2 A BRIEF OF CONSENSUS AND

FAIRNESS IN PoW AND PoS

SYSTEMS

Fairness is an important concern for the design of

various mechanisms in blockchain technology e.g.

transaction, payment, incentive, and the consensus

protocol itself. Through consensus algorithms, the

blockchain network participants come to a common

point of agreement about the present state of the dis-

tributed ledger. In this section, we will brieﬂy discuss

the working principles of some of the most important

consensus algorithms and their pros and cons from a

fairness point of view. Such a brief will provide an

idea as to how fairness is maintained in blockchain

platforms or the challenges of arriving at fairness.

Due to space limitations, we conﬁne our discussion

of fairness requirements to the Ripple consensus pro-

tocol.

• Proof of Work (PoW):

PoW was introduced to set all transactions in a

decentralized manner by eliminating the role of

intermediaries. Like other networks, the PoW

system is maintained by some nodes known as

miners that solve a complex computationally in-

tensive puzzle for purposes of block formation.

On average, mining takes 10 minutes in the Bit-

coin system to create a new block. The entire

process is highly expensive in terms of cost and

energy. PoW system lacks scalability though it

is highly secure and reliable (Nakamoto, 2009).

Popular examples of PoW cryptocurrency are Bit-

coin, Litecoin, and Dogecoin.

Pros:

1. The consensus algorithm provides complete de-

centralization.

2. It works on a permissionless model.

Cons:

1. It fails to defend against 51% attack.

2. Consumes a lot of energy for achieving consen-

sus and has no energy-saving mechanism.

3. Very high transaction speed >100s.

4. Very low throughput <100tps

• Proof of Stake (PoS):

The PoS consensus algorithm is the best-ﬁtted al-

ternative to PoW to reduce cost and energy (Ge

et al., 2022). Block validation is based on the

number of coins staked by the node. More the

stake, the holder is more likely to be chosen as a

block validator. Popular examples of PoS cryp-

tocurrency are Ethereum, Cardano, Solana and

Polkadot, Tezos, Cosmos, Algorand, and Syn-

thetix Network.

Pros:

1. Energy efﬁcient consensus algorithm.

2. Works on a permissionless model and offers

high scalability as compared to PoW.

3. Better veriﬁcation speed <100s and throughput

<1000tps as compared to PoW

Cons:

1. It’s semi-centralized and not fully decentralized

like PoW.

2. Does not offer protection against 51% attack as

the validator with the highest stake of coins can

dominate and perform malicious activity.

3. Less secure than PoW.

4. Rich-gets-richer.

Huang et. al. (Huang et al., ) focus on rich-

gets-richer concern in terms of incentives/rewards for

rich and poor miners. In PoS, the majority of the

stake/coin is controlled by the rich miner i.e., who has

invested more money. And the number of rich miners

is very less. The authors (Huang et al., ) propose two

types of fairness: – expectational fairness and robust

fairness. In expectational fairness, the reward should

be proportional to the amount of investment; i.e., the

reward is identical for every miner/investor. In robust

fairness, the relationship between initial investment

and reward is characterized in a more sophisticated

way taking into account all possible outcomes.

Liu et. al. (Taherdoost, 2023) introduces fair-

ness in blockchain consensus through an intermediary

where the protocol is fair towards the owner and inter-

mediary but not to the users. That is, the intermediary

is asked to create a transaction contract for the owner

with a hash value. If the hash value is unpublished

earlier, then the transaction is committed through an

intermediary under certain conditions like a valid sig-

nature. In the entire scenario, the intermediary is re-

sponsible for preventing the double spending attack.

Such a protocol is not fair toward Sybil attack as an

intermediary and the owner can be the same person.

Ahmed et al. (Ahmed and Kostiainen, 2018) dis-

cuss unfairness in a random selection of participants

. As the distributed number selection itself is a difﬁ-

cult task, the authors introduce a Robust Round Robin

method for leader selection where the selection pro-

cess happens deterministically in every round. Round

Robin algorithm is applied with some initial predeter-

mined identities to avoid vulnerabilities. This method

SECRYPT 2023 - 20th International Conference on Security and Cryptography

568

achieves fairness in permissionless blockchain con-

sensus but lacks resistance to Denial of Service (DoS)

attacks.

Other PoS-based consensus protocols suffer from

fairness from various perspectives. In Ouroboros

Praos(David et al., 2017), the randomness is provided

in each round and the selection of a leader can be bi-

ased. RapidChain (Zamani et al., 2018) introduced a

“selection committee” through which the distributed

randomness generation protocol is done. In this case,

the target is the committee and this protocol is very

expensive.

Apart from these consensus protocols, there are

several other PoS-based consensus protocols that suf-

fer from various aspects of fairness. For example,

in Delegated Proof of Stake (DPoS) more stake you

have, the more block reward you will get (Binance,

2023). Witnesses can make a crew and hence can

start a monopoly in ruling the network. It is semi-

centralized and hence exposed to 51% attacks by ma-

licious nodes. It is not safe against double-spending.

Power is in the hands of a selected few nodes. Hence,

the unfair distribution of incentives takes place.

To determine validators, Proof of Time (PoT) em-

ploys a voting system and considers validators’ net-

work active time as well as their reputation in the net-

work (Zebpay, ). The base of this consensus is DPoS

which is a modiﬁed version of PoS. The more you

perform diligently; you will get a chance for higher

incentives. Although the system is more equitable,

establishing a reputation may take a long time. If you

want to jump in and start validating right away, PoT

may discourage you by not selecting you as a valida-

tor.

In Proof of Elapsed Time (PoET), a signed timer

object is assigned randomly to every node and when

the timer expires for a node, that node becomes block

leader and generates a new block (Curran, ). Though

PoET is good for permissioned networks, as dis-

cussed earlier, the third-party involvement itself is an

unfair decision.

Proof-of-Weight (PoWeight) is a blockchain con-

sensus mechanism that assigns a ‘weight’ to users

based on the amount of cryptocurrency they own

(Frankenﬁeld, ). The network is protected from dou-

ble spending attacks until a majority of the weighted

users are honest. But it can not provide resistance

against 51% attack.

Proof of Importance (PoI), which is based on PoS,

rewards users who actively transact on the network.

PoI needs nodes having enough invested currency

with Importance Score (Mark, ). The Importance

Score is calculated based on the hoarding time of cur-

rency. The node having a higher stake with less hoard-

ing time gets more Importance Score. This consensus

suffers from the rich-gets-richer problem.

Except for this incentive-centric fairness, the other

concern of fairness is transaction ordering. Orda et.

al. (Orda and Rottenstreich, 2019) consider pro-

posal validation based on the combined information

or agreement from the members/nodes of the net-

work. Helix protocol (Asayag et al., 2018) introduced

equal probability distribution for a transaction to be

selected for a block. According to age-aware fairness

(Sokolik and Rottenstreich, 2020), the transaction is

prioritized if the latency is high. Other works which

focus on transaction ordering fairness are Fair share

(Lev-Ari et al., 2019), Receive-order-fairness (Kelkar

et al., 2020), Relative order fairness (Kursawe, 2020)

etc.

Liu et. al. (Liu et al., 2018) analyzed fairness

in cryptocurrency payments. They surveyed differ-

ent protocols which are modeled in leverage fairness

in the “payment-for-receipt” exchange mechanism. If

service is provided properly, the payment should be

done on time and properly, and vice versa.

Lagaillardie et. al. (Lagaillardie et al., 2019) dis-

cussed fairness in the Tendermint blockchain. If the

system is fair, a user tends to stay in the system oth-

erwise they tend to leave. Tendermint is a committee-

based system that ﬁnds agreement among the valida-

tors. It provides a fair platform for validators.

Some consensus protocols have been designed by

combining PoW and PoS to get the best results e.g.,

Proof of Activity (PoA) (Seth, ). Proof of Activity

combines the mechanisms of PoW and PoS. Initially,

by using PoW, the miner, mines an empty block hav-

ing only header information and the address of the

reward. Once the empty block is mined, PoS comes

to the sensation for the next step of work, where val-

idators are chosen randomly to validate and sign the

new block. The protocol suffers from the following:

• High energy consumption for mining blocks.

• Due to massive computation, the mining process

takes a lot of time.

• Requires expensive hardware for computation.

• There’s nothing at stake from both miners and val-

idators leading to internal conﬂicts and a bad rep-

utation.

• The number of validators could be less due to a

lack of interest.

From the above discussion

, it is clear that most

of the algorithms suffer in terms of fairness and scal-

There have been several subtle aspects of PoS systems

that have been incorporated in the recent switch over from

POW to POS in the Ethereum blockchain platform; we shall

not be discussing them here.

A Rand Index-Based Analysis of Consensus Protocols

569

ability. Consensus algorithms are either energy inef-

ﬁcient or suffered from monopoly. Some consensus

tried to hybridize the basic consensus algorithms e.g.,

hybridization of PoW and PoS. But the entire voting

system for the selection of validators is a matter of

question and it is even harder in the presence of mali-

cious users.

In this paper, we analyze fairness in the agreement

process in the Ripple protocol. The aspect of fairness

is to reduce the monopoly in the validation system and

we show how fairness can be achieved in the presence

of malicious users. We have considered the underly-

ing Byzantine Fault Tolerance problem and analyzed

the agreement and fairness in Ripple protocol using

Rand Index.

3 RIPPLE CONSENSUS

ALGORITHM (RPCA): A BRIEF

In this section, we brieﬂy describe the Ripple consen-

sus algorithm (Schwartz et al., 2014). Unlike Bitcoin

and Ethereum, the native cryptocurrency XRP uses

the RPCA which provides faster transactions. It is

also low-cost in nature, scalable, more stable, sustain-

able, and decentralized ledger. All the consensus al-

gorithms are designed based on Byzantine Generals’

Problem (BGP). PoW and PoS are two different vari-

ations used by Bitcoin and Ethereum respectively to

come to grips with the Byzantine Problem. Accord-

ing to BGP, let’s say η number of generals want to

take decisive measures to attack a target. For taking

a decision, generals can only communicate with each

other through messengers. In this scenario, the fol-

lowing cases can occur:

• Few generals may agree to attack, rest are not

agreed.

• Few generals can conspire to spoil the plan as they

can be corrupted.

• If messengers are corrupted, they may deliver

false messages to a few generals.

• Messengers may get delayed to reach a general

unintentionally / intentionally.

RPCA is used to handle these types of situations in

blockchain networks where a conjugate decision of a

group of nodes will be considered to take a proper

decision in a trustless environment.

3.1 RCPA Working Principle

In this section, we will make a component comparison

between BGP and RPCA. Table 1 depicts the equiva-

lent components of BGP and RPCA.

Table 1: Component comparison between BGP and RPCA.

Byzantine Generals’

Problem

RPCA

Battalion Blockchain network

General Server/Node

Messenger Connection

Loyal General Loyal Node

Traitor General Faulty Node

Set of Generals having

the same decision

UNL (Unique node

list)

• According to RPCA (the strategist) all loyal nodes

should come up with the same decision or no de-

cision at all. The strategist cannot tolerate any de-

cision in between.

• Strategist asks each node to select the other nodes

of similar interests or to whom they can trust. The

outcome of this choice will create a Unique Node

List (UNL).

• If the decision in a UNL is agreed upon by 80%

of the other nodes in that particular UNL, the de-

cision will be ﬁnalized by the server.

• As the strategist (RPCA) is following Byzantine

Fault Tolerance which is 20%, according to it, the

system can only tolerate 20%, fault or less than it.

• The method will be repeated by each server in ev-

ery UNL.

In short, the distribution of nodes is done in such

a way that different sub-nets will communicate with

each other considering network fault and latency so

that consensus will be established throughout the en-

tire network. The authors of the Ripple protocol pro-

posed a concept of a list of nodes known as a Unique

Node List (UNL). It is shown that, in the blockchain

network, it is enough to have a subset/subnet for

broadcasting the transaction as well as voting. But

the entire operation must be done inside a single sub-

net. If the subnets are separate from each other, an

agreement cannot be established as subnets cannot

communicate with each other. Only nodes within a

single UNL can communicate with each other, hence

forking will be high. If the connection is established

among subnets, forking will be minimized and strong

acceptance will be realized. An analysis of the Ripple

protocol is given below.

3.2 RPCA Analysis

The Ripple protocol that focuses on distributed pay-

ment systems achieves correctness, agreement, and

utility using certain levels of “tolerance” threshold.

The consensus process considers a network of a given

SECRYPT 2023 - 20th International Conference on Security and Cryptography

570

size, a number of malicious users, and some latency

over communication. When all these properties con-

verge at a certain point, we can say that nodes have

reached a correct agreement.

According to the Ripple protocol consensus, there

are n number of servers, say s

, where i = 1,2,.. ., n,

and server s

contains n

number of nodes, say N

i j

where j = 1,2, .. ., n

. Notice that here n

can be equal

to n

for some i and j. Now for some servers, s

a fraudulent transaction can be seen as a Byzantine

fault, and the loss of service due to it requires con-

sensus and it can be seen as a Byzantine failure. In a

server, if we assume X as the total number of Byzan-

tine failures, then the correctness will be maintained

as long as the total number of Byzantine failures is

less than equal to some tolerance level, that is

X ≤ (n

− 1)(1 −

100

) (1)

where t denotes the tolerance level. According to

Lamport et. al. (Lamport et al., 1982), the Byzan-

tine General Problem does not allow more than

(n−1)

byzantine faults or we can say, not more than 33%

nodes can act as a malicious node. The other interpre-

tation is, if there exists n number of nodes in a UNL,

then the broadcast message can reach at max (n − 1)

nodes and not more than one-third of those (n − 1)

nodes can act as malicious nodes. To achieve this,

we can simply put the value of tolerance t as 67%

in 1 to achieve byzantine failure. Similarly, several

other algorithms reported different Byzantine consen-

sus: Fab Paxox (Martin and Alvisi, 2006) reported

(n−1)

Byzantine failure, i.e tolerance t is 80%, Attiya

et. al. (Attiya et al., 1984) reported

(n−1)

Byzantine

failure, i.e tolerance t is 60%.

Note that in a server, s

, each node, say N

i j

, where

j = 1,2, ...n

has two choices to decide either to col-

lude and join a nefarious cartel or not to collude. If

we assume that the probability that a node, N

i j

joins a

nefarious cartel is p

then the probability a node does

not collude is simply 1 − p

. Now each node can be

seen as a Bernoulli trial with exactly two outcomes

i j

(

1 with probability p

0 with probability(1 − p

)

Here 1 represents that the node is colluding and 0

represents that the node is not colluding. In other

words, 1 can be seen as the occurrence of a Byzan-

tine failure. Since there are n

number of nodes

in the server s

, and our interest lies in the proba-

bility of a total number of nodes colluding in the

server or a total number of Byzantine failures. There-

fore, we can have X =

∑

i= j

i j

, here an event A

i j

= 1 on the j-th trial}, and so X can have val-

ues 0,1, .. ., n

. Note that A

,. .. ,A

are inde-

pendent. Therefore, for one particular outcome, say

∩ A

∩ ...,A

i−1

∩ A

, the probability of

occurrence of this particular outcome is given by

P(A

∩ A

∩ ...,A

i−1

∩ A

)

= p

(1 − p

). .. p

(1 − p

) = p

(1 − p

)

−x

Here the calculation is not dependent on which set of

x A

i j

s occur, only some set of x occurs. Also, the

event X = x will occur no matter which set of x A

i j

occurs. Putting this all together we see that a proba-

bility of a particular outcome with exactly x number

of colluding has the probability p

(1 − p

)

−x

of oc-

currence. However, there are n

number of nodes and

if interest lies in selecting exactly x number of collu-

sion, then there can be a total





number of different

outcomes. Therefore we have

P(X = x|n

, p

) =





(1 − p

)

−x

;x = 0, 1,2,...,n

Note that, random variable X denotes the total

number of nodes colluding in a server s

(having n

number of nodes) follows Binomial distribution with

parameters n

and p

, denoted as Binomial(n

, p

) with

the above-given probability mass function. Recall

that the correctness will be maintained as long the to-

tal number of Byzantine failures are less than a toler-

ance level that is X ≤ (n

−1)(1−

100

). Therefore the

probability of correctness is given by

P(X ≤ ⌈(n

− 1)(1 −

100

)⌉)

⌈(n

−1)(1−

100

)⌉

∑

x=0





(1 − p

)

−x

(2)

Here ⌈.⌉ denotes the ceiling function. The reason

to consider it is that X can only take integer values

between 0 and n

, and for a given value t the value

of (n

− 1)(1 −

100

) may turn out have positive real

value.

Next, we consider different tolerance levels of t,

the number of nodes, and the probabilities that a node

joins a nefarious cartel, and calculate the probabili-

ties of correctness using (2) and are shown in Table

2. From the tabulated values it can be seen that with

a ﬁxed value of p

, increasing the number of nodes

provides a higher probability of correctness. Also

with higher values of tolerance t probability of cor-

rectness decreases. Further, note that if in a network,

we consider all the servers having the same probabil-

ity of colluding that is p

= p

= . .. = p

= p, then

X ∼ Binomial(N, p) distribution, where N =

∑

i=1

is the total number of nodes in the network having n

number of servers. It can be seen that the probability

A Rand Index-Based Analysis of Consensus Protocols

571

Table 2: Probability of correctness for different values of n

and p

t = 70 t = 75 t = 80

0.10 0.15 0.20 0.10 0.15 0.20 0.10 0.15 0.20

50 0.9999 0.9980 0.9691 0.9997 0.9868 0.8894 0.9906 0.8800 0.5835

100 1.0000 0.9999 0.9939 0.9999 0.9970 0.9125 0.9991 0.9336 0.5594

150 1.0000 0.9999 0.9987 1.0000 0.9996 0.9554 0.9999 0.9621 0.5486

200 1.0000 1.0000 0.9997 1.0000 0.9999 0.9655 0.9999 0.9780 0.5421

300 1.0000 1.0000 0.9999 1.0000 0.9999 0.9856 0.9999 0.9922 0.5344

of correctness increases in such cases. In (Schwartz

et al., 2014), the authors have considered 80% toler-

ance that is t = 80 with 200 nodes, and have reported

the probability of correctness to be 0.9780. This can

be interpreted as achieving the 0.9780 probability of

correctness with 80% tolerance and p

= 0.15, in the

network having at least 200 nodes. As the number

of nodes decreases below 200, the probability of cor-

rectness also decreases, and vice versa. If one is inter-

ested to achieve a given probability of correctness, say

with a given tolerance and p

, the required number

of nodes can be calculated by solving the following

equation.

P(X ≤ ⌈(n

− 1)(1 −

100

)⌉) = P

(3)

In fact, one can see the probability of correctness

given by (2) as a function of t, n

, and p

, and for a

ﬁxed probability of correctness to achieve the value

of any one of the t, n

and p

can be computed by

giving any of the two values in (3). This can be useful

to analyze:

• How many nodes are required in a server to

achieve a ﬁxed probability of correctness by giv-

ing the values of t and p

• How much tolerance can be allowed in a server to

achieve a ﬁxed probability of correctness by giv-

ing the values of n

and p

• How much probability of colluding can be enter-

tained in a server to achieve a ﬁxed probability of

correctness by giving the values of n

and t?

4 APPLICATION OF

CLUSTER-BASED ANALYSIS

OF RPCA

In this section, we analyze RPCA by treating the sub-

nets as clusters that preserve some intended proper-

ties, treating the faults in general as general byzan-

tine, and the activity of each subnet as the activity of

a cluster preserving similarity property. Our analysis

below shows that connectivity among clusters plays

a vital role in accepting new transactions and block

creation to increase the chain of blocks.

According to RPCA, every UNL needs 80% nodes

to agree at a single point of decision as the network

cannot tolerate more than 20% faulty nodes. All

servers contact their own UNL and come to a point

to agree upon. For instance, consider two different

UNLs, one UNL is full of traitor nodes and the other

one is full of loyal nodes. In both cases, UNLs will

conclude as per their own decision and hence, they

separately come to a point of agreement. This il-

lustrates how the two UNLs can make contradictory

decisions. If the interconnection is established be-

tween the above-said UNLs (traitors and loyal), then

as per the Byzantine Generals’ Problem at most 20%

of traitor nodes can be replaced by 20% loyal nodes

and hence, the traitors’ UNL cannot make any wrong

decision. Before capturing the UNL criterion for con-

sensus formally in the cluster-based analysis, we shall

deﬁne the notion of rand index.

4.1 Rand Index: A Brief Overview

Rand Index is a similarity measurement of two data

clusters (Wikipedia, 2022). By Rand Index, we can

calculate the number of agreements and disagree-

ments in terms of node pairs from the same or dif-

ferent clusters.

Consider a network with N number of nodes

having two (2) different partitions or clusters of

the network, say C

′

= (C

′

,. .. ,C

′

) and let

′′

= (C

′′

,. .. ,C

′′

). Here the meaning of parti-

tion/clusters is that of non-empty disjoint subsets of

the network such that their union equals N. Observe

that the set of all unordered pairs of the network hav-

ing





pairs is the disjoint union of the following

deﬁned sets:

A = {pairs that are in the same clusters under C

′

and

′′

}

B = {pairs that are in different clusters under C

′

and

′′

}

SECRYPT 2023 - 20th International Conference on Security and Cryptography

572

C = {pairs that are in the same cluster under C

′

but

different in cluster C

′′

}

D = {pairs that are in different cluster under C

′

but in

the same cluster under C

′′

}

Therefore the Rand index to measure the similarity

between two clustering C

′

and C

′′

is given by

R =

|A| + |B|

|A| + |B| + |C| + |D|

|A| + |B|





2(|A| + |B|)

N(N − 1)

Here |A| + |B| can be considered as the number of

agreements between C

′

and C

′′

, and |C| + |D| as the

number of disagreements between C

′

and C

′′

. Notice

that as the denominator |A| + |B| + |C|+ |D| is the to-

tal number of unordered pairs of nodes, it can be writ-

ten as





. Now here the Rand index represents the

frequency of occurrence of agreements over the total

pairs of nodes, or the probability that C

′

and C

′′

will

agree on a randomly chosen pair of nodes. Mathemat-

ically the sets can be written as:

A = {(o

) | o

∈ C

′

∈ C

′′

}

B = {(o

) | o

∈ C

′

∈ C

′

∈ C

′′

∈ C

′′

}

C = {(o

) | o

∈ C

′

∈ C

′′

∈ C

′′

}

D = {(o

) | o

∈ C

′

∈ C

′

∈ C

′′

}

for some 1 ≤ i, j ≤ n,i ̸= j,1 ≤ k,k

≤ r,k

̸=

,1 ≤ l,l

≤ s,l

̸= l

For illustrative purposes, consider a network (Fig-

ure 2 {a,b,c,d,e, f ,g,h,i, j, k}. Further, let us have

two partitions C

′

= {{a,b,c,d,e, f },{g,h, i, j, k}}

and C

′′

= {{a,b, c,d, e},{ f , g},{h, i, j,k}}.

The meaning of these clusters is - network 1

has 6 nodes ({a, b,c, d,e, f }) and network 2

has 5 nodes ({g,h, i, j,k}) and they have two

common nodes { f ,g}. Then we have A =

{(a,b), (a,c), (a,d), (a,e),(b,c),(b,d),(b,e),(c,d),

(c,e)(d, e),(h, i),(h, j),(h,k),(i, j),(i,k),( j,k)}

with |A| = 16. Further B =

{(a,g), (a,h), (a,i),(a, j),(a,k), (b,g), (b,h)...}

with |B| = 29. Therefore we get R =

2(16 + 29)/(110) = 0.81. Now if we consider

′′

= {{a,b,c,d},{e, f ,g,h},{i, j, k}} i.e. Figure 4,

then rand index turn out 0.67. This means the fork has

been reduced from 0.81 to 0.67 just by considering

another partition, and therefore Rand Index is highly

dependent upon the number of clusters. Rand index

can be computed easily using the following code in

R-statistical programming language:

library(fossil)

#define clusters C1 and C2

C1 = c(1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2)

C2 = c(1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3)

#calculate Rand index between C1 and C2

rand.index(C1, C2)

We have analysed a spectrum of cases of agree-

ment and it is clear that the more the interconnections

among clusters, better is the fairness in terms of in-

centive and load/node distribution in the blockchain

network. In a similar manner, we can consider these

intersection nodes as open permissioned nodes which

actually support PoS consensus. Figure 1 to Figure 4

diagrams show the importance of interconnections to

inﬂuence fairness.

Figure 1 shows Cluster 1 and Cluster 2 and ini-

tially that do not have any common nodes or mem-

bers. Each cluster achieves correct consensus inde-

pendently, and hence, they violate the agreement. The

connectivity of the two clusters reduces disagreement

between them. The connectivity represents the com-

mon members from both clusters who arrive at a sin-

gle point of agreement. More the common members,

the higher the agreement. Fig 1 represents two sep-

arate clusters having independent consensus to fol-

low. In this case, the fork formation is maximum as

there is no point of agreement (no common members).

Through rand-index as explained above, we calculate

the number of times a pair of elements belong to the

same cluster across two different clustering methods

along with the number of times a pair of elements are

in different clusters across two different clusters over

all possibilities.

In Figure 2, the rand-index is 81% where the com-

mon members are 18% of the total nodes of two clus-

ters. That means, unlike 100% fork as in Figure 1,

in Figure 2 fork is reduced to 81%. As we increase

the common members’ percentage of two clusters, we

can observe the fork percentage gets reduced. In Fig-

ure 3, the rand index is 74% whereas the common

member involved percentage is 27%. In Figure 4, val-

ues are 67% and 36% respectively.

Figure 1: Two separate clusters having independent consen-

sus.

Our further step is to distribute the percentage of

nodes of the entire network among permissionless

and permissioned consensus under a byzantine fault-

A Rand Index-Based Analysis of Consensus Protocols

573

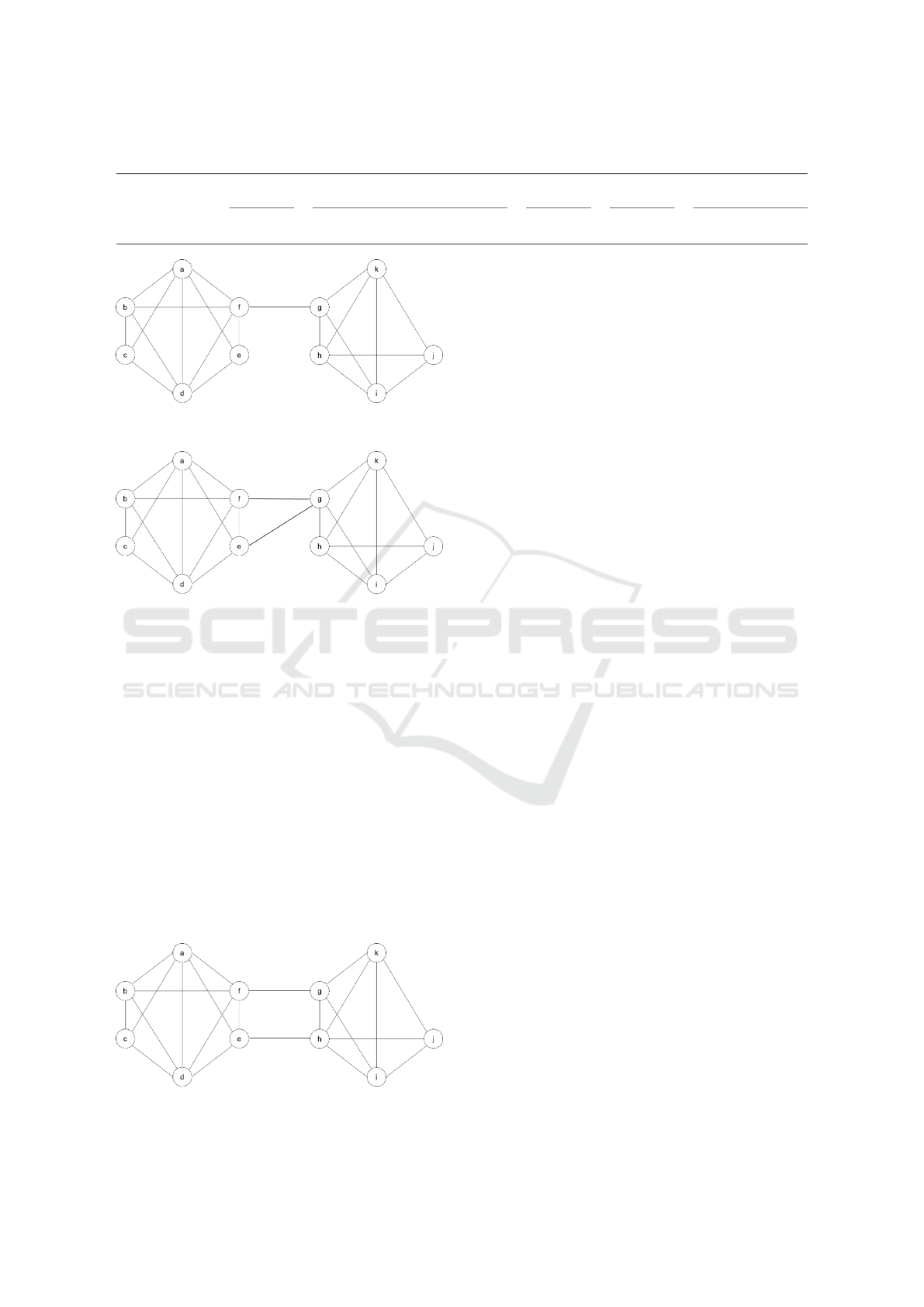
Table 3: Stake distribution over network nodes.

Nodes A B C D E F G H I J K L M N O P

Stake 42 42 39 38 37 37 37 33 27 22 10 13 9 7 6 1

Cluster C1 C2 C3 C4 C5

Stake percentage 21% 55.25% 12% 5.7% 5.7%

Figure 2: Two common members from two different clus-

ters.

Figure 3: Three common members from two different clus-

ters.

tolerant environment for fairness analysis.

5 FAIRNESS ANALYSIS

In section 3, we have shown how the connections be-

tween two different consensus-driven networks can

agree upon a single agreement. The analysis shows

how minimal connections between two different con-

sensus decisions can impact on agreement and hence,

fairness. In the Ripple protocol, there are two aspects

of fairness analysis:

• One is communication latency and

• the other one is validator selection.

If we go for the basic validator’s role in a PoS pro-

Figure 4: Four common members from two different clus-

ters.

tocol, we can come to the conclusion that PoS has

several advantages over PoW in terms of energy sav-

ing, computational requirements, and time. Despite it,

PoS suffers from many drawbacks, and few of which

are listed below:

• The control of the network is fully under the um-

brella of stakeholders. The more stake you have

the more control you have.

• As the control is under the stakeholders, the sys-

tem is more prone to act in a centralized manner.

• It has the potential of getting a 51% attack by the

malicious user because anyone can hold that much

stake of the total network stake hence the chance

of malicious activities.

• Smaller nodes have very less power in the vali-

dation of transactions and hence PoS possesses a

lack of proper decentralization which is the key

factor of BlockChain technology.

• Scalability is poor as the transaction speed is com-

paratively slower than PoW and fees are also very

high.

• As priority plays a big role in the PoS-enabled

network, there is a chance of inefﬁcient use of re-

sources as compared to energy consumption.

• Last but not least, if there are multiple stakehold-

ers having the same stake/priority, what should be

the way to break the tie?

In the Ripple protocol, if we consider different

UNLs and the role of nodes separately, we can design

the user’s role in a decentralized manner with efﬁcient

resource utilization. It also can solve the priority is-

sues hence the rich-gets-richer problem can be solved.

For example, consider a network of 16 nodes (say

A to P). The minimum stake possessed by node P

is 1 and the maximum stake is 42 possessed by two

nodes A and B. The network is subdivided into sev-

eral clusters based on their stake value. The range of

each cluster is 0 to 9, 10 to 19, 20 to 29, and so on.

Based on this clustering scheme, we have 5 clusters

in our example. Instead of calculating each node’s

stake percentage, we calculate cluster-wise stake per-

centage. For example, cluster 1 has two nodes A and

B and their stakes are 42 and 42 respectively. So the

percentage of cluster stake is (42+42)/400 where 400

is the total stake of the network. In this example, we

can see two tie conditions and one attack condition:

SECRYPT 2023 - 20th International Conference on Security and Cryptography

574

• Two or more nodes (A-B and E-F-G) having the

same stake inside a cluster.

• Two clusters (4, 5) have the same percentage of

stake.

• Cluster 2 has more than 51% stake i.e. 55.25%.

The Algorithm 1 describes the validator selection pro-

cess. The following terms are used in the Algorithm

Total Number of Clusters =⇒ C (C

.. . C

) Block

Validator =⇒ B Total Number of Nodes in a Cluster

=⇒ NC Block having highest Stake in a Cluster =⇒

NC Total Stake of Network =⇒ ST Stake Percentage

=⇒ SP

1. Total Number of Clusters =⇒ C (C

.. . C

)

2. Block Validator =⇒ B

3. Total Number of Nodes in a Cluster =⇒ NC

4. Block having highest Stake in a Cluster =⇒ NC

5. Total Stake of Network =⇒ ST

6. Stake Percentage =⇒ SP

Data: C, N

Result: B

min stake ← 1;

max stake ← 49% o f ST ;

B ← b;

Aged Node Flag ← ON;

for Cluster in C

to C

if SP < 49% o f ST and SP(C

) >

SP(C

i+1

) then

for node in C

, i = 1 .. .NC do

if node[i] > node[i+1] then

while

min stake ≤ b ≤ max stake

B ← b, min stake ≤ b ≤

max stake

end

else

Aged Node Flag ← OFF

end

else

Divide Cluster into two parts

end

Algorithm 1: Selection of Block Validator.

The informal interpretation of the Algorithm 1 is

given below:

Step 1: First we check the cluster stake percentage.

It should not cross 49% of the total stake.

Step 2:

If( no attack condition)

Block selection can be done by the highest cluster

stake.

Else

The aged node of the highest cluster will be inacti-

vated until the next block is created.

Step 3: Once the next block is created, the aged

node can be shifted to another cluster having a low

percentage of stakes by adding or subtracting stakes

to fulﬁll the cluster range.

Step 4: If there is a collision between two or more

clusters, the aged node can be removed in the same

manner to break the tie.

Step 5: Except for the publishing nodes, other nodes

will take part in validation in a round-robin manner

as per their chronological order of stake percentage.

6 CONCLUSIONS

In this paper, we have introduced a cluster-based anal-

ysis to provide an analysis of RPCA and its validator

selection fairly. For the agreement analysis, we have

used the Rand Index and shown that more the com-

mon members, the more the reduction in forking. We

have observed that to achieve the 0.9780 probability

of correctness with 80% tolerance and pi = 0.15, there

should be at least 200 nodes required. We further

have provided an idea of fair validator selection infor-

mally. A full formalization of the ”fair validator” is

being carried out. We have also brieﬂy discussed var-

ious several fairness aspects of different blockchain

consensus protocols that shall indicate the application

of our approach for formalizing the respective fair-

ness requirements of the different consensus proto-

cols; while we have analyzed RPCA in this paper, we

are working on formalizing the others in our frame-

work. Further, we are exploring the various hybrid

consensus protocols like Redbelly (Crain et al., 2021)

etc., in our framework for arriving at a theoretical

analysis that needs to be validated against the demon-

strated effectiveness of the Redbelly blockchain.

REFERENCES

Ahmed, M. and Kostiainen, K. (2018). Identity aging: Efﬁ-

cient blockchain consensus. CoRR, abs/1804.07391.

Asayag, A., Cohen, G., Grayevsky, I., Leshkowitz, M., Rot-

tenstreich, O., Tamari, R., and Yakira, D. (2018). A

fair consensus protocol for transaction ordering. pages

55–65.

Attiya, H., Dolev, D., and Gil, J. (1984). Asynchronous

A Rand Index-Based Analysis of Consensus Protocols

575

byzantine consensus. In ACM SIGACT-SIGOPS Sym-

posium on Principles of Distributed Computing.

Binance, A. (2023). Delegated Proof of Stake Ex-

plained. https://academy.binance.com/en/articles/

delegated-proof-of-stake-explained. [Online; ac-

cessed 01-February-2023].

Crain, T., Natoli, C., and Gramoli, V. (2021). Red belly: A

secure, fair and scalable open blockchain.

Curran, B. What is Proof of Elapsed Time Consen-

sus? (PoET) Complete Beginner’s Guide. https:

//blockonomi.com/proof-of-elapsed-time-consensus/.

[Online; accessed 01-February-2023].

David, B., Ga

zi, P., Kiayias, A., and Russell, A.

(2017). Ouroboros praos: An adaptively-secure,

semi-synchronous proof-of-stake protocol. Cryptol-

ogy ePrint Archive, Paper 2017/573. https://eprint.

iacr.org/2017/573.

Frankenﬁeld, J. Proof-of-Weight. https:

//www.investopedia.com/terms/p/

proof-elapsed-time-cryptocurrency.asp. [Online;

accessed 13-March-2023].

Ge, L., Wang, J., and Zhang, G. (2022). Survey of consen-

sus algorithms for proof of stake in blockchain. Secu-

rity and Communication Networks, 2022.

Huang, Y., Tang, J., Cong, Q., Lim, A., and Xu, J. Do

the rich get richer? fairness analysis for blockchain

incentives.

Kelkar, M., Zhang, F., Goldfeder, S., and Juels, A. (2020).

Order-fairness for byzantine consensus. Cryptology

ePrint Archive, Paper 2020/269. https://eprint.iacr.

org/2020/269.

Kursawe, K. (2020). Wendy, the good little fairness wid-

get: Achieving order fairness for blockchains. In Pro-

ceedings of the 2nd ACM Conference on Advances in

Financial Technologies, AFT ’20, page 25–36, New

York, NY, USA. Association for Computing Machin-

ery.

Lagaillardie, N., Djari, M. A., and G

urcan, n. (2019).

A computational study on fairness of the tendermint

blockchain protocol. Information, 10(12).

Lamport, L., Shostak, R., and Pease, M. (1982). The byzan-

tine generals problem. ACM Trans. Program. Lang.

Syst., 4(3):382–401.

Lev-Ari, K., Spiegelman, A., Keidar, I., and Malkhi, D.

(2019). Fairledger: A fair blockchain protocol for ﬁ-

nancial institutions.

Liu, J., Li, W., Karame, G. O., and Asokan, N. (2018). To-

ward Fairness of Cryptocurrency Payments. IEEE Se-

curity and Privacy, Volume 16, issue 3:9.

Mark. Proof of Importance. https://www.mycryptopedia.

com/proof-of-importance/. [Online; accessed 20-

March-2023].

Martin, J.-P. and Alvisi, L. (2006). Fast byzantine con-

sensus. IEEE Trans. Dependable Secur. Comput.,

3(3):202–215.

Nakamoto, S. (2009). Bitcoin: A peer-to-peer electronic

cash system.

Orda, A. and Rottenstreich, O. (2019). Enforcing fairness

in blockchain transaction ordering.

Schwartz, D., Youngs, N., and Britto, A. (2014). The ripple

protocol consensus algorithm.

Seth, S. Proof-of-Activity (PoA). https:

//www.investopedia.com/terms/p/

proof-activity-cryptocurrency.asp#:

∼

:text=Proof%

2Dof%2Dactivity%20(PoA)%. [Online; accessed

20-March-2023].

Sokolik, Y. and Rottenstreich, O. (2020). Age-aware fair-

ness in blockchain transaction ordering. pages 1–9.

Taherdoost, H. (2023). Smart contracts in blockchain tech-

nology: A critical review. Information, 14(2).

Wikipedia (2022). Rand index. [Online; accessed 30-Dec-

2022].

Zamani, M., Movahedi, M., and Raykova, M. (2018).

Rapidchain: Scaling blockchain via full sharding. In

Proceedings of the 2018 ACM SIGSAC Conference on

Computer and Communications Security, CCS ’18,

page 931–948, New York, NY, USA. Association for

Computing Machinery.

Zebpay. What Is Proof Of Time Consensus? https:

//zebpay.com/in/blog/what-is-proof-of-time. [Online;

accessed 01-February-2023].

SECRYPT 2023 - 20th International Conference on Security and Cryptography

576