A Successive Quadratic Approximation Approach for Tuning Parameters

in a Previously Proposed Regression Algorithm

Patrick Hosein

, Kris Manohar and Ken Manohar

Department of Computer Science, The University of the West Indies, St. Augustine, Trinidad

Keywords:

Regression, Parameter Tuning, Convex Optimization, Machine Learning.

Abstract:

We investigate a previously proposed regression algorithm that provides excellent performance but requires

signiﬁcant computing resources for parameter optimization. We summarize this previously proposed algo-

rithm and introduce an efﬁcient approach for parameter tuning. The speedup provided by this optimization

approach is illustrated over a wide range of examples. This speedup in parameter tuning increases the practi-

cability of the proposed regression algorithm.

1 INTRODUCTION

Parameter optimization or tuning is the process of

evaluating potential parameter values to identify the

optimal value for the related objective function. This

optimal value results in an output value for the objec-

tive function that is either the minimum output if it is

a cost function or the maximum output if it is a util-

ity function. Parameter optimization can be a time-

consuming and even a manual process. However, it

is important to invest the time to complete this and

achieve the best possible performance.

The proposed regression algorithm in (Hosein,

2023) addresses the bias-variance trade-off and deter-

mines the optimal trade-off between personalization

and robustness and illustrates the approach using an

automobile insurance claims dataset. This algorithm

depends on a tuning parameter κ with an objective

function of Mean Square Error (MSE). As MSE is a

cost function, the optimal value of κ will result in the

minimum MSE value.

The relationship between MSE and κ was ob-

served to be a nonlinear function with a consistent

shape. The function is initially convex but then be-

comes concave and approaches a limiting value from

below. Therefore, the optimal value of κ that mini-

mizes the MSE lies in the convex region but note that

this is not a pure convex optimization problem.

Gradient descent is a popular optimization algo-

rithm. It can iterate and move along the direction of

https://orcid.org/0000-0003-1729-559X

https://orcid.org/0000-0001-9079-2475

the steepest negative gradient until the minimum point

is reached. However, it may get stuck at saddle points

and it introduces additional hyper-parameter tuning

for its learning rate. Newton’s method can potentially

converge faster than gradient descent but this requires

an analytic function for which the second derivative

exists and can be computed. For our problem this is

not the case.

Quadratic approximation involves approximating

a nonlinear function with a simpler quadratic func-

tion. Successive quadratic approximation (SQA) it-

eratively approximates an objective function with a

quadratic function and then solves to ﬁnd the mini-

mum point of the quadratic function. On each iter-

ation, the minimum point of the quadratic function

move towards converging with the minimum point

of the objective function. Given that a single pa-

rameter is to be optimized, i.e. κ, and the observed

shape properties of the function, we use a successive

quadratic approximation approach which we describe

in detail later.

2 PREVIOUS WORK AND

CONTRIBUTIONS

Since the previously proposed regression algorithm is

relatively new there are no publications on the param-

eter optimization aspect which is our focus. There

are papers on parameter optimization for regression

as for example the work done in (Wang et al., 2021).

However their focus is on developing a tuning-free

Hosein, P., Manohar, K. and Manohar, K.

A Successive Quadratic Approximation Approach for Tuning Parameters in a Previously Proposed Regression Algorithm.

DOI: 10.5220/0012148900003541

In Proceedings of the 12th International Conference on Data Science, Technology and Applications (DATA 2023), pages 629-633

ISBN: 978-989-758-664-4; ISSN: 2184-285X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

629

Huber Regression approach whereas we are looking

at a completely different regression approach which

we describe later.

In the paper (Stuke et al., 2020) the authors as-

sess three different hyperparameter selection meth-

ods: grid search, random search and an efﬁcient au-

tomated optimization technique based on Bayesian

optimization. They found that for a large number

of hyper-parameters, Bayesian Optimization and ran-

dom search are more efﬁcient than a grid search. We

also illustrate that our proposed hyper-parameter tun-

ing approach is more efﬁcient than a grid search.

Our contribution is an improvement on the param-

eter optimization method used for the regression algo-

rithm presented in (Hosein, 2023). We demonstrate,

through examples, the potential speedup in computa-

tion thus increasing the usability of their regression

algorithm.

3 PROBLEM DESCRIPTION

Let us ﬁrst consider the case of a single feature with

ordinal independent values (e.g., age). Denote the de-

pendent value of sample i by y

and the independent

value by x

. Suppose we need to predict the dependent

value for a test sample with independent value ˆx. One

predictor is the average of the dependent variable over

all samples with independent value ˆx. However there

may be none, or few samples, to obtain a robust pre-

diction. We can instead include nearby samples in the

prediction (i.e., aggregation) but how “big” should the

neighbourhood be and how much weight should we

assign to our neighbours. We use the following ap-

proach. We take a weighted average of the dependent

values over all samples but weight the average based

on the distance between the independent values of the

test sample and each training sample. In particular we

use the following predictor.

ˆy(κ) ≡

∑

s∈S

(1+d

)

∑

s∈S

(1+d

)

(1)

where d

= | ˆx−x

|, S is the set of training samples and

κ is a hyper-parameter. Note that, if κ = 0 then the

predictor is simply the average taken over dependent

values of all samples. If there are one or more sam-

ples such that x

= ˆx then as κ goes to inﬁnity then the

predictor tends to the average of these samples. The

optimal κ typically lies somewhere between these ex-

tremes. One can ﬁnd the optimal value of κ by doing

a linear search but that requires a signiﬁcant amount

of computing. We introduce an efﬁcient approach to

ﬁnding the optimal value of κ.

Note that one can perform a similar computation

in the case of categorical data. In this case the dis-

tance between two samples is deﬁned as the absolute

difference between the average dependent values of

the categories of the two samples. In addition, this

approach can be extended to multiple features. In

this case the distance between two samples is the Eu-

clidean distance based on the single feature distances

(with some normalization). However, we again need

to optimize over κ. We provide examples for this case

as well. More details on the regression algorithm can

be found in (Hosein, 2023).

4 AN ILLUSTRATIVE EXAMPLE

We determine the optimal κ as follows. For a given

κ we use K-Fold validation to determine the resulting

Normalized Mean Square Error. This is the MSE di-

vided by the MSE obtained if the predictor was just

the average over all samples of the dependent vari-

ables (in the training set). Hence we obtain a value of

1 at κ = 0. We then ﬁnd the value of κ that minimizes

this NMSE.

Let E(κ) represent the Normalized Mean Square

Error given a parameter value κ. In practice, we have

found that this function has the shape illustrated in

Figure 1. The function is convex to the left of the

dashed line and concave and increasing to the right.

The minimum point lies within the convex region. We

can summarise the proposed optimization approach as

follows. Starting with any three points on the curve

we determine the quadratic function passing through

these points. If this quadratic function is convex then

we ﬁnd the minimum point and replace the maximum

of the previous three points with this new point. If,

however, this quadratic function is concave then we

know that the minimum lies to the left of the point

with the smallest κ value. In this case we replace

the three points with (1) the point with the lowest κ

value, (2) the point at κ = 0 and (3) the point midway

between these two. The quadratic function through

these three points is guaranteed to be convex and so

we can continue the process. This ensures that we

gradually move to the convex region and, once there,

we converge to the minimum value. Pseudo-code for

this algorithm is provided in Algorithm 1.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

630

Algorithm 1: Pseudo-code for Quadratic approximation Algorithm.

1: E(κ) ≡ normalized mean square error for κ

2: If E(0.5) ≥ 1 then κ

∗

< 0.5 so EXIT (feature is not useful)

3: Set κ

= 0, κ

= 10, κ

= 20, κ

∗

= κ

argmin

{E(κ

)}

4: Set ε = 1 + ν (ν determines the level of accuracy obtained)

5: while (ε > ν) do

6: (a, b, c) ← coefﬁcients of quadratic through points at κ

, κ

and κ

7: if (a ≤ 0) then

8: κ

= min

{κ

}, κ

, κ

= 0

9: else

10: κ

argmax

{E(κ

)}

←

−2a

11: end if

12: ε = |κ

∗

− κ

argmin

{E(κ

)}

13: κ

∗

← κ

argmin

{E(κ

)}

14: end while

15: Return κ

∗

E(κ)

Figure 1: Typical Shape of the E(κ) Function.

5 NUMERICAL EXAMPLES

5.1 Computation Comparison

In this section we provide some numerical examples

to compare the number of evaluations required before

we obtain an acceptable value for κ. We compare

this with the number of iterations required for a lin-

ear search. Suppose our stopping criterion is when

ε ≤ ν. If we were to do a grid search then, in order to

obtain similar performance, the grid search spacing

must be at least ν. We therefore must start at κ = 0

and increase κ by at most ν in each iteration. If the

resulting optimal value is κ

∗

then once we reach this

point the NMSE will start increasing and we can then

stop. Therefore the number of iterations required is

approximately

∗

and hence we can use this to de-

termine the number of iterations required with a linear

search.

5.2 Insurance Risk Assessment

In this section we use the dataset that was used in (Ho-

sein, 2023) to illustrate the potential computation sav-

ings. We used six features from the Comprehensive

policies of the dataset and a threshold of ν = 0.01.

In Table 1 we provide the values for each step of the

process. In Step 0 we initialize the ﬁrst 3 points. Note

that we only need to evaluate the function for κ = 10

and κ = 20 since we know the value at κ = 0 is 1. The

minimum point for the associated quadratic function

occurs at κ = 14.88 and so we replace the point at zero

(which has a value greater than the other two points)

with this point. However, these three points now form

a concave function and so in Step 2 we choose κ val-

ues of (0, 5, 10). In all remaining steps the three

points form a convex quadratic and we repeat until

there is very little change in the best (so far) value of

κ.

After 9 iterations we converge for the chosen

threshold of ν = 0.01. A linear search would have

taken approximately 9.20/0.01 = 920 iterations. In

other words the computation time of the proposed ap-

proach would be approximately 1% of the time for a

linear search. If we had instead set ν = 0.1 then the

A Successive Quadratic Approximation Approach for Tuning Parameters in a Previously Proposed Regression Algorithm

631

7.5

8.5

9.5

10.5

11.5

0.649

0.650

0.651

0.652

0.653

E(κ)

Unit-Spaced Samples

Quadratic Approximation Samples

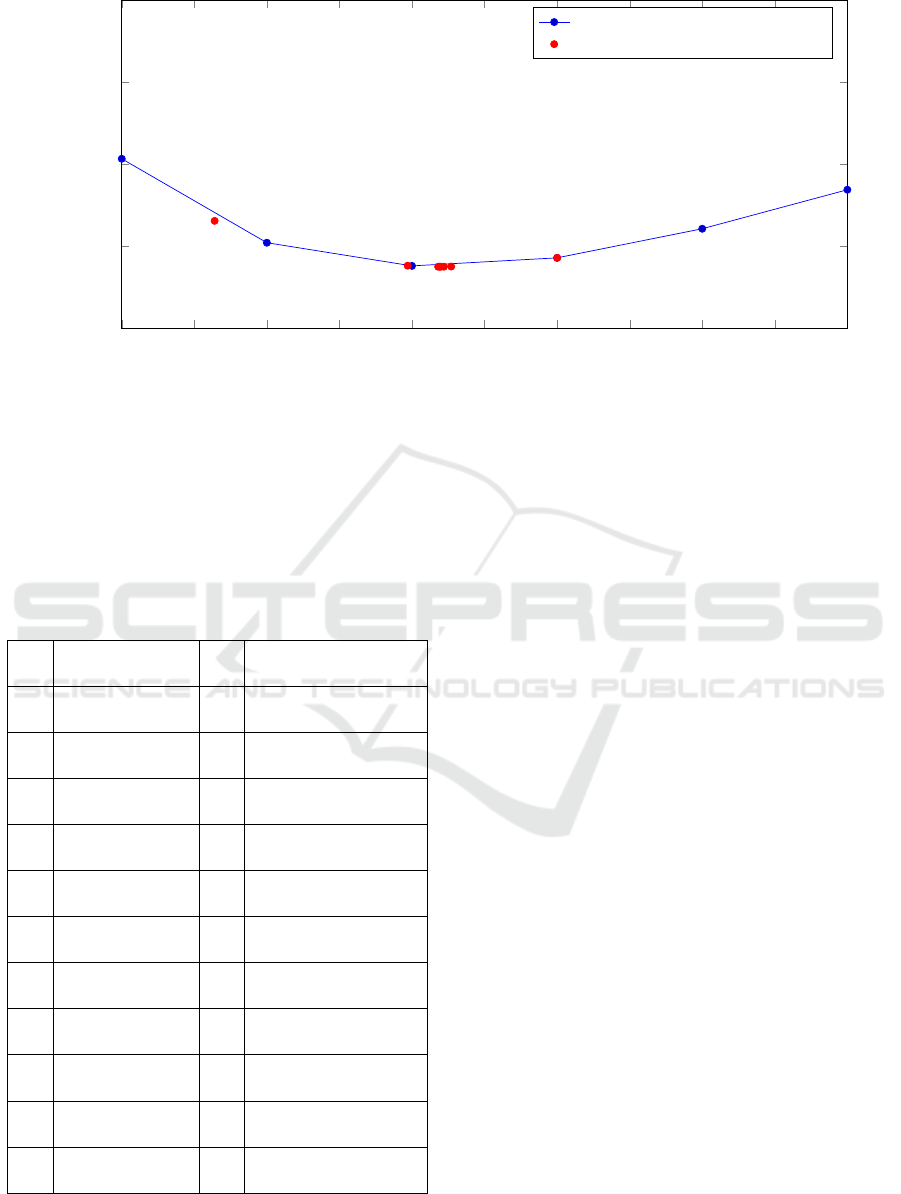
Figure 2: E(κ) as a function of κ for Selected Features.

speed up would have been (9.2/0.1)/6 = 15. In Figure

2 we plot the minimum values for each iteration but

only for points near the optimum. We ﬁnd that, after

4 iterations, we already have a reasonable result (at

κ = 8.97) and for most practical purposes this result

is sufﬁcient.

Table 1: Summary of Steps in the Algorithm.

Step (κ

, κ

) κ

∗

E(κ

∗

)

0 (0, 10, 20) 10.0 0.6498572510787386

1 (10, 14.88, 20) 10.0 0.6498572510787386

2 (0, 5, 10) 10.0 0.6498572510787386

3 (5, 7.64, 10) 10.0 0.6498572510787386

4 (7.64, 8.97, 10) 8.97 0.6497613579708842

5 (8.97, 9.27, 10) 9.27 0.6497511801524423

6 (8.97, 9.22, 9.27) 9.22 0.6497490840222766

7 (9.18, 9.22, 9.27) 9.18 0.6497489707751954

8 (9.18, 9.22, 9.20) 9.20 0.6497489687581092

9 (9.18, 9.19, 9.20) 9.19 0.6497489655206691

10 (9.19, 9.19, 9.20) 9.19 0.6497489655206691

6 ADDITIONAL NUMERICAL

EXAMPLES

We ran several additional examples and determined

the speedup provided for each of them for different

levels of κ accuracy. The datasets for these examples

were taken from the UCI Machine Learning Reposi-

tory (Dua and Graff, 2017). The details of these ex-

amples are as follows:

1. Single Ordinal Feature. We used the age feature

of the student-math dataset (Cortez, 2014).

2. Singe Categorical Feature. We used the internet

feature of the student-math dataset (Cortez, 2014).

3. Mix of Categorical and Ordinal Features. We

used the internet, age, health, and absences fea-

tures of the student-math dataset (Cortez, 2014).

4. Multiple Ordinal Features. We used the cylin-

ders, displacement, hp, weight, acceleration and

year features of the auto-mpg dataset (Quinlan,

1993).

The speedup is the ratio of the number of itera-

tions required for a linear search to the number re-

quired for the proposed approach. These are provided

in Table 2 for different values of ν. We note that as

we increase the level of accuracy the proposed ap-

proach provides increased speedup. Also, as the num-

ber of features increases, the speedup also increases.

In practice a problem may have tens of features and

hence we expect even better performance for such

cases.

DATA 2023 - 12th International Conference on Data Science, Technology and Applications

632

Table 2: Speed up values for different levels of accuracy.

Example ν = 0.1 ν = 0.01 ν = 0.001

1 17 177 1776

2 12 123 1233

3 42 426 4260

4 91 918 9188

7 CONCLUSION AND FUTURE

WORK

We described a regression approach that was previ-

ously proposed in the literature but which required

signiﬁcant computational resources. We introduce

an approach to speed up parameter optimization and

showed that it could result in as much as two orders of

magnitude decrease in computation. In the future we

plan to further improve this optimization approach,

provide additional examples and provide a proof of

convergence.

REFERENCES

Cortez, P. (2014). Student Performance. UCI Machine

Learning Repository.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory.

Hosein, P. (2023). A data science approach to risk assess-

ment for automobile insurance policies. International

Journal of Data Science and Analytics, pages 1–12.

Quinlan, R. (1993). Auto MPG. UCI Machine Learning

Repository.

Stuke, A., Rinke, P., and Todorovi

c, M. (2020). Efﬁcient hy-

perparameter tuning for kernel ridge regression with

bayesian optimization. Machine Learning: Science

and Technology, 2.

Wang, L., Zheng, C., Zhou, W.-X., and Zhou, W.-X. (2021).

A new principle for tuning-free huber regression. Sta-

tistica Sinica.

A Successive Quadratic Approximation Approach for Tuning Parameters in a Previously Proposed Regression Algorithm

633