Finite Element Simulation on the Tensile Property of Steel Cord at

Different Lay Lengths Under Axial Loading

Shanling Han

, Lingkang Kong

, Yanmeng Chi

, Long Chen

and Yong Li

College of Mechanical and Electronic Engineering, Shandong University of Science and Technology,

Qingdao, Shandong, China

College of Materials Science and Engineering, Shandong University of Science and Technology,

Qingdao, Shandong, China

Keywords: Steel Cord, Lay Length, Tensile Property, Finite Element Analysis, Axial Loading.

Abstract: Steel cord is the primary load-bearing component of a tire, and as the tire environment becomes more

complicated and variable, greater tensile property demands are placed on the cord. There are several factors

that affect the tensile property of steel cord, with lay length being an important factor that is closely related to

the durability and quality of steel cord. Therefore, this paper takes 3×0.20+6×0.35HT steel cord as the

research object, establishes the parametric model with varying lay lengths, and employs the finite element

method to examine the effect of varying lay lengths on the tensile property. The results indicate that the

breaking strain of steel cord is lowest at the standard lay length. Furthermore, the breaking strain of steel cord

increases regardless of whether the lay length of the inner and outer monofilaments increases or decreases.

This study provides a basis and reference for the optimal design and manufacture of steel cord.

1 INTRODUCTION

Steel cord is widely used in rubber products (Zhang,

2019) such as tires and transportation belts because of

its high tensile strength, malleability, and stability

(Prawoto, 2012). The load-bearing capacity and

service life of steel cord are crucial to the safe

operation of rubber products. As the primary skeleton

material of rubber products, steel cord is subjected to

loads such as tension (Gurevich, 2022) and impact (Li,

2021), and its load-bearing strength and safe

operation are crucial to the service life (Kruzel, 2019).

During use, the steel cord will be abrasive and loose

between the monofilaments; as a result, the failure of

the steel cord due to stretching has become a major

concern among engineering designers and end-users.

To improve the safety factor of steel cord, the lay

length must be investigated. Nonetheless, in the

development of steel cord, the steel cord must be

repeatedly tested to determine its optimal parameters,

which is poorly oriented, time-consuming, and

wasteful of resources. For analyzing the stress-strain

analysis of complex metal structural products, finite

element analysis is more intuitive, highly accurate,

and widely used in the industry (Korunović, 2019).

Numerous scholars have conducted extensive

research on this topic, concentrating primarily on the

axial tensile property of steel cord.

Stanova (Stanova, 2011; Stanova, 2011)

developed mathematical geometric models of single

and double-layered wire ropes with specified initial

parameters, discussed the application of the derived

mathematical models, and carried out numerical

simulations of the established finite element models

for multilateral strands subjected to tension tests.

Chen (Chen,2021) and Abdullah (Abdullah, 2016)

have proposed techniques for modeling that are more

refined. Extensive research has been conducted on the

stress distribution law of the wire during tensioning

of the locking coil wire rope, as well as the behavior

of the prestressed strand after stress and fracture.

Fedorko (Fedorko, 2014) proposed a criterion for the

failure of locking coil wire ropes. And proposed an

accurate computational three-dimensional solid

modeling method for two-layer triangular wire

strands for finite element analysis, and used the three-

dimensional computational model for finite element

analysis of two-layer triangular steel strands

subjected to tensile loads. Ma (Ma, 2022) simulated

the multi-pass tensile process of wire with and

without eccentric inclusion under different back

tensions using the finite element method. All previous

finite element analyses made use of steel cord with a

standard lay length, ignoring the effect of lay length

Han, S., Kong, L., Chi, Y., Chen, L. and Li, Y.

Finite Element Simulation on The Tensile Property of Steel Cord at Different Lay Lengths Under Axial Loading.

DOI: 10.5220/0012149500003562

In Proceedings of the 1st International Conference on Data Processing, Control and Simulation (ICDPCS 2023), pages 64-71

ISBN: 978-989-758-675-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

on the tensile property of the steel cord. In general,

the breaking strain decreases as the lay length

increases. 3 × 4 × 0.22HE compared with 3 + 9 ×

0.22HE, the former lay length (3.15S/6.3S) than the

latter lay length (6.3S/12.5S) is twice as small,

although the diameter of the two monofilament and

the number of filaments is the same, but the former

break strain of up to 5-10%, the latter only about 2%;

from the physical test data, the former break tension

of 912 N, the latter is 830 N. the strength twist loss of

high elongation cord is often above 20%. Therefore,

the influence of lay length on tensile property needs

to be further explored.

This paper first will obtain the tensile curve of

3×0.20+6×0.35HT using a tensile machine, then will

establish the parametric model of 3×0.20+6×0.35HT

and verify the accuracy and feasibility of the

simulation by comparing it with experimental data.

Finally, models with an inner lay length of 10 mm and

an outer lay length of 12.5, 14.0, 16.0, 18.0, 20.0, and

22.4 mm will be created, as well as models with an

inner lay length of 8.0, 9.0, 10.0, 11.2, 12.5 and 14.0

mm and an outer lay length of 18 mm. To examine the

effect of different lay lengths on tensile property.

2 FINITE ELEMENT ANALYSIS

OF TENSILE STEEL CORD

2.1 The Establishment of the Finite

Element Model

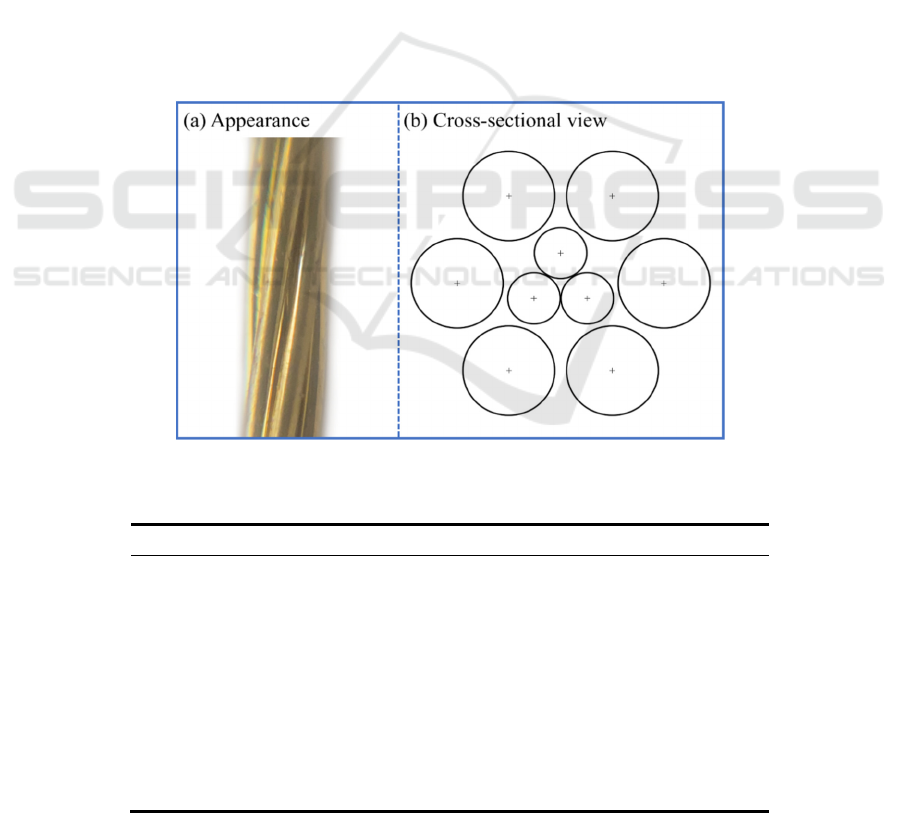
As an example, this study models a steel cord of type

3×0.20+6×0.35HT (Fig. 1a). The cross-sectional

view of this cord is shown in Fig. 1(b). This type of

cord is one of the simpler cord structures, consisting

of two layers of steel monofilaments twisted inside

and outside, with each layer evenly distributed along

the circumference and both layers in a single spiral

structure. The parameters such as diameter, lay length,

diameter, distance from inner and outer cord to the

center are listed in Table 1.

Figure 1: Steel cord: (a) appearance, (b) cross-sectional view.

Table 1: 3×0.20+6×0.35HT steel cord parameters.

Material properties Value

Length (mm) 15

Diameter (mm) 1.13

Inner cord lay length (mm) 10

Outer cord lay length (mm) 18

Inner cord diameter (mm) 0.2

Outer cord diameter (mm) 0.35

The distance from the inner cord to the center (mm) 0.118

The distance from the outer cord to the center (mm) 0.394

Breaking stress (MPa) 2918.68

Breaking strain (%) 0.0208

Finite Element Simulation on The Tensile Property of Steel Cord at Different Lay Lengths Under Axial Loading

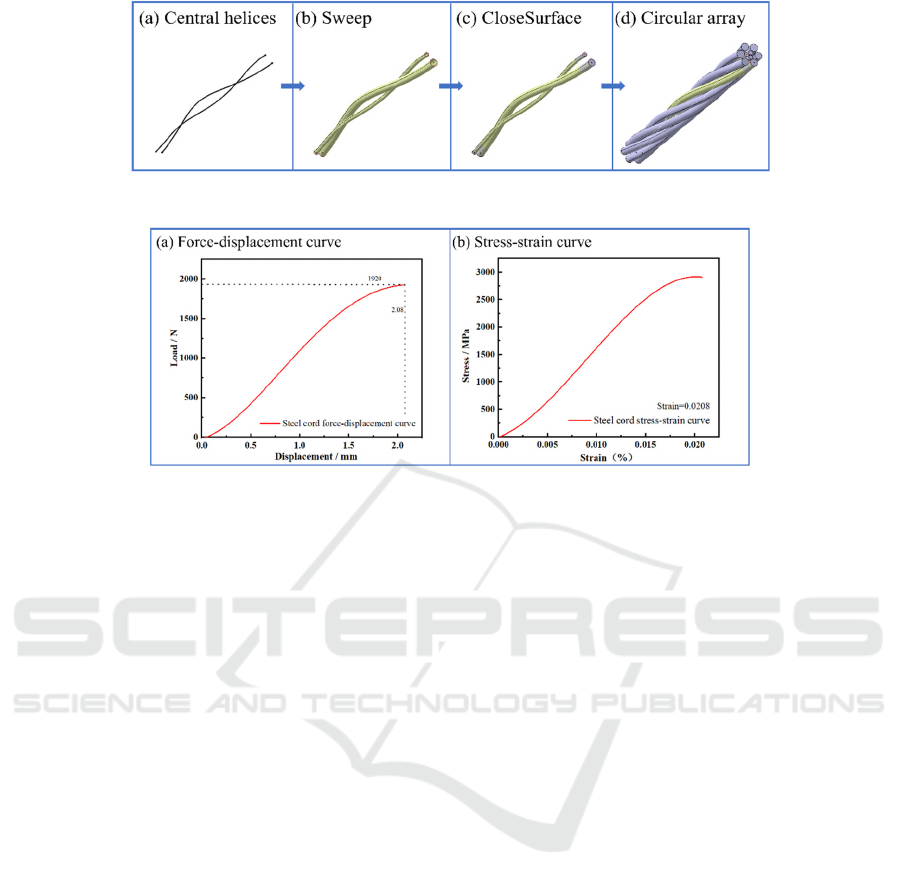
Figure 2: Specific procedure: (a) generates center helices, (b) sweep, (c) closed, (d) circular array.

Figure 3: 3×0.20+6×0.35HT steel cord: (a) force- displacement curve, (b) stress-strain curve.

The standard lay lengths are 2.5, 2.8, 3.1, 3.5, 4.0,

4.5, 5.0, 5.6, 6.3, 7.1, 8.0, 9.0, 10.0, 11.2, 12.5, 14.0,

16.0, 18.0, 20.0, 22.4, 25.0, etc. 3×0.20+6×0.35HT is

used as the research object, and models with inner lay

length of 10 mm and an outer lay length of 12.5, 14.0,

16.0, 18.0, 20.0, and 22.4 mm are established, as well

as models with inner lay lengths of 8.0, 9.0, 10.0, 11.2,

12.5, and 14.0 mm and outer lay lengths of 18 mm.

These models are used to examine the effect of

different lay lengths on the stress distribution and

strain.

Based on the above parameters, parametric

modeling of the steel cord can be achieved by the

spiral sweep and circular array functions. Firstly, the

center line of the steel cord and the cross section of

two kinds of monofilaments are established (Fig. 2a),

then the helices are generated, and the curve

smoothing is used to adjust the curvature

inconsistency of the intersection point of the helix,

then the solid model of the monofilaments is

completed with the sweep (Fig. 2b) and closed

surface (Fig. 2c) commands, and finally the complete

steel cord is completed with the circular array (Fig.

2d) command.

2.2 Material Properties

Analysis of steel cord using finite elements is a

nonlinear problem requiring the definition of material

parameters, the construction of the mesh system, the

configuration of the solver, the construction of

connection relations, the establishment of boundary

conditions, and post-processing. Based on the explicit

dynamic solver, a simulation study of the tensile steel

cord is carried out

The steel cord is a high-carbon steel, and the

steel cord is an elastoplastic material. In material

systems, elastoplastic materials are usually defined by

the following parameters: ductile damage, density,

elasticity, and plasticity. To simulate a real cord

stretching experiment, the steel cord is pulled off by

the traditional German Zwick electronic universal

testing machine with a tensile speed of 100 mm/min.

The stress-strain curve is calculated from the force-

displacement curve of the cord stretched in the press,

and the curve is measured and plotted using

specialized tools. these parameters are calculated

from the stress-strain curve (Fig. 3a) obtained by

stretching 3×0.20+6×0.35HT cord in a press, and the

stress-strain curve is shown in Fig. 3(b).

The density of steel cord is

7.95 10 /tmm

−

;

Young's modulus of elastic property is

11 2

1.81 10 /Nmm×

, Poisson's ratio is 0.3; breaking

strain, stress triaxiality, strain ratio and damage

evolution of ductile damage are 0.207, 0.333, 0.001

and 0.02 respectively. The experimental data of the

press are given in terms of nominal stress and nominal

strain and considering the effect of material necking

on the data. The real stress and real strain are used to

define the plasticity data. Therefore, the

transformation from nominal stress/strain to real

stress/strain has to be realized, and the transformed

stress-strain curve is shown in Fig. 3.

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

Figure 4: Key steps of finite element analysis: (a) mesh generation, (b) coupling.

Figure 5: Boundary conditions at both ends of the steel cord.

2.3 Mesh Generation and Contact

Condition

Because each monofilament within the steel cord has

central symmetry, the mesh division of each

monofilament also has central symmetry. In

consideration of the geometric characteristics of the

monofilament and contact, etc., and to eliminate the

influence of the mesh type on the analysis of

experimental results, the uniform use of C3D4 mesh

type, and to consider the accuracy of simulation

results and calculation time. Meshes with dimensions

of 0.05 mm are used for the finite element analysis.

The meshed model can be seen in Fig. 4(a).

Considering the contact between the

monofilaments of the steel cord during the tensile

process, the surface-to-surface contact type is defined.

This method yields more accurate results, but it is

time-consuming. Therefore, instead of setting up

contact pairs for two individual monofilaments, a

global setup is used with a contact behavior of hard

contact normal to the steel cord surface and a friction

coefficient of 0.19 between brasses of the steel cord

surface material in the radial direction.

To accurately simulate the tensile experiment on

both ends of the steel cord testing machine's

stretching state, the simulation incorporated the

following boundary conditions: one end of the steel

cord degrees of freedom by way of motion coupling

constraint to the reference point RP-1 (Fig. 4b). the

reference point RP-1 coupling steel cord end surface

into a fixed relationship, the reference point has six

degrees of freedom, specifically three translational

degrees of freedom, three rotational degrees of

freedom. The load is only applied in the axial

direction to the monofilament, and the remaining

degrees of freedom are null.

2.4 Boundary Conditions

The boundary conditions of the steel cord are imposed

as shown in Fig. 5, where the reference point RP-1

moves uniformly along the axial direction at 0.6 mm

in 0.15 s under axial tension, and the other end of the

steel cord is fixedly restrained.

Finite Element Simulation on The Tensile Property of Steel Cord at Different Lay Lengths Under Axial Loading

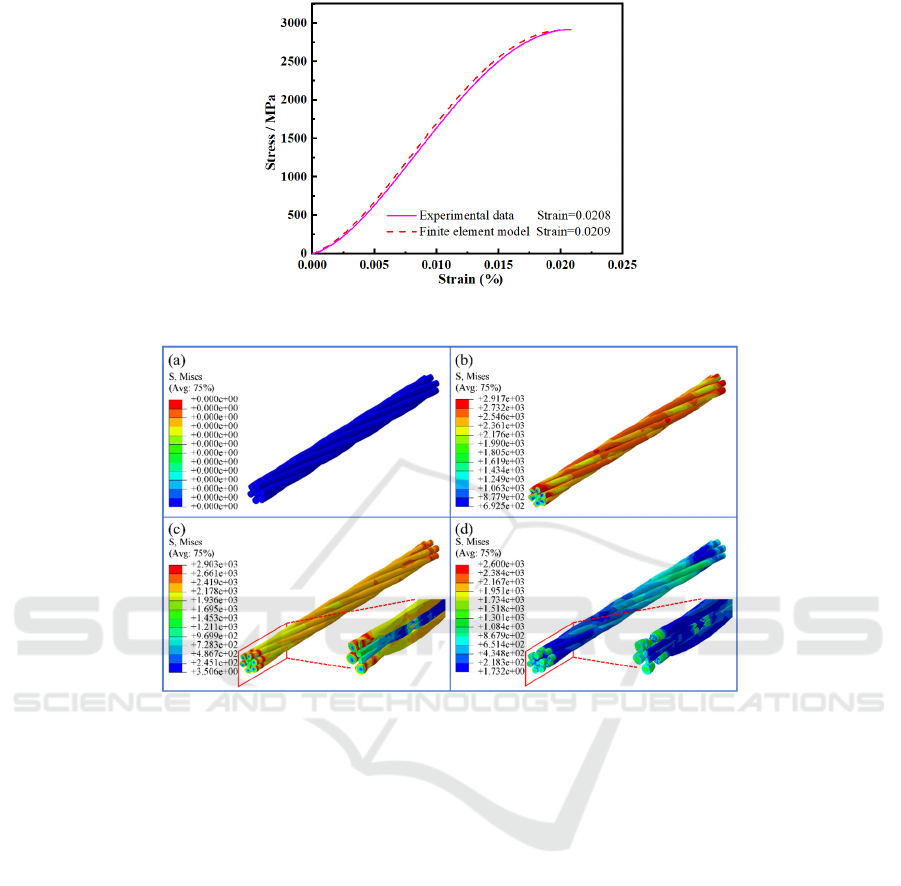
Figure 6: Experimental data and finite element model of tensile stress-strain curves.

Figure 7: Tensile process of steel cord: (a) initial state, (b) maximum stress reached, (c) inner layer monofilament breakage,

(d) outer layer monofilament breakage.

3 RESULTS AND DISCUSSION

Two types of results to study the overall mechanical

property of the tensile action steel cord are analyzed

in this article: stress distribution and strain.

(1) First, the tensile simulation is conducted for

the finite element model with the standard inner lay

length of 10 mm and outer lay length of 18 mm, and

the stress-strain curve obtained is shown in Fig. 6.

The breaking strain is 2.09%, and the deviation from

the tensile test is only 0.625%; the tensile property of

the steel cord obtained from the simulation result are

consistent with the actual measured value, which

provides a comparison of the tensile property of the

steel cord. This provides a basis for the tensile

comparison of finite element models with different

lay lengths, and the finite element analysis process is

also authentic and reliable.

(2) The finite element model tensile process

and the stresses in its cross section are shown in Fig.

7 and Fig. 8. The stresses within the steel cord cross

section exhibit a centrally symmetrical distribution

and a decreasing trend outward. Compared to the

outer layer, the inner layer of the cord is subjected to

a greater stress, which means that the inner

monofilament is subjected to a larger load. As a result,

inner monofilament breaks first (Fig. 7c), followed by

the outer monofilament (Fig. 7d). Due to the different

lay lengths of the steel cord, the cross section of the

steel cord is roughly divided into three cases from a

radial perspective: first (Fig. 8b1), there is a small gap

between the monofilaments of the steel cord,

relatively independent, there is no extrusion

phenomenon, the steel cord is only subject to axial

tensile load, when the load distribution is relatively

uniform and no stress concentration phenomenon

arises. Second (Fig. 8b2), the inner three

monofilaments are extruded by the outer six

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

Figure 8: Stress distribution: (a) steel cord in the stretched state, (b) three typical cross-sections.

Figure 9: Steel cords with inner lay lengths of 10 mm and outer lay lengths of (a) 12.5, (b) 14.0, (c) 16.0, (d) 18.0, (e) 20.0,

and (f) 22.4 mm.

Figure 10: Steel cords with inner lay lengths of (a) 8.0, (b) 9.0, (c) 10.0, (d) 11.2, (e) 12.5, and (f) 14.0 mm and outer lay

lengths of 18 mm.

monofilaments, and the inner three monofilaments are

extruded from one another. When the inner

monofilaments are subjected to axial tensile and

extrusion, the stress is the highest; therefore, it is also

easy to break in this section. Third (Fig. 8b3), the

inner three monofilaments don’t receive the extrusion

of the outer layer of steel cord; only the inner three

monofilaments extrude each other. At this group, the

steel cord received tensile and extrusion force, and the

stress is higher.

(3) The breaking strains at 2918 MPa for models

with inner lay lengths of 10 mm and outer lay lengths

of 12.5, 14.0, 16.0, 18.0, 20.0, and 22.4 mm and for

models with inner lay lengths of 8.0, 9.0, 10.0, 11.2,

12.5, and 14.0 mm and outer lay lengths of 18 mm are

depicted in Fig. 9 and Fig. 10. When the inner layer

lay length is 10 mm and the outer layer lay length is

12.5 mm, the maximum breaking strain is 2.69%,

with a deviation of 28.71% from the breaking strain

of steel cord at the standard lay length. The breaking

strain tends to decrease with increasing lay length for

both the inner and outer layers. The minimum

breaking strain for 3×0.20+6×0.35HT with standard

lay lengths of 10 mm for the inner layer and 18 mm

for the outer layer is 2.09%, while the breaking strain

increases with increasing lay length when the inner

layer lay length is greater than 10 mm and the outer

layer lay length is greater than 18 mm. As shown in

Finite Element Simulation on The Tensile Property of Steel Cord at Different Lay Lengths Under Axial Loading

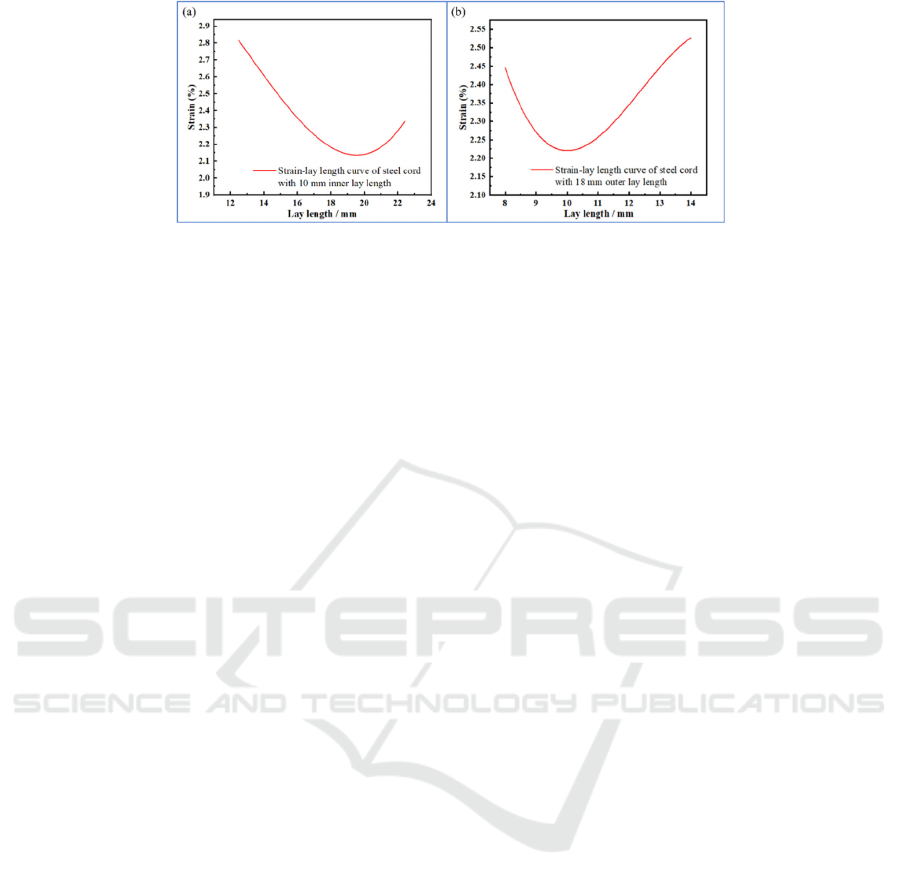
Figure 11: Strain-lay length curves: (a)steel cord with 10 mm inner lay length, (b) steel cord with 18 mm outer

lay length.

Fig. 11, it can be observed that the breaking strain of

the steel cord increase regardless of whether the lay

length is increased or decreased in comparison to the

standard lay length, which is consistent with the

results of actual steel cord manufacture.

4 CONCLUSION

Steel cord tensile property are influenced by several

parameters, including lay length. A parametric model

of 3×0.20+6×0.35HT steel cord is developed and

compared to the stress-strain curve obtained from a

tensile test. The deviation of the breaking strain from

the tensile test is only 0.625%, which proves the

simulation's accuracy and prepares for the upcoming

experiments.

In this paper, the steel cord loading cross-section

is categorized based on the difference in stress

distribution: first, each monofilament of the inner and

outer layers is extrusion-free and only experiences

tensile stress. Second, the inner monofilaments

extrude each other and receive the extruding effect of

the six outer monofilaments simultaneously, at which

group the inner monofilaments carry the most stress

and will break first, followed by the outer

monofilaments. Third, just the inner monofilaments

extrude each other while the outer monofilaments do

not exert any pressure. This research also compares

the breaking strain of steel cords with various lay

lengths and standard lay lengths. When the lay length

is standard, the steel cord's breaking strain is minimal.

Whether the lay length of the inner or outer

monofilaments increases or decreases, the steel cord

fracture strain increases. Also consistent with actual

steel cord manufacturing results.

ACKNOWLEDGMENT

This work was supported by National Nature Science

Foundation of Shandong Province of China (Grant

No. ZR2022ME118).

CONFLICTS OF INTEREST

The authors declare that they have no known

competing financial interests or personal

relationships that could have appeared to influence

the work reported in this paper.

REFERENCES

Zhang P, Duan M, Ma J, zhang Y. (2019). A precise

mathematical model for geometric modeling of wire

rope strands structure. Applied Mathematical

Modelling. 76:151-71.

Prawoto Y, Mazlan RB. (2012). Wire ropes: Computational,

mechanical, and metallurgical properties under tension

loading. Computational Materials Science. 56:174-8.

Gurevich L, Danenko V, Bogdanov A, Kulevich V. (2022).

Analysis of the stress-strain state of steel closed ropes

under tension and torsion. International Journal of

Advanced Manufacturing Technology. 118:15-22.

Li Y, Sun X, Song J, Zhang S, Han S. (2021). Topological

structure and experimental investigation of a novel

whole tire bead. Materials & Design. 203:109592.

Kruzel R, Ulewicz M. (2019). The fatigue strength of

bidirectionally bent steel cord used in tyres.

Engineering Failure Analysis. 105:176-81.

Korunović N, Fragassa C, Marinković D, Vitković N,

Trajanović M. (2019). Performance evaluation of cord

material models applied to structural analysis of tires.

Composite Structures. 224:111006.

Stanova E, Fedorko G, Fabian M, Kmet S. (2011).

Computer modelling of wire strands and ropes Part I:

Theory and computer implementation. Advances in

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

Engineering Software. 42:305-15.

Stanova E, Fedorko G, Fabian M, Kmet S. (2011).

Computer modelling of wire strands and ropes part II:

Finite element-based applications. Advances in

Engineering Software. 42:322-31.

Chen Z, Guo L, Liu H, Chen H. (2021). Finite element

study of behaviour and interface force conditions of

locked coil wire rope under axial loading.

Construction and Building Materials. 272:121961.

Abdullah ABM, Rice JA, Hamilton HR, Consolazio GR.

(2016). An investigation on stressing and breakage

response of a prestressing strand using an efficient

finite element model. Engineering Structures.

123:213-24.

Fedorko G, Stanova E, Molnar V, Husakova N, Kmet S.

(2014). Computer modelling and finite element

analysis of spiral triangular strands. Advances in

Engineering Software. 73:11-21.

Ma A, Zhang Y, Dong L, Yan H, Fang F, Li Z. (2022).

Damage and fracture analyses of wire with off-center

inclusion on multi-pass drawing under different back

tensions. Engineering Failure Analysis. 139:106512.

Finite Element Simulation on The Tensile Property of Steel Cord at Different Lay Lengths Under Axial Loading