Goertzel Algorithm Based on Matlab Platform System Simulation for

Listening Dial Tone Recognition Research

Yucheng Li

, Yang Zhang, Yongtian Li and Yifeng Wu

Aviation Maintenance NCO Academy of Air Force Engineering University, Xinyang 464000, Henan, China

Keywords: Goertzel Algorithm, DTMF, Matlab Simulation, Dial Tone Identification.

Abstract: In order to improve the security of using mobile phones and prevent the theft of mobile banking passwords,

this paper makes a deep research on the recognition technology of listening dial tone based on Goertzel

algorithm of Matlab platform system simulation. Goertzel algorithm is the most classical and practical method

to estimate the power spectrum of Dual Tone multi-frequency (DTMF) signal. DTMF dialing system has the

advantages of convenient frequency domain analysis and strong anti-interference ability. The algorithm only

estimates the power spectrum at two specific frequency points of DTMF signal, and it can deduce the key

value from the corresponding relationship of frequency array on the keyboard.

1 INTRODUCTION

Nowadays, smart phones have been completely

integrated into our daily life. We frequently tap the

mobile phone keyboard, input the phone number,

input a variety of passwords or verification code, edit

wechat or SMS, operation of online banking, online

shopping, often hear the "du tick" button sound, all of

these voices are potentially telltale. There are many

places in real life where secrets can be divulged. For

example, when interviewing public figures on

television and audio media, be careful not to play the

dialing sound as well. When we usually use mobile

phones to make calls, we must pay attention to

whether someone is recording the phone number or

password, otherwise it is easy to restore out, causing

serious hidden dangers. To prevent password leakage,

the phone banking system often changes the tone

when entering your password to make the dial tone

sound strange, so that no one can identify your dial

tone.

The Dual Tone multi-frequency (DTMF) signal

is used to send commands to the switch. When we

press a key on the phone keyboard, two different

frequencies of sound are emitted simultaneously,

which are converted into electricity for analysis.

Through some software means can restore the number

key tone, and then resolve the number (Yeh, 2019;

Siddhant, 2020).

A complete telephone keypad is shown in Figure

1, with 10 numeric keys and 2 character keys.

According to ITU recommendations, each number or

character is transmitted by using a combination of two

single-frequency signals. Therefore, the signal

corresponding to each key on the keyboard can be

expressed as:

𝑋(𝑡)=Asin(2πf



𝑡)+Bsin(2πf



𝑡) (1)

In this equation, where f

and f

respectively

represent the frequency values corresponding to the

row and column where the key is located. The

frequency values marked on the 4 rows 697 Hz, 770

Hz, 852 Hz and 941 Hz, which constitute the low-

frequency group, and the frequency values marked on

the 3 columns 1209 Hz, 1336 Hz and 1477 Hz, which

constitute the high-frequency group.

The corresponding relationship between

keyboard number and frequency is shown in Figure 1.

The values of these frequencies are specially

designed: A. These frequencies are within the audible

range of a person, so that when a key is pressed, a

person can hear it; B. None of these seven frequencies

is a multiple of any of the other frequencies; C. No

combination, addition, or subtraction of any two

frequencies is equal to any other frequency. Therefore,

these features not only simplify the decoding of dual-

tone multifrequency signals, but also reduce the

probability of misdetection of dual-tone

multifrequency signals.

According to the regulations of the international

telegraph and telephone advisory committee, it is

required to transmit a keyboard number or symbol

every 100ms, and the duration of the audio signal

114

Li, Y., Zhang, Y., Li, Y. and Wu, Y.

Goertzel Algorithm Based on Matlab Platform System Simulation for Listening Dial Tone Recognition Research.

DOI: 10.5220/0012150300003562

In Proceedings of the 1st International Conference on Data Processing, Control and Simulation (ICDPCS 2023), pages 114-121

ISBN: 978-989-758-675-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Figure 1: Frequency array of telephone keypad.

Figure 2: Time-domain and frequency-domain waveforms of key 1.

representing the number must be 45 ~55ms. In order

to distinguish between two consecutive key numbers,

the rest of the time during the 100ms should be silent

(no signal) and the sampling frequency of the

telephone signal should be 8kHz. As long as you are

familiar with the time-frequency transformation

relationship of signal processing, it is easy to see the

corresponding frequency value of different time

periods, and then according to the principle of DTMF

signal, you can immediately deduce the key value.

In other words, the DTMF signal is converted

into the frequency domain through Discrete Fourier

Transformation (DFT), and then the energy of each

frequency point is determined in the frequency

domain. Through matlab simulation, Figure 2 shows

the time-domain waveform and frequency-domain

waveform of key 1. It can be seen intuitively that

button 1 is actually composed of two single-frequency

signals (697Hz and 1209Hz).

Fig. 3 shows the time-domain waveform and

frequence-domain waveform of keys 0-9. It can be

seen intuitively that each key is actually composed of

two single-frequency signals. The spectral amplitude

of DTMF signal is very large at high and low

frequencies, and almost zero at other frequencies.

DTMF signals are converted into discrete time series,

and then DFT is performed to detect the two largest

frequencies of the amplitude spectrum. The encoding

and decoding of DTMF signals realized in this paper

is an ideal situation. In practice, DTMF signals will

be aliased and have a lot of noise in the transmission

process, and the frequency components of signals

cannot be determined simply by calculating the

amplitude at a fixed frequency.

Goertzel Algorithm Based on Matlab Platform System Simulation for Listening Dial Tone Recognition Research

115

Figure 3: Time domain waveform and frequency domain waveform of keys 0~9.

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

116

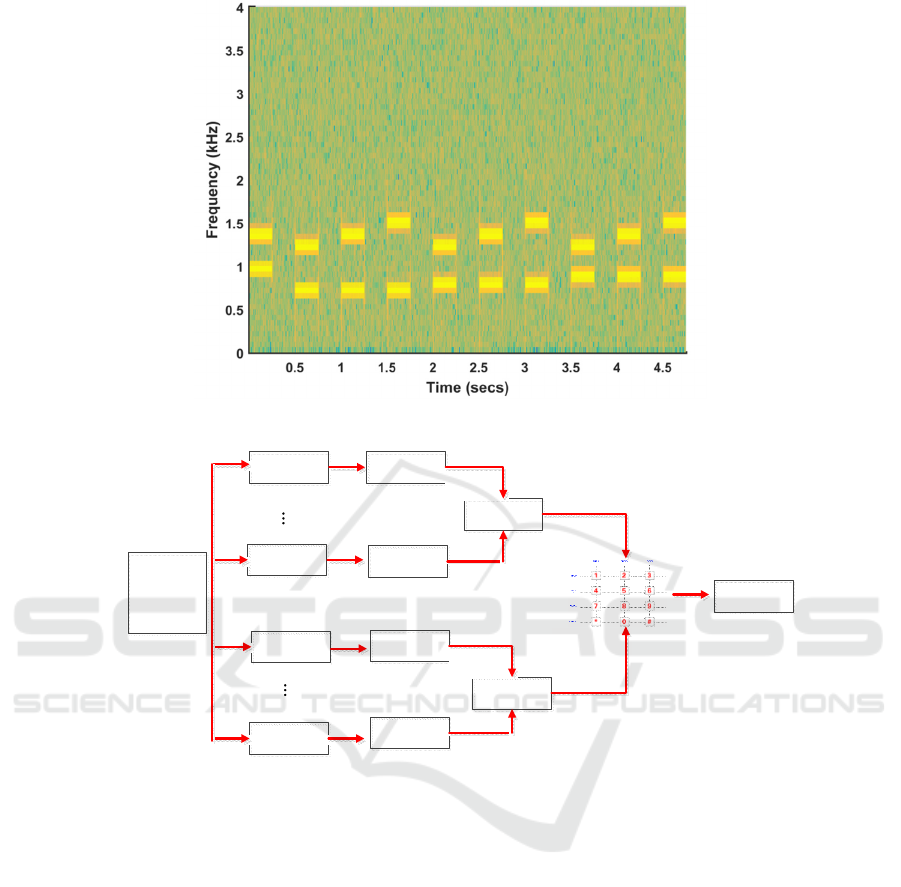
Figure 4: Time-frequency diagram of keys 0-9.

Fc1 filter

Fc4 filter

Fr1 filter

Fr4 filter

FFT

DTM F

signal

waveform

max(.)

min(.)

K ey value

Figure 5. Filter method to identify key values.

In Figure 4, the time-frequency diagram of dial

tone 0-9 is given. In order to better simulate the real

situation, the simulation program also introduced two

simulation parameters in the source code, namely,

dialing interval time (BLK) and transmission noise.

As can be seen from the results in Figure 4, keys 1,2

and 3 have the same low-frequency signals (697Hz),

while their high-frequency signals rise one by one.

The frequency transformation relationship of other

keys is similar (Getu, 2015; Porterfield, 2020).

Direct calculation of DFT requires a large

amount of calculation, while DTMF signal detection

only needs to calculate the spectrum of a few

frequency points. Therefore, engineers usually use

filter method or Goertzel algorithm to complete the

detection of DTMF signal.

2 FILTER RECOGNITION AND

SIMULATION RESULTS

The principle of filter method to identify keys is

shown in Figure 5. The most critical step of this

method is to design 7 bandpass filters, and the center

frequency of each bandpass filter corresponds to each

frequency point of the low/high frequency group. The

dial-tone numbers to be identified (DTMF signal

waveform) are passed through the 7 bandpass filters

in turn. Theoretically, only the signals whose

frequency components are consistent with the center

frequency of the filter can pass through. The low/high

frequency serial number can be determined by

detecting the one with the most energy at the output

end of the filter. Finally, the key value can be

inversely deduced by the corresponding relationship

Goertzel Algorithm Based on Matlab Platform System Simulation for Listening Dial Tone Recognition Research

117

Figure 6: Comparison of amplitude-frequency characteristics of bandpass filters.

of the frequency array on the keyboard.

The input value (Dial Number) is arbitrarily

changed to different key values on the telephone

keyboard, and the estimated value (key number) is

checked one by one. We found that the filter method

could not achieve 100% accuracy in identifying a

single key value. The recognition effect is sensitive to

input signal duration, Fast Fourier Transform (FFT)

points and filter order. The bottleneck of filter

recognition is that the amplitude-frequency

characteristics of bandpass filters are not ideal.

Figure 6 shows the amplitude-frequency

characteristics of bandpass filters with center

frequencies of 697Hz, 770Hz, 852Hz and 941Hz

respectively. In the source code, a method based on

frequency sampling is used to design digital filters. As

can be seen from Figure 6, the passband parts of the

four bandpass filters are all overlapped together, and

the single-frequency signals of 770Hz, 852Hz and

941Hz can mostly pass the bandpass filter of 697Hz.

In other words, 697Hz bandpass filter is not ideal for

770Hz, 852Hz, and 941Hz single-frequency signals

3 GOERTZEL ALGORITHM AND

SIMULATION RESULTS

In theory, DTMF signals only have energy at two

fixed frequency points, how to estimate these two

frequencies accurately and efficiently is the key to

identify dial tone. For the traditional spectrum

estimation method, it obtains the estimation results of

all frequency points through a frequency range, while

for THE DTMF signal, we only care about the power

spectrum estimation values at the seven fixed

frequency points.

Goertzel algorithm is the most classical and

practical method to estimate the power spectrum of

DTMF signal. The algorithm only estimates the

power spectrum at specific frequency points of

DTMF signal. This algorithm makes full use of the

periodic characteristics of sequence 𝑊





to reduce the

computation of DFT.

The calculation formula is as follows:

𝑦



(

𝑛

)

= 𝑥

(

𝑛

)

+ 𝑊





𝑦



(

𝑛−1

)

,0≤𝑛≤𝑁 (2)

In the equation,

−

, N is the

number of sampling points, and k is the serial number

vector of frequency points to calculate DFT. The

computation amount of Goertzel algorithm in

application is determined by N value. The larger the

calculated N value is, the longer the sampling

sequence is. In the case that fs has been determined

(8000 in this paper), its signal has stronger frequency

resolution and bring longer delay. Therefore, the

selection of sampling points N depends on the

frequency resolution required by the system. If the

value of N is too small, adjacent audio will fall into

the same detection window during signal detection

and it cannot be distinguished, resulting in

misjudgment; if the N value is too large, it not only

increases the useless calculation amount, but also

causes the delay to increase. Therefore, when the N

sampling points are finished, the amplitude judgment

of the specified frequency of the signal can be

completed, which greatly improves the real-time

performance of the system. Goertzel algorithm only

calculates the Fourier component of one frequency

point at a time. In this paper, N is 205

(Vasu, 2019;

Slekas, 2017; KULAÇ, 2015; Onchis, 2014).

As can be seen from Figure 7, the lower signal.

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

118

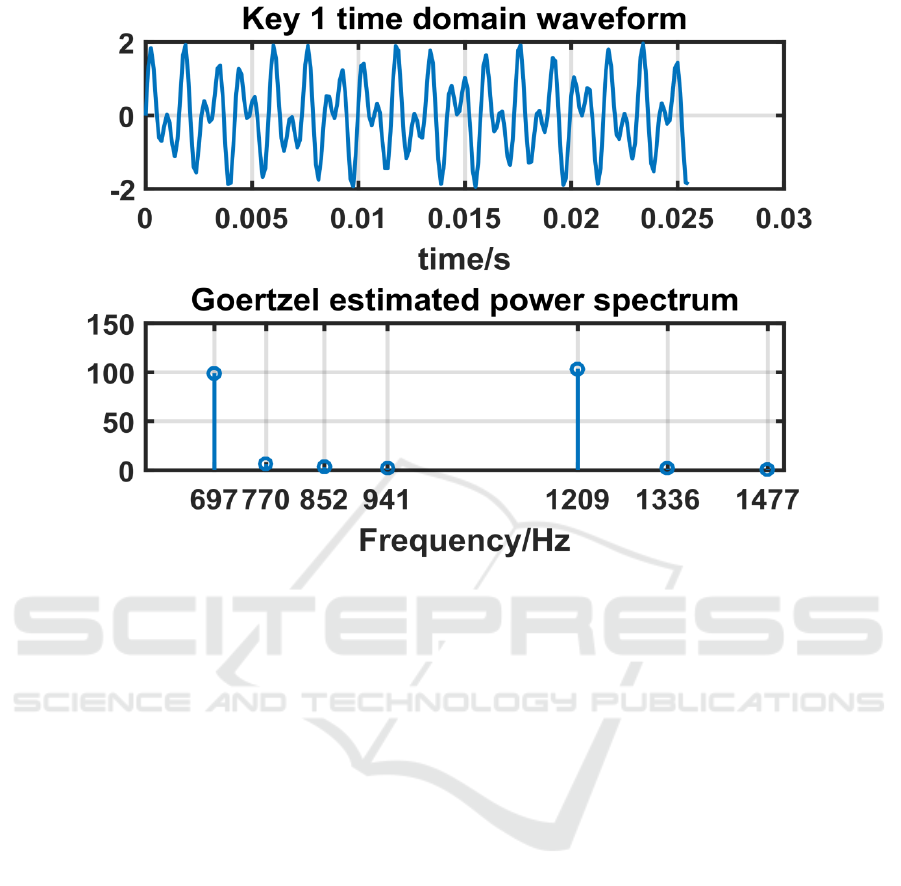
Figure 7: Power spectrum estimation of DTMF signal using Goertzel algorithm (Key 1).

on the left is the frequency component of 697Hz

signal, and the other one is 1209Hz signal. The

Goertzel algorithm calculates only the frequency

amplitude for the specified audio 697Hz. It can be

seen from the figure that the power difference

between audio signal and background noise is quite

large, which is also the basis for judging the existence

of audio by threshold method.

As can be seen from Figure 8, Goertzel

algorithm only estimates the power spectrum at the 7

frequency points given in advance (only 7 frequency

values are needed to represent pure digital keys). At

this point, only the frequency points corresponding to

the two largest energy values need to be detected, and

the key value can be derived from the corresponding

relationship of frequency array on the keyboard.

Through this method, some important operation keys

of users can be recorded, and then the recording data

can be detected in the time domain, and then the

effective area is converted to the frequency domain

for digital classification by Goertzel algorithm, and

all key data of users can be obtained by comparing

with the DTMF coding table.

Using Goertzel algorithm to identify mobile

phone numbers, the recognition effect is much better

than filter method, and has certain anti-interference

ability to transmission noise. It should be noted that

the program directly divides the dial tone of mobile

phone into 10 DTMF signals for power spectrum

estimation, eliminating the process of voice signal

endpoint detection, which is essential in practical

application, in addition, when the signal length is

extended, the calculation amount of DFT will also

increase. However, because DTMF signal detection

does not care about the phase information of the

spectrum, but only the amplitude information of the

spectrum, the Goertzel algorithm only needs N

iterations to quickly calculate the amplitude of the

spectrum. In essence, Goertzel algorithm is a fast

calculation of DFT, but it can selectively calculate

DFT values at individual frequency points, so as to

avoid the waste of memory and computing resources

(Pediredla, 2018; Mahmooda, 2013).

4 CONCLUSION

In this paper "Goertzel algorithm based on Matlab

platform system simulation for listening dial tone

recognition research", introducing how to use the

combination of two single frequency signals to

simulate telephone dial tone. This paper based on the

DTMF signal waveform infer the key value by

estimating the frequency value.

Goertzel Algorithm Based on Matlab Platform System Simulation for Listening Dial Tone Recognition Research

119

Figure 8: Power spectrum estimation of DTMF signal using Goertzel algorithm (keys 0~9).

Dual-tone multi-frequency dialing system is a

typical signal processing system, which can realize

the generation, detection and recognition of dual-tone

multi-frequency signals. Goertzel algorithm only

calculates the spectral components corresponding to a

single frequency, which simplifies the calculation of

phase in signal detection, so the calculation amount is

simplified. Goertzel is more complex for covering the

full spectrum, but it is more efficient for a single

frequency, making it suitable for a variety of small

processors and embedded devices. For audio

detection, Goertzel algorithm can use recursive

method to start calculation while storing data, saving

a large number of storage units, eliminating the delay

required by data collection, and improving the real-

time communication. In terms of hardware cost and

computational efficiency, Goertzel algorithm is

superior not only to traditional independent

recognition methods, but also to software decoding

schemes using DFT.

To sum up, Matlab platform can generate and

detect DTMF signal well. Goertzel algorithm is a

feasible method to calculate sequential DFT and

detect DTMF and calculate input numbers.

REFERENCES

Yeh, CY (Yeh, Cheng-Yu), Hwang, SH (Hwang, Shaw-Hwa)

2019 Efficient Detection Approach for DTMF Signal

Detection Applied Sciences 9(3) 422

Siddhant Kadam, Tanvi Bhat, Tanmay Pawar 2020 DTMF

based multifunctional device International Journal of

Scientific Research in Engineering and Management

4(5) 1-4

Getu B N, Hamad N A, Attia H A 2015 Remote controlling

of an agricultural pump system based on the dual tone

multi-frequency (DTMF) technique Journal of

Engineering Science and Technology 10(10) 1261-

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

120

1274

Porterfield R, Melissa J 2020 Signals and Images: Advances

and Results in Speech, Estimation, Compression,

Recognition, Filtering, and Processing

Photogrammetric Engineering & Remote Sensing 86(2)

77-78

Vasu M, Lenine D, Kiranmayi R 2019 Goertzel algorithm

based islanding detection method based on small

second order harmonic component for grid integrated

PV systems Journal of Scientific and Industrial

Research 78(11) 782-787

Slekas, Gediminas; Kancleris, Zilvinas; Ragulis, Paulius;

Seliuta, Dalius 2017 Using of Generalized Goertzel

Algorithm for FDTD Calculation of the Transmission

and Reflection Spectra of Periodic Structures IEEE

Transactions on Electromagnetic Compatibility 59(6)

2038-2041

KULAÇ, Selman; SAZLI, Murat Hüsnü 2015 Effective

cooperative DTV detection using the Goertzel

algorithm Turkish Journal of Electrical Engineering

and Computer Sciences 23(5) 1384-1392

Onchis, Darian M; Rajmic, Pavel 2014 Generalized

Goertzel algorithm for computing the natural

frequencies of cantilever beams Signal Processing

96(A) 45-50

Pediredla Hima Bindu, Sateesh Virothu, M. Satya Anuradha

2018 Comparison of FFT and Goertzel Algorithms

Used in DTMF Detection System Using GUI

International Journal of Research in Electronics and

Computer Engineering 6(4) 69-75

Mahmooda M, Vinod Kumar Reddy, Sagar Nayakanti 2013

Implementation of Spectrum Analyzer using

GOERTZEL Algorithm International Journal of

Scientific and Research Publications 3(3) 1-7

Goertzel Algorithm Based on Matlab Platform System Simulation for Listening Dial Tone Recognition Research

121