Sliding Mode Formation Control for Multiple Hypersonic Glide

Vehicles

Dongdong Yao

1,*

Yandong Hu

, Dawei Liu

and Qunli Xia

School of Aerospace, Beijing Institute of Technology, Beijing, China

Zhengzhou University of Aeronautics, Zhengzhou, China

China Research Development Academy of Machinery, Beijing, China

Keywords: Hypersonic Glide Vehicle, Formation Controller, Sliding Mode Control, State Observer, Sign of Bank

Angle.

Abstract: Aiming at the formation flying problem multiple hypersonic gliding vehicles, a formation controller design

method based on sliding mode control theory is proposed. Firstly, according to the vehicle motion model

and the multi-body "leader-follower" motion model, the trajectory of the leader and the state equation of the

follower are obtained. Based on the sliding mode control theory, a formation controller is designed to

maintain the relative position between the follower and the leader in terms of altitude and speed. The

extended state observer is designed to eliminate formation modeling errors and flight process errors. On this

basis, the control variable is transformed from acceleration to attack angle and bank angle. According to the

lateral relative position and heading angle direction, the sign change logic of the bank angle is designed to

ensure that the lateral relative position can meet the formation distance requirements. Simulation results

show that the proposed control method can achieve the desired multi-hypersonic vehicle formation flying.

1 INTRODUCTION

Hypersonic glide vehicle has become the focus of

research in many countries because of its high speed,

high precision and long range (ZHAO, 2014).

Facing the complex battlefield environment and

diverse combat tasks, with the improvement of

vehicle performance, multiple hypersonic vehicles

can improve the communication and detection

ability during glide by flying in formation, and is

conducive to the realization of coordinated attack on

the target during the terminal guidance period.

Therefore, it is important to study the formation

control method of multiple hypersonic glide vehicles

(GUO, 2022; SHUI, 2020).

Hypersonic glide vehicle has the characteristics

of strong nonlinear model, severe flight environment,

wide flight space and strict flight constraints. Its

only control force is aerodynamic, so accurate

formation control of hypersonic vehicles is very

complicated and difficult to achieve (An, 2022).

Therefore, when considering the formation space

configuration, it is not necessary to keep an accurate

space configuration of multiple aircraft, but only

need to maintain the relative position in a certain

space to form an "inaccurate formation", so as to

ensure that the aircrafts can realize the

communication, detection, middle and terminal

guidance transition and other functions during the

flight.

The cooperative formation control of

hypersonic glide vehicles can be based on three

methods (WANG, 2019). The first is based on the

cooperative trajectory planning of multiple aircraft,

and obtains the trajectory of each aircraft by setting

various constraints of the aircraft (CHU, 2017; YU,

2020; GAO, 2022). The second is based on the

formation controller, which is usually based on the

"leader-follower" formation model. The formation

controller is designed to keep the following aircraft

(hereinafter referred to as "follower") in relative

space position (ZHANG, 2021; ZHANG, 2021; WEI,

2022). The third is based on the distributed

consensus algorithm, and according to the

communication topology, the consistency control

law is designed to realize the formation flight of

multiple aircraft (Wei, 2021; Zhao, 2017; LI, 2020).

Among them, the first method can fully consider the

flight capability of the aircraft, but it usually

establishes the cooperative control law through the

flight time, and the cooperative trajectory planning

method through the formation space configuration

Yao, D., Hu, Y., Liu, D. and Xia, Q.

Sliding Mode Formation Control for Multiple Hypersonic Glide Vehicles.

DOI: 10.5220/0012150900003562

In Proceedings of the 1st International Conference on Data Processing, Control and Simulation (ICDPCS 2023), pages 133-140

ISBN: 978-989-758-675-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

133

still needs further research. The second method is

easier and more efficient to realize formation and

maintenance, but the formation members are highly

dependent on the information of the leading aircraft

(hereinafter referred to as "leader"), which is easy to

be interfered with. The third method can also

quickly form and maintain formation, and is less

affected by a single aircraft, but it puts forward

higher requirements on the ability of aircraft to

communicate and process information. In addition,

due to the lack of thrust and the under-saturation and

strong coupling characteristics of the gliding vehicle

(WANG, 2018), the three-axis’s acceleration cannot

be projected directly into the aerodynamic force,

which makes it difficult to deal with the control

variable obtained by the latter two methods above.

Based on the above research, this paper takes

the hypersonic glide vehicle as the research object

and designs a sliding mode formation controller

based on the "leader-follower" formation model to

ensure that multiple vehicles maintain relative

configuration within a certain range during flight.

Firstly, according to the aircraft motion model and

the "leader-follower" formation model, the leader

trajectory is given and the follower state equation is

obtained. Then, according to the sliding mode

control theory, a formation controller with extended

state observer (ESO) is designed to satisfy the

formation requirements of multiple aircraft.

Considering that attack angle and bank angle are the

actual control variables, the calculation method of

the attack angle and the sign change method of the

bank angle are designed so that the horizontal

direction of aircraft can meet the relative distance

constraints. Simulation results show the

effectiveness of the method.

2 HYPERSONIC VEHICLE

MODEL DESCRIPTION

The motion model of the aircraft refers to the

literature (Lu, 2014), and there is a three-degree-of-

freedom motion equation in the half-velocity

coordinate system, as shown in fig.1.

where, r is the distance between the vehicle and

the center of the earth, λ and φ denote latitude and

longitude respectively, v is the velocity of the

vehicle, θ and ψ denote flight path angle and

azimuth angle respectively, m is for mass, σ is the

bank angle, g is the acceleration of gravity. D and L

represent drag and lift, whose calculation formula is

shown as fig. 2.

rvsin

vcos sin

rcos

vcos

cos

vDgsin

L cos g cos

vcos

mv v

Lsin v

tan c s s n

cos

θψ

σθθ







=− −



=−+



=−





−



(1)

Figure 1: Relative motion relation of the leader and

follower

qSC

DqSC







(2)

where, q is the dynamic pressure, S is the

aerodynamic reference area, C

and C

represent lift

coefficient and drag coefficient.

Considering the dynamic pressure, heat flux

density and overload constraints of the leader, there

max

≤





≤









(3)

where,



is the heat flux density, n is the overload,

the subscript

max indicates the maximum value.

The formation model is established according to

the reference (Amer, 2020), as shown in fig.1.

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

134

Taking the leader trajectory coordinate system as the reference system, the relative motion equations for the

leader and follower are give:

()

cos cos cos sin sin cos

sin cos cos cos sin sin

cos sin cos sin

cos

lf lff lffl lll

ll lff lffl ll

f l f f ll ll

vvyzv

yvvxz

zvxy

θθ ψψ θθ θ θψ

θψψ θψ θψ



=−++−−



=− − + − +



=−+−







=−











(4)

()

cos

sin

cos

lfflffl l x

llffffllly

lffl ll z

xvvyzd

yvvxzd

zvxyd

ψψ θθ θ ψ

θψψ θ θθψ

ψψ ψ θψ



=−++−+



=− − + − + +



=−+−+







=−











(5)

where, the subscript

l indicates the states of the

leader, the subscript f indicates the states of

followers, x, y and z represent three-axis’s relative

position of followers,

, a

and a

are three-axis’s

acceleration.

For the formation model shown in equation (4),

since the relative position equation of the follower is

established in the leader trajectory coordinate system,

and the earth curvature is not taken into

consideration, the reference inertial coordinate

system of the leader and the followers is the ground

coordinate system (NUE coordinate system) during

the coordinate system transformation. However,

when the curvature of the earth is considered, the

ground coordinate system of the two will no longer

coincide. At this time, the relative position obtained

ccording to equation (3) will result in modeling

errors caused by curvature. When two vehicles are

10km apart, the error value is about 8m, when the

they are 100km apart, the error value is about 0.8km.

It can be seen that if the relative position of the

leader and follower is less than 100km, the relative

error is less than 1%, but as the distance increases,

the absolute error also increases, and the error needs

to be properly processed according to the

requirements.

In the simulation of most literatures (Brian, 2021;

Wang, 2018; Wang, 2017), the absolute value of

flight path angle is no more than 10°, so it can be

simplified as follows: sin

θ = θ, cosθ = 1. Meanwhile,

considering the modeling and process errors d

, d

and d

, equation (3) can be simplified as equation (5)

3 DESIGN OF SLIDING MODE

FORMATION CONTROLLER

According to reference (LI, 2021), keeping a specific

space configuration during the flight of multiple

hypersonic vehicles can improve the detection ability

of the group. In this paper, the formation space

configuration of multi-vehicle is "one-line". Due to

the constraint of aircraft control ability, the distance

between two aircraft in Z-axis direction should be

given within a certain range. The minimum distance

min

is given according to the safe distance between

the two aircraft, and the maximum distance R

max

given according to the communication ability.

3.1 Sliding Mode Controller Design

According to equation (5), the state equation of

Sliding Mode Formation Control for Multiple Hypersonic Glide Vehicles

135

aircraft can be written as equation (6). Since the

distance in the

z direction is controlled by the bank

angle symbol, it only needs to design the sliding

mode surface that controls the state in the

x and y

directions.

112

AX BX F D

XGU



=+++











(6)

[]

()

fff xy

lf l

lfl

XxyX v v Uaa

cos

Ddd

ψψ θ

ψψθ

θψ



== =





−





−

−−



−−













According to the design principle of sliding mode

control (Li, 2005), the function of sliding mode and

the approach law are taken

()

11 1

22 2

sgn >0, 0

sce e

ssksk

eX X

εε







=− − >





=−



(7)

where, X

and X

are the expected values of X

and

. For X

. Using the backstepping method, X

can

be expressed as

()

2111d

BkeAXFD

−

=−−−−

(8)

In order to track and keep the relative position of

the follower, according to equation (7), there is

()( )

()

11 1

22 2

11 2 2

sgn

sce e

eX X

cX X X X s ks

=−

−+ − =− −

  

(9)

The control law is obtained by taking equation (6)

into equation (8), show as in equation (10)

()

112

c X AX BX F D

Xsgnsks

−



−−−−+







(10)

The design of the sliding mode surface and the

reaching law above can ensure

0ss ≤



, that is,

Lyapunov function

2Vs/=

is positive definite

and its derivative is negative definite. The system

can stabilize on the sliding mode surface after

reaching it, that is, the error tends to zero.

3.2 Extended State Observer Design

According to reference (Li, 2005), an extended state

observer is designed to estimate the bounded

composite disturbance D.

First define the expanded state X

, assuming



, considering the first formula in equation (6),

the state equation can be written as

112 1

AX BX F X



=+++











(11)

The ESO is used to estimate X

and X

, and the

calculation formula is

()

1111

11 1 2 12 11 1

12 12 1

EZ X

AX BX F Z E

ZfalE,,

βαδ

=−





=+++−





=−





(12)

where, E1 is the observation error of X

, Z

and Z

are the observation values of X

and X

respectively.

>0 and

>0 are the observed gain of ESO,

0and

>0 are the parameters to be designed.

The function fal(E

) is defined as

()

111

EsgnE E

fal E , ,

E/ E

αδ

δδ

−







≤





(13)

By designing a reasonable value of

and

it can be ensured that ESO can observe and

dynamically compensate X

and X

well.

Substituting D with the observed variable Z

equation (10) can be rewritten as

()

112 12

c X AX BX F Z

Xsgnsks

−



−−−−+







(14)

Since the error is less than 1% of the expected

distance, the error is bounded and does not affect in

the stability of the controller.

3.3 Control Instruction Assignment

Design

The control instruction obtained Section 3.1 is

acceleration, U = [a

, a

]

. However, the actual

control variables of the aircraft are the attack angle

and the bank angle, so, it is also necessary to obtain

the relationship between acceleration and angle.

According to equation (1), (2) and (5), there is

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

136

av Cgsin

qS v cos

av Ccos gcos

θσθ



==− −







== − +







(15)

where, (C

、C

) = f (α，Ma). It can be seen that the

control variables a

has a direct mapping relationship

with the attack angle, which can be obtained by

aerodynamic inverse interpolation. However, the

attack angle and the bank angle are coupled items, so

they cannot be solved directly by a

. It is necessary

to use the angle of attack and a

to solve the value of

the bank angle.

For the sign of the course angle, the classical

method adopts the course angle corridor to

determine the sign (Ma, 2017). First set the course

angle error threshold. When the course angle error

exceeds the preset error threshold, change the bank

angle sign to make the course angle return to the

corridor; when the course angle error does not

exceed the error corridor, keep the course angle sign

unchanged.

In this paper, based on the idea of the error

threshold, the sign change logic of the bank angle is

designed to ensure the follower can maintain the

relative position in the z-axis direction. At the same

time, the error threshold is designed according to the

relative position error in the z-axis direction and

cruse angle. Take R

and R

to satisfy R

min

< R

max

. There is

()

min

fld

max

sgn R R R R

gn sgn R R R

sgn R R R R

σψψψ



−<



=− − − < <





−<





(16)

where,

represents the error threshold. This is to

ensure that when the aerodynamic force meets the

control requirements, the aircraft will stay away

when it is close and close when it is far away, so that

the relative position can be kept within the expected

distance range. In the relatively centered distance

range, try to keep the speed direction consistent with

the leader.

4 SIMULATION

The Common Aero Vehicle (CAV) is selected as the

simulation object, its aerodynamic model is (CHEN,

2014)

3.025 10

29.49510

0.232 2.94 0.295

0.024 2.38 0.406

−

−×



=− + +





=+ +





(17)

The US 1976 atmospheric model is selected as the

atmospheric environment, the characteristic area of

the aircraft is S = 0.48378m

, and the mass of the

aircraft is m = 907kg. The maximum attack angle is

25°, and the maximum bank angle is ±90°.

The leader adopts a balanced gliding trajectory,

with



, satisfying

()

cos

Lcos v



+− =





(18)

The bank angle of the leader is always 0°, and the

gliding reaches a height of 30km. The heat flow,

dynamic pressure and overload constraints during

flight are: Q

max

= 2000Kw/m

max

= 500kPa, n

max

15. R

min

=5km, R

=8km, R

=13km, R

max

=15km. The

initial states of the leader, follower 1 and follower 2

are shown in Table 1.

Table 1: The initial state of the leader and followers.

h/km

(λ

、φ)/°

v/m·s

-1

θ/° ψ/°

Leader 60

（0、0）

5000 0 0

follower1 65

（0.13、0.01）

5000 0 0.1

follower2 63

（-0.12、-0.01）

5000 0 0.1

The simulation results are as follows.

Sliding Mode Formation Control for Multiple Hypersonic Glide Vehicles

137

Figure 2: Trajectory of leader and followers. Figure 3: Longitudinal and lateral trajectory.

Figure 4: Curves of attack angle and bank angle. Figure 5: Curves of speed, flight path angle and course angle.

Figure 6: Followers position of x,y and z. Figure 7: H-V flight corridor.

It can be seen from Figure 2-Figure 7 that the

two followers can maintain the spatial configuration:

the initial errors in the x-axis direction are 1km and -

1km respectively, and with the adjustment during the

flight, the errors tend to 0 but are not stable at 0. This

is because the limitation of aircraft control capability

and the coupling of control variables. During the

flight, the error in the x direction of follower1 does

not exceed 2km, and that of follower2 does not

exceed 1km. Similarly, the initial altitudes of the two

followers are 63km and 65km, respectively, and the

altitude error (y-direction error) also approaches 0

during the flight, and the steady-state error is not

maintained at 0, but the error does not exceed 1.5km.

0 20 40 60 80 100 120 140 160 180

/°

follower1

follower2

0 20 40 60 80 100 120 140 160 180

t/s

-100

-50

/°

0 20 40 60 80 100 120 140 160 180

4700

4800

4900

5000

v/m s

-1

0 20 40 60 80 100 120 140 160 180

-0.06

-0.04

-0.02

/°

0 20 40 60 80 100 120 140 160 180

t/s

-0.04

-0.02

0.02

/°

leader

follower1

follower2

0 20 40 60 80 100 120 140 160 180

-2000

2000

0 20 40 60 80 100 120 140 160 180

-2000

2000

4000

follower1

follower2

0 20 40 60 80 100 120 140 160 180

t/s

-2

1000 1500 2000 2500 3000 3500 4000 4500 5000 5500 6000

v/m s

-1

h/km

dynamic pressure

heat flow

overload

leader

follower1

follower2

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

138

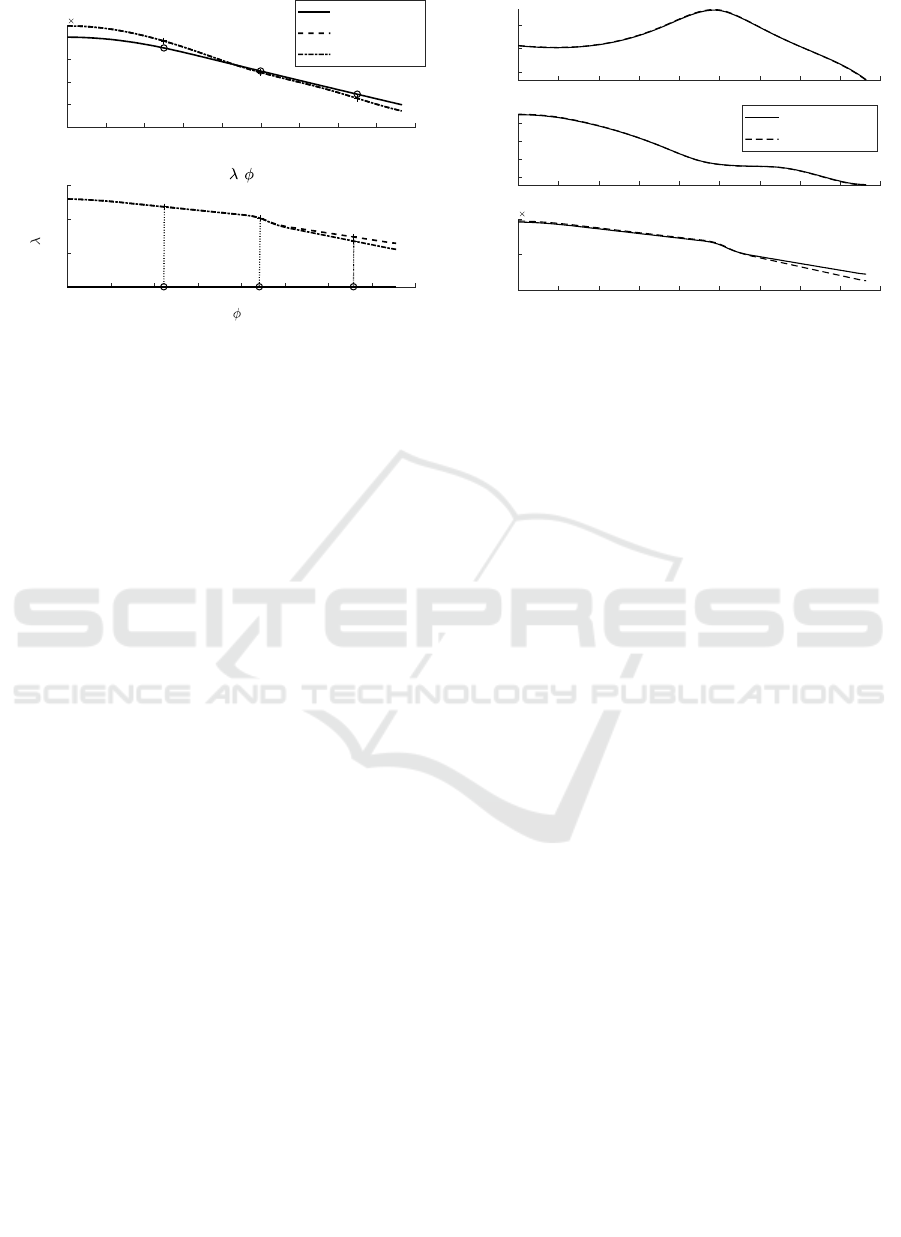
Figure 8: Comparison of trajectories. Figure 9: Comparison of position.

In the z direction, the two followers approach

the leader after 100s and stabilize at about 8km. In

addition, the H-V curves of the leading aircraft are

all within the corridor constraints, satisfying the

flight process constraints.

Add 1% error to the relative position, and add

ESO to the controller at the same time. The observer

constants are respectively selected as

= 0.15，

0.15

，

= 25，

= 50. Taking follower1 as the

research object, the trajectory simulation comparison

results are obtained.

It can be seen from Figure 8 and Figure 9 that

after increasing the position error and the observer,

the trajectory of follower1 will change. The

trajectories have little difference in the x and y

directions, but as the flight time increases, the

relative position in the z direction gradually develops.

This is because the z-direction is expected to have a

relatively farther distance, and the error will be

larger under the same error ratio. Since the z-

direction distance is only controlled by the sign of

the bank angle, the accuracy cannot be guaranteed

and thus the deviation will occur. However, the

distance between the follower and the leader is still

within expectations, and the formation configuration

can be considered to meet formation requirements.

5 CONCLUSION

1) The sliding mode formation controller designed in

this paper can realize the relative position tracking of

the leader aircraft by multiple hypersonic glide

vehicles in the "leader-follower" mode;

2) Adding ESO to the controller can reduce the

modeling error and make the calculation of the

follower’s trajectory more accurate;

3) The transformation method of control variables

in this paper can realize the mapping of aircraft

control variables from acceleration to attack angle

and bank angle, so as to keep the relative position of

the aircraft within the expected distance and realize

formation flight.

CONFLICTS OF INTEREST

There is no conflict of interest.

REFERENCES

ZHAO J. Progress in reentry trajectory planning for

hypersonic vehicle. Journal of Systems Engineering

and Electronics, 2014, 25(4):627-639.

GUO M K. Review on cooperative guidance technology

for hypersonic flight vehicle. Aerospace Technology,

2022(02):75-84. DOI:10.16338/j.issn.2097-0714.

20220615.

SHUI X B. A Formation Control Method of Multiple

Hypersonic Missiles. Tactical Missile Technology,

2020(05):139-148. DOI:10.16358/j.issn.1009-

1300.2020.1.050.

An Kai. Research Progress of Formation-Cooperative Cont

rol Methods for Low-Speed and High-Speed Vehicle

Systems. Aero Weaponry. https://kns.cnki.net/ kcms/d

etail/41.1228.TJ.20220613.1050.001.html.

WANG X. Time-cooperative entry guidance based on

analytical profile. Acta Aeronautica et Astronautica

Sinica, 2019,40(03):239-250.

CHU H. Improved MPSP Methodbased cooperative re-

entry guidance for hypersonic gliding

vehicles∥MATEC Web of Conferences, 2017.

YU J L. Cooperative guidance strategy for multiple

hypersonic gliding vehicles system. Chinese Journal

of Aeronautics, 2020, 33(3):990-1005.

0 20406080100120140160180

t/s

h/m

h-t

leader

without error

with error

012345678

/°

0.05

0.1

0.15

/°

0 20406080100120140160180

1000

2000

x/m

0 20406080100120140160180

-2000

2000

4000

y/m

without error

with error

0 20406080100120140160180

t/s

0.5

1.5

z/m

Sliding Mode Formation Control for Multiple Hypersonic Glide Vehicles

139

GAO Y. Improved predictor-corrector guidance method

for time-coordination entry. Journal of Beijing

University of Aeronautics and Astronautics, 1-

15[2022-10-11]. DOI:10.13700/j.bh.1001-5965.2022.

0530.

ZHANG Z L ． Cooperative control method of multi-

missile formation under uncontrollable speed.

Journal of Northwestern Polytechnical University,

2021, 39(2):249-257.

ZHANG M Y. Research on Three-dimensional Guidance

Law for Cooperative Attack of Multi-unpowered

Missiles. Journal of Projectiles, Rockets, Missiles and

Guidance, 2021, 41(06):1-6. DOI:10.15892/

j.cnki.djzdxb.2021.06.001.

WEI S H. Research on a New Multi-missile Formation Co

ntroller Design Method. Journal of Projectiles, Rocke

ts, Missiles and Guidance, 2022,42(03): 69-73. DOI:1

0.15892/j.cnki.djzdxb.2022.03.014.

Wei Li. Distributed formation control of multiple flight

vehicles with considering communication delay. The

12th International Conference on Mechanical and

Aerospace Engineering, 2021.

Zhao Q, Dong X, Liang Z, et al. Distributed Cooperative

Guidance for Multiple Missiles with Fixed and

Switching Communication Topologies. Chinese

Journal of Aeronautics, 2017, 30(4):1761570-1581.

LI W. Research on Time-cooperative Guidance of Multiple

Flight Vehicles with Time-varying Velocity. Acta

Armamentarii, 2020, 41(6):1096-1110.

WANG Z Y. Research on Cooperative Guidance and

Formation Flight with Multiple Constraints. Beijing:

Beijing Institute of Technology, 2018:155-158.

Lu P. Entry guidance: a unified method. Journal of

Guidance, Control, and Dynamics, 2014, 37(3):713-

728.

Amer Al-Radaideh. Relative Dynamics Modeling and

Three-Dimensional Formation Control for Leader-

Follower UAVs in the Presence of Wind. AIAA 2020-

0878. AIAA Scitech 2020 Forum. January 2020.

Brian Coulter. Hypersonic Trajectory Optimization with

High-Fidelity Aerothermodynamic Models. AIAA

2021-0715. AIAA Scitech 2021 Forum. January 2021.

Wang Z B , Michael J. Grant. Autonomous Entry Guidance

for Hypersonic Vehicles by Convex Optimization.

Journal of Spacecraft and Rockets, 2018, 55:4,993-

1006

Wang Z P. Hypersonic Skipping Trajectory Planning for

High L/D Gliding Vehicles. AIAA 2017-2135. 21st

AIAA International Space Planes and Hypersonics

Technologies Conference. March 2017.

LI M Y. Research on Cooperative Distribution and Strike

Strategy of Multi-aircraft to Multi-target. Beijing:

Beijing Institute of Technology, 2021, 37-45.

Li S C. Profile Tracking Guidance Law Based on Sliding

Mode Control. Acta Aeronautica et Astronautica

Sinica, 2005, 10-25.

Ma Z. Research on the attitude control of quad-rotor UAV

based on active disturbance rejection control. 2017

3rd IEEE International Conference on Control

Science and Systems Engineering (ICCSSE), 2017, pp.

45-49. doi: 10.1109/CCSSE.2017.8087892.

CHEN K J. Launch Vehicle Flight Dynamics and

Guidance. Beijing: National Defense Industry Press,

2014, 319-320.

WANG G L. Predictor-corrector Reentry Guidance for

Hypersonic Vehicles. Harbin: Harbin Institute of

Technology, 2010, 22-31.

ICDPCS 2023 - The International Conference on Data Processing, Control and Simulation

140