Advanced Trajectory Planning and 3D Waypoints Navigation of
Unmanned Underwater Vehicles Based Fuzzy Logic Control with LOS
Guidance Technique
Fethi Demim
1
a
, Hadjira Belaidi
2 b
, Abdenebi Rouigueb
3 c
, Ali Zakaria Me ssaoui
4
,
Kahina Lo uadj
5
d
, Sofian S aghour
4
, Mohamed Akram Benatia
3
, Mohamed Chergui
6
,
Abdelkrim Nemra
1
e
, Ahmed Allam
6
and Elha ouari Kobzili
6
1
Laboratory of Guidance and Navigation, Ecole Milit aire Polytechnique, Bordj El Bahri, Algiers, Algeria
2
Signals and Systems Laboratory, Institute of Electrical and Electronic Engineering,
University M’Hamed Bougara of Boumerdes, Boumerdes, Algeria
3
Laboratory of Artificial Intelligence and Virtual Reality, Ecole Militaire Polytechnique, Bordj El Bahri, Algiers, Algeria
4
Laboratory of Complex Systems Control and Simulators, Ecole Mil itaire Polytechnique, Algiers, Algeria
5
Laboratoire d’Informatique, Mathmatiques, et Physique pour l’Agriculture et les Forˆets, Universit´e de Bouira, Algeria
6
Ecole Nationale Polytechnique, Algiers, Algeria
Keywords:
Unmanned Underwater Vehicles, RRT, LOS Based Navigation Guidance, Fuzzy Logic Control, Avoiding
Obstacle.
Abstract:
Trajectory planning is a critical action for achieving the objectives of Unmanned Underwater Vehicles (UUVs).
To navigate through complex environments, this study investigates motion trajectory planning using Rapidly-
exploring R andom Trees (R RT) and Fuzzy Logic Control (FLC). Our goal is to explore the use of the RRT
trajectory planning algorithm to generate waypoints in a known static environment. In this case, the UUV’s
planned trajectory can meet the required conditions for obstacle avoidance. B y using various objective func-
tions, the model can be solved, and the corresponding control variables can be adjusted to effectively ac-
complish the requirements of underwater navigation. This technique has been successfully applied in various
experimental scenarios, demonstrating the effectiveness of the FLC regulator. For instance, The 3D way-
point navigation challenge has been tackled by implementing the Fuzzy Controller, which utilizes the robust
Line-Of-Sight (LOS) guidance technique. Experimental results demonstrate that the FLC regulator efficiently
navigates through the waypoints, maintains an accurate course, controls t he pitch and yaw angles of the UUV,
and successfully reaches the final destination.
1 INTRODUCTION
Navigating Unmanned Underwater Vehicles (UUVs)
in d ynamic and uncertain underwater environments
remains a formidable challenge. To tackle this, re-
searchers are delving into advanced UUV navigation
techniques like traje ctory planning and control. Tra-
a
https://orcid.org/0000-0003-0687-0800
b
https://orcid.org/0000-0003-2424-626X
c
https://orcid.org/0000-0001-5699-2721
d
https://orcid.org/0000-0002-4203-6357
e
https://orcid.org/0000-0001-9237-9449
jectory planning, a critical facet of UUV navigation,
involves charting a viable path from the current UUV
position to the intended destination. This path must
account for obstacle avoidance, seabed distance main-
tenance (Issac et al., 1979), disturbance compensation
(e.g., ocean currents), and the preservation of desired
stability levels (Breivik and Fossen, 2000).
To navigate around obstacles, UUVs often require
additional power to come to a stop and remain sta-
tionary. In efforts to mitigate this challenge and en-
hance precision and effectiveness, researc h has ven-
tured into employing Fuzzy Logic Controllers (FLCs)
and artificial inte lligence techniques (Blidbe rg, 2003)
538
Demim, F., Belaidi, H., Rouigueb, A., Messaoui, A., Louadj, K., Saghour, S., Benatia, M., Chergui, M., Nemra, A., Allam, A. and Kobzili, E.
Advanced Trajectory Planning and 3D Waypoints Navigation of Unmanned Underwater Vehicles Based Fuzzy Logic Control with LOS Guidance Technique.
DOI: 10.5220/0012153200003543
In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 538-545
ISBN: 978-989-758-670-5; ISSN: 2184-2809
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

(Coleman, 20 03). Nonetheless, steering underwater
vehicles remains intrica te due to intricate intercon-
nections, substantial nonlinearities in modeling, un-
certainty in model pa rameters, and the complexities
of handling disturb ances like ocean currents and wave
influences (Blidberg, 2003).
Over the past decade, a multitude of control
techniques have emerged and undergo ne te stin g
for autonomous un derwater vehicles (AUVs). In
2018, diverse methods were introduced, inc luding
Optimization- te chnique based Ada ptive Model-Free
Control (OAMFC), adaptive backstepping terminal
sliding mode contro l employing Recurrent Neural
Networks (RNN), and an intelligent controller for co-
operative missions with limited or no commun ic ation
(Safaei and Mahyuddin, 2018) (Yang et al., 201 8).
In 2022, two stud ie s successfully add ressed the
challenge of fixed- time trajectory tracking control for
undera c tuated AUVs in the presence of external dis-
turbance s. This achievement was attained by integrat-
ing the backstepping contro l technique with a fixed-
time control approach (Peng et al., 2022) and (An
et al., 2022). Looking ahead to 2023, an innovative
trajectory planning method for AU V obstacle avoid-
ance in complex environments emerged. This ap-
proach leveraged the Gauss Pseudo-spectral Method
(GPM) and deep reinfor cement learning to for mulate
a versatile trajectory planning model that accommo-
dates multiple constraints (Gan et al., 2023).
This article intr oduces an advanced 3D trajectory
planning and fuzzy logic control m ethod for U UV s.
The approach encompasses path generation with di-
rect methods like the pseudo- spectral method (Kim
and Kim, 2017), spanning theoretical foundations,
practical implementation, and performance assess-
ment. The article addresses fuzzy logic controller
parameter optimization using techniques like Sim-
ulated Annealing, Genetic Algorithm, and Particle
Swarm Optimization (Poppinga et al., 2011). To over-
come current trajectory planning limitations, an en -
hanced mathematical model w ith dynamic constraints
is proposed for precise navigation in complex un -
derwater environments. The study employs an RRT-
based algorithm and FLC controller for UUV trajec-
tory planning and control, yielding enhanced naviga-
tion efficiency and empir ic al validation. Further more,
it explores Fuzzy Controller integration for ”Way-
points navigation” using RRT-generated way-points
with LOS guidance, leveraging Simultaneous Local-
ization and Mapping for advanced trajectory planning
techniques (Demim et al., 2018), (Demim and et al.,
2019), and (Demim et al., 2022).
The structure of the article is outlined as follows.
Section II delves into UUV modeling, encom passing
both kinematic and dynamic equations. In Section
III, a comprehensive exploration of the fuzzy logic
control- based RRT algorithm is presented as a piv-
otal approach for UUV obstacle avoidance during 3D
waypoint navigation. Moving on to Section IV, em-
pirical findings are shared to validate the efficacy of
the prop osed methodologies. Finally, Section V con-
cludes the paper by suggesting areas for future re-
search work.
2 MATHEMATICAL
REPRESENTATION OF UUV
SYSTEM
2.1 Kinematic Modeling of UUV Sys tem
This section introduces a U UV trajectory planning
method considering its physical capabilities and con-
straints. The dynamic model is descr ibed by six non-
linear equations for kinematics and dy namics, incor-
porating hydro dynamic and hydrostatic relationships
governing 3D movement and stability. Euler a n-
gles (φ,θ,ψ) in a local coordinate system define the
UUV’s orientation, representing roll, pitch , and yaw
rotations around the body-fixed frame’s X , Y , and Z
axes (see Figure 1). Two coordinate systems are de-
fined: the body-fixed frame and th e e a rth-fixed frame,
aligned with the UUV’s ce nter of gravity, fo rming the
foundation for control and movement analysis. The
Figure 1: UUV presentation in the body-fixed frame.
UUV’s center of gravity is defined in the absolute ref-
erence frame R
0
by its Cartesian coordinates:
η
1
= [x, y, z]
T
(1)
The orientation of the vehicle, defined in the absolute
referenc e frame, is expressed as:
η
2
= [φ, θ, ψ]
T
(2)
The position vector is expressed as:
η = [η
T
1
,η
T
2
]
T
= [x, y, z, φ, θ, ψ]
T
(3)
Advanced Trajectory Planning and 3D Waypoints Navigation of Unmanned Underwater Vehicles Based Fuzzy Logic Control with LOS
Guidance Technique
539

The body-fixed velocity vector v of UUV is given by:
v = [v
T
1
,v
T
2
]
T
= [u, v, w, p, q, r]
T
(4)
In this context, the vector v
1
= [u, v, w]
T
denotes th e
linear velocities in surge (u), sway (v), and heave (w)
directions, corresponding to x, y, and z axes. The vec-
tor v
2
= [p, q, r]
T
signifies the angular velocities for
roll, pitch, and yaw. The UUV’s kinematic model
allows trajectory determination based on initial con-
figuration and translational and rotational velocities.
The inertial reference frame linked to th e earth yields
the trajectory via the following kinematic relation ship
(Fossen, 2011):
˙
η = Jv (5)
The Jacobian matrix J = T (φ,θ,ψ), as derived from
(Fossen, 1994), simplifies the translation of the
UUV’s position between global and local reference
frames. This matrix enable s the smooth conversion of
coordinates be twe en these frames, connecting the m
effectively. The relationship between global an d local
linear velocities [x; y; z] and [u; v; w] is encapsulated
in the transfo rmation equation:


u
v
w


= f (φ,θ,ψ) ×


˙x
˙y
˙z


(6)
Modeling UUVs is a comp lex task and often involves
challenges in determining hydrodynamic pa rameters,
which can be addressed using empir ic a l equations or
tank tests. To simplify the modeling process, various
assumptions can be made . First, we assume the UUV
is neutrally buoyant and has a uniformly distributed
mass. We also disregard roll motion, and external fac-
tors like wind, waves, and currents. Additionally, the
dynamic equations incorpo rate a hydrodynamic drag
term of less than two, while th e UUV’s structure is as-
sumed symmetric acro ss three main symmetry planes.
The simplified kinematic equations (Eq. 5) (Liang
et al., 2018) can be represented by neglecting r oll mo-
tion (φ = 0):









˙x = u cos(ψ)cos(θ) − v sin(ψ) + w cos(ψ)sin(θ)
˙y = u sin(ψ)cos(θ) + v cos(ψ) + wsin(ψ)sin(θ)
˙z = −u sin(θ) + wcos(θ)
˙
θ = q
˙
ψ = r/cos(θ)
(7)
2.2 Dynamic Modeling of UUV System
The equation of motion for an U U V depends on the
effects of various control a ctions, such as rudd e r ori-
entation, propulsion, gravity force, and buoyancy. As
UUVs are nonlinear systems, their dynamics can be
modeled by the next eq uation (Yu et al., 2019):
M ˙v = C
ext
(v)v + D(v)v + τ
g
+ τ
c
(8)
where M represents the positive definite symm e tric
inertia matrix, D(v) den otes the damping matrix, an d
C
ext
(v) is the antisymmetric Coriolis and centrifugal
forces matrix incorporatin g added mass effects. The
vector τ
ext
, extracted from (Fossen, 2011), captures
the forces and moments actin g on the vehicle and can
be deconstructed as follows:
τ
ext
= τ
g
+ τ
c
(9)
The vector τ
ext
of applied forces and mo ments can be
partitioned into τ
g
and τ
c
. The former encompa sses
gravity and buoyancy-related fo rces a nd moments,
while the latter originates from the vehicle’s actuators.
Hydrodynamic actu ators can be categorized into rud-
ders and de pth control surfaces (corresponding to τ
5
and τ
6
, respectively), as well as propulsion force (rep-
resented by τ
1
). Consequently, the vector of forc e s
and moments resulting from the vehicle’s actuators is
given by:
τ
c
= [τ
1
, 0, 0, 0, τ
5
, τ
6
]
T
(10)
The UUV’s dynamic model center s on the pivotal ma-
trix M, encompassing m ass and moments of inertia
distribution. T his matr ix is pivotal for UUV motion
modeling and force/moment calculations in response
to water movements. Symmetrical UUV stru cture
condenses M into a diagonal form, enh ancing dynam-
ics analysis across three princip al symmetry planes.
M = diag[m
11
, m
22
, m
33
, m
44
, m
55
, m
66
] (11)
Assuming that our vehicle is a rigid body with neutr al
buoyancy that satisfies W = B and has a homogeneous
mass distribution, an even simpler representation can
be obtained by locating the center o f gravity and the
center of buoyancy on the z-axis. This results in a
simplified h ydrostatic force representation as (Fossen,
2011):
τ
g
= diag[0, 0, 0, 0 , − (z
G
W −z
B
B)sin(θ), 0] (12)
The variables z
B
and z
G
represent the z position be-
tween the geometric center of the UUV a nd its center
of buoyancy and center of gravity, respectively. We
can rewrite equation 8 as follows:













m
11
˙u = m
22
vr − m
33
wq − X
u
u − X
u
|u|u|u| + τ
1
m
22
˙v = −m
11
ur −Y
v
v −Y
v
|v|v|v|
m
33
˙w = m
11
uq − Z
w
w − Z
w
|w|w|w|
m
55
˙q = (m
33
− m
11
)uw − M
q
|q|q|q| − (z
G
w − z
B
B)
sin(θ) + τ
5
m
66
˙r = (m
11
− m
22
)uv − N
r
r − N
r
|r|r|r| + τ
6
(13)
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
540

where τ
1
refers to the propulsion force, τ
5
and τ
6
express the pitch and yaw torques, respectively, and
X
u
,X
u
|u|,Y
v
,Y
v
|v|,Z
w
,Z
w
|w|,N
r
, and N
r
|r| are the lin-
ear and quadratic drag terms c oefficients (Fossen,
2011) (Liang et al., 2018).
3 FUZZY LOGIC CONTROLLER
BASED UUV TRAJECTORY
PLANNING
Waypoint navigation employing pred etermined points
for guiding UUVs through obstacle-rich environ-
ments is a widely utilized strategy. The Rapidly-
Exploring Random Tree (RRT) algorithm excels at
tackling intricate motion p la nning tasks, even within
high-dimensional sp aces. RRT’s configuration tree
construction and utilization of local planners make it
particularly effective in dynamic and uncertain con-
texts. Moreover, the inc orpora tion of advanced algo-
rithms and optimization techniques enh a nces obsta-
cle avoidance strategies and controllers, ena bling the
generation of real-time trajectories that adapt to ex-
ternal factors. In our study, we implemented the PD
controller, a traditional option characterized by:
u(t) = K
p
e(t) + K
d
˙e
dt
(14)
where e represents the error between the setpoint and
the output, K
p
and K
d
represent the proportional and
derivative gains, respectively. T he fuzzy values are
described as follows: NV B (Negative Very Big), NB
(Negative Big), NS (N egative Small), Z (Zero), PS
(Positive Small), PB (Positive Big), PV B (Positive
Very Big), i ∈ {1,2, 3,4,5,6,7}. The inference rule s
based on the Takagi-Sugeno technique are given in
Ta ble 1 which present the FLC Infer e nce Rules for
˜
ψ
Table 1: FLC Inference Rules.
˜
ψ/
˜
θ 
˙
˜
ψ/
˙
˜
θ
NB NS Zero PS PB
NB NVB NVB NB NS PS
NS NVB NB NS PS PS
Zero NB NS Z PS PB
PS NS NS PS PB PVB
PB NS PS PB PVB PVB
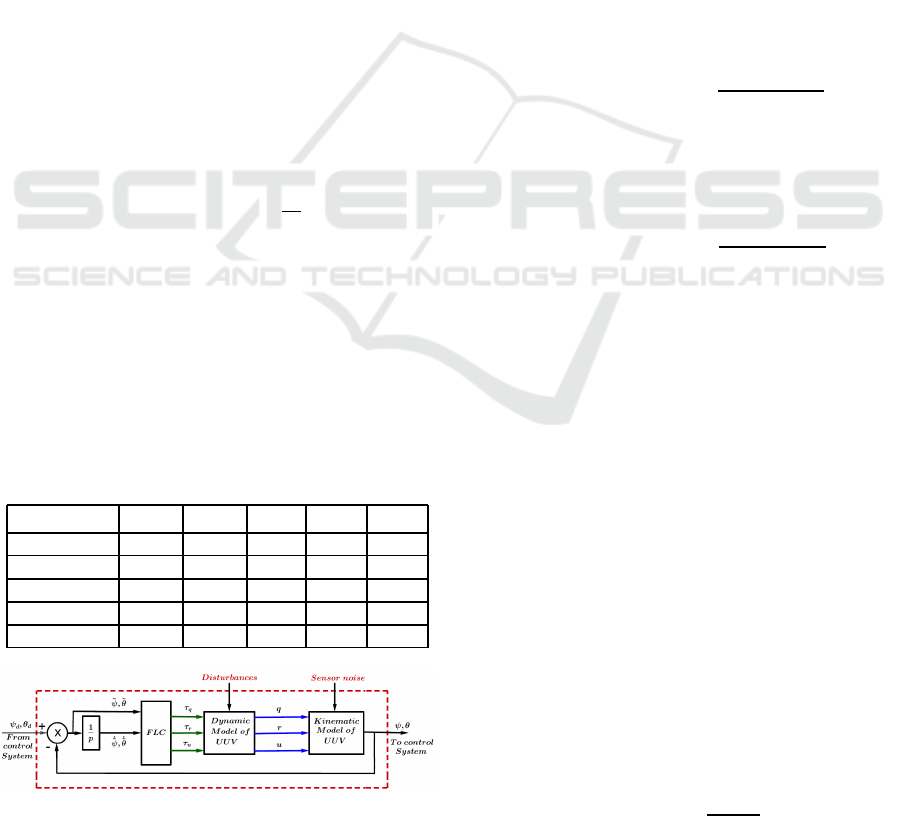
Figure 2: Fuzzy logic controller design.
and
˜
θ, respectively. The problem of navigating UUVs
through multiple passage points can be tac kled by em-
ploying the RRT algorithm to generate a set of way-
points. This a pproach ensures a safe and viable tra-
jectory in a known static environmen t. For control-
ling the UUV’s pitch and yaw angles during 3D way-
point n avigation, a Fuzzy Logic Controller (FLC) is
implemented. The FLC g overns the UUV’s actions
using the Line-Of-Sight (LOS) guidance method, e n-
abling trajectory tracking while avoiding obstacles
and maintaining stability. The integration of RRT
and FLC streamlines wayp oint navigation in chal-
lenging underwater conditions. The FLC c ontrol pro-
cess, depicted in Figure 2, involves transforming input
data using membership functions to linguistic terms
and fuzzifying them to obtain degrees of member-
ship. These are then used in a fuzzy inf e rence system
to generate an output control signal, which is subse-
quently defuzzified and converted into a specific value
for UUV control. Notably, th e calculation of τ
q
and
τ
r
is as follows:
τ
5
= τ
q
= FLC(e
θ
, ˙e
θ
) =
∑
m
i=1
k
i
µA(k
i
)
∑
m
i=1
µA(k
i
)
(15)
where µA(k
i
) represents the degree of
membersh ip of the fuzzy variable τ
q
and
k
i
∈ {−200,−175, −100, 0,100,175,200} as
shown in Figure 3(a).
τ
6
= τ
r
= FLC(e
ψ
, ˙e
ψ
) =
∑
m
i=1
k
i
µA(k
i
)
∑
m
i=1
µA(k
i
)
(16)
where µA(k
i
) represents the degree of
membersh ip of the fuzzy variable τ
r
and
k
i
∈ {−200, −100,−50,0,50,100, 200} as shown in
Figure 3(b).
4 LOS GUIDANCE PRINCIPLE
FOR 3D TRAJECTORY
PLANNING
The desired way-points p
d
= (x
d
, y
d
, z
d
) determine
the input of the control structure. The desired head-
ing and pitch angles are calculated based on the 3D
LOS (Line-Of-Sight) guidance law. The FLC con-
troller then assigns the desired torques to the vehicle
to reach these way-points. The LOS strategy is based
on aligning the vehicle as closely as possible to an
imaginary straight line connecting the vehicle p osi-
tion and the target. Assuming it moves at a c onstant
velocity u, the simple 2D-LOS for the desired he ading
angle ψ
d
can be defined as fo llows:
ψ
d
i
= tan
−1

y
d
i
− y
x
d
i
− x

(17)
Advanced Trajectory Planning and 3D Waypoints Navigation of Unmanned Underwater Vehicles Based Fuzzy Logic Control with LOS
Guidance Technique
541

(a) Membership degrees of the output τ
q
.
(b) Membership degrees of the output τ
r
.
Figure 3: Presentation membership degrees of the output τ
q
and τ
r
.
The 3D guidance system is designed to ad just the de-
sired depth of the UUV proportionally to its horizon -
tal distanc e to the target. To achieve this, consider
that the UUV needs to move from its current position
(x,y,z) to the target waypoint (x
d
,y
d
,z
d
). The desired
angle between the line connec ting the UUV an d the
target and the horizontal plane , and can be calculated
as follows:
θ
d
= tan
−1

z
d
i
− z
p
(x
d
i
− x )
2
+ (y
d
i
− y )
2

(18)
where x
d
i
, y
d
i
z
d
i
: i = {1, 2, 3,..., N}, N are the co-
ordinates of the N waypoints in the plane XY , and
(x, y, z) is the planar position of the UUV at time t.
5 EXPERIMENTS AND
DISCUSSION
Our simulation re sults show that c ombining RRT with
a fuzzy controller offers a effective and secure method
for mission planning in r ealistic AUV operations.
Fuzzy logic allows the creation of accurate models
that closely resemble human reasoning. With its sim-
plicity and versatility, fuzzy logic has remained a vi-
brant research area for several decades. Studies in
fuzzy logic for process control have centered on es-
tablishing general d esign rules for fuzzy controllers,
assessing stability criteria, and creating optimization
algorithm s for these controllers.
5.1 Tuning of the Controller Parameters
The simulation platform consists of an underactuated
UUV model controlled by three independent inputs:
propulsion force, pitch torque, and yaw torque. Its
nominal values and hydrodynamic para meters are:
• Inertia Terms: ˆm
11
= 215 Kg, ˆm
22
= ˆm
33
=
255 Kg, ˆm
55
= ˆm
66
= 80 Kg.m
2
;
• Linear Drag Hydrodynamic Coefficient
Terms:
ˆ
X
u
= 70 Kg/s,
ˆ
Y
v
=
ˆ
Z
w
= 100 Kg/s,
ˆ
M
q
=
ˆ
N
r
= 50 Kg.m
2
/s;
• Quadratic Drag Hy drodyna mic Coefficient
Terms:
ˆ
X
u
|u| =
ˆ
M
q
|q| =
ˆ
N
r
|r|100 Kg/m,
ˆ
Y
v
|v| =
ˆ
Y
w
|w| = 200 Kg/m;
• Other Parameters: m = 185 Kg,W =
B = 1813 N, z
G
= z
B
= 0.01 m,
˜
ψ =
˜
θ ∈
[−180
◦
,+180
◦
],
˙
˜
ψ =
˙
˜
θ ∈ [−3,+3] and
τ
q
,τ
r
∈ [−200,+200].
The control of the an gles ψ a nd θ is carried out by
PD controller. These angles of the latter are written
as follows:
(
τ
r
= τ
6
= K
p
˜
ψ + K
d
˙
˜
ψ
dt
τ
q
= τ
5
= K
p
˜
θ + K
d
˙
˜
θ
dt
(19)
The error signals represent the differences between
the desired an d actual values of ψ and θ as d e picted
in Figure 4. After incorporating th e FLC controller
with the calculated parameters into our system to reg-
ulate the angles ψ and θ, we performed simulation s
and obtained the following re sults, as depicted in Fig-
ure 6: ψ
d
= 0.57 rad,θ
d
= 0.52 rad,K
p
r
= K
p
q
=
7000, K
d
r
= 155.25,K
d
q
= 346. Th e FLC receives er-
ror sign als, which rep resent the disparities be tween
the desired and actual values of ψ and θ, and employs
fuzzy logic-based control rules to generate two con-
trol signals.
5.2 Comparison Between FLC and PD
Controllers of Angles ψ and θ
We applied PD and FLC techniques for pitch and yaw
angle control, with the objective of identifying an op-
timal controller that achieves steady-state error elimi-
nation, minimal overshoot, reduced settling time, a nd
effective process regulation. Our aim is to devise a
system characterized by precision, speed, stability,
and robustness. To evaluate contro ller performance ,
the Mean Square Error (MSE) is commonly used as a
parameter optimization metric, calculated as follows:
MS E
ψ
=
1
N
N
∑
1
˜
ψ
2
, MSE
θ
=
1
N
N
∑
1
˜
θ
2
(20)
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
542

0 1 2 3 4 5 6 7 8 9 10
0
0.5
1
1.5
2
Proportional Derivative (PD)
Yaw angle ψ (rad)
Time (s)
Yaw angle control ψ with PD
Desired value ψ
d
ψ
d
– 5%
(a) ψ angle control using PD.
0 1 2 3 4 5 6 7 8 9 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Proportional Derivative (PD)
Pitch angle θ (rad)
Time (s)
Desired value θ
d
θ
d
– 5%
Pitch angle control θ with PD
(b) θ angle control using PD.
Figure 4: Control based PD of the angles ψ and θ.
0 1 2 3 4 5 6 7 8 9 10
0
0.5
1
1.5
2
Yaw angle ψ (rad)
Time (s)
Fuzzy Logic Controller (FLC)
ψ
d
– 5%
Desired value ψ
d
Yaw angle ψ control with FLC
(a) ψ angle control using FLC.
0 1 2 3 4 5 6 7 8 9 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Fuzzy Logic Controller (FLC)
Pitch angle θ (rad)
Time (s)
θ
d
– 5%
Desired value θ
d
Pitch angle control θ with FLC
(b) θ angle control using FLC.
Figure 5: Control based FL C of the angles ψ and θ.
where N represents the number of samples.
In performance evaluation, accuracy is determined by
comparing achieved go a ls to desired ones. This in-
volves assessing the gap between desired setpoint and
steady-state measurement, where
˜
ψ and
˜
θ tend to-
wards infinity. Speed is gauged by response time
(T
r
ψ
,T
r
θ
), representing time to stable output within
± 5% of range. Damping links to damping ratio, indi-
cating oscillation attenuation. Higher dampin g yields
quicker dampin g, seen in overshoot (D
ψ
,D
θ
). Re-
sults in Table 2 show comparable, satisfactory perfor-
mance of both controllers under steady-state. How-
ever, FLC surpasses PD, with reduced overshoot, en -
hanced p recision, and lower mean squared error. PD
has quicker response, but FLC boasts better damp-
ing, minimiz ing oscillations. FLC excels in precision,
closely tracking tr ajectory with low MSE and aligned
output. PD achieves speedier steady-state, yet larger
overshoot could lead to oscillation s (Table 2). Based
on the findings in Table 2, the FLC controller proves
advantageous for this system, exhibiting superior per-
formance in terms of overshoot, p recision, and MSE .
However, if prioritizin g speed over minimizing over-
shoot is crucial, the PD controller could be favored.
Notably, our simulations reveal the FLC’s overall su-
periority over the PD controller, except for respo nse
time. Figure 6 sh owcases a comparative analysis of
the FLC-based and PD controllers’ pe rformance for ψ
and θ, affirming the FLC’s superior tracking accuracy
and overall perfo rmance. Furthermore, Figures 7 and
8 demonstrate the FLC-based control’s effectiveness
in r egulating rotation velocities (q and r) an d torque s
(τ
q
and τ
r
). The former illustrates angular velocity
q and torque τ
q
aligning with the desired ang le θ
d
,
while the latter depicts an gular velocity r and torque
τ
r
aligning with the desired angle ψ
d
.
5.3 3D N avigation by Waypoint Usi ng
the F LC-Based LOS Guidance
Method
Figure 9 illustrates the UUV’s 3D navigation along
automatically generated waypoints from the RRT* a l-
gorithm. The FL C-guided LOS controller ensures
waypoint traversal while maintaining constant veloc-
ity. The control of ψ a nd θ angles during navigation
is displayed in Figures 10 and 11. The FLC employs
input fuzzy sets fo r pitch and yaw angle errors an d
output fuzzy sets for pitch and yaw torques.
6 CONCLUSIONS
This article offers a comprehensive exploration of
UUV trajec tory planning, employing ad vanced RRT
and fuzzy logic-ba sed strategies. Our simulation re-
sults highlight the efficacy of combining RRT an d
fuzzy controllers for secure and efficient mission
planning in challenging marine environments. Fuzzy
Advanced Trajectory Planning and 3D Waypoints Navigation of Unmanned Underwater Vehicles Based Fuzzy Logic Control with LOS
Guidance Technique
543

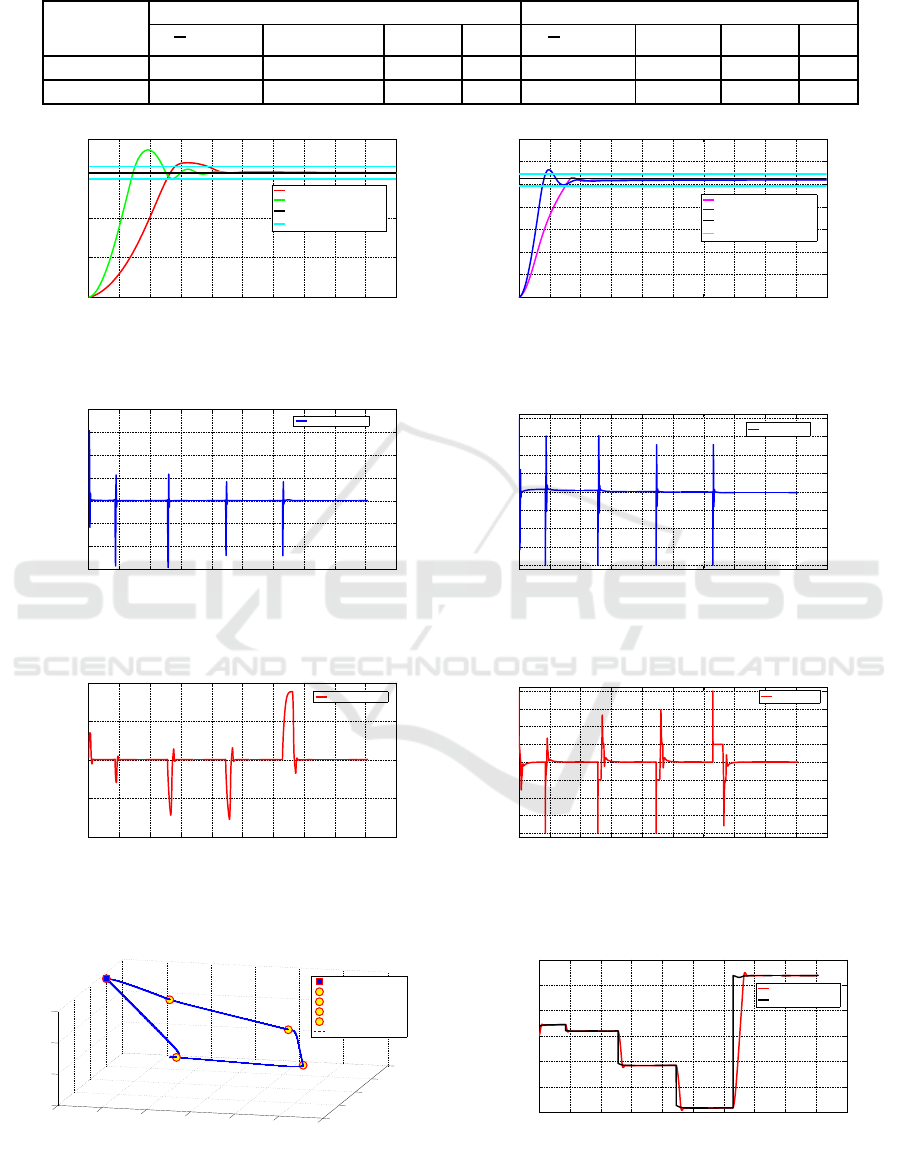
Table 2: Comparison of the angle ψ and θ between FLC and PD Controllers.
ψ θ
Controller
1
N
∑
N
1
˜
ψ
2
lim
t←∞
˜
ψ
D
ψ
T
r
ψ
1
N
∑
N
1
˜
θ
2
lim
t←∞
˜
θ D
θ
T
r
θ
FLC 9.2379e-11 -3.0409e -04 0.1271 3.88 1.4955e-08 -0.0039 0.0048 1.52
PD 1.1407e-10 3.3792e -04 0.2889 2.42 2.900 2e-08 -0.00 54 0.0397 1.12
0 1 2 3 4 5 6 7 8 9 10
0
0.5
1
1.5
2
Comparison of yaw angle (ψ) control between FLC and PD
Yaw angle ψ (rad)
Time (s)
Yaw angle ψ control with FLC
Yaw angle ψ control with PD
Desired value ψ
d
ψ
d
– 5%
(a) Comparison of ψ angle control using FLC and PD.
0 1 2 3 4 5 6 7 8 9 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Comparison of pitch angle (θ) control between FLC and PD
Pitch angle θ (rad)
Time (s)
Pitch angle θ control with FLC
Pitch angle θ control with PD
Desired value θ
d
θ
d
– 5%
(b) Comparison of θ angle control using FLC and PD.
Figure 6: Comparison control based FLC and PD of the angles ψ and θ.
0 20 40 60 80 100 120 140 160 180 200
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
The angular velocities (q) for 3D navigation using waypoints
q (rad/s)
Time (s)
Angular velocity q
(a) Control of the rotation velocity q.
0 20 40 60 80 100 120 140 160 180 200
-200
-150
-100
-50
0
50
100
150
200
τ
q
(N)
Time (s)
Pitch torque (τ
q
) applied on the AUV to produce angular motion around Y−axis
Pitch torque τ
q
(b) Control of torque τ
q
.
Figure 7: Control of the rotation velocity q and torque τ
q
.
0 20 40 60 80 100 120 140 160 180 200
-1
-0.5
0
0.5
1
The angular velocities (r) for 3D navigation using waypoints
r (rad/s)
Time (s)
Angular velocity r
(a) Control of the rotation velocity r.
0 20 40 60 80 100 120 140 160 180 200
-200
-150
-100
-50
0
50
100
150
200
τ
r
(N)
Time (s)
Yaw torque (τ
r
) applied on the AUV to produce angular motion around Z−axis
Yaw torque τ
r
(b) Control of torque τ
r
.
Figure 8: Control of the rotation velocity r and torque τ
r
.
0
20
40
60
80
100
120
-60
-40
-20
0
20
-15
-10
-5
0
Y (m)
X (m)
3D navigation of UUV by following waypoints
Z (m)
Starting and endpoints
Waypoint n1
Waypoint n2
Waypoint n3
Waypoint n4
UUV trajectory
Point n°2
Point n°1
Point n°4
Point n°3
Figure 9: 3D navigation of the UUV by following way-
points.
0 20 40 60 80 100 120 140 160 180 200
-3
-2
-1
0
1
2
3
Fuzzy logic control the yaw angle (ψ) of the AUV during 3D navigation
Yaw angle ψ (rad)
Time (s)
Control yaw angle ψ
Desired value ψ
d
Figure 10: FLC controls the ψ angle during the 3D naviga-
tion trajectory.
ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics
544

0 20 40 60 80 100 120 140 160 180 200
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
Fuzzy logic control the pitch angle (θ) of the AUV during 3D navigation
Pitch angle θ (rad)
Time (s)
Control pitch angle θ
Desired value θ
d
Figure 11: FLC controls the θ angle during the 3D naviga-
tion trajectory.
logic mim ic s human-like representation and reason-
ing, making it a prolific research domain. Ongoing
efforts in pr ocess control foc us on developing gen-
eral fu zzy controller rules, stability analysis, and op-
timization algorithms.
In our future research, we aim to incorpo rate in-
tegral square e rror analysis for a deeper understand-
ing of FLC system perform ance co mpared to differ-
ent controllers, emphasizing trajectory accuracy and
stability. While our study holds potential, we recog-
nize ongoing challenges in advancing UUV trajectory
planning, requirin g adaptable algorithms, seamless
sensor integration, and addressing intricate mission
scenarios. Tackling these challenges in upco ming re-
search could greatly enhanc e trajectory planning ef-
ficiency, impacting diverse fields like oceanography,
surveillance, exploration, and resou rce management.
REFERENCES
An, S., Wang, L., and He, Y. (2022). Robust fixed-
time tracking control for underactuated auvs based on
fixed-time disturbance observer.
Blidberg, D. (2003). The development of autonomous
underwater vehicles (auv). I n A Brief Summary,
Autonomous Undersea Systems Institute, Lee New
Hampshire, USA.
Breivik, M. and Fossen, T. (2000). Guidance laws for au-
tonomous underwater vehicles. In Norwegian Univer-
sity of Science and Technology, Norway.
Coleman, J. (2003). Undersea drones pull duty in iraq hunt-
ing mines. In C ape Code Times.
Demim, F., Benmansour, S., Nemra, A., Rouigueb, A.,
Hamerlain, M., and Bazoula, A. (2022). Simultane-
ous localization and mapping for autonomous under-
water vehicle using a combined smooth variable struc-
ture filter and extended kalman filter. pages 621–650.
Demim, F. and et al., A. N. (2019). NH-∞-SLAM algorithm
for autonomous underwater vehicle. Springer Interna-
tional Publishing.
Demim, F., Nemra, A., Abdelkadri, H., Louadj, K., Hamer-
lain, M., and Bazoula, A. (2018). Slam problem for
autonomous underwater vehicle using svsf filter. In
Proceeding of 25th IEEE International Conference
on Systems, Signals and Image Processing, Maribor,
Slovenia, pages 1–5. IEEE.
Fossen, T. (1994). Guidance and Control of Ocean Vehicles.
Fossen, T. (2011). Handbook of Marine Craft Hydrodynam-
ics and Motion Control.
Gan, W. , Su, L., and Chu, Z. (2023). Trajectory planning of
autonomous underwater vehicles based on gauss pseu-
dospectral method.
Issac, M., Adams, S., He, M., Neil, W., Christopher, D.,
and Bachmayer, R. (1979). Manoeuvring experiments
using the mun explorer auv. In In proceeding.
Kim, Y. and Kim, B. (2017). Time-optimal trajectory plan-
ning based on dynamics for differential-wheeled mo-
bile robots with a geometric corridor. pages 5502–
5512.
Liang, X., Qu, X., Hou, Y., and Ma, Q. (2018). Three-
dimensional trajectory tracking control of an underac-
tuated autonomous underwater vehicle based on ocean
current observer. pages 1–9.
Peng, Y., Guo, L., and Meng, Q. (2022). Backstepping
control strategy of an autonomous underwater vehicle
based on probability gain. pages 39–58.
Poppinga, J., Birk, A., Pathak, K., and Vaskevicius, N.
(2011). Fast 6-dof path planning for autonomous un-
derwater vehicles (auv) based on 3d plane mapping.
Safaei, A. and Mahyuddin, M. (2018). Application of
the optimal adaptive model-free control algorithm on
an autonomous underwater vehicle. Proceedings 3rd
of the IEEE International Conference on Advanced
Robotics and Mechatronics, Singapore, Singapore.
Yang, C., Yao, F., and Zhang, M. (2018). Adaptive back-
stepping terminal sliding mode control method based
on recurrent neural networks for autonomous under-
water vehicle. pages 1–16.
Yu, H., Guo, C., and Yan, Z. (2019). Globally finite-time
stable three-dimensional trajectory-tracking control of
underactuated uuvs.
Advanced Trajectory Planning and 3D Waypoints Navigation of Unmanned Underwater Vehicles Based Fuzzy Logic Control with LOS
Guidance Technique
545