A Dynamic Computational Model of Head Sway Responses in Human

Upright Stance Postural Control During Support Surface Tilt

Vittorio Lippi

1,2 a

, Christoph Maurer

and Stefan Kammermeier

Institute of Digitalization in medicine, Faculty of Medicine and Medical Center, University of Freiburg,

Freiburg im Breisgau, Germany

Clinic of Neurology and Neurophysiology, Medical Centre-University of Freiburg, Faculty of Medicine,

University of Freiburg, Breisacher Straße 64, 79106, Freiburg im Breisgau, Germany

Klinikum der Universität München, Ludwig-Maximilians-Universität LMU, Neurologische Klinik und Poliklinik,

Marchioninistraße 15, 81377 München, Germany

Keywords: Modelling, Computational Model, Feedback Control Systems, Parameters Identiﬁcation, Posture Control,

Human Motor Control.

Abstract: Human and humanoid posture control models usually rely on single or multiple degrees of freedom inverted

pendulum representation of upright stance associated with a feedback controller. In models typically focused

on the action between ankles, hips, and knees, the control of head position is often neglected, and the head is

considered one with the upper body. However, two of the three main contributors to the human motion

sensorium reside in the head: the vestibular and the visual system. As the third contributor, the proprioceptive

system is distributed throughout the body. In human neurodegenerative brain diseases of motor control, like

Progressive Supranuclear Palsy PSP and Idiopathic Parkinson’s Disease IPD, clinical studies have

demonstrated the importance of head motion deﬁcits. is work speciﬁcally addresses the control of the head

during a perturbed upright stance. A control model for the neck is proposed following the hypothesis of a

modular posture control from previous studies. Data from human experiments are used to ﬁt the model and

retrieve sets of parameters representative of the behavior obtained in diﬀerent conditions. e result of the

analysis is twofold: validate the model and its underlying hypothesis and provide a system to assess the

diﬀerences in posture control that can be used to identify the diﬀerences between healthy subjects and patients

with diﬀerent conditions. Implications for clinical pathology and application in humanoid and assistive

robotics are discussed.

1 INTRODUCTION

1.1 Overview

The analysis of body segment sway during a

perturbed upright stance is an established

experimental method to investigate posture control

and the underlying neurological processes in human

subjects (e.g., Assländer & Peterka, 2016; Goodworth

& Peterka, 2018) and to test the balance capabilities

of humanoid robots (Pasma et al., 2018; Zebenay et

al., 2015). Perturbation of upright stance allows

insights into the internal control mechanisms'

https://orcid.org/0000-0001-5520-8974

https://orcid.org/0000-0001-9050-279X

https://orcid.org/0000-0003-0158-889X

limitations and pinpoint the cause of possible deficits.

These alterations may be externally applied or

initiated by voluntary motion of the subject itself.

For the underlying data of our proposed model,

upright standing subjects were studied during the

passively applied small-angle rotational disturbance

with multiple superimposed sinusoidal frequencies of

their support surface, where the center of rotation was

placed at the ankle joint. Three groups of subjects

were investigated: healthy control subjects and

neurodegenerative disorders with movement control

impairment: Progressive Supranuclear Palsy PSP and

Idiopathic Parkinson’s Disease IPD. The body

Lippi, V., Maurer, C. and Kammermeier, S.

A Dynamic Computational Model of Head Sway Responses in Human Upright Stance Postural Control During Support Surface Tilt.

DOI: 10.5220/0012154300003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 17-28

ISBN: 978-989-758-670-5; ISSN: 2184-2809

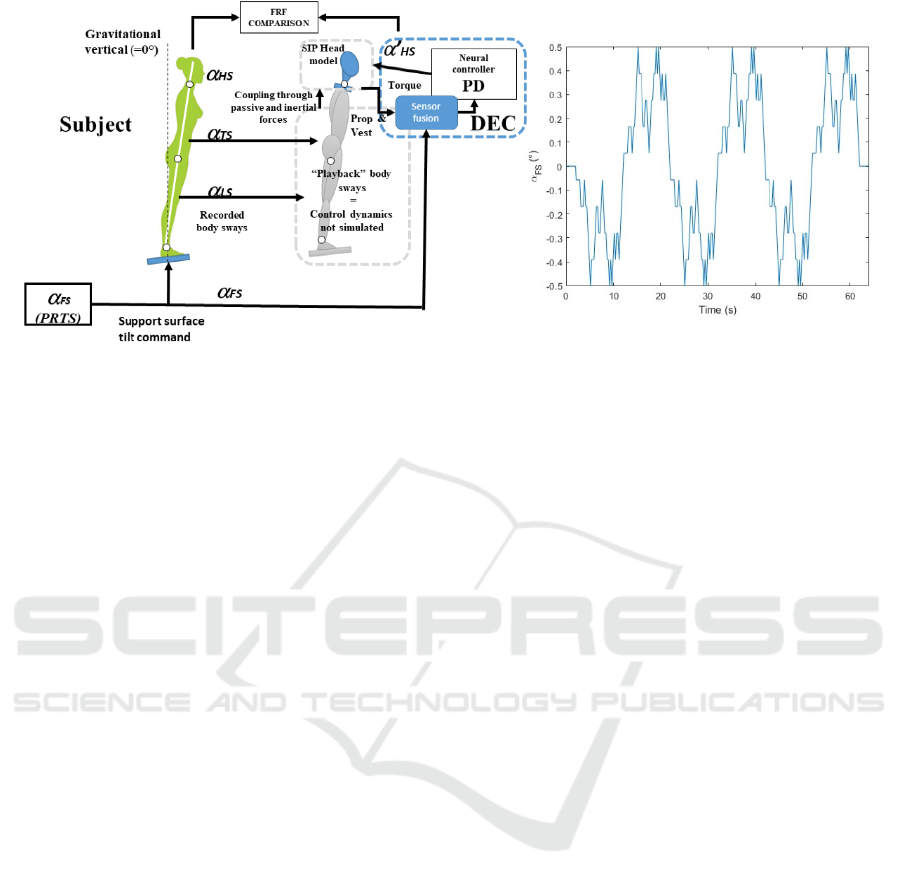
Figure 1: General Scheme of the simulated system. The recorded sways for the legs and trunk and the known PRTS input

profile are used to simulate the neck movement. On the left, the profile of the PRTS stimulus 𝛼



with peak-to-peak amplitude

1°.

segment movements were recorded with 3D

ultrasound motion capture detailed in Methods and

Kammermeier et al., 2018. The proposed model fits

data from human experiments in different conditions,

i.e., eyes-open, and eyes-closed, combined with two

amplitudes. The model was implemented with and

without including nonlinearities observed in previous

experiments to test how they capture the nonlinear

responses typical of humans. Usually, larger

disturbances are, in proportion, compensated more

than smaller ones (Hettich et al., 2013 and 2015).

Based on these results, a model for a quantitative

description of the posture control task in terms of

input (perturbation stimulus) and output (body

segment sway) was constructed, focusing on the head

segment. The response can be represented as a

transfer function in the frequency domain and

developed further as a dynamic system of response

regulation. The inherently unstable human upright

posture requires dynamic feedback control based on

sensory input.

The degrees of freedom vary depending on the

scenario: a single-inverted-pendulum model (SIP),

representing the torque provided around the ankles, is

suitable to describe small movements produced by

small perturbations. An added hip segment with

intersegmental coordination (Hettich et al., 2014)

results in a double-inverted pendulum model (DIP).

Involving the knees in the compensation of more

intense and challenging disturbances with a third

degree of freedom (Atkeson & Stephens 2007)

suggests that responses could be possibly dictated by

optimization criteria penalizing the amplitudes of

joint angles excursions and the applied torques, at

least in transient responses to impulsive disturbances.

More than 2 degrees of freedom are usually modeled

when applying posture control models to humanoids

in order to cover the number of actuators in their

kinematics (e.g., three in Ott et al., 2016) or to model

the interaction between a human and a wearable

exoskeleton (e.g., four in Lippi & Mergner, 2020). In

most cases, the control of the head is not taken into

account, and the head is considered together with the

rest of the upper body since the head is considered a

minor fraction of the upper body's mass (about 16%,

in De Leva, 1996).

This paper addresses the modeling of head control

as a modular control system, associating each degree

of freedom with a feedback controller (Hettich et al.,

2014; Lippi & Mergner, 2017). The specific

formulation of the control problem (§ 2.1) allows the

identification of the control parameters just for the

module controlling the neck without including a full

model of the other joints.

The internal representation of human body motion

in space is construed from three main sensory input

qualities for the purpose of motor control (e.g.,

summarized in Dieterich & Brandt, 2019): vestibular

angular acceleration and gravitational tilt from the

inner ear; visual alignment to vertical and horizontal

references from the eyes; and proprioceptive joint and

muscle sensors for their mutual relative positions

throughout the body. Each biological sensor type has

optimal sensory operating ranges of kinetic motion

and stationary position to overlap with the weak

ranges of other sensors. Two of these three sensory

contributors reside in the freely mobile human head,

unlike in current self-propelled humanoid robots

(e.g., Boston Dynamics Atlas). Positioning vision and

vestibular system in a small mobile mass on top

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

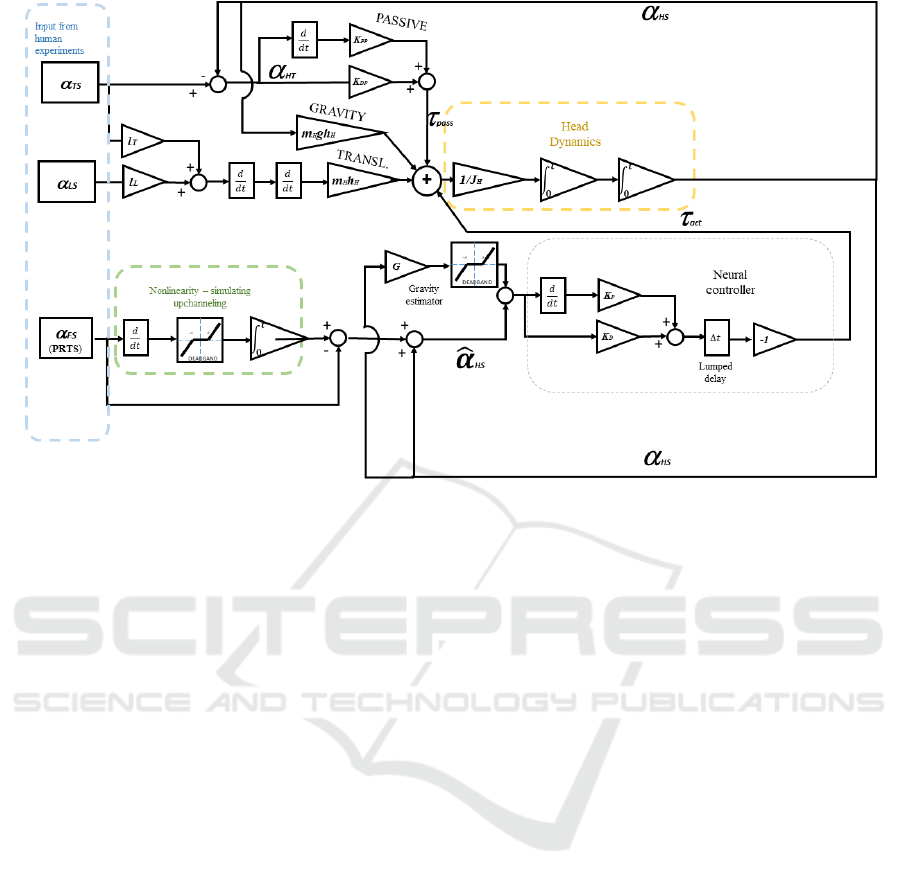
Figure 2: The Dynamic system from equations (1) to (7). Here the controlled variable is the head-in-space angle 𝛼



. To

control the head-to-trunk angle 𝛼



, such a variable should be provided as input for the neural controller instead of 𝛼



. As

the reference is assumed to be 0° the controlled variable equals the error 𝜀 in (1). The recorded body sway for the trunk and

legs is used as input. In contrast, the recorded head sway is used outside the simulation to optimize the parameters and evaluate

the result.

instead of within the main mass of the body has

several practical and evolutionary advantages. This

feature could not yet be practically implemented in

humanoid robotics by abundant technical and

computational constraints.

Therefore, understanding this sensorimotor

integration in healthy humans, in comparison to

human disease conditions, which particularly impair

the integration of head-based sensory information in

motor control, may be considered essential to future

developments in several fields of science:

- A model that can emulate healthy and

degenerative brain diseases may help to

understand analogies in neuroanatomical and

physiological networks so that tools for

diagnosis, progression monitoring, and effect

graduation of possible targeted therapies for

specific aspects of the degenerating neural

network might be developed.

- For humanoid robotics, a functional model

with known weak points similar to human

disease conditions may help to develop a

robust computational framework to integrate

sensor arrays remote to the main robot body,

analog to the human head. This may

indirectly open the main robotic body space

for other systems, like advanced propulsion

or increased payload.

1.2 State of the Art

The modeling of posture control as a dynamic system

is widespread in the analysis of human experiments

and humanoid robotics. There is no consent about

how the "actual human control system" is, and

various approaches are proposed in the literature,

depending on the analyzed task and the question

under investigation. Usually, models describe the

system as an inverted pendulum (single or multiple)

where the joint torques are controlled (Hettich et al.,

2014; Maurer et al., 2006; Thomas Mergner, 2010;

Peterka, 2002); other models include muscle activity

(Souza et al., 2022) and tendon dynamics (Loram et

al., 2004, 2005b, 2005a; P. G. Morasso & Schieppati,

1999) specifically. The effort in designing the

controller can be oriented toward representing the

biomechanics (Alexandrov et al., 2017, 2015),

investigating some neurological processes such as

sensor fusion (Thomas Mergner, 2010; Peterka,

2002), or a more general model of human neural

control (Jafari et al., 2019; McNeal & Hunt, 2023), or

based on some optimization (Atkeson & Stephens,

2007; Jafari & Gustafsson, 2023; Kuo, 2005). While

A Dynamic Computational Model of Head Sway Responses in Human Upright Stance Postural Control During Support Surface Tilt

Pictures from Kammermeier et al. (2018).

Figure 3: The experimental setup: the test subject stands on

a tilting platform. The subject's feet were placed within

marked positions, with the heels together and the tips spread

15° apart, while the arms hung loosely by the sides.

the optimization provides an interesting insight into

why the subjects may behave in a certain way and, by

definition, optimized controls for humanoids, the

optimal control is rarely totally human-like as human

behavior is reasonably the result of a trade-off

between typical control system requirements as

tracking precision and energy efficiency and

biological peculiarities that are less obvious from the

engineering point of view such as reducing the effort

of the nervous system or dealing with the fear of

falling.

In general, the more a task is complicated, the

more degrees of freedom are involved; for example,

quiet stance can be modeled with a single inverted

pendulum where the body sway is controlled by ankle

torque (P. Morasso et al., 2019) at least to predict

center of mass (COM) sway. However, there is a

small activity of other joints (Pinter et al., 2008).

Applying optimization to the compensation of

disturbances (push) of different amplitudes reveals

the emergence of strategies involving more joints,

going for ankle strategies for small pushes to knee

bend for larger ones, passing through hip-ankle

strategies for stimuli in between (Atkeson &

Stephens, 2007). As anticipated above, the control of

the neck is not common in literature, as usually, the

upper body is considered altogether and referred to as

HAT (head, arms, and trunk). In (Kilby et al., 2015),

kinematic 3D models with different numbers of

degrees of freedom (ranging from 1 to 7) for posture

control are proposed for the analysis of different tasks

recorded with subjects, i.e., quiet standing, standing

on foam, and standing on one leg. The simple model

has just the ankle joint, while the most complex has

ankles, knees, hips, and neck. No control system is

proposed, and the analysis is performed on the

variance of joint angles. The results show that the

model with the neck (7 DOF) is the most accurate in

fitting the sway of the center of mass and confirm that

with increasingly difficult tasks (standing on foam is

more demanding than quiet standing on a firm

surface, and standing on one leg is even more

difficult). This suggests that including the neck in the

control system can be beneficial in understanding

human posture control in the general case.

In this paper, the focus is on the neck with the

twofold objective of, on the one hand, exploring how

the DEC model can be extended with an additional

degree of freedom and testing whether the modularity

of the DEC control can be applied to study local

characteristics of the control, e.g., in this case, the

stiffness of the neck, and, on the other hand, provide

a tool for the specific analysis of PSP and IPD

patients.

2 MATERIALS AND METHODS

2.1 Clinical Experimental Data

The proposed model emulates the 3D motion analysis

data obtained from three groups of human subjects.

The overall setup is described in detail in

Kammermeier et al. 2018; here, 19 healthy elderly

subjects are considered. All participants gave written

informed consent, and data was anonymized at study

inclusion following the Helsinki Declaration and the

local ethics committee (142/04; Ethikkommission der

Medizinischen Fakultät).

All subjects were placed on a remotely

controllable platform (Toennis) as shown in Fig. 3,

allowing a front-to-back tilt through the ankle joint

axis. The stimulation paradigm involved a resting

condition and small-angle (0.5° and-1°) rotational

disturbances with multiple superimposed sinusoidal

frequencies (0.05-2.2Hz) for 60 seconds; each

maximum angular displacement was tested in eyes

open EO and eyes closed EC conditions.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

3D motion capture was performed with

ultrasound receivers (Zebris 3D) and re-sampled to

100Hz. The sensors placement is shown in Fig. 4 The

final dataset included the platform motion track and

the position signals of three markers for the head,

three for the chest, one for the lower spine, and one

each at the knees along the time domain.

2.2 Posture Control Model

e Control Model is based on the disturbance

identiﬁcation and compensation (DEC) principle

(omas Mergner, 2010) and its implementation as a

modular control system (Hettich et al., 2014; Lippi et

al., 2016; Lippi & Mergner, 2017). e DEC is based

on the hypothesis of a servo controller for body

position (Merton, 1953), complemented with the

estimation and compensation of external disturbances

based on sensory input (T Mergner et al., 1997;

omas Mergner & Rosemeier, 1998). e servo

controller is implemented as a PD, proportional

derivative controller. e compensation, which

generally includes support surface tilt and

acceleration, gravity, and external push, here is

considered only for gravity and support surface tilt.

Such compensation is implemented in a

Störgrößenaufschaltung fashion, literally meaning

disturbance control in German, i.e., a feed-forward

compensation of disturbances based on sensory input

that allows us to estimate the disturbance itself

(Bleisteiner et al., 1961). e DEC controller is

mainly used to predict steady-state responses, unlike

other models oriented to transient responses (e.g.,

Allum & Honegger, 1992; Küng et al., 2009).

e Control Equations regulating the action of

the servo controller for the neck are:

Active Torque

𝜏



=(𝐾



+ 𝐾



𝑑

𝑑𝑡

) (𝜀+ 𝐺



)

(1)

Passive Torque

𝜏



=(𝐾



+ 𝐾



𝑑

𝑑𝑡

) (𝛼



)

(2)

Gravity

Compensation

𝐺



=𝐾



𝜗



(𝛼



)

(3)

Support Surface

Tilt Compensation

𝛼



=𝛼



+𝛼



−𝛼



(4)

Where 𝐾



a n d 𝐾



are the coeﬃcients of the PD

controller, 𝜀 the error on the controlled variable that

can be the estimated head in space position 𝛼



from

(4) or 𝛼



, the angle between head and trunk, and 𝐺



is the estimated gravity torque from (3). Expressing

the disturbance as an additional input for the PD

exploits the derivative as an anticipation eﬀect. In

robotics applications, the compensation can have its

own PD parameter to allow for ﬁne control (Ott et al.,

2016), here only a PD according to previous works

where the DEC is used to model human responses

(e.g., Georg Hettich et al., 2014; omas Mergner et

al., 2009). 𝐾



and 𝐾



are the passive stiﬀness and

damping associated with the neck. 𝛼



in (3) and (4)

is the head-in-space angle (with respect to the

gravitational vertical) that here is assumed to come

from the vestibular system without any modeled

noise. 𝐾



is a coeﬃcient associated with gravity (that

usually, in humans, is slightly under-compensated,

taking into account the additional torque produced by

the servo loop). e function 𝜗



() is a dead-zone

nonlinearity deﬁned as

𝜗



(𝛼)=

𝛼+𝜃



𝛼<−𝜃



0−𝜃



<𝛼<𝜃



𝛼−𝜃



𝛼>𝜃



(5)

Where the threshold 𝜃



is a non-negative

parameter, the estimation of support surface tilt is

aﬀected by a nonlinearity also reﬂected in the

estimated 𝛼



in (4). Speciﬁcally, the foot-in-space

estimation is performed by fusing the vestibular

angular velocity signal with the proprioception of all

the joints from the head to the ankle, a nonlinear

function 𝜗



() with the same formal expression of (5)

and another threshold 𝜃



is then applied to the

resulting velocity signal. Here, as the proprioception

and vestibular signals are modeled as ideal, the 𝛼



known from the experiment design (§2.2.) is used to

produce the following estimation

𝛼





= 𝜗



(

𝑑

𝑑𝑡

𝛼



)







𝑑𝜏

(6)

Where 𝑡



is the current time and the initial

condition of the estimator is assumed to be 𝛼



=0.

Again for the assumption of ideal proprioceptive

signals, the error 𝛼



−𝛼



is propagated directly to

𝛼



, leading to eq. (4). e nonlinearity 𝜗



()

explains the fact observed in subjects that smaller

stimuli are associated with larger gains in the

responses (Hettich et al., 2011). Although introducing

an error in the tracking of body sway that prevents

asymptotic stability, the dead band does not make the

system unstable; in fact, it can be demonstrated that

the system is Lyapunov stable (Lippi & Molinari,

2020).

A Dynamic Computational Model of Head Sway Responses in Human Upright Stance Postural Control During Support Surface Tilt

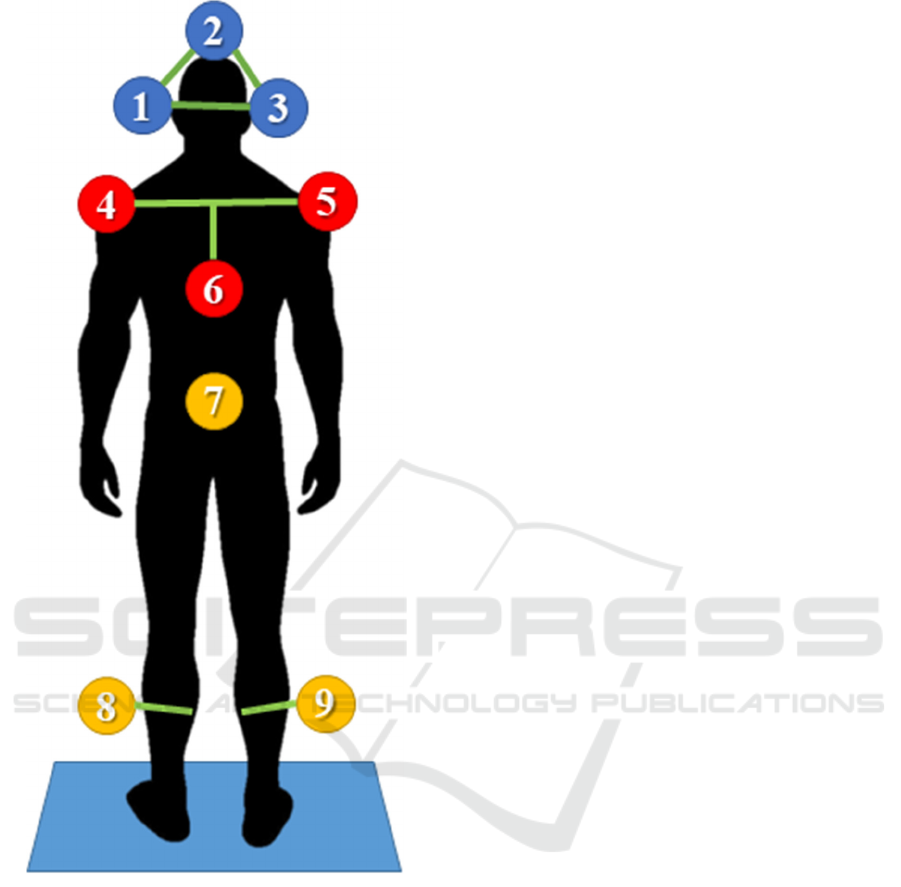
Figure 4: 3D ultrasound position markers (Zebris system)

placement: head (1,2,3), upper chest (4,5,6), hip (7) and

lateral femoral epicondyles (8,9).

A lumped delay ∆𝑡 representing all the delays in

the loop aﬀects the active control (it is in series with

the PD). e sources of the delay are the sensory input

and the motor control. For the control of the ankle,

they are usually estimated to be between 80 and 200

ms, depending on the subject and the test conditions

(Antritter et al., 2014; Li et al., 2012; Molnar et al.,

2021). In general, the delay of peripheral body joints

is expected to be larger than the one associated with

joints closer to the brain, e.g., the delay in the control

loop of the hip is smaller than the one of the ankle

(e.g., 70 ms and 180 ms respectively in G Hettich et

al., 2011). is suggests that the delay in the neck

control loop will be smaller (as conﬁrmed in the

Results §3). Delay is an important parameter as it is

observed that an added delay of about 70 – 80 ms can

already be perceived (Morice et al., 2008) and can

degrade the performance in tracking tasks (Lippi et

al., 2010) and; hence it is reasonably one of the

parameters characterizing the performance also in

posture control as suggested by (Li et al., 2012;

Lockhart & Ting, 2007; Molnar et al., 2021; Van Der

Kooij et al., 1999; Vette et al., 2010). Furthermore,

delay appears to be a determining factor in the

diﬀerent performances between young and elderly

subjects (Davidson et al., 2011; Qu et al., 2009).

A schema of the simulated system with an

overview of the DEC control, including the simulated

dynamic system, is shown in Fig. 1.

e Dynamic of the Head is simulated as a single

inverted pendulum (SIP) characterized by the weight

and the moment of inertia of the head on which the

active toques 𝜏



and 𝜏



from (1) and (2). e

translation produces a further eﬀect due to the sway

of the legs and the trunk resulting in the following

dynamic system, where the small angle

approximations sin𝛼𝛼 and cos𝛼=1 are

applied:

⎩

⎨

⎧

𝛼



=𝛼



𝛼



=𝜏



+𝜏



+𝐺+𝑇



/𝐽



𝐺= 𝑚



𝑔ℎ



𝛼



𝑇



(

𝛼



𝑙



+𝛼



𝑙



)

ℎ



𝑚



(7)

where 𝐽



is the head moment of inertia, 𝑚



i s t h e

head mass, ℎ e is the height of the head center of

mass, and 𝑔=9.81 𝑚/𝑠



is the gravity acceleration

constant. 𝑙



and 𝑙



are the lengths of the trunk and leg

segments, respectively. A standard set of

anthropometric parameters (De Leva, 1996; Winter,

2009) is used in all the simulations with no speciﬁc

adaptation to the single subject. Anthropometric

parameters are reported in Table 1. e full dynamic

system is shown in detail in Fig. 2.

2.3 The Dataset

e Frequency Response Function, FRF, is an

empirical transfer function between the stimulus and

the body sway. e input support surface tilt has a

Pseudo Random Ternary Sequence (PRTS) proﬁle

(Peterka, 2002). e fact that the system is pseudo-

random prevents the subjects from using prediction,

as it is expected that the user can learn the sequence

(omas Mergner, 2010). However, a study

(Assländer et al., 2020) suggests that the adaptation

observed in subjects after repeating the experiments

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

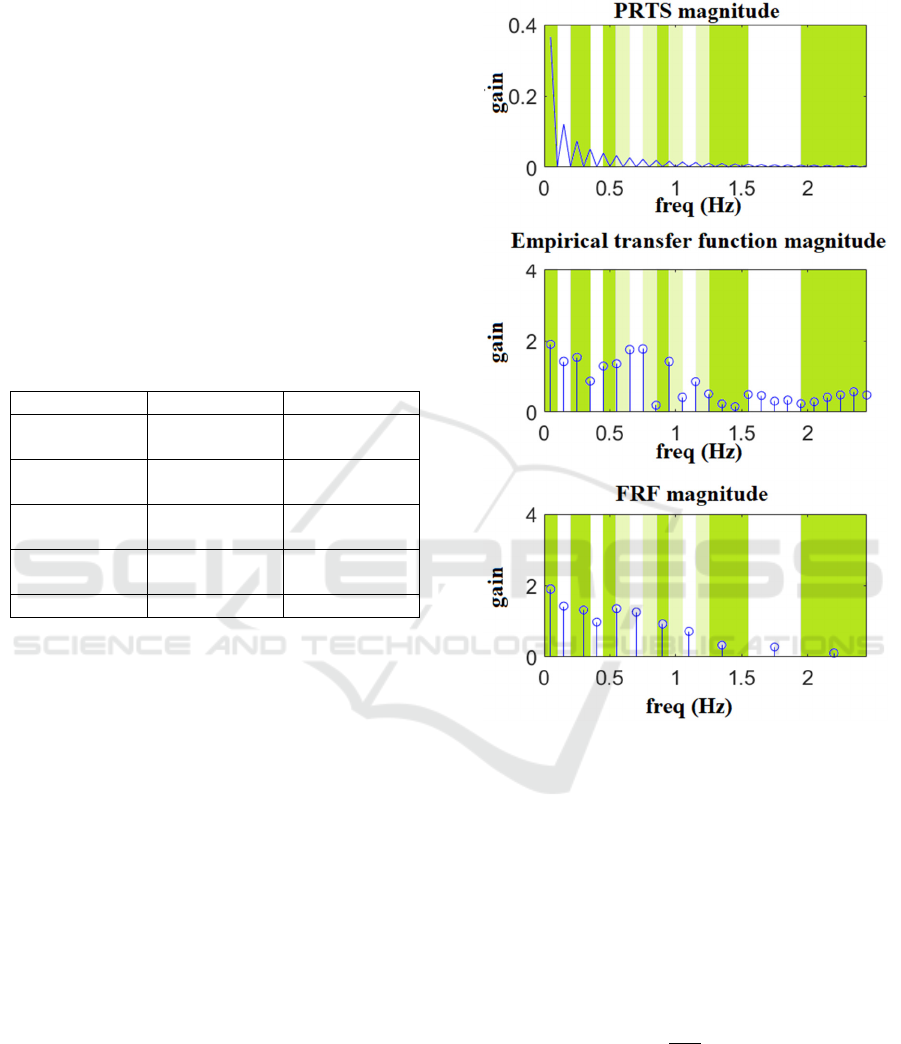
may be due to learning the dynamics of the body in

the experimental scenario, as they occur both with

pseudo-random and rhythmic stimuli. Robotic

experiments showed how DEC could improve

performance when integrating an online learning

system to predict future disturbances (Lippi, 2018). In

the presented model, no prediction or learning will be

taken into account. e peak-to-peak amplitudes used

in the presented experiments are 0.5° and 1°. e

PRTS power spectrum has a proﬁle with peaks

separated by ranges of frequencies with no power

(Joseph Jilk et al., 2014; Lippi et al., 2020; Peterka,

2002). e response is evaluated for speciﬁc

frequencies where the PRTS spectrum has peaks (see

Fig. 5, top). e FRF is computed with the Fourier

transform of the input U and the output Y as

Table 1: Anthropometric parameters used in all the

simulations.

Parameter Symbol Value

Head moment

of inertia

𝐽



0.4797 kg/m

Leg length

(ankle to hip)

𝑙



0.8543 m

Trunk length

(hip to neck)

𝑙



0.5011 m

Head COM

height

ℎ



0.2053 m

Head mass 𝑚



4.5 kg

where 𝐺



=𝑈∗𝑌 and 𝐺



=𝑈∗𝑈 are empirical

estimations of the cross-power spectrum and the input

power spectrum (∗ is the element-wise product). e

spectrum is then transformed into a vector of 11

components by averaging the FRF over neighboring

ranges of frequencies, as illustrated in Fig. 5. e

choice of the frequencies and their overlapping

follows the method described in (Peterka, 2002), but

here is adapted to the 11 frequencies considered as the

PRTS used here is shorter in time (one cycle is 20

seconds, and the signal is repeated three, in contrast

to the six cycles of 60.5 s of the original work). e

averaging was initially proposed to obtain a

visualization with the frequencies almost equally

spaced on a logarithmic scale, typically used to plot

the FRF. e ﬁnal representation of the FRF is a

function of the 11 frequencies

𝒇=



0.1,0.3,0.6,0.8,1.1,1.4,1.8,2.2,2.7,3.5,4.4



𝐻𝑧

Notice that a transfer function represents a linear

system input-output relationship assuming no

transient eﬀect due to initial conditions. It is known

that human postural responses are nonlinear (e.g., see

sensory reweighting in Assländer & Peterka, 2016),

so the FRF is intended as a representation of the

output of a trial and not as a general model for the

subject.

Figure 5: Spectrum and example of FRF. Above: The

magnitude of the DFT of the PRTS. Center: empirical

transfer function from (8). Below: FRF resulting from the

averaging of frequency bands. The bands on the

background show the frequency ranges over which the

spectrum is averaged: white and dark green represent

ranges associated with groups of frequencies. The sets of

frequencies overlap, with light green bands belonging to

both contiguous groups, and a sample on the transition

between two bands belongs to both groups. As the FRF is

averaged in the complex domain, the average shown in the

plot is not the average of the magnitudes.

𝐻=

𝐺



𝐺



(8)

2.4 Fitting the Model

e model ﬁts the data using a numeric research

algorithm (Lagarias et al., 1998) implemented by the

A Dynamic Computational Model of Head Sway Responses in Human Upright Stance Postural Control During Support Surface Tilt

Matlab function fminsearch.

e objective function to be minimized is the

diﬀerence between the FRF from the experimental

trial and the one produced by the simulation. e

threshold 𝜃



is set to 0.065 rad/s, as Georg Hettich

et al. (2014) reported. Some variations of the model

have been tested, speciﬁcally: i. a linear model with

no dead bands (𝜃



=0 , and 𝜃



=0 ), ii. a model

with no dead band on gravity (𝜃



=0.065 , and

𝜃



=0), and iii. a model where the threshold 𝜃



was

unknown a priori and considered a parameter to be

selected to ﬁt the model. e best model, in the sense

of having the smallest ﬁtting error on average, was ii.

is may sound paradoxical as the model iii. includes

the possibility of setting 𝜃



=0; hence, it is expected

to perform at least equally to ii. e problem is that

adding one free parameter can sometimes decrease

the performance of fminsearch. Speciﬁcally, in

this setup, the gain nonlinearity introduced by the

dead bands may not be easy to distinguish from the

eﬀect of the control gains.

It should be noted that the linear model can

reproduce the nonlinear response (compare the

diﬀerent gains associated with the two diﬀerent

amplitudes in Fig. 6) as the parameters are optimized

for each trial separately, showing a reweighting in

diﬀerent conditions. e introduction (6) improves

the average result. It leads to a smaller variance in the

gains parameters suggesting that it can explain the

nonlinear response "automatically," as shown more in

detail in the next section.

In the following model ii. is discussed, and the

identiﬁed parameters are 𝐾



, 𝐾



from (1), 𝐾



, 𝐾



from (2), 𝐾



from (3), and the lumped delay ∆𝑡.

3 RESULTS

The average and the standard deviation parameters

for the different conditions, i.e., Eyes closed (EC),

eyes open EO, and peak-to-peak amplitudes of 0.5°

and 1°, are reported in Table 2. In the following, the

error consists of the norm of the difference between

the FRFs of the data and the simulated model. For this

reason, it has no unit of measure being a ratio between

angles as the FRFs.

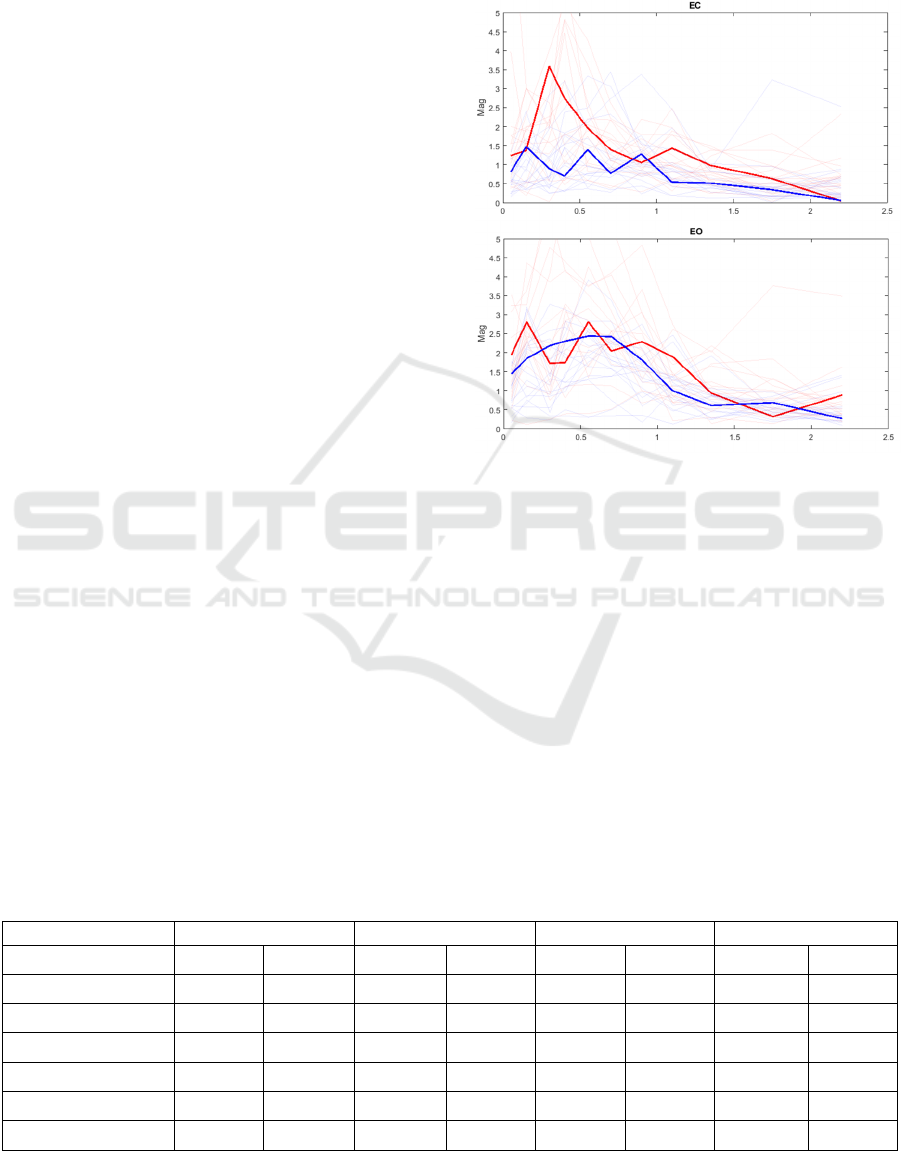
Figure 6: Average FRF magnitude for eyes closed (above)

and eyes open (below) conditions. The red line is the

response to 0.5°, and the blue line to 1°. The transparent

lines on the background represent FRFs from single trials.

The average is performed in a complex domain. The effect

of the nonlinearity is evident with eyes closed: the gain is

larger with the smaller stimulus that is under-compensated

due to the effect of the thresholds as demonstrated in (Lippi

& Molinari, 2020)

There is a significant difference in passive

stiffness between the response to the stimuli of 0.5

and 1° amplitudes with EC (𝐾



was larger at 0.5°

with p=0.04 tested with ANOVA). In contrast, the

difference was smaller and not significant for EO

(p=0.24). Slightly modified models have fit for

comparison, and the detailed report of such fits goes

beyond the space allowed for this work. The result

Table 2: Results of model fit for different visual conditions (EC, EO) and peak-to-peak (pp) amplitudes.

EC pp 0.5° EC pp 1° EO pp 0.5° EO pp 1°

Paramete

mean

td mean Std mean

td mean Std

𝑲

𝑷

[Nm/rad]

11.129 10.34 7.1597 1.1701 8.4829 5.2197 5.5033 1.7324

𝑲

𝑫

[Nms/rad]

1.5208 1.465 1.1701 0.91631 1.5034 0.85115 1.5213 0.8278

𝑲

𝑷𝑷

[Nm/rad]

12.379 9.8733 6.9293 4.6557 13.583 11.079 10.139 5.3557

𝑲

𝑷𝑫

[

Nms/rad]

3.3978 3.1578 3.7765 3.0908 2.3834 1.1103 2.4437 0.85655

𝑲

𝑮

1.049 0.49004 0.8516 0.56258 0.90084 0.45227 0.96701 0.36248

∆𝒕

[s]

0.060489 0.040352 0.085444 0.061062 0.036357 0.028749 0.053899 0.017607

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

can be summarized as follows: The linear model

(with no dead-bands produces a larger error (2.7

compared to 2.1 of the final model) and a larger

variance in the parameters (1.7) compared to the final

model (1.4). A model where the proprioceptive

variable (head-to-trunk angle 𝛼



) was used instead

of head-in-space 𝛼



as the control variable has

produced worse results on average. e standard

deviation of the proportional gains, both active (𝐾



)

and passive (𝐾



), is relatively large in the group of

responses associated with 0.5°, especially for the EC

case. is may be because when the oscillations of the

trunk are small, the eﬀect of those two gains is

diﬃcult to distinguish as 𝛼



≅𝛼



4 DISCUSSION CONCLUSIONS

AND FUTURE WORK

The model that produced the best fit included the dead

band nonlinearity from eq (6) but not the one on the

gravity compensation. It is interesting to notice that

the evident difference between EO and EC (see Fig.

6) is not reflected by a significant difference in the

parameters in the neck control. This suggests that the

differences in behavior between EC and EO are

expressed in the sway of the trunk and the leg

segments that affect the head as an input. The more

relevant difference observed in parameters is the

larger stiffness with small oscillations, suggesting

that, with 0.5°, the head is moving with the trunk.

These considerations suggest, on the one hand, that

the DIP model is enough to predict the behavior of the

upper body in healthy subjects (at least for the small

oscillations considered). On the other hand, modeling

the behavior of the neck may be beneficial for

applications where head movements are involved

explicitly, e.g., when the DEC is applied to an

assistive device (Lippi & Mergner, 2020) if the

device supports the head as well (e.g., an active

version of Garosi et al., 2022). The patient's behavior

is currently under investigation.

Models for perturbed posture control are used to

explain the differences in body sway responses in

terms of meaningful parameters, for example, sensory

weighting in different conditions (Assländer &

Peterka, 2014) or different subject characteristics

such as stiffness or delay (A. Goodworth et al., 2023).

In particular, the possibility to exploit the modularity

of the DEC control to identify parameters relative to

different joints will be used to identify differences

between normal and pathological behavior expressed

locally, e.g., see if the neck is stiffer in a group of

patients.

The application to a bioinspired humanoid control

system of the proposed neck model is

straightforward: the up-channeled 𝛼



value can be

provided by the sensor fusion between the neck

proprioceptive input (encoder) and the output of the

module controlling the trunk 𝛼



as speciﬁed in

(Lippi & Mergner, 2017).

In this work, the ﬁt of the model was performed

with small amplitudes that are safe for patients (hence

in the range of interest for future experiments). Future

improvement in the model's validation can be

achieved by integrating experiments with larger

amplitudes. This may reveal nonlinear effects that are

not visible with small head movements and, by

producing larger trunk sways, allow for better

differentiation between the effects of active and

passive stiffness. For example, the gravity threshold

that was not relevant in these experiments may

become more visible.

REFERENCES

Alexandrov, A. V., Lippi, V., Mergner, T., Frolov, A. A.,

Hettich, G., & Husek, D. (2017). Human-inspired

Eigenmovement concept provides coupling-free

sensorimotor control in humanoid robots. Frontiers in

Neurorobotics, 11(APR). https://doi.org/10.3389/

fnbot.2017.00022

Alexandrov, A. V, Frolov, A. A., Horak, F. B., Carlson-

Kuhta, P., Park, S., Audren, H., Vaillant, J., Kheddar,

A., Escande, A., Kaneko, K., Yoshida, E., Elhasairi, A.,

Pechev, A., Faraji, S., Colasanto, L., Ijspeert, A. J.,

Gams, A., den Kieboom, J., Dzeladini, F., … Abiko, S.

(2015). Biologically inspired kinematic synergies

provide a new paradigm for balance control of

humanoid robots. Robotics and Automation, 2001.

Proceedings 2001 ICRA. IEEE International

Conference On, 2(5), 4030–4035.

Allum, J. H. J., & Honegger, F. (1992). A postural model

of balance-correcting movement strategies. Journal of

Vestibular Research, 2(4), 323 – 347.

https://doi.org/10.3233/ves-1992-2406

Antritter, F., Scholz, F., Hettich, G., & Mergner, T. (2014).

Stability analysis of human stance control from the

system theoretic point of view. Control Conference

(ECC), 2014 European, 1849–1855. https://doi.org/10.

1109/ECC.2014.6862198

Assländer, L., Gruber, M., & Giboin, L. S. (2020).

Reductions in body sway responses to a rhythmic

support surface tilt perturbation can be caused by other

mechanisms than prediction. Experimental Brain

Research, 238(2). https://doi.org/10.1007/s00221-020-

05723-z

A Dynamic Computational Model of Head Sway Responses in Human Upright Stance Postural Control During Support Surface Tilt

Assländer, L., & Peterka, R. J. (2014). Sensory reweighting

dynamics in human postural control. Journal of

Neurophysiology, 111(9). https://doi.org/10.1152/

jn.00669.2013

Assländer, L., & Peterka, R. J. (2016). Sensory reweighting

dynamics following removal and addition of visual and

proprioceptive cues. Journal of Neurophysiology.

https://doi.org/10.1152/jn.01145.2015

Atkeson, C. G., & Stephens, B. (2007). Multiple Balance

Strategies From One Optimization Criterion.

Proceedings of the 2007 7th IEEE-RAS International

Conference on Humanoid Robots, HUMANOIDS 2007,

57–64. https://doi.org/10.1109/ICHR.2007.4813849

Bleisteiner, G. V., Mangoldt, W., Henninger, H., & Oetker,

R. (1961). Handbuch der Regelungstechnik. Springer.

Davidson, B. S., Madigan, M. L., Southward, S. C., &

Nussbaum, M. A. (2011). Neural control of posture

during small magnitude perturbations: Effects of aging

and localized muscle fatigue. IEEE Transactions on

Biomedical Engineering, 58(6). https://doi.org/10.1

109/TBME.2010.2095500

De Leva, P. (1996). Adjustments to Zatsiorsky-seluyanov's

segment inertia parameters. Journal of Biomechanics,

29(9). https://doi.org/10.1016/0021-9290(95)00178-6

Dieterich, M., & Brandt, T. (2019). Perception of verticality

and vestibular disorders of balance and falls. Frontiers

in Neurology, 10(APR). https://doi.org/10.3389/

fneur.2019.00172

Garosi, E., Mazloumi, A., Jafari, A. H., Keihani, A.,

Shamsipour, M., Kordi, R., & Kazemi, Z. (2022).

Design and ergonomic assessment of a passive

head/neck supporting exoskeleton for overhead work

use. Applied Ergonomics, 101. https://doi.org/

10.1016/j.apergo.2022.103699

Goodworth, A. D., & Peterka, R. J. (2018). Identifying

mechanisms of stance control: a single stimulus

multiple output model-fit approach. Journal of

Neuroscience Methods, 296, 44–56. https://doi.

org/10.1016/j.jneumeth.2017.12.015

Goodworth, A., Felmlee, D., & Karmali, F. (2023).

Variation between individuals in sensorimotor

feedback control of standing balance. Journal of

Neurophysiology, 130(2), 303–318. https://doi.

org/10.1152/jn.00353.2022

Hettich, G., Assländer, L., Gollhofer, A., & Mergner, T.

(2014). Human hip-ankle coordination emerging from

multisensory feedback control. Human Movement

Science. https://doi.org/10.1016/j.humov.2014.07.004

Hettich, G., Fennell, L., & Mergner, T. (2011). Double

Inverted Pendulum Model of Reactive Human Stance

Control. Multibody Dynamics 2011.

Hettich, G., Lippi, V., & Mergner, T. (2015). Human-Like

Sensor Fusion Implemented in the Posture Control of a

Bipedal Robot. In Neurotechnology, Electronics, and

Informatics (pp. 29–45). Springer. https://doi.

org/10.1007/978-3-319-15997-3_3

Hettich, G., Lippi, V., & Mergner, T. (2013). Human-like

sensor fusion mechanisms in a postural control robot.

NEUROTECHNIX 2013 - Proceedings of the

International Congress on Neurotechnology,

Electronics and Informatics, 152–160.

https://doi.org/10.5220/0004642701520160

Jafari, H., & Gustafsson, T. (2023). Optimal controllers

resembling postural sway during upright stance. PLOS

ONE, 18(5), 1–23. https://doi.org/10.1371/journal.

pone.0285098

Jafari, H., Nikolakopoulos, G., & Gustafsson, T. (2019).

Stabilization of an inverted pendulum via human brain-

inspired controller design. IEEE-RAS International

Conference on Humanoid Robots. https://doi.

org/10.1109/Humanoids43949.2019.9035019

Joseph Jilk, D., Safavynia, S. A., & Ting, L. H. (2014).

Contribution of vision to postural behaviors during

continuous support-surface translations. Experimental

Brain Research. https://doi.org/10.1007/s00221-013-

3729-4

Kammermeier, S., Maierbeck, K., Dietrich, L., Plate, A.,

Lorenzl, S., Singh, A., Bötzel, K., & Maurer, C. (2018).

Qualitative postural control differences in Idiopathic

Parkinson’s Disease vs. Progressive Supranuclear Palsy

with dynamic-on-static platform tilt. Clinical

Neurophysiology, 129(6). https://doi.org/10.1016/

j.clinph.2018.03.002

Kilby, M. C., Molenaar, P. C. M., & Newell, K. M. (2015).

Models of postural control: Shared variance in joint and

COM motions. PLoS ONE, 10(5). https://doi.

org/10.1371/journal.pone.0126379

Küng, U. M., Horlings, C. G. C., Honegger, F., Duysens, J.

E. J., & Allum, J. H. J. (2009). Control of roll and pitch

motion during multi-directional balance perturbations.

Experimental Brain Research, 194(4). https://doi.

org/10.1007/s00221-009-1743-3

Kuo, A. D. (2005). An optimal state estimation model of

sensory integration in human postural balance. Journal

of Neural Engineering, 2(3). https://doi.org/10.

1088/1741-2560/2/3/S07

Lagarias, J. C., Reeds, J. A., Wright, M. H., & Wright, P.

E. (1998). Convergence properties of the Nelder-Mead

simplex method in low dimensions. SIAM Journal on

Optimization, 9(1). https://doi.org/10.1137/S105262

3496303470

Li, Y., Levine, W. S., & Loeb, G. E. (2012). A two-joint

human posture control model with realistic neural

delays. IEEE Transactions on Neural Systems and

Rehabilitation Engineering, 20(5). https://doi.org/10.

1109/TNSRE.2012.2199333

Lippi, V. (2018). Prediction in the context of a human-

inspired posture control model. Robotics and

Autonomous Systems. https://doi.org/10.1016/j.robot.

2018.05.012

Lippi, V., Avizzano, C. A., Mottet, D., & Ruffaldi, E.

(2010). Effect of delay on dynamic targets tracking

performance and behavior in a virtual environment.

Proceedings - IEEE International Workshop on Robot

and Human Interactive Communication, 446–451.

https://doi.org/10.1109/ROMAN.2010.5598607

Lippi, V., Brands, K. G., & Seel, T. (2020). Real-time

implementation and evaluation of magnetometers

tracking system for human and humanoid posture

control benchmarking based on inertial sensors.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

ICINCO 2020 - Proceedings of the 17th International

Conference on Informatics in Control, Automation and

Robotics, 675–680. https://doi.org/10.5220/0009869

106750680

Lippi, V., & Mergner, T. (2017). Human-derived

disturbance estimation and compensation (DEC)

method lends itself to a modular sensorimotor control

in a humanoid robot. Frontiers in Neurorobotics,

11(SEP). https://doi.org/10.3389/fnbot.2017.00049

Lippi, V., & Mergner, T. (2020). A challenge: Support of

standing balance in assistive robotic devices. Applied

Sciences, 10(15), 5240. https://doi.org/10.3390/

APP10155240

Lippi, V., Mergner, T., Szumowski, M., Zurawska, M. S.,

& Zielińska, T. (2016). Human-inspired Humanoid

Balancing and Posture Control in Frontal Plane. In

ROMANSY 21-Robot Design, Dynamics and Control

(pp. 285–292). Springer, Cham. https://doi.org/10.

1007/978-3-319-33714-2_32

Lippi, V., & Molinari, F. (2020). Lyapunov stability of a

nonlinear bio-inspired system for the control of

humanoid balance. ICINCO 2020 - Proceedings of the

17th International Conference on Informatics in

Control, Automation and Robotics, 726–733.

https://doi.org/10.5220/0009970307260733

Lockhart, D. B., & Ting, L. H. (2007). Optimal

sensorimotor transformations for balance. Nature

Neuroscience, 10(10). https://doi.org/10.1038/nn1986

Loram, I. D., Maganaris, C. N., & Lakie, M. (2004).

Paradoxical muscle movement in human standing.

Journal of Physiology, 556(3). https://doi.org/10.

1113/jphysiol.2004.062398

Loram, I. D., Maganaris, C. N., & Lakie, M. (2005a).

Active, non-spring-like muscle movements in human

postural sway: How might paradoxical changes in

muscle length be produced? Journal of Physiology,

564(1). https://doi.org/10.1113/jphysiol.2004.073437

Loram, I. D., Maganaris, C. N., & Lakie, M. (2005b).

Human postural sway results from frequent ballistic

bias impulses by the soleus and gastrocnemius. Journal

of Physiology, 564(1). https://doi.org/10.1113/

jphysiol.2004.076307

Maurer, C., Mergner, T., & Peterka, R. J. (2006).

Multisensory control of human upright stance.

Experimental Brain Research, 171(2), 231–250.

https://doi.org/10.1007/s00221-005-0256-y

McNeal, J. S., & Hunt, A. (2023). A Simple Dynamic

Controller for Emulating Human Balance Control. In F.

Meder, A. Hunt, L. Margheri, A. Mura, & B. Mazzolai

(Eds.), Biomimetic and Biohybrid Systems (pp. 227–

239). Springer Nature Switzerland.

Mergner, T, Huber, W., & Becker, W. (1997). Vestibular-

neck interaction and transformation of sensory

coordinates. Journal of Vestibular Research :

Equilibrium & Orientation, 7(4), 347–367.

Mergner, Thomas. (2010). A neurological view on reactive

human stance control. Annual Reviews in Control

34(2), 177–198. https://doi.org/10.1016/j.arcontrol.

2010.z08.001

Mergner, Thomas, & Rosemeier, T. (1998). Interaction of

vestibular, somatosensory and visual signals for

postural control and motion perception under terrestrial

and microgravity conditions - A conceptual model.

Brain Research Reviews, 28(1–2). https://doi.org/

10.1016/S0165-0173(98)00032-0

Mergner, Thomas, Schweigart, G., & Fennell, L. (2009).

Vestibular humanoid postural control. Journal of

Physiology Paris, 103(3–5), 178–194.

https://doi.org/10.1016/j.jphysparis.2009.08.002

Merton, P. A. (1953). Speculations on the Servo-Control of

Movement. In In Ciba Foundation Symposium - The

Spinal Cord, G.E.W. Wolstenholme (Ed.).

https://doi.org/10.1002/9780470718827.ch18

Molnar, C. A., Zelei, A., & Insperger, T. (2021). Rolling

balance board of adjustable geometry as a tool to assess

balancing skill and to estimate reaction time delay.

Journal of the Royal Society Interface, 18(176).

https://doi.org/10.1098/rsif.2020.0956

Morasso, P., Cherif, A., & Zenzeri, J. (2019). Quiet

standing: The single inverted pendulum model is not so

bad after all. PLoS ONE, 14(3).

https://doi.org/10.1371/journal.pone.0213870

Morasso, P. G., & Schieppati, M. (1999). Can muscle

stiffness alone stabilize upright standing? Journal of

Neurophysiology, 82(3). https://doi.org/10.1152/jn.

1999.82.3.1622

Morice, A. H. P., Siegler, I. A., & Bardy, B. G. (2008).

Action perception patterns in the virtual ball bouncing:

combating system latency and tracking functional

validity. J Neurosci Methods, 1(255), 255–266.

Ott, C., Henze, B., Hettich, G., Seyde, T. N., Roa, M. A.,

Lippi, V., & Mergner, T. (2016). Good Posture, Good

Balance: Comparison of Bioinspired and Model-Based

Approaches for Posture Control of Humanoid Robots.

IEEE Robotics & Automation Magazine, 23(1), 22–33.

https://doi.org/10.1109/MRA.2015.2507098

Pasma, J. H., Assländer, L., van Kordelaar, J., de Kam, D.,

Mergner, T., & Schouten, A. C. (2018). Evidence in

support of the independent channel model describing

the sensorimotor control of human stance using a

humanoid robot. Frontiers in Computational

Neuroscience, 12. https://doi.org/10.3389/fncom.

2018.00013

Peterka, R. J. (2002). Sensorimotor integration in human

postural control. Journal of Neurophysiology.

https://doi.org/10.1152/jn.2002.88.3.1097

Pinter, I. J., Van Swigchem, R., Van Soest, A. J., &

Rozendaal, L. A. (2008). The dynamics of postural

sway cannot be captured using a one-segment inverted

pendulum model: A PCA on segment rotations during

unperturbed stance. Journal of Neurophysiology,

100(6). https://doi.org/10.1152/jn.01312.2007

Qu, X., Nussbaum, M. A., & Madigan, M. L. (2009).

Model-based assessments of the effects of age and

ankle fatigue on the control of upright posture in

humans. Gait and Posture, 30(4).

https://doi.org/10.1016/j.gaitpost.2009.07.127

Souza, T. R., Schallig, W., Veerkamp, K., Magalhães, F.

A., Okai-Nóbrega, L. A., Fonseca, S. T., & van der

A Dynamic Computational Model of Head Sway Responses in Human Upright Stance Postural Control During Support Surface Tilt

Krogt, M. M. (2022). Muscle actions on crossed and

non-crossed joints during upright standing and gait: A

comprehensive description based on induced

acceleration analysis. Journal of Biomechanics, 130.

https://doi.org/10.1016/j.jbiomech.2021.110874

Van Der Kooij, H., Jacobs, R., Koopman, B., &

Grootenboer, H. (1999). A multisensory integration

model of human stance control. Biological Cybernetics,

80(5). https://doi.org/10.1007/s004220050527

Vette, A. H., Masani, K., Nakazawa, K., Popovic, M. R., &

Member, S. S. S. S. (2010). Neural-Mechanical

Feedback Control Scheme Fluctuation During Quiet

Stance. Rehabilitation, 18(1).

Winter, D. A. (2009). Biomechanics and Motor Control of

Human Movement: Fourth Edition. In Biomechanics

and Motor Control of Human Movement: Fourth

Edition. https://doi.org/10.1002/9780470549148

Zebenay, M., Lippi, V., & Mergener, T. (2015). Human-

like humanoid robot posture control. ICINCO 2015 -

12th International Conference on Informatics in

Control, Automation and Robotics, Proceedings, 2,

304–309. https://doi.org/10.5220/0005542603040309.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics