Identifying Similar Top-K Household Electricity Consumption Patterns

Nadeem Iftikhar

, Akos Madarasz and Finn Ebertsen Nordbjerg

University College of Northern Denmark, Aalborg 9200, Denmark

Keywords:

Nearest Neighbors, Unsupervised Learning, KNN, Brute Force, KD Tree, Ball Tree, Similarity Search,

Top-K Query.

Abstract:

Gaining insight into household electricity consumption patterns is crucial within the energy sector, particularly

for tasks such as forecasting periods of heightened demand. The consumption patterns can furnish insights into

advancements in energy efﬁciency, exemplify energy conservation and demonstrate structural transformations

to speciﬁc clusters of households. This paper introduces different practical approaches for identifying similar

households through their consumption patterns. Initially different data sets are merged, followed by aggre-

gating data to a higher granularity for short-term or long-term forecasts. Subsequently, unsupervised nearest

neighbors learning algorithms are employed to ﬁnd similar patterns. These proposed approaches are valu-

able for utility companies in offering tailored energy-saving recommendations, predicting demand, engaging

consumers based on consumption patterns, visualizing energy use, and more. Furthermore, these approaches

can serve to generate authentic synthetic data sets with minimal initial data. To validate the accuracy of these

approaches, a real data set spanning eight years and encompassing 100 homes has been employed.

1 INTRODUCTION

Over 40% carbon dioxide (CO2) emissions are due to

electricity generation, which results in negative im-

pact on sustainability. In addition, many regions ex-

perience a shortage in energy supplies and increas-

ing prices. Hence, optimizing power consumption is

becoming increasingly important for both households

and society as such. In this paper, grouping of elec-

tricity consumers is investigated according to similar

consumption patterns. Traditionally, electricity con-

sumers are classiﬁed based on coarse-grained group-

ing, such as residential, industrial and commercial.

This classiﬁcation is inadequately correlated with the

actual consumption behaviour of different types of

consumers (Trotta et al., 2020). Hence, a ﬁne-grained

grouping of consumers based on consumption pat-

terns is needed. Further, grouping of consumption

data is important in many aspects, for example util-

ity suppliers may use it for demand management and

demand prediction (by understanding consumer be-

havior through consumption patterns in different geo-

graphical sectors facilitates demand management and

demand prediction). This is important in order to

optimize power production and distribution network

load. Furthermore, knowledge of consumer proﬁles

https://orcid.org/0000-0003-4872-8546

is also necessary in order to give consumers relevant

and focused advice on how to reduce and/or optimize

consumption. To ﬁnd similar top-k consumption pat-

terns, pattern based clustering algorithms with simi-

larity measures may be used. Clustering is a set of un-

supervised machine learning methods where objects

are group according to some (unknown) similarities.

Clustering may help to discover unknown groups in

data sets (Rahim et al., 2021). Nearest neighbors

method is chosen in this paper as it is one of the

widely used clustering techniques relying on a sim-

ilarity measure (Cembranel et al., 2019). In order to

ﬁnd similar top-k consumption patterns this paper im-

plements three different types of unsupervised nearest

neighbors learning algorithms: modiﬁed brute force,

Ball tree and KD tree.

To summarize, the main contributions in this pa-

per are as follow:

• Transforming time series data sets for further

analysis;

• Presenting different practical approaches for per-

forming similar household consumption pattern

search based on unsupervised learning;

• Using search results and performance as a mea-

sure for accuracy, different algorithms are com-

pared utilizing real-world data sets, consisting of

eight years of hourly readings from 100 homes.

Iftikhar, N., Madarasz, A. and Nordbjerg, F.

Identifying Similar Top-K Household Electricity Consumption Patterns.

DOI: 10.5220/0012154500003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 167-174

ISBN: 978-989-758-671-2; ISSN: 2184-3228

167

The paper is structured as follows. Section 2 ex-

plains the motivation and solution overview. Sec-

tion 3 presents the related work. Section 4 describes

the approaches to ﬁnd the similar consumption pat-

terns. Section 5 describes the experimental results.

Section 6 concludes the paper and points out the fu-

ture research directions.

2 MOTIVATION AND SOLUTION

OVERVIEW

In this section, the overview of the proposed solu-

tion and the motivation behind it is provided. One of

the main goals of this study “is to identify residential

electricity consumption patterns based on electricity

consumption, household characteristics, external fac-

tors (time, weather etc.) as well as working day and

holiday data”. As an illustration, Table 1 provides a

snapshot of smart meter data, displaying the hourly

kWh consumption for a sample household.

Table 1: Snapshot of electricity consumption raw data

(hourly granularity).

Meter id Read date Hour Reading

1 2012-06-01 1 1.011

1 2012-06-01 2 0.451

1 2012-06-01 3 0.505

1 2012-06-01 4 0.441

1 2012-06-01 5 0.468

The data employed in this paper comprises four

data sets: involving time series data of household con-

sumption over an eight-year span, with hourly gran-

ularity, weather time series data that consists of ex-

ternal temperature values for the same time span and

granularity, household characteristics as well as holi-

day data for the same time span (further details about

the data sources are omitted to preserve privacy). As

the goal of this study is to compute the similarity in

the consumption patterns for each hour of the day.

For that reason the consumption data is transformed

into 24 hourly readings, aggregated at daily granular-

ity (with the help of a pivot table). In this way ev-

ery instance in the consumption data has a pattern

for each speciﬁc day (Table 2). Depending on the

requirements analysis, it is possible to narrow down

the consumption pattern to different times of the day,

for example, morning period [00:00-08:00], day pe-

riod [09:00-16:00] and evening period [17:00-23:00]

as well as based on weekdays and weekends. In addi-

tion, it is also possible to aggregate the consumption

patterns to a higher time granularity, such as monthly,

quarterly and annually. Although, hourly consump-

tion readings can exhibit some information about the

consumption habits of a household, however com-

bining household consumption data with other data

sources such as, external temperature and house char-

acterises would help the utility companies in gain-

ing deeper understanding and wider views of their

consumers. Given the smart meter and temperature

time series data, household characteristics as well as

weekends/weekdays, 52 dimensions are created. To

ﬁnd the top-k most similar instances in the training

set based on a test instance, three approaches to ﬁnd

the nearest neighbours of a test instance are used in

this paper (depending on data set size, data set spar-

sity and feature dimensionality). After data cleans-

ing, data transformation, merging and data normaliz-

ing, the general ﬂow of the neighbor-based method is

the following: build a data structure, the distance be-

tween the query instance and the data instances in the

underlying data structure is calculated and the k most

similar instances are returned. Further details of the

proposed method are presented in Section 4.

3 RELATED WORK

This section primarily focuses on the prior research

conducted concerning consumption patterns that ex-

hibit similarities. A novel method for retrieving the

k nearest neighbours by using an inverted index and

compute only nonzero terms for document similar-

ity is proposed by (Feremans et al., 2020). A hierar-

chical clustering based method for identifying house-

hold electricity consumption patterns is presented by

(Yang et al., 2018). A technique to segment house-

hold based on their consumption patterns by using

the combination of k-means and hierarchical cluster-

ing is presented by (Kwac et al., 2014). Further,

(Ardakanian et al., 2014) used a periodic auto re-

gression based model for computing electricity con-

sumption proﬁles. The input to the model consists

of two time series, consumption readings and exter-

nal temperature measurements. A household classi-

ﬁcation supervised machine learning algorithm based

on k nearest neighbor and support vector machine is

presented by (Hopf et al., 2016). Also, a electric-

ity load forecasting method is proposed by (Humeau

et al., 2013). The proposed method ﬁrst group house-

holds into clusters using k-means, afterward it pre-

dicts the consumption for each cluster as well as ag-

gregate these predictions and ﬁnally obtain a better

load forecast. In addition, (Okereke et al., 2023) sug-

gested an unsupervised k-means clustering approach

for categorizing consumers based on the similarity of

their typical electricity consumption behaviors. Like-

wise, an improved k-means algorithm, in which prin-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

168

Table 2: Snapshot of 24-hour electricity consumption data (daily granularity).

Meter id Read date Daily Hour 0 Hour 1 Hour 2 ... Hour 21 Hour 22 Hour 23

1 2012-06-01 19.476 0.8115 1.011 0.451 ... 0.752 1.584 4.188

1 2012-06-02 20.331 0.6130 0.442 0.496 ... 0.935 0.871 0.942

1 2012-06-03 22.844 1.1330 1.428 0.435 ... 1.274 1.298 1.319

1 2012-06-04 25.610 1.3370 1.351 1.536 ... 0.586 0.586 0.598

1 2012-06-05 24.127 0.6180 0.644 0.472 ... 1.177 1.222 1.261

cipal component analysis is used to reduce the di-

mensions of time series data is presented by (Wen

et al., 2019). Further, the work by (Wu et al., 2023)

proposed various visual analysis methods including

customer segmentation to analyze energy consump-

tion data. A household clustering solution using k-

means and auto-encoder based on water consumption

behaviour is developed by (Lange et al., 2023). More-

over, an adaptive hybrid ensemble model with pattern

similarity and short-term load forecasting is proposed

by (Laouaﬁ et al., 2022). The pattern similarity part

consists of calendar-based grouping along with me-

dian ﬁltering and k nearest neighbor algorithm. Simi-

larly, (Gholizadeh and Musilek, 2022) suggested fed-

erated learning with hyper parameter-based cluster-

ing approach for electricity load forecasting. Fur-

thermore, an auto-encoder based clustering approach

is presented by (Eskandarnia et al., 2022) and feder-

ated learning approaches for electricity consumption

based on k-means clustering are suggested by (Wang

et al., 2022). Machine learning based approaches are

recommended by (Tang et al., 2022) and (Guo et al.,

2022) that uses k-medoids clustering for discovering

residential energy consumption patterns. The unique-

ness of the research presented in this paper lies in its

analysis of outcomes achieved through the applica-

tion of unsupervised nearest neighbors algorithms to

real-world data sets comprising over 2 million data

instances. This analysis showcases a notable combi-

nation of accuracy and performance. Furthermore,

smart meter data generators proposed by (Iftikhar

et al., 2016) and (Iftikhar et al., 2017) have the ability

to generate realistic energy consumption data using

periodic auto regressive models. Likewise, the nearest

neighbours based approaches presented in this paper

can also be used for generating realistic synthetic data

sets based on consumption patterns. This can be ac-

complished with a modest seed and a reasonable level

of accuracy.

On the whole the focus of these previous works is

on various aspects and recent advancements of simi-

larity search. The work presented in this paper con-

siders a number of recommendations presented in

those previous works. Further, most of them focus

on theoretical rather than practical issues in relation

to similar consumption patterns, while the focus of

this paper is to provide practical methods based on

unsupervised learning.

4 METHODS

This section begins with an overview of the unsuper-

vised nearest neighbors learning and the chosen dis-

tance function (Section 4.1), followed by describing

the need and working of modiﬁed brute force algo-

rithm (Section 4.2) and explaining the KD tree and

Ball tree algorithms (Section 4.3) and (Section 4.4),

respectively.

4.1 Overview

To ﬁnd the top-k most similar data instances based on

a search query, multiple approaches can be used, de-

pending on the size of data, sparsity of data (which

commonly occurs in high-dimensional data) and di-

mensionality of data. The general ﬂow of the unsu-

pervised nearest neighbors learning is the following:

a data structure is constructed, the distance of the new

testing query/pattern is compared with the data in-

stances present in the underlying data structure to ﬁnd

the k nearest neighbours based on a predeﬁned dis-

tance measure and the k most similar data instances

are returned. Depending on the data dimensions, dif-

ferent data structures/algorithms can be used.

Cosine Similarity =

A · B

∥A∥∥B∥

∑

i=1

∑

i=1

∑

i=1

(1)

In order for any nearest neighbors algorithm to

work properly, it is important to choose the suitable

distance measure depending on the need. There are

a lot of different distance metrics available, where

Euclidean distance function is the most popular one

among all of them and it is also set as the default dis-

tance function in the Scikit-learn Nearest Neighbors

library in Python. The Euclidean distance computes

a similarity based on the magnitude of the data in-

stances. On the other hand, Cosine distance, which is

calculated as (Cosine distance = 1- Cosine similarity)

measures the angle between two data instances. The

cosine similarity is calculated in Equation 1, where

Identifying Similar Top-K Household Electricity Consumption Patterns

169

A · B represents the dot product of vectors A and B,

while ∥A∥ and ∥B∥ represent the magnitudes of vec-

tors A and B, respectively. The Cosine similarity ﬁnds

two data instances similar even if their values differ in

magnitude, as long as their direction in space is same.

The similarity lies within the range of 0 to 1, wherein

0 signiﬁes complete similarity between the data in-

stances, while 1 denotes no similarity whatsoever.

4.2 Modiﬁed Brute Force

When a data set is sparse (especially in the case of

high-dimensional data), it means it has a large num-

ber of zero feature values that are not meaningful for

the analysis purposes. Further, for the sparse data set

the querying time of any algorithm will be signiﬁ-

cantly large. The standard nearest neighbors method

works by ﬁnding the k most similar neighbours for

each query instance. Where, the query instance has

to be compared with each instance in the training data

(including the zero feature values). In order to over-

come this performance inefﬁciency, a modiﬁed brute

force algorithm is proposed in this paper. First, a

hashmap data structure is created from the training

data. The hashmap only stores non-zero feature val-

ues. Then, the distance is calculated based on the

instances stored in the hashmap rather than the in-

stances present in the training data. The following two

algorithms explain the modiﬁed version of the brute

force approach.

Input: Dataset

HM = HASHMAP

for for each row in dataset

for for each non-zero feature in row

HM[feature] += [row, feature]

return HM

end

Algorithm 1: Create hashmap.

Algorithm 1 generates a data structure that maps

each feature in a given data set to the corresponding

rows and feature values that contain that feature. It

does this by iterating over each row in the data set

and, for each non-zero feature in the row, updating

the corresponding entry in the hashmap. The algo-

rithm creates a list associated with each feature in the

hashmap and appends a tuple containing the row in-

dex and the feature value to that list. After iterating

over all the rows and features, the resulting hashmap

contains all the features in the data set as keys, and

each key maps to a list of tuples. Each tuple contains

the row index and feature value for a row that contains

the corresponding feature.

Input: query, k, hashmap

RESULT = HASHMAP

HEAP = MINHEAP(SIZE=K)

for every non-zero feature in query

for every tuple in hashmap[feature]

rowIndex = tuple[0]

feature-from-hashmap = tuple[1]

RESULT[rowIndex][0] +=

feature-from-hashmap

RESULT[rowIndex][1] += feature

end

for every instance in RESULT

HEAP.PUSH(CosineSimilarity(instance[0],

instance[1]))

HEAP.POPMIN()

end

return HEAP

Algorithm 2: Find top-k similar instances.

Further, Algorithm 2 ﬁnds the k most similar in-

stances to a given query by computing the cosine

similarity between the query and all the instances

in the hashmap. It works by ﬁrst initializing a RE-

SULT variable with the values from the hashmap and

a HEAP with size k. Then, for each non-zero feature

in the query, the algorithm updates the corresponding

values in the RESULT matrix by adding the feature

value from the hashmap and the feature value from

the query. Next, the algorithm computes the cosine

similarity between the query and each instance in the

RESULT matrix, and adds the computed similarity to

the HEAP while popping out the minimum value if

the size of HEAP exceeds k. Finally, the algorithm

returns the HEAP that contains the k most similar in-

stances.

4.3 KD Tree

KD tree is a binary tree structure. It addresses the

computational inefﬁciencies of the brute-force ap-

proach. In KD tree, the training data is divided into

multiple blocks and when a query instance comes,

the distance is calculated only with the data instances

with in that block instead of calculating with all the

training data instances. The tree construction time

takes most of the computation load. KD tree is quite

efﬁcient with low-dimensional data and big data sets.

Further, Algorithm 3 is a recursive method that

constructs a KD tree from a set of data instances

(training set) in a k-dimensional space. The algorithm

starts by checking that the training set is not empty,

afterwards it calculates the splitting axis for partition-

ing. Further, the training set is sorted based on the

selected axis and the median value of the instances

along that axis is calculated. It then creates a new

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

170

node object for the KD tree with the median value as

its data. The left and right sub-trees are constructed by

recursively applying the algorithm to the left and right

halves of the sorted training set, splitting each subset

along the next axis in sequence. The recursion termi-

nates when the size of the training set is zero. The

resulting KD-tree can be used to efﬁciently search for

nearest neighbors to a given query instance in the k-

dimensional space by traversing the tree and pruning

sub-trees that cannot contain a closer instance.

Input: trainset, depth, k

Function constructKDTree(trainset, depth, k):

if trainset is empty then

return null

end

axis = depth mod k

sorted trainset = sort(trainset, axis)

medianIndex = length(sorted

trainset) div 2

median = sorted trainset[medianIndex]

node = new node(median)

node.left = constructKDTree(sorted trainset[1

to medianIndex - 1, depth+1, k]

node.right = constructKDTree(medianIndex +

1 to length(sorted trainset), depth+1, k]

return node

End Function

Algorithm 3: Create KD tree.

Input: root, query, depth, k, KNN (MAXHEAP of

size k)

Function

KNearestNeighbors(root, query, depth, k, KNN):

if root is null then

return

end

axis = depth mod k

queryPoint = query[axis]

distance := cosineDistance(queryPoint, root)

if kNN.size < k then

kNN.insert(distance, root)

else if distance < kNN.Max() then

kNN.removeMax()

kNN.insert(distance, root)

end

if queryPoint <= root[axis] then

KNearestNeighbors(root.left, query, depth

+ 1, k, kNN)

else

KNearestNeighbors(root.right, query,

depth + 1, k, kNN)

end

return KNN

End Function

Algorithm 4: Find K-nearest neighbours in KD tree.

Furthermore, Algorithm 4 ﬁnds the k nearest

neighbors of a query instance in a k-dimensional

space using a KD tree. The algorithm ﬁrst computes

the current axis of partitioning and calculates the co-

sine distance between the query instance and the root

of the KD tree. If the KNN MAXHEAP is not yet full

(its size is less than k), then it inserts the current dis-

tance and the root into the MAXHEAP. On the other

hand, if the MAXHEAP is already full then it replaces

the farthest neighbor and inserts the current distance

and root into the MAXHEAP. Next, the algorithm de-

termines which subtree to traverse by comparing the

query instance with the root along the current axis.

If the query instance is less than or equal to the root,

it recursively call the KNearestNeighbors on the left

subtree of the current node; otherwise, right subtree.

The same process is then repeated recursively for each

subtree until a leaf node or a null node is reached. Fi-

nally, the algorithm returns the k nearest neighbors to

the query instance.

4.4 Ball Tree

One of the primary challenges of KD trees lies in han-

dling high-dimensional data. In order to address this

challenge, Ball tree can be considered. Within the

Ball Tree structure, the total space of training data

is divided into circular balls. The distance from a

test query is computed solely with the centroid of the

nearest ball to the query. Subsequently, the training

instances contained within that speciﬁc ball are uti-

lized for forecasting the output of the test query. Ball

tree is quite similar to KD tree as it uses hyper-spheres

(balls) instead of boxes (blocks) for that reason further

details about Ball tree are omitted to avoid duplica-

tion.

5 EXPERIMENTS

In this section, an assessment is conducted on the ap-

proaches used for identifying nearest neighbours of

a query instance. The evaluation is based on search

outcomes and performance, serving as indicators of

accuracy. The data sets encompasses various parame-

ters, including electricity consumption, outdoor tem-

perature, house characteristics and holiday data.

5.1 Setup

In order to ﬁnd similar top-k consumption patterns,

three distinct unsupervised nearest neighbors learn-

ing algorithms (modiﬁed brute force, Ball tree and

KD tree) are subjected to experimentation. Overall,

the experimentation involves the utilization of Python

(version 3.11), along with scikit-learn (version 1.2),

pandas (version 2.0) and NumPy (version 1.24), to

Identifying Similar Top-K Household Electricity Consumption Patterns

171

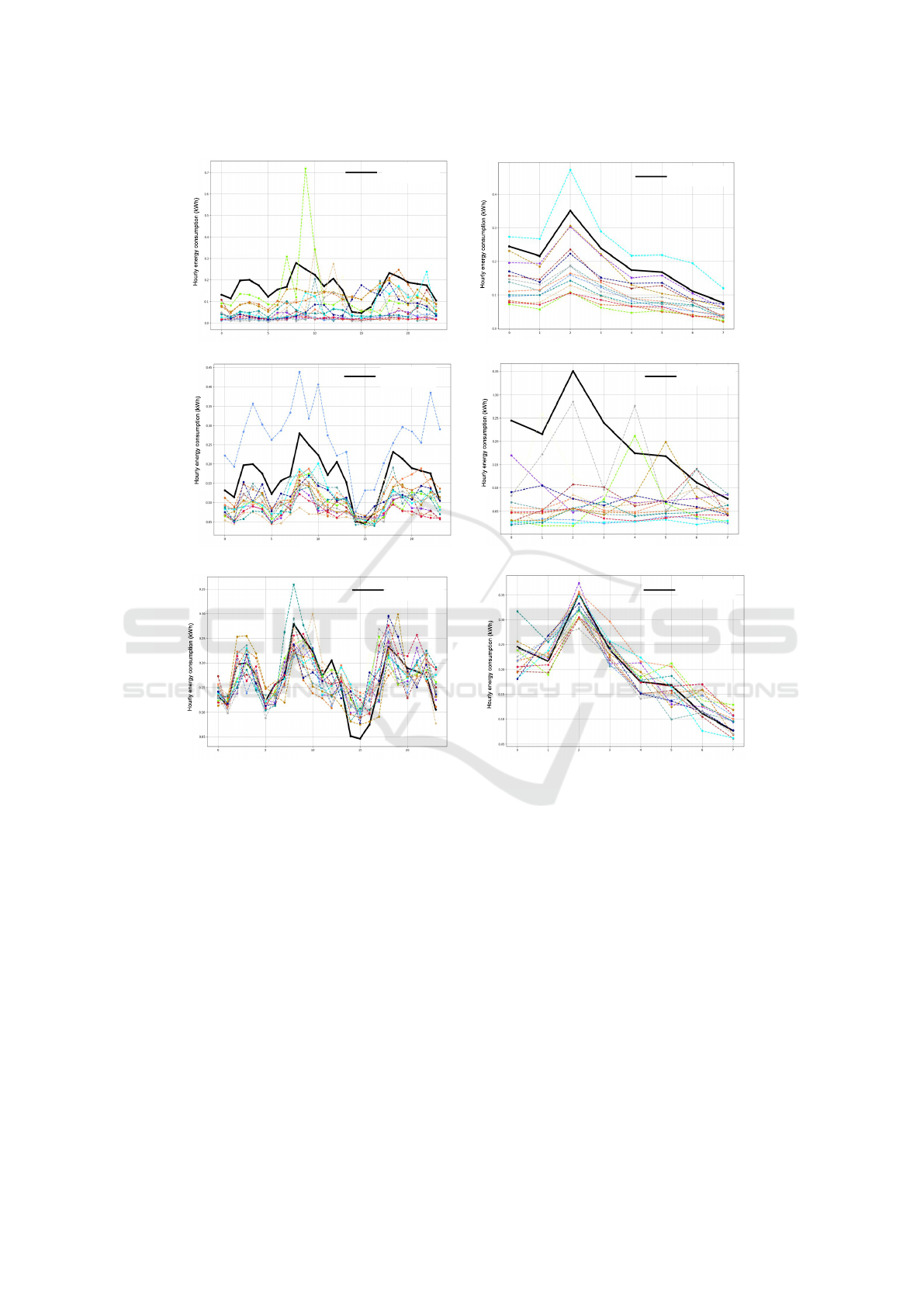
Modified brute force (low-dimensional data)

KD tree (low-dimensional data)

KD tree (high-dimensional data)

Ball tree (low-dimensional data)

Ball tree (high-dimensional data)

Time of day

Modified brute force (high-dimensional data)

Time of day

Search query/pattern

Figure 1: Top-15 similar consumption patterns based on the given query/pattern using three different nearest neighbours

algorithms.

assess all the algorithms. The electricity consump-

tion data set employed for the experiments amounts to

188 Megabytes in size. The algorithms were executed

on a hardware platform consisting of a single node,

8th Generation Intel Core i7-8565U 1.8 GHz proces-

sor, 32GB DDR4 RAM and 1TB SSD. The reported

results were obtained by running each algorithm 20

times with averaging over the best 5 executions.

5.2 Results and Discussion

The results of top 15 most similar consumption pat-

terns using three types of algorithms with high-

dimensional data (52 dimensions) are presented in

(Fig. 1). It can be observed in Fig. 1 (left hand side)

that KD tree performed the best by returning the most

relevant results against the search query, however Ball

tree also performed reasonably well by returning the

results that have similar patterns even so the magni-

tude of the values varies. Further, the results with low-

dimensional data (10 dimensions) in Fig. 1 (right hand

side) demonstrates that again KD tree performed the

best while modiﬁed brute force also performed well

by capturing the similar patterns, however not nec-

essary with the same magnitude. Further, it can be

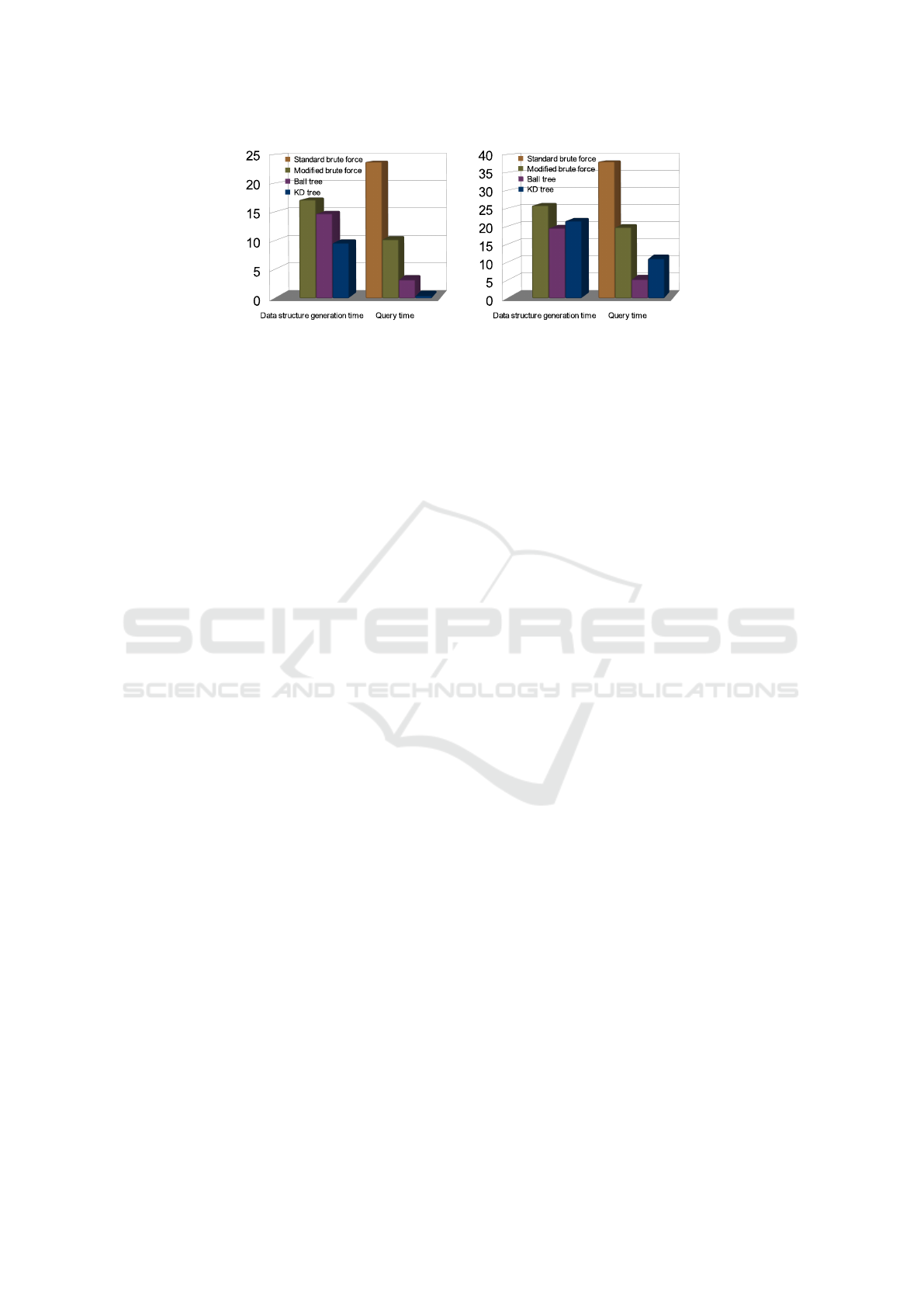
noticed in Fig. 2 (a) with low-dimensional data the

time of building the data structures and query time

to ﬁnd similar patterns, KD tree achieves the best

overall performance, while Ball tree accomplish bet-

ter query time than modiﬁed brute-force. The mod-

iﬁed brute force algorithm performed better at query

time in comparison to the standard brute force algo-

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

172

(a)

(b)

Figure 2: (a) low-dimensional data; (b) high-dimensional data.

rithm, however it could perform even better in case

of a sparse data set since the modiﬁed algorithm re-

duces the amount of data instances the query have to

traverse through. An example of sparse data set could

be a time series of solar electricity production, where

more than 60% of the data values are zero as the PV

stations cannot produce solar energy at night. Fur-

thermore, Fig. 2 (b) with high-dimensional data the

Ball tree performed the best. Likewise, the modiﬁed

brute force algorithm performed better at query time

in comparison to the standard brute force algorithm.

To summarize, standard brute force algorithm is

the slowest of all approaches for the reason that it

does almost all of the work during testing phase. On

the contrary, modiﬁed brute force, Ball tree and KD

tree need to build the data structure ﬁrst (equivalent to

the training phase). Both KD tree and Ball tree algo-

rithms are effective if the data size is large. Moreover,

Ball tree performs much better in higher dimensions

as compared to KD tree. On the other hand, if the data

size is small or data is sparse, modiﬁed brute force al-

gorithm could perform better.

6 CONCLUSIONS

This paper has presented practical approaches for

identifying similar patterns in household electricity

consumption within the energy sector. Identifying

similar consumption patterns aids utility suppliers in

segmenting households for customized energy saving

plans, forecasting short-term/long-term electricity de-

mand, providing off-peak prices during speciﬁc inter-

vals, creating household proﬁles to enhance and sus-

tain energy efﬁciency, and more. The proposed solu-

tion relies on K nearest neighbors (KNN) methods, in-

cluding brute force, KD tree and Ball tree. Moreover,

to optimize the functionality of the standard brute

force algorithm, a modiﬁed version has been created.

The enhanced version employes a hashmap and co-

sine similarity to efﬁciently compute K nearest neigh-

bors for high-dimensional sparse data. The accuracy

of search outcomes and the operational performance

of unsupervised nearest neighbours algorithms were

assessed using real-world data set, yielding promis-

ing results. The presented approaches are applicable

across various sectors within energy industry.

For the future work, an investigation into the

performance of the modiﬁed brute force algorithm

with high-dimensional sparse data would be valuable.

Additionally, evaluating the presented algorithms on

well-known energy data sets and comparing their ac-

curacy and performance against state-of-the-art sim-

ilarity search algorithms could provide insightful re-

sults.

REFERENCES

Ardakanian, O., Koochakzadeh, N., R. P. Singh, L. G.,

and Keshav, S. (2014). Computing electricity con-

sumption proﬁles from household smart meter data.

In EDBT/ICDT Workshops, pages 140–147. CEUR-

WS.org.

Cembranel, S. S., Lezama, F., Soares, J., Ramos, S., Gomes,

A., and Vale, Z. (2019). A short review on data mining

techniques for electricity customers characterization.

In IEEE PES GTD Grand International Conference

and Exposition Asia, pages 194–199. IEEE.

Eskandarnia, E., Al-Ammal, H. M., and Ksantini, R.

(2022). An embedded deep-clustering-based load pro-

ﬁling framework. Sustainable Cities and Society,

78:103618.

Feremans, L., Cule, B., Vens, C., and Goethals, B. (2020).

Combining instance and feature neighbours for ex-

treme multi-label classiﬁcation. International Journal

of Data Science and Analytics, 10:215–231.

Gholizadeh, N. and Musilek, P. (2022). Federated learn-

ing with hyperparameter-based clustering for electri-

cal load forecasting. Internet of Things, 17:100470.

Guo, Z., O’Hanley, J. R., and Gibson, S. (2022). Predicting

residential electricity consumption patterns based on

smart meter and household data: A case study from

the republic of ireland. Utilities Policy, 79:101446.

Hopf, K., Sodenkamp, M., Kozlovkiy, I., and Staake, T.

Identifying Similar Top-K Household Electricity Consumption Patterns

173

(2016). Feature extraction and ﬁltering for house-

hold classiﬁcation based on smart electricity meter

data. Computer Science - Research and Development,

31:141–148.

Humeau, S., Wijaya, T. K., Vasirani, M., and Aberer, K.

(2013). Electricity load forecasting for residential cus-

tomers: Exploiting aggregation and correlation be-

tween households. In Sustainable Internet and ICT

for Sustainability, pages 1–6. IEEE.

Iftikhar, N., Liu, X., Danalachi, S., Nordbjerg, F. E., and

Vollesen, J. H. (2017). A scalable smart meter data

generator using spark. In On the Move to Meaningful

Internet Systems.OTM 2017 Conferences, pages 21–

36. Springer.

Iftikhar, N., Liu, X., Nordbjerg, F. E., and Danalachi, S.

(2016). A prediction-based smart meter data gener-

ator. In 19th International Conference on Network-

Based Information Systems, pages 173–180. IEEE.

Kwac, J., Flora, J., and Rajagopal, R. (2014). Household

energy consumption segmentation using hourly data.

IEEE Transactions on Smart Grid, 5(1):420–430.

Lange, D., Ribalta, M., Echeverria, L., and Pocock, J.

(2023). Proﬁling urban water consumption using au-

toencoders and time-series clustering techniques. In

14th International Conference on Hydroinformatics,

page 1136 012005. IOP Publishing.

Laouaﬁ, A., Laouaﬁ, F., and Boukelia, T. E. (2022). An

adaptive hybrid ensemble with pattern similarity anal-

ysis and error correction for short-term load forecast-

ing. Applied Energy, 322:119525.

Okereke, G. E., Bali, M. C., Okwueze, C. N., Ukekwe,

E. C., Echezona, S. C., and Ugwu, C. I. (2023). K-

means clustering of electricity consumers using time-

domain features from smart meter data. Journal

of Electrical Systems and Information Technology,

10(1):1–18.

Rahim, M. S., Nguyen, K. A., Stewart, R. A., Ahmed, T.,

Giurco, D., and Blumenstein, M. (2021). A clustering

solution for analyzing residential water consumption

patterns. Knowledge-Based Systems, 233:107522.

Tang, W., Wang, H., Lee, X. L., and Yang, H. T. (2022).

Machine learning approach to uncovering residential

energy consumption patterns based on socioeconomic

and smart meter data. Energy, 240:122500.

Trotta, G., Gram-Hanssen, K., and rgensen, P. L. J. (2020).

Heterogeneity of electricity consumption patterns in

vulnerable households. Energies, 13(18):4713.

Wang, Y., Jia, M., Gao, N., Krannichfeldt, L. V., Sun, M.,

and Hug, G. (2022). Federated clustering for elec-

tricity consumption pattern extraction. IEEE Transac-

tions on Smart Grid, 13(3):2425–2439.

Wen, L., Zhou, K., and Yang, S. (2019). A shape-based

clustering method for pattern recognition of residen-

tial electricity consumption. Journal of cleaner pro-

duction, 212:475–488.

Wu, J., Niu, Z., Li, X., Huang, L., Nielsen, P. S., and Liu,

X. (2023). Understanding multi-scale spatiotemporal

energy consumption data: A visual analysis approach.

Energy, 263:125939.

Yang, T., Ren, M., and Zhou, K. (2018). Identifying house-

hold electricity consumption patterns: A case study of

kunshan, china. Renewable and Sustainable Energy

Reviews, 91:861–868.

APPENDIX

The implementation of the modiﬁed brute force al-

gorithm, as outlined in Section 4.2 has been realised

through the following Python code.

#create hashMap

def createhashMap(feature_set):

hashmap = {}

#fill hashmap with keys from feature columns

train_instance_num = feature_set.shape[0]

#for each row in dataset

for i, row in enumerate(feature_set):

#for each feature in row

for j, feature in enumerate(row):

if (i == 0):

hashmap[j] = []

if (feature != 0):

hashmap[j].append([i,

feature])

return hashmap

#Given a test query (xq) return the k most

#similar consumption patterns

def knnSearch(xq, k, hashmap):

S = {}

heap = []

#loop through all the query features

for j,feature in enumerate(xq):

#loop through all the tuples for the

#non-zero query feature in the hashmap

if (feature != 0):

for tuples in hashmap[j]:

#if it is the first feature,

#then create an empty array

if(j == 0):

S[tuples[0]] = [[],[]]

#Append to S at [tuples[0]]

S[tuples[0]][0].append(tuples[1])

S[tuples[0]][1].append(feature)

counter = 0

for rowid in S:

if(counter < k):

heapq.heappush(heap,

(cosine_sim(S[rowid][0],S[rowid][1])

,rowid))

else:

heapq.heappushpop(heap,

(cosine_sim(S[rowid][0],S[rowid][1])

,rowid))

counter += 1

heaplist = heapq.nlargest(k,heap)

return heaplist

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

174