Validation of a Biomechanical Performance Assessment Platform

Applying an Inertial-Bpased Biosensor and Axis Vector Computation

Wangdo Kim

1,2 a

, Sean S. Kohles

3,4,5 b

, Emir A. Vela

1,2 c

and Victor Huayamave

Ingeniería Mecánica, Universidad de Ingeniería y Tecnología -UTEC, Lima, Peru

Research Center in Bioengineering, Ingeniería Mecánica, Universidad de Ingeniería y Tecnología-UTEC, Lima, Peru

Kohles Bioengineering, Cape Meares, OR, U.S.A.

Division of Biomaterials & Biomechanics, School of Dentistry, and Department of Emergency Medicine,

School of Medicine, Oregon Health & Science University, Portland, OR, U.S.A.

Department of Human Physiology and Knight Campus for Accelerating Scientific Impact, University of Oregon,

Eugene, OR, U.S.A.

Department of Mechanical Engineering, Embry-Riddle Aeronautical University, Daytona Beach, FL, U.S.A.

Keywords: Biosensors, Instantaneous Axis-Angle Representations, IMU Sensors, Inertial Measurement Units, Quaternions,

Inverse Kinematics, Forward Kinematics, Instantaneous Axis of Rotation, Motion Tracking Sensors.

Abstract: Inertial kinetics and kinematics have substantial influences on human biomechanical function. A new

algorithm for IMU-based motion tracking is presented in this work. This study combines recent developments

in improved biosensor technology with mainstream motion-tracking hardware to measure the overall

performance of human movement based on joint axis-angle representations of limb rotation. This study

proposes an alternative approach to representing three-dimensional rotations using a normalized vector around

which an identified joint angle defines the overall rotation, rather than a traditional Euler angle approach.

Contrast the procedure of Euler angles with the procedure of Axis angle, Euler angles force the body to move

along a certain route which it had arbitrarily chosen but which the body had not chosen; in fact, the body

would not take any of its routes separately, though it would take all of them together in the most embarrassing

manner-goal-directed behavior. But axis angle had no preconceived scheme as to the nature of the movements

to be expressed. Although the axis-angle representation requires vector quotient algebra (quaternions) to

define rotation, this approach may be preferred for many graphics, vision, and virtual reality software

applications. Elbow flexion and extension motion was used to validate the analytical methods. The results

suggest that the novel approach could reasonably predict a detailed analysis of axis-angle migration. The

described algorithm could play a notable role in the biomechanical analysis of human joints and offers a

harbinger of IMU-based biosensors which may assess the control of skilled manipulation.

1 INTRODUCTION

Human motion capture systems, constructed from

Inertial Measurement Units (IMUs), have been the

subject of recent development and validation. Lapresa

et al. (2022) presented the validation of inertial

systems using an anthropomorphic robot (Lapresa et

al., 2022). These approaches rely on measuring the

three-dimensional linear and angular positions and

accelerations of subject joints and limbs generated by

https://orcid.org/0000-0003-0527-5129

https://orcid.org/0000-0002-5869-7715

https://orcid.org/0000-0002-9397-2452

https://orcid.org/0000-0003-0837-6849

micro-electromechanical systems (MEMS) such as

an IMU. Effectively, an IMU is a localized biosensor

accelerometer and gyroscope estimating an object’s

biomechanical position and orientation. IMUs can be

single-point sensors or more complex single-pack

arrays when including an additional magnetometer

and sensor fusion algorithm, providing more accurate

movement data and reduced sensor drift. A common

artifact of accelerometer measurements is manifested

in velocity and displacement trajectory drift obtained

when integrating the raw acceleration record.

Kim, W., Kohles, S., Vela, E. and Huayamave, V.

Validation of a Biomechanical Performance Assessment Platform Applying an Inertial-Bpased Biosensor and Axis Vector Computation.

DOI: 10.5220/0012157900003587

In Proceedings of the 11th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2023), pages 93-100

ISBN: 978-989-758-673-6; ISSN: 2184-3201

MEMS-based IMU sensors can be used in

computer vision techniques that track the location of

a person through a combination of their pose and

orientation with applications in robotics, personal

navigation, and virtual reality. Furthermore, recent

studies confirm IMU sensor applications for human

motion analysis, enhancing biomechanics,

rehabilitation, ergonomics, and sports assessments

(González-Alonso et al., 2021). This research

includes refined quantification of human movements

and movement classification. These studies

concentrate on obtaining the kinematic Identification

of a particular activity, which helps identify

biomechanical disorders such as disease or injury, as

well as longer-term patterns of atypical

neuromuscular control. Compact, self-contained

systems for the kinematic Identification of human

motion, such as that offered by IMUs, are

independent of the subject’s mobility environment

and free of obstructions that may affect optical

position sensors (D'Amore, Ciarleglio, & Akin,

2015).

Current swing dynamic performance indices seem

to be insufficient to represent the fundamental of golf

dynamic performance because full-body models may

be easily affected by the rotation of individual

anatomical segments (Teu, Kim, Fuss, & Tan, 2006).

Recent studies have suggested that the inertia tensor,

a physical property whose values are time- and

coordinate-independent, may be an important

informational invariant haptic perception of which is

not influenced by the segment rotations. Previous

work addressing the biomechanical performance

assessment platform used an optical-based system

(Figure 1) and identified the geometric change to a

certain axis, such that if the club is rotated around this

axis through a determinate angle, the desired

movement will be effected. The perception-action

dynamic alignment between the inertia of the club

and the instantaneous axis was indexed as an

influence on the swing phase of the golf training

system (Kim, Veloso, Araújo, Machado, et al., 2013).

We found that perception and action were more

highly correlated with each other in the more skilled

player (Figure 2b) compared to the less experienced

player (Figure 2a).

The present study describes the characteristics of

an IMU wearable sensor platform that provides a

critical biomechanical parameter during the

assessment of joint disease and injury. Here, the

instantaneous axis-angle representation (IAA) of

limb function is a vector that is identified as a metric

to assist human movement analysis for use in

rehabilitation and sports. The estimation of the IAA

and its variant motion is strongly related to the joint's

functionality and ligament health (Kim, Araujo,

Kohles, Kim, & Alvarez Sanchez, 2020) as well as

the overall performance of locomotion perception and

motor control (Kim, 2020). Joint kinematics depend

on a postural balance or equilibrium, meaning that the

components of the resultant moment about the axis of

rotation sum to zero. In this work, we confirm the

accuracy of IMU-based inverse kinematics and

forward kinematics as applied to upper limb

movement.

Figure 1: Position of attached markers on the body of the

subject that adopted the stance at the instance of the club

addressing the ball. The separate panel depicts individual

markers attached to the hand. The labeled markers were

used to build an anatomical reference frame within which

the grip reference frame was coincident at the beginning of

the downswing. The origin of the global frame coincides

with the first COP location of the left foot.

The specific objective of this work is to present a new

algorithm for Inertial measurements unit (IMU)-

based motion tracking with quaternions. Axis-angle

representation for rotation, instead of representing a

3D rotation using a sequence of rotations around the

sensor coordinates system, as Euler angles do, the

axis-angle representation uses a normalized vector S

around which the rotation is defined by some angle θ

and can track a sequence of events in terms of a one-

one correspondence of IAA. Although the IAA is not

fixed, it is indeed moving about in such an

embarrassing manner that has unity relative to the

posture and behaviors of the subject being

considered.

There are two main advantages to using the axis

angle representation for describing limb kinematics.

The first is that they allow a global description of rigid

body motion that does not suffer from singularities

due to local coordinates. Such singularities are

inevitable when one represents rotation via Euler

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

Figure 2: (a), (b). Player A, the novice golf player, produced a three-dimensional spatiotemporal view on the instantaneous

axis-angle (IAA, solid lines) and the instantaneous principal axes of inertia (e3, dashed lines) for small motion steps (300Hz)

that were projected onto the posteromedial side of the player (a). The endpoints of axes are at the intersections with anterior

(Ant) and Posterior (Pos) planes, which are located 100 and 300 cm off the origin of the global frame. The first axis, indicated

by 1, represents the beginning of the downswing. The arrow indicates where the subsequent axes have migrated at every

0.0333 second of time step (units in cm).

Player B, the skilled player, produced a three-dimensional spatiotemporal view on the instantaneous axis-angle (IAA, solid

lines) and the instantaneous principal axes of inertia (e3, dashed lines) for small motion step (300Hz) that were projected onto

the posteromedial side of the player (a) and onto the superior side of the player (b). In an effort to verify positioning perception

and action relation in time-sequence of motion data, the club IAA is shown to be regularly projective to the e3. This

representative analysis indicates a close connection (Spatial-temporal representation of IAA versus the e3) during the

downswing for player B.

angles. The second advantage is that the axis-angle

provides a very geometric description of rigid motion,

which significantly simplifies the analysis of

biomechanisms and is handy for describing the

kinesthesis, "feeling of movement," in all skeletal and

muscle structures. The axis vector is not moving

instantaneously, occupying a stationary axis in the

global frames.

2 MATERIAL AND METHODS

2.1 Inertial Measurement Unit Device

and Model Foundation

The newest generation of cost-efficient inertial

motion trackers features a lightweight design,

wireless connectivity (Bluetooth Low Energy, BLE),

and robust sensor fusion algorithms to provide

accurate data for human movement applications

(DOT Wearable Sensor, Xsens Technologies B.V.,

Enschede, the Netherlands). Software manipulation

tools are provided (Software Development Kit, SDK)

to facilitate the customization of mobile applications

based on the available output data, thereby allowing

developers to integrate the sensor into a wide range of

solutions. Robust algorithms (Strap Down

Integration, SDI) and a sensor fusion framework

(Xsens Kalman Filter Core, XKF) run onboard the

sensor to provide accurate physical orientation

estimates and minimize the effects of magnetic

distortion (González-Alonso et al., 2021).

The IMUs applied in this work contain MEMS

type gyroscopes, accelerometers, and

magnetometers. These individual sensor signals are

fused through a statistical estimation framework to

obtain three-dimensional (3D) limb and joint

orientation. The output provided by the three main

device components is then fed into the signal

processing pipeline. The two main algorithms noted

above are run onboard the motion tracking sensor

(Schumacher, 2006). The sensors are primarily

designed to connect to mobile devices such as

smartphones that must be BLE-capable (Figure 3).

Before describing the output data, it is prudent to

present the types of reference systems used in this

paper. Data shall be expressed in terms of local

(Sensor Coordinate System, SCS) and global, earth-

fixed (Global Reference Coordinate System, GRCS)

coordinate systems. The SCS is a right-handed,

Validation of a Biomechanical Performance Assessment Platform Applying an Inertial-Bpased Biosensor and Axis Vector Computation

Figure 3: Wireless communication between the sensors and

a mobile device was used in this study.

Cartesian coordinate system that is body-fixed within

each sensor identified with lowercase x, y, and z axes

(Figure 4). The local earth-fixed RC is also defined as

a right-handed, Cartesian coordinate system with the

following global orientations:

 X positive to the East (E).

 Y positive to the North (N).

 Z positive when pointing Up (U)

Figure 4: The local sensor coordinate system (SCS) is

associated with the sensor as indicated by the (x,y,z)

Cartesian coordinate system, while the global reference

coordinate system (GRCS) is matched to the elbow joint

and anatomic orientation as indicated by the (X, Y, Z)

Cartesian coordinate system. Since the SCS is not aligned

with the GRCS in this anatomic configuration, the data

measured by the SCS is transformed through vector algebra

by applying the unit quaternion cos

𝜋



,0,0,sin

𝜋



 ,

which rotates data in SCS by 90 degrees about the Z axis.

This coordinate system is known as East-North-Up

(ENU) and is the standard framework in inertial

navigation for aviation and geodetic applications.

Note that positive global orientations can be

established for any application while maintaining the

right-hand configuration, i.e., X positive to the South

(S).

The wearable sensors produce instantaneous 3D

coordinate axis orientation and acceleration data. The

data available for the experiment can be classified

into two categories: inertial data and sensor fusion

data. The inertial data is comprised of linear

acceleration (units of m/s

) and angular velocity

(units of ◦/s) as provided in the SCS. These IMU-

based sensors output angular velocities as a direct

measurement from the internal gyroscopes. The 3D

orientation output takes the quotient of the axis

vectors as unit quaternions. The orientation can be

represented by a normalized quaternion, q = [W X Y

Z] with W being the real component and X, Y, Z as

the imaginary global coordinate components. This

sensor output is within the ENU localized global

reference coordinate system. The output IMU

measurement vector 𝑆



contains the individual

measurements stacked together as ten state variables:

𝑆



𝑎



, 𝑎



, 𝑎



, 𝜛



, 𝜛



, 𝜛



, 𝑞



, 𝑞



, 𝑞



, 𝑞





(1)

The optimal filtering problem is then to determine the

angular acceleration state variables, 𝛼



, 𝛼



, 𝛼



 as

well as their numerical derivatives as the angular

velocity vector components 𝜔



, 𝜔



, 𝜔



. Further, the

problem is then constructing the new state variables,

which provide the best match with the data within

𝑆



but also have a degree of numerical smoothness.

The regularization method is then applied to solve

this numerical challenge (Trujullo & Busby, 1997).

In this study, we estimated the identified state

variables by applying L-curve Tikhonov

regularization filtering (TRF). The TRF algorithm

was previously applied in the optimization of

smoothing parameters (Ancillao, Vochten, Verduyn,

De Schutter, & Aertbeliën, 2022) during multiscale

cell-tissue level (Kim, Tretheway, & Kohles, 2009)

and joint level (Kim, Kim, Veloso, & Kohles, 2013)

biomechanical analyses. As a result of the TRF,

thirteen numerically smoothed state variables are then

present in the filtered vector 𝑆



𝑆





𝑎



, 𝑎



, 𝑎



, 𝜛



, 𝜛



, 𝜛



, 𝑞



, 𝑞



𝑞



𝑞



, 𝛼



, 𝛼



, 𝛼





(2)

The data in this application was recorded through

local resources (VR Motion Laboratory, Department

of Mechanical Engineering, UTEC, Lima, Peru). One

healthy, well-trained subject (1 man) gave his written

informed consent to participate in this study.

It has frequently been assumed in previous

methods that the point of observation for motion is

unoccupied because it is measured in a Sensor

Coordinate System (SCS), while the point of

observation in this work is occupied in global

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

reference coordinate systems (GRCS.) When a point

of observation is occupied, there is also information

to specify the motion of himself, and the limb of the

person in action instantaneously occupies some

portion of the space in a way that is unique to the

person as presented as the instantaneous axis-angle

representation (IAA.) This information is unique to

that person. The IAA is not moving and stationary in

the GRCS, occupying the specific axis in the freedom

space. Therefore, the innovation brought by this

research is to propose the measure of the feeling of

the self-movement, i.e., proprioception, in terms of

the IAA, meaning that it specifies the self-movement

as distinguished from an object moving in the

environment.

2.2 Inverse Kinematic Solutions Using

Quaternions

Our solution method is based on an axis-angle

representation by applying vector algebra quaternions

as a motion operator. All rotating screw motions are

represented as a rotation about an axis with respect to

the global GRCS. Two quaternions describe general

movement positioning: one for orientation and the

second for translation.

All the data processing was implemented in a

commercial programming and computing platform

(MATLB, The MathWorks, Natick, MA, USA).

Here, the module “Quaternion.m” was applied

(Tincknell, 2023). Quaternion.m implements

quaternion mathematical operations, including three-

dimensional rotations, transformations, and

numerical propagation of the governing equations of

rotational motion, most of which are fully vectorized.

Quaternions represent complex numbers within a

four-dimensional vector space (rank 4) over a real

number field (Kuipers, 1999). A quaternion is

generalized as

𝑞𝑤𝑥𝑖𝑦𝑗𝑧𝑘



𝑞



, 𝑞



, 𝑞



, 𝑞





(3)

𝑞



𝑞



, 𝒒

𝒗



(4)

where 𝑞



represents a scalar and 𝒒

𝐯





𝑞



, 𝑞



, 𝑞





represents a vector. A quaternion of 𝒒

𝐯

 0 is called

a real quaternion, and a quaternion of 𝒒

𝟎

 0 is

identified as a pure quaternion. Multiplication of two

quaternion vectors can be expressed as

𝑞



⊗𝑞



𝑞



𝑞



−𝑞



⋅𝑞



, 𝑞



𝑞



𝑞



𝑞



𝑞



𝑞



(5)

where the symbols “ ⊗ ”,” ⋅ ”,”  ” denote the

quaternion product, dot product, and cross product

actions, respectively. Quaternion multiplication is not

considered commutative. The conjugate of the

quaternion can be expressed as:

𝑞

∗





𝑞



, −𝒒

𝒗







𝑞



, −𝑞



, −𝑞



, −𝑞





(6)

and thus defining the quaternion norm

‖

𝑞

‖

as:

𝑞



𝑞⊗𝑞

∗

𝑞





𝑞





𝑞



𝑞





(7)

With the relationship

‖

𝑞

‖



 1, a unit quaternion is

present whereby any quaternion



𝑞



can be

normalized by dividing by its norm. The inverse of a

quaternion is then expressed as:

𝑞





𝑞



𝑞

∗

𝑎𝑛𝑑

‖

𝑞

‖

 0

(8)

and thereby for a unit-quaternion, the relationship is

reduced to:

𝑞



𝑞

∗

(9)

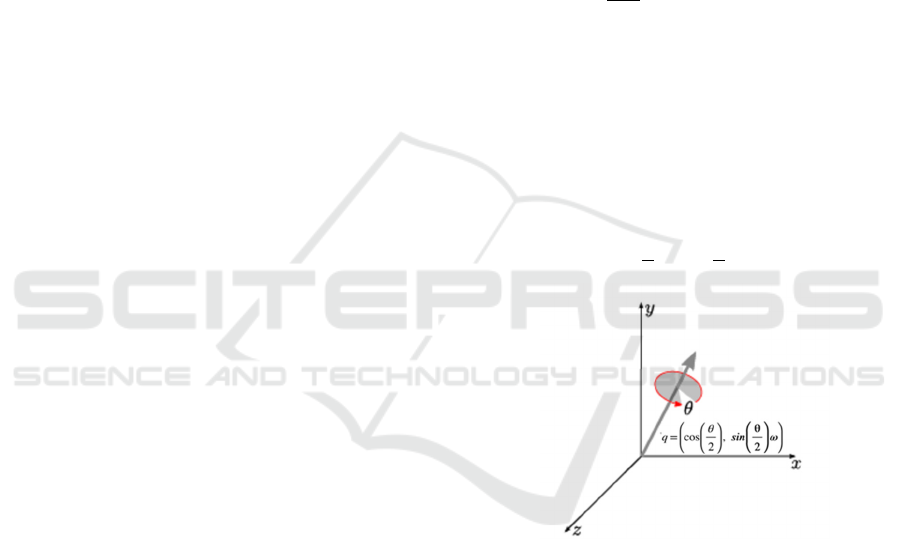
A unit quaternion can be further defined as a vector

rotation operator. Rotation about a unit axis 𝜔 with

an angle 𝜃 is then defined by the axis-angle

representation (Figure 5).

𝑞cos 

𝜃

,sin

𝜃

𝜔

(10)

Figure 5: Graphical axis-angle representation for vector

rotations. The approach described here uses a normalized

quaternion q around which the rotation is defined by four

kinematic variables instead of three. Applications include

computer-aided graphics, vision, and virtual reality

computation.

2.3 Biomechanical Orientation

Tracking with Quaternions

Earlier work has demonstrated how human

perception and motor control interact continuously

between external physical systems (Gibson, 1979).

The axis-angle representation effectively establishes

a global description of the individual as a rigid body

during environmental interactions and avoids

mathematical singularities due to the use of the local

Validation of a Biomechanical Performance Assessment Platform Applying an Inertial-Bpased Biosensor and Axis Vector Computation

coordinates. The benefits of using quaternions during

axis-angle representation as described in the

presented approach are the well-defined sets of

operations for vector addition, multiplication, and

interpolation while converting the representations

directly to rotational matrices. Such singularities are

inevitable when representing rotations traditionally

via Euler angles.

A general rigid-body transformation has 6 degrees

of freedom (DOF) accounting for linear and angular

translations or as defined here: 3 DOF for orientation

and 3 DOF for translation. A unit-quaternion can be

used as a rotation operator as shown in Equation 10

and Figure 3. A vector 𝒗 can be transformed into a

vector 𝒘 such that:

𝒘 = 𝑞⊗𝒗⊗𝑞

∗

(11)

where 𝑞 is a unit quaternion and 𝒗 is a pure

quaternion. The unit quaternion can be used to

transform a vector, but not through rigid

transformation. Therefore, an alternative quaternion

will implement translation:

𝑡 = 𝒑−𝑞⊗𝒑⊗𝑞

∗

(12)

Where 𝒑 is the position vector of an arbitrary point on

the axis within a pure quaternion.

In this study, we use the axis-angle representation

to obtain the inverse kinematics solution of the elbow

during simple flexion and extension within the

healthy range of motion of upper limb movement.

The immediate objective is to identify the forward

kinematics of the hand. For this purpose, it suffices to

identify the values of the axis-angle of the elbow joint

and its location with respect to the GRCS system. The

estimation of the IAA representation of limb

movement, also known as a biomechanical screw axis

(Ball, 1900), can play a notable role in the

biomechanical analysis of biological joints (healthy,

diseased, and injured). We assume that the amplitude

of the angle of the instantaneous axis is minute, in

conformity with a small angle assumption when

combined in the same manner as force values.

3 RESULTS

We demonstrate the described IMU-based approach

by applying the axis-angle representation of healthy

upper limb movements. These experiments: (i)

demonstrate the calculation of the IAA and the

analysis of IAA migration using quaternion

operators; (ii) check the accuracy of both the IMU-

based inverse kinematics and forward kinematics. A

single male adult subject was used to validate the

mathematical approach with data functional anatomic

data produced during elbow flexion-extension

postures of the upper limb within the sagittal plane of

motion. The UTEC human-subjects ethics committee

approved the data collection.

The forward kinematics was performed in that

sensor trajectories were reconstructed as x,y, z

Cartesian coordinates with the help of the IAA. The

RC frame was defined for the elbow joint as follows

(Figure 4): The origin location is the midpoint of the

projection between the medial and lateral bony

aspects of the distal humerus. The X-axis defines the

lateral aspects of the elbow joint. The X-axis is also

coincident with the South (S) orientation according to

the ENU global reference coordinate system, the Y-

axis is positive to the East (E), and the Z-axis is

positive when pointing up (U).

Data were generated by the IMU accelerometer

and gyroscope, as provided in the sensor-fixed frame

(SCS) and combined through a sensor fusion

algorithm measuring the orientation with respect to

the global reference frame (GRCS). Therefore, it is

necessary to align the SCS frame in which three linear

accelerations and three rotational rate gyroscopes are

measured to the global coordinates as described

above, allowing the IAA to be computed by the global

system.

The virtual sagittal plane was defined relative to

the geometric representation of the IAA from the

geometric center (Figure 6). This allows us to assess

variability in the direction of the functional IAA

during the flexion-extension movement of the

forearm. In addition, the intersection of the functional

IAA with this plane was analyzed, while the

migration of IAA was observed for small motion

steps (acquired at 60 Hz).

Contrast the procedure of Euler angles with the

procedure of Axis angle, Euler angles tried to force

the body to move along the certain route which it had

arbitrarily chosen but which the body had not chosen;

in fact, the body would not take any one of its routes

separately, though it would take all of them together

in the most embarrassing manner—goal-directed

behavior. But axis angle had no preconceived scheme

as to the nature of the movements to be expressed. A

subject simply found the body in a certain position,

A, and then he coaxed the body to move, not in this

way or in that particular way, but any way the body

liked to any new position B.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

Figure 6: A sequence of IAAs from the single human

subject elbow is represented relative to the origin of the

global frame (units in meters, m).

Once the IAA was defined, forward kinematics

obtained the vector trajectories (Figure 7). Finally, the

position of the end effector, the IMU sensor located

in the palm of the subject’s hand, is given by

trajectories as viewed in the oblique and on the

sagittal plane.

4 CONCLUSIONS

In theoretical terms, inverse kinematics, which in

itself is ruled by an IAA, is formed to visualize the

migration of biomechanical action. Another piece of

information provided by forward kinematics as ruled

by the end effector is formed by visualizing the

migration of the motion at the distal or proximal ends

of the limb itself. In this way, the characteristics of

the elbow motion can be estimated intuitively based

on the shape and alignment relative to each of the

limb segments. From a mechatronic perspective, we

use position and orientation data to control the end

effector of a robotic arm. From that application,

identifying the joint variables that generate that

desired position and orientation will ultimately

control the end effector. However, human movement

control is continuous and processed concurrently with

afferent and efferent inherent modulation.

Limitations of this study are that one IMU sensor

was used during the activity of a single subject. The

optimal system for joint biomechanics should be

characterized using two IMUs where each sensor is

worn at the proximal and distal segments containing

the target joint. Future research will focus on

increasing the use of IMUs when defining limb

movements while studying the model performance in

clinical and laboratory settings.

Figure 7: The elbow IAA trajectories as viewed at the

oblique angle (a) and the sagittal plane containing the

motion of flexion and extension (b). (units in meters, m).

By using the traditional optical-based motion

tracking system, we have characterized the concept of

a "knee axis" and further the concept of "invariant.

(Kim & Vela, 2021; Kim, Veloso, Araújo, Vleck, &

João, 2013)" We found that the line of the ground

reaction force (GRF) vector is very close to the knee

instantaneous axis (KIA). It aligns the knee joint with

the GRF such that the reaction forces are torqueless.

This insight shows that locating KIA is equivalent to

the dynamic alignment measurement. This method

can be used for the optimal design of braces and

orthoses for the conservative treatment of knee

osteoarthritis. Having validated the axis-angle with

the optical-based system, we applied the same

approach with the imu-based system to track the

occupied motion of the subject.

The invariant combination of the axis-angle

representation could open a new era of quantifying

biomechanical perception-action systems as

interactions with the natural or built environment.

The overall performance metrics of many motor

activities could be extended to real-world and clinical

settings within multiple spatial and temporal

frameworks. Further, this approach may then be

extended to understanding the causal nature of

biomechanical injury and disease, especially that

associated with inertial kinetics and kinematics.

The kinesthesis, the awareness of one's own

motion, cannot be measured in a sensor coordinate

system (SCS.) However, they have unity relative to

the posture and behavior of the subject being

(a)

(b)

Validation of a Biomechanical Performance Assessment Platform Applying an Inertial-Bpased Biosensor and Axis Vector Computation

considered. The results exert goal-directed feedback

control by using the IAA to guide our motion

continuously. Our assumption is that goal-directed

feedback could be applied to many more

rehabilitation application routines. Real-time posture

correction and motion change instruction could

ultimately optimize motor learning, reducing injuries

caused by excessive motion and bad postures.

Therefore, the shape of the IAA surface relative to the

goal-directed behavior of the performer can be

regarded as the “genome” of golf swing performance.

ACKNOWLEDGEMENTS

This study was funded by PROCIENCIA under

contract N° PE501080681-2022-PROCIENCIA

Proyectos Especiales: Proyectos de Investigadores

Visitantes, the MIT-Peru UTEC Seed Fund,

“Development of Proper Tunnel Syndrome

Placement Device to Avoid Impingement”, the UTEC

Fondo Semilla 2022, “Aprendizaje Perceptivo de los

Movimientos de las Piernas y Pateo de Infantes con

Espina Bífida utilizando un Sistema de

Entrenamiento de Realidad Virtual.”, the National

Institutes of Health, USA (Grants: R03 DE014288,

R15 EB007077, and P20 MD003350), and the US

National Science Foundation CAREER award

CMMI-2238859.

REFERENCES

Ancillao, A., Vochten, M., Verduyn, A., De Schutter, J., &

Aertbeliën, E. (2022). An optimal method for

calculating an average screw axis for a joint, with

improved sensitivity to noise and providing an analysis

of the dispersion of the instantaneous axes. Plos one,

17(10), e0275218.

Ball, R. (1900). A Treatise on the Theory of Screws:

Cambridge University Press.

D'Amore, N., Ciarleglio, C., & Akin, D. L. (2015). Imu-based

Manipulator kinematic identification. Paper presented at

the 2015 IEEE International Conf. on robotics and

automation (ICRA).

Gibson, J. J. (1979). The Ecological Approach to Visual

perception: Houghton Mifflin.

González-Alonso, J., Oviedo-Pastor, D., Aguado, H. J., Díaz-

Pernas, F. J., González-Ortega, D., & Martínez-Zarzuela,

M. (2021). Custom IMU-based wearable system for

robust 2.4 GHz wireless human body parts orientation

tracking and 3D movement visualization on an avatar.

Sensors, 21(19), 6642.

Kim, W. (2020). The Knee Proprioception as Patient-

Dependent Outcome Measures within Surgical and Non-

Surgical Interventions Proprioception: IntechOpen.

Kim, W., Araujo, D., Kohles, S. S., Kim, S.-G., & Alvarez

Sanchez, H. H. (2020). Affordance-Based Surgical

Design Methods Considering Biomechanical Artifacts.

Ecological Psychology, 1-15. doi:10.1080/10407413.

2020.1792782

Kim, W., Kim, Y.-H., Veloso, A. P., & Kohles, S. S. (2013).

Tracking knee joint functional axes through Tikhonov

filtering and Plűcker coordinates. Journal of Novel

Physiotherapies(1).

Kim, W., Tretheway, D. C., & Kohles, S. S. (2009). An

inverse method for predicting tissue-level mechanics

from cellular mechanical input. Journal of

Biomechanics, 42(3), 395-399.

Kim, W., & Vela, E. A. (2021). A Tensional Network in the

Knee. Biomedical Journal of Scientific & Technical

Research, 40(2), 32073-32078.

Kim, W., Veloso, A., Araújo, D., Machado, M., Vleck, V.,

Aguiar, L., .Vieira, F. (2013). Haptic perception-action

coupling manifold of effective golf swing.

International Journal of Golf Science, 2(1), 10-32.

Kim, W., Veloso, A. P., Araújo, D., Vleck, V., & João, F.

(2013). An informational framework to predict reaction

of constraints using a reciprocally connected knee

model. Computer Methods in Biomechanics and

Biomedical Engineering, 1-12. doi:10.1080/10255842.

2013.779682

Kuipers, J. B. (1999). Quaternions and Rotation Sequences.

Princeton: Princeton University Press.

Lapresa, M., Tamantini, C., di Luzio, F. S., Ferlazzo, M.,

Sorrenti, G., Corpina, F., & Zollo, L. (2022). Validation

of Magneto-Inertial Measurement Units for Upper-

Limb Motion Analysis Through an Anthropomorphic

Robot. IEEE Sensors Journal, 22(17), 16920-16928.

Schumacher, A. (2006). Integration of a gps aided

strapdown inertial navigation system for land vehicles.

Master of Science Thesis, KTH Electrical Engineering.

Teu, K. K., Kim, W., Fuss, F. K., & Tan, J. (2006). The

analysis of golf swing as a kinematic chain using dual

Euler angle algorithm. Journal of Biomechanics, 39(7),

1227-1238.

Tincknell, M. (2023). Quaternion. MATLAB Central File

Exchange. Retrieved from https://www.mathworks.

com/matlabcentral/fileexchange/33341-quaternion

Trujullo, D. M., & Busby, H. R. (1997). Practical Inverse

Anlaysis in Engineering. Boca Raton: CRC Press.

icSPORTS 2023 - 11th International Conference on Sport Sciences Research and Technology Support

100