A Flexible Approach for Retrieving Geometrically Similar Finite

Element Models Using Point Cloud Autoencoders

Sonja Schlenz

1,2 a

, Simon M

oßner

, Carl Henrik Ek

3 b

and Fabian Duddeck

2 c

BMW Group, Knorrstr. 147, Munich, Germany

School of Engineering and Design, Technical University of Munich, Arcisstr. 21, Munich, Germany

Department of Computer Science and Technology, University of Cambridge, 15 JJ Thomson Avenue, Cambridge, U.K.

Keywords:

Shape Retrieval, Autoencoder, Similarity Search.

Abstract:

For the development of complex products like vehicle components, knowledge about previous solutions is a

key factor. Complete solutions or parts thereof can often be reused if a similar previous model can be identiﬁed.

To gain independence from the individual experience of single engineers about previous models and a tedious

search process, identifying and retrieving the most similar models from large databases offers great potential.

Accordingly, this paper introduces a method to achieve this kind of shape retrieval based on engineering data.

3D geometries are represented as point clouds and reduced to one single vector with an autoencoder to identify

similarities in the latent space. The method can be used in a ﬂexible way to identify global or local similarities

as well as to emphasize different parts of the structure in the similarity search. The method is evaluated on an

industrial dataset containing real-world engineering data.

1 INTRODUCTION

New car models are most often not developed from

scratch, but build upon previously established basic

concepts and knowledge. Multiple car models are

commonly based on one shared platform in order to

save cost, increase ﬂexibility and manage complex-

ity (Muffatto, 1999). The car models originating from

the same platform often share principal parts of the

design, like the body in white, while individualising

other segments. Additionally, different product fami-

lies can exist, where similar car body styles like SUVs

are clustered and share similarities. Because of this,

car models from the same company are usually not

inherently different as there are relations to at least

some other models.

In addition to these general similarities between

different car models, knowledge is also transferred

between unrelated models. During the structural de-

sign process, ﬁnite element (FE) models are simu-

lated to predict performance values without conduct-

ing many expensive hardware tests. When a model

does not satisfy required target values, changes have

https://orcid.org/0009-0000-9485-2340

https://orcid.org/0000-0003-1302-6309

https://orcid.org/0000-0001-8077-5014

to be made to the geometry to improve the results.

Classical optimization approaches are often not feasi-

ble in such complex models with multiple objectives,

so that engineers have to take the decisions on how

to change the model. The solutions highly depend on

the individual skills and experience of the responsible

engineer. Therefore, knowledge is an important factor

in the automotive industry, for general car concepts as

well as for the detailed design.

To facilitate and objectify the structural design

process, it would be beneﬁcial to have the possibil-

ity to search a large database with all models of a

company for similar models compared to a model cur-

rently under development. Since similarities to previ-

ous models often exist, it is likely that solutions could

be transferred from past processes. Having informa-

tion about similar models from the complete database

would enable the engineer to consider solutions from

many models, in contrast to only using limited per-

sonal knowledge about similar models. Since mod-

els frequently share some common features, while the

complete models are more different, the consideration

of local similarities could also be of interest to obtain

the most relevant results. To maximize the beneﬁt for

an engineer, the possibility to ﬂexibly choose the de-

sired local area for the similarity search would be ad-

vantageous.

188

Schlenz, S., Mößner, S., Ek, C. and Duddeck, F.

A Flexible Approach for Retrieving Geometrically Similar Finite Element Models Using Point Cloud Autoencoders.

DOI: 10.5220/0012158700003598

In Proceedings of the 15th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2023) - Volume 1: KDIR, pages 188-195

ISBN: 978-989-758-671-2; ISSN: 2184-3228

In this paper, we propose a method to retrieve the

most similar ﬁnite element models from a database to

an arbitrary input model. The models are represented

as point clouds, whose dimensionality is reduced with

an autoencoder. The obtained latent vectors are then

used for the assessment of similarity and the subse-

quent retrieval of the models. Depending on the sam-

pling strategy of the point clouds, global and local

similarities can be retrieved as well as putting empha-

sis on different aspects of the geometry. We show that

meaningful models can be retrieved with our method,

that can then be used by engineers for the transfer of

previous solutions in similar situations.

2 STATE OF THE ART

Geometric engineering data can be available in dif-

ferent data formats. Computer Aided Design (CAD)

models e.g. consist of Boundary Representation (B-

Rep) objects, Constructive Solid Geometry (CSG) or

combinations thereof (Xu et al., 2021), while ﬁnite

element (FE) models used for simulations are meshed

models deﬁned by a number of nodes and elements.

Other possible formats of geometric engineering data

include e.g. surface meshes for additive manufac-

turing or mathematically deﬁned curves like Non-

Uniform Rational B-Splines (NURBS) for exchange

formats (Starly et al., 2005).

Data formats like these are naturally unstructured

and cannot directly be used for comparison. There-

fore, a representation of the data is a necessary ﬁrst

step for the retrieval of models with similar geomet-

ric characteristics. In this section, we ﬁrst introduce

different possibilities for 3D data representations in

Section 2.1, before we present previous approaches

of shape retrieval in the engineering domain in Sec-

tion 2.2.

2.1 3D Data Representation

A multitude of approaches exist to transform unstruc-

tured 3D data into usable representations. A common

approach is to convert the data into a format for which

established algorithms can be applied. Similar to 2D

images consisting of pixels, 3D data can be approxi-

mated by a volumetric grid consisting of voxels (Mat-

urana and Scherer, 2015). Another common option to

allow the use of algorithms proven in 2D is the pro-

jection of the 3D data to a 2D space by taking images

from deﬁned viewpoints (Su et al., 2015). The use of

hand-crafted features or basic shape descriptors usu-

ally leads to a high explainability, but previous knowl-

edge about the data is required to chose adequate de-

scriptors (Bustos et al., 2005).

In recent years, great progress has been made on

learning directly on non-euclidean data. PointNet (Qi

et al., 2017) is a well known architecture taking point

clouds as input without further preprocessing. This is

advantageous compared to other approaches because

of its efﬁciency and compact representation, while

having the ability to describe geometric details. Simi-

larly, systems learning directly on meshes were intro-

duced, transforming convolutional algorithms to the

mesh domain (Hanocka et al., 2019). Other recent ap-

proaches are based on graph representations (Shi and

Rajkumar, 2020).

A more speciﬁc option to reduce data to one de-

scriptive vector are autoencoders. As neural net-

works, these use an encoder to reduce the dimension-

ality of the input data to one latent vector and a de-

coder to retrieve an output resembling the input. They

are trained by minimizing the difference between in-

put and output. In recent years, approaches using au-

toencoders directly on point clouds led to promising

results (Achlioptas et al., 2018; Yang et al., 2018).

2.2 Engineering Shape Retrieval

Approaches

Shape retrieval has been a longstanding problem in

the engineering domain and has inspired a multitude

of approaches. Many of these are based on shape de-

scriptors that represent the geometry in a simpliﬁed

way. Examples are the use of shape distribution his-

tograms (Li et al., 2011; Hong et al., 2006), Opitz

Coding (Zehtaban and Roller, 2013), attribute adja-

cency graphs and surface line distribution (Ma et al.,

2019) or distance distribution histograms (Zhuang

et al., 2017). Other similar approaches not only aim

at the retrieval of parts with global similarity, but of-

fer the possibility for partial retrieval by partitioning

models into segments (Tao et al., 2013; Ji et al., 2023;

Bai et al., 2010). However, the segmentation in these

approaches is ﬁxed for each model, leading to an in-

ﬂexible process without taking into account the en-

gineer’s speciﬁc needs. Approaches based on shape

descriptors as described above are often geared to-

wards a speciﬁc dataset or use case and their general-

ization to other datasets is not proven (Bustos et al.,

2005). Additionally, most previous approaches are

based on the retrieval of CAD models. They are lim-

ited to CAD formats and not applicable to similarity

searches for data formats like ﬁnite elements.

An approach that does not suffer from these re-

strictions was introduced by (Krahe et al., 2022). In

this approach, an autoencoder is used together with

point cloud representations to describe CAD mod-

A Flexible Approach for Retrieving Geometrically Similar Finite Element Models Using Point Cloud Autoencoders

189

els for similarity search. Bickel et al. also use an

autoencoder in their approach, but combine it with

a projection of vertices of meshed models onto a

sphere to obtain a matrix representation (Bickel et al.,

2023). Another approach using autoencoders is based

on multi-view projections of 3D shapes to 2D im-

ages (Zhu et al., 2016). All of these approaches focus

only on global similarity. Furthermore, the methods

were evaluated based on datasets consisting of differ-

ent classes, considering if retrieved parts belong to

the same class as the input model. There, the goal

is to identify models for potential reuse (Krahe et al.,

2022). While this is sufﬁcient based on the speciﬁc

use case, the focus of our proposed approach is the

discovery of similarities between different variants of

the same class to enable knowledge transfer on a more

detailed level.

Our goal of a shape retrieval method that is not

dependent on speciﬁc data formats like CAD models,

that generalizes well to diverse shapes and that can be

used for global or local shape retrieval in a ﬂexible

way has yet to be fully addressed.

3 METHODOLOGY

For our proposed shape retrieval method, the geome-

try is ﬁrst represented as point clouds. These are then

used as an input for an autoencoder, that reduces the

dimensionality of the representation to one latent vec-

tor. Based on these vectors, the similarity search and

retrieval is performed. We introduce our database in

Section 3.1, the processing of the geometry to obtain

relevant point clouds in Section 3.2 and the architec-

ture of the point cloud autoencoder in Section 3.3.

Finally, we explain our method of retrieving similar

geometries in Section 3.4.

3.1 Database

The data used in this work originates from the car

development process at BMW, consisting of meshed

models of car bonnets from previously performed FE

simulations. Figure 1 shows the parts considered for

an exemplary model.

3145 complete models based on 37 different car

projects were retrieved from our database. The focus

of our work is on the retrieval of similar parts from

the same class, where the inner sheet is used as ex-

emplary part. The inner sheet is a part present in

every car that is crucial for its stability and stiffness

as well as for crash functionality. Some exemplary

inner sheets from different car models are shown in

Figure 2. For evaluation purposes, the method is ad-

Figure 1: Explosion view of parts from an exemplary bon-

net.

ditionally applied to a dataset consisting of the ﬁve

different classes of parts shown in Figure 1.

3.2 Sampling of Points

The input format required by our autoencoder are

point clouds. Since our database consists of meshed

models, their nodes can directly be considered as

points. For other engineering data formats, methods

like ray tracing can be employed to obtain point cloud

representations. To make use of the autoencoder, a

consistent input size is needed. We chose an input size

of 1024 points for a balance of detailed representation

and efﬁciency and sample this number of points from

each of the original point clouds in different ways.

Depending on the desired kind of similarity, it is

possible to sample points from only the edges of a

part, from all of its points or a combination thereof.

When sampling only from the edges, more emphasis

is put on the outer contour of the parts, while consid-

ering all points leads to a higher importance of the 3D

structures. When representing complete inner sheets,

we randomly sample half of the points from the edges

of each part and half from the rest of the existing

points as a middle ground between the options. Fig-

ure 3 shows the obtained point cloud representation

of the parts from Figure 2.

In order to retrieve models with a locally high sim-

ilarity, points can be sampled from a smaller area of

each part. We propose to deﬁne a circle around the

area of interest with an arbitrarily chosen center and

radius, and sample points only inside this circle. To

account for the different sizes of the parts from differ-

ent car projects, the center of the circles is deﬁned rel-

atively considering the bounding box dimensions of

each part. If not stated otherwise, points are sampled

from all relevant nodes for this approach, since de-

pending on the chosen area no edges might be present.

Figure 4 shows the sampled sections for exemplary

parts, location and radius.

Important similarity information might not only

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

190

Figure 2: Exemplary inner sheets, rendered from meshes, viewed from top.

Figure 3: Exemplary sampled point clouds, viewed from top.

be present in individual parts, but also in the relative

location of a bonnet’s assembled parts towards each

other or the distances between them. To consider this

information in the similarity search, the complete as-

sembly can be used as a basis. A center and radius

are deﬁned as explained above, while instead of a cir-

cle, a sphere is deﬁned as a boundary. The points

are then sampled inside this sphere for all assemblies,

considering all sections of parts lying within the de-

ﬁned sphere. This is shown in Figure 5 for exemplary

models.

3.3 Point Cloud Autoencoder

As basis for the retrieval, the point cloud autoencoder

proposed by (Achlioptas et al., 2018) is chosen be-

cause of its competitive results for different tasks. The

input is a 3D geometry represented as point cloud

with a size of N points times three dimensions. The

autoencoder consists of ﬁve 1D convolutional layers

with a kernel size of one as an encoder, and three

fully-connected layers as a decoder. As loss func-

tion, the chamfer distance is chosen to account for

the permutation-invariance of point clouds. The input

point clouds are normalized. More information about

the point cloud autoencoder can be found in (Achliop-

tas et al., 2018). Figure 6 shows the principal archi-

tecture of the point cloud autoencoder.

3.4 Retrieval Process

After the training of the autoencoder with the sam-

pled point clouds is completed, the most similar mod-

els to an arbitrary input point cloud can be retrieved.

A point cloud with the appropriate number of points

is sampled from the test model and encoded with the

trained autoencoder to obtain a latent representation.

The cosine distance is calculated between this repre-

sentation and all other latent representations from the

dataset, as shown in Equation 1 for exemplary vectors

a and b. The n most similar models, having the low-

est cosine distance, are retrieved and returned to the

engineer for further use.

cos

(a, b) = 1 −

a · b

||a||

||b||

(1)

4 RETRIEVAL RESULTS

The main focus of our work lies on the retrieval of

similar models from the same class, which we present

in Section 4.2. For evaluation purposes and compar-

ison with previous methods, we additionally consider

a multi-class setting in Section 4.1. In both cases, we

sample 1024 points from each part in different ways

and train the autoencoder for 50 epochs. For the size

of the latent vector, we use 128 dimensions.

A Flexible Approach for Retrieving Geometrically Similar Finite Element Models Using Point Cloud Autoencoders

191

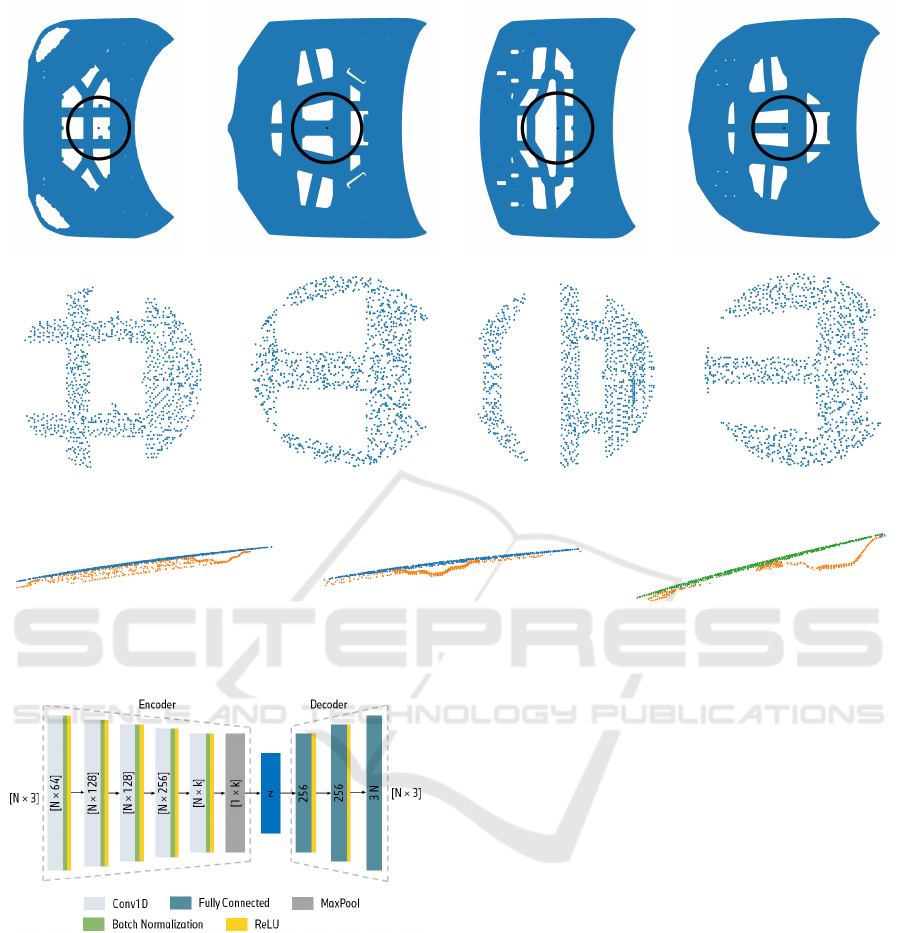
Figure 4: Exemplary sampled circle sections from the center with radius = 250 mm, viewed from top.

Figure 5: Exemplary sampled sphere sections from the center with radius = 250 mm, viewed from the side. Different colors

indicate different parts.

Figure 6: Autoencoder architecture where N is the number

of points, z is the latent vector and k is the size of the latent

vector. Visualization adapted from (Saha et al., 2021).

4.1 Retrieval of Similar Parts from

Different Classes

For the multi-class setting, we train our autoencoder

with the dataset consisting of parts from the ﬁve dif-

ferent classes shown in Figure 1. Since we only use

unique part models and different parts are modiﬁed

more or less frequently during a vehicle development

process, different numbers of parts are obtained per

class. Our multi-class dataset consists of 2595 inner

sheets, 433 outer skins, 790 front reinforcments, 406

hinge reinforcments and 177 lock reinforcements.

We sample points from both edges and surfaces

proportionate to the total numbers of points. Anal-

ogously to (Bickel et al., 2023), we use the com-

plete dataset for training and evaluate the performance

based on multiple metrics. Retrievals are considered

to be correct, if they originate from the same class as

the input model. The following metrics are used:

Nearest Neighbour (NN):

Precision of the most similar retrieval result.

First Tier (FT):

Recall results of the best n − 1 results, where n is

the number of models in the relevant class.

Second Tier (ST):

Recall results of the best 2 · (n − 1) results, where

n is the number of models in the relevant class.

The relevant values are retrieved for every model in

the dataset and the average resulting values reported

in Table 1, divided into individual classes.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

192

(a) Distance 0.0076. (b) Distance 0.021. (c) Distance 0.21.

Figure 7: Global similarity of different models (orange) to the test model (blue) viewed from top. Most similar model in (a),

intermediate similarity in (b), least similar model in (c).

Table 1: Shape retrieval results for the multi-class setting.

Best: 1.0, worst: 0.0.

NN FT ST

Outer skin 0.991 0.289 0.446

Inner sheet 0.999 0.863 1.0

Reinforcement front 1.0 0.929 0.996

Reinforcement hinge 1.0 0.873 0.957

Reinforcement lock 1.0 0.926 0.994

Complete 0.999 0.822 0.941

4.2 Retrieval of Similar Parts from a

Single Class

Since the use case of interest is the retrieval of simi-

lar parts to a newly developed model, one individual

inner sheet model is deﬁned as test model and only

parts from different car projects are used for training.

This process is performed for multiple exemplary test

models.

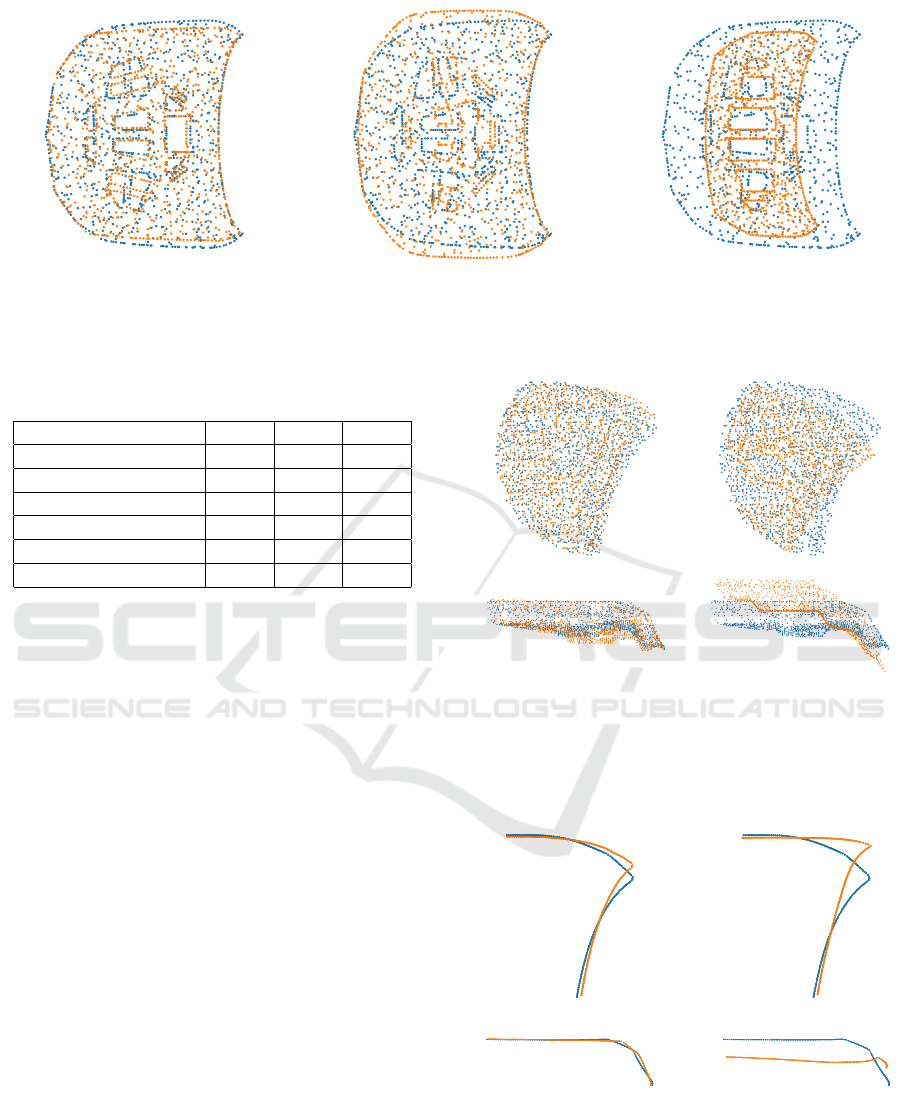
First, we consider the global similarity of individ-

ual parts, where points are sampled from complete in-

ner sheet models. Figure 7 shows one exemplary test

model together with different models and their indi-

cated similarity values. Figure 7a shows the most sim-

ilar model from the dataset, Figure 7c the least similar

one.

Next, location and radius are deﬁned and points

sampled within the circle to investigate local similar-

ities. The autoencoder is trained with only the points

from the local sections. Analogously to the global

similarity, we use one part as test model and remove

the rest of the parts originating from the same car

project. The most and least similar models for an ex-

emplary input model are shown in Figure 8 for the

corner of the parts.

Depending on the kind of similarity that is re-

quired, different sampling strategies can lead to dif-

(a) Distance 0.0044. (b) Distance 0.29.

Figure 8: Similarity of most and least similar models (or-

ange) to the test model (blue) for a section in the corner,

sampled from all points. Upper row is the view from top,

lower row the view from front. Radius = 250 mm.

(a) Distance 0.0011. (b) Distance 0.37.

Figure 9: Similarity of most and least similar models (or-

ange) to the test model (blue) for a section in the corner,

sampled only from the edges. Upper row is the view from

top, lower row the view from front. Radius = 250 mm.

A Flexible Approach for Retrieving Geometrically Similar Finite Element Models Using Point Cloud Autoencoders

193

(a) Distance 0.00043. (b) Distance 0.17.

Figure 10: Similarity of most and least similar models (or-

ange) to the test model (blue) for a sphere section in the

center of an assembly. View from side. Radius = 250 mm.

ferent similarity values. In the next example, we sam-

ple points from only the contour of the parts from the

corner section to obtain the input point clouds. With

this, different models are retrieved and shown in Fig-

ure 9.

In our ﬁnal example complete assemblies are con-

sidered. Points are sampled within a sphere boundary

around a point on the outer skin at the center of the

bonnet. Retrieval results are shown in Figure 10.

The number of models used for training varies,

since only unique models are considered. Models can

have differences in some parts outside the section of

interest, leading to a lower number of models for local

similarities compared to global similarity.

5 DISCUSSION

The main advantage of our proposed approach lies in

its ﬂexibility. Point clouds can be obtained from all

common engineering representations of 3D geometry,

while the similarity search can be guided by the sam-

pling strategy of the input points. For the local sim-

ilarity, the section can be chosen completely ﬂexible,

in contrast to previous approaches. While we only

considered sections in the shape of a circle or sphere,

it is generally possible to use any shape for obtaining

sections. By adjusting the sampling ratio between the

edges and the complete part, engineers can guide the

results into the desired direction to obtain the most

relevant results.

The presented results show that our proposed

method leads to promising results, as models with a

high visual similarity to the input model are identiﬁed.

An objective evaluation is however difﬁcult, since

no ground truth about desired levels of similarity is

available. To prove the validity of the proposed ap-

proach, we additionally used our method with a multi-

class dataset, as quantitative evaluation approaches

are available for this problem formulation.

The multi-class setting is evaluated according to

common metrics from literature. While high values

are reached for the complete dataset, big differences

are noticeable for the individual classes. The values of

the outer skin are signiﬁcantly behind the rest of the

data for the ﬁrst and second tier metric. A possible

reason is the generally high similarity between outer

skins and inner sheets. In the same car model, the

outer contour of these two parts is predominantly the

same, since they are assembled on top of each other. It

is likely that similarities are higher between an outer

skin and an inner sheet from the same model than two

outer skins from more different car models. These

results indicate that these geometries were encoded

and retrieved according to their geometric similarity,

which is suitable for our use case that focuses more

on geometric similarity and less on speciﬁc classes.

This emphasizes our different focus compared

to the related approaches introduced in Section 2.2.

While the state of the art primarily focuses on the re-

trieval of parts from the correct class in a multi-class

setting, our goal is the identiﬁcation of the highest

similarity within one class. In this setting, local sim-

ilarities are of particular interest for applications and

can be obtained in a ﬂexible way, opposed to previous

approaches that focus on global similarity or ﬁxed lo-

cal segments.

6 CONCLUSION

In this paper, we presented a method for similarity

search and retrieval of 3D engineering data. We used

a point cloud autoencoder for representation of ge-

ometry and assessed similarity values in its latent

space. The results we show originate from real in-

dustrial engineering data, showing the method’s rele-

vance for real-world application. The key novelty of

this paper lies in the ﬂexibility of our method to guide

the retrieval process towards desired kinds of similar-

ity. Compared to previous approaches that focus on

global retrieval or partial retrieval of ﬁxed segments,

local similarity can be retrieved for any section with

our method. A further novelty is the retrieval of sim-

ilar models for arbitrary sections from complete as-

semblies.

We achieved promising results for a variety of

sampling strategies, whose relevance was conﬁrmed

by engineers. While the most similar models are un-

ambiguous for many examples, there are other mod-

els where engineers can disagree on the most relevant

results. Future research activities should therefore in-

clude a study about perceived similarity of the models

by multiple engineers to enable a more quantitative

evaluation. Additionally, a meaningful description of

similarity opens up possibilities for more advanced

future applications. This could e.g. include automatic

quality checks or consideration of simulation results

to retrieve relevant models even more precisely.

KDIR 2023 - 15th International Conference on Knowledge Discovery and Information Retrieval

194

ACKNOWLEDGEMENTS

The contribution of this paper was written as part

of the joint project newAIDE under the consortium

leadership of BMW AG with the partners Altair En-

gineering GmbH, divis intelligent solutions GmbH,

MSC Software GmbH, Technical University of Mu-

nich, TWT GmbH. The project is supported by the

Federal Ministry of Economics and Energy (BMWi)

on the basis of a decision of the German Bundestag.

REFERENCES

Achlioptas, P., Diamanti, O., Mitliagkas, I., and Guibas, L.

(2018). Learning representations and generative mod-

els for 3d point clouds. In Dy, Krause (Hg.) 2018 –

Proceedings of the 35th International Conference on

Machine Learning, volume 80, pages 40–49.

Bai, J., Gao, S., Tang, W., Liu, Y., and Guo, S. (2010).

Design reuse oriented partial retrieval of cad models.

Computer-Aided Design, 42(12):1069–1084.

Bickel, S., Schleich, B., and Wartzack, S. (2023). A novel

shape retrieval method for 3d mechanical components

based on object projection, pre-trained deep learning

models and autoencoder. Computer-Aided Design,

154:103417.

Bustos, B., Keim, D. A., Saupe, D., Schreck, T., and Vrani

D. V. (2005). Feature-based similarity search in 3d ob-

ject databases. ACM Computing Surveys, 37(4):345–

387.

Hanocka, R., Hertz, A., Fish, N., Giryes, R., Fleishman, S.,

and Cohen-Or, D. (2019). Meshcnn: A network with

an edge. ACM Transactions on Graphics, 38(4):1–12.

Hong, T., Lee, K., and Kim, S. (2006). Similarity com-

parison of mechanical parts to reuse existing designs.

Computer-Aided Design, 38(9):973–984.

Ji, B., Zhang, J., Li, Y., and Pang, J. (2023). Free-form cad

model retrieval approach for engineering reuse based

on local feature segmentation. Computers & Graph-

ics, 111:111–121.

Krahe, C., Marinov, M., Schmutz, T., Hermann, Y., Bonny,

M., May, M., and Lanza, G. (2022). Ai based geo-

metric similarity search supporting component reuse

in engineering design. Procedia CIRP, 109:275–280.

Li, M., Zhang, Y. F., Fuh, J., and Qiu, Z. M. (2011). De-

sign reusability assessment for effective cad model re-

trieval and reuse. International Journal of Computer

Applications in Technology, 40(1/2):3.

Ma, W., Wang, P., Cai, D., and Wang, D. (102019). Re-

search on 3d cad model retrieval algorithm based on

global and local similarity. In 2019 IEEE Interna-

tional Conferences on Ubiquitous Computing & Com-

munications (IUCC) and Data Science and Computa-

tional Intelligence (DSCI) and Smart Computing, Net-

working and Services (SmartCNS), pages 349–355.

IEEE.

Maturana, D. and Scherer, S. (9/28/2015 - 10/2/2015).

Voxnet: A 3d convolutional neural network for real-

time object recognition. In 2015 IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS), pages 922–928. IEEE.

Muffatto, M. (1999). Introducing a platform strategy in

product development. International Journal of Pro-

duction Economics, 60-61:145–153.

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Pointnet:

Deep learning on point sets for 3d classiﬁcation and

segmentation. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition (CVPR).

Saha, S., Rios, T., Minku, L., van Stein, B., Wollstadt,

P., Yao, X., B

ack, T., Sendhoff, B., and Menzel, S.

(2021). Exploiting generative models for performance

predictions of 3d car designs. In IEEE Symposium Se-

ries on Computational Intelligence (IEEE SSCI 2021).

IEEE.

Shi, W. and Rajkumar, R. (2020). Point-gnn: Graph neural

network for 3d object detection in a point cloud. In

The IEEE Conference on Computer Vision and Pattern

Recognition (CVPR).

Starly, B., Lau, A., Sun, W., Lau, W., and Bradbury, T.

(2005). Direct slicing of step based nurbs models

for layered manufacturing. Computer-Aided Design,

37(4):387–397.

Su, H., Maji, S., Kalogerakis, E., and Learned-Miller, E.

(12/7/2015 - 12/13/2015). Multi-view convolutional

neural networks for 3d shape recognition. In 2015

IEEE International Conference on Computer Vision

(ICCV), pages 945–953. IEEE.

Tao, S., Huang, Z., Ma, L., Guo, S., Wang, S., and Xie,

Y. (2013). Partial retrieval of cad models based on

local surface region decomposition. Computer-Aided

Design, 45(11):1239–1252.

Xu, X., Peng, W., Cheng, C.-Y., Willis, K. D., and Ritchie,

D. (62021). Inferring cad modeling sequences using

zone graphs. In 2021 IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition (CVPR), pages

6058–6066. IEEE.

Yang, Y., Feng, C., Shen, Y., and Tian, D. (2018). Fold-

ingnet: Point cloud auto-encoder via deep grid defor-

mation. In 2018 IEEE/CVF Conference on Computer

Vision and Pattern Recognition (CVPR 2018), pages

206–215, Piscataway, NJ. IEEE.

Zehtaban, L. and Roller, D. (2013). Beyond similarity

comparison: Intelligent data retrieval for cad/cam

designs. Computer-Aided Design and Applications,

10(5):789–802.

Zhu, Z., Wang, X., Bai, S., Yao, C., and Bai, X. (2016).

Deep learning representation using autoencoder for 3d

shape retrieval. Neurocomputing, 204:41–50.

Zhuang, T., Zhang, X., Hou, Z., Zuo, W., and Liu, Y. (2017).

A novel 3d cad model retrieval method based on ver-

tices classiﬁcation and weights combination optimiza-

tion. Mathematical Problems in Engineering, 2017:1–

12.

A Flexible Approach for Retrieving Geometrically Similar Finite Element Models Using Point Cloud Autoencoders

195