Fractional Order-Sliding-Mode Controller for Regulation of a Nonlinear

Chemical Process with Variable Delay

Antonio Di Teodoro

, Marco Herrera

and Oscar Camacho

Colegio de Ciencias e Ingenier

ıas ¨El Polit

ecnico”, Universidad San Francisco de Quito USFQ, Quito, Ecuador

Keywords:

Sliding Mode Control, Fractional Order Calculus, Reduced Order Model, Chemical Processes, Simulation.

Abstract:

The present work shows the application of a new controller based on combining the fractional order calculus

concepts with the sliding mode theory to a non-linear system with variable delay. The power of fractional-order

calculus is used to identify the real process and represent it as a reduced-order model. From this model, the

controller is developed using the sliding-mode control procedure. An SMC based on FOPDT and one based

on fractional calculus are compared using some performance indicators to assess performance quantitatively.

1 INTRODUCTION

The chemical and biochemical engineering ﬁeld has

a lot of control problems, one of which is the pri-

mary focus of current work: regulating variable time

delay processes. In real applications, plant behav-

ior is often affected by unexpected dynamics, out-

side disturbances, etc. (Obando et al., 2023). Dis-

turbances, model errors, unmodeled dynamics, ele-

vated time delay, and poorly deﬁned plant charac-

teristics reduce the efﬁcacy of conventional regula-

tion schemes even for linear time-invariant systems in

chemical processes, especially at the industrial scale.

When designing a process controller, the control

actions become slow if it has a time delay, decreas-

ing the total process performance. Furthermore, in

some cases, it has been seen that delays produce in-

stability in the system, as in (Prado et al., 2022), lead-

ing to the search for more advanced control proposals.

Thus, controlling dynamical systems with delay time

has become a major topic in control theory.

The variable structure control has a method called

the sliding mode control (SMC). SMC is a simple

and reliable method for creating controllers for linear

and non-linear processes, according to (Camacho and

Smith, 2000; Utkin et al., 2020). SMC is one of the

most widely used techniques for managing dynamical

systems because it is relatively insensitive to uncer-

tainties(Camacho and Smith, 2000; Esp

ın et al., 2022;

https://orcid.org/0000-0002-8766-0356

https://orcid.org/0000-0002-3124-2403

https://orcid.org/0000-0001-8827-5938

Utkin et al., 2020). The traditional sliding mode con-

trol always maintains a predesigned sliding variable

S(t), which is generated by a so-called reaching con-

dition, such as S(t)

S(t) < 0, to be zero under high-

frequency switching (Utkin et al., 2020).

Substantial research has been published on the ap-

plication of SMC in industrial engineering process

control; we can name some of them here(Esp

ın et al.,

2022; Xiao and Li, 2016; Dimassi et al., 2019; Ra-

sul and Pathak, 2016; Sardella et al., 2020; Siddiqui

et al., 2020; Herrera et al., 2020; Salinas et al., 2018;

Kadu et al., 2018). Although few studies on SMC de-

sign employ fractional order calculus techniques for

chemical processes, we can highlight some of them

(Di Teodoro et al., 2023; Di Teodoro et al., 2022;

Ullah and Mohammad, 2022; Allahem et al., 2022;

Mehri and Tabatabaei, 2021; Haghighi and Ziaratban,

2020; Ardjal et al., 2021).

The current work illustrates the application of a

novel controller based on fusing notions from sliding

mode theory and fractional order calculus to a non-

linear system with variable delay. First, the actual

process is represented as a reduced-order model us-

ing the strength of fractional-order calculus. Then,

the sliding-mode control approach is used to create

the controller from this model. Finally, some perfor-

mance measures were used to evaluate and compare

an SMC based on FOPDT and an SMC based on frac-

tional calculus.

The paper is divided as follows: in Section

two, some fundamentals are described; Section three

shows the methodology of design; in Section four, the

Di Teodoro, A., Herrera, M. and Camacho, O.

Fractional Order-Sliding-Mode Controller for Regulation of a Nonlinear Chemical Process with Variable Delay.

DOI: 10.5220/0012159400003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 131-139

ISBN: 978-989-758-670-5; ISSN: 2184-2809

131

results by simulations are presented; and ﬁnally, the

conclusion.

2 BACKGROUND

2.1 Sliding Mode Control

The SMC is a variable structure controller created uti-

lizing nonlinear control techniques. It is a robust con-

trol that reacts appropriately to nonlinear systems un-

der unknown conditions. Furthermore, it is immune

to changes in modeling parameters. The SMC consid-

ers a sliding surface that allows the controlled variable

to transition from an initial state to the desired ﬁnal

state. For this reason, its control law includes a con-

tinuous component to move on the sliding surface and

a discontinuous part for the reachability phase. The

motion of the system on a sliding surface is known as

the sliding mode (Utkin et al., 2020).

The SMC control law U(t), as expressed in (1):

U(t) = U

(t) +U

(t) (1)

(t): It is obtained from the equivalent control

method (Utkin et al., 2020). Keep the controlled vari-

able on the sliding surface σ(t) = 0. The equivalent

control is deduced, considering that the derivative of

the surface is zero.

The sliding condition is given by:

dσ(t)

= 0 (2)

Combined with the previous equation and the

model of the process system, U

(t) is obtained.

(t): It is the discontinuous control part; it al-

lows the system to reach the sliding surface. It incor-

porates a nonlinear element that includes the switch-

ing element of the control law; therefore, U

(t) con-

tains the switching element and is given by:

(t) = K

sign(σ(t)) (3)

is a tuning parameter responsible for the reach-

ing mode.

SMC transitions on the sliding surface cause chat-

tering. Chattering excites system dynamics not mod-

eled, causes vibration of the actuator with wear, and

degrades performance. One way to reduce such im-

pacts is to smooth the non-linear switching function

using soft functions such as the sigmoid function (Ca-

macho and Smith, 2000). Therefore, the discontinu-

ous controller utilizes the sigmoid function:

(t) = K

σ(t)

|σ(t)| + δ

(4)

The convergence condition, often known as at-

tractiveness, ensures that the system dynamics will

always converge on the sliding surface(Utkin et al.,

2020). It is necessary to formulate a Lyapunov func-

tion V (t) > 0 with ﬁnite energy. The candidate Lya-

punov function is deﬁned as follows.

V (t) = 1/2σ

(t) (5)

It is sufﬁcient to make sure that the derivative of

the function V (t) is negative for it to be possible for

the function V (t) to be reduced. Therefore, the condi-

tion of convergence can be written as follows:

dV (t)

dσ(t)

σ(t) < 0 (6)

It states that if the projection of the system trajec-

tories on the sliding surface is stable, then the system

is stable (Li et al., 2010).

2.2 Briefs About Fractional Calculus

2.2.1 Deﬁnitions of Caputo and

Riemann-Liouville Derivative and Their

Connection

Deﬁnition 1. The Riemann − Liouville fractional in-

tegral of order α > 0 is given by (see (Kilbas et al.,

2006; Miller and Ross, 1993; Podlubny, 1994; Kilbas

et al., 1993))





(x) =

Γ(α)

h(t)

(x −t)

1−α

dt, x > a. (7)

We denote by I

) the class of functions h, rep-

resented by the fractional integral (7) of a summable

function, that is, h = I

ϕ, where ϕ ∈ L

(a,b). A de-

scription of this class of functions is given in (Kilbas

et al., 2006; Kilbas et al., 1993; Abbas et al., 2023;

Patel et al., 2023) (L

[a,b] space can be deﬁned as a

space of measurable functions for which the absolute

value is Lebesgue-integrable).

Deﬁnition 2. Let





(x) denote the fractional

Riemann–Liouville derivative of order α > 0, where

h ∈ L

(a,b) (see (Kilbas et al., 2006; Miller and Ross,

1993; Podlubny, 1994; Kilbas et al., 1993; Abbas

et al., 2023))





(x) =





Γ(s−α)

h(t)

(x−t)

α−s+1

dt, (8)

s = [α] + 1,x > a, (9)

where [α] denotes the integer part of α and Γ is the

gamma function.

When 0 < α < 1, then (8) takes the form





(x) =



1−α



(x). (10)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

132

Example 1.

f (x − a)

(

0, γ = α − 1,

γ+1

γ−α+1

(x − a)

γ−α

, otherwise

With α ∈ (0,1), a > 0, k ∈ N and γ > −1, and an

appropriate f . (See (Ceballos et al., 2020; Ceballos

et al., 2022; Kilbas et al., 1993))

Deﬁnition 3. Let α ≥ 0 and m = [α]. Then, we can

deﬁne the operator

f := I

m−α





f ,

when





f ∈ L

[a,b].

Example 2.

(x − a)

= 0 if β ∈ {0,1,2,. . ., m −

1}.

Lemma 1. Let α ≥ 0 and m = [α] + 1. Suppose that

f is such that

and

exists. Then

f =

f −

m−1

∑

k=0

(x − a)

k−α

Γ(k − α + 1)





f (a).

See (Kilbas et al., 2006; Podlubny, 1994; Kilbas et al.,

1993))

consequently, we have the following lemma:

Lemma 2. Let α ≥ 0 and m = [α] + 1. Suppose that

f is such that

and

exists.

Then

f =

f = D

f . If and only if





f (a) = 0 for all k = 0,..., m − 1.

The semigroup property for the composition of frac-

tional derivatives does not hold in general (see (Pod-

lubny, 1994, Sect. 2.3.6)). In fact, the property:





= D

α+γ

h (11)

holds whenever

( j)

) = 0, j = 0,1,... ,s − 1, (12)

and h ∈ AC

s−1

([a,b]), h

(s)

∈ L

(a,b) and s = [γ] + 1

( AC

([a,b]) denotes the class of functions h, which

are continuously differentiable in the segment [a,b],

up to order s − 1 and h

(s−1)

is absolutely continuous

in [a,b]).

Remark 1. In this paper, we use D

to identify the

fractional operator because we assume that the initial

conditions are equal to zero.

2.2.2 Laplace Transform of Fractional

Derivatives

Deﬁnition 4. Let F(s) := (L f )(s), i.e., say, the

Laplace transform of the function f and α > 0

(See([(Kilbas et al., 1993)])).



L D



(s) = s

F(s) −

l−1

∑

j=0

( j)

α− j−1

where l = [α] + 1 and f

( j)

) =

f (t)|

t−→0

, j =

0,...,l −1. Clearly, if α ∈ (0,1) then



L D



(s) = s

F(s) − f (0

α−1

(13)

2.2.3 The Use of the Mittag-Lefﬂer for G(s)

In order to develop our model, we will make use of the

two-parameter Mittag-Lefﬂer function. This function

is deﬁned classically as

Deﬁnition 5. Let z ∈ C and α > 0. The two-

parameter Mittag-Lefﬂer function is given by

α,β

(z) =

+∞

∑

k=0

Γ(αk + β)

, ∀z ∈ C. (14)

Remark 2. Note that E

α,β

(z) > 0 for all z ∈ C

and

when β = 1, then E

α,β

(z) = E

(z) This function is uni-

formly convergent over C. For α, β ≥ 0 If n = 1 and

r = 1. E

1,1

(z) = E

(z) = exp(z). (see (Kilbas et al.,

2006; Podlubny, 1994; Kilbas et al., 1993))

3 CONTROL DESIGN APPROACH

IN THE CAPUTO SENSE

This section presents the mathematical development

of the sliding mode control based on a FOPID surface.

Since SMC is a model-based controller, let us use an

empirical model of the actual process. Using the reac-

tion curve procedure, the nonlinear process can be ap-

proximated for a ﬁrst-order plus dead time (FOPDT)

model (Smith and Corripio, 2005).

X(s)

U(s)

−t

τs + 1

. (15)

3.1 Time Delay Approximation

A ﬁrst problem encounter in the realization of this

fractional controller is the time delay part (Camacho

and Smith, 2000). In the complex settings, the natu-

ral exponential function e

can be represented as the

well–known Taylor series centered at 0 which is abso-

lutely convergent for z ∈ C. A simple linear approx-

imation is 1 + z where the absolute error

− 1 − z

equals the Taylor remainder R

. On the other hand,

we have that e

−z

thus we can approximate e

−z

1+z

. Indeed, to see this let the approximation

error,



−z

−

1+z



, be bounded by ε

max

> 0. Then,



−z

−

1+z



≤

|z|

|1+z|

max

1,e

−Re

{

}

= ε

max

For example, the time delay e

−t

can be approxi-

mated to

s+1

and, in turn, the FOPDT transfer func-

tion is as follows:

−t

τs + 1

≈

(τs + 1)(t

s + 1)

, (16)

Fractional Order-Sliding-Mode Controller for Regulation of a Nonlinear Chemical Process with Variable Delay

133

that has a second order differential equation form (Ca-

macho and Smith, 2000).

Remark 3. A discussion that seems interesting to us

about the role of the fractional parameter in the expo-

nential function is a future work. A further conjecture

is that we believe that the parameter β is not neces-

sary. Which makes the calculation of the Laplace in-

verse much simpler.

3.2 Fractional Transfer Functions

Let α, β ∈ R, r,n ≥ 0. Then, we deﬁne the fractional

transfer function plus dead time as

X(s)

U(s)



τ(s

) + 1





n,r

))



(17)

where α and β can be interpreted as orders of frac-

tional derivatives and integrals. Note that transfer

function (15) is obtained when α and β approach to

−

Transfer function (17) can be approximated by (see

sec. 3.1 above)

X(s)

U(s)



τ(s

) + 1





n,r

))



≈



τ(s

) + 1



Γ(n)Γ(n + r)

Γ(n + r) +



)



Γ(n)

. (18)

and can be changed to a fractional differential equa-

tion form. Using this approximation in equation (17)

we obtain

Γ(n) s

α+β



Γ(n + r)





Γ(n)



τt

Γ(n + r)

X(s)

τt

[K Γ(n) Γ(n + r)]U (s)

(19)

Using deﬁnition 4 whenever the function X satisﬁes

the conditions of lemma 2 , then



α+β



(t)+



Γ(n + r)

Γ(n)



X)(t)









(t)+



τt

Γ(n + r)

Γ(n)



X(t) =

τt

[K Γ(n + r)]U (t)

(20)

3.3 Fractional Sliding Surface

Let us deﬁne the fractional sliding surface according

to (18) and (20). In the following, we assume the con-

ditions of lemma 2.

Deﬁnition 6. Let α,β ∈ R, m = [α + β], e(t) ∈

m−1

([a,b]) and e

(m)

∈ L

(a,b). Then, the frac-

tional slinding surface, S

α,β

, is deﬁned as



α,β



(t)



α+β

+ λ







(t).

(21)

where λ

,λ

are selected such that S

α,β

= 0, giving

a closed-loop stable response.

Remark 4. In the classical sense (Camacho and

Smith, 2000), our operator converge to (22)

(S e)(t) =



+ λ



e(t)dt. (22)

when n = 2 as α,β approach to 1

−

. The binomial

theorem can be used to generalize n. This is a fasci-

nating topic for further research. Just emphasize that

fractional computation for outside-interval parame-

ters (0,1) is much more difﬁcult to calculate.

Remark 5. Note that the deﬁnitions 2 and 3 allow us

to commute the classical integral operator I

in the

fractional sliding surface operator in deﬁnition 6, i.e.,



α+β

+ λ





α+β

+ λ



. (23)

Classical derivation of operator 6 will be needed in

the following:



α,β



(t) =



α+β

+ λ



[e(t)] .

(24)

where we have used the result in remark 5 followed by

the application of the Fundamental Theorem of Cal-

culus.

The next theorem shows how we can construct the

fractional equivalent control law U

α,β

(t).

Theorem 1. Let α, β ∈ R, m = [α + β], e(t) ∈

m−1

([a,b]) and R

(m)

(t), X

(m)

(t) ∈ L

(a,b). Then,

the fractional control law u

α,β

(t) based in the frac-

tional sliding surface deﬁned in 6 is

α,β

(t) =

τt

K Γ(n + r)









α+β



(t)+ λ





(t)+





(t)+ λ

R(t)+



Γ(n + r)

Γ(n)

− λ







(t)+



− λ







(t)+



τt

Γ(n + r)

Γ(n)

− λ



X(t)







(25)

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

134

Let e(t) = R(t) − X(t). First, we apply operator

(24) to function e(t) to obtain



α,β



(t) =



α,β



(t) −



α,β



(t).

(26)

by the linearity of this fractional operator. Next,



α,β



(t) = 0 guides us, combining equation (20)



α+β



(t)+ λ





(t)+ λ





(t)+ λ

R(t)+



α+β



(t)+



Γ(n + r)

Γ(n)







(t)+









(t)+



τt

Γ(n + r)

Γ(n)



X(t) =



α+β



(t)+





(t)+ λ





(t)+ λ

X(t)+

τt

[K Γ(n + r)]U(t)

(27)

The result follows.

Remark 6. If R : R → R such that R = c, where c ∈

R. Then

R = 0, consequently, D

R(t) = 0 and D

(t) = 0.

The derivatives of the reference value can be ignored

(Camacho and Smith, 2000) without affecting the

control performance, which allows a simpler con-

troller.

Thus, the resulting equivalent controller law is given

as follows:

α,β

(t) =

τt

K Γ(n + r)







R(t)+



Γ(n + r)

Γ(n)

− λ







(t)+



− λ







(t)+



τt

Γ(n + r)

Γ(n)

− λ



X(t)







(28)

The previous equation can be simpliﬁed by letting,

Γ(n + r)

Γ(n)

= λ

(29)

and

= λ

(30)

The sliding (continuous) control law is:

α,β

(t) =

τt

K Γ(n+r)



e(t) +



τt

Γ(n+r)

Γ(n)



X(t)



(31)

The reaching (discontinuous) control law U

α,β

(t) is

deﬁned as follows:

α,β

(t) = K

(α,β)

α,β

(t)



α,β

(t)



+ δ

α,β

(32)

Where K

(α,β)

is the switching gain.

Once the continuous and discontinuous parts of the

SMC, based on the fractional reduced order, have

been obtained; the total fractional order SMC law can

be represented as follows:

α,β

(t) = u

α,β

(t) + K

(α,β)

α,β

(t)



α,β

(t)



+ δ

α,β

. (33)

Until now, to our knowledge, there are no tuning

equations for K

(α,β)

neither δ

α,β

; hence in this paper

they are tuned by trial and error.

3.4 Fractional Results Using r = α and

n = β = 1

M U

α,1

(t) =



α+1

+ λ



R(t)



Γ(α + 1)

− λ







(t)



− λ







(t) +



Γ(α + 1)

τt

− λ



X(t)

(34)

Where M =

τt

Γ(α + 1) and Γ(1) = 0! = 1

3.5 Stability Condition

The dynamics of the system will always converge on

the sliding surface according to the convergence con-

dition; to reach the sliding surface, it is necessary to

create a Lyapunov candidate function V (t) > 0 with

ﬁnite energy. We use the Mittag–Lefﬂer stability the-

orem to do this and get the corresponding systems’

asymptotic stability.

Theorem 2 (See Theorem 5.1 in (Li et al., 2010)). Let

x = 0 be an equilibrium point for the system

x(t) = f (x(t)), t ≥ t

where 0 < α ≤ 1 and I ⊂ R be a domain containing

the origin f ∈ C

(I). Let V (t, x(t)) : [0,∞) × I → R

be a continuously differentiable function and locally

Lipschitz with respect to x such that

i) A||x||

≤ V (t,x(t)) ≤ B||x||

ii) D

V (t, x(t)) ≤ −F||x||

where t ≥ 0, x ∈ I,α ∈ (0, 1), A,B, F,a, and b. are

arbitrary positive constants. Then x = 0 is Mit-

tag–Lefﬂer stable. If the assumptions hold globally

on R, then x = 0 is globally Mittag–Lefﬂer stable.

V (t, x(t)) = x(t)

(2)α−1

α,α

(−λx(t)

(2)α−1

). (35)

Fractional Order-Sliding-Mode Controller for Regulation of a Nonlinear Chemical Process with Variable Delay

135

Setpoint

Control

Valve

Agitator

Figure 1: Mixing Tank process.

Where α ∈ (0,1) , E

α,β

is the Mittag-Lefﬂer function

deﬁned in (14).

This function is locally Lipschitz any interval of R

and satisﬁes

(i 0 < V (t,x(t)) ≤ B||x||

for x ∈ I ⊂ R and any B ∈

R. See (Coloma et al., 2021; Ceballos et al., 2020;

Ceballos et al., 2022)

(ii D

V (t, x(t)) = −λV (t,x(t)) ≤ −F||x||

for any

F,a,b ∈ R, see (Kilbas et al., 2006).

in consequence x = 0 is Mittag–Lefﬂer stable, using

the Remark 4.4 in (Li et al., 2010) (Mittag–Lefﬂer sta-

bility and Generalized Mittag–Lefﬂer stability imply

asymptotic stability) we guarantee asymptotic stabil-

ity of our system.

4 RESULTS AND DISCUSSION

4.1 Mixing Tank Process

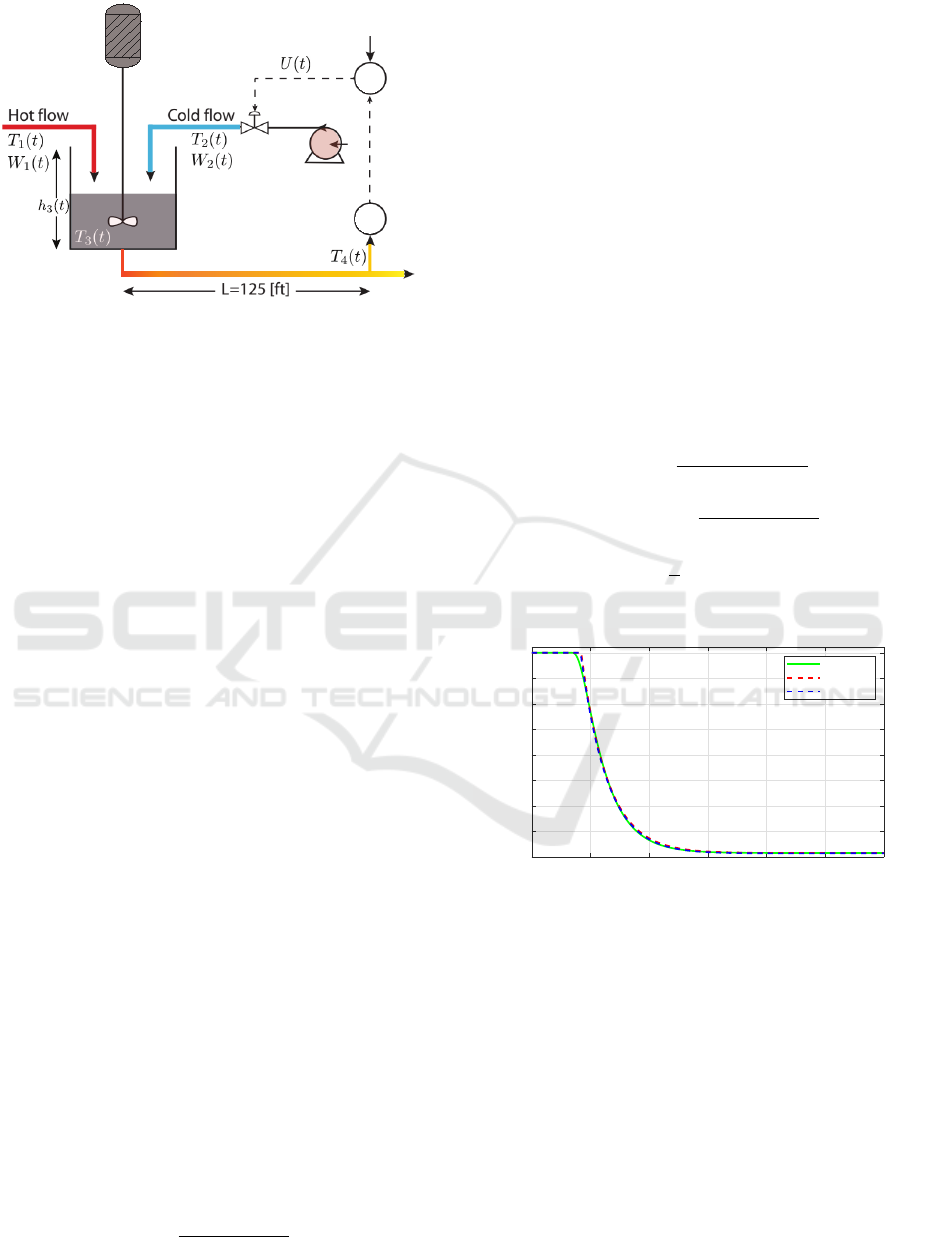
The mixing tank shown in Fig. 1 consists of the si-

multaneous entry of the hot W

(t) and cold ﬂow W

(t)

into the process with temperatures T

(t) and T

(t), re-

spectively. The output T

(t) is the temperature of the

mixture measured at a point 125 ft downstream of the

mixing tank. The Fail-Closed (FC) actuator regulates

the cold stream to maintain the desired temperature

within the mixing tank. The control objective con-

sists of maintaining the required mixing temperature

(t) despite disturbances in the hot ﬂow W

(t). The

following determines the time delay between the tank

and the sensor’s position.

(t) = T

(t −t

) (36)

with, transportation lag or delay time:

LAρ

(t) +W

(t)

(37)

where A is the cross section of the pipe, the length

of the pipe L and the density ρ of the contents of the

mixing tank. A complete description of the non-linear

model and parameters in a stationary state and the sys-

tem variables can be found in (Camacho and Smith,

2000).

4.2 Identiﬁcation and Validation of

FOPDT and FO-FOPDT Models

The reaction curve method is used to identify an ap-

proximate model of the non-linear mixing tank pro-

cess. Thus, 10% of the input of the process (m(t))

is made. Figure 2 shows the responses of the tank

mix process, the approximate FOPDT model (Smith

and Corripio, 2005) and the approximate fractional

FO-FOPDT model (Gude and Garc

ıa Bringas, 2022).

Equations (38) and (39) show the approximate mod-

els:

G(s)

FOPDT

−0.8207e

−4.206s

2.227s + 1

(38)

G(s)

FO−FOPDT

−0.8207e

4.142s

2.262s

1.01

+ 1

(39)

As can be seen in the Eqs. (38) and (39). The

controllability relation



> 1



, which makes it dif-

ﬁcult to control (Obando et al., 2023). Also, it can be

considered as a process with a long delay.

0 5 10 15 20 25 30

Time [min]

0.46

0.465

0.47

0.475

0.48

0.485

0.49

0.495

0.5

Transmitter units [pu]

Process

FOPDT

FO-FOPDT

Figure 2: Open Loop Output Responses for step process

input.

The mean square error (MSE) is used to vali-

date the models obtained. Where: MSE

FOPDT

1.4192x10

−7

and MSE

F0−FOPDT

= 9.3819x10

−8

. Al-

though both indices are low, the MSE of the fractional

model was the lowest.

To analyze the performance of the FO-SMC con-

troller, it is compared with a conventional SMC con-

troller presented in (Camacho and Smith, 2000). FO-

SMC controller parameters λ

, λ

and λ

are tuned

according to Section 3. SMC controller parameters

and the FO-FOPDT K

and δ parameters are tuned

according to (Camacho and Smith, 2000). These pa-

rameters are shown in Table 1.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

136

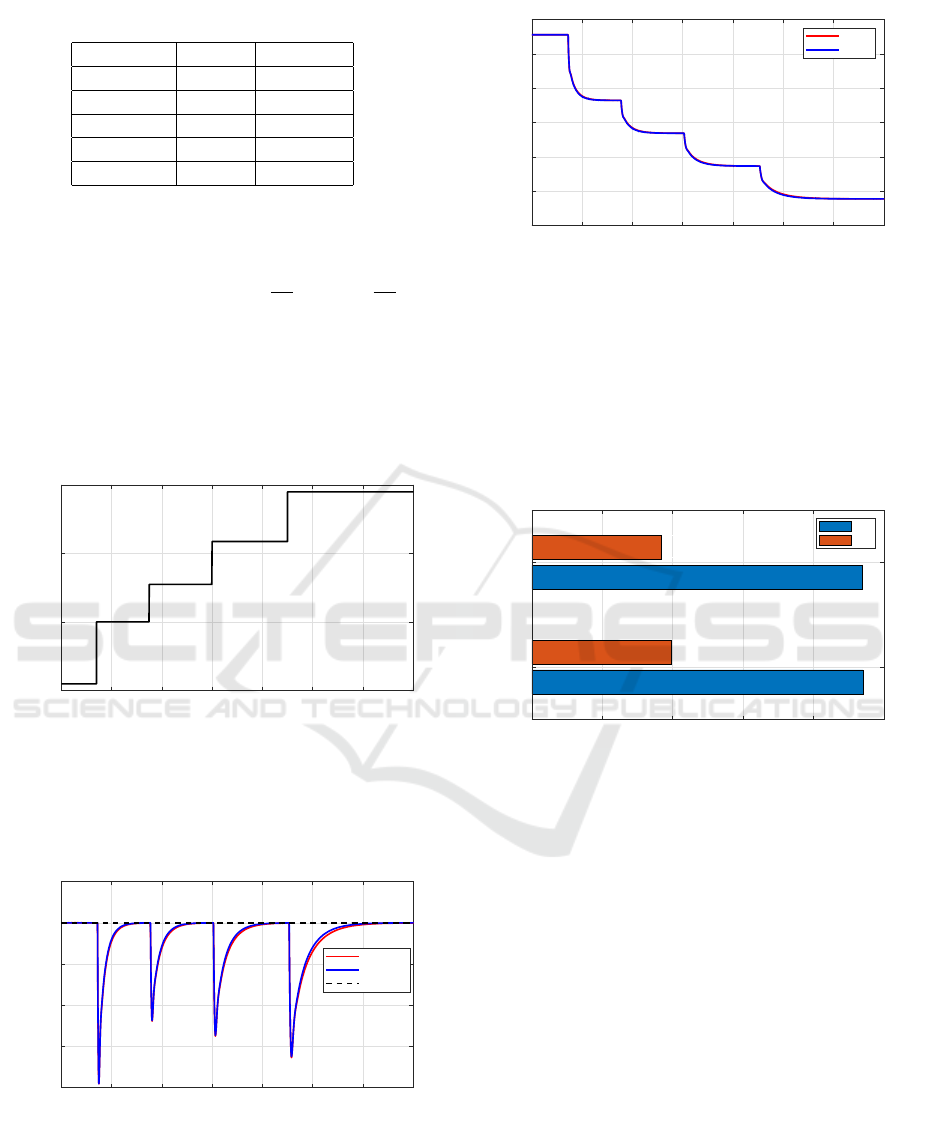
Table 1: Controller design parameters.

Parameter SMC FO-SMC

0.1179 0.1171

0.6867 0.2425

− 0.4419

0.3833 0.3925

δ 0.7059 0.6894

4.3 Disturbance Rejection Test

In this test, from the operating point T

(t) = 150[

F],

the variations in steps from 250



min



to 150



min



the hot ﬂow W

(t).

Due to the distance of the pipe L = 120[ f t], the

outlet temperature is measured downstream. Further-

more, due to the effect of the disturbance, the varia-

tion of W

(t) causes the time delay of the processes to

increase stepwise from 3.58 to 4.9[min], as shown in

Fig. 3.

0 200 400 600 800 1000 1200 1400

Time [min]

3.5

4.5

Time-Delay [min]

Figure 3: Dead Time variation.

Figure 4 shows the temperature responses for the

disturbance rejection test. It can be seen that for the

last two disturbances, the response of the FO-SMC

controller presents a slight improvement.

0 200 400 600 800 1000 1200 1400

Time [min]

142

144

146

148

150

152

Temperature [

SMC

FO-SMC

Reference

Figure 4: Temperature responses.

The control actions for both controllers have very

similar behavior, as shown in Fig. 5.

0 200 400 600 800 1000 1200 1400

Time [min]

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Controller output [pu]

SMC

F-SMC

Figure 5: Action Controllers.

4.4 Performance Indices Comparison

In Fig. 6 the comparison of the performance indices

of the SMC controller and the FO-SMC is shown. It

can be seen that the performance values obtained for

both controllers are very similar. However, the FO-

SMC controller presents slightly lower ISE and IAE

values.

0 5 10 15 20 25

SMC

FO-SMC

TVu

IAE

23.5

23.51

9.164

9.912

Figure 6: Comparative of performance indexes of the con-

trollers.

5 CONCLUSION

The paper applied a novel SMC based on a fractional-

order model to a variable time-delayed nonlinear pro-

cess. The results showed that the proposed approach

is promising, requiring more exploration of the tun-

ing equations and the effects of λ and β to reach the

sliding surface and reduce chattering.

ACKNOWLEDGEMENTS

The Universidad San Francisco de Quito (USFQ) sup-

ported this work through the Poli-Grants Program un-

der Grant 17965.

Fractional Order-Sliding-Mode Controller for Regulation of a Nonlinear Chemical Process with Variable Delay

137

REFERENCES

Abbas, S. et al. (2023). Fractional Differential Equations

and Inclusions. World Scientiﬁc.

Allahem, A., Karthikeyan, A., Varadharajan, M., and

Rajagopal, K. (2022). Computational model of a

fractional-order chemical reactor system and its con-

trol using adaptive sliding mode control. Fractals,

30(10):2240243–87.

Ardjal, A., Bettayeb, M., Mansouri, R., and Zouak, B.

(2021). Design and implementation of a model-free

fractional order intelligent pi fractional order sliding

mode controller for water level tank system. ISA

transactions.

Camacho, O. and Smith, C. A. (2000). Sliding mode con-

trol: an approach to regulate nonlinear chemical pro-

cesses. ISA transactions, 39(2):205–218.

Ceballos, J., Coloma, N., Di Teodoro, A., and Ochoa-

Tocachi, D. (2020). Generalized fractional cauchy–

riemann operator associated with the fractional

cauchy–riemann operator. Advances in Applied Clif-

ford Algebras, 30(5):1–22.

Ceballos, J., Coloma, N., Di Teodoro, A., Ochoa-Tocachi,

D., and Ponce, F. (2022). Fractional multicomplex

polynomials. Complex Analysis and Operator Theory,

16(4):1–30.

Coloma, N., Di Teodoro, A., Ochoa-Tocachi, D., and

Ponce, F. (2021). Fractional elementary bicomplex

functions in the riemann–liouville sense. Advances in

Applied Clifford Algebras, 31(61).

Di Teodoro, A., Ochoa-Tocachi, D., Aboukheir, H., and

Camacho, O. (2022). Sliding-mode controller based

on fractional order calculus for chemical processes.

In 2022 IEEE International Conference on Automa-

tion/XXV Congress of the Chilean Association of Au-

tomatic Control (ICA-ACCA), pages 1–6. IEEE.

Di Teodoro, A., Ochoa-Tocachi, D., Aboukheir, H., and Ca-

macho, O. (2023). Sliding mode control based on a

generalized reduced fractional order model: Theoret-

ical approach. In The conference on Latin America

Control Congress, pages 47–58. Springer.

Dimassi, H., Winkin, J. J., and Wouwer, A. V. (2019).

A sliding mode observer for a linear reaction–

convection–diffusion equation with disturbances. Sys-

tems & Control Letters, 124:40–48.

Esp

ın, J., Castrillon, F., Leiva, H., and Camacho, O. (2022).

A modiﬁed smith predictor based–sliding mode con-

trol approach for integrating processes with dead

time. Alexandria Engineering Journal, 61(12):10119–

10137.

Gude, J. J. and Garc

ıa Bringas, P. (2022). Inﬂuence of the

selection of reaction curve’s representative points on

the accuracy of the identiﬁed fractional-order model.

Journal of Mathematics, 2022.

Haghighi, A. and Ziaratban, R. (2020). A non-integer slid-

ing mode controller to stabilize fractional-order non-

linear systems. Advances in Difference Equations,

2020(1):1–19.

Herrera, M., Camacho, O., Leiva, H., and Smith, C. (2020).

An approach of dynamic sliding mode control for

chemical processes. Journal of Process Control,

85:112–120.

Kadu, C., Khandekar, A., and Patil, C. (2018). Design

of sliding mode controller with proportional integral

sliding surface for robust regulation and tracking of

process control systems. Journal of Dynamic Systems,

Measurement, and Control, 140(9):091004.

Kilbas, A. A., Marichev, O., and Samko, S. (1993). Frac-

tional integrals and derivatives (theory and applica-

tions).

Kilbas, A. A., Srivastava, H. M., and Trujillo, J. J.

(2006). Theory and applications of fractional differ-

ential equations, volume 204. elsevier.

Li, Y., Chen, Y., and Podlubny, I. (2010). Stability

of fractional-order nonlinear dynamic systems: Lya-

punov direct method and generalized mittag–lefﬂer

stability. Computers & Mathematics with Applica-

tions, 59(5):1810–1821.

Mehri, E. and Tabatabaei, M. (2021). Control of quadruple

tank process using an adaptive fractional-order sliding

mode controller. Journal of Control, Automation and

Electrical Systems, 32:605–614.

Miller, K. S. and Ross, B. (1993). An introduction to the

fractional calculus and fractional differential equa-

tions. Wiley.

Obando, C., Rojas, R., Ulloa, F., and Camacho, O.

(2023). Dual-mode based sliding mode control ap-

proach for nonlinear chemical processes. ACS omega,

8(10):9511–9525.

Patel, V., Guha, D., and Purwar, S. (2023). Distur-

bance observer-based higher-order sliding mode con-

troller for frequency regulation of hybrid power sys-

tems. International Journal of Automation and Con-

trol, 17(2):188–226.

Podlubny, I. (1994). Fractional-order systems and

fractional-order controllers. Institute of Experimen-

tal Physics, Slovak Academy of Sciences, Kosice,

12(3):1–18.

Prado, A. J., Herrera, M., Dominguez, X., Torres, J., and

Camacho, O. (2022). Integral windup resetting en-

hancement for sliding mode control of chemical pro-

cesses with longtime delay. Electronics, 11(24):4220.

Rasul, T. and Pathak, M. (2016). Control of nonlinear chem-

ical process using sliding mode control. In 2016 IEEE

1st International Conference on Power Electronics,

Intelligent Control and Energy Systems (ICPEICES),

pages 1–5. IEEE.

Salinas, L. R., Santiago, D., Slawi

nski, E., Mut, V. A.,

Chavez, D., Leica, P., and Camacho, O. (2018). P+

d plus sliding mode control for bilateral teleoperation

of a mobile robot. International Journal of Control,

Automation and Systems, 16(4):1927–1937.

Sardella, M. F., Serrano, E., Camacho, O., and Scaglia, G.

(2020). Linear algebra controller design based on the

integral of desired closed-loop behavior: Application

to regulation and trajectory tracking in a typical chem-

ical process. Industrial & Engineering Chemistry Re-

search, 59(45):20131–20140.

Siddiqui, M. A., Anwar, M. N., and Laskar, S. H. (2020).

Sliding mode controller design for second-order un-

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

138

stable processes with dead-time. Journal of Electrical

Engineering, 71(4):237–245.

Smith, C. A. and Corripio, A. B. (2005). Principles and

practices of automatic process control. John wiley &

sons.

Ullah, N. and Mohammad, A. (2022). A simulation ap-

proach for closed-loop control of coupled four tank

system. International Journal of Modeling, Simula-

tion, and Scientiﬁc Computing, 13(04):2250029.

Utkin, V., Poznyak, A., Orlov, Y. V., and Polyakov, A.

(2020). Road map for sliding mode control design.

Springer.

Xiao, T. and Li, H.-X. (2016). Sliding mode control de-

sign for a rapid thermal processing system. Chemical

Engineering Science, 143:76–85.

Fractional Order-Sliding-Mode Controller for Regulation of a Nonlinear Chemical Process with Variable Delay

139