Closing the Sim-to-Real Gap with Physics-Enhanced Neural ODEs

Tobias Kamp

, Johannes Ultsch

and Jonathan Brembeck

German Aerospace Center, Institute of System Dynamics and Control (SR), Germany

Keywords:

Dynamical Systems, Hybrid Modelling, Neural Ordinary Differential Equations, Scientiﬁc Machine Learning,

Physics-Enhanced Neural ODEs.

Abstract:

A central task in engineering is the modelling of dynamical systems. In addition to ﬁrst-principle methods,

data-driven approaches leverage recent developments in machine learning to infer models from observations.

Hybrid models aim to inherit the advantages of both, white- and black-box modelling approaches by combin-

ing the two methods in various ways. In this sense, Neural Ordinary Differential Equations (NODEs) proved

to be a promising approach that deploys state-of-the-art ODE solvers and offers great modelling ﬂexibility. In

this work, an exemplary NODE setup is used to train low-dimensional artiﬁcial neural networks with phys-

ically meaningful outputs to enhance a dynamical model. The approach maintains the physical integrity of

the model and offers the possibility to enforce physical laws during the training. Further, this work outlines

how a conﬁdence interval for the learned functions can be inferred based on the deployed training data. The

robustness of the approach against noisy data and model uncertainties is investigated and a way to optimize

model parameters alongside the neural networks is shown. Finally, the training routine is optimized with mini-

batching and sub-sampling, which reduces the training duration in the given example by over 80 %.

1 INTRODUCTION

The modelling of dynamical systems is an impor-

tant and challenging engineering task which forms

the foundation for subsequent controller design, op-

timization, visualization and many more. Models are

usually optimized for speciﬁc applications, since ex-

act (white-box) modelling of complex systems soon

becomes infeasible. In order to optimize a model re-

garding its prediction quality or computational com-

plexity, conventional data-driven approaches like pa-

rameter optimization, system identiﬁcation and the

usage of look-up tables are common practice.

Black-Box Modelling

With the rise of machine learning (ML) algorithms

and toolboxes, manifold data-driven modelling ap-

proaches for dynamical systems emerged. Espe-

cially recurrent neural networks (RNNs) proved to

be well suited to learn time-dependent correlations

(Haber and Ruthotto, 2017), (Chang et al., 2019).

Neural Ordinary Differential Equations (NODEs), as

https://orcid.org/0009-0006-5584-2928

https://orcid.org/0000-0001-6483-8468

https://orcid.org/0000-0002-7671-5251

introduced by Chen (Chen et al., 2018), pose an-

other promising approach. NODEs only approxi-

mate the right-hand side of the differential equations

with neural networks (NNs) and beneﬁt from the us-

age of well-established ODE solvers that enable time-

continuous simulation and the handling of stiff sys-

tems and time events. However, pure black-box ap-

proaches generally suffer from poor extrapolation,

high data demand and instability. Knowledge of the

fundamental dynamics of a system can be used to mit-

igate these disadvantages using a hybrid modelling

approach.

Hybrid Modelling

Hybrid models combine ﬁrst-principle methods with

machine learning and aim to leverage the advan-

tages of both. One way to use the existing knowl-

edge is to enforce physically meaningful behaviour

of the black-box model during the training. Raissi in-

troduced Physics-informed neural networks (PINNs)

(Raissi et al., 2019) to solve problems that involve

partial differential equations. These networks lever-

age the power of automatic differentiation to incor-

porate knowledge about the derivatives into the loss

function. Another way to use the physical equations is

the explicit combination with black-box components.

Kamp, T., Ultsch, J. and Brembeck, J.

Closing the Sim-to-Real Gap with Physics-Enhanced Neural ODEs.

DOI: 10.5220/0012160100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 2, pages 77-84

ISBN: 978-989-758-670-5; ISSN: 2184-2809

In this case, the white-box part serves e.g. to pre-

process the inputs, initialize hidden states of recur-

rent architectures or to provide an a-priori estimation

that is afterwards corrected by data-driven compo-

nents (cf. residual-physics, (Daw et al., 2022), (Zeng

et al., 2020)). The idea of residual-physics formed the

basis for dedicated hybrid simulators which allow the

incorporation and training of NNs in physics-based

models (Ajay et al., 2018), (Heiden et al., 2020). For

a more complete overview of current developments

in hybrid modelling, we refer the interested reader to

the surveys of Willard (Willard et al., 2020), Rai (Rai

and Sahu, 2020) and Karniadakis (Karniadakis et al.,

2021).

Universal Differential Equations

Universal differential equations (UDEs) (Rackauckas

et al., 2020) expand the basic idea of Neural ODEs

and allow arbitrary designs of the differential equa-

tions. This enables the enrichment of dynamical

models with NNs to expand or replace equations or

computational costly parts. The concept was used

in several works and in different domains, for in-

stance in vehicle dynamics (Bruder and Mikelsons,

2021), (Thummerer et al., 2022), chemistry (Owoyele

and Pal, 2022), climate modelling (Ramadhan et al.,

2022) or ﬂuid dynamics (Thummerer et al., 2021).

Contribution

The generality and physical integrity of a hybrid

model diminishes with increasing inﬂuence and com-

plexity of its black-box components, while the de-

mand for training data rises. In the reviewed ap-

plications of NODEs, the physical model is either

combined with data-driven components to form a

higher-order model (Thummerer et al., 2021), (Thum-

merer et al., 2022) or the NNs approximate the right-

hand side of single differential equations (Bruder and

Mikelsons, 2021), (Owoyele and Pal, 2022). While

the obtained models demonstrate the potentials of hy-

brid approaches, y NODEs are prone to instability is-

sues and/or local optima (Turan and Jaschke, 2022)

and the analysis of the physical feasibility and extrap-

olation is not trivial. Inspired by the idea of “ﬁne-

grained data-driven models” (Heiden et al., 2020), we

propose to go one step deeper and insert physically

meaningful neural components into the given differ-

ential equations, forming a Physics-enhanced NODE

(PeNODE). This has the advantage, that the learned

functions can be analysed directly and physical prop-

erties can be enforced during the training. In addi-

tion, we show how a conﬁdence interval can be de-

rived from the training data, which serves to deﬁne

the application boundaries of the hybrid model. An-

other beneﬁt of the presented approach is the limited

inﬂuence of the data-driven components, which re-

duces stability and convergence issues and minimises

the data-demand.

Outline

This work is structured as follows: In Section 2, we

present the concept of PeNODEs and how the loss-

function can be used to enforce physical laws. In

Section 3, the training routine and the beneﬁts of

mini-batching and sub-sampling are described. Our

demonstrator, a quarter vehicle model, is introduced

in Section 4. The conducted experiments and cor-

responding results are presented in Section 5 before

concluding with Section 6.

2 METHOD

This section presents a method to formulate PeN-

ODEs and how to enforce properties with regularizing

terms. Further, the idea of simultaneous parameter ﬁt-

ting is introduced.

2.1 Terminology

The meaningful combination of physical equations

and NNs is referred to as Physics-enhanced Neu-

ral ODE (PeNODE). The additional usage of reg-

ularizing terms that guide the optimization and en-

force certain properties would be a “Physics-Informed

Physics-enhanced Neural ODE” (cf. PINNs, (Raissi

et al., 2019)). For the sake of simplicity, we however

assume that a Physics-enhanced Neural ODE can also

be Physics-Informed.

2.2 Prerequisites

This work postulates the existence of a dynamical

model, which fairly represents the fundamental dy-

namics of the considered system. The model must be

given in the general form

˙x(t) = f (x,u,t) (1)

y(t) = g(x,u,t) , (2)

with a state-vector x, input-vector u and output-vector

2.3 Deriving a PeNODE

In order to obtain a neural ODE, the right-hand side

of the differential equation (1) is enhanced with one

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

or more NNs with parameters Θ:

˙x(t) = f (x,u,t, NN(x,u,t, Θ)) . (3)

The analogy of systems in different domains (Hogan

and Breedveld, 2005) offers the possibility to sketch

a general approach to obtain a PeNODE, i.e. a mean-

ingful combination of the physical equations and

NNs:

In the context of systems analogy, the three ba-

sic components of a dynamical system are compli-

ance, inductance and resistance. Further, a domain-

speciﬁc pair of power conjugated variables, i.e. one

ﬂow variable and one potential variable can be de-

ﬁned. Component-speciﬁc (differential-) equations

correlate ﬂow and potential (e.g. U = RI for an

electrical resistance) and/or deﬁne the transition to

another domain. The differential equations of the

system can be derived by setting the potentials to

be equal and the sum of ﬂows equal to zero for

each connection of the components and substitute the

component-speciﬁc equations (Zimmer, 2016).

Based on the described formalism, we propose to

introduce neural components into the systems equa-

tions that obey the same fundamental rules and learn

the correlation of ﬂow and potential. The number

of relevant inputs for these neural components is ex-

pected to be low, since they capture but one aspect

of the complex system they compose. The NNs thus

have a low-dimensional input and an one-dimensional

output. This “ﬁne-grained” approach is advanta-

geous, because the obtained neural components are

easy to analyse regarding their physical feasibility

and extrapolation properties. Furthermore, physically

meaningful behaviour can be encouraged during the

training by punishing unphysical outputs. Finally, the

limited inﬂuence of the black-boxes avoids stability

issues and minimises the data demand.

The presented approach is well suited to enhance

models which already capture the fundamental dy-

namics of the real system. In this case, the neural

components can account for secondary effects like

friction, elasticities or non-linear characteristics that

cause the Sim-to-Real Gap, i.e. the residuum between

model predictions and real observations.

2.4 Physics-Informed Training

During the training, the parameters of the neural com-

ponents are adapted to minimise the error (or loss) of

the model-predictions with respect to given training

data. In order to obtain physically reasonable neu-

ral components, regularizing terms that punish un-

physical behaviour can be added to the loss function.

For example, zero-crossing of learned functions is de-

sirable in many cases: Consider a neural resistance

(damper) with trainable parameters Θ which intro-

duces a damper force F

R,NN

(v) that depends on a ve-

locity v. For v = 0, this force must be equal to zero.

Thus, a possible regularizing term is given by

zcross

(Θ) = F

R,NN

(0,Θ)

. (4)

Since a regularizing term in the loss function cannot

enforce exact zero-crossing, the remaining offset can

be eliminated after the training by subtraction:

R,NN

(v) = F

R,NN

(v) − F

R,NN

(0) . (5)

If secondary dependencies, i.e. more inputs are added

to the neural component, the concepts of regularizing

and offset-correction are still applicable. In that case,

the zero-crossing values of arbitrary sample points of

the input space of the secondary inputs can be used for

the regularization. In the given example, if a depen-

dency of the temperature T is added, the regularizer

can be adapted to

zcross

(Θ) =

∑

i=0

R,NN

(0,T

,Θ)

, (6)

with N samples from the temperature input-space.

The given example shows how a regularizer for a

single neural component can be formulated. In addi-

tion to such speciﬁc terms, general knowledge about

system properties like stability and oscillation capa-

bility can be incorporated using eigen-informed regu-

larizers (Thummerer and Mikelsons, 2023).

2.5 Optimizing Model Parameters

The presented approach relies on low-dimensional

NNs whose inﬂuence is limited by design. In order

to add further degrees of freedom to the optimiza-

tion, certain model parameters, e.g. the masses or

inertia, can be optimized alongside the parameters of

the NNs. To optimize model parameters {p

, p

,...},

we propose to deﬁne a vector of parameter-modiﬁers

∆

= [δp

, δp

,...]

that is concatenated with the

vector of the NN-parameters and subjected to the

gradient-based optimization. To ensure stability of

the model and limit the impact of the modiﬁers, a

smooth saturation with a hyperbolic tangent function

can be used. The modiﬁed model parameters ˜p

are

then given by

˜p

= (1 + δp

(7)

δp

= γtanh(δp

) . (8)

The hyper-parameter γ ∈ (0, 1) ensures that the pa-

rameters can only be changed by max . ± γ, e.g.

±20 %.

Closing the Sim-to-Real Gap with Physics-Enhanced Neural ODEs

3 TRAINING DETAILS

In this section, the training process for a NODE is

brieﬂy sketched, revealing how mini-batching and

sub-sampling help to reduce the computational com-

plexity and how to use model outputs as physical fea-

tures.

3.1 Basic Training

The basic training routine of a NODE is to repeat-

edly simulate the model for a given time horizon, cal-

culate the loss with respect to all or a subset of the

states and adapt the weights of the NNs in a step

of a gradient-based algorithm, e.g. gradient descent.

The loss function can be any common metric like the

(root) mean squared error over all time-points and

states. The gradient-based optimization requires the

usage of a differentiable ODE-solver, as provided in

Julia (Bezanson et al., 2017) or PyTorch

. This con-

sequently assumes that the model is (re)implemented

in the training environment. With FMIFlux.jl

, the

model exchange standard FMI

can be used to facili-

tate this process and integrate FMUs into Julia appli-

cations.

3.2 Mini-Batching and Sub-Sampling

The computational complexity of the gradient calcu-

lation increases signiﬁcantly with the length and sam-

ple rate of the deployed training trajectories. Mini-

batching can be used to eliminate this effect and make

the training scalable to arbitrary datasets by using a

number of short sequences from the original dataset

for each update. A further reduction of complex-

ity can be achieved by sub-sampling, i.e. calculat-

ing the loss for a subset of the data points. To intro-

duce randomness and avoid aliasing, the points can be

sampled randomly instead of using equidistant time-

intervals.

3.3 Model Outputs as Physical Features

In many cases, not all states of a system are mea-

surable with reasonable effort. While methods for

state estimation can be used to ﬁll in missing mea-

surements, the NODE can also be trained on a subset

of states or other quantities. In this case, the model

observation function (cf. Equation (2)) is used to

transform the state trajectory into an output trajectory

https://github.com/rtqichen/torchdiffeq

https://github.com/ThummeTo/FMIFlux.jl

https://fmi-standard.org/

which reﬂects the available measurements. Using the

model outputs for the training is a form of feature ex-

traction and can serve to condense the possibly high-

dimensional state-space to a set of (relevant) quanti-

ties. Note, that if measurement for states are missing,

the usage of mini-batching is impeded, since the ini-

tial state for each sequence must be given to solve the

differential equations correctly.

4 DEMONSTRATOR

In this section we introduce our demonstrator, a quar-

ter vehicle model (QVM). A non-linear version of the

QVM serves to generate training data and the linear

QVM is transformed into a PeNODE that is used in

several training-setups to demonstrate our method.

4.1 The Linear QVM

The QVM is commonly used to represent the vertical

dynamics of road vehicles. It consists of two masses,

one for the wheel (m

) and one for one quarter of

the body (m

) (cf. Figure 1). The two masses are

connected by a linear spring-damper pair with coefﬁ-

cients c

and d

, representing the vehicle suspension

(index s). Another linear spring-damper pair with co-

efﬁcients c

and d

represents the tire that connects the

vehicle to the ground (index t). The state vector x con-

sists of the road height z

, the position and velocity of

the wheel z

and v

and the position and velocity of

the body z

and v

. The input u(t) is the differential

road height ˙z

and the model output y contains the ac-

celerations of the wheel and the body a

and a

x = [x

,...,x

]

= [z

, v

, z

, v

, z

]

(9)

y = [ ˙x

, ˙x

]

= [a

, a

]

(10)

u = ˙z

(11)

The linear differential equations that describe the sys-

tem (12 - 16) can be derived using the Newtonian laws

of motion.

˙x

= v

(12)

˙x

= m

−1

∆z

+ d

∆v

) (13)

˙x

= v

(14)

˙x

= m

−1

∆z

+ d

∆v

− c

∆z

− d

∆v

) (15)

˙x

= u (16)

∆z

= z

− z

, ∆v

= v

− v

∆z

= z

− z

, ∆v

= ˙z

− v

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

∆z

NN,c

NN,d

∆

∆v

Figure 1: Scheme of the hybrid quarter vehicle model with

the incorporated black-box components.

4.2 Data Generation

For the generation of training data, the linear QVM

is extended by two non-linear effects in the suspen-

sion. A translational friction force F

f r

, consisting

of Stribeck-, Coulomb and viscous friction, is added

(cf. Simscape: Translational Friction

) and the spring

is modiﬁed towards a progressive characteristic by

adding a quadratic term F

. The model equations

(13) and (15) are consequently changed to

˙x

= m

−1

∆z

+ d

∆v

+ F

(∆z

) + F

f r

(∆v

)) (17)

˙x

= m

−1

∆z

+ d

∆v

− c

∆z

− d

∆v

− F

(∆z

) − F

f r

(∆v

)) . (18)

To obtain the trajectory of states and outputs, the non-

linear model is simulated over time for a given input

u(t). The input is derived from a realistic road proﬁle

(ISO8608, Type D (M

cka, 2017)), imitating a rather

rough road. The generated states and observables are

sampled with 1000 Hz and are artiﬁcially disturbed

by Gaussian noise. The training dataset consists of a

single trajectory of 42 s length.

4.3 The Neural QVM

For the demonstration of our method, the basic linear

model is augmented with two NNs to learn the miss-

ing effects from the data. The NNs are interpreted as

neural compliance and -resistance (here: spring and

damper) that induce the forces F

NN,c

and F

NN,d

. They

consequently add to the sum of forces in the given

https://www.mathworks.com/help/simscape/ref/

translationalfriction.html, accessed 27.04.2023

Table 1: Architecture of the deployed neural networks.

Layer Dimensions Activation

1 16 × 1 ReLU

2 16 × 16 ReLU

3 1 × 16 Identity

differential equations according to:

˙x

= m

−1

∆z

+ d

∆v

+ F

NN,c

(∆z

)

+ F

NN,d

(∆v

)) (19)

˙x

= m

−1

∆z

+ d

∆v

− c

∆z

− d

∆v

− F

NN,c

(∆z

) − F

NN,d

(∆v

)) . (20)

The architecture of the neural networks is summa-

rized in Table 1. In our approach, the neural compo-

nents capture single effects within a complex system.

In most cases, the learned functions will be simple

and small NNs with few nodes sufﬁce. In the given

setup, the two NNs only have 321 parameters each.

In a realistic setup, the accelerations a

and a

are

comparably easy to measure. Therefore, the model

output y is used for the optimization. The loss func-

tion is a normalized root mean squared error (RMSE,

Eq. (21)) with N quantities (here a

and a

) and M

data points q

i j

with labels ˆq

i j

. To account for different

orders of magnitude of the quantities, the standard de-

viation σ

is derived from the training data and used

for the normalization. Further, a regularizer to enforce

zero-crossing r

zcross

(cf. Eq. (6)) with a weight factor

of λ = 0.01 is added.

L =

∑

i=1

∑

j=1

(

i j

− ˆq

i j

)

+ λ||[F

NN,c

(0),F

NN,d

(0)]

(21)

When mini-batching is used, the presented loss is cal-

culated for each sequence of the batch and averaged

over all sequences.

4.4 Implementation Details

The model is implemented and trained in Julia, us-

ing the packages OrdinaryDiffEq.jl for the solu-

tion of the ODEs, Zygote.jl for the automatic dif-

ferentiation and tools like the ADAM optimizer from

Flux.jl. All trainings were conducted on a notebook

with a 10th generation intel i7 CPU.

5 EXPERIMENTAL RESULTS

We use the neural QVM to prove the concept of PeN-

ODEs and the sketched training methods in several

Closing the Sim-to-Real Gap with Physics-Enhanced Neural ODEs

−0.5 −0.25

0.25 0.5

−100

100

∆v

(m/s)

Force (N)

ref.

learned

(a) Friction Force

−40 −20 0 20 40

500

1,000

∆z

(mm)

Force (N)

(b) Spring Characteristic

Figure 2: Comparison of the learned forces to their refer-

ences. The dashed and dotted lines indicate the 1σ- and

2σ-intervals of the inputs that occurred during the training.

experiments. First, we show the results of a basic

training and analyse them with respect to physical

feasibility, interpretability and extrapolation proper-

ties. Second, the beneﬁts of mini-batching and sub-

sampling are presented. Finally, the robustness of the

training against model uncertainties and noisy data is

investigated and the advantages of optimizing model

parameters alongside the NNs are illustrated.

5.1 Basic Training: Results and

Interpretation

The results in this paragraph are obtained with the

straightforward approach to use the whole sequence

with full sample rate for each update. The train-

ing comprised 1000 epochs, i.e. simulation, loss-

calculation, gradient-calculation and one update-step

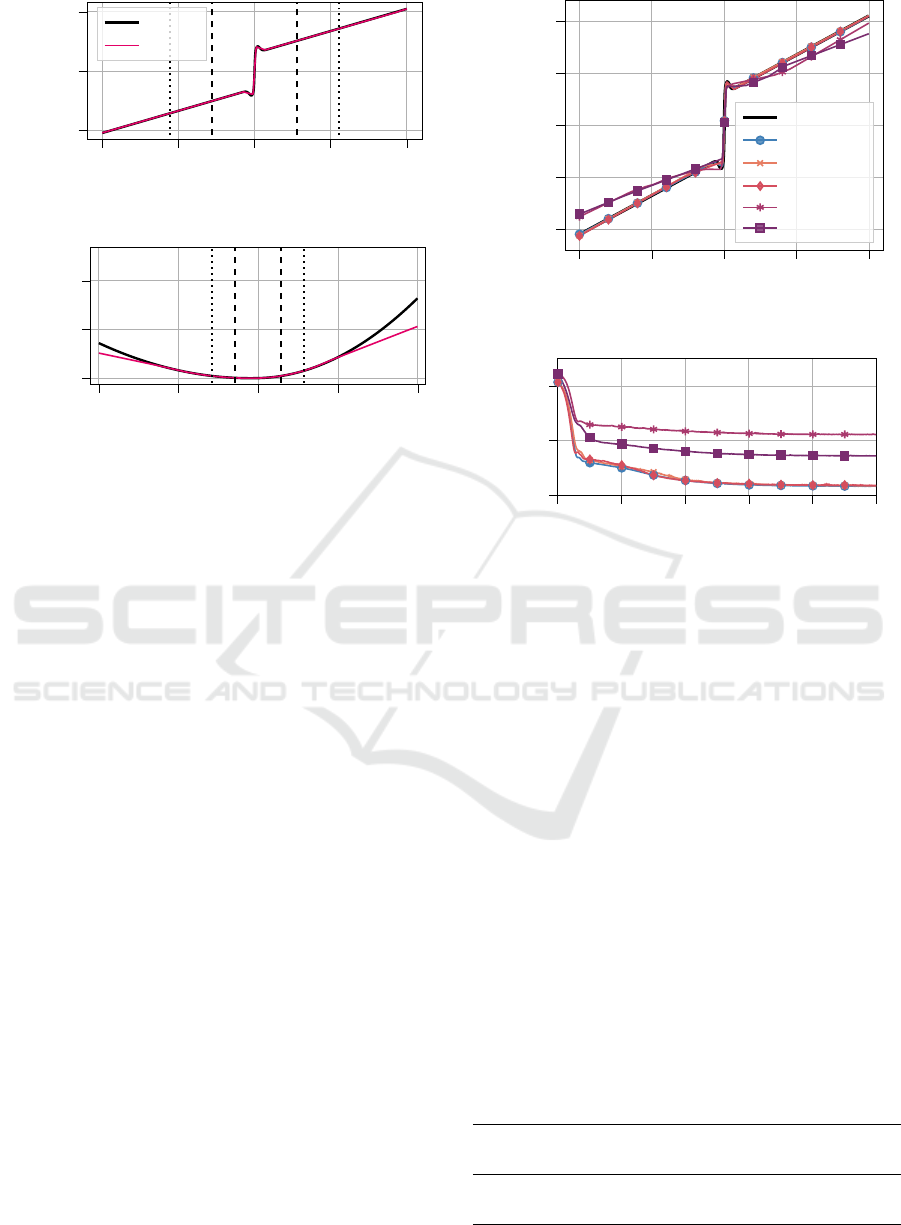
of the optimization. In Figure 2, the learned neural

forces are compared to the non-linearities that were

incorporated during the data generation. The dashed

and dotted lines depict the 1σ- and 2σ-intervals (i.e.

one/two standard deviations) of the NN-inputs that

occurred during the training.

It shows, that the underlying non-linearities are

fairly well captured by the neural components within

the 2σ-conﬁdence-interval. The outputs outside the

interval are interpreted as extrapolations, since less

than 10 % of the training inputs lay outside this in-

terval. Both neural forces show a linear extrapola-

−0.5 −0.25

0.25 0.5

−100

−50

100

∆v

(m/s)

Force (N)

ref.

baseline

batch

batch+subs

nsy+par

paramopt

(a) Learned neural friction forces.

0 200 400

600

800 1,000

0.2

0.4

E poch ()

Loss ()

(b) Convergence of the training-loss.

Figure 3: Overview of the learned neural friction forces and

the convergence of the loss for different training setups (cf.

Section 5.1 - 5.4).

tion behaviour that results from the ReLU activation

function. Consequently, if a saturating extrapolation

is preferred, the usage of a tanh activation in the last

hidden layer can be considered.

We would like to emphasize that the underlying

non-linearities were precisely learned from only one

training sequence of 42 s length. In this case, more

data would be beneﬁcial only if the induced inputs

expand the conﬁdence intervals of the learned forces.

5.2 Mini-Batching and Sub-Sampling

As described in Section 3, mini-batching and sub-

sampling reduce the computational complexity of the

training routine and allow the usage of larger datasets.

As an indicator of the computational complexity, the

Table 2: Comparison of the training and average epoch du-

ration.

Baseline Batching Batching +

Sub-sampling

Overall duration 33 h 6.5 h 4.5 h

Per epoch 120 s 24 s 17 s

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

5 6

7 8

−2

·10

−2

(m)

ref. lin. model PeNODE

5 6

7 8

−5

·10

−2

(m/s)

5 6

7 8

−0.5

−0.25

0.25

0.5

Time (s)

(m/s

)

Figure 4: Detail of the model predictions for body-height,

-velocity and -acceleration of the linear model compared to

the trained neural ODE.

duration of one training with 1000 epochs for differ-

ent setups is measured and the results are compared

in Table 2. During the baseline training, each update

is based on the complete sequence of 42 s and the full

sample rate of 1000 Hz. In contrast, the batch updates

only use a set of 3 randomly sampled sequences, each

of 4 s length. With sub-sampling, the same settings (3

× 4 s) are used, but the loss is only calculated for 25 %

of the available points that are also randomly sampled.

The learned neural damper forces can be compared in

Figure 3a (baseline, batch, batch+subs). Additionally,

Figure 3b depicts the convergence of the loss over the

course of the training. It shows, that the learned forces

only differ slightly and the loss reaches almost the

same optimum, while mini-batching decreases the du-

ration by roughly 80 % and sub-sampling by another

30 %.

All following results were obtained with 1000

training-epochs and mini-batching as presented. Sub-

sampling was not used, since the beneﬁt is not as sig-

niﬁcant and the training becomes more prone to local

optima.

5.3 Model Uncertainties and Noisy Data

The previously presented results prove the princi-

ple of learning underlying non-linearities from model

output data. However, the simulated data was of high

0 200 400

600

800 1,000

−0.1

0.1

E poch ()

Modi f ier ()

δm

δd

δc

Figure 5: Convergence of the simultaneously optimized pa-

rameter modiﬁers.

quality and the physical part of the hybrid model used

the nominal parameters. In the following, the robust-

ness of the approach against noisy data and model

uncertainties is investigated. To this end, the added

noise is increased by a factor of ﬁve and the parame-

ters of the neural QVM, i.e. the masses m

, m

and

the coefﬁcients of the tire spring-damper pair c

and d

are disturbed by ± 10 % with respect to the nominal

value.

The training results under these circumstances are

included in Figure 3 (nsy+par). It shows, that the neu-

ral damper still captures the non-linear friction, with a

minor loss of precision. The same is true for the neu-

ral spring. Figure 4 gives an impression of the model

predictions before and after the training in this case,

illustrating how the learned components enhance the

model predictions despite the disturbed parameters

and presence of noise.

5.4 Simultaneous Parameter Fitting

Here we used the same setup as before (in-

creased noise, disturbed parameters) but the model-

parameters m

, m

, c

and d

are optimized alongside

the parameters of the NNs. The corresponding mod-

iﬁers are saturated with γ = 0.2 as presented in Sec-

tion 2 (Eq. (7) and (8)). Figure 5 illustrates how the

modiﬁers converge to a near optimal value over the

course of the training. The target values for the modi-

ﬁers marked with plus-markers are +0.1 and the mod-

iﬁers with triangles −0.1 respectively. Figure 3, lines

“nsy+par” versus “paramopt”, shows the signiﬁcant

decrease of the remaining loss after the optimization

that can be attributed to the corrected model parame-

ters.

Closing the Sim-to-Real Gap with Physics-Enhanced Neural ODEs

6 CONCLUSIONS

In this work, we presented an approach to incorpo-

rate low-dimensional neural networks into the differ-

ential equations of a given model, forming a Physics-

enhanced Neural ODE. It showed, that missing ef-

fects are effectively learned by these neural compo-

nents, while physically meaningful behaviour can be

enforced during the training. The usage of single-

output neural networks yields the possibility to as-

sign a conﬁdence interval to the obtained functions,

which increases the credibility of the hybrid model.

We are conﬁdent, that the presented method poses a

straightforward approach to enhance existing dynami-

cal models without sacriﬁcing their physical integrity.

ACKNOWLEDGEMENTS

This work was organized within the European ITEA3

Call6 project UPSIM - Unleash Potentials in Simula-

tion (number 19006). The work was partially funded

by the German Federal Ministry of Education and Re-

search (BMBF, grant number 01IS20072H).

The term Physics-enhanced Neural ODEs (PeN-

ODE) was created in the proposal for the ITEA 4

project OpenSCALING.

REFERENCES

Ajay, A., Wu, J., Fazeli, N., Bauza, M., Kaelbling, L. P.,

Tenenbaum, J. B., and Rodriguez, A. (2018). Aug-

menting Physical Simulators with Stochastic Neural

Networks: Case Study of Planar Pushing and Bounc-

ing. In 2018 IEEE/RSJ International Conference on

Intelligent Robots and Systems (IROS). IEEE.

Bezanson, J., Edelman, A., Karpinski, S., and Shah, V. B.

(2017). Julia: A fresh approach to numerical comput-

ing. SIAM Review.

Bruder, F. and Mikelsons, L. (2021). Modia and Julia for

Grey Box Modeling. In Link

oping Electronic Con-

ference Proceedings. Link

oping University Electronic

Press.

Chang, B., Chen, M., Haber, E., and Chi, E. H. (2019). An-

tisymmetricRNN: A Dynamical System view on re-

current Neural Networks. ICLR 2019.

Chen, R. T. Q., Rubanova, Y., Bettencourt, J., and Duve-

naud, D. (2018). Neural Ordinary Differential Equa-

tions. Neural Information Processing Systems.

Daw, A., Karpatne, A., Watkins, W. D., Read, J. S.,

and Kumar, V. (2022). Physics-Guided Neural Net-

works (PGNN): An Application in Lake Temperature

Modeling. In Knowledge-Guided Machine Learning.

Chapman and Hall.

Haber, E. and Ruthotto, L. (2017). Stable Architectures for

Deep Neural Networks. Inverse Problems, Volume 34.

Heiden, E., Millard, D., Coumans, E., Sheng, Y., and

Sukhatme, G. S. (2020). NeuralSim: Augment-

ing Differentiable Simulators with Neural Networks.

IEEE International Conference on Robotics and Au-

tomation (ICRA) 2021.

Hogan, N. and Breedveld, P. (2005). The Physical Basis of

Analogies in Physical System Models. In Mechatron-

ics - An Introduction. CRC Press.

Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris,

P., Wang, S., and Yang, L. (2021). Physics-informed

Machine Learning. Nature Reviews Physics.

cka, P. (2017). Simulated Road Proﬁles According to

ISO 8608 in Vibration Analysis. Journal of Testing

and Evaluation.

Owoyele, O. and Pal, P. (2022). ChemNODE: A neural Or-

dinary Differential Equations Framework for efﬁcient

Chemical Dinetic Solvers. Energy and AI.

Rackauckas, C., Ma, Y., Martensen, J., Warner, C., Zubov,

K., Supekar, R., Skinner, D., Ramadhan, A., and Edel-

man, A. (2020). Universal Differential Equations for

Scientiﬁc Machine Learning.

Rai, R. and Sahu, C. K. (2020). Driven by Data or De-

rived through Physics? a Review of Hybrid Physics

Guided Machine Learning Techniques with Cyber-

Physical System (CPS) Focus. IEEE Access.

Raissi, M., Perdikaris, P., and Karniadakis, G. (2019).

Physics-Informed Neural Networks: A deep Learn-

ing Framework for Solving Forward and Inverse Prob-

lems involving nonlinear Partial Differential Equa-

tions. Journal of Computational Physics.

Ramadhan, A., Marshall, J. C., Souza, A. N., Lee, X. K.,

Piterbarg, U., Hillier, A., Wagner, G. L., Rackauckas,

C., Hill, C., Campin, J.-M., and Ferrari, R. (2022).

Capturing missing Physics in Climate Model Parame-

terizations using Neural Differential Equations. Jour-

nal of Advances in Modeling Earth Systems (JAMES).

Thummerer, T. and Mikelsons, L. (2023). Eigen-informed

NeuralODEs: Dealing with stability and convergence

issues of NeuralODEs.

Thummerer, T., Stoljar, J., and Mikelsons, L. (2022). Neu-

ralFMU: Presenting a Workﬂow for integrating hybrid

NeuralODEs into Real-World Applications. Electron-

ics.

Thummerer, T., Tintenherr, J., and Mikelsons, L. (2021).

Hybrid Modeling of the Human Cardiovascular Sys-

tem using NeuralFMUs. 10th International Confer-

ence on Mathematical Modeling in Physical Sciences.

Turan, E. M. and Jaschke, J. (2022). Multiple shooting for

training neural differential equations on time series.

IEEE Control Systems Letters.

Willard, J., Jia, X., Xu, S., Steinbach, M., and Kumar, V.

(2020). Integrating Physics-Based Modeling with Ma-

chine Learning: A Survey. ACM Computing Surveys.

Zeng, A., Song, S., Lee, J., Rodriguez, A., and Funkhouser,

T. (2020). TossingBot: Learning to Throw Arbitrary

Objects with Residual Physics. IEEE Transactions on

Robotics.

Zimmer, D. (2016). Equation-Based Modeling with Mod-

elica – Principles and Future Challenges. SNE Simu-

lation Notes Europe.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics