Computing the Traversability of the Environment by Means of Sparse

Convolutional 3D Neural Networks

Antonio Santo

1,2 a

, Arturo Gil

1 b

, David Valiente

1 c

, M

onica Ballesta

1 d

and Adri

an Peidr

1 e

University Institute for Engineering Research, Miguel Hern

andez University,

Avda. de la Universidad s/n, 03202 Elche (Alicante), Spain

Valencian Graduate School and Research Network of Artiﬁcial Intelligence (valgrAI),

Cam

ı de Vera S/N, Ediﬁcio 3Q, 46022 Valencia, Spain

Keywords:

Autonomous Mobile Robots, Artiﬁcial Intelligence, Neural Networks, Point Clouds, Sparse Convolution.

Abstract:

The correct assessment of the environment in terms of traversability is strictly necessary during the naviga-

tion task in autonomous mobile robots. In particular, navigating along unknown, natural and unstructured

environments requires techniques to select which areas can be traversed by the robot. In order to increase

the autonomy of the system’s decisions, this paper proposes a method for the evaluation of 3D point clouds

obtained by a LiDAR sensor in order to obtain the transitable areas, both in road and natural environments.

Speciﬁcally, a trained sparse encoder-decoder conﬁguration with rotation invariant features is proposed to

replicate the input data by associating to each point the learned traversability features. Experimental results

show the robustness and effectiveness of the proposed method in outdoor environments, improving the results

of other approaches.

1 INTRODUCTION

The answer to the question ”Where should I walk?”,

formulated in (Wellhausen et al., 2019) implicitly

contains the understanding of everything that sur-

rounds the robot in order to be able to navigate along

the environment. This concept, which is assumed to

be innate to humans, should be extrapolated to au-

tonomous mobile robots, as it enables safe planning

and navigation in various applications such as explo-

ration of unknown environments, autonomous driv-

ing, search and rescue applications.

To date, path planning algorithms have been clas-

siﬁed according to two fundamental concepts: a) the

manner in which the space is deﬁned and represented;

b) the form in which the transitable zones are rep-

resented on the map. Thus, according to the ﬁrst

concept, different representations of the space can be

found, such as: 2D occupancy maps (Moravec and

Elfes, 1985), 3D voxel-based occupancy maps (Hor-

nung et al., 2013; Oleynikova et al., 2017; Han et al.,

https://orcid.org/0009-0006-0085-6273

https://orcid.org/0000-0001-7811-8955

https://orcid.org/0000-0002-2245-0542

https://orcid.org/0000-0002-8029-5085

https://orcid.org/0000-0002-4565-496X

2019) or elevation maps (DEM) (Langer et al., 1994),

in which a probability value deﬁnes that a certain

space is free or occupied, and may be traversed by

the robot considering the physical parameters of the

robot.

However, the classical approaches mentioned

above are not sufﬁciently robust when applied to all

types of environments (Xiao et al., 2022), since au-

tonomous driving can be understood differently de-

pending on the environment in which it is intended

to navigate. Mainly in structured environments, the

free space refers to regular roads, whereas for natural

environments the concept is a bit abstract. The latter

are environments complex and diverse and can hide

invisible obstacles for the robots sensors.

This fact, together with a more sophisticated sen-

sorization of the equipment (considering character-

istics such as cost, resolution and lightness), justi-

ﬁes an approaching to compute traversability under

a new paradigm: supervised machine learning, based

on neural networks. Speciﬁcally, in recent years the

use of LiDAR sensors in combination with Neural

Networks has become popular. In particular, LiDAR

sensors are immutable to different lighting conditions

compared to other optical sensors such as cameras.

This paper proposes a contribution to the estima-

Santo, A., Gil, A., Valiente, D., Ballesta, M. and Peidró, A.

Computing the Traversability of the Environment by Means of Sparse Convolutional 3D Neural Networks.

DOI: 10.5220/0012160300003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 383-393

ISBN: 978-989-758-670-5; ISSN: 2184-2809

383

tion of traversability in complex terrains using deep

learning techniques, in particular segmentation meth-

ods of a scene described by means of 3D point clouds.

The rest of the paper is organized as follows: Sec-

tion 2 presents a summary of the most signiﬁcant ap-

proaches in the ﬁeld of Deep Learning for the calcula-

tion of traversability. Then, the concepts on which our

method is based will be discussed and explained in

Section 3. Finally, a set of experimental results is pre-

sented, that considers different types of environments

that have been used in the training process. Finally,

Section 5 presents the main conclusions that can be

drawn from this approach.

2 RELATED WORK

This section describes some proposals in the ﬁeld of

traversability calculation using neural networks and

machine learning. The contributions have been di-

vided into two main blocks: conventional machine

learning methods and methods based on the use of

neural networks.

2.1 Conventional ML Methods

These group comprises algorithms that generally start

from alternative representations of the input data, i.e.,

act on features extracted from the data which are con-

sidered to be discriminating for the problem to be

solved. This strategy is employed in (Bellone et al.,

2017), where stereo image pairs are used as input

data. In (Vapnik, 1999), a study of the most dis-

criminating geometric and appearance features for the

traversability problem in urban environments is per-

formed based on the training of an SVM classiﬁer,

concluding that features that include normal vectors

are the most suitable for this task. In (Kragh et al.,

2015), the calculation of features based on a local

neighborhood for each point (obtained using a 3D Li-

DAR sensor) is proposed, in order to classify them

into: soil, vegetation or object. In this proposal, an

adaptive neighborhood radius is proposed to alleviate

the loss of point density as a function of the distance

to the sensor, which is inherent to LiDAR sensors. In

this way, high resolutions are guaranteed at short dis-

tances, whereas noisy features at long distances are

diminished.

One of the biggest problems with previous meth-

ods is the need for an expert to generate labels of the

class to which each point belongs. Therefore, there

are methods that automate this process by training

the classiﬁers with simulated data such as (Martinez

et al., 2020) which tries to describe point clouds ex-

tracted from the GAZEBO simulator from the analy-

sis of the principal directions (PCA) in a given neigh-

borhood environment.

2.2 Neural Networks

LiDAR sensors generate, at their output, the position

of a set of 3D points. These 3D points correspond

to the ﬁrst reﬂection produced by an object when it

is illuminated by a collimated laser beam. In rela-

tion to this fact, alternatives have been developed to

efﬁciently work with three-dimensional data. For ex-

ample, in (Velas et al., 2018), point clouds are trans-

formed into multichannel images that store the depth,

height and reﬂectivity of each point. These images

are processed through dense convolutional layers to

learn which areas are traversable. Another solution

is presented in (Razani et al., 2021) where spherical

projections of the point clouds are carried out. Next

2D convolutional layers are applied to solve a seman-

tic segmentation problem. A different solution is pre-

sented in (Wang et al., 2017), where octal trees or oc-

trees are used to reduce the complexity of the space

described by the point clouds. In this manner, dense

convolution operations are restricted to those octrees

that are occupied. The same idea is extended in (Frey

et al., 2022), where the traversability of the space is

computed by means of a generalization of the con-

volution operation to n-dimensions and employing a

sparse encoder-decoder setup (Choy et al., 2019).

On the other hand there are methods that combine

the information provided by LiDAR with image in-

formation. (Gu et al., 2019) propose a road detec-

tion method by merging the color information pro-

vided by the camera and the range information ob-

tained with the LiDAR. The point clouds are projected

to their corresponding images and feed a 2D convolu-

tional neural network. (Fan et al., 2020), fuses the

features of both types of data once they have been ex-

tracted by different architectures of neural networks.

(Chen et al., 2019) proposes a progressive adaptation

of the LiDAR representation to make it more compat-

ible with the visual information from the camera. To

do so, the point cloud is transformed into an alterna-

tive representation where roads are more distinguish-

able.

3 PROPOSED APPROACH

This section deﬁnes the traversability problem. Next,

a detailed description of the approach is presented.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

384

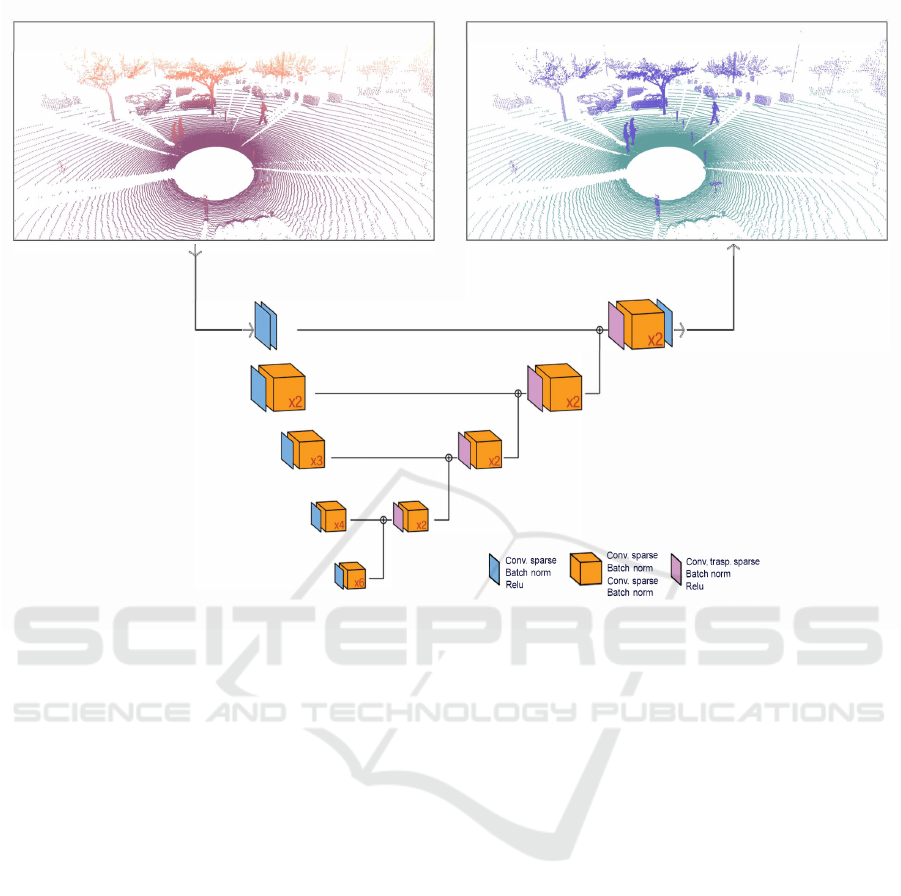
Figure 1: Encoder-decoder conﬁguration employed, MinkUnet34 (Choy et al., 2019).

3.1 Problem Statement

The problem of traversability evaluation is considered

as a semantic segmentation task. A point cloud B is

deﬁned as a set B = {(⃗p

⃗

), i = 1, ... , N}, where

N is the total number of points in the cloud, each

point with coordinates ⃗p

∈ R

expressed in the Li-

DAR reference frame. The traversability condition

of each point is denoted as l

. We consider that each

point is associated to a feature vector

⃗

∈ R

, being

the dimensionality of the input features associated

with each point in the cloud. Each point originated by

the LiDAR sensor is considered to have coordinates

⃗p

= (x

), according to the coordinate system of

the LiDAR sensor itself. The aim is to infer a classiﬁ-

cation l

∈ [0,1] that represents the traversavility con-

dition of the LiDAR point, that is: traversable (1) or

not traversable (0). Thus, the problem can be deﬁned

as a point-wise binary classiﬁcation problem.

3.2 Sparse Convolution

The discrete convolution operation was originally

born in the ﬁeld of signal processing. However, it is

profusely used in image processing and in convolu-

tional Neural Networks.

This type of neural networks, despite being com-

putationally expensive, show great results in problems

such as image classiﬁcation and segmentation. How-

ever, their possible application to sparse data, such as

point clouds, understanding sparsity as the distanc-

ing of the set of values that constitute the data, would

be computationally inefﬁcient due to their sequential

and iterative nature. The operations to be performed

would increase by a cubic factor. As a result, the gen-

eralization of the 2D convolution in images gives rise

to the sparse convolution operation.

This type of discrete convolution allows to fo-

cus the convolution kernel on those discretized spaces

where a non-zero value exists, thus departing from the

classical constant displacement of a 2D mask when

the convolution operation is applied on images. This

idea is particularly efﬁcient in point clouds since there

are many void zones in the cloud and, therefore, the

convolution operation on those areas would only re-

sult in unnecessary time and resource consumption.

Therefore, given any point cloud B, a sparse tensor

S is deﬁned, in turn, formed by two tensors S(T

• T

is deﬁned as a function of the coordinates of

the points that constitute the original cloud B =

{(⃗p

⃗

), i = 1, .. . , N}. An integer part func-

tion is applied to discretize the space. The points

Computing the Traversability of the Environment by Means of Sparse Convolutional 3D Neural Networks

385

are modiﬁed according to a scaling factor, v, that

determines the discretization of the space. In ad-

dition, the batch b

to which each point cloud be-

longs is added to facilitate the training of the net-

work. Thus, the tensor T

is deﬁned as:







¯p







(1)

with ¯p

= f loor(⃗p

) = f loor





As a result, m points belonging to the point cloud

could be discretized in the same voxel ¯p

. Each of

the m points having a different feature vector

⃗

• T

stores and averages the features

⃗

associated

with the m points, that share the same space, i.e.

belong to the same voxel, ¯p

, after applying the

scale factor v and the integer part function.













(2)

where

∑

i=1

⃗

∀

⃗

∈ ¯p

The processing of the input data is carried out using

the Minkowski Engine library

(Choy et al., 2019).

3.3 Sparse 3D Neural Networks

The method presented in this document uses a neu-

ral network with an encoder-decoder conﬁguration,

whose implementation is a sparse variety of the con-

volutional neural network Resnet20 (He et al., 2016)

and the U-net architecture (Ronneberger et al., 2015).

Therefore, the network is mainly divided into two

parts:

• Encoder. The encoding part of the network is

in charge of generating point descriptors based

on the 3D sparse convolution of the features be-

longing to each point. In this case, during this

research, different combinations of input features

were tested, such as: the coordinates of each

point ⃗p

= (x

), the normal vectors of each

point

⃗

= (n

)

and several combinations

of these features. Finally, in this approach the fea-

ture vector is deﬁned as:

⃗

= (n

,Z) where n

https://github.com/NVIDIA/MinkowskiEngine

the Z coordinate of the normal unit vector

⃗

and

the normalized coordinate Z ∈ [0, 1]. This feature

vector includes a natural invariance to rotation to

the point cloud along the vertical axis and, in the

experiments carried out, allowed to obtain the best

results.

• Decoder. The decoding part of the network tries

to reconstruct and extrapolate the latent informa-

tion generated by the encoder to the coordinates

of the input point cloud. For this purpose, trans-

posed convolution layers are used.

The network conﬁguration is shown in Figure 1.

The ﬁgure represents different levels of the neural net-

work in a top-down way, by means of sparse convo-

lutions and sparse residual blocks. In addition, once

the encoder is ﬁnished, the scheme continues in an

ascending way through the concatenation of the de-

scriptors of different levels, indicated by the symbol

⊕, and transposed convolutions to recover the original

shape of the input point cloud.

4 EXPERIMENTAL RESULTS

This section presents the experimental results ob-

tained by the proposed method under different train-

ing conﬁgurations.

4.1 Datasets

A set of freely available databases have been used for

training, validation and testing of the neural network,

in particular:

1) SemanticKITTI: This is a dataset based on the

KITTI Vision Benchmark (Geiger et al., 2012). It

combines odometry positions and point clouds from

different paths through the city of Karlsruhe, Ger-

many, collected by the Velodyne HDL-64E sensor

model. It includes, in total, 22 urban sequences, de-

scribing highly structured environments. Ten of these

sequences contain labels for each point, oriented to

semantic segmentation problems.

2) Rellis-3D (Jiang et al., 2021): It consists of

a dataset of 13,556 point clouds divided into 4 dis-

tinct sequences captured by means of an OS1-64 Li-

DAR. There are labels for each point, and unlike the

SemanticKITTI it describes highly unstructured envi-

ronments and rural roads.

3) SemanticUSL (Jiang and Saripalli, 2021): This

dataset, employed a Clearpath Warthog equipped with

an OS1-64 LiDAR. It includes footage of the cam-

pus and research facilities of the University of Texas.

It contains 1200 point clouds labeled under the same

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

386

(a) KITTI translated. (b) Rellis-3D translated.

Figure 2: Translation of the original labels to two traversability labels.

format as the SemanticKITTI including road scenes,

pedestrian streets and natural environments.

All the mentioned databases contain, approxi-

mately, 25 different labels to which a point can be-

long. These labels include semantic concepts such as:

bush, mud, asphalt, sidewalk... etc. The datasets were

relabeled, attending to the traversability condition,

giving, as a result, only two classes (“traversable” and

“non-traversable”). Figure 2 shows the modiﬁcations

made to the data to ﬁt a binary segmentation problem.

The original classes that have been converted to the

“traversable” class are: sidewalk, asphalt, low vegeta-

tion or grass, dirt, cement and mud. The classes that

have been converted to the class “non-traversable”

are: tree, person, car, truck, building, among others.

4.2 Implementation Details

The neural network model is implemented using the

Minkowski Engine (Choy et al., 2019) and Pytorch.

The network training has been performed using two

NVIDIA 3090 TURBO graphics cards and a ter-

mination criterion that optimizes the F1 metric on

a given balanced validation set. All the code, in-

cluding a guide to the changes made to the original

datasets mentioned in section 4.1, has been developed

in Python and is available at https://github.com/

ARVCUMH/transitability_minkowski.git

As for the training parameters we have employed

a learning ratio of 0.01 and the stochastic gradient de-

scent method (SGD) as the optimizer. In addition,

given the binary nature of our approach we employed

the binary cross-entropy loss function.

In order to reduce the feature processing time in

a real application, the point clouds are voxelized at 3

centimeters. Thus the calculation of the normal vec-

tors is supported by the search of the 6 nearest neigh-

bors of each point by means of a KDtree algorithm

implemented by open3D library (Zhou et al., 2018).

4.3 Training Network

The training stage of the aforementioned datasets has

been carried out using only some SemanticKITTI se-

quences and all of the Rellis-3D sequences. The rea-

son for this choice is to have a balanced number of

training examples including, equally, urban, unstruc-

tured and natural environments. This prevents the net-

work from specializing in a particular type of environ-

ment. The use of the SemanticUSL database is lim-

ited exclusively to test processes in order to demon-

strate the generalization capabilities of the network in

environments never seen during training.

In addition, during the experiments, the network

has been trained using variations of the scaling pa-

rameter v to discretize the space, as it will be shown

in the following sections.

Computing the Traversability of the Environment by Means of Sparse Convolutional 3D Neural Networks

387

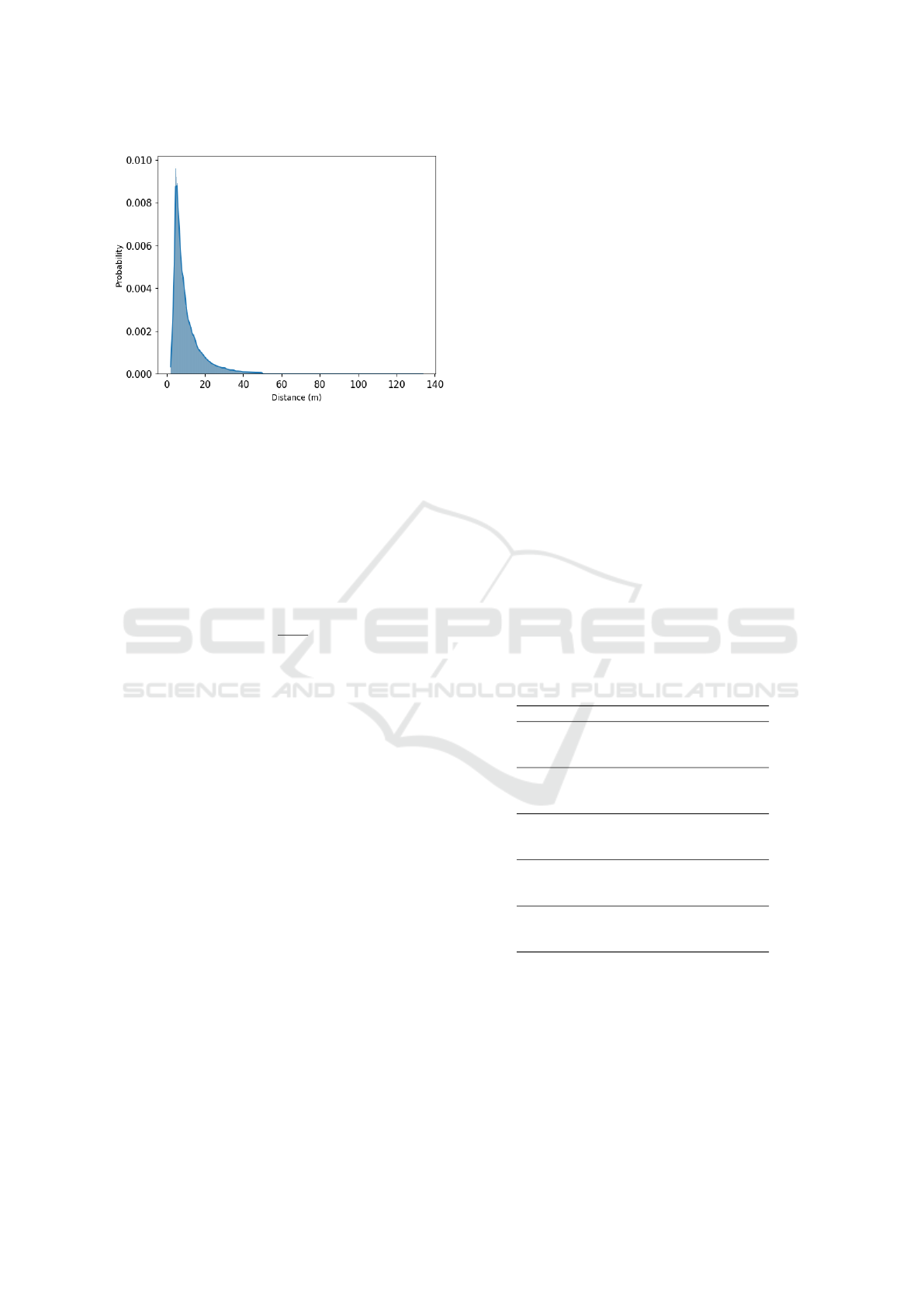
Figure 3: Probability density function according to the dis-

tance of each point to the sensor.

4.4 Distance Effect

By studying how LiDAR planes interact with the sur-

rounding environment, it is clear that the distance, d,

between consecutive LiDAR planes and the ground

plane depends on the angle formed by the intersection

of the two planes mentioned above, α, and the height,

h, at which the LiDAR is located. This relationship is

governed by:

d =

tanα

(3)

Thus, at very far distances, the different laser

planes are far apart. This effect is easy to appreciate

in Figure 2. Consequently, the description of some

regions in the robot environment is very inaccurate,

since the LiDAR point density is very low. This con-

cept is represented in Figure 3, which shows the prob-

ability of the existence of points based on the distance

to the sensor. The probability density function is com-

puted based on the observations of 100 point clouds.

It can be seen how, above 45 meters, the probabil-

ity of ﬁnding points is almost zero. Therefore, as a

solution, it was proposed to consider only the points

that are within a radius of 45 meters from the sensor

and, all the evaluations have been performed under

this condition.

4.5 Quantitative Evaluation

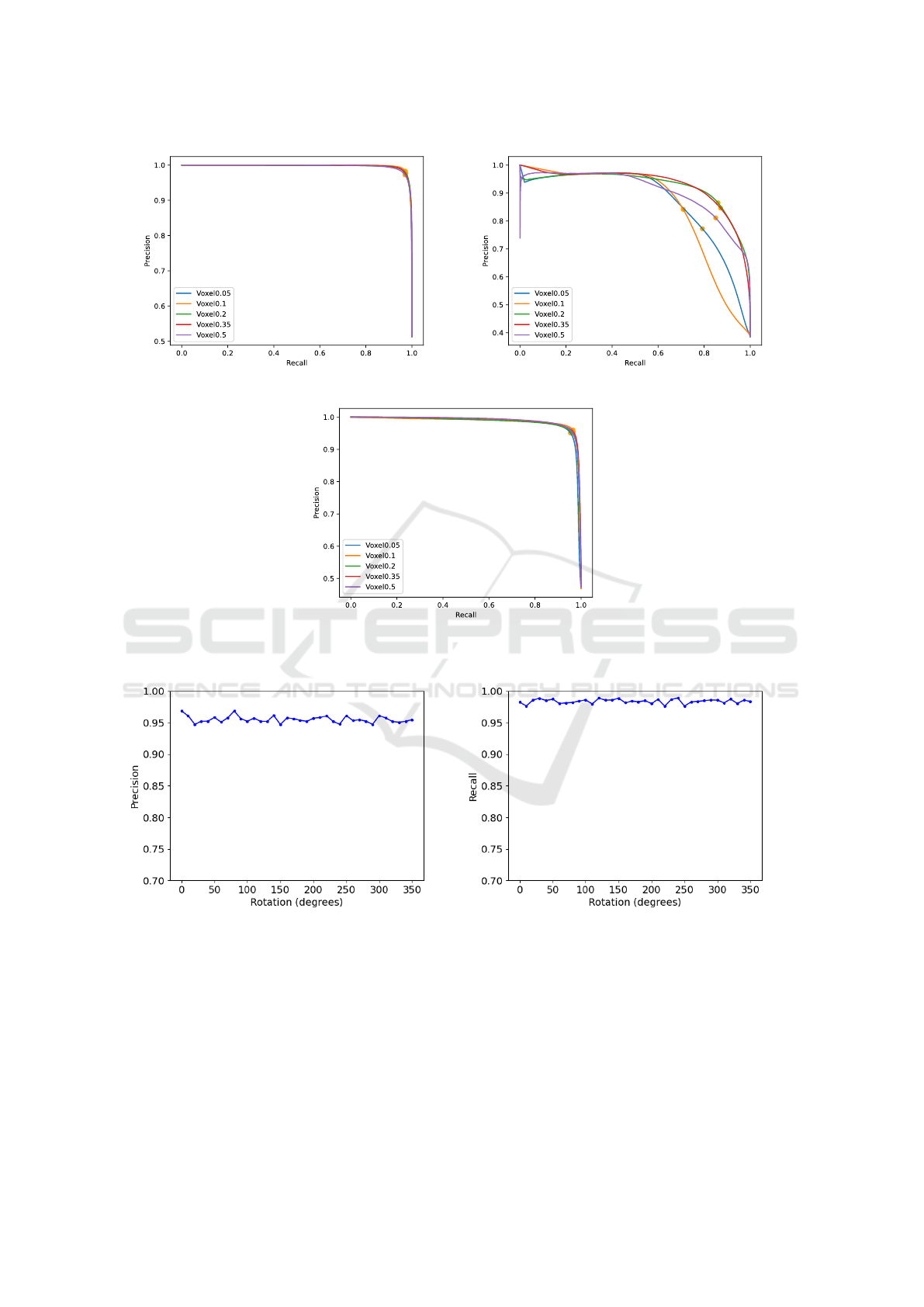
Figure 4 presents the results in terms of precision and

recall. For this purpose, inferences have been made

on all the point clouds that make up the test dataset.

The classiﬁcation of each point inferred by the net-

work is compared with its ground truth, giving rise to

true positives, true negatives, false positives and false

negatives. Figures 4(a) and 4(c), present the results

in urban and structured environments corresponding

to SemanticKITTI and USL datasets. In both ﬁgures,

the precision-recall curve is very close to the maxi-

mum (upper right corner). Therefore we can assume

that the trained models learn the traversable and non-

traversable zones very consistently, achieving accu-

racy and recall values higher than 95% for certain

working points. Moreover, these curves show that the

performance of the network does not depend on the

discretization parameter v (size of voxel, or scale pa-

rameter), since very similar values are achieved.

On the other hand, Figure 4(b) presents the re-

sults when the method is applied to an unstructured

environment. As expected, the results suggest that

it is more difﬁcult to correctly infer which areas are

traversable. Likewise, in this case, the discretization

of the point cloud space is a determining factor, since

differences in performance are observed depending

on this factor. The improvement of some voxels with

respect to others does not seem to follow a logical or-

der for these speciﬁc environments.

Table 1 shows in detail the performance met-

rics obtained according to the scale factor mentioned

above. It can be observed in a more analytical

way how the datasets describing urban environments

lead to very similar results (SemanticKITTI, Seman-

ticUSL). However, in highly unstructured datasets the

performance of the neural network is lower and more

dependent on the discretization of the point cloud.

Table 1: Results with different discretizations of the space

on the described databases.

Dataset Voxel F1 Acc. MIOU

Rellis3D

0.05

0.72 0.82 0.58

Kitti 0.97 0.97 0.94

USL 0.91 0.90 0.83

Rellis3D

0.1

0.72 0.83 0.57

Kitti 0.97 0.97 0.95

USL 0.93 0.93 0.87

Rellis3D

0.2

0.79 0.85 0.66

Kitti 0.97 0.97 0.94

USL 0.93 0.93 0.87

Rellis3D

0.35

0.79 0.86 0.66

Kitti 0.97 0.97 0.94

USL 0.95 0.95 0.91

Rellis3D

0.5

0.78 0.84 0.65

Kitti 0.97 0.97 0.93

USL 0.94 0.94 0.89

In addition, a comparison has been made with

other results found in the literature (Table 2). The

comparison presented in Table 2 includes different

methods focused on semantic segmentation. Accord-

ing to (Fusaro et al., 2023), the datasets were adapted

to a binary problem as we do in section 4.1.

Finally, an experiment was carried out with the

aim of demonstrating the invariance of the obtained

features. Figure 5 shows the variation of the precision

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

388

(a) P-R curve on the SemanticKITTI dataset. (b) P-R curve on the Rellis-3D dataset.

Figure 4: Precision-Recall curves of network inference on test data.

(a) Precision metric in relation to rotation. (b) Recall metric in relation to rotation.

Figure 5: Rotationally invariant results.

and recall metrics of a point cloud rotated between 0

and 360 degrees. Ideally the graph should present a

completely horizontal line, however, due to the dif-

ferent discretization of the space when rotating, the

results vary very slightly, and it can be considered to

be invariant to rotation.

4.6 Qualitative Evaluation

In Figure 6, the results are presented in a visual form,

in which the parameters that compose the confusion

matrix are shown in different colors: true positives

(green), true negatives (purple), false positives (red)

and false negatives (orange). Figures 6(a), 6(c) and

6(e) represent a perfectly labeled point clouds of the

Computing the Traversability of the Environment by Means of Sparse Convolutional 3D Neural Networks

389

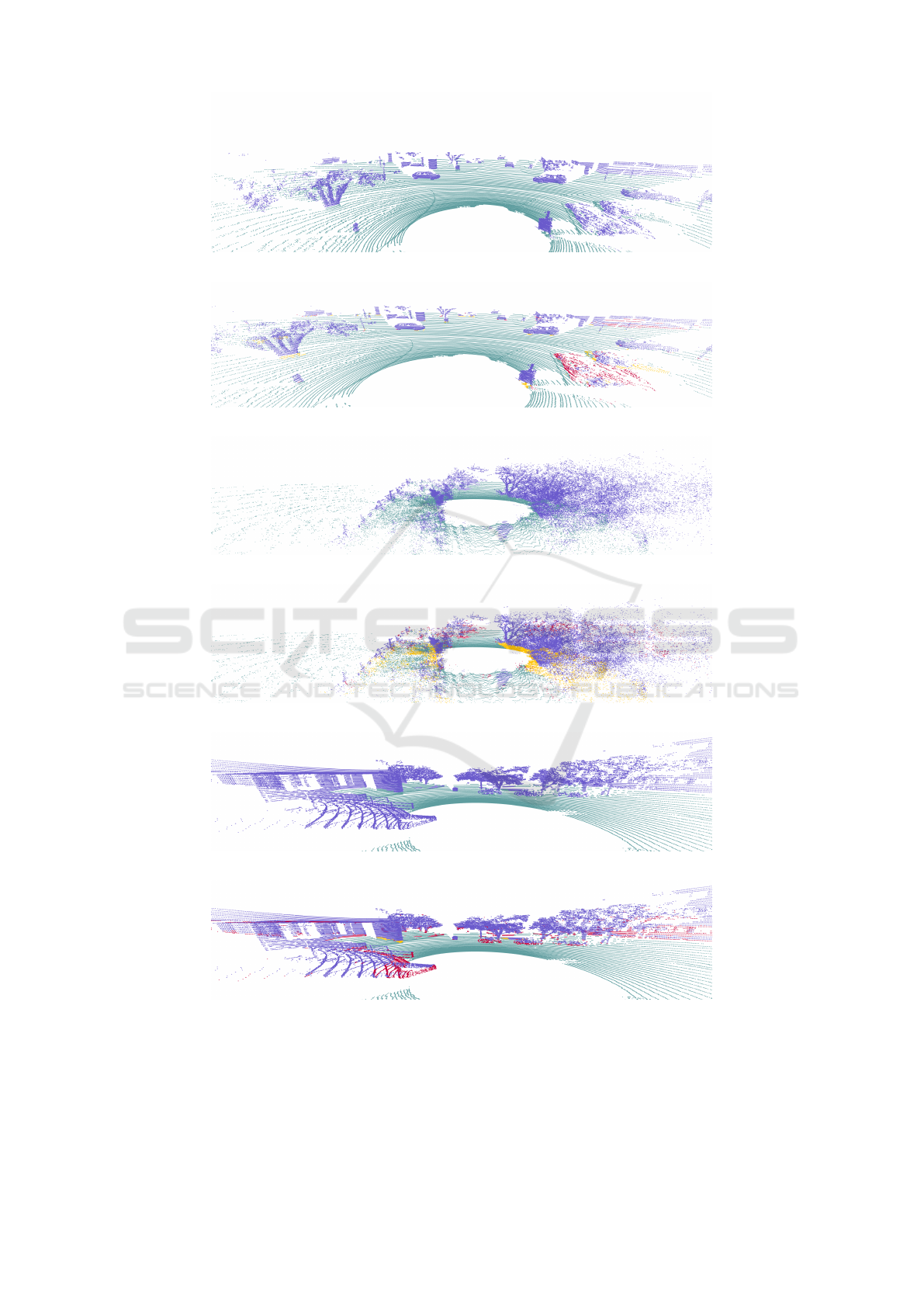
(a) Labeled point cloud from SemanticKITTI dataset.

(b) Network inference from SemanticKITTI dataset.

(d) Network inference from Rellis-3D dataset.

(e) Labeled point cloud from USL dataset.

(f) Network inference from USL dataset.

Figure 6: Visual representation of the inference results of the network. Green: true positives (TP). Purple: true negatives

(TN). Red: false positives (FP). Orange: false negatives (FN).

different datasets with which the method has been

evaluated. On the other hand, Figure 6(b), 6(d) and

6(f) represent the neural network inferences with the

errors in orange and red and the hits in green and pur-

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

390

(a) Original point cloud. (b) Point cloud rotated 45 degrees.

Figure 7: Inference invariant to rotation.

Table 2: Results of different approaches on SemanticKITTI

sequences 0-10. With [1]: (Redmon and Farhadi, 2018),

[2]: (Wu et al., 2018), [3]: (Wu et al., 2019), [4]: (Qi et al.,

2017), [5]: (Fusaro et al., 2023).

Method Accuracy F1 mIoU

[1] 93.4 93.0 87.4

[2] 90.1 89.4 81.4

[3] 92.3 91.9 85.5

[4] 90.0 93.0 87.4

[5] 89.2 91.4 84.9

Ours 96.6 95.9 92.3

ple as described above. False positives tend to appear

in highly unstructured areas. False negatives appear

near the edges found between two adjacent geome-

tries.

At this point, it is important to consider that false

positives (classiﬁed by the network as traversable, but

which are really not traversable) are really dangerous

in a robot navigation task.

In the same way that before it has been shown that

the method is invariant to rotation in a general way,

we can directly observe this fact in Figure 7. This ﬁg-

ure shows the inferences of the neural network for the

same point cloud rotated 45 and 90 degrees in Figures

7(b) and Figure 7(c) respectively.

5 CONCLUSION

In this paper have been presented a method for

traversability estimation in point clouds using a sparse

neural network with an encoder-decoder conﬁgura-

tion. An analysis in terms of voxel size has been per-

formed on different datasets.

The results obtained demonstrate a high robust-

ness of the solution both in highly structured and nat-

ural environments and improve the results of the ap-

proaches that are found in the literature. In particular,

the study shows that the estimation of traversability

performs very well in semi-structured environments

(SemanticKITTI, SemanticUSL). It is a more compli-

cated task in highly disordered natural environments

(Rellis-3D). It has also been shown that the results are

invariant to changes in rotation in the same environ-

ment, giving rise to small variations that do not gen-

erally affect the assessment of the traversability of the

space.

As future work, we plan to merge the visual in-

formation with the LiDAR representation to make the

method more consistent. In addition, we plan to test

the neural network on different robots with different

sensors. Finally, we plan to address the problem of

space traversability under a continuous (non-binary)

paradigm that depends in some way also on the phys-

ical characteristics of the robot and not only on the

terrain.

Computing the Traversability of the Environment by Means of Sparse Convolutional 3D Neural Networks

391

ACKNOWLEDGEMENTS

This work has been funded by the ValgrAI

Foundation, Valencian Graduate School and Re-

search Network of Artiﬁcial Intelligence through

a predoctoral grant. In addition, this publica-

tion is part of the project TED2021-130901B-I00,

funded by MCIN/AEI/10.13039/501100011033 and

by the European Union “NextGenerationE”/PRTR”

and of the projects PROMETEO/2021/075, and

GIGE/2021/150, funded by the Generalitat Valen-

ciana.

REFERENCES

Bellone, M., Reina, G., Caltagirone, L., and Wahde, M.

(2017). Learning traversability from point clouds in

challenging scenarios. IEEE Transactions on Intelli-

gent Transportation Systems, 19(1):296–305.

Chen, Z., Zhang, J., and Tao, D. (2019). Progressive lidar

adaptation for road detection. IEEE/CAA Journal of

Automatica Sinica, 6(3):693–702.

Choy, C., Gwak, J., and Savarese, S. (2019). 4D spatio-

temporal convnets: Minkowski convolutional neural

networks. In Proceedings of the IEEE/CVF con-

ference on computer vision and pattern recognition,

pages 3075–3084.

Fan, R., Wang, H., Cai, P., and Liu, M. (2020). Sne-

roadseg: Incorporating surface normal information

into semantic segmentation for accurate freespace de-

tection. In European Conference on Computer Vision,

pages 340–356. Springer.

Frey, J., Hoeller, D., Khattak, S., and Hutter, M. (2022). Lo-

comotion policy guided traversability learning using

volumetric representations of complex environments.

In 2022 IEEE/RSJ Int. Conf. on Intelligent Robots and

Systems (IROS), pages 5722–5729. IEEE.

Fusaro, D., Olivastri, E., Evangelista, D., Imperoli, M.,

Menegatti, E., and Pretto, A. (2023). Pushing the

limits of learning-based traversability analysis for au-

tonomous driving on cpu. In Intelligent Autonomous

Systems 17: Proceedings of the 17th Int. Conf. IAS-17,

pages 529–545. Springer.

Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready

for autonomous driving? the kitti vision benchmark

suite. In 2012 IEEE conference on computer vision

and pattern recognition, pages 3354–3361. IEEE.

Gu, S., Zhang, Y., Tang, J., Yang, J., and Kong, H. (2019).

Road detection through crf based lidar-camera fusion.

In 2019 International Conference on Robotics and Au-

tomation (ICRA), pages 3832–3838. IEEE.

Han, L., Gao, F., Zhou, B., and Shen, S. (2019). Fiesta:

Fast incremental euclidean distance ﬁelds for online

motion planning of aerial robots. In 2019 IEEE/RSJ

Int. Conf. on Intelligent Robots and Systems (IROS),

pages 4423–4430. IEEE.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-

ual learning for image recognition. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 770–778.

Hornung, A., Wurm, K. M., Bennewitz, M., Stachniss, C.,

and Burgard, W. (2013). Octomap: An efﬁcient prob-

abilistic 3D mapping framework based on octrees. Au-

tonomous robots, 34:189–206.

Jiang, P., Osteen, P., Wigness, M., and Saripalli, S. (2021).

Rellis-3D dataset: Data, benchmarks and analysis.

In 2021 IEEE Int. Conf. on robotics and automation

(ICRA), pages 1110–1116. IEEE.

Jiang, P. and Saripalli, S. (2021). Lidarnet: A boundary-

aware domain adaptation model for point cloud se-

mantic segmentation. In 2021 IEEE Int. Conf. on

Robotics and Automation (ICRA), pages 2457–2464.

IEEE.

Kragh, M., Jørgensen, R. N., and Pedersen, H. (2015). Ob-

ject detection and terrain classiﬁcation in agricultural

ﬁelds using 3D lidar data. In Computer Vision Sys-

tems: 10th Int. Conf., ICVS 2015, Copenhagen, Den-

mark, July 6-9, 2015, Proceedings, pages 188–197.

Springer.

Langer, D., Rosenblatt, J., and Hebert, M. (1994). A

behavior-based system for off-road navigation. IEEE

Transactions on Robotics and Automation, 10(6):776–

783.

Martinez, J. L., Moran, M., Morales, J., Robles, A., and

Sanchez, M. (2020). Supervised learning of natural-

terrain traversability with synthetic 3D laser scans.

Applied Sciences, 10(3):1140.

Moravec, H. and Elfes, A. (1985). High resolution maps

from wide angle sonar. In Proceedings. 1985 IEEE

Int. Conf. on robotics and automation, volume 2,

pages 116–121. IEEE.

Oleynikova, H., Taylor, Z., Fehr, M., Siegwart, R., and Ni-

eto, J. (2017). Voxblox: Incremental 3D euclidean

signed distance ﬁelds for on-board mav planning. In

2017 IEEE/RSJ Int. Conf. on Intelligent Robots and

Systems (IROS), pages 1366–1373. IEEE.

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Point-

net: Deep learning on point sets for 3D classiﬁcation

and segmentation. In Proceedings of the IEEE con-

ference on computer vision and pattern recognition,

pages 652–660.

Razani, R., Cheng, R., Taghavi, E., and Bingbing, L.

(2021). Lite-hdseg: Lidar semantic segmentation us-

ing lite harmonic dense convolutions. In 2021 IEEE

Int. Conf. on Robotics and Automation (ICRA), pages

9550–9556. IEEE.

Redmon, J. and Farhadi, A. (2018). Yolov3: An incremental

improvement. arXiv preprint arXiv:1804.02767.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-

net: Convolutional networks for biomedical image

segmentation. In Medical Image Computing and

Computer-Assisted Intervention–MICCAI 2015: 18th

Int. Conf., Munich, Germany, October 5-9, 2015, Pro-

ceedings, Part III 18, pages 234–241. Springer.

Vapnik, V. (1999). The nature of statistical learning theory.

Springer science & business media.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

392

Velas, M., Spanel, M., Hradis, M., and Herout, A. (2018).

CNN for very fast ground segmentation in velodyne

lidar data. In 2018 IEEE Int. Conf. on Autonomous

Robot Systems and Competitions (ICARSC), pages

97–103. IEEE.

Wang, P.-S., Liu, Y., Guo, Y.-X., Sun, C.-Y., and Tong, X.

(2017). O-CNN: Octree-based convolutional neural

networks for 3D shape analysis. ACM Transactions

On Graphics (TOG), 36(4):1–11.

Wellhausen, L., Dosovitskiy, A., Ranftl, R., Walas, K., Ca-

dena, C., and Hutter, M. (2019). Where should i

walk? predicting terrain properties from images via

self-supervised learning. IEEE Robotics and Automa-

tion Letters, 4(2):1509–1516.

Wu, B., Wan, A., Yue, X., and Keutzer, K. (2018). Squeeze-

seg: Convolutional neural nets with recurrent crf

for real-time road-object segmentation from 3D lidar

point cloud. In 2018 IEEE Int. Conf. on robotics and

automation (ICRA), pages 1887–1893. IEEE.

Wu, B., Zhou, X., Zhao, S., Yue, X., and Keutzer, K. (2019).

Squeezesegv2: Improved model structure and unsu-

pervised domain adaptation for road-object segmenta-

tion from a lidar point cloud. In 2019 Int. Conf. on

Robotics and Automation (ICRA), pages 4376–4382.

IEEE.

Xiao, X., Liu, B., Warnell, G., and Stone, P. (2022). Motion

planning and control for mobile robot navigation us-

ing machine learning: a survey. Autonomous Robots,

46(5):569–597.

Zhou, Q.-Y., Park, J., and Koltun, V. (2018). Open3d: A

modern library for 3d data processing. arXiv preprint

arXiv:1801.09847.

Computing the Traversability of the Environment by Means of Sparse Convolutional 3D Neural Networks

393