Experimental Validation of an Actor-Critic Model Predictive Force

Controller for Robot-Environment Interaction Tasks

Alessandro Pozzi

1 a

, Luca Puricelli

1 b

, Vincenzo Petrone

2 c

, Enrico Ferrentino

2 d

Pasquale Chiacchio

2 e

, Francesco Braghin

1 f

and Loris Roveda

3 g

Department of Mechanical Engineering, Politecnico di Milano, 20133 Milano, Italy

Department of Computer Engineering, Electrical Engineering and Applied Mathematics (DIEM), University of Salerno,

84084 Fisciano, Italy

Istituto Dalle Molle di Studi sull’Intelligenza Artiﬁciale (IDSIA), Scuola Universitaria Professionale della Svizzera

Italiana (SUPSI), Universit

a della Svizzera Italiana (USI), 6962 Lugano, Switzerland

Keywords:

Physical Robot-Environment Interaction, Artiﬁcial Neural Networks, Optimized Interaction Control,

Impedance Control.

Abstract:

In industrial settings, robots are typically employed to accurately track a reference force to exert on the sur-

rounding environment to complete interaction tasks. Interaction controllers are typically used to achieve this

goal. Still, they either require manual tuning, which demands a signiﬁcant amount of time, or exact modeling

of the environment the robot will interact with, thus possibly failing during the actual application. A signiﬁcant

advancement in this area would be a high-performance force controller that does not need operator calibration

and is quick to be deployed in any scenario. With this aim, this paper proposes an Actor-Critic Model Pre-

dictive Force Controller (ACMPFC), which outputs the optimal setpoint to follow in order to guarantee force

tracking, computed by continuously trained neural networks. This strategy is an extension of a reinforcement

learning-based one, born in the context of human-robot collaboration, suitably adapted to robot-environment

interaction. We validate the ACMPFC in a real-case scenario featuring a Franka Emika Panda robot. Com-

pared with a base force controller and a learning-based approach, the proposed controller yields a reduction

of the force tracking MSE, attaining fast convergence: with respect to the base force controller, ACMPFC

reduces the MSE by a factor of 4.35.

1 INTRODUCTION

1.1 Context

Most of nowadays manufacturing processes require

the massive employment of robots. Industries are in-

creasingly deploying manipulators in their production

processes to accomplish interaction tasks like polish-

ing, deburring, or assembly, with the aim of increas-

ing the levels of quality and customization of the de-

livered products.

https://orcid.org/0000-0002-6460-4669

https://orcid.org/0000-0003-1736-0822

https://orcid.org/0000-0003-4777-1761

https://orcid.org/0000-0003-0768-8541

https://orcid.org/0000-0003-3385-8866

https://orcid.org/0000-0002-0476-4118

https://orcid.org/0000-0002-4427-536X

Given the wide range of practical scenarios ma-

nipulators are employed in, robot control is one of

the major interests of the current scientiﬁc research,

especially in the industrial sector. In order to accom-

modate the propensity of manufacturers to improve

the cost, accuracy and throughput of their production

plants, in the last decades researchers have proposed

a vast spectrum of advantageous alternatives to classi-

cal control techniques like the well-known and largely

used linear PID controllers.

Optimal control is among the most consolidated

disciplines in advanced control, given its capability

of explicitly optimizing a certain objective function,

appropriately parameterized to maximize desired per-

formance indices, according to the task requirements.

Generally speaking, the ﬁelds of application of opti-

mal control frameworks cover a broad variety of sce-

narios: in principle, they are suitable to optimize any

394

Pozzi, A., Puricelli, L., Petrone, V., Ferrentino, E., Chiacchio, P., Braghin, F. and Roveda, L.

Experimental Validation of an Actor-Critic Model Predictive Force Controller for Robot-Environment Interaction Tasks.

DOI: 10.5220/0012160700003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 394-404

ISBN: 978-989-758-670-5; ISSN: 2184-2809

system formulated as a dynamic model, from simple

linear integrators (Preitl et al., 2006) to complex bio-

logical systems (Rigatos et al., 2016).

In robotics, one can beneﬁt from optimizing nu-

merous quantities, e.g. trajectory tracking or joint vi-

bration (Mohd Hanif et al., 2021), to ensure accu-

racy in the performed task. This fundamental prob-

lem can be addressed with various approaches, such

as fractional-order control (Atas¸lar-Ayyıldız, 2023) or

double PID controllers to manage both motor position

and velocity (Ucgun et al., 2022). Another popular

technique in this context is fuzzy logic control, used

to improve the system stability, rise time, and steady-

state error (Obadina et al., 2022). Furthermore, ex-

ploiting optimization algorithms like spiral dynam-

ics algorithms (Kasruddin Nasir et al., 2021) and

particle swarm optimization (Sathish Kumar et al.,

2023), fuzzy logic controllers can be optimally tuned

to tackle trajectory and velocity tracking (Liu et al.,

2022).

1.2 Related Works

Trajectory-tracking accuracy is not the only perfor-

mance roboticists aim at optimizing: indeed, one fun-

damental feature to control, particularly in industrial

applications, is robot-environment interaction. To this

aim, interaction controllers are adopted to guaran-

tee stability and safety of the working environment

while accurately tracking precise force proﬁles, so as

to maximize the production quality.

Delivering the aforementioned characteristics is

the core objective of interaction controllers: the pi-

oneering work in (Mason, 1981) set off the divi-

sions of interaction control strategies into two macro-

categories: direct force control (Khatib, 1987) and

impedance control (Hogan, 1984), with the latter be-

ing typically preferred to the former for its capability

of inherently providing the manipulator with a com-

pliant behavior. Unfortunately, impedance controllers

lack accurate force tracking, a feature requiring, as

demonstrated in (Jung et al., 2004), a complete and

exact characterization of the environment, which is,

in general, a utopian intent to accomplish.

Therefore, impedance controllers with force-

tracking capabilities have been widely addressed

in literature with various strategies, from variable

impedance (Jung et al., 2004; Duan et al., 2018;

Roveda et al., 2020; Shu et al., 2021) or variable

stiffness (Lee and Buss, 2008) techniques to refer-

ence generation methods (Seraji and Colbaugh, 1997;

Liang et al., 2018; Roveda et al., 2020; Li et al.,

2023): recently, (Roveda and Piga, 2021) proposed

using a PI direct force control law as reference gener-

ator for an inner-loop impedance controller.

Learning methods are speciﬁcally suitable

for robot-environment interaction tasks: these

optimization-based approaches are indeed a powerful

tool to learn unmodeled effects that can inﬂuence

the dynamics of the controlled plant, overcoming

the main limitation of the abovementioned standard

techniques, i.e. the human effort in tuning the

additional parameters needed by the introduced

force control law. For this reason, researchers are

currently focusing on applying AI-based strategies

on impedance controllers for parameter tuning

(Zhang et al., 2021) or residual action computation

(Johannink et al., 2019; Puricelli et al., 2023). Other

common approaches are exploiting neural networks

to estimate the human-robot (Roveda et al., 2022)

or robot-environment (Peng et al., 2021) interaction

dynamics, or adopting reinforcement learning (Jo-

hannink et al., 2019; Roveda et al., 2022) to optimize

a certain task. Most of them are task-speciﬁc, e.g.

(Zhang et al., 2021), and require a considerable

amount of trials (or simulation-to-real transfer) to

reach optimal performance (Johannink et al., 2019).

1.3 Contribution

This paper proposes an Actor-Critic Model Predictive

Force Controller (ACMPFC) capable of providing

force-tracking capabilities to a low-level impedance

controller. The ACMPFC is composed of two con-

trol loops: the outer loop (which we also term high-

level controller) computes a setpoint for the inner-

loop impedance controller to accurately follow a de-

sired force reference.

The high-level control strategy makes use of a

Reinforcement Learning (RL) approach, previously

used for physical human-robot collaboration (Roveda

et al., 2022): the contribution of this work is hence

to demonstrate how such a technique can be adapted

for robot-environment interaction tasks, guaranteeing

precise force tracking. This feature is fundamental

in several practical use-cases, e.g. welding, cutting or

polishing, for which our method delivers better per-

formance compared to standard controllers.

We have discussed in Sections 1.1 and 1.2 that op-

timal control and learning control are paramount for

improving the performance of robot-environment in-

teraction controllers. Therefore, motivated by the dis-

cussed necessities, our method exploits both frame-

works. Indeed, the ACMPFC makes uses of Neural

Networks (NNs) for a two-fold objective: (i) form-

ing a Model Approximator (MA), used for estimating

the interaction dynamics, and (ii) developing an Ac-

tor-Critic strategy for the computation of the optimal

Experimental Validation of an Actor-Critic Model Predictive Force Controller for Robot-Environment Interaction Tasks

395

setpoint to track.

We show that ACMPFC can reduce the force-

tracking error when compared to both a general-

purpose PI Force Controller (PIFC) (Roveda and

Piga, 2021) and a different AI-based optimal con-

troller, known as ORACLE (Puricelli et al., 2023).

In particular, ACMPFC outperforms PIFC in terms of

tracking accuracy, and, at the same time, it overcomes

the main disadvantage of ORACLE, which is a con-

sistent time delay in exerting the desired force proﬁle.

All the experiments are run on a real manipulator, i.e.

the Franka Emika’s Panda robot shown in Figure 1,

whose kinematic structure consists of 7 serial revo-

lute joints.

The remainder of this article is structured as fol-

lows. Section 2 elaborates on the design of the pro-

posed methodology, whereas Section 3 presents the

results obtained by its employment; Section 4 con-

cludes the paper, discussing on the attained achieve-

ments and brieﬂy presenting possible future develop-

ments.

2 METHODOLOGY

The ACMPFC is a RL-based strategy that provides

enhanced force-tracking capabilities to an impedance

controller. Given a desired wrench to exert on the

environment, it provides the underlying impedance

controller, not able to follow the reference wrench

by itself, with the correct setpoint to track. The

whole architecture, illustrated in the diagram of Fig-

ure 2, consists of the following components: (i) an

inner-loop impedance controller, that ensures a sta-

ble compliant behavior with respect to the envi-

ronment; (ii) three Feed-Forward Neural Networks

(FFNNs) that, by cooperation, constitute the out-

er-loop controller, computing the optimal setpoint for

the low-level impedance controller; (iii) data stor-

age, including the trajectories to execute to train the

ACMPFC over the episodes. All these components

are described in detail in the next sections.

2.1 Impedance Controller

In order to be able to compare the ACMPFC with the

control architectures in (Roveda and Piga, 2021; Puri-

celli et al., 2023), it is necessary to adopt the same

low-level impedance controller. This inner-loop con-

troller imposes the desired compliance on the robot’s

end-effector (EE) while controlling a setpoint pose,

that will be provided in advance by the outer-loop ref-

erence generator.

A manipulator robot with n Degrees of Freedom

Figure 1: Real scenario testing bench. It features a Franka

Emika’s Panda robot coming into contact with the environ-

ment, represented by the white thin block (a) rigidly at-

tached to a larger surface (b) that slides over the plane (c).

This particular conﬁguration reduces stick-slip effects dur-

ing the interaction. The 3D-printed spherical end-effector

(d) provides a small interaction surface with the material,

making it possible to model the contact with the environ-

ment as a spring in the exploration phase (i.e. the phase dur-

ing which the Actor’s bounds are computed, as mentioned

in Section 2.3.4).

(DOFs), performing an m-dimensional task, with m ≤

6 ≤ n, can be described by the following dynamic

model:

M(q

q +C

C(q

q + τ

(

q) + g

g(q

q) = τ

− J

q) f

where M

M(q

q) ∈ R

n×n

is the manipulator’s inertia ma-

trix, C

C(q

q) ∈ R

n×n

is the matrix accounting for the

Coriolis and centrifugal effects, τ

(

q) ∈ R

n×1

ac-

counts for static and viscous friction, g

g(q

q) ∈ R

n×1

represents the torque exerted on the links by grav-

ity, τ

∈ R

n×1

indicates the impedance control ac-

tion, J

J(q

q) ∈ R

m×n

is the geometric Jacobian, f

∈

m×1

is the vector of wrenches exerted by the robot

end-effector (EE) on the environment. The vectors

q ∈ R

n×1

represent positions, velocities, and ac-

celerations of the manipulator’s joints, respectively.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

396

RL data

storage

Model

Approximator

Critic

Bellman (2)

CEM

Actor

Environment

Robotic arm

Impedance

controller (1)

Force

controller

(Actor)

Reference

wrench and pose

k+1

–

k+1

MA error

–

k+1

∗

Critic error

k+1

...

k+T

∗

k+1

−

k+1

Actor error

Weigths

update

Online block

Physical plant

Input block

Ofﬂine block

Figure 2: ACMPFC functioning scheme. The RL data storage includes the system’s states and actions over the execution of a

trajectory, and forwards them to the NNs for off-line training between consecutive episodes.

The impedance control law with robot dynam-

ics compensation can be written as (Formenti et al.,

2022):

= J

q) f

C(q

q + g

g(q

q), (1)

with

− f

q)M

−1

imp

( f

− K

imp

∆x

x − D

imp

∆

x),

where M

q) ≜





†

M(q



J(q



†

∈ R

m×m

the task-space inertia matrix, with (·)

†

indicating the

pseudo-inverse matrix. ∆x

x ≜ x

− x

x is the error be-

tween the desired EE pose x

and the actual pose

x. With m = 6, x

x = (x,y,z, φ,ϑ, ψ)

represents the

full robot EE pose, composed of position (x,y,z)

and orientation (φ,ϑ, ψ). ∆

x ≜

−

x represents the

pose error derivative. M

imp

∈ R

m×m

are

the impedance control parameters (i.e., mass, damp-

ing, and stiffness diagonal matrices, respectively),

which can be tuned, in accordance to the rules in

(Roveda and Piga, 2021), to ensure a medium-soft

robot-environment interaction and a bandwidth of

2.5Hz. Typically, the coefﬁcients of D

imp

are chosen

as d

imp,i

= 2ξ

imp,i

, with ξ

being the damp-

ing ratio and i = 1,2,.. ., m is the axis index.

2.2 Control Architecture

The high-level controller relies on an Actor-Critic

structure, a RL technique consisting of an agent inter-

acting with an environment with the goal of optimiz-

ing the reward received by performing actions on it.

The system to be controlled is modeled as a Markov

Decision Process (MDP) (Bellman, 1958), i.e. it is

represented as a tuple ⟨S ,A,P,R,λ⟩, where S repre-

sents the ﬁnite set of the system’s states, A is the ﬁnite

set of actions the actor can execute, P(s

k+1

| s

) is

the state transition probability matrix from state s

state s

k+1

by taking the action a

, R(s,a) = E [r | s,a]

is the reward function outputting the expectation of

the reward r obtained from the environment at state s

if the agent’s action is a, and λ ∈ [0; 1] is the discount

factor.

Depending on the environment conﬁguration, the

task objective, and the semantics of the reward func-

tion, the optimization problem can be stated as either

maximization or minimization of the reward function.

In the latter case, the reward function can be inter-

preted, without loss of generality, as a cost function.

Henceforth, we will use the term “reward function”

for convenience.

As a RL algorithm, the ACMPFC’s goal is to ﬁnd

the optimal control policy π

∗

(a | s), which optimizes

the cumulative reward, by continuously interacting

with the environment. The components of the Actor-

Critic strategy are (i) the Actor, i.e. the agent that ap-

plies actions on the environment, modifying its state

and receiving rewards; (ii) the Critic, i.e. the entity

that establishes the value of actions taken by the ac-

tor, given the predicted evolution of the system.

In our case, the system to be controlled is the

robot-environment physical plant: its state is deﬁned

as s

s = (x

x, f

,∆

∆

∆ f

f ), while the action is the control

variable a

a = x

, whose tracking minimizes the force

error ∆ f

f ≜ f

− f

, where f

is the force reference

to exert on the environment, speciﬁed by the task re-

quirements.

Experimental Validation of an Actor-Critic Model Predictive Force Controller for Robot-Environment Interaction Tasks

397

In brief, the controller design is led by the follow-

ing optimization problem:

= argmin {R

R(∆

∆

f )},

where R

R(∆

∆

f ) is the reward function, which will be

formalized later. Note that its argument is the ex-

pected force error ∆

∆

f ≜ f

−

, which depends on

the expected interaction force

. The actual inter-

action force f

is unknown because it strictly de-

pends on the environment, and is known by the agent

through measurements only after the control action x

is applied and the next state is observed.

Here follows a brief explanation of the entities in-

volved in the ACMPFC; additional implementation

details, together with a proof of convergence of the

RL-based algorithm, can be found in (Roveda et al.,

2022).

2.2.1 Actor

The Actor computes the action

a to be taken at state

s, with a FFNN approximating the optimal policy

∗

a | s

s). By minimizing the MSE with respect to

the optimal action a

∗

, computed by the Critic via

the Cross-Entropy Method (which will be explained

next), the learning process will make the Actor’s ac-

tual policy

π tend to the optimal policy π

∗

More speciﬁcally, the Actor’s NN is trained in

agreement with the following optimization problem:

min

∑

i=0



∗

−







with the NN parameters θ

updated applying a

Stochastic Gradient Descent (SGD) optimization.

2.2.2 Critic

The Critic assesses the value of the Actor’s policy by

approximating the action-value function (also called

Q-function) Q

(s,a), returning the value associated

with taking a particular action a in the state s, imple-

mented with a FFNN. Let

≜

Q(s

) be the out-

put of the Critic at time k, computing a different value

for each control direction. The Critic’s NN learning

goal is minimizing the MSE with respect to the op-

timal Q-value Q

∗

, computed according to Bellman’s

equation (Bellman, 1952):

∗

= R

+ λ

k+1

, (2)

where Q

∗

≜ Q

∗

) and R

≜ R

R(s

More formally, the minimization problem yield-

ing the Critic’s NN’s training is the following:

min

∑

i=0



∗

−







with the NN parameters θ

updated applying a SGD

optimization.

It is now worth discussing how our architecture

compares to other common Actor-Critic structures,

i.e. DDPG (Lillicrap et al., 2015), SAC (Haarnoja

et al., 2018) and TD3 (Fujimoto et al., 2018). The

most immediate aspect to highlight is that our archi-

tecture foresees a single NN to implement the Critic,

whereas both SAC and TD3 require two Critic net-

works to explicitly leverage the problem of maxi-

mization bias, with the former employing an addi-

tional value network to compute the Q-value. On the

other hand, DDPG uses a single network, similarly

to our controller: the only difference is that DDPG

exploits two additional NNs, namely the target Ac-

tor and Critic networks, used to compute the target

Q-value Q

∗

needed to train the Critic, while in our ar-

chitecture it is computed with the Bellman equation

in (2).

2.2.3 Cross-Entropy Method

The Cross-Entropy Method (CEM) (de Boer et al.,

2005) computes the optimal action a

∗

so as to maxi-

mize the cumulative reward over a prediction horizon

T , computed by making inference on the Critic, in

fact implementing a Model Predictive Control (MPC)

strategy. The future states {s

}

k+T

i=k+1

are inferred from

the Model Approximator (MA).

The strategy of the algorithm is to sample the ac-

tion space, approximating the distributions of suitable

solutions, assumed to be, e.g., Gaussian. Sampling

from these distributions generates possible candidate

sequences of solutions. The distributions are itera-

tively updated on the basis of the best candidate se-

quences, i.e., in our case, the ones maximizing the cu-

mulative reward. As the algorithm progresses, the dis-

tributions become more and more reﬁned, until con-

vergence to optimal solutions. The pseudo-code de-

scribing its implementation is given in Algorithm 1.

The reader should note that the CEM algorithm

overcomes the problem of overestimation bias, which

is one of the main issues with most Deep Actor-

Critic RL methods. Indeed, by randomly sampling

sequences of actions/states and updating the stochas-

tic distributions’ parameters according to the best se-

quences, the Actor is less inﬂuenced by the inherent

bias of explicitly selecting the action that optimizes

the Q-value computed by only one Critic.

2.2.4 Model Approximator

The Model Approximator estimates the robot-

environment system’s dynamics; thus, it considers the

reduced state s

≜ (x

x, f

) and its evolution over

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

398

Data: current state s

from the RL data

storage

Parameters: T , N

, N

samples

, N

elites

, α

Result: optimal control action a

∗

initialize the mean µ and the standard

deviation σ of the T stochastic distributions

∼ N (µ

,σ

)}

T −1

t=0

;

for iter = 1,2,.. .,N

for j = 1, 2,.. ., N

samples

sample a random sequence of actions

}

T −1

t=0

from D

;

predict the system evolution through

the MA: {s

}

T −1

t=1

, with s

= s

;

evaluate the cumulative reward as

∑

T −1

t=0

T −1

;

end

sort the sequences a

with respect to r

increasing order;

let a

elites

be the best N

elites

sequences;

for t = 0,1, ...,T − 1 do

compute mean µ

elites

and standard

deviation σ

elites

of a

elites

;

update µ

← (1 − α)µ

+ αµ

elites

;

update σ

← (1 − α)σ

+ ασ

elites

;

update D

with the new values of µ

and σ

;

end

Algorithm 1: Cross-Entropy Method (CEM).

time, as the state variable ∆

∆

∆ f

f is not related to its

actual dynamics. In particular, it embeds the transi-

tion of the system between two consecutive states, i.e.

k+1

= s

+ δ





, under action a

, where δ

s is

the MA’s output (Nagabandi et al., 2018), computed

by an ensemble of FFNNs (Chua et al., 2018) at each

time step k. It is exploited by the CEM to propagate

the system’s state over time, hence predicting its evo-

lution.

Thanks to the NN ensemble, the MA allows for

a data-efﬁcient learning, as demonstrated in (Chua

et al., 2018). Opting for different architectures, e.g. a

single FFNN, would result in a less efﬁcient training,

thus requiring either more data or a different learning

process, as in (Nagabandi et al., 2018).

The training procedure aims at minimizing the

MSE with respect to the actual state s

, recorded dur-

ing the execution of an episode, according to the fol-

lowing minimization problem:

min

∑

i=0



−







with the NN parameters θ

updated applying a SGD

optimization.

2.3 Learning Procedure

The control architecture described in Section 2.2

was originally developed and employed in the Q-

Learning-based Model Predictive Variable Impedance

Controller (QLMPVIC) (Roveda et al., 2022), instan-

tiated for a Human-Robot Collaboration (HRC) sce-

nario. Therein, an online learning strategy for the

NNs is implemented: the high-level control loop fre-

quency is set to 6 Hz and every 5 control steps, whose

data are collected in the buffer, the training is per-

formed and the networks’ weights are updated. With

respect to the work in (Roveda et al., 2022), several

modiﬁcations are needed to adapt the learning proce-

dure to a robot-environment scenario.

2.3.1 Ofﬂine Reinforcement Learning

The training of the NNs is performed ofﬂine, i.e.

between two consecutive episodes. This allows the

ACMPFC to work at 1 kHz since, as shown in Fig-

ure 2, during the online phase, the Actor’s weights

are ﬁxed, and its NN is only used to infer the con-

trol action x

. During the episode execution, the sys-

tem’s states and the controller actions are stored in

the buffer, and used in the next episode. This modiﬁ-

cation is crucial for the robot-environment interaction

problem, as the controller must work at the robot’s

control frequency in order to properly manage the in-

teraction forces.

2.3.2 Reward Function

In (Roveda et al., 2022), the objective is minimizing

the exerted wrench f

, so as to make the human in-

teraction as comfortable as possible. So, we intro-

duce a modiﬁcation in the reward function in order to

properly pursue the objective of force tracking. In our

case, the reward function is hence the following:

= c

· | f

(k) − f

(k)| + c

· |x

(k) − x

(k − 1)|,

(3)

where the term | f

(k) − f

(k)| is needed for force

tracking purposes, whereas the term |x

(k) − x

(k −

1)| is needed to reduce overshoot or excessive varia-

tions of the desired set point x

, with operator ‘·’ indi-

cating the element-wise product between vectors. The

coefﬁcients in c

and c

balance the trade-off between

these relative contributions and must be selected by

the user.

2.3.3 Impedance Control Setpoint

The hybrid force/position control law that generates

the setpoint for the impedance controller can be writ-

Experimental Validation of an Actor-Critic Model Predictive Force Controller for Robot-Environment Interaction Tasks

399

ten as follows:

= (I

I − Γ

Γ)x

+ Γ

Γx

where x

is the reference pose, I

I ∈ R

m×m

is the iden-

tity matrix, and, assuming the common case in which

m = 6, Γ

Γ ≜ diag



,γ



is the task speci-

ﬁcation matrix (Khatib, 1987), with γ

= 1 if the i−th

direction is subject to force control, 0 otherwise.

2.3.4 Actor’s Action Space Bounds

Since the controller must always guarantee the safety

of both the robot structure and the working environ-

ment, the Actor’s control action must be limited to

a ﬁxed range. The bounds of this range, as well as

the environment’s rest position x

, can be retrieved in

a preliminary phase, in which the ACMPFC is deac-

tivated, with only the impedance controller running.

During this phase, the robot slowly approaches the

environment, until a force threshold is registered. The

lower bound on x

is set to the position at which x

reached, while the upper bound is set to the position

at which the force threshold is measured.

2.3.5 Contact Position Information Embedment

The last modiﬁcation applied to the Q-LMPVIC

comes consequently to the change of use case. In-

deed, a problem occurs when feeding the NNs with

the data as collected during training: x

x represents an

absolute pose, so if the position of the environment

changes, even slightly, from episode to episode, the

NNs are not able to account for it. Therefore, we pro-

cess the data before the training process, to make all

poses relative. Consider, for instance, the case where

the force reference has to be tracked along the z di-

rection. The resultant ∆z position that will be fed to

the NNs will be ∆z ≜ z − z

. Instead of feeding the

robot’s EE z coordinate directly, subtracting the envi-

ronment position z

allows making the NNs training

and execution independent of the contact position and

dealing only with penetrations.

3 RESULTS

We employ the proposed control approach on a real

scenario, after ﬁrst testing it in simulation. The

real robot test is shown in the attached video

. The

GitHub source code

makes it possible, for interested

users, to reproduce our simulation and test it on new

trajectories.

https://youtu.be/7ysG4lz5lVY

https://github.com/unisa-acg/actor-critic-model-

predictive-force-controller

Table 1: Hyperparameters for ACMPFC NNs: depth indi-

cates the number of fully-connected layers, width indicates

the number of neurons per layer.

Parameter Actor Critic MA

Depth 2 2 3

Width 200 128 300

Learning rate 1e−4 1e−4 1e−3

Optimizer Adam Adam Adam

Loss function MSE MSE MSE

Dropout probability 0.1 0.1 0.2

Activation function ReLU ReLU ReLU

3.1 Task Setup and Materials

Both in simulation and real environments, the

ACMPFC strategy is tested on a Franka Emika’s

Panda robot, a 7-DOF robotic arm. This platform ex-

poses an interface to retrieve, via software, estima-

tions of f

from joint torque measurements. Alterna-

tively, one can use ﬂange-mounted force/torque sen-

sors. The simulation tests are performed in MuJoCo

(Todorov et al., 2012) for a realistic representation of

the real-case scenario. The task consists of moving

the EE, with a ﬁxed orientation, along a planar tra-

jectory, so as to exert a force normal (i.e. along the z

axis) to the xy plane, also termed contact surface, i.e.

Γ = diag (0,0,1, 0,0, 0).

Novel force control techniques are typically val-

idated by assessing their performance, in terms of

force-tracking error, against speciﬁc 1-dimensional

force proﬁles, e.g. constants (Seraji and Colbaugh,

1997; Jung et al., 2004; Liang et al., 2018; Roveda

et al., 2020; Li et al., 2023), step functions (Iskandar

et al., 2023), or sine waves with periods in the order

of seconds (Duan et al., 2018; Shu et al., 2021).

In our scenarios, the manipulator is asked to learn

to track a mixed force reference, consisting of three

subsequent sections: a ramp from 25 N to 35 N, a con-

stant at 35 N, and ﬁnally a sine wave, whose mean

value linearly decreases down to 15 N, of amplitude

8 N and frequency 1.5 Hz, chosen as in (Puricelli

et al., 2023) for a fair comparison.

The ACMPFC performances are placed in opposi-

tion to two other force control strategies, already com-

pared to each other in (Puricelli et al., 2023): one is

based on classical control theory, i.e. a Proportional-

Integral Force Controller (PIFC) (Roveda and Piga,

2021), the other is based on a pre-trained NNs ensem-

ble (ORACLE) (Puricelli et al., 2023). Both control

approaches are conﬁgured with the same parameters

as proposed in (Puricelli et al., 2023).

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

400

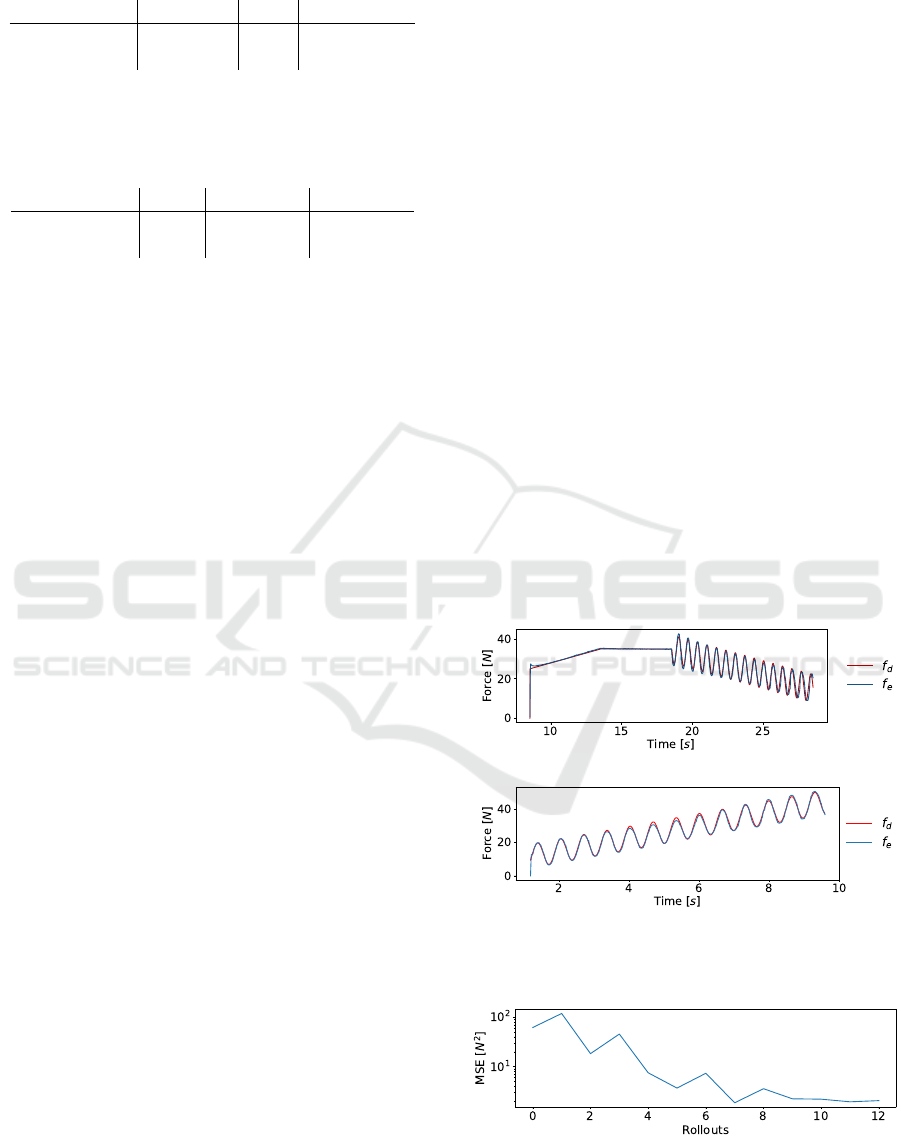
Table 2: Impedance control parameters along the z axis.

Environment M

imp

[kg] ξ K

imp

[N/m]

Simulated 8 1.42 12000

Real 10 1.42 10500

Table 3: MSE [N

] comparison between the PIFC (Roveda

and Piga, 2021), the ORACLE (Puricelli et al., 2023) and

the ACMPFC (ours), with force control active only along

the z axis.

Environment PIFC ORACLE ACMPFC

Simulated 8.16 1.55 3.07

Real 9.62 3.45 2.21

3.2 Implementation Setup

All the modules involved in the architecture shown

in Figure 2 interface with each other via ROS

(Robot Operating System) communication mecha-

nisms. They are developed in Python3, with the NNs

implemented through the PyTorch framework (Paszke

et al., 2019). The discount factor in (2) is set to

λ = 0.95, while the coefﬁcients of the reward func-

tion (3) are chosen as c

= 1 and c

= 2. The param-

eters for the CEM are T = 5, N

= 3, N

samples

= 128,

elites

= 4, and α = 0.95 (see Algorithm 1).

As regards the NNs design, their hyperparameters

are listed in Table 1. In particular, the model approx-

imator column refers to the values of the 3 base esti-

mators of the ensemble. An exponential epoch-based

scheduler is applied to the learning rate to improve the

training speed.

The low-level impedance controller is tuned fol-

lowing the principles of (Roveda and Piga, 2021);

the resulting parameters are listed in Table 2, which

solely reports the gains for the z axis since it is the

only direction of interest for the polishing-like task

considered in this work.

3.3 Simulation Results

As mentioned in Section 3.1, the simulation setup is

set to mimic the real environment of Figure 1 ex-

ploiting the Robosuite framework (Zhu et al., 2020)

to control the virtual robot in the MuJoCo simula-

tor (Todorov et al., 2012). The manipulator is com-

manded via the control scheme of Figure 2, whose

control loop frequency is set at 1 kHz.

The robot, during the execution of a trajectory,

slowly approaches the table and, once the contact

is established, the high-level force control loop is

activated. The gains of the base PIFC are K

0.0008m/N and K

= 0.008 s m/N.

The simulation results are collected in Table 3:

after convergence, the ACMPFC strategy improves

the performances compared to the PIFC, while they

are slightly worse than ORACLE. The force-tracking

MSE = ( f

− f

)

is computed on the reference tra-

jectory described in Section 3.1.

As regards training and convergence, 10 episodes

are needed to reach a stable MSE in tracking. Each

reference trajectory takes 30 seconds and, between

episodes, the NNs training time takes, on average, ca.

60 seconds. These times are achieved on a conﬁgu-

ration composed of an i5-7300HQ CPU, GTX1050Ti

GPU (Mobile), and Ubuntu 20.04.

3.4 Experimental Results

In the real scenario, a thin block is placed onto a

larger and stiffer thin layer, sliding over the table, and

dragged by the robot during motion. Figure 1 dis-

plays the experimental conﬁguration. The parame-

ters are the same as those in Section 3.2, while the

PIFC’s parameters are, as in (Puricelli et al., 2023),

= 0.001 m/N and K

= 0.008 s m/N.

As reported in Table 3, the real-world experiments

conﬁrm a performance improvement for the force

proﬁles under test, plotted in Figure 3. In fact, once

convergence is reached (around the 10

episode, as

shown in Figure 4), the MSE obtained by the PIFC

(Roveda and Piga, 2021) is reduced by a factor of

4.35; also, compared to the ORACLE learning-based

(a) Training trajectory

(b) Test trajectory

Figure 3: ACMPFC force tracking along z direction in the

real scenario after convergence.

Figure 4: ACMPFC Mean Squared Error trend evolution

over the training episodes. Force tracking is active only

along the z direction. Convergence is reached after the 10

episode.

Experimental Validation of an Actor-Critic Model Predictive Force Controller for Robot-Environment Interaction Tasks

401

strategy (Puricelli et al., 2023), our ACMPFC further

reduces the MSE by a factor of 1.56.

It can be noticed that the MSE is high at the be-

ginning of the training process, since the Actor be-

haves almost randomly (in the limited action range,

as speciﬁed in Section 2.3.4), and decreases exponen-

tially as the rollouts progress, demonstrating the ef-

fectiveness of the Actor-Critic RL strategy. The evi-

dent non-monotonic trend might be avoided by low-

ering the NN’s learning rate; however, this would re-

quire more rollouts for convergence. Thus, the MSE

trend is justiﬁed by jumps in the action’s policy space

during the Actor’s training throughout the episodes.

The effect of the convergent phenomenon can be bet-

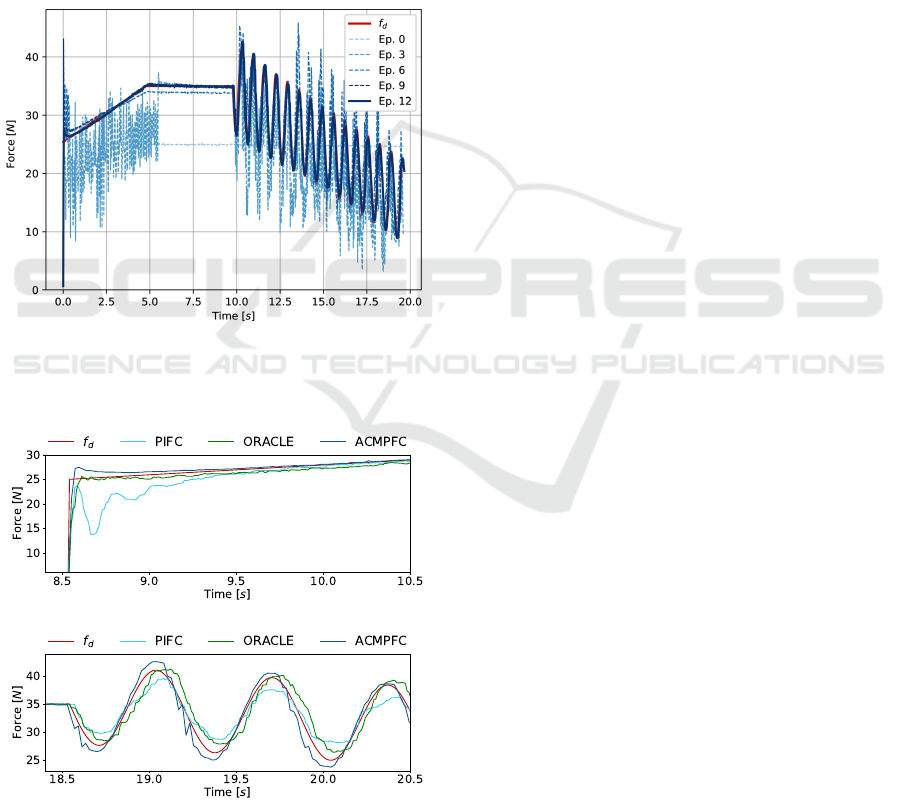
Figure 5: Exerted force over the episodes: throughout the

rollouts, the actual force tends to the desired force, demon-

strating the convergence of the Actor’s policy to the optimal

one.

(a) Contact phase

(b) Sine wave

Figure 6: Force tracking at some critical points. Three

control strategies are compared: PIFC (Roveda and Piga,

2021), ORACLE (Puricelli et al., 2023), and ACMPFC

(ours).

ter visualized in Figure 5: it is immediate to deduce

that, as the rollouts advance, the exerted force proﬁle

tends to the desired one, proving that the Actor’s pol-

icy converges to the optimal one.

Figure 6 shows the performance of the three dif-

ferent strategies at particular points of the trajectory.

The ACMPFC is able to track the reference, with

overshoots of ca. 2 N during the initial contact and

sine peaks. However, the ACMPFC strategy, com-

pared to ORACLE (Puricelli et al., 2023), does not

present any delay in tracking the desired force proﬁle

(as evident from Figure 6b), thus its performances in

terms of MSE are in general better, as quantitatively

conﬁrmed by the results in Table 3.

Finally, the fact that the system is capable of track-

ing force references accurately, by efﬁciently learn-

ing the interaction dynamics, is proven by asking the

robot to perform a validation trajectory, different than

the training one. The training trajectory is that of Fig-

ure 3a, while the system’s performance on the valida-

tion trajectory is reported in Figure 3b; in the latter,

MSE = 2.73 N

is achieved, which is comparable to

the result obtained on the former.

4 CONCLUSIONS

This work proposes an Actor-Critic Model-Predictive

Force Controller (ACMPFC), adapting and validat-

ing an already existing methodology (Roveda et al.,

2022) in a context of accurate force tracking, i.e. ex-

tending its scope from human-robot collaboration to

robot-environment interaction. The strategy is com-

posed of two control loops: a low-level Cartesian

impedance controller, and a high-level NN-based con-

troller, whose inference optimizes the impedance con-

troller’s setpoint, allowing for accurate force tracking

when performing a contact task in an unknown envi-

ronment.

The NNs constituting the high-level controller are

trained according to a RL-based approach. An Actor-

Critic learning strategy computes optimal actions by

making use of a model approximator, i.e. a NN en-

semble modeling the robot-environment interaction

dynamics.

The ACMPFC is tested both through MuJoCo

simulations and in a real scenario, proving capable

of overcoming the performance of a PI direct force

controller (Roveda and Piga, 2021) and the AI-based

ORACLE strategy (Puricelli et al., 2023), in terms

of force-tracking MSE, while achieving fast conver-

gence.

Future work could be devoted to the employment

of the proposed strategy in higher-dimensional tasks.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

402

REFERENCES

Atas¸lar-Ayyıldız, B. (2023). Robust Trajectory Tracking

Control for Serial Robotic Manipulators Using Frac-

tional Order-Based PTID Controller. Fractal and

Fractional, 7(3):250.

Bellman, R. (1952). On the Theory of Dynamic Program-

ming. Proceedings of the National Academy of Sci-

ences, 38(8):716–719.

Bellman, R. (1958). Dynamic programming and stochastic

control processes. Information and Control, 1(3):228–

239.

Chua, K., Calandra, R., McAllister, R., and Levine, S.

(2018). Deep Reinforcement Learning in a Handful of

Trials using Probabilistic Dynamics Models. In Proc.

Adv. Neural Inform. Process. Syst., volume 31, pages

4754–4765.

de Boer, P.-T., Kroese, D. P., Mannor, S., and Rubin-

stein, R. Y. (2005). A Tutorial on the Cross-Entropy

Method. Annals of Operations Research, 134:19–67.

Duan, J., Gan, Y., Chen, M., and Dai, X. (2018). Adap-

tive variable impedance control for dynamic contact

force tracking in uncertain environment. Robot. Au-

ton. Syst., 102:54–65.

Formenti, A., Bucca, G., Shahid, A. A., Piga, D., and

Roveda, L. (2022). Improved impedance/admittance

switching controller for the interaction with a variable

stiffness environment. Complex Eng. Syst., 2(3):12.

Fujimoto, S., van Hoof, H., and Meger, D. (2018). Address-

ing Function Approximation Error in Actor-Critic

Methods. arXiv preprint.

Haarnoja, T., Zhou, A., Abbeel, P., and Levine, S.

(2018). Soft Actor-Critic: Off-Policy Maximum En-

tropy Deep Reinforcement Learning with a Stochastic

Actor. arXiv preprint.

Hogan, N. (1984). Impedance Control: An Approach to

Manipulation. In Proc. Amer. Contrl. Conf., pages

304–313, San Diego, CA, USA.

Iskandar, M., Ott, C., Albu-Sch

affer, A., Siciliano, B., and

Dietrich, A. (2023). Hybrid Force-Impedance Control

for Fast End-Effector Motions. IEEE Robotics and

Automation Letters, 8(7):3931–3938.

Johannink, T., Bahl, S., Nair, A., Luo, J., Kumar, A.,

Loskyll, M., Ojea, J. A., Solowjow, E., and Levine, S.

(2019). Residual Reinforcement Learning for Robot

Control. In Proc. IEEE Int. Conf. Robot. Autom.,

pages 6023–6029, Montreal, QC, Canada.

Jung, S., Hsia, T. C. S., and Bonitz, R. G. (2004). Force

Tracking Impedance Control of Robot Manipulators

Under Unknown Environment. IEEE Trans. Control

Syst. Technol., 12(3):474–483.

Kasruddin Nasir, A. N., Ahmad, M. A., and Tokhi, M. O.

(2021). Hybrid spiral-bacterial foraging algorithm for

a fuzzy control design of a ﬂexible manipulator. Jour-

nal of Low Frequency Noise, Vibration and Active

Control, 41(1):340–358.

Khatib, O. (1987). A uniﬁed approach for motion and force

control of robot manipulators: The operational space

formulation. IEEE J. Robot. Autom., 3(1):43–53.

Lee, K.-k. and Buss, M. (2008). Force Tracking Impedance

Control with Variable Target Stiffness. IFAC Proc.

Vol., 41(2):6751–6756.

Li, K., He, Y., Li, K., and Liu, C. (2023). Adaptive

fractional-order admittance control for force tracking

in highly dynamic unknown environments. Industrial

Robot: the international journal of robotics research

and application.

Liang, X., Zhao, H., Li, X., and Ding, H. (2018). Force

tracking impedance control with unknown environ-

ment via an iterative learning algorithm. In Proc.

IEEE 3rd Int. Conf. Adv. Robot. Mechatron., pages

158–164, Singapore, Singapore.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-

uous control with deep reinforcement learning. arXiv

preprint.

Liu, Y., Jiang, D., Yun, J., Sun, Y., Li, C., Jiang, G., Kong,

J., Tao, B., and Fang, Z. (2022). Self-Tuning Con-

trol of Manipulator Positioning Based on Fuzzy PID

and PSO Algorithm. Frontiers in Bioengineering and

Biotechnology, 9.

Mason, M. T. (1981). Compliance and Force Control for

Computer Controlled Manipulators. IEEE Trans. Syst.

Man Cybern.: Syst., 11(6):418–432.

Mohd Hanif, M. I. F., Ahmad, M. A., and Jui, J. J. (2021).

PID Tuning Method Using Chaotic Safe Experimen-

tation Dynamics Algorithm for Elastic Joint Manip-

ulator. Journal Europ

een des Syst

emes Automatis

es,

54(5):693–698.

Nagabandi, A., Kahn, G., Fearing, R. S., and Levine, S.

(2018). Neural Network Dynamics for Model-Based

Deep Reinforcement Learning with Model-Free Fine-

Tuning. In Proc. IEEE Int. Conf. Robot. Autom., Bris-

bane, QLD, Australia.

Obadina, O. O., Thaha, M. A., Mohamed, Z., and Sha-

heed, M. H. (2022). Grey-box modelling and fuzzy

logic control of a Leader–Follower robot manipulator

system: A hybrid Grey Wolf–Whale Optimisation ap-

proach. ISA Transactions, 129:572–593.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., K

opf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).

PyTorch: An Imperative Style, High-Performance

Deep Learning Library. In Proc. Adv. Neural Inform.

Process. Syst., Red Hook, NY, USA. Curran Asso-

ciates Inc.

Peng, G., Philip Chen, C. L., He, W., and Yang, C. (2021).

Neural-Learning-Based Force Sensorless Admittance

Control for Robots With Input Deadzone. IEEE Trans.

Ind. Electron., 68(6):5184–5196.

Preitl, Z., Precup, R.-E., Tar, J. K., and Tak

acs, M. (2006).

Use of multi-parametric quadratic programming in

fuzzy control systems. Acta Polytechnica Hungarica,

3(3):29–43.

Puricelli, L., Pozzi, A., Petrone, V., Ferrentino, E., Chi-

acchio, P., Braghin, F., and Roveda, L. (2023). Op-

timized Residual Action for Interaction Control with

Learned Environments. TechRxiv Preprint.

Experimental Validation of an Actor-Critic Model Predictive Force Controller for Robot-Environment Interaction Tasks

403

Rigatos, G., Siano, P., Selisteanu, D., and Precup, R.-E.

(2016). Nonlinear Optimal Control of Oxygen and

Carbon Dioxide Levels in Blood. Intelligent Indus-

trial Systems, 3(2):61–75.

Roveda, L., Castaman, N., Franceschi, P., Ghidoni, S., and

Pedrocchi, N. (2020). A Control Framework Deﬁni-

tion to Overcome Position/Interaction Dynamics Un-

certainties in Force-Controlled Tasks. In 2020 IEEE

International Conference on Robotics and Automation

(ICRA), pages 6819–6825.

Roveda, L. and Piga, D. (2021). Sensorless environ-

ment stiffness and interaction force estimation for

impedance control tuning in robotized interaction

tasks. Auton. Robots, 45(3):371–388.

Roveda, L., Testa, A., Shahid, A. A., Braghin, F., and Piga,

D. (2022). Q-Learning-based model predictive vari-

able impedance control for physical human-robot col-

laboration. Artiﬁcial Intelligence, 312:103771.

Sathish Kumar, A., Naveen, S., Vijayakumar, R., Suresh,

V., Asary, A. R., Madhu, S., and Palani, K.

(2023). An intelligent fuzzy-particle swarm optimiza-

tion supervisory-based control of robot manipulator

for industrial welding applications. Scientiﬁc Reports,

13(1):8253.

Seraji, H. and Colbaugh, R. D. (1997). Force Tracking in

Impedance Control. Int. J. Robot. Res., 16(1):97–117.

Shu, X., Ni, F., Min, K., Liu, Y., and Liu, H. (2021).

An Adaptive Force Control Architecture with Fast-

Response and Robustness in Uncertain Environment.

In Proc. IEEE Int. Conf. Robot. Biomim., pages 1040–

1045, Sanya, China.

Todorov, E., Erez, T., and Tassa, Y. (2012). MuJoCo:

A physics engine for model-based control. In Proc.

IEEE Int. Conf. Intell. Robots Syst., pages 5026–5033,

Vilamoura-Algarve, Portugal. IEEE.

Ucgun, H., Okten, I., Yuzgec, U., and Kesler, M. (2022).

Test Platform and Graphical User Interface Design

for Vertical Take-Off and Landing Drones. Roma-

nian Journal of Information Science and Technology,

25(3–4):350–367.

Zhang, X., Sun, L., Kuang, Z., and Tomizuka, M. (2021).

Learning Variable Impedance Control via Inverse Re-

inforcement Learning for Force-Related Tasks. IEEE

Robot. Autom. Lett., 6(2):2225–2232.

Zhu, Y., Wong, J., Mandlekar, A., Mart

ın-Mart

ın, R., Joshi,

A., Nasiriany, S., and Zhu, Y. (2020). robosuite: A

Modular Simulation Framework and Benchmark for

Robot Learning. arXiv preprint.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

404