Robot Path Planning with Safety Zones

Evis Plaku

1 a

, Arben C¸ ela

1,2 b

and Erion Plaku

3 c

AI Laboratory, Tirana Metropolitan University, Sotir Kolea Street, Tirana, Albania

Laboratory of Images, Signals, and Intelligent Systems, ESIEE Paris, Noisy-le-Grand CEDEX, France

Department of Computer Science, George Mason University, Fairfax, Virginia, U.S.A.

Keywords:

Robot Path Planning, Safety Zones.

Abstract:

Path planning is essential for guiding a robot to its destination while avoiding obstacles. In practical scenarios,

the robot is often required to remain within predeﬁned safe areas during navigation. This allows the robot

to divert from its main path during emergencies and follow alternative routes to a safety center. This paper

introduces a novel method to incorporate safety zones into path planning. Each zone is deﬁned by a central

point and a radius. Our approach efﬁciently plans paths to the goal, ensuring that the robot can reach a

safety center without having to travel more than the radius of the safety zone. Using sampling, our approach

constructs a roadmap with navigation routes and identiﬁes safe locations that satisfy the distance requirements

for reaching a safety center. The safe portion of the roadmap is then searched to ﬁnd a path to the goal.

We demonstrate the effectiveness of our approach through simulated experiments in obstacle-rich 2D and 3D

environments, utilizing car and blimp robot models.

1 INTRODUCTION

Path planning plays a crucial role in ensuring that

a robot can successfully reach its destination while

avoiding collisions (Choset et al., 2005). To enhance

safety, a practical approach is to require the robot to

adhere to designated safe areas so that it can promptly

respond to emergencies by diverting from its intended

path and following alternative routes to safety centers.

This is imperative for reducing potential risks and en-

suring the safety of the robot and its surroundings.

Path planning with safety zones holds potential

for diverse domains. Robots in industrial settings or

search-and-rescue missions could utilize path plan-

ning with safety zones to navigate hazardous envi-

ronments or unstable terrains. Autonomous vehicles

could employ safety zones for lane adherence, ob-

stacle response, and handling unpredictable behavior.

Healthcare robots could adhere to safety zones to pri-

oritize patient and staff well-being while delivering

supplies and performing tasks. Overall, the adoption

of path planning with safety zones could enhance re-

liability, efﬁciency, and safety across domains.

https://orcid.org/0009-0002-4042-2673

https://orcid.org/0000-0001-5708-1743

https://orcid.org/0000-0002-6622-386X

Figure 1: Example of path planning with safety zones for

a car robot model. Each safety zone is deﬁned by its cen-

ter (blue cylinder) and radius (blue circle). For each inter-

mediate conﬁguration along the main path to the goal, the

ﬁgure also shows the emergency route (black segments) to

reach a safety center within the distance constraints. If an

emergency path partially overlaps with the main path, only

the non-overlapping portion is visible. The safe locations

(from which a safety center can be reached within the dis-

tance constraints) are shown in yellow, cyan, magenta, and

blue for safety zones 1, 2, 3, and 4, respectively. Videos can

be found at https://tinyurl.com/y4d2urcf.

Toward this objective, this paper makes it possible

to incorporate safety zones into path planning. Each

safety zone consists of a center location and a corre-

sponding radius, representing the maximum permis-

sible distance the robot can travel to reach the cen-

ter. A location is deemed safe if the robot is able

Plaku, E., Çela, A. and Plaku, E.

Robot Path Planning with Safety Zones.

DOI: 10.5220/0012162100003543

In Proceedings of the 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023) - Volume 1, pages 405-412

ISBN: 978-989-758-670-5; ISSN: 2184-2809

405

to reach a safety center while avoiding collisions and

without traveling more than the radius associated with

the safety center. The objective is then to compute a

collision-free path that enables the robot to reach its

goal while remaining within safe locations. In this

way, the robot can always detour to a safety center

in response to emergency situations. Fig. 1 shows an

example of path planning with safety zones.

Path planning with safety zones presents signif-

icant challenges. Even without considering safety

zones, planning a collision-free path is challenging,

particularly in unstructured and obstacle-rich envi-

ronments. The robot must navigate around several

obstacles and maneuver through narrow passages to

reach its goal. When safety zones must be taken into

account, the complexity increases further. The path

planner must now reason about location safety and

generate safety paths from each intermediate location

along the main path. Consequently, this gives rise to

numerous path-planning problems, demanding novel

methods to ensure efﬁcient and safe robot navigation.

To overcome these challenges, our approach

combines sampling-based exploration with discrete

search, enabling safe navigation in unstructured and

obstacle-rich environments. Our approach facili-

tates navigation by constructing a dense roadmap that

connects neighboring locations through collision-free

paths. Safe locations are identiﬁed by searching over

the roadmap from each safety center. Finally, the

path to the goal is computed through a shortest-path

search restricted to the safe portion of the roadmap.

If no such path exists, we add more samples and cre-

ate new connections to improve the roadmap cover-

age. This process of enhancing the roadmap, iden-

tifying safe locations, and searching the safe portion

continues until a solution is found or a runtime limit is

reached. We demonstrate the efﬁcacy of our approach

by conducting simulated experiments in unstructured

2D and 3D environments with numerous obstacles,

employing both car and blimp robot models.

2 RELATED WORK

Sampling-based approaches have proven effective for

path planning in complex environments. One pop-

ular approach is the Probabilistic RoadMap (PRM)

(Kavraki et al., 1996), which constructs a roadmap by

sampling and connecting neighboring robot conﬁgu-

rations to capture the connectivity of the environment.

Various techniques seek to improve sampling near ob-

stacles (Cao et al., 2019), deferring collision checking

(Bohlin and Kavraki, 2000), utilizing machine learn-

ing (Baldoni et al., 2022), or provide asymptotically

optimal solutions (Karaman and Frazzoli, 2011).

Other approaches utilize Rapidly-exploring Ran-

dom Tree (RRT) (LaValle and Kuffner, 2001). En-

hancements include multi-step connections (Kuffner

and LaValle, 2000), regions (Denny et al., 2020), ob-

stacle clearance (Plaku et al., 2017), direct-path su-

perfacets (Plaku et al., 2018), and machine learning

(Wang et al., 2020; Zhao et al., 2022; Bui et al., 2022).

Risk-aware methods aim to compute collision-

free paths that reduce a risk metric (Feyzabadi and

Carpin, 2014; Primatesta et al., 2019). Other methods

incorporate uncertainty reasoning to ensure the safe

execution of planned paths by the robot (Schouwe-

naars et al., 2004; Pepy and Lambert, 2006).

Our proposed approach leverages from PRM the

idea of constructing a roadmap to capture the connec-

tivity of the environment. The roadmap in our case is

denser to provide alternative connections between lo-

cations. Moreover, we introduce the concept of safety

zones and leverage the roadmap to identify safe loca-

tions. By searching the safe portion of the roadmap,

our approach ﬁnds collision-free paths to the goal, en-

suring detours to safe centers from any intermediate

conﬁguration along the planned path. This adaptive

capability is essential to reducing potential risks.

3 PROBLEM FORMULATION

This section deﬁnes the environment, safety zones,

robot models, and the overall problem.

The environment, denoted as W , consists of

obstacles O = {O

,...,O

} and safety zones S =

,...,S

}. Obstacles are often represented as 2D

polygons or 3D triangular meshes. Each S

∈ S is de-

ﬁned by its center and radius, denoted as S

.c and S

.r.

The robot model is a tuple R =

⟨

P , C

⟩

, where P

denotes its geometric shape and C denotes the conﬁg-

uration space. A conﬁguration c =

⟨

p,θ

⟩

∈ C deﬁnes

the position p and orientation θ. The robot models

used in the experiments are shown in Fig. 2. For the

car model, c =

⟨

p = (x,y),θ

⟩

, where θ denotes the ro-

tation in the xy-plane. The blimp can ﬂy parallel to

the xy-plane, so c =

⟨

p = (x,y,z),θ

⟩

A local motion from conﬁguration c

∈ C to

∈ C is denoted as c

⇝ c

and is deﬁned via in-

terpolation, i.e., interp : C × C × [0,1] → C, where

interp(c

,t) = (1 − t)c

+tc

A path is deﬁned as a sequence of conﬁgurations

σ : {1,...,ℓ} → C, where the robot follows the in-

terpolated motion from σ

to σ

i+1

. The notation |σ|

denotes the number of conﬁgurations, i.e., |σ| = ℓ.

The path length is deﬁned as the distance traveled,

i.e., dist(σ) =

∑

|σ|−1

i=1

dist(σ

,σ

i+1

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

406

Figure 2: The robot models used in the experiments.

It is often desirable to ensure that the intermediate

conﬁgurations in σ are no more than a distance d ∈

from each other, i.e., dist(σ, σ

i+1

) ≤ d.

A conﬁguration c ∈ C is collision-free if the robot

does not collide with an obstacle when placed accord-

ing to c. PQP (Larsen et al., 2000) is used to check for

collisions. A path is collision-free if every conﬁgura-

tion in the sequence and the interpolated motions be-

tween intermediate conﬁgurations are collision-free.

A conﬁguration c ∈ C is safe if there is a collision-

free path λ from c to a safety center S

.c such that

dist(λ) ≤ S

.r. Note that some locations within the

ball deﬁned by S

.c and S

.r could be unsafe since, due

to obstacles, there may not be a collision-free path to

a safety center that satisﬁes the distance constraints.

Putting it all together, the input to path planning

with safety zones is the environment W , obstacles

O = {O

,...,O

}, safety zones S = {S

,...,S

}, the

robot model R =

⟨

P , C

⟩

, a maximum distance d be-

tween conﬁgurations, and the initial and goal conﬁg-

urations c

init

goal

∈ C. The objective is to compute a

collision-free path σ from c

init

to c

goal

consisting en-

tirely of safe conﬁgurations. In addition, the approach

should compute a safety path λ

for each intermedi-

ate conﬁguration c

∈ σ. Intermediate conﬁgurations

along σ and each λ

should be within a maximum dis-

tance d from each other. Figs. 1 and 3 provide several

illustrations of path planning with safety zones.

4 METHOD

Our approach has three components. The ﬁrst com-

ponent constructs a roadmap to facilitate navigation

within the safe zones. The second component identi-

ﬁes the safe roadmap nodes, i.e., nodes that can reach

a safety center with a path whose length does not ex-

ceed the radius of the safety zone. The third compo-

nent searches over the safe portion of the roadmap to

ﬁnd a path from the initial to the goal conﬁguration.

Pseudocode is shown in Alg. 1. Details follow.

4.1 Roadmap Construction Within

Safety Zones

The roadmap is represented as a graph G = (V ,E).

Each node v ∈ G.V corresponds to a collision-free

conﬁguration, denoted as v.c. Each edge

⟨

v, u

⟩

∈ G.E

Algorithm 1: Path planning with safety zones.

Input: W : environment; O: obstacles;

S = {S

,.. .,S

}: safety zones; R =

⟨

P ,C

⟩

: robot

model; d: maximum roadmap edge distance; k:

number of roadmap neighbors; nrSamplesToAdd:

roadmap batch size; c

init

goal

∈ C : initial and goal

conﬁgurations; t

max

: runtime limit.

Output: A collision-free path σ from c

init

to c

goal

consisting entirely of safe conﬁgurations, and a

collision-free safety path λ

for each c

∈ σ.

1 G = (V , E) ← (

0);

2 for c ∈ {c

init

goal

.c,...,S

.c} do

3 v.

⟨

c,safe,d

,...,d

⟩

←

ADDNODE(

⟨

c,false,∞, . . . ,∞

⟩

);

4 while TIME() ≤ t

max

5 nrNodes ← |G.V |;

6 for i = 1, . ..,nrSamplesToAdd do

7 c ← SAMPLEVALIDCFG(W ,O, S);

8 v.

⟨

c,safe,d

,...,d

⟩

←

ADDNODE(G,

⟨

c,false,∞, . . . ,∞

⟩

);

9 for i = nrNodes, . ..,|G.V | − 1 do

10 v ← GETNODE(G, i);

11 for u ∈ NEIGHBORS(G,v.c,k) do

12 if ¬COLLISION(W , O,v.c ⇝ u.c)

then ADDEDGE(G,

⟨

v,u

⟩

,d);

13 for S

∈ S do

14 S

.parents ← FINDSAFE(G, S

.c,S

.r);

15 for

⟨

v,parent,cost

⟩

∈ S

.parents do

16 v.safe ← true; v.d

← cost;

17 V

safe

← {v : v ∈ G.V ∧ v.safe = true};

18 E

safe

← G.E ∩ (V

safe

× V

safe

);

19 G

safe

←



safe



;

20 if CONNECTED(G

safe

init

goal

) then

21 σ ← SHORTESTPATH(G

safe

init

goal

);

22 for i = 1, . ..,|σ| do

23 λ

← RETRIEVESAFEPATH(S, σ

);

24 return



σ,λ

,...,λ

|σ|



;

25 return

indicates a collision-free path from v.c to u.c, which

is obtained by interpolation and denoted by v.c ⇝ u.c.

Moreover, each node v maintains information about

the shortest-path distances to each safety center, rep-

resented as v.d

,...,v.d

. The node v is marked as

safe (indicated by a Boolean ﬂag v.safe) if one of these

shortest paths reaches its safety center within the dis-

tance constraints, i.e., v.d

≤ S

.r. In this way, the

roadmap corresponds to a network of collision-free

conﬁgurations interconnected via collision-free paths,

designed to facilitate efﬁcient and safe navigation.

The roadmap construction starts by adding the ini-

tial and goal conﬁgurations, along with the center of

each safety zone, as roadmap nodes (Alg. 1:1–3). The

Robot Path Planning with Safety Zones

407

roadmap is further populated by adding randomly-

generated collision-free conﬁgurations (Alg. 1:6–8).

SAMPLEVALIDCFG repeatedly samples a conﬁguration

until it is not in collision. The sampling is exclusively

conducted within the safety zones, as conﬁgurations

outside these zones are inherently unsafe.

The next stage seeks to connect each node v to its

k-nearest conﬁgurations through collision-free paths

(Alg. 1:9–12). As mentioned earlier, the path from

v to a neighbor u is obtained through interpolation

from v.c to u.c. If any intermediate conﬁguration is

in collision, the edge (v,u) is discarded. To stream-

line this process, we create a mesh that encompasses

all the robot placements along the intermediate con-

ﬁgurations. Subsequently, we employ efﬁcient colli-

sion checking, e.g., PQP, to assess whether the mesh

is in collision. This allows us to efﬁciently determine

the collision-free nature of the entire path, without the

need for individual conﬁguration checks.

If the path from v.c to u.c is collision-free, we con-

nect v and u in the roadmap (Alg. 1:12). However,

if this edge is long, the function ADDEDGE divides it

into smaller segments, each no longer than a speciﬁed

distance d. These segments are then added as individ-

ual edges to the roadmap. This approach ensures that

the roadmap captures the connectivity between nodes

accurately, even for longer edges.

4.2 Identifying Safe Roadmap Nodes

After constructing the roadmap, the next task is to de-

termine which roadmap nodes are safe. To qualify as

safe, a node v must have a roadmap path λ that reaches

the center of a safety zone S

such that dist(λ) ≤ S

.r.

One possible approach to identify the safe nodes is

to perform a shortest-path search from each node in

the roadmap. However, this can be computationally

expensive, especially when the roadmap is dense.

To address this, we utilize Dijkstra’s shortest-path

algorithm (Dijkstra, 1959) and initiate the search from

each safety center (Alg. 1:13–16). The search starting

from S

.c ends when a node is removed from the pri-

ority queue with a path length exceeding S

.r. This is

possible because all the remaining nodes in the queue

will have a path length greater than S

.r, and thus, they

can be excluded from further consideration. By em-

ploying this optimization, we can efﬁciently identify

the safe nodes without the need to run shortest-path

searches from every roadmap node.

Upon completion of the search, we are able to

identify all the nodes that are accessible from S

through paths with a length that does not surpass S

.r.

For each of these nodes, we maintain records of both

the index of the corresponding safety center and the

path length required to reach that safety center. This

information allows us to keep track of the connection

between the nodes and their associated safety centers,

as well as the corresponding path distances. In addi-

tion, each S

maintains the parent map generated by

Dijkstra’s algorithm. The entries in the parent map

are tuples

⟨

v, parent, cost

⟩

, where v serves as the in-

dex key, parent denotes the parent node of v, and cost

represents the path length from S

.c to v. This data

structure enables efﬁcient retrieval and reconstruction

of the paths from the safe nodes to S

.c.

4.3 Searching over the Safe Portion of

the Roadmap

When considering safety zones, the planned path

must only traverse safe nodes. To achieve this, we

eliminate all nodes (and their edges) that are not

marked as safe. This reﬁned subset of the roadmap,

consisting exclusively of safe nodes and edges, is re-

ferred to as the “safe portion” of the roadmap, and is

denoted as G

safe



safe



(Alg. 1:17–19).

To determine the shortest path, we employ A*

(Hart et al., 1968) on G

safe

(Alg. 1:20–21). To save

computational time, we run A* only when we are cer-

tain that a path exists in G

safe

from c

init

to c

goal

. This

certainty is achieved by utilizing a disjoint-set data

structure (Galler and Fisher, 1964), which helps us

keep track of the connected components within G

safe

Let σ denote the path obtained from A*. In ad-

dition to σ, we also require the sub-paths from each

conﬁguration in σ to a corresponding safety center

(Alg. 1:24–25). To reconstruct these sub-paths, we

utilize the parent maps generated by Dijkstra’s algo-

rithm, which are stored by each safety zone S

. In

cases where σ

is associated with multiple safety cen-

ters, we select the shortest path among them. This en-

sures that we obtain the most efﬁcient path from each

conﬁguration in σ to its corresponding safety center.

If it is determined that there is no path connect-

ing the initial and goal conﬁgurations within the G

safe

graph, it could be due to inadequate sampling or in-

sufﬁcient connections within the roadmap. In such

cases, we return to the roadmap construction stage

and continue populating the roadmap with additional

nodes and establishing new connections.

Following the updated roadmap construction, we

once again identify the nodes that are considered

safe and perform a search exclusively within the safe

portion of the roadmap. This iterative process of

augmenting the roadmap, determining safe nodes,

and conducting searches over the safe portion of the

roadmap is repeated until a solution path is discovered

or a predeﬁned runtime limit is reached.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

408

5 EXPERIMENTS AND RESULTS

Experiments are conducted in simulation using a car

and a blimp robot model operating in unstructured en-

vironments with numerous obstacles.

5.1 Tree-Based Path Planner for

Baseline Comparison

To the best of our knowledge, there is no existing ap-

proach that addresses the speciﬁc problem considered

in this paper. To establish a baseline, we developed

an alternative method comprised of a a main and an

auxiliary planner, both based on RRT. Before adding

a node to the main tree, the auxiliary planner is in-

voked to compute a safety path from the node to the

center of a safety zone, ensuring the path length stays

within the safety zone’s radius. The node is added to

the tree only if a valid safety path is found.

Pseudocode is shown in Alg. 2. In each iteration, a

target conﬁguration is randomly sampled. Small steps

are then taken from the nearest tree node v

near

toward

the target along an interpolation path until the target

is reached or a collision is detected. If the goal is

reached, a solution is found. This process of sampling

a target and expanding a branch from the nearest node

toward the target is repeated until a solution is found

or a runtime limit is reached.

The auxiliary and main planners utilize dif-

ferent strategies for implementing SELECTTARGET,

ACCEPTABLE(v), and REACHEDGOAL(v). In the auxil-

iary planner, targets are sampled from the entire con-

ﬁguration space, with occasional guidance toward a

random safety center. ACCEPTABLE(v) checks if it is

still possible to reach any safety center. If the dis-

tance from the root of the tree to v and from v to the

center of a safety zone S

exceeds S

’s radius, v cannot

reach the center of S

. If none of the centers are reach-

able, v is deemed unacceptable. REACHEDGOAL(v) is

satisﬁed when v reaches any of the safety centers.

In the main planner, targets are generally sam-

pled from the entire conﬁguration space, but occa-

sionally the goal conﬁguration c

goal

is selected as the

target. REACHEDGOAL(v) is considered satisﬁed when

v reaches c

goal

. ACCEPTABLE(v) utilizes the auxiliary

planner to check if there exists a path from v to a

safety center that satisﬁes the distance constraints.

5.2 Environments

The experiments are conducted using four scene

types: maze, random, waves, and 3D rooms, as shown

in Figs. 1 and 3. These scenes pose signiﬁcant chal-

lenges, as the robot must avoid numerous obstacles

Algorithm 2: Tree-based path planning with safety zones

for baseline comparisons.

Input: W : environment; O: obstacles;

S = {S

,.. .,S

}: safety zones; R =

⟨

P ,C

⟩

robot; b: sampling bias; t

max

: runtime limit.

Output: A collision-free path σ from c

init

to c

goal

consisting entirely of safe conﬁgurations, and a

collision-free safety path λ

for each c

∈ σ.

1 T ← INITIALIZETREE(c

root

);

2 while TIME() < t

max

3 c

target

← SAMPLETARGET();

4 v ← v

near

← NEAREST(T ,c);

5 ℓ ← NRSTEPSPATH(v.c, c

target

);

6 for i = 1, . ..,ℓ do

7 v

new

← NEWNODE();

8 v

new

.c ← interp(v

near

.c,c

target

,i/ℓ);

9 v

new

.parent ← v;

10 v

new

.d ← v.d + dist(v.c,c);

11 if ¬COLLISION(v) then break;

12 if ¬ACCEPTABLE(v) then break;

13 ADDNODE(T ,v

new

);

14 if REACHEDGOAL(v

new

) then

15 return SOLUTION(T , v

new

);

16 v ← v

new

;

17 return

Auxiliary Planner

SAMPLETARGET()

if RAND() < b then

return select one of the S

.c at random;

else return random cfg from entire space;

ACCEPTABLE(v)

return ∃S

∈ S : v.d + dist(v.c, S

.c) ≤ S

.r;

REACHEDGOAL(v)

return ∃S

∈ S : dist(v.c,S

.c) ≤ ε;

Main Planner

SAMPLETARGET()

if RAND() < b then return c

goal

;

else return random cfg from entire space;

ACCEPTABLE(v): return auxPlanner.PLAN(v) ̸=

REACHEDGOAL(v): return dist(v.c, c

goal

) ≤ ε

and navigate narrow passages to reach its destination.

For the maze, random, and waves scenes, we cre-

ated three difﬁculty levels, with L3 being the most

challenging. Maze levels L1, L2, and L3 corre-

spond to maze dimensions of 10 × 10, 14 × 14, and

18 × 18, respectively. During maze generation, we

used Kruskal’s algorithm to set the grid dimensions

and randomly place walls. However, to introduce al-

ternative paths in the maze, approximately 10% of

the walls were removed. This modiﬁcation allows

for multiple navigation options, but the maze remains

Robot Path Planning with Safety Zones

409

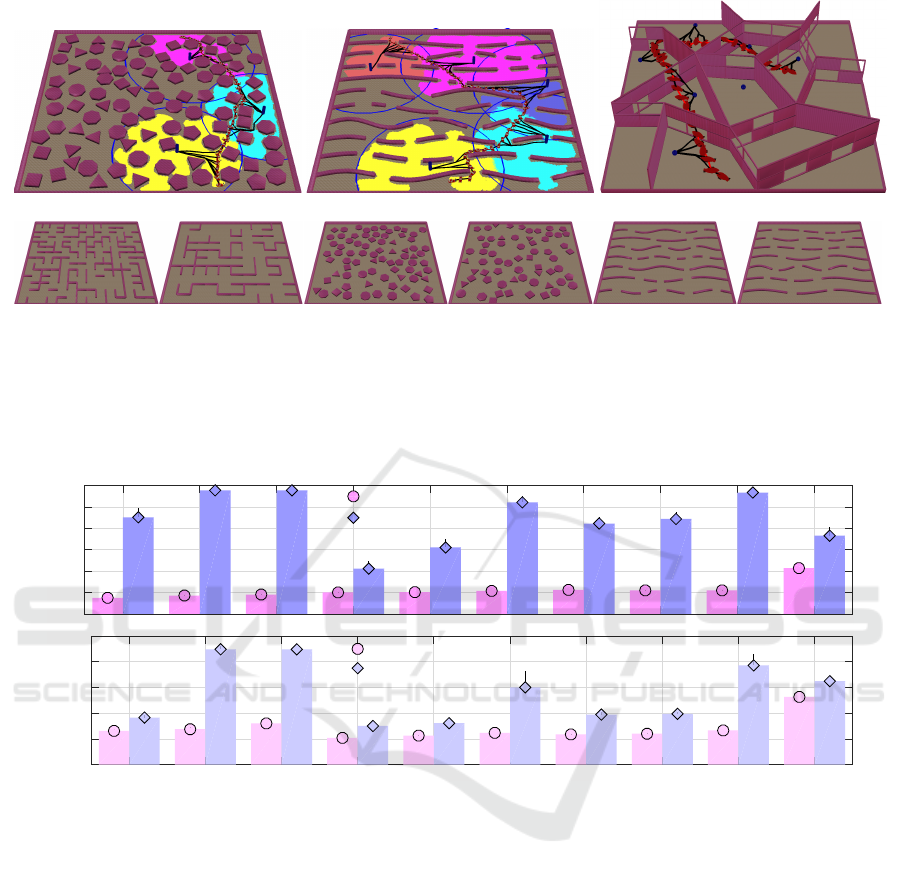
random:L3 waves:L3 rooms:3D

maze:L2 maze:L1 random:L2 random:L1 waves:L2 waves:L1

Figure 3: The other scene types (random, waves, rooms) used in the experiments. The maze scene type is shown in Fig. 1.

For the maze, random, and waves scene types, we have three levels of difﬁculty with L3 being the most challenging. In the

random and waves scene types at the L3 difﬁculty level, the ﬁgures also illustrate safety zones, along with the safe locations

and solutions determined by our approach. Due to the visual complexity of presenting safety zones and safe locations in the

3D rooms scene, we opted to showcase solely the centers of the safety zones and the solution computed by our approach. The

car model is used in the maze, random, and waves scene types, while the blimp model is used in the 3D rooms scene.

mazes:L1

1.7

23.0

mazes:L2

1.8

mazes:L3

1.9

random:L1

2.0

4.3

random:L2

2.0

8.6

random:L3

2.1

37.3

waves:L1

2.2

18.8

waves:L2

2.1

21.8

waves:L3

2.1

51.3

rooms:3D

4.4

12.7

our planner

baseline planner

runtime [s]

mazes:L1

mazes:L2

mazes:L3

random:L1

random:L2

random:L3

waves:L1

waves:L2

waves:L3

116

rooms:3D

128

256

our planner

baseline planner

distance [m]

Figure 4: Runtime and solution length results on a logarithmic scale. These results correspond to problem instances where the

radii of safety zones are randomly set within the interval I

= [4m,6m]. Entries marked with X indicate failure by the baseline

planner to solve the problem instances within the 60s time limit per run.

challenging due to its density and zigzag paths.

The random scenes consist of randomly placed

obstacles, with varying difﬁculty levels determined by

the percentage of area covered by these obstacles. L1,

L2, and L3 correspond to 20%, 25%, and 30% cover-

age, respectively. These levels create dense environ-

ments with limited passages for the robot.

The waves scene type consists of wavy obstacles

spaced slightly apart from each other. Each wave

contains randomly positioned gaps of varying width.

However, these gaps are relatively narrow, requiring

the robot to maneuver with precision. Different difﬁ-

culty levels are achieved by adjusting the number of

wave obstacles. L1, L2, and L3 levels contain 5, 7,

and 10 wave obstacles, respectively.

The 3D rooms scene comprises multiple rooms,

each containing small openings positioned at various

heights that the blimp robot can traverse. This creates

a challenging environment, as the blimp robot must

navigate with precision, ﬂying from one room to an-

other in order to reach its destination.

5.3 Problem Instances

For the maze, random, and waves scene types, we cre-

ated 3 scenes for each level of difﬁculty for a total of

27 scenes. We have one scene for the 3D rooms, so

28 different scenes were used in the experiments.

A problem instance is deﬁned by placing the ini-

tial and goal conﬁgurations and the safety zones. The

initial and goal conﬁgurations are placed at collision-

free locations near the bottom and top, respectively,

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

410

2.9

1.9

2.0

2.6

2.0

2.1

24.6

2.1

37.3

2.2

20.3

2.2

17.3

2.2

27.8

1.9

51.4

2.1

51.3

1.9

40.6

2.2

38.5

2.2

31.8

4.5

7.0

4.4

12.7

5.5

12.4

4.6

18.9

5.6

18.2

mazes:L3 random:L3 waves:L3 rooms:3D

our planner

baseline planner

runtime [s]

120

116

mazes:L3 random:L3 waves:L3 rooms:3D

128

256

our planner

baseline planner

distance [m]

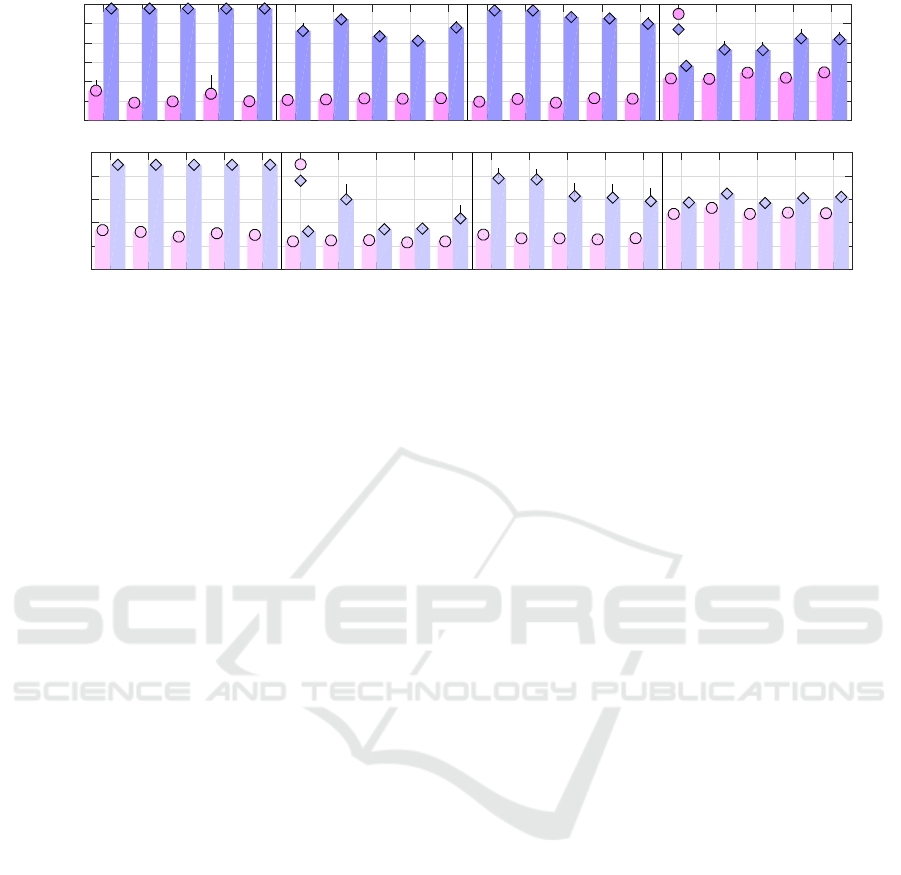
Figure 5: Runtime and solution length results when varying the intervals used to set the radii of the safety zones, where

= [2m, 4m], I

= [4m, 6m], I

= [6m, 8m], I

= [8m, 10m], and I

= [10m, 12m].

requiring the robot to navigate a considerable dis-

tance. The safety zones are created by randomly po-

sitioning their centers and setting their radii at ran-

dom within speciﬁed minimum and maximum val-

ues. These safety zones cover both the initial and goal

conﬁgurations and form a connected component, with

overlaps between zones considered as connections.

For the experiments, we generated problem in-

stances with safety zone radii falling into ﬁve inter-

vals: I

= [2m,4m], I

= [4m,6m], I

= [6m,8m],

= [8m,10m], and I

= [10m,12m]. For each scene

and interval I

, we created 30 instances following the

procedure described above. As a result, we generated

a total of 28 × 5 × 30 = 4200 problem instances.

5.4 Measuring Performance

The experiments were conducted on a computing

cluster comprising nodes with Dell PowerEdge R640

Intel(R) Xeon(R) Gold 6240R CPU 2.40GHz, each

equipped with 48 cores. The experiments did not uti-

lize parallelism or multi-threading; instead, each in-

stance was executed on a single core. The code was

implemented in C++ and compiled using g++-9.3.0.

The results provide information on the runtime

and solution length for our approach and the baseline

planner. The runtime includes the time taken from

reading the input until a solution is found or until the

runtime limit of 60s per run is reached. To obtain

more reliable statistics, the mean and standard devia-

tion are calculated after removing the top and bottom

25% of the results to mitigate the inﬂuence of outliers.

5.5 Results

Results over All Scene Types: Fig. 4 presents

the runtime and solution length results for all the

scene types utilized in the experiments. The ﬁndings

demonstrate the computational efﬁciency of our ap-

proach, as it is able to rapidly discover solutions even

in highly challenging environments. This efﬁciency

stems from a combination of roadmap construction,

identiﬁcation of safe locations, and search over the

safe portion of the roadmap. The roadmap captures

the connectivity of the environment, facilitating ef-

ﬁcient navigation within and between safety zones.

The search-based approaches quickly identify the safe

nodes within the roadmap and ﬁnd a collision-free

path to the goal, ensuring that each intermediate con-

ﬁguration along the path can reach a safety center

within the distance constraints.

The baseline planner is capable of solving some of

the problem types, but requires signiﬁcant time, and

even fails, in the more challenging problems where

the robot has to navigate around numerous obstacles

and pass through several narrow passages to reach its

goal. This outcome is anticipated due to the nature of

the baseline planner, which requires invoking the aux-

iliary planner multiple times to determine paths to-

wards safety centers for each node added to the main

tree. Consequently, this process incurs a signiﬁcant

computational cost, making it less efﬁcient and effec-

tive in complex problem instances.

When comparing solution lengths, our approach

consistently produces signiﬁcantly shorter solutions

than the baseline planner. This is due to the shortest-

path searches over the roadmap, enabling our ap-

proach to reduce the distance required to reach the

safety centers and the goal.

Results When Varying the Area of Safety Zones:

Fig. 5 shows the runtime and solution length results

obtained by varying the radii of the safety zones

across different intervals. These results further high-

light the computational efﬁciency of our approach

and its ability to generate short solutions. Our ap-

proach consistently performs well across all problem

Robot Path Planning with Safety Zones

411

instances, beneﬁting from the roadmap construction

that facilitates navigation within and between safety

zones, even when their areas change. The shortest-

path searches conducted over the roadmap enable our

approach to identify safe locations and determine a

safe path to the goal. In contrast, the baseline planner

faces challenges in expanding the tree effectively to

satisfy the distance constraints imposed by the safety

zones. This further highlights the advantage of our

approach in handling varying safety zone radii.

6 DISCUSSION

This paper presented a novel approach to incorporate

safety zones into path planning. The approach made

it possible to plan the path of a robot to reach its goal

while always being able to detour to a safety cen-

ter within the speciﬁed distance constraints in case of

emergencies. Experiments in challenging 2D and 3D

environments, involving car and blimp robot models,

demonstrated the efﬁcacy of the approach.

This work opens up several potential research di-

rections. One direction is leveraging machine learn-

ing to predict safe locations. Another is to handle

complex tasks, including multiple goals, exploration,

and even extend the approach to multiple robots.

REFERENCES

Baldoni, P., McMahon, J., and Plaku, E. (2022). Leveraging

neural networks to guide path planning: Improving

dataset generation and planning efﬁciency. In IEEE

International Conference on Automation Science and

Engineering, pages 667–674.

Bohlin, R. and Kavraki, L. E. (2000). Path planning us-

ing lazy PRM. In IEEE International Conference on

Robotics and Automation, volume 1, pages 521–528.

Bui, H.-D., Lu, Y., and Plaku, E. (2022). Improving the

efﬁciency of sampling-based motion planners via run-

time predictions for motion-planning problems with

dynamics. In IEEE/RSJ International Conference on

Intelligent Robots and Systems, pages 4486–4491.

Cao, K., Cheng, Q., Gao, S., Chen, Y., and Chen, C. (2019).

Improved PRM for path planning in narrow passages.

In IEEE International Conference on Mechatronics

and Automation, pages 45–50.

Choset, H., Lynch, K. M., Hutchinson, S., Kantor, G., Bur-

gard, W., Kavraki, L. E., and Thrun, S. (2005). Prin-

ciples of Robot Motion: Theory, Algorithms, and Im-

plementations. MIT Press.

Denny, J., Sandstr

om, R., Bregger, A., and Amato, N. M.

(2020). Dynamic region-biased rapidly-exploring ran-

dom trees. In Workshop on the Algorithmic Founda-

tions of Robotics, pages 640–655.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische Mathematik, 1:269–271.

Feyzabadi, S. and Carpin, S. (2014). Risk-aware path plan-

ning using hirerachical constrained markov decision

processes. In IEEE International Conference on Au-

tomation Science and Engineering, pages 297–303.

Galler, B. A. and Fisher, M. J. (1964). An improved

equivalence algorithm. Communications of the ACM,

7(5):301–303.

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A for-

mal basis for the heuristic determination of minimum

cost paths. IEEE Transactions on Systems Science and

Cybernetics, 4(2):100–107.

Karaman, S. and Frazzoli, E. (2011). Sampling-based algo-

rithms for optimal motion planning. The International

Journal of Robotics Research, 30(7):846–894.

Kavraki, L. E.,

Svestka, P., Latombe, J. C., and Overmars,

M. H. (1996). Probabilistic roadmaps for path plan-

ning in high-dimensional conﬁguration spaces. IEEE

Transactions on Robotics and Automation, 12(4):566–

580.

Kuffner, J. J. and LaValle, S. M. (2000). RRT-connect: An

efﬁcient approach to single-query path planning. In

IEEE International Conference on Robotics and Au-

tomation, volume 2, pages 995–1001.

Larsen, E., Gottschalk, S., Lin, M., and Manocha, D.

(2000). Fast proximity queries with swept sphere vol-

umes. In IEEE International Conference on Robotics

and Automation, pages 3719–3726.

LaValle, S. M. and Kuffner, J. J. (2001). Randomized kino-

dynamic planning. International Journal of Robotics

Research, 20(5):378–400.

Pepy, R. and Lambert, A. (2006). Safe path plan-

ning in an uncertain-conﬁguration space using RRT.

In IEEE/RSJ International Conference on Intelligent

Robots and Systems, pages 5376–5381.

Plaku, E., Plaku, E., and Simari, P. (2017). Direct path

superfacets: An intermediate representation for mo-

tion planning. IEEE Robotics and Automation Letters,

2(1):350–357.

Plaku, E., Plaku, E., and Simari, P. (2018). Clearance-

driven motion planning for mobile robots with differ-

ential constraints. Robotica, 36(7):971–993.

Primatesta, S., Guglieri, G., and Rizzo, A. (2019). A risk-

aware path planning strategy for UAVs in urban envi-

ronments. Journal of Intelligent & Robotic Systems,

95:629–643.

Schouwenaars, T., How, J., and Feron, E. (2004). Reced-

ing horizon path planning with implicit safety guar-

antees. In American Control Conference, volume 6,

pages 5576–5581.

Wang, J., Chi, W., Li, C., Wang, C., and Meng, M. Q.-H.

(2020). Neural RRT*: Learning-based optimal path

planning. IEEE Transactions on Automation Science

and Engineering, 17(4):1748–1758.

Zhao, C., Zhu, Y., Du, Y., Liao, F., and Chan, C.-Y. (2022).

A novel direct trajectory planning approach based on

generative adversarial networks and rapidly-exploring

random tree. IEEE Transactions on Intelligent Trans-

portation Systems, 23(10):17910–17921.

ICINCO 2023 - 20th International Conference on Informatics in Control, Automation and Robotics

412