Maximizing Particle Coverage with Fixed-Area Rectangles

Seung-Yeol Hong

and Yong-Hyuk Kim

Department of Computer Science, Kwangwoon University, Seoul, Republic of Korea

Keywords: Genetic Algorithm, Optimization, Deployment.

Abstract: In this study, our primary focus is on enhancing particle coverage through the effective deployment of

rectangles with fixed areas and flexible shapes within a two-dimensional space. These rectangles represent

areas optimally managed by various units like CCTV cameras, police personnel, search and rescue units and

robots. Particles are objects designated for processing by these units. To realize this objective, we presented

an efficient technique for deploying rectangles in a two-dimensional space using a genetic algorithm (GA).

The GA searches for the optimal deployment of rectangles that maximizes the sum of the particle densities

represented int the heat map. We experimented by applying our problem to maritime search and rescue

planning. The main application of our method in maritime search and rescue planning is the deployment of

search and rescue units in the ocean. As a result, the GA outperformed the greedy method by up to 14%. The

experimental outcomes demonstrate the superiority of our proposed method compared to existing techniques.

Specifically, its effectiveness becomes more pronounced when the total area covered by the placed rectangles

is smaller than the entire search area.

1 INTRODUCTION

Determining a maritime search and rescue (SAR)

plan considers a variety of factors, including the

expected location of the search target, the availability

of search and rescue units (SRU). So, determining a

maritime SAR plan is a challenging task.

With the advancement of science and technology,

research is being conducted on decision-making

systems for maritime SAR planning. One study

improved the mathematical model used for SAR and

used genetic simulated annealing algorithm (GSAA)

to support SRU resource scheduling (Ai et al. 2019).

They designed a search area allocation algorithm that

considers spatio-temporal characteristics. Another

study conducted a comprehensive review on decision

support in maritime emergencies and proposed a

decision support method using two optimization

algorithms (Xiong et al. 2020). They are used

differential evolution (DE) (Storn et al. 1997) and

NSGA-II (Deb et al. 2000) to find appropriate SAR

plans and support SRU resource scheduling.

Determining a search area for SRUs is an

important part of SAR planning. Existing studies set

up one large rectangle that represents the entire search

https://orcid.org/0009-0006-5806-3401

https://orcid.org/0000-0002-0492-0889

area and then divide it to deploy SRUs. However,

there are two problems with this approach. First,

efficiency is reduced when SRUs cannot cover the

entire search area. Second, SRUs may be wasted on

unimportant areas because all search areas are

explored.

In this paper, we present a generalization of the

problem of placing SRUs in SAR planning. The

generalized problem has broader applicability and

can be extended to various other problems.

Furthermore, we propose an optimal rectangle

deployment method using a genetic algorithm (GA)

that improves upon the existing studies. We deploy

rectangles in the two-dimensional space where search

targets represented by particle exists. The rectangles

represent areas that can be explored by SRUs. These

rectangles are deployed to contain as many particles

as possible.

The problem of deploying rectangles to cover as

many particles as possible can be applicable not only

to SAR planning but also to various other problems.

For example, police can be distributed on heavily

travelled streets to clear traffic and prevent accidents.

In another example, sensors can be deployed on most

sensitive areas. One study (Yoon et al. 2022) used a

172

Hong, S. and Kim, Y.

Maximizing Particle Coverage with Fixed-Area Rectangles.

DOI: 10.5220/0012162900003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 172-178

ISBN: 978-989-758-674-3; ISSN: 2184-3236

GA to deploy sensors and maximize space coverage,

while another study (Seo et al. 2017) used a GA for

the efficient deployment of CCTVs on streets.

However, the limitation of previous studies is the

representation of sensors as fixed-size circles or fans,

restricting their applicability to diverse problem

scenarios. In particular, configuring the search area as

a curve in SAR planning presents disadvantages.

During the path planning phase, when the search area

contains curves, obtaining crucial variables like the

probability of detection becomes challenging. Hence,

the circle and fan shapes, as employed in prior studies,

are not suitable for SAR planning, and rectangles

prove to be a better fit for such scenarios.

Meanwhile, research is also being conducted on a

problem similar to SAR planning: planning paths for

Unmanned Aerial Vehicles (UAVs) (Mansouri et al.

2017, Akshya et al. 2020). These problems involve

deploying a rectangle that covers a specific polygon

or object and devising a path around the rectangle's

center point. However, these problems typically

assume that the UAV can cover the entire area. If the

UAV lacks the time to explore the entire region, it

necessitates a strategy to explore the crucial sections

first. Our suggested rectangle placement method

positions rectangles exclusively in important areas,

making it suitable for UAV path planning under time

constraints.

This paper is organized as follows. Section 2

describes how SRUs have been deployed in previous

studies of SAR. We modify this method to our

problem and compare it to our proposed method.

Section 3 describes our proposed method. Section 4

describes the environment we experimented in and

the setup for our experimental methods. Section 5

discusses the results of our experiments. Finally, in

Section 6, we outline potential directions for future

work.

2 PREVIOUS METHOD

In this part, we introduce how previous studies (Ai et

al. 2019 & Xiong et al. 2020) have deployed the

search area of SRUs. In existing studies, the entire

search area is divided into equal-sized cells, and then

the following algorithm is performed.

Step 1: select a cell with the highest value, among

the areas where the SRU is not placed.

Step 2: expand the selected area by one column or

one row in the direction of the higher fitness value

(up, down, right, and left).

Step 3: repeat process Step 2 until the fitness value

does not increase.

Step 4: when Step 3 ends, place the SRU in the

selected area.

Step 5: repeat process Step 1 through Step 4 until

the entire search area is covered.

Previous studies have employed specific

functions to evaluate fitness values. The utilized

function takes into consideration the rectangle's

dimensions and the cumulative values of the cells it

encompasses. If only the cumulative cell values were

considered, the rectangle would expand indefinitely.

However, the function uses a ratio of the size of the

rectangle to the sum of the cell values so that the

evaluation value decreases after the rectangle is large

enough.

3 PROPOSED METHOD

3.1 Data

In the two-dimensional space where the rectangles are

deployed, there are search targets represented by

particles. If there are too many particles, the

subsequent process, GA deploying rectangles, will

take a long time. To address this, we simplify the two-

dimensional space into a heat map. The heat map

consists of N-by-N cells. Each cell has as its value the

density of the particles it contains. Figure 1 shows the

heat map we used in our experiment. Higher values in

the cells are colored as red, and lower values in the

cells are colored as blue. Cells with very few particles

and therefore not important at all are colored as white.

3.2 Genetic Algorithm

A genetic algorithm (GA) is one of the most famous

evolutionary algorithms. It is an optimization

algorithm developed to mimic the evolutionary

process of living organism (Holland, 1975).

GA (offspring size n, max generation

max

) {

P ← generate 200 random initial solutions

for generation g ← 1 to g

max

for i ← 1 to n

, p

← select two parent chromosomes

using

Roulette wheel

← generate offspring chromosome from

, p

using uniform crossover

← mutation(o

)

← repair(o

)

end for

replace n chromosomes in P with o

to o

end for

return best chromosome in P

}

orithm 1: Pseudo-code of ou

GA.

Maximizing Particle Coverage with Fixed-Area Rectangles

173

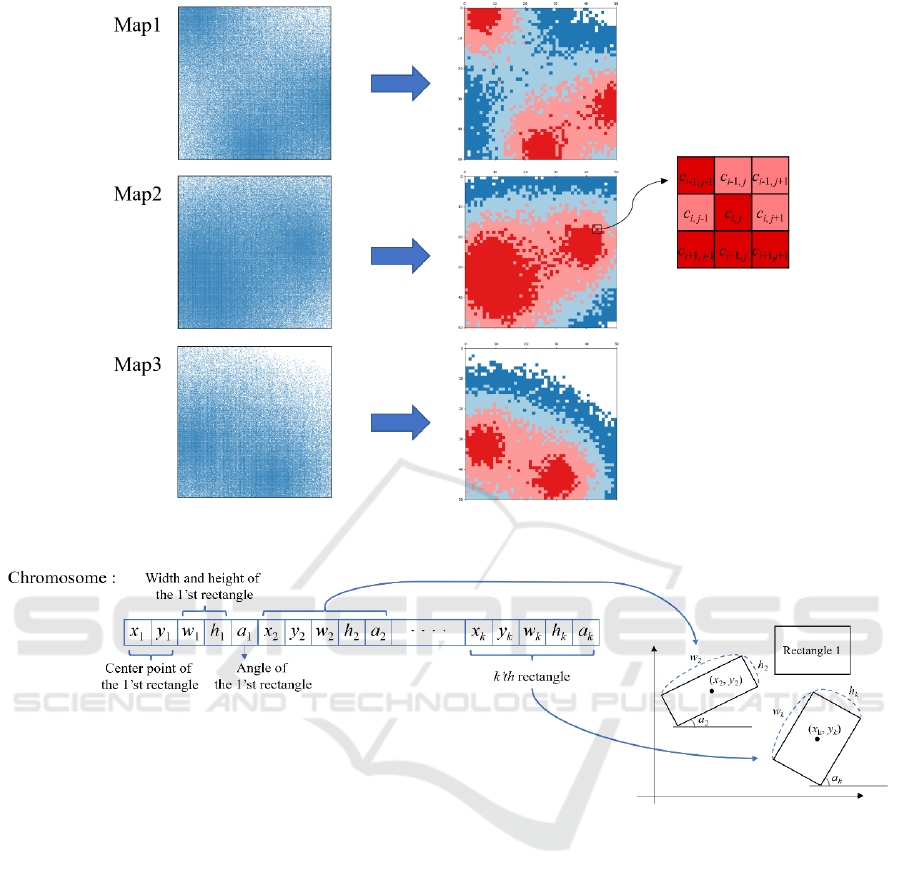
Figure 1: Heat map of particles in a given domain.

Figure 2: Example illustration of the genotype (left) and the phenotype (right) of a chromosome.

We propose using the GA to deploy rectangles on

the data described in Section 3.1. We designed a

method for representing rectangles in the two-

dimensional space and evaluating their performance.

Additionally, we designed a repair operator to

maintain a fixed rectangle area, which is applied after

the mutation operation. The structure of our proposed

GA is shown in Algorithm 1.

3.2.1 Encoding

Rectangles are deployed in the heat map to indicate

that the SRU is limited. The shape of the rectangles is

free; however, its area (the product of width and

height) must be fixed at a certain value. This is

indicating that SRUs can only search a limited area.

Encoding defines the way how the solution is

represented. In this study, a rectangle (gene) is

represented by an array of {x-coordinate of the center

, y-coordinate of the center, width (w), height (h), and

angle(a)}.

Thus, the chromosome with k rectangles is

represented by a one-dimensional array with 5k

elements. Figure 2 shows how we represent

rectangles as chromosome. a is the angle the rectangle

is rotated with respect to the x-axis. The number

under each variable is the number of the rectangle.

For example, x

is the x-coordinate of the center of the

first rectangle.

3.2.2 Objective Function

As the objective function we compute a fitness score,

which indicates how well the chromosome is suited

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

174

Figure 3: How to apply a penalty to the objective function to exclude overlapping regions.

to the problem. It evaluates the chromosomes by

summing up the values of all cells within the heat map

that are covered by the rectangle. The objective

function considers a rectangle to contain a cell if the

cell's center point falls within the rectangle.

To incentivize rectangles to cover as many cells

as possible, we introduce a penalty for overlapping

regions. If a rectangle overlaps with another, the

overlapping area is excluded from the calculation of

the objective function. Figure 3 illustrates the

application of penalties in the objective function. The

fitness score is computed by considering the values of

the cells within the colored region. However, cells in

the uncolored region, where the rectangles overlap,

are not taken into account for the fitness score

computation. This penalty is applied for the following

two reasons.

Firstly, when rectangles overlap, it undermines

our objective of maximizing cell coverage with a

limited number of rectangles. If the rectangles

overlap, it is natural that the number of cells they can

cover will be reduced. So, by applying a penalty and

excluding the overlapping areas within the objective

function, our genetic algorithm can converge towards

optimal solutions more effectively.

Secondly, in real-world scenarios, the overlap of

rectangles can lead to negative consequences. In the

context of SAR planning, when rectangles overlap, it

indicates that the search areas of SRUs also overlap.

This overlap can result in adverse outcomes, such as

collisions or an increased scale of accidents. Thus,

penalizing overlapping areas helps to avoid such

undesirable situations.

Equation (1) represents our objective function.

Let c

i,j

denote the value of the cell in row i and column

j. A variable w

i,j

determines whether or not a penalty

is applied. If only one rectangle contains the cell in

row i and column j, w

i,j

is set to 1. On the other hand,

if no rectangle contains the cell in row i and column j

or if multiple rectangles contain the cell in row i and

column j, w

i,j

is set to 0. A set of rectangles with no

overlapping areas will receive a better evaluation

when using this objective function.

𝑓

∑∑

𝑐

,

×𝑤

,









where

𝑤

,

=

exatl

one rectangle contain 𝑐

,

0 otherwise

(1)

3.2.3 Repair Operator

The repair operator fixes the height or width using the

fitness score. The repair operator divides the fixed-

area by the height to get the modified width.

Conversely, the modified height is obtained by

dividing the fixed-area by the width. Then, the repair

operator selects the one that has a higher fitness score

when the modified height or modified width is

applied. The pseudo-code for the repair operation is

presented in Algorithm 2.

4 EXPERIMENTAL SETUP

We conduct experiments using three different

methods, all share the following two settings.

First, to represent a resource scarce situation, we

set the number of rectangles, k, to 3. Thus, the

chromosome length in our experiment is 15 (= 3 × 5).

Second, we set the size of the heat map, N, to 50.

4.1 GA Parameters

The GA selection operation uses a Roulette wheel.

The variable to control the selection pressure of the

Roulette wheel is set to 3. For the crossover

operation, uniform crossover and a mutation

probability of 0.05 are applied. When mutations

occur, different ranges of random values are applied

to each gene. For the genes x and y, which represent

Maximizing Particle Coverage with Fixed-Area Rectangles

175

Table 1: Experiment results of 30 runs.

Greedy method Random multi-start GA

- Generation = 1000 Generation = 1500 Generation = 1000 Generation = 1500

Run 1 time

O.A.

Run 30 times O.A.

Map1

Best 887.0

Best 806.6

17.8

Best 812.6

12.6

Best 917.9

0.9

Best 923.5

1.2 Ave. - Ave. 790.6 Ave. 794.7 Ave. 887.4 Ave. 893.8

Std. - Std. 8.3 Std. 8.6 Std. 16.4 Std. 18.8

Map2

Best 942.1

Best 984.1

28.6

Best 991.6

22.6

Best 1071.2

4.1

Best 1077.1

3.4 Ave. - Ave. 966.7 Ave. 973.2 Ave. 1035.3 Ave. 1042.4

Std. - Std. 8.9 Std. 9.6 Std. 18.8 Std. 18.4

Map3

Best 827.6

Best 808.2

51.6

Best 808.2

48.9

Best 892.1

11.2

Best 897.2

8.5

Ave. - Ave. 782.1 Ave. 786.1 Ave. 865.4 Ave. 869.0

Std. - Std. 10.7 Std. 10.2 Std. 14.6 Std. 20.7

The greedy method always produces the same result in the same data.

Average of the area where the rectangles overlap.

the coordinates of the rectangle's center point, a real

number between 0 and N is randomly assigned. The

genes w and h, representing the width and height of

the rectangle, are assigned a real number between 1

and the value of fixed-area. The changes of the area

are not considered at this stage, as the repair operation

is carried out after the mutation operation. The gene

a, representing the angle, is randomly assigned a real

number between 0 and 180 degrees. After the

mutation operation, the chromosome is repaired to fix

the rectangular area. Fifty offspring chromosomes are

generated and replace the parent chromosomes with

lower fitness scores. This process is repeated for

1,000 and 1,500 generations with a population of 200

per generation.

4.2 Greedy Method

The greedy method is designed as a variation of a

previous method. The difference from previous

method

is that the present study does not cover all

highest value in the heat map as the initial area. The

selected area is then extended in the direction that

could have a higher fitness score. The rectangle

cannot encroach on another rectangular area. The

rectangle can also extend outside of the heat map, and

the outside of the heat map does not affect the

rectangle's fitness score. The rectangle does not

expand further after filling a fixed size. After the

rectangle is deployed, the chromosome is repaired.

4.3 Random Multi-Start

Random multi-start randomly generates as many

chromosomes as the number of chromosomes

generated by the GA, and it repairs them. It selects the

best chromosome among them. The pseudo-code for

the random multi-start is presented in Algorithm 3.

5 RESULTS

The rectangles are deployed on a heat map using the

greedy

method, GA, and random multi-start. Table 1

Repair (chromosome = {

, … ,

}) {

for each rectangle r

= {x

, y

, w

, h

, d

}

← maximum coverage area of r

fix

← {x

, y

, w

, c

/ w

, d

}

fix

← {x

, y

, c

/ h

, h

, d

}

if fitness(h

fix

) > fitness(w

fix

) then

← h

fix

if fitness(h

fix

) < fitness(w

fix

) then

← w

fix

end for

return repaired chromosome

}

Algorithm 2: Pseudo-code of repair operation.

RandomMultiStar

(offspring size n,

max generation g

max

population P) {

R ← | P | + n × g

max

for i ← 1 to R

← randomly-generated chromosome

← repair(o

)

end for

return best in O = {o

, o

, …, o

}

orithm 3: Pseudo-code of random multi-start.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

176

Figure 4: Best solutions in Map 3.

shows the highest, average, and standard deviation of

the fitness score, and the average overlap area for 30

runs for each method. The greedy method exhibits

significant performance differences depending on the

characteristics of the data. In Map1 (left of Figure 1),

the dense regions are separated; thus, the greedy

method performs well. In contrast, in Map2 (middle

of Figure 1), the dense regions are clustered together,

and the greedy method does not perform well. On

average, the GA exhibits a stable performance. The

GA outperforms the greedy method by an average of

5% and a maximum of 14 %. The GA also reduces

the average overlap area by 86% on average and 95%

compared to random multi-start. Figure 4 shows the

best solutions obtained from the greedy method,

random multi-start, and GA in Map3.

The GA, executed on an Intel i7-7700 3.60GHz

CPU with 16GB of memory, Microsoft Windows 10

operating system, and implemented using the C++

programming language, achieves an average

completion time of 90 seconds. In contrast, the

random multi-start approach takes approximately 58

seconds on average, while the Greedy Method

exhibits a runtime of around 1 second.

6 CONCLUSIONS

In this study, we presented an efficient approach for

deploying rectangles with flexible shapes and fixed

sizes. While the problem we addressed has potential

applications in various fields, our main goal was to

apply it to SAR planning. Existing researches about

SAR planning typically assumes that the search area

can be completely covered. However, real-world

scenarios may involve limitations in number of SRU

or time availability. We successfully deployed

rectangles within a heat map that represent the

significance of search areas. This approach was

particularly effective when not all regions could be

thoroughly explored due to constraints in SRU

availability or time constraints, thereby mitigating the

drawbacks of prior methodologies.

7 FUTURE WORK

Future research can be conducted as follows. First,

accommodating changes in the area of rectangles is

important. In the real world, there is a travel time for

resources to reach the deployed area. As resources are

active for a fixed duration, the coverage area they can

handle may decrease or p depending on their travel

time. Therefore, it would be more realistic to adjust

the size of the rectangles based on their deployment

location.

Second, considering overlapping rectangles under

specific conditions can be beneficial. The types of

robots used in search and rescue operations (ground,

air, marine, etc.) are becoming increasingly diverse

(Queralta et al. 2020). When different types of robots

are involved, overlapping search areas may not pose

a risk of accidents. By incorporating this

consideration, our approach can be applied to a wider

range of problems by designing an objective function

that cancels the penalty for overlapping rectangles

under certain conditions.

Third, more experimentation is required.

Although we have enhanced the performance of

rectangular deployment compared to existing

methods, we have not yet established a diverse

comparison group. It would hold more significance to

compare the effectiveness of GA with metaheuristic

algorithms and other optimization techniques like

NSGA-II.

Maximizing Particle Coverage with Fixed-Area Rectangles

177

In last, expanding the objective function to

include additional variables is worth exploring. Our

study focuses on a simple objective of placing

rectangles to cover as many particles as possible.

However, in real-world scenarios, multiple

environmental factors need to be taken into account.

For instance, in maritime SAR planning, it is crucial

to consider factors such as the probability of coverage

(POC) and the probability of detection (POD) of a

rescue target (Ototoe et al. 2019). Furthermore,

various factors like the marine environment and the

likelihood of the rescue target's survival should also

be taken into account. Therefore, designing the

objective function to incorporate more variables

would enable more accurate experiments.

ACKNOWLEDGEMENTS

This research was supported by Korea Institute of

Marine Science & Technology Promotion (KIMST)

funded by Korea Coast Guard (20220463)."

REFERENCES

B. Ai, B. Li, S. Gao, J. Xu and H. Shang, (2019). An

intelligent decision algorithm for the generation of

maritime search and rescue emergency response plans.

In IEEE Access, vol. 7, pp. 155835-155850.

W. Xiong, P.H.A.J.M. van Gelder, K. Yang, (2020). A

decision support method for design and

operationalization of search and rescue in maritime

emergency. In Ocean Engineering, vol. 207, 107399.

R. Storn, K. Price, (1997). Differential evolution–a simple

and efficient heuristic for global optimization over

continuous spaces. In Journal of Global Optimization

11, 341–359.

K. Deb, S. Agrawal, A. Pratap, T. Meyarivan, (2000). A fast

elitist non-dominated sorting genetic algorithm for

multi-objective optimization: NSGA-II. In Parallel

Problem Solving from Nature PPSN VI, pp 849-858.

Y. Yoon and Y. H. Kim, (2022). Maximizing the coverage

of sensor deployments using a memetic algorithm and

fast coverage estimation. In IEEE Transactions on

Cybernetics, vol. 52, no. 7, pp. 6531-6542.

J.H. Seo, Y. Yoon, Y.H. Kim, (2017). Coverage problem in

camera-based sensor networks using the CUDA

platform. In International Journal of Distributed

Sensor Networks, vol. 13, no. 12.

S.S. Mansouri, G. Georgoulas, T. Gustafsson and G.

Nikolakopoulos, (2017). On the covering of a

polygonal region with fixed size rectangles with an

application towards aerial inspection. In 2017 25th

Mediterranean Conference on Control and Automation

(MED), pp. 1219-1224.

J. Akshya, P.L.K. Priyadarsini, (2020). Graph-based path

planning for intelligent UAVs in area coverage

applications. In Journal of Intelligent & Fuzzy Systems,

vol. 39, issue 6, pp. 8191-8203.

J. H. Holland, (1975). Adaptation in Natural and Artificial

Systems. University of Michigan Press, Ann Arbor, MI.

second edition 1992.

J.P. Queralta, J. Taipalmaa, B.C. Pullinen, V.K. Sarker,

T.N. Gia, H. Tenhunen, M. Gabbouj, J. Raitoharju,

T. Westerlund, (2020). Collaborative multi-robot

search and rescue: planning, coordination, perception,

and active vision. In IEEE Access, vol. 8, pp. 191617-

191643.

D.A. Otote, B. Li, B. Ai, S. Gao, J. Xu, X. Chen, G. Lv,

(2019). A decision-making algorithm for maritime

search and rescue plan. In Sustainability 2019, 11,

2084.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

178