CoreSelect: A New Approach to Select Landmarks for Dissimilarity

Space Embedding

Sylvain Chabanet

, Philippe Thomas

and Hind Bril El-Haouzi

Université de Lorraine, CNRS, CRAN, F-88000 Epinal, France

Keywords:

Machine Learning, Proximity Learning, Surrogate Modeling, Sawmill Simulation.

Abstract:

This paper studies an application of indeﬁnite proximity learning to the prediction of baskets of products of

logs in the sawmill industry. More precisely, it focuses on the usage of the dissimilarity space embedding

framework to generate a set of features representing wood logs. According to this framework, data points are

represented by a vector of dissimilarity measures toward a set of representative data points named landmarks.

This representation can then be used to train any of the large variety of available ML models requiring struc-

tured features. However, this framework raises the problem of selecting these landmarks. A new method is

proposed to select these landmarks which is compared with four other methods from the literature. Numer-

ical experiments are run to compare these methods on a dataset from the Canadian sawmill industry. The

data representations obtained are used to train random forests and neural networks ensemble models. Re-

sults demonstrate that both the Partition Around Medoids (PAM) method and the newly proposed CoreSelect

methods lead to a small but signiﬁcant reduction in the mean square error of the predictions.

1 INTRODUCTION

The process of sawing a wood log into lumber is di-

verging and in co-production. From a single log, a

sawmill will obtain simultaneously several products

with different dimensions and grades. In addition, the

heterogeneity of shape and internal defects between

logs make it difﬁcult to anticipate what set of lum-

ber would be obtained from sawing a log. All these

factors greatly complicate production planning and

control in this industry. Simulation tools have been,

however, widely studied alone or in conjunction with

other decision-support tools to alleviate these prob-

lems (Chabanet et al., 2023). Simulators can, in par-

ticular, be used to predict the set of lumber that would

be obtained by sawing a speciﬁc log. This set of lum-

ber is named the Basket of Products (BoP) of the log

in the following of this study. To repeat this operation

over all logs to be sawed, or at least a representative

sample, allow to approximate the mix of product that

would be obtained by a speciﬁc production plan.

Several authors, however, have mentioned the

important computational time associated with saw-

https://orcid.org/0000-0002-3706-293X

https://orcid.org/0000-0001-9426-3570

https://orcid.org/0000-0003-4746-5342

ing simulation models (Morneau-Pereira et al., 2014;

Wery et al., 2018). This complicates their use for

short-term decision problems which might still re-

quire several thousand simulation runs. To alleviate

this problem, (Morin et al., 2015), in particular, pro-

posed to train machine learning surrogate models of

these simulation models. These surrogate models,

equivalently called metamodels, are machine learn-

ing models trained on past simulation results to pre-

dict the BoP of logs. These surrogate models are,

therefore, approximations of the simulation models

for speciﬁc sawmill conﬁgurations.

Many different sawmill simulation surrogate mod-

els have been studied in the literature. They can

be distinguished, in particular, by the input consid-

ered to describe a log and predict its BoP. Some saw-

ing simulation models like Optitek (Goulet, 2006) or

SAWSIM

can, indeed, process logs described by 3D

scans of their surfaces. These scans are 3D point

clouds providing information over the shape of the

logs. Few ML models are, however, able to process

this type of input directly. For this reason, (Morin

et al., 2015; Morin et al., 2020) propose surrogate

models making predictions from structured represen-

https://www.halcosoftware.com/software-1-sawsim,

last accessed May 2023

Chabanet, S., Thomas, P. and El-Haouzi, H.

CoreSelect: A New Approach to Select Landmarks for Dissimilarity Space Embedding.

DOI: 10.5220/0012163500003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 479-486

ISBN: 978-989-758-674-3; ISSN: 2184-3236

479

tations of the logs based on know-how features com-

monly used in the industry. In particular, they use

the length of the logs, their volumes, diameter at

both extremities, curvature, and shrinking. (Selma

et al., 2018) propose to use a dissimilarity function

to compare pairs of logs from their scans and predict

their BoP using a nearest-neighbors scheme. More

precisely, they propose to use the Iterative Closest

Point (ICP) dissimilarity which is a consequence of

the ICP algorithm commonly used to align 3D shapes

(Besl and McKay, 1992). The idea of using pairwise

ICP dissimilarity toward class medoids as features for

other ML models was investigated, for example, by

(Chabanet et al., 2021b) in the case of neural network

surrogate models. Lastly, (Martineau et al., 2021)

study several neural network surrogate models, in-

cluding models based on the architecture pointnet (Qi

et al., 2017), which is able to learn directly from 3D

point clouds.

This study focuses on surrogate models predicting

BoP from pairwise dissimilarities. Several previous

studies have, in particular, proposed sawing simula-

tion surrogate models able to predict the BoP of a log

based on a vector of features composed of the dis-

similarities of this log toward a set of representative

logs from the model training dataset. This strategy is

called the dissimilarity space embedding framework

in the literature (Duin and P˛ekalska, 2009). For ex-

ample, (Chabanet et al., 2021b) use such vectors as in-

put to multi-layer perceptrons, while (Chabanet et al.,

2021a) use a variant of a naïve Bayes classiﬁer. These

past studies, however, do not study alternative meth-

ods for the selection of the representative data points,

also called landmarks, used to generate the vectors of

dissimilarity features fed to the classiﬁer.

The main contribution of this study is, therefore,

the proposition of a novel method to select landmarks

and its comparison with four other methods from the

literature. The landmarks selected by these methods

are used to train two types of ensemble models to pre-

dict BoP of logs.

The remainder of this article is organized as fol-

lows. Section 2 reviews the literature on indeﬁnite

proximity learning and formally introduces the dis-

similarity space embedding framework. Section 3

presents the learning problem studied, the landmarks

selection methods compared in this study as well as

the dataset used during experiments. Experimental

results are detailed in section 4. Lastly, section 5 con-

cludes this study.

2 INDEFINITE PROXIMITY

LEARNING

Non-metric proximity (similarity or dissimilarity)

functions naturally arise in many ﬁelds to compare

how alike two data items are. For example, the dy-

namic time warping dissimilarity (Müller, 2007) is a

popular method to compare time series, or the Jaccard

dissimilarity (Luo et al., 2009) has been used in many

studies to compare text documents. Learning from

these proximity functions can be an attractive alterna-

tive to learning from descriptive features. Most of the

common methods proposed to learn from proximity

function require speciﬁc properties such as symmetry

or semi-deﬁniteness which are not always respected

in practice. Several families of methods have been,

however, proposed by the literature to deal with the

non-metric case (Schleif and Tino, 2015).

Many methods, for example, rely on applying

transformations to the proximity matrix M that con-

tains the pairwise proximity evaluation on the train-

ing dataset to make it positive semi-deﬁnite (Munoz

and de Diego, 2006). Once transformed, the matrix

M can, then, be used to train kernel-based models like

Support Vectors Machines (SVM). The out-of-sample

extension of these methods, i.e, their extension to data

points not in the training dataset to make new pre-

dictions, is, however, often not straightforward, and

computationally costly (Schleif and Tino, 2015).

Other authors, like (Ong et al., 2004), extend the

theory of reproducing kernel Hilbert spaces, which

underlie, for example, SVM, to reproducing Krein

spaces. Learning algorithms in a Krein space can

consider non-deﬁnite proximity matrices. This theory

leads, in particular, to training models that are linear

combinations of dissimilarities toward training data

points.

Lastly, another general method, which is the one

considered in this study, is the proximity (similarity

or dissimilarity) space embedding method (Duin and

P˛ekalska, 2009). Such a scheme ﬁrst selects a small

set of prototypes, called landmarks, in the training

dataset. A point is, then, represented by the vec-

tor of dissimilarities toward these prototypes. More

precisely, considering a training set D and a subset

R = {r

, ..., r

} ⊆ D, a data point x is represented by:

D(x, R) = (d(x, r

), ..., d(x, r

)), , (1)

where d denotes the proximity function. The

points r

, ..., r

are the landmarks.

The use of dissimilarity space embedding has

been, in particular, extensively studied in the context

of labeled graph classiﬁcation (Livi et al., 2014). This

framework has been, similarly, applied to time series

NCTA 2023 - 15th International Conference on Neural Computation Theory and Applications

480

classiﬁcation. (Jain and Spiegel, 2015), for exam-

ple, study a method to train SVM models for time se-

ries classiﬁcation, using the time warping dissimilar-

ity and a dissimilarity space embedding framework.

Lastly, this framework has been used to predict BoP

of logs based on the ICP dissimilarity in (Chabanet

et al., 2021a; Chabanet et al., 2021b).

This method has, in particular, two main advan-

tages which motivate its choice in this study. The ﬁrst

advantage is that it does not restrict the choice of the

ML model used. Data points are effectively embed-

ded in a vector feature space. Therefore, any of the

many and extensively studied ML models designed

to learn in this classic setting can be used. For the

speciﬁc problem studied in this paper, this allows, for

example, to train Random Forests (RF) or multi-layer

perceptrons to predict BoP from the ICP dissimilarity

space. RF were, in particular, proven effective when

trained on know-how features (Morin et al., 2020).

The second advantage is that it allows the user to se-

lect the dimension of the proximity space. This is im-

portant because, while a larger proximity space might

lead to better models, at least up to some point, it

also means that more proximity function evaluations

are required to embed new data points before mak-

ing a prediction. Such evaluations can, however, be

computationally expensive. The ICP dissimilarity, for

example, is the result of an iterative optimization al-

gorithm whose complexity is dependent on the num-

ber of points in the point clouds. Computational ef-

ﬁciency is, however, very important in the context of

surrogate models.

Such a method, however, raises the problem of

how to select landmarks. The best selection method,

however, is dependent on the learning problem and

dataset (P˛ekalska et al., 2006).

3 CASE STUDY

This study focuses on the usage of the dissimilarity

space embedding framework to train sawing simula-

tion surrogate models to predict baskets of products

of logs from 3D scans of their surface. From a ma-

chine learning perspective, this problem can be mod-

eled and has been modeled as either a classiﬁcation

problem or as a regression problem.

If the problem is modeled as a classiﬁcation prob-

lem, every BoP present in the training dataset is asso-

ciated with a class to be predicted. The main advan-

tage of this method is that the surrogate model will

always predict a feasible BoP. However, these train-

ing datasets can contain many different BoP, some of

them appearing only once in the training dataset. It is

Figure 1: Example of a 3D scan of a log.

also possible that the training dataset does not contain

all of the possible BoP.

If the problem is modeled as a (multi-output) re-

gression problem, a BoP is modeled as a vector of

size p where p is the number of standard products that

can be sawed in the sawmill considered. The i

ele-

ment of this vector correspond to the quantity of the

type of lumber present in the BoP. While this elimi-

nates the problem caused by rare and unobserved BoP,

it also means that unfeasible BoP will be predicted.

Typically, BoP predicted by regression model con-

tains fractional quantities of product. It should be no-

ticed, however, that these predictions are not designed

to be used individually, but aggregated by batches of

logs and fed to operational research models. For these

reasons, in this study, the problem of predicting BoP

of logs is modeled as a regression problem.

3.1 Dataset

The dataset used in this study originates from the

Canadian forest-product industry. It contains infor-

mation over 2219 pine, ﬁr, and spruce wood logs.

More precisely, each log has a 3D scan, a set of six

know-how features, and a BoP obtained by simulat-

ing the sawing of the log with the software Optitek.

The 3D scans are point clouds, describing the sur-

face of the logs. They are, therefore, constituted of an

unordered list of points with three coordinates each.

The number of points in a cloud varies from scan to

scan and is, in particular, dependent on the length of

the logs. The points are ordered in rough ellipsoids

spanning the log surface. An example of such a scan

is provided in ﬁgure 1.

In addition to these scans, each log is described by

six know-how features: its length, diameters at both

extremities, curvature, shrinking, and volume. These

features are, in particular, used by (Morin et al., 2015)

to predict BoP of logs. Models trained to predict BoP

from these descriptive features are, therefore, used as

baselines in this study.

Some of these features are used in this industry to

classify logs in the log yard. This is, in particular, the

CoreSelect: A New Approach to Select Landmarks for Dissimilarity Space Embedding

481

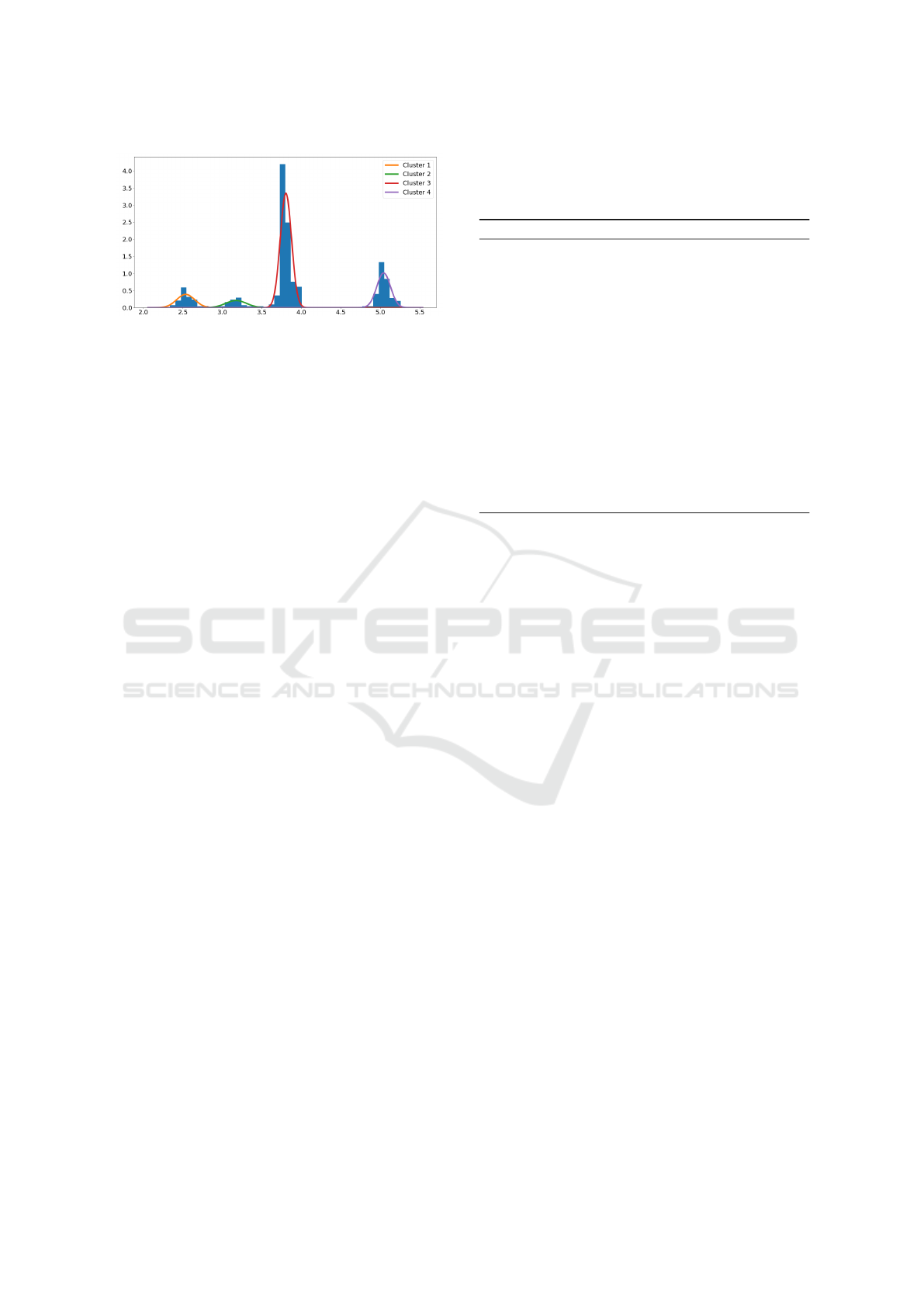
Figure 2: Histogram of the length of the logs in the dataset.

case of the length and diameters. Logs from differ-

ent clusters would have different possible BoP. This

dataset, in particular, can be divided into four clus-

ters, based on the length of the logs. Figure 2 presents

the histogram of the length of logs, to which was ﬁtted

a mixture of four Gaussian distributions.

The sawmill model set to the simulator Optitek to

generate this dataset was able to produce 47 types of

products. The BoP are, therefore, modeled as vec-

tors of dimension 47. In total, 870 different BoP are

present in this dataset, of which 614 appear only once.

3.2 Landmarks Selection

In this study, ﬁve methods will be compared to select

landmarks to train dissimilarity features. These dis-

similarity features will also be compared to the know-

how features introduced in the previous section.

The ﬁrst and simplest method is to select land-

marks at random in the training dataset. It is used as

a baseline, for example, by (P˛ekalska et al., 2006) on

binary and multi-class classiﬁcation problems. While

systematic methods perform, overall, better, the dif-

ference is sometimes small and depends on the num-

ber of landmarks selected.

The second method is an algorithm providing a

locally optimal solution to the k-medoid clustering

problem. It is often named alternate in the litera-

ture. The k-medoid problem consist in ﬁnding a sub-

set R = (r

, ..., r

) in a dataset D = (x

, ..., x

) so that

R minimize:

∑

i=1

∑

x∈C

d(x, r

), (2)

with x ∈ C

if d(x, r

) = min

r∈R

d(x, r).

This method is named k-center in (P˛ekalska et al.,

2006) and is, overall, the best-performing method on

the classiﬁcation problems it was tested on. While

(P˛ekalska et al., 2006) apply it on a class-by-class ba-

sis, however, it is applied on the whole dataset here.

This method is based on a k-medoids algorithm, i.e, a

generalization of the well-known k-means algorithm

for data clustering. The landmarks correspond to the

cluster centers. The general principle of this algo-

rithm is presented in algorithm 1.

Algorithm 1: Alternate.

Input D = (x

, ..., x

), set of training inputs

Output R = (r

, ..., r

), set of landmarks

Initialize R = (r

, ..., r

) at random or following an

heuristic.

Initialize clusters C

, ..., C

so that D =

j∈J1,qK

while End condition is False do

for x ∈ D do

i ← max

j∈J1,qK

(d(x, r

))

set x into C

end for

for i ∈ J1, qK do

← argmin

x∈C

(

∑

x∈C

(d(x, r

))

end for

end while

This algorithm is iterative. The complexity of one

iteration is O(n

) with n the size of the training dataset

(Schubert and Rousseeuw, 2021). Iterations are per-

formed until some ending condition appends, either

that a maximum number of iterations is reached or

that the set of landmarks stops changing.

The third method is based on the Partitioning

Around Medoids (PAM) algorithm (Sarle, 1991). It

solves the same k-medoid problem and is more com-

putationally intensive but more accurate (Schubert

and Rousseeuw, 2021). PAM is constituted of two

parts: Build, which initializes the centers of the clus-

ters, and Swap, which swaps cluster centers with

other data points in order to decrease the clustering

cost deﬁned in equation 2. An outline of the Swap

procedure is presented in algorithm 2. Depending on

the exact implementation, the complexity of one iter-

ation ranges from O(n

) to O(q

) with n the size of

the training dataset and q the number of clusters. The

implementation used for this article is O(q(n − q)

)

(Maranzana, 1963).

The fourth method evaluated in this study is

named Dselect and proposed by (Kar and Jain, 2011).

This heuristic is based on the idea that landmarks

should be as dissimilar from one another as possi-

ble. In particular, they introduced a heuristic, named

Dselect, that iteratively selects new landmarks as the

ones minimizing the average dissimilarity toward pre-

viously selected landmarks. A pseudocode of this

heuristic is presented in algorithm 3. It is an itera-

tive greedy algorithm. Contrary to k-medoids where

all landmarks are reevaluated at every iteration, Dse-

lect starts from an empty set of landmarks and adds

NCTA 2023 - 15th International Conference on Neural Computation Theory and Applications

482

Algorithm 2: PAM Swap.

Input D = (x

, ..., x

), set of training inputs

Output R = (r

, ..., r

), set of landmarks

R ← Build(D)

Initialize clusters C

, ..., C

empty

for x ∈ D do

i ← max

j∈J1,qK

(d(x, r

))

set x into C

end for

while cost decrease do

for r ∈ R do

for x ∈ D \ R do

Compute cost change when swapping r

and x

end for

perform the best swap

end while

them one by one until the set is completed. As such,

the complexity of the whole algorithm is O(nq

) with

n the size of the training dataset and q the number of

landmarks. It is, therefore, less costly than Alternate

and PAM as long as the number of landmarks remains

small in comparison with the dataset size.

Algorithm 3: Dselect.

Input D = (x

, ..., x

), set of training inputs

Output R = (r

, ..., r

), set of landmarks

← random element from D

for i ∈ J1, qK do

← argmax

x∈D\R

(

∑

∈R

d(x, r

))

end for

The ﬁfth method evaluated is a variant of Dselect

which is proposed in this study. This method is named

CoreSelect. A pseudocode is given in algorithm 4.

Like Dselect, it is a greedy algorithm. The difference

is that at every iteration, the next landmark is selected

as the data point that maximizes their minimal dis-

similarity with previously selected landmarks. A mo-

tivation for this modiﬁcation of Dselect is that, in the

metric case, this strategy yields an approximate solu-

tion to a q-center problem (Dyer and Frieze, 1985):

min

R=(r

,...,r

)⊂X

∆(r

, ..., r

), (3)

with

∆(r

, ..., r

) = max

x∈X

min

d(x, r

). (4)

More precisely, it ensures that the maximum dis-

tance between a point and the nearest selected land-

mark is at most twice that of the optimal solution. It

should be noticed that this q-center problem is dif-

ferent from the one solved by the alternate and PAM

algorithms. These algorithms minimize the sum of

distances toward cluster centers. On the other hand,

this method has been proven to be an approximate so-

lution to the problem of minimizing the radiuses of

the clusters. The complexity of this algorithm is the

same as Dselect: O(nq

Algorithm 4: CoreSelect.

Input D = (x

, ..., x

), set of training inputs

Output R = (r

, ..., r

), set of landmarks

← random element from D

for i ∈ J1, qK do

← argmax

x∈D\R

(min

∈R

(d(x, r

))

end for

3.3 Surrogate Models

Two ensemble models are used as sawing simulation

surrogate models in this study. The ﬁrst is the Ran-

dom Forest (RF) algorithm (Breiman, 2001). The pre-

diction of the forest is the average of the prediction

of individual decision trees. Random forests were,

in particular, selected for their good performances as

sawmill simulator surrogate models in (Morin et al.,

2015; Morin et al., 2020) on know-how features. An

important characteristic of random forest is that, to

lower the correlation between the base trees and fur-

ther reduce the variance of the ensemble, trees are

trained on bootstrap samples of the training dataset.

In addition, every split of the tree is optimized on a

random subsample of the available features. Hyper-

parameters for this model were selected by trial and

error. In particular, the number of trees in the forest

was set to 500, the total number of landmarks used for

the dissimilarity space embedding was set to 100 and

the fraction of the number of features considered to

optimize each split was set to 10, except for the base-

line using the know-how features. In this case, all six

features are considered for each split selection.

The second ensemble model investigated in this

study is an ensemble of small artiﬁcial neural net-

work (ANN) models. These neural networks are feed-

forward models with a single hidden layer, trained

with the Levenberg-Marquardt algorithm. Similarly

to what was done in (Chabanet et al., 2021b), the ac-

tivation function of the hidden layer is a hyperbolic

tangent and the activation function of the output layer

is a sigmoid. The sigmoid output, in particular, ensure

CoreSelect: A New Approach to Select Landmarks for Dissimilarity Space Embedding

483

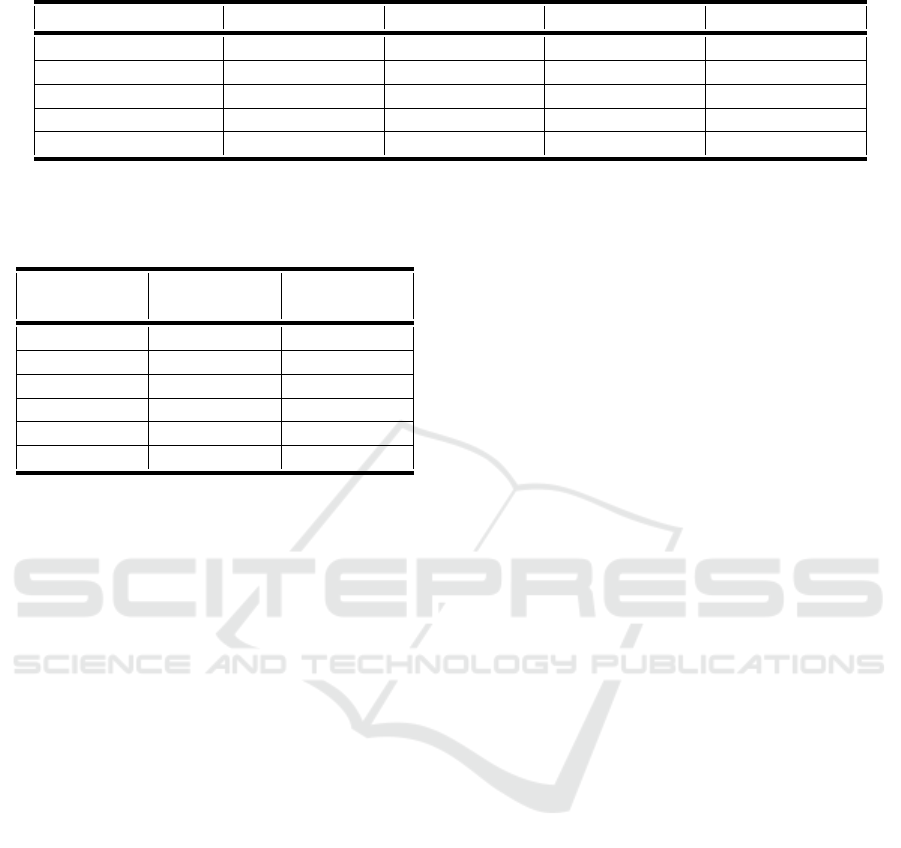
Table 1: Average number and standard deviation over 30 repetitions of the number of landmarks in each length cluster.

Selection method Cluster 1 Cluster 2 Cluster 3 Cluster 4

Random 12.0 (3.1) 6.7 (2.5) 59.9 (5.9) 21.5 (4.4)

Alternate 3.3 (1.2) 3.0 (1.3) 90.2 (2.0) 3.5 (1.0)

PAM 23.8 (2.9) 16.3 (2.6) 40.0 (2.4) 19.9 (2.2)

Dselect 48.8 (0.5) 0.03 (0.2) 0.9 (0.6) 50.3 (0.6)

CoreSelect 27.5 (3.0) 17.2 (3.0) 35.9 (3.1) 19.4 (1.8)

Table 2: Average and standard deviation over 30 experi-

ment repetitions of the MSE obtained for each model on the

evaluation set.

Selection

method

Random

Forest

ANN

ensemble

Know-how 1.819 (0.035) 1.968 (0.020)

Random 1.773 (0.027) 1.828 (0.020)

Alternate 1.847 (0.035) 1.985 (0.041)

PAM 1.762 (0.029) 1.823 (0.020)

Dselect 1.781 (0.034) 1.855 (0.023)

CoreSelect 1.763 (0.029) 1.830 (0.020)

that, after rescaling the predictions, the quantities of

lumber predicted are always between 0 and the max-

imum quantity observed in the training dataset. The

number of neurons in the hidden layer was set by tri-

als and errors to 2, which is consistent with the results

of (Chabanet et al., 2021b). As for the random forest

model, the number of landmarks was set to 100 and

the number of weak learners to 500. The number of

features used as input for each network was set to 10.

4 EXPERIMENTAL RESULTS

Experiments are run as follows. The dataset is, ﬁrst,

divided at random into a small training set of size 500,

and an evaluation set of size 1719. For each landmark

selection method, 100 landmarks are selected on the

training set and used to embed the data in a dissimi-

larity space. The know-how features are also used to

obtain a sixth representation of the data. For each rep-

resentation, a random forest and an ANN ensemble

are trained on the training set. The Mean Square Error

(MSE) of the prediction is measured on the evaluation

set. To average out the impact of the exact train-test

separation of the dataset, this process is repeated 30

times.

Table 1 presents the number of landmarks selected

by each method in each of the 4 length clusters de-

ﬁned in section 3.1. These numbers are averaged over

30 repetitions of the experiments. Different selection

methods have different behavior. The number of land-

marks selected by the random method in each cluster

is, naturally, proportional to the size of each cluster.

Therefore, the largest cluster, cluster 3, which repre-

sents 60% of the dataset, has, on average, approxi-

mately 60% of the landmarks. Similarly, cluster 4,

which represents 22% of the dataset, contains, on av-

erage, approximately 22% of the landmarks. On the

opposite, the smallest cluster, cluster 2, contains only

6.7% of the landmarks.

Both PAM and CoreSelect smooth slightly the dis-

tribution of the landmarks over the clusters. In partic-

ular, 40.0 and 35.9 landmarks are selected in average

in cluster 3 by PAM and CoreSelect respectively. This

is less than the amount selected by the random selec-

tion method. On the opposite, they select respectively

16.3 and 17.2 landmarks in cluster 2.

Dselect and Alternate have very different behav-

ior. Dselect, in particular, mostly selects landmarks in

the two extremal clusters, clusters 1 and 4. This might

be explained, in the metric case, by the tendency of

DSelect to select the next point far from the geometric

median of the previously selected landmarks, which is

the point minimizing the sum of distances toward the

landmarks. On the opposite, Alternate selects most of

the landmarks, 90 on average, from cluster 3 which is

the largest cluster.

The MSE evaluated on the evaluation test for the

different landmark selection methods and surrogate

models are presented in table 2. Several facts have to

be mentioned. First, the lowest MSE is obtained for

the RF surrogate model and the PAM and CoreSelect

landmark selection results. These two MSE cannot

be said to be statistically different from these exper-

iments. In particular, a paired student test over the

MSE measured on the 30 repetitions of the experi-

ment has a p-value of 0.41. It should be noticed, how-

ever, that CoreSelect has a lower computational cost

than PAM. Comparing both these methods to the third

best method, i.e., the RF model with random land-

marks, yields p-values lower than 3 × 10

−5

in both

cases. Therefore, both PAM and the newly proposed

CoreSelect selection methods allow to improve upon

the random baseline, as well as the know-how fea-

tures. On the contrary, both the Dselect and Alternate

NCTA 2023 - 15th International Conference on Neural Computation Theory and Applications

484

selection methods show signiﬁcantly worse MSE for

the Random Forest model. P-values of the students

test are 3 × 10

−10

and 5 × 10

−4

respectively. This

might be due to the highly irregular dispersion of the

landmarks across clusters.

In general, ANN ensemble surrogate models have

higher MSE than RF surrogates. The impact of the

various landmarks selection methods over the average

MSE is, however, different. In particular, in this case,

the method with the lowest MSE is PAM alone. This

time, using CoreSelect does not lead to lower MSE

than the random method. In particular, the p-value

of a paired student test is, here, 0.32. Both Dselect

and Alternate, however, lead to higher MSE than the

random selection method.

Table 3: Average and standard deviation over 100 repeti-

tions of the time required by each method to select 100 land-

marks in a subset of size 500 of the dataset.

Selection

method

Selection Time

Random

8.9 × 10

−5

(2.8 × 10

−4

)

Alternate

2.6 × 10

−2

(1.9 × 10

−3

)

PAM 15.7 (0.6)

Dselect

2.0 × 10

−2

(6.7 × 10

−4

)

CoreSelect

2.3 × 10

−2

(6.8 × 10

−4

)

To complement the previous experimental results,

the computation times required by the selection meth-

ods with the implementation used for these experi-

ments were estimated. Dselect and CoreSelect were

implemented from scratch in Python using the numpy

library. Alternate and PAM were implemented as

wrapper around clustering functions from the scikit-

learn-extra

library. All experiments were run on a

computer with an intel Core i7 vPRO 10

generation

CPU at 2.70GHz. Table 3 presents the average times

required by each landmark selection method, over a

hundred new random subsets of size 500 of the whole

dataset. Unsurprisingly, the fastest method is by far

the random selection. Dselect, CoreSelect, and Alter-

nate have very similar computational times, between

0.020 and 0.026 seconds in these experiments. On

the opposite, PAM is very slow, as it needs, on av-

erage, 15.7 seconds to select the landmarks. Consid-

ering that the two best methods are, here CoreSelect

and PAM which perform similarly with random forest

models, Coreselect present a clear advantage in terms

of time.

https://scikit-learn-extra.readthedocs.io/en/stable/

install.html, last accessed in May 2023

5 CONCLUSION

This article studies surrogate models for sawmill sim-

ulation. In particular, it focuses on the use of the

dissimilarity space embedding framework to create a

feature space used to train models and make predic-

tions. Because this framework raises the question of

the methods used to select the landmarks which form

its core, ﬁve landmarks selection methods are com-

pared on this method.

Numerical experiments were run using a dataset

from the Canadian Sawmill industry to train RF and

ANN ensemble models on data representations ob-

tained from each method. Results were also com-

pared with baselines obtained from know-how repre-

sentation of the data points.

Among the combinations of landmarks selection

methods and ML models evaluated, the lowest MSE

was obtained for the RF model, with landmarks ob-

tained from either the PAM or the newly proposed

CoreSelect method. CoreSelect, however, has lower

computational complexity than PAM.

Several limits to this study should, however, be

mentioned and lead to future works. First, previous

works have shown that the performances of these sur-

rogate models can change widely from one sawmill to

another, especially depending on the number of stan-

dard products they produce. Therefore, the experi-

ments presented in this study should be repeated on

other independent datasets. Similarly, the impact of

the size of the training dataset and of the number of

landmarks should be investigated in detail. Lastly, the

reason why CoreSelect leads to lower MSE than the

random baseline with the RF models but not with the

ANN ensemble should be explored as it might lead to

a deeper insight into the behavior of these models on

dissimilarity spaces.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge the ﬁnancial

support of the ANR-20-THIA-0010-01 Projet LOR-

AI (Lorraine Intellgence Artiﬁcielle) and the région

Grand EST. We are also extremely grateful to FPInno-

vation, who gathered and processed the dataset used

in this study.

REFERENCES

Besl, P. J. and McKay, N. D. (1992). Method for regis-

tration of 3-d shapes. In Sensor fusion IV: control

CoreSelect: A New Approach to Select Landmarks for Dissimilarity Space Embedding

485

paradigms and data structures, volume 1611, pages

586–606. Spie.

Breiman, L. (2001). Random forests. Machine learning,

45:5–32.

Chabanet, S., Bril El-Haouzi, H., Morin, M., Gaudreault,

J., and Thomas, P. (2023). Toward digital twins for

sawmill production planning and control: beneﬁts, op-

portunities, and challenges. International Journal of

Production Research, 61(7):2190–2213.

Chabanet, S., Chazelle, V., Thomas, P., and El-Haouzi,

H. B. (2021a). Dissimilarity to class medoids as fea-

tures for 3d point cloud classiﬁcation. In Advances

in Production Management Systems. Artiﬁcial Intelli-

gence for Sustainable and Resilient Production Sys-

tems: IFIP WG 5.7 International Conference, APMS

2021, Nantes, France, September 5–9, 2021, Proceed-

ings, Part III, pages 573–581. Springer.

Chabanet, S., Thomas, P., and El-Haouzi, H. B. (2021b).

Medoid-based mlp: an application to wood sawing

simulator metamodeling. In 13th International Con-

ference on Neural Computation Theory and Applica-

tions, NCTA 2021.

Duin, R. and P˛ekalska, E. (2009). The dissimilarity repre-

sentation for pattern recognition: a tutorial. Technical

Report.

Dyer, M. and Frieze, A. (1985). A simple heuristic for

the p-centre problem. Operations Research Letters,

3(6):285–288.

Goulet, P. (2006). Optitek: User’s manual.

Jain, B. J. and Spiegel, S. (2015). Time series classiﬁcation

in dissimilarity spaces. In AALTD@ PKDD/ECML.

Kar, P. and Jain, P. (2011). Similarity-based learning via

data driven embeddings. Advances in neural informa-

tion processing systems, 24.

Livi, L., Rizzi, A., and Sadeghian, A. (2014). Optimized

dissimilarity space embedding for labeled graphs. In-

formation Sciences, 266:47–64.

Luo, C., Li, Y., and Chung, S. M. (2009). Text document

clustering based on neighbors. Data & Knowledge

Engineering, 68(11):1271–1288.

Maranzana, F. E. (1963). On the location of supply points to

minimize transportation costs. IBM Systems Journal,

2(2):129–135.

Martineau, V., Morin, M., Gaudreault, J., Thomas, P., and

El-Haouzi, H. B. (2021). Neural network architectures

and feature extraction for lumber production predic-

tion. In The 34th Canadian Conference on Artiﬁcial

Intelligence.

Morin, M., Gaudreault, J., Brotherton, E., Paradis, F., Rol-

land, A., Wery, J., and Laviolette, F. (2020). Machine

learning-based models of sawmills for better wood al-

location planning. International Journal of Produc-

tion Economics, 222:107508.

Morin, M., Paradis, F., Rolland, A., Wery, J., Laviolette,

F., and Laviolette, F. (2015). Machine learning-based

metamodels for sawing simulation. In 2015 Win-

ter Simulation Conference (WSC), pages 2160–2171.

IEEE.

Morneau-Pereira, M., Arabi, M., Gaudreault, J., Nourelfath,

M., and Ouhimmou, M. (2014). An optimization and

simulation framework for integrated tactical planning

of wood harvesting operations, wood allocation and

lumber production. In MOSIM 2014, 10eme Con-

férence Francophone de Modélisation, Optimisation

et Simulation.

Müller, M. (2007). Dynamic time warping. Information

retrieval for music and motion, pages 69–84.

Munoz, A. and de Diego, I. M. n. (2006). From indeﬁnite

to positive semi-deﬁnite matrices. In Structural, Syn-

tactic, and Statistical Pattern Recognition: Joint IAPR

International Workshops, SSPR 2006 and SPR 2006,

Hong Kong, China, August 17-19, 2006. Proceedings,

pages 764–772. Springer.

Ong, C. S., Mary, X., Canu, S., and Smola, A. J. (2004).

Learning with non-positive kernels. In Proceedings of

the twenty-ﬁrst international conference on Machine

learning, page 81.

P˛ekalska, E., Duin, R. P., and Paclík, P. (2006). Prototype

selection for dissimilarity-based classiﬁers. Pattern

Recognition, 39(2):189–208.

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Point-

net: Deep learning on point sets for 3d classiﬁcation

and segmentation. In Proceedings of the IEEE con-

ference on computer vision and pattern recognition,

pages 652–660.

Sarle, W. S. (1991). Finding groups in data: An introduction

to cluster analysis.

Schleif, F.-M. and Tino, P. (2015). Indeﬁnite prox-

imity learning: A review. Neural Computation,

27(10):2039–2096.

Schubert, E. and Rousseeuw, P. J. (2021). Fast and eager

k-medoids clustering: O (k) runtime improvement of

the pam, clara, and clarans algorithms. Information

Systems, 101:101804.

Selma, C., Bril El Haouzi, H., Thomas, P., Gaudreault,

J., and Morin, M. (2018). An iterative closest point

method for measuring the level of similarity of 3d

log scans in wood industry. Service Orientation in

Holonic and Multi-Agent Manufacturing: Proceed-

ings of SOHOMA 2017, pages 433–444.

Wery, J., Gaudreault, J., Thomas, A., and Marier, P. (2018).

Simulation-optimisation based framework for sales

and operations planning taking into account new prod-

ucts opportunities in a co-production context. Com-

puters in industry, 94:41–51.

NCTA 2023 - 15th International Conference on Neural Computation Theory and Applications

486