Shaping the Behavior Space with Counterfactual Agents in

Multi-Objective Map Elites

Anna Nickelson, Nicholas Zerbel, Gaurav Dixit and Kagan Tumer

Collaborative Robotics and Intelligent Systems (CoRIS) Institute, Oregon State University, Corvallis, OR, U.S.A.

Keywords:

Counterfactuals, Quality Diversity, Multi-Objective, Evolutionary Learning.

Abstract:

Success in many real-world problems cannot be adequately deﬁned under a single objective and instead re-

quires multiple, sometimes competing, objectives to deﬁne the problem. To perform well in these environ-

ments, autonomous agents need to have a variety of skills and behaviors to balance these objectives. The

combination of Multi-Objective Optimization (MOO) and Quality Diversity (QD) methods, such as in Multi-

Objective Map Elites (MOME), aim to provide a set of policies with diverse behaviors that cover multiple

objectives. However, MOME is unable to diversify its search across the behavior space, resulting in signif-

icantly reduced coverage of the global Pareto front. This paper introduces Counterfactual Behavior Shaping

for Multi-Objective Map Elites (C-MOME), a method that superimposes counterfactual agents onto the state

space of a learning agent to more richly deﬁne the diversity of agent behaviors. Counterfactuals explicitly

introduce new forms of diversity in agent behaviors, resulting in C-MOME’s effective coverage of behavioral

niches; this provides a broader set of Pareto optimal policies. We show that C-MOME covers more than twice

as much of the behavior space compared to MOME while increasing the hypervolume of the global Pareto

front by over 40%.

1 INTRODUCTION

When optimizing over a single objective, learning-

based approaches seek to ﬁnd the best solution avail-

able that represents the global optimum. Although

some problems can be adequately deﬁned under a sin-

gle objective, many real-world problems are complex

and deﬁne success using multiple competing objec-

tives that need to be balanced. For example, engi-

neering design tasks often aim to maximize safety

while minimizing costs (Coello Coello, 2006) and in

multi-robot exploration tasks, designers try to maxi-

mize exploration while minimizing energy consump-

tion, travel time, or distance (Burgard et al., 2005; Al-

itappeh and Jeddisaravi, 2022). While many Multi-

Objective Optimization (MOO) algorithms have been

introduced to ﬁnd well-balanced solutions to these

problems, they typically consider objective trade-

offs under a particular set of operating conditions.

For long-term deployments and dynamic environ-

ments, autonomous agents need to be able to adapt to

changes in the environment while continuing to bal-

ance multiple goals. This is a challenging problem for

agents as they need to learn what tasks to accomplish,

how to accomplish the tasks, how different tasks cor-

relate with different objectives, and what the best bal-

ance between objectives is for the current system con-

ditions.

One way to provide a stepping stone to this level

of reasoning is to train a diverse set of policies or

skills for the agent to enact in different scenarios.

Quality Diversity (QD) methods can be used to ad-

dress this training step as they intentionally diver-

sify the search by focusing on policies that cover a

wide range of behaviors in order to provide a breadth

of policies (Mouret and Clune, 2015). Popular QD

approaches, such as Multi-dimensional Archive of

Phenotypic Elites (MAP-Elites) (Mouret and Clune,

2015), aim to ﬁnd policies that ﬁll different behav-

ioral niches, but these methods still typically focus

on ﬁnding policies that solve for a singular objective.

Multi-Objective Map Elites (MOME) addresses this

issue by maintaining a local Pareto front within each

behavioral niche to cover multiple objectives (Pierrot

et al., 2022). However, MOME is unable to fully di-

versify its search across the behavior space, leading

to poor coverage across the Pareto front and behavior

space.

In this work we propose Counterfactual Behavior

Shaping for Multi-Objective Map Elites (C-MOME).

Nickelson, A., Zerbel, N., Dixit, G. and Tumer, K.

Shaping the Behavior Space with Counterfactual Agents in Multi-Objective Map Elites.

DOI: 10.5220/0012164800003595

In Proceedings of the 15th International Joint Conference on Computational Intelligence (IJCCI 2023), pages 41-52

ISBN: 978-989-758-674-3; ISSN: 2184-3236

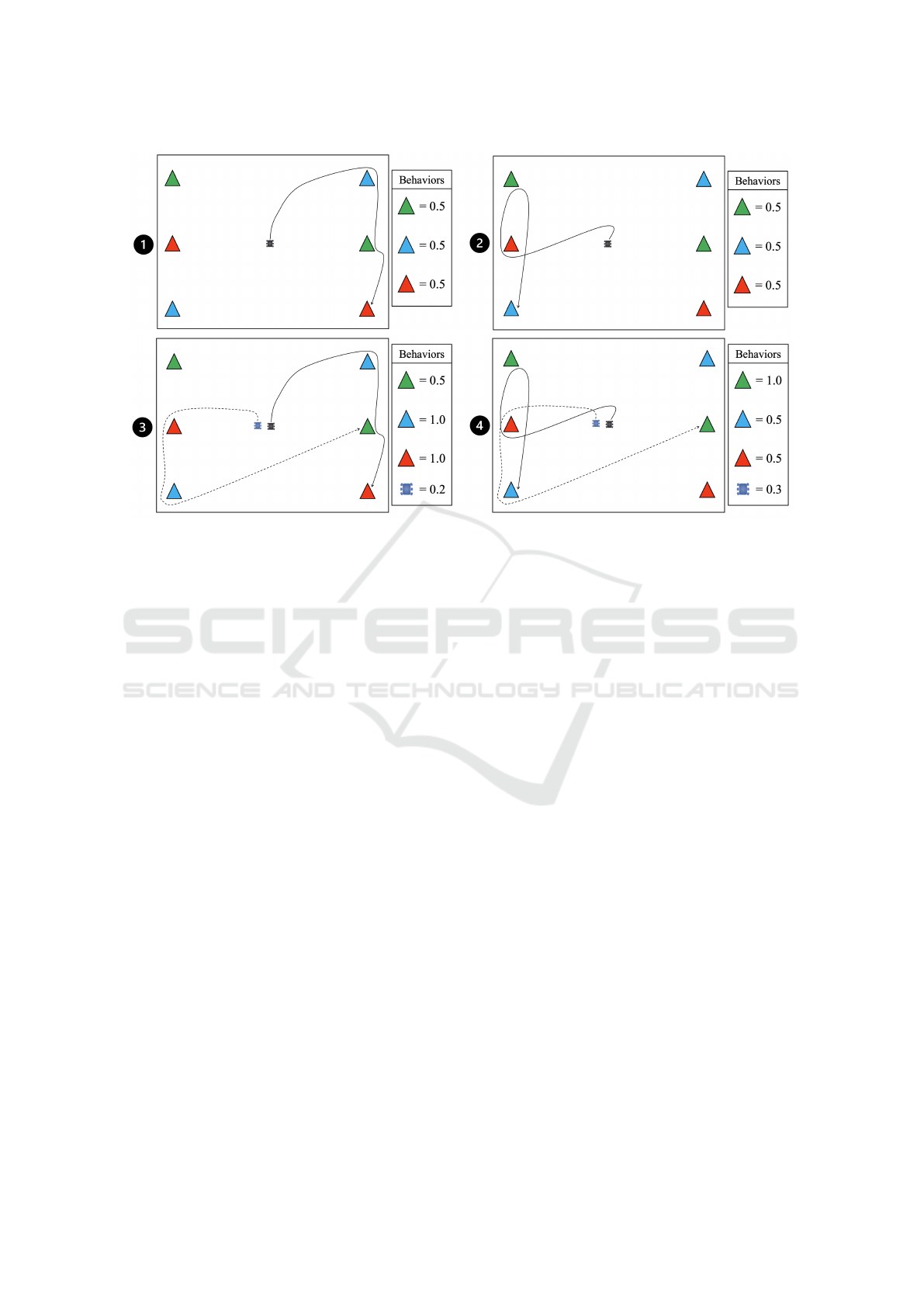
Figure 1: In sub-ﬁgures (1) and (2), we show two distinct agent behaviors resulting from different policies in a multi-objective

tasks observation problem. In (1) and (2) behaviors are deﬁned by the percentage of each tasks type an agent observes.

However, this deﬁnition of behaviors does not effectively capture the distinctiveness of the two agent behaviors. By injecting

a counterfactual agent, we redeﬁne the learning agent’s behaviors to more accurately capture this diversity. In this scenario,

adding a counterfactual agent also adds a new behavioral measure that describes tasks exploration overlap between agents.

Applying these counterfactual behaviors we see that agent behavior (1) can be redeﬁned as (3) and agent behavior (2) can be

redeﬁned as (4). While MOME would sort the policies for behaviors (1) and (2) into the same behavioral niche, C-MOME

sorts these policies into separate niches. This helps C-MOME diversify its search across both the behavior and objective

spaces.

C-MOME superimposes counterfactual states con-

taining agent representations onto the state space of

learning agents. Counterfactual agents inject struc-

tured dynamics into agent behaviors, which enables

a broader deﬁnition of diversity within the behavior

space of MAP-Elites. This enables C-MOME di-

versify its search across the behavior space; in turn,

C-MOME provides signiﬁcantly greater coverage of

effective policies along the global Pareto front and

across the behavior space.

To illustrate how counterfactuals redeﬁne agent

behaviors, we consider a multi-objective observation

task within a conﬁned environment involving multi-

ple types of targets. In this example, the behavior

space is deﬁned by the types of targets the agent vis-

its and how it chooses to interact with them. As in

many QD problems, this deﬁnition is constrained by

the environment. As a result, MOME is unable to ef-

fectively expand its search across the entire behavior

space. This constricts down the search resulting in a

lack of coverage of the global Pareto front. By intro-

ducing new behaviors deﬁned through counterfactual

agents, C-MOME more richly deﬁnes agent behaviors

and expands the search to cover the entire behavior

space. We illustrate this in Figure 1.

The contributions of this work are to:

1. Reﬁne the behavior space of an agent by inject-

ing counterfactual agents into the state space of a

learning agent,

2. Provide a greater coverage of policies along the

global Pareto front and behavior space in multi-

objective problems,

3. Analyze how counterfactuals impact the quality

and diversity of agent policies.

In a Multi-Objective tasks observation problem,

we show that C-MOME improves coverage of both

the behavior space by more than 2x and the global

Pareto front by more than 40% compared with

MOME. We compare the performance of MOME

and C-MOME to other state-of-the-art MOO algo-

rithms (namely Nondominated Sorting Genetic Algo-

rithm II (NSGA-II)). We also demonstrate the impact

of different counterfactuals on agent policies by com-

paring the policies found along the Pareto front with

overall coverage of niches within the behavior space.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

2 BACKGROUND

In many real-world problems, success is seldom de-

ﬁned under a singular objective. To solve these prob-

lems, autonomous agents typically need to learn a

wide range of different policies that can balance trade-

offs between multiple different objectives in various

ways. In this section we discuss several areas of study

relevant to this problem including Multi-Objective

Optimization and Quality Diversity. We also discuss

related works such as MOME and the use of counter-

factuals in machine learning.

2.1 Multi-Objective Optimization

Problems that do not have a single, optimal solu-

tion and are classiﬁed as Multi-Objective Optimiza-

tion (MOO) problems. Many problems use multiple

different objectives to deﬁne success, many of which

are conﬂicting. When the preferred balance between

objectives is known in advance, the objectives can be

scalarized and an optimal solution can be found with

traditional single-objective searches (Das and Den-

nis Jr, 1996; Drugan and Nowe, 2013; Van Moffaert

et al., 2013). In many cases, the preferred balance

may not be known or may change based on the sit-

uation. Most strategies to MOO aim to provide a set

of solutions that optimize different trade-offs between

objectives. The goal of MOO methods is to ﬁnd cov-

erage of the optimal region of the objective space,

known as the Pareto front, in order to present a set

of solutions that provide different balances between

objectives.

Evolutionary search-based methods are a natural

ﬁt for this problem, as they are able to ﬁnd, com-

pare, and iterate over a population of policies to

ﬁnd incrementally better solutions. Two of the most

prominent evolutionary multi-objective methods are

Strength Pareto Evolutionary Algorithm 2 (SPEA2)

(Zitzler et al., 2001) and Nondominated Sorting Ge-

netic Algorithm II (NSGA-II) (Deb et al., 2002).

NSGA-II uses a non-dominated sorting method for

ranking and sorting each solution, and it also in-

cludes a measure of crowding distance among solu-

tions to force the search to diversify across the objec-

tive space. SPEA2 computes a strength value for each

solution found, and it stores stores previously found

non-dominated solutions. This set of stored solutions

is updated after every generation. The ﬁtness of each

solution is calculated based on the number of solu-

tions that dominate it and that are dominated by it.

2.2 Quality Diversity

Where MOO aims to solutions that provide cover-

age over the objective space, Quality Diversity (QD)

seeks ﬁnd diversiﬁed policies that capture a broad

set of behaviors. This builds on previous techniques

in novelty search that focus on ﬁnding substantially

different solutions (Eysenbach et al., 2019; Lehman

and Stanley, 2011). QD aims to diversify across a

pre-deﬁned “behavior space”, a reduced-dimensional

summary of the actions or behaviors of each policy.

QD methods separate the behavior space into many

local regions, called niches, then keeps the best pol-

icy found in each niche. One notable example of

QD methods is Multi-dimensional Archive of Pheno-

typic Elites (MAP-Elites) (Mouret and Clune, 2015).

MAP-Elites is an evolutionary method that aims to

ﬁnd many different solutions for a given task. Specif-

ically, MAP-Elites aims to ﬁnd a diverse set of poli-

cies that do not necessarily solve a task optimally, but

solve a task using a variety of unique behaviors.

2.2.1 Multi-Objective Map Elites (MOME)

Multi-Objective Map Elites (MOME) (Pierrot et al.,

2022) incorporates the principles of both MOO and

QD search by building on the MAP-Elites framework.

Instead of a singular policy, MOME keeps the set

of policies in each niche that are locally Pareto op-

timal. In doing so, they are able to provide solutions

that are diverse across both the objective and behav-

ior spaces. However, combining these two methods

leads to extensive time spent searching and optimiz-

ing in unhelpful or sub-optimal regions of the behav-

ior space. By keeping locally Pareto optimal policies,

this method keeps many policies that result in no re-

ward as there are many niches where zeroes across all

objectives is locally Pareto optimal. These policies

are then used for mutation and crossover; without an-

other mechanism to add back diversity, the search is

weighed down and has a difﬁcult time escaping these

local minima.

2.3 Counterfactuals in Agent Learning

Counterfactual thought is a strategy people often

use to analyze alternative outcomes to real events

and learn from “what-if” scenarios (Boninger et al.,

1994; Byrne, 2016). This concept has also been

adopted in agent-based learning paradigms, most no-

tably in applications of reward shaping that aim to ad-

dress the issue of credit assignment within multiagent

learning problems. For example, Difference Evalua-

tions compare rewards generated from counterfactual

states with the actual rewards agents received to pro-

Shaping the Behavior Space with Counterfactual Agents in Multi-Objective Map Elites

vide individuals with ﬁnely-tuned reward feedback in

cooperative multiagent learning problems (Agogino

and Tumer, 2004). In a similar work, Counterfac-

tual Multi-Agent (COMA) policy gradients rely on

a counterfactual baseline in reinforcement learning

contexts to single out individual agent actions while

keeping the actions of others ﬁxed so more informa-

tive rewards can be evaluated (Foerster et al., 2018).

Counterfactuals have also been used in multiagent

coordination problems to produce “stepping stone”

rewards to make learning easier in situations where

task completion depends on simultaneous action in-

puts from multiple different agents. For example,

D++ compares the reward given by the current state

of a system with a reward generated from a counter-

factual state where n partner agents were available

to cooperate with a speciﬁc individual (Rahmattal-

abi et al., 2016). Counterfactuals have also been ex-

tended beyond reward shaping in applications such

as explainability in AI (Verma et al., 2020; Olson

et al., 2021), inference and decision making (Johans-

son et al., 2016; Kusner et al., 2017), and ethics in

machine learning (Kasirzadeh and Smart, 2021).

Regardless of the application, counterfactuals in

agent-based learning seek to shape available informa-

tion to provide richer learning signals or more trans-

parent decision making. In this work we apply coun-

terfactuals to quality diversity within multi-objective

problems to shape the state and behavior spaces using

counterfactual agents.

3 COUNTERFACTUAL

BEHAVIOR SPACE SHAPING

In this work, we introduce C-MOME, a novel ex-

tension to MOME that superimposes counterfac-

tual agents onto a learning agent’s state space and

shapes the behavior space used for policy search in

MAP-Elites and MOME. By injecting counterfac-

tual agents exhibiting different behaviors into the state

space, we more richly deﬁne the behaviors of a learn-

ing agent. This provides structured diversity at the be-

havior level enabling substantially better coverage the

behavior space. In turn, C-MOME ﬁnds a more use-

ful and diverse set of policies along the global Pareto

front.

To illustrate how counterfactuals can be used to

redeﬁne the behavior space of an agent, we present an

example of an agent observing different types of tasks

in Figure 1. In this example, we deﬁne behaviors as

the percentage of each task type observed by an agent.

In Figure 1-1 and Figure 1-2, we see two different be-

haviors encoded within different agent policies. Al-

though the outcomes are similar in terms of observed

tasks, the policies exhibit two distinctive agent be-

haviors. However, based on the deﬁnition of the be-

havior space, these behaviors appear as non-distinct

and would be sorted into the same behavioral niche

within MOME. By injecting counterfactual agents,

we can redeﬁne the behavior space to better capture

the differences between agent behaviors (Figure 1-

3 and Figure 1-4). Using these redeﬁned behaviors,

the differences in the learning agent’s behaviors are

more distinct allowing C-MOME to sort the underly-

ing policies into more more representative behavioral

niches. By providing this form of structured diver-

sity, C-MOME builds a set of Pareto optimal poli-

cies that provide a greater coverage along the global

Pareto front.

Using counterfactual agents also allows the learn-

ing agent to learn different behaviors in a single agent

formulation while being sensitive to future learning

with real agent partners. This implementation of

C-MOME is designed to be the ﬁrst step in a curricu-

lum learning solution for multiagent teaming, which

we discuss in the future work section (Section 6).

3.1 Counterfactual Representation

Counterfactuals are “counter to the facts”. They are

represented as non-learning agents and exhibit behav-

iors that impact the state space and re-deﬁne the be-

havior space for the learning agent. For example,

counterfactuals can be static or dynamic. The coun-

terfactual agents can also impact the tasks within the

state space or have no impact on tasks. A key factor is

that counterfactuals do not impact any of the agent re-

wards or the completion of objectives directly. Learn-

ing agents merely perceive that counterfactual agents

are impacting task completion and act according to

their state perception and policies. This limits the im-

pact of the counterfactuals to the state space and be-

havior space of the agent to improve the ﬁdelity of the

policy search within the behavior space.

Counterfactuals impact the agent’s perception in

three distinct ways. In the state space, counterfactuals

can have a direct impact by (1) appearing as agents;

they can also indirectly impact it by (2) ‘completing’

tasks. Finally, counterfactuals can be used to (3) re-

deﬁne the behavior space to decouple it from a sta-

tionary environment. Each of these changes in the

agent’s perception injects structured diversity to im-

prove the overall policy search.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

3.2 Counterfactual State Space

Counterfactuals impact the agent’s state space in two

ways. First, they are perceived by the learning agent’s

sensors as agents in the environment. This allows the

agent to learn the impact of simple behaviors, such as

moving closer to or further from other agents. Coun-

terfactuals can also impact the completeness of tasks

in the environment but only through the perceptions

of the learning agent. This leads to the deﬁnition of

the learning agent’s state as described in Equation 1

where the state, s, is deﬁned by the ground truth state

of the world, s

, and the superimposed counterfactual

state, s

s = s

+ s

(1)

Agent sensors provide a summary of the distance,

, to any real agents, a ∈ A, within the sensor range in

a given region, r, as shown in equation 2. Counterfac-

tual agents, c ∈ CF, are added in the same manner, as

shown in the highlighted portion of Equation 2. In this

work, we do not consider other non-counterfactual

agents, a.

∑

a∈r

+ 1

∑

c∈r

+ 1

(2)

Agent sensors also summarize the distance, d, and

completion percentage, p, for tasks of a given group,

t ∈ T

, in a region, r. This is shown in Equations 3

and 4, respectively. Counterfactuals, c ∈ CF, can im-

pact the completeness of each task, shown in the high-

lighted region of Equation 4. Once again, the coun-

terfactual agents impact on task completion is only re-

ﬂected in the learning agent’s state space; counterfac-

tual agents cannot directly contribute to the rewards

earned by the learning agent.

∑

t∈r

+ 1

(3)

∑

t∈r

∑

t∈r

(4)

where t ∈ T

, a ∈ A, c ∈ CF

Collectively, equations 2, 3, and 4 combine to cre-

ate the agent’s state, s. The highlighted portions of

these equations denoted with the subscript c form the

counterfactual state, s

, while the rest makes up the

world state, s

as seen in Equations 6 and 5, respec-

tively. In Equation 5, b is a state variable representing

the agent’s current battery level. This provides a con-

straint on the agent, forcing it to be strategic about

how it competes tasks.

∑

a∈r

+ 1

∑

t∈r

+ 1

∑

t∈r

(5)

∑

c∈r

+ 1



∑

t∈r



(6)

3.3 Counterfactual Behavior Space

Counterfactual agents enable C-MOME to more

richly deﬁne agent behaviors allowing for broader be-

havioral diversity. By incorporating counterfactuals

into the state space, agents are able to detect and react

to the perceived actions and behaviors of counterfac-

tual agents. The behavior space is deﬁned to capture

the diverse ways in which the learning agent can react

to these counterfactuals.

Similar to the state space, the behavior space, beh,

is deﬁned by the agent’s behaviors in the world, beh

and the agent’s behaviors in relation to the counter-

factuals, beh

beh = [beh

, beh

] (7)

The counterfactual behavior space, beh

, includes

summary statistics of the distance from the agent to

the counterfactual agents. This is summarized using

three different variables: the closest the agent got to

a counterfactual, the furthest an agent got away from

a counterfactual, and the average distance to all coun-

terfactuals across an episode.

beh

min(d

), max(d

(8)

4 EXPERIMENTAL SETUP

In this work, we test C-MOME in a continuous, multi-

objective observation problem where an agent must

observe different types of targets. Exploration of each

type of target is considered a separate task (or objec-

tive). While the overall goal is for the agent to com-

plete as many tasks as possible, the agent has to bal-

ance different, competing objectives by observing dif-

ferent task types during its mission.

Objectives are deﬁned by how complete tasks are

in each task group, T

. The ﬁtness calculation for each

objective is the sum of the completion percentage of

each task of a given type as described in Equation 9.

In this work, we use two task groups and therefore

have two objectives to optimize over. We note that

it is not possible for the agent to complete 100% of

Shaping the Behavior Space with Counterfactual Agents in Multi-Objective Map Elites

the tasks within the time provided. This is an inten-

tional quality of the environment, as the agent must

be strategic about how to spend its time and balance

the tasks it aims to accomplish.

∑

t∈T

(9)

4.1 Learning Agents

Learning agents have two sets of sensors, one set de-

tects agents and the other detects tasks. Agents have

four sensors of each type to collect information within

four quadrants of a 360 degree circular area centered

around the agent. The agent’s state includes one in-

put for each agent sensor that detects the distance to

other agents in each region. The agent’s state also in-

clude two inputs for each task sensor that detects task

completeness and the distance to tasks; each task type

has a separate set of sensors. One additional sensor

input deﬁnes the current charge of the agent’s battery

(b). These collectively become the learning agent’s

state, s

. The counterfactual state, s

, is added to

the learning agent’s state in order to more richly de-

ﬁne the agent’s behavior. An agent’s sensors collect

state information deﬁning s

and s

(Equations 5 and

6).

The learning agent is represented by a neural net-

work policy with a single hidden layer (30 nodes).

Using this policy, the agent selects which region to go

toward, which task type to accomplish in that region,

how much effort to put into that task, and its velocity,

v. A separate navigation policy navigates the agent to

the closest task of the chosen type in that region. In

this work, we assume the agent has optimized naviga-

tion and control policies for travelling between differ-

ent tasks in the environment. The battery is drained

at a rate of the velocity squared, so the agent must

balance speed and energy (Equation 10).

The agent outputs two variables that determine

how much effort it puts in to the chosen task, e

and

. The battery, b, drains at the rate of their product

(Equation 10), and the product of these two scalars

adds to the task’s completion percentage, p

, up to

100% (Equation 11).

= b − v

− (e

∗ e

)

(10)

= p

+ (e

∗ e

) (11)

4.2 Behavior Space

The tasks in this problem form the baseline for deﬁn-

ing the behavior space used by MOME. The behav-

iors are direct outputs from the agent’s policy, namely

the velocity, v, and effort, e

and e

. The behavior

space is deﬁned as the mean of each of variable across

an episode, separated by task group g. For our im-

plementation, we test with two task groups creating a

6-dimensional behavior space (Equation 12).

beh

= beh

= [[ ¯e

0,g

, ¯e

1,g

, ¯v

] ∀g] (12)

For C-MOME, we reduce the world behavior

space (beh

) to two dimensions by taking the mean

of all three variables for each group in (Equation 12).

As a result, the behavior space with counterfactuals

is 5-dimensional: two task groups in beh

and three

summary statistics in beh

(Equation 8). We do this

to make the behavior space dimensions more closely

aligned and comparable in the cases with and without

counterfactuals (5 vs 6 dimensions).

beh



beh



[ ¯e

0,g

, ¯e

1,g

, ¯v

] ∀g

min(d

), max(d

(13)

4.3 Counterfactual Parameters

To gain a more thorough understanding of how coun-

terfactual agents impact both the behavior space and

objective space in C-MOME, we test a number of dif-

ferent parameters that dictate the creation of coun-

terfactual agents. First, we test how different types

of counterfactual agents impact performance (Section

5.2). We evaluate C-MOME with Static counterfac-

tual agents that are present in the environment but do

not move, Move counterfactuals where counterfactual

agents move but do not effect task completion within

the learning agent’s state space, and Task counterfac-

tuals where counterfactual agents move and impact

task completion. Next, we analyze how the number

of counterfactual agents impacts performance (Sec-

tion 5.3). Finally, we test how adding counterfactuals

to three different portions of the agent’s perception

impacts the overall search (Section 5.4). In the state,

counterfactuals can (1) impact task completion or (2)

appear as agents; they can also impact (3) the deﬁni-

tion of the behavior space. In each experiment, we

compare against MOME which has no counterfactual

agents to form a baseline for comparison.

When there are no counterfactuals (MOME), the

state is deﬁned by the true world state, s

, and the

behavior space is deﬁned by the agent’s interactions

with the world, beh

(Equations 5 and 12). With

counterfactuals (C-MOME), the counterfactual infor-

mation is injected in the state space, s

+ s

, and the

behavior space beh

+ beh

(Equations 6 and 13) un-

less otherwise noted.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

4.4 Experimental Parameters

We run experiments in the multi-objective exploration

problem in a 20x20, 2D continuous environment. The

learning agent starts at a randomized position within

one unit of the center of the map. The agent can move

at up to 2 units per time step; the speed at each time

step is determined by the velocity output, v, multi-

plied by the max speed. Learning agents have a bat-

tery life of 30 units at the start of each episode and

episodes last for 50 time steps. Counterfactuals move

at one unit per time step. Each counterfactual has a

randomly generated list of tasks they visit in order.

There are 16 tasks in the environment that are laid

out in a circle with a radius of 6 units with alternating

types; the position of each task is randomly perturbed

by up to 1 unit in the x and y-directions. Agents

can interact with any task less than 2 units away, and

counterfactual agents can interact with any task up to

1 unit away. All results are averaged across 20 statis-

tical runs unless otherwise stated. Error is reported as

the standard error in the mean.

5 RESULTS

In this work, we compare C-MOME against two

baseline methods representing the state-of-the-art in

multi-objective and QD search: Multi-Objective Map

Elites (MOME) (Pierrot et al., 2022) and Nondomi-

nated Sorting Genetic Algorithm II (NSGA-II) (Deb

et al., 2002). C-MOME builds on the MOME frame-

work by using counterfactual agents to shape the state

and behavior spaces of the search. By comparing

C-MOME with MOME, we characterize the impact

counterfactuals have on both the coverage of behav-

ioral niches within the behavior space and the cov-

erage of policies along the global Pareto front in the

objective space. Comparing C-MOME with NSGA-II

characterizes the performance of this method against

an algorithm that is considered state-of-the-art in

multi-objective search. We expand our study on the

positive impact of counterfactual states by adding

counterfactual agents to the agent’s state space in

NSGA-II.

5.1 Performance Measures

To test the overall performance of each method, we

compare them in both the objective space and the be-

havior space. The work introducing MOME, (Pierrot

et al., 2022), uses the hypervolume of the Pareto front

to test the quality of the multi-objective search. The

hypervolume measures the volume of the geometric

Figure 2: This compares the effects of different types of

counterfactual agents on the hypervolume of the Pareto

front. Results show the ﬁnal Pareto hypervolume found af-

ter testing 200,000 policies per run, averaged over 20 stat

runs. Move and Task counterfactuals result in a greater hy-

pervolume compared to Static counterfactuals and MOME

(No cf).

shape created by the points on the Pareto front along

with a reference point; we use [0, 0] for our compar-

isons. Note that in a 2D objective space, this equates

to the area of the polygon created by the Pareto front

and the origin. For the behavior space, we compare

the percent of niches ﬁlled by each method. When

plots are shown for individual runs, such as for the

Pareto front, we chose a run that was closest to the

mean.

5.2 Counterfactual Types

First, we examine how different types of counterfac-

tuals perform in C-MOME compared with MOME.

As outlined in Section 4.3, we test Static, Move, and

Task counterfactual types. For this test, we use 9

counterfactual agents for each type. These results are

summarized in Figure 2.

The results in Figure 2 demonstrate that Static

counterfactual agents have a small impact on perfor-

mance. This is a positive result, as Static counterfac-

tuals do not express unique behaviors that can effec-

tively redeﬁne the behaviors of a learning agent. This

result shows that the change in behavior space deﬁ-

nition, beh

to beh

c f

, and the inclusion of agents in

the state provides some beneﬁt. Similarly, we see that

the hypervolume impact of Task counterfactuals com-

pared with Move counterfactuals is also negligible.

However, we see a noticeable increase in performance

between having no counterfactuals or static counter-

factuals and counterfactuals that move. The Move and

Task counterfactuals both show signiﬁcant improve-

ment of the ﬁnal Pareto hypervolume, increasing it by

Shaping the Behavior Space with Counterfactual Agents in Multi-Objective Map Elites

(a) MOME Pareto Front

(b) C-MOME Pareto Front

Figure 3: Representative global Pareto fronts found af-

ter searching through 200,000 policies for MOME and

C-MOME with Task counterfactuals. Policies that are

Pareto dominant are represented as blue dots while non-

Pareto dominant policies are in red. The counterfactual

agents used in C-MOME result in a greater coverage of

Pareto optimal policies compared with MOME and keeps

signiﬁcantly fewer policies in unhelpful regions, near [0, 0].

These graphs were chosen as representatives because they

are closest to the mean for their population.

over 40%, each with approximately 3% standard error

after 20 stat runs.

While measuring the hypervolume characterizes

the coverage of the Pareto front as a whole, we also

show examples of typical Pareto fronts generated by

MOME (no counterfactuals) and C-MOME with Task

counterfactuals in Figures 3a and 3b, respectively.

These plots provide a more detailed view of how the

introduction of moving, counterfactual agents can re-

deﬁne the behavior space resulting in more substan-

tial policies along the global Pareto front. These also

highlight how MOME spends signiﬁcant time search-

ing a sub-optimal region, near [0, 0], while C-MOME

Figure 4: Comparing the effect of different types of coun-

terfactual agents on the coverage of behavioral niches. We

show that Move and Task counterfactuals successfully cover

more than twice the area of the behavior space, with Task

cfs achieving over 95% coverage.

is able to spread the search across the objective space.

Impact on Behavior Space: To characterize the

impact counterfactuals have on the behavior space

within MOME, we measure the total number of

niches that contain policies. Note that for these re-

sults, we do not include counterfactuals in the behav-

ior space and use beh

for all cases. This is done to

make the results directly comparable, as the counter-

factual behavior space, beh

, has signiﬁcantly differ-

ent constraints. By comparing the amount of “ﬁlled”

niches to the total number of niches, we can estimate

the total coverage of policies over the behavior space.

We present these ﬁndings in Figure 4. The total num-

ber of niches ﬁlled by C-MOME is 2.3x the number

of niches ﬁlled by MOME (with no counterfactuals).

This result shows that C-MOME leverages the struc-

tured diversity provided by counterfactuals to provide

signiﬁcantly better coverage of both the behavior and

objective spaces.

Compared against both MOME and C-MOME

with Static counterfactuals, dynamic counterfactuals

improve the overall search in the objective space.

By comparing against the Static counterfactuals, we

show that the redeﬁnition of the behavior space and

inclusion of additional information in the state is not

what causes the improvement. The dynamic coun-

terfactuals provide structured variability in the envi-

ronment, which allows C-MOME to more richly de-

ﬁne agent behaviors and effectively cover the behav-

ior space as seen in Figure 4. This diversiﬁes the

search across the behavior space, which in turn im-

proves the performance in the objective space.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

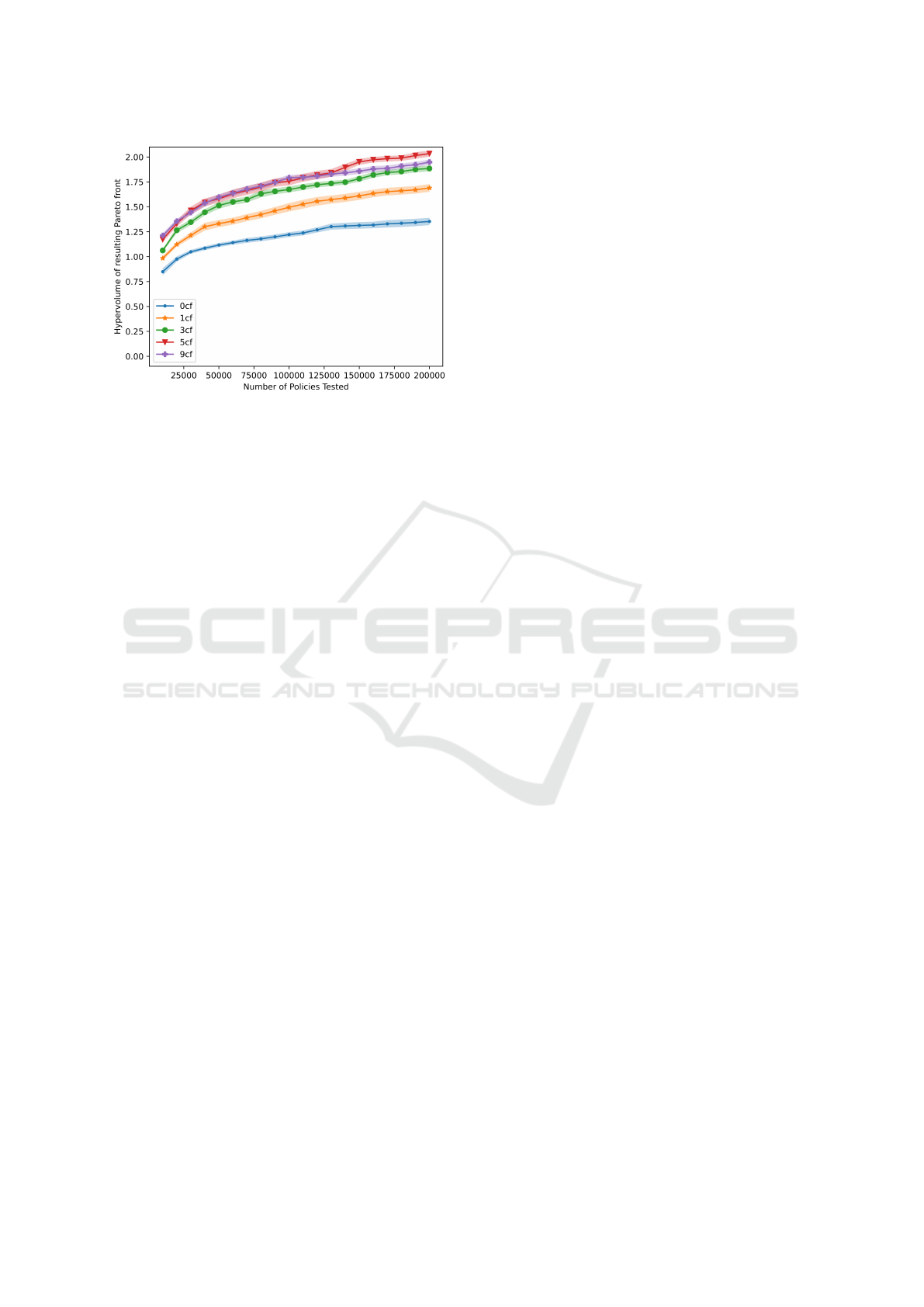
Figure 5: Comparing the impact of different numbers of

Task counterfactual agents on the hypervolume of the global

Pareto front. Increasing the number of counterfactual agents

results in an increase in the total hypervolume. However,

the gain in hypervolume becomes less signiﬁcant as more

agents are added beyond 5 agents.

5.3 Number of Counterfactual Agents

In testing the type of counterfactuals used in

C-MOME, we found that dynamic counterfactual

agents resulted in a marked increase in the hyper-

volume of the global Pareto front. To further under-

stand the effect counterfactual agents have on learn-

ing and shaping the behavior space, we also examine

the number of counterfactual agents used. Using Task

counterfactuals we tested all cases from 0 to 9 Task

counterfactual agents and found that hypervolume in-

creases with more counterfactual agents; however, it

does so incrementally. We show a representative sam-

pling of these results in Figure 5 where, for simplicity,

we present the results for 0, 1, 3, 5, and 9 counterfac-

tuals.

In Figure 5, we see a larger initial increase in hy-

pervolume when we compare MOME with no coun-

terfactuals against C-MOME with 1 counterfactual.

The hypervolume between 1 counterfactual and 5

counterfactuals is also relatively large; however, the

rate of hypervolume increase for each added agent di-

minishes after 5 agents.

Impact on Behavior Space: We see a similar trend

when comparing the impact of the number of counter-

factual agents on the behavior space coverage. Figure

6 shows a visual representation of two dimensions of

the behavior space for 0, 1, and 9 counterfactuals. The

No cf case achieves 40.1% coverage of the behavior

space, 1 CF achieves 67.8%, and the 9 Task CFs is

able to cover 96.6%. We found this trend holds across

all tests run from 0 to 9 agents.

5.4 Counterfactuals Shaping Perception

As presented in Section 3, there are three distinct

ways in which counterfactuals impact agent percep-

tions. As part of the state, counterfactuals can im-

pact the (1) percieved task completion or (2) appear

as agents. Additionally, counterfactuals can impact

(3) the deﬁnition of the behavior space. We explored

the impact of these three factors on the performance

of C-MOME. These results are presented in Figure 7

and Table 1.

These results show that each of the three compo-

nents have a moderate impact on the hypervolume of

the pareto front. The most surprising result is that

the behavior deﬁnition has a small impact alone, but

when combined with either the task completion or

agent state, it has a signiﬁcantly better impact. Over-

all we show that the synergy of all three is what pro-

vides the best coverage of the objective space, and

therefore the best policies.

5.5 Counterfactuals in MOME and

NSGA-II

The previous results demonstrate the impact counter-

factual agents have on shaping the behavior space in

MOME. To gain a better understanding of overall

performance within MOO, we also compare MOME,

C-MOME, NSGA-II, and NSGA-II with counterfac-

tuals. While the counterfactuals in C-MOME are pri-

marily used to redeﬁne the behavior space, NSGA-II

does not rely on a behavior space. Therefore, the

counterfactual states we add to NSGA-II only have an

impact on the state space of the learning agent. Sim-

ilar to the counterfactuals in C-MOME, the counter-

factual agents do not impact the objectives.

We ﬁrst explore the effect of counterfactuals in

NSGA-II by testing the types of counterfactuals de-

ﬁned in Section 4.3. We plot the effect these coun-

terfactuals have on NSGA-II hypervolume in Figure

8. Similar to the trends observed in C-MOME, we

see that dynamic counterfactual agents lead to an in-

crease in the hypervolume of the global Pareto front.

However, unlike in C-MOME, the results indicate no

change in hypervolume with static counterfactuals.

We also include the hypervolume comparison be-

tween MOME, C-MOME, and NSGA-II in Figure 8.

Overall we see that NSGA-II outperforms MOME in

this task with a substantial increase in the hypervol-

ume of the global Pareto front. We also see that Task

counterfactuals in both MOME and NSGA-II leads to

a signiﬁcant increase in hypervolume. It is worth not-

ing that NSGA-II only solves half of the originally

stated problem, as it provides diversity across the ob-

Shaping the Behavior Space with Counterfactual Agents in Multi-Objective Map Elites

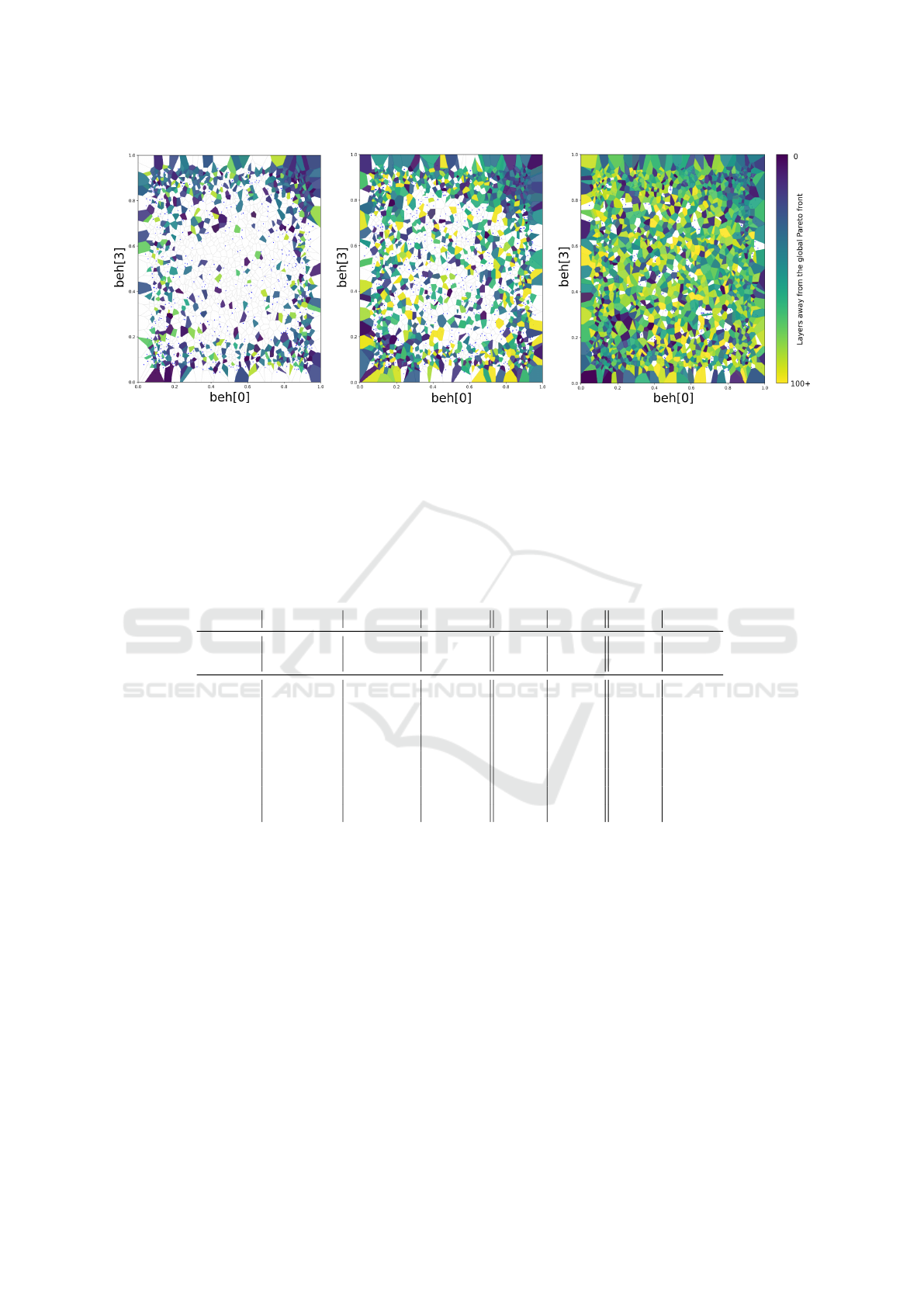
(a) No CF Behavior Space

(b) 1 CF Behavior Space

Figure 6: Representative behavior spaces found after searching through 200,000 policies for the No CF (Fig. 6a), 1 Task CF

(Fig. 6b), and 9 Task CFs (Fig. 6c) cases. Niches that have a policy that is globally Pareto optimal are represented in purple;

the color scales to yellow as the policies get further from the global Pareto front. All three cases use the beh

behavior space

in order to show a direct comparison. The No cf case achieves 40.1% coverage of the behavior space, 1 CF achieves 67.8%,

and the 9 Task CFs is able to cover 96.6%.

Table 1: Hypervolume of the Pareto front and coverage of the niches in the behavior space, broken down by conﬁguration.

We present situations with 0 counterfactuals (MOME) or 9 counterfactuals (C-MOME). Note that we do not present niche

coverage results for the conﬁgurations that have counterfactuals in the behavior space; the behavior space is signiﬁcantly

different and bounded, so the results are not comparable.

Perception Shaping Hypervolume Niche coverage

Num cf (1) Task p (2) Agent (3) Beh. Mean St.Err. Mean St.Err

- - - 1.281 0.079 0.401 0.0069

- • - 1.353 0.037 0.431 0.0084

- - - 1.298 0.025 0.420 0.0056

• - - 1.636 0.042 0.884 0.0029

- • - 1.709 0.027 0.902 0.0030

- - • 1.414 0.032 - -

• • - 1.862 0.036 0.966 0.0015

• - • 1.831 0.037 - -

- • • 1.925 0.028 - -

• • • 1.949 0.027 - -

jective space but not across the behavior space.

Although NSGA-II does not use a behavior space

for discovering new policies, the process of adding

counterfactual agents to the learning agent’s state

space had a noticeable impact on the hypervolume.

This result mirrors the study of the impact of coun-

terfactuals in agent perceptions, outlined in Section

5.4. It also reinforces the power of counterfactuals,

given that they do not have a direct impact on re-

ward functions or objective measures. We believe

this increase in performance is the result of struc-

tured dynamic elements added by the counterfactual

agents. The added counterfactual dynamics in the

state space helps NSGA-II avoid local minima when

assessing the ﬁtnesses of various policies during the

policy search.

6 CONCLUSION

In this work we introduce C-MOME, a novel ex-

tension to MOME that uses counterfactual agents to

better deﬁne agent behaviors thus shaping the be-

havior space. This shaped behavior space enables

C-MOME to more richly deﬁne agent behaviors,

diversify the search in the behavior and objective

spaces, and bias the search toward more productive

regions. We explored how different types of counter-

factual agents can inﬂuence both the behavior space

within MAP-Elites, and the coverage of policies along

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications

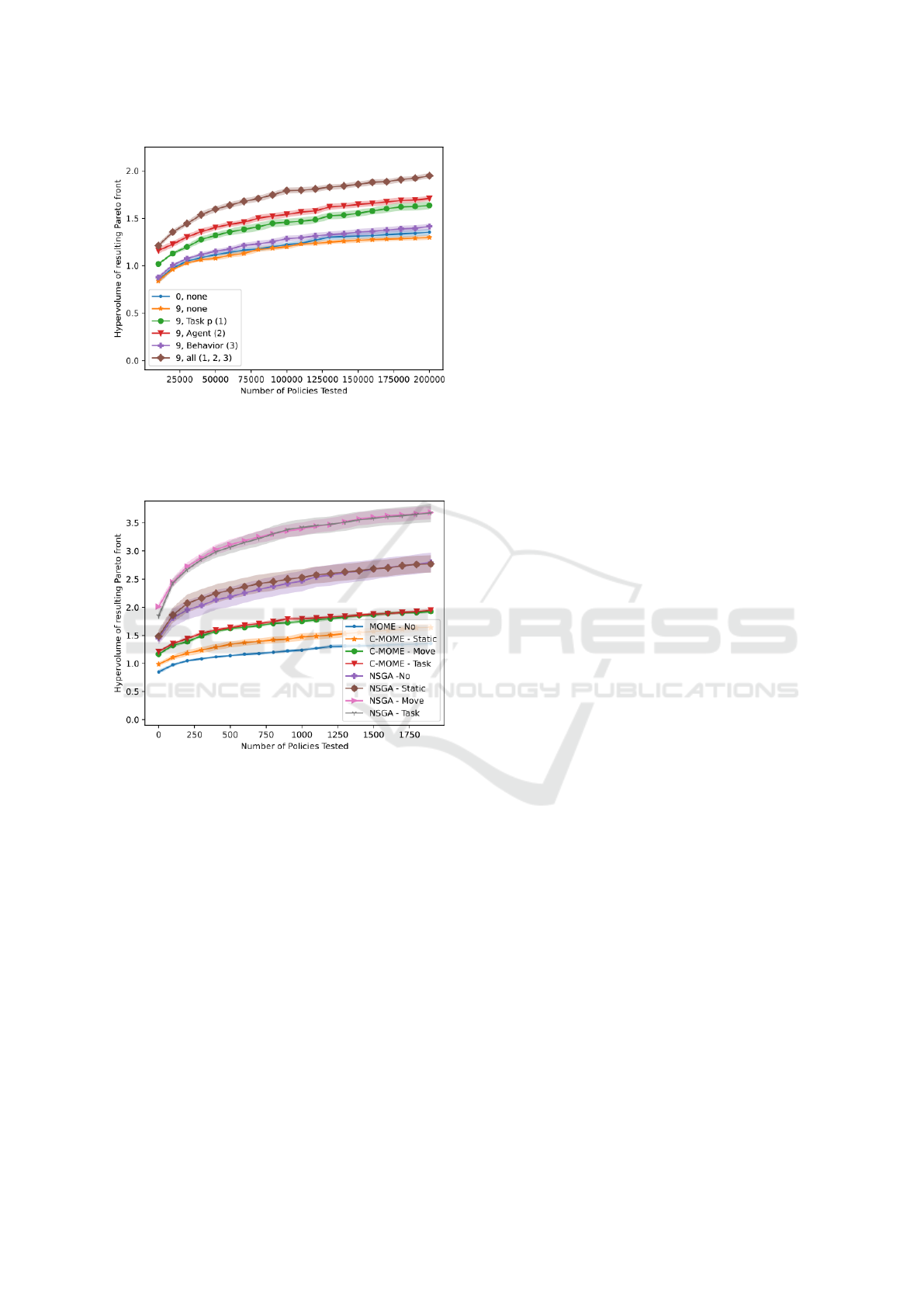
Figure 7: Comparing the impact of including counterfacu-

tals in the learning agents’ perceptions. In the state, coun-

terfactuals can (1) impact task completion or (2) appear as

agents; they can also impact (3) the deﬁnition of the behav-

ior space.

Figure 8: Comparing the effect of different counterfactual

types on NSGA-II. Similar to C-MOME, Move and Task

counterfactuals have a signiﬁcant impact on hypervolume.

Unlike C-MOME, the static counterfactuals have no impact

on hypervolume instead of a minimal impact.

the global Pareto front. We found that dynamic coun-

terfactual agents led to an increase in the hypervol-

ume along the global Pareto front, ﬁlling over 96%

of the niches of the behavior space; MOME is only

able to achieve 40% coverage. Finally, in comparing

MOME and NSGA-II, we found that NSGA-II out-

performed this implementation of MOME. However,

adding dynamic counterfactual agents improved the

performance of NSGA-II despite it relying on policy

search through the objective space.

This work demonstrates the impact of adding

counterfactual agents into a single agent MOO prob-

lem. C-MOME is intended to be the preliminary

learning phase in a curriculum style approach to mul-

tiagent, multi-objective coordination. By reducing the

learning of policies to a single agent problem, we de-

crease the noise typically associated with a multia-

gent learning environment, which simpliﬁes learning

enough to focus on the challenge of discovering a di-

verse set of policies that can balance multiple objec-

tives. Although the counterfactual agents are repre-

sentative of learning in an environment where multi-

ple agents are acting, it cannot fully account for real

agents that impact all aspects of the system. Future

work will extend C-MOME via curriculum learning

with the next step focusing on coordination and team

formation.

ACKNOWLEDGEMENTS

This work was partially supported by the National

Science Foundation under grant IIS-2112633 and the

Air Force Ofﬁce of Scientiﬁc Research under grant

No. FA9550-19-1-0195.

REFERENCES

Agogino, A. and Tumer, K. (2004). Efﬁcient evaluation

functions for multi-rover systems. In Genetic and

Evolutionary Computation – GECCO 2004, volume

3102, pages 1–11, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Alitappeh, R. J. and Jeddisaravi, K. (2022). Multi-robot

exploration in task allocation problem. Applied Intel-

ligence, 52(2):2189–2211.

Boninger, D. S., Gleicher, F., and Strathman, A. (1994).

Counterfactual thinking: From what might have been

to what may be. Journal of personality and social psy-

chology, 67(2):297.

Burgard, W., Moors, M., Stachniss, C., and Schneider, F. E.

(2005). Coordinated multi-robot exploration. IEEE

Transactions on robotics, 21(3):376–386.

Byrne, R. M. (2016). Counterfactual thought. Annual re-

view of psychology, 67:135–157.

Coello Coello, C. A. (2006). Evolutionary multi-objective

optimization: A historical view of the ﬁeld. Comp.

Intell. Mag., 1(1):28–36.

Das, I. and Dennis Jr, J. E. (1996). A closer look at

drawbacks of minimizing weighted sums of objectives

for pareto set generation in multicriteria optimization

problems. Technical report.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

Nsga-ii. Trans. Evol. Comp, 6(2):182–197.

Drugan, M. M. and Nowe, A. (2013). Designing multi-

objective multi-armed bandits algorithms: A study. In

The 2013 international joint conference on neural net-

works (IJCNN), pages 1–8. IEEE.

Shaping the Behavior Space with Counterfactual Agents in Multi-Objective Map Elites

Eysenbach, B., Gupta, A., Ibarz, J., and Levine, S. (2019).

Diversity is all you need: Learning skills without a re-

ward function. In International Conference on Learn-

ing Representations.

Foerster, J. N., Farquhar, G., Afouras, T., Nardelli, N.,

and Whiteson, S. (2018). Counterfactual multi-

agent policy gradients. In Proceedings of the Thirty-

Second AAAI Conference on Artiﬁcial Intelligence

and Thirtieth Innovative Applications of Artiﬁcial In-

telligence Conference and Eighth AAAI Symposium

on Educational Advances in Artiﬁcial Intelligence,

AAAI’18/IAAI’18/EAAI’18. AAAI Press.

Johansson, F. D., Shalit, U., and Sontag, D. (2016). Learn-

ing representations for counterfactual inference. In

Proceedings of the 33rd International Conference on

International Conference on Machine Learning - Vol-

ume 48, ICML’16, page 3020–3029. JMLR.org.

Kasirzadeh, A. and Smart, A. (2021). The use and misuse

of counterfactuals in ethical machine learning. In Pro-

ceedings of the 2021 ACM Conference on Fairness,

Accountability, and Transparency, FAccT ’21, page

228–236, New York, NY, USA. Association for Com-

puting Machinery.

Kusner, M., Loftus, J., Russell, C., and Silva, R. (2017).

Counterfactual fairness. page 4069–4079.

Lehman, J. and Stanley, K. O. (2011). Novelty search and

the problem with objectives. Genetic programming

theory and practice IX, pages 37–56.

Mouret, J.-B. and Clune, J. (2015). Illuminating

search spaces by mapping elites. arXiv preprint

arXiv:1504.04909.

Olson, M. L., Khanna, R., Neal, L., Li, F., and Wong, W.-

K. (2021). Counterfactual state explanations for rein-

forcement learning agents via generative deep learn-

ing. Artiﬁcial Intelligence, 295:103455.

Pierrot, T., Richard, G., Beguir, K., and Cully, A. (2022).

Multi-objective quality diversity optimization. In Pro-

ceedings of the Genetic and Evolutionary Computa-

tion Conference, GECCO ’22, page 139–147, New

York, NY, USA. Association for Computing Machin-

ery.

Rahmattalabi, A., Chung, J. J., Colby, M., and Tumer, K.

(2016). D++: Structural Credit Assignment in Tightly

Coupled Multiagent Domains. In 2016 IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems (IROS), pages 4424–4429, Daejeon, South Ko-

rea. IEEE.

Van Moffaert, K., Drugan, M. M., and Now

e, A. (2013).

Scalarized multi-objective reinforcement learning:

Novel design techniques. In 2013 IEEE Symposium on

Adaptive Dynamic Programming and Reinforcement

Learning (ADPRL), pages 191–199.

Verma, S., Boonsanong, V., Hoang, M., Hines, K. E., Dick-

erson, J. P., and Shah, C. (2020). Counterfactual

explanations and algorithmic recourses for machine

learning: a review. arXiv preprint arXiv:2010.10596.

Zitzler, E., Laumanns, M., and Thiele, L. (2001). Spea2:

Improving the strength pareto evolutionary algorithm.

TIK-report, 103.

ECTA 2023 - 15th International Conference on Evolutionary Computation Theory and Applications